#matrice de pauli

[wisdomrays]

TAFAKKUR: Part 347

THE UNIVERSE IN THE LIGHT OF MODERN PHYSICS

‘The least understood aspect of the universe is its being understandable,’ said Einstein.

These words attempt to pierce the veil of habit that develops in our minds from not looking into the reason for things. The perfection of the order operative in the universe is of such a degree that it prevents us from being aware of it. In the same way, we only become aware of the faultless operation of the watches we have worn on our wrists for years when they stop working.

In the world-view developed upon the foundation of Newton’s laws of motion, the universe was likened to a flawlessly operating watch. Events were tied to one another in a cause-effect relationship and our knowing the laws of this relationship allowed us to predict events with great accuracy. It was possible to determine with mathematical exactness a wide range of phenomena, from the times of eclipses of sun and moon to the amount of fuel and the speed needed to put an object into orbit around the earth. The success of these ‘natural laws’ led many people to believe that they completely expressed and ‘ruled’ the whole order of the universe.

Because God creates and sustains all things and events from behind the veil of universal general laws, because certain events (causes) are followed reliably by similar events (effects) each time they (the causes) occur, it begins to be supposed that the causes are responsible for or ‘create’ the effects. This is, of course, a gross error, as no number of causes suffices to create even a little effect; for every event even the tiniest, the whole universe must be presupposed first, including the laws operative within it. Moment by moment, all things and all events are created and sustained by God, Who wills from an infinite range of alternative possibilities a particular actuality.

The clockwork model of the universe derived from Newtonian or classical physics is not a complete account of the phenomena which we observe in the universe. Already in the late 19th century, scientists had been bewildered by the lines that turned up in the light spectra emitted by heated gases: the steady, stable clockwork model predicted did not happen. Also, there were problems explaining the behaviour of light: sometimes it made more sense as a beam of particles, sometimes as a wave.

Today our understanding of the universe is very far from the ‘clockwork’ model. The shift in understanding occurred in the first quarter of the 20th century, beginning in 1900 with the publication of Max Planck’s work on radiation. The problem Planck worked on for six years was that the actually measured radiation from hot bodies did not conform to the values predicted by the classical theory. He put forward the suggestion that bodies radiating energy did so, not evenly and continuously, but unevenly and discontinuously in tiny packets or ‘quanta’. So startling was this suggestion that, despite confirmation by experiment, Planck himself thought of his theory as solving the problem of radiation by a sort of trick.

But then, in 1905, Albert Einstein published an article using the notion of packets of energy of definite sizes to explain how electrons are ejected from metal when light (radiation) falls on it. Whereas classical theory had predicted that the voltage (measure of the energy of the electrons ejected) would be proportional to the intensity of the light (radiation), Einstein showed that it was proportional instead to the frequency of the radiation. The conformity of this explanation with experimentally observed results gained Einstein the Nobel Prize. (Einstein didn’t receive the prize for his famous theory of relativity.) The significance of these findings and theories was not fully appreciated at the time.

A few years later in 1910, Ernest Rutherford did a ground-breaking experiment. He bombarded a thin layer made up of gold atoms with high energy particles and showed that the atom contained an extremely small positively-charged nucleus with negatively-charged electrons moving around it. Following the classical physics model, these electrons should have been small particles orbiting the nucleus in the same way as the planets orbit the sun, steadily losing energy until they fell on to the nucleus-in other words, the atom should have been unstable. Again it was a rejection of the classical model, three years later, by Niels Bohr, that helped solve the problem. Bohr argued that the electrons must move in fixed orbits until deflected by the absorption or emission of a unit of energy.

Atoms emit radiation after various external signals and only at specific wave lengths. As Einstein said, every different color of light is composed of energy packets inversely proportional to its wave-length (frequency). Because the Planck constant (h) is very small, the energy of these packets is also very, very small. For example, a normal light bulb emits 1020 light packets (photons) a second. Each of these photons is created when an activated atom or molecule passes to its normal or ‘basic state.’ Thus light, which allows us to see and which is a basic building block of life, develops as a result of the motions (in wave form) of electrons. The concepts of classical physics could successfully explain many of the events of daily life, but it couldn’t explain events on the subatomic level.

During those years (1910-1925) physics fell into a state of confusion because of the many measurements that conflicted with general theory and could not be explained by it. This situation was to lead W. Pauli (later to discover the principle fundamental to the understanding of the structure and characteristics of elements) to say he would rather have been a singer or gambler than a physicist. Actually in order to explain the observations being made, the whole way in which physical events had been understood required fundamental revision by wholly new methods. This was achieved by Werner Heisenberg, a 24 year-old physicist described by his teachers as a person who dealt with the essence of a subject rather than getting bogged down in detail, a person with powerful concentration and ambition. Perhaps the success of this young mind can be explained by the critical perspective he developed through reading the works of great men such as Kant and Plato, which was later supported with sound knowledge he got from great physicists. Heisenberg, who relaxed from work by climbing rocks and reading poetry, said: ‘It was around three in the morning when the calculations were completed and the solution to the problem appeared in front of me. First I experienced a great shock. I was so excited that I didn’t even think about sleeping. I left the house and, sitting on a rock, I waited for the sunrise.’

Like the other scientists who established quantum physics, Heisenberg was a philosopher-physicist. The philosophy he accepted and advocated that allowed him to interpret atomic events is as follows: ‘Even though it is successful with classical physics, the language we use to explain physical events in the atom or its surroundings is insufficient. For this reason, after making a specific measurement in a quantum system (for example, an atom), using that knowledge we can get a theory that will tell us what kind of results we can find in the next measurement. But it’s not possible to say anything about what takes place between the two measurements.’

What pushed Heisenberg to make such a statement was that the mathematical tools he used to develop a theory that could explain the observed discontinuity of energy in light and atoms were abstract concepts that had not been used before. In classical physics the numbers we know were used to give value to matter’s position, speed, size, etc. In Heisenberg’s quantum mechanics, these sizes were expressed with infinite dimensional n x n matrices which enabled physicists to calculate the properties attributed to electrons (energy, position, momentum, angular momentum) in an approximate way. Because these abstract mathematical expressions didn’t have an equivalent in everyday spoken language, it wasn’t possible to approach them with a classical understanding. It was observed that in order to measure the position of an electron, the experimenter necessarily altered its velocity. This problem was formally expressed in 1927 in Heisenberg’s famous Uncertainty Principle.

Independently of Heisenberg, Erwin Schrodinger made another significant breakthrough in mathematical description of electrons. Inspired by the hypothesis put forward two years earlier by De Broglie about the wave properties of matter particles, Schrodinger developed a ‘wave mechanics’ by which the movement of particles could be calculated. (figure: 1) But the fundamental question remained as to what these strange and original ‘waves of matter particles’ or ‘waves accompanying matter particles’ were.

The mathematical formulations devised by Heisenberg and Schrodinger are complementary in the sense that physicists use whichever best resolves the particular calculations they are trying to make. There is no formally distinct space between the scientists and the phenomena they are seeking to understand and manipulate: their means of observation and manipulation (the mathematics) in some sense ‘posit’, put in place, the very phenomena whose place (among other properties) they are trying to determine. Alongside the notion of an infinite array of rows and points, as invented by Heisenberg, to plot the position or motion of a sub-atomic particle, physicists and philosophers of physics have begun to speak of arrays of events or ‘stories’ to try to explain, in something resembling ordinary language, the ideas they are handling. This cannot be described as a world-view in the way that the Newtonian physics confirmed and sustained a world-view, but it is nevertheless a clear and distinct disposition which, instead of excluding God as the Force Who wound up the clockwork and then retired from His creation, admits the in-completeness and uncertainty of human knowledge as a structural element of reality-in other words, the uncertainty is not a function of our present ignorance (to be relieved by future knowledge), but an actual constituent of the way reality is.

Quantum physics, at least figuratively and metaphorically, has became a vehicle for the interpretation of such concepts as matter, beyond-matter, energy, existence and non-existence in a way nearer to Divine sources; and led to many physicists settling accounts with their conscience and turning towards God Who is understood to be simultaneously transcendent and immanent, there and here.

[unpeudephysique]

Algèbre de Lie

Une algèbre de Lie de dimension n est un espace vectoriel L de dimension n muni d’une application bilinéaire [ . , . ] : 

qui a les propriétés suivantes :

Cette application est appelée crochet de Lie.

Soient ea les éléments d’une base de L. Le crochet de Lie appliqué à ces éléments se décompose dans cette base de la manière suivante :

Les coefficients fcab sont appelés constantes de structure de l’algèbre de Lie L. Ces constantes de structure définissent complètement l’algèbre de Lie considérée.

Algèbre de Lie d’un groupe de Lie

Soit un groupe de Lie G tel que ceux définis dans le post sur les groupes de Lie. On définit la notion de chemin sur ce groupe de la manière suivante. Un chemin est une application différentiable du segment [-1 1] sur ce groupe : 

la valeur t = 0 correspondant à la matrice identité Id (l’élément neutre du groupe).

C étant différentiable on peut définir la dérivée de g(t) à l’origine :

On démontre que l’ensemble de toutes les matrices m obtenues par dérivation sur tous les chemins passant par l’application Id est une algèbre de Lie. C’est l’algèbre de Lie du groupe de Lie G. Elle est notée Lie(G).

Espace tangent au groupe de Lie

Revenons à la définition des matrices m ci-dessus. Lorsque t est petit, on peut la réécrire de la manière suivante : 

Cette équation explique pourquoi on donne aussi à Lie(G) le nom d’espace tangent à l’élément neutre du groupe G.

Représentation exponentielle et générateurs de G

Parmi tous les chemins associés à un même élément m de Lie(G), il en est un (et un seul) qui a la propriété suivante :

Sur ce chemin, l’équation suivante est vérifiée :

Ce qui permet d’écrire :

Les éléments de toute base de Lie(G) sont appelés générateurs du groupe G. Il est en effet facile de générer à partir de ces éléments l’action d’un élément de G appartenant au voisinage de l’élément neutre.

Algèbre de Lie du groupe SO(3)

Les matrices R du groupe SO(3) peuvent s’écrire de la manière suivante :

Les matrices réelles antisymétriques GU sont les générateurs des matrices RU.  

L’ensemble so(3) des matrices réelles antisymétriques GU est l’algèbre de Lie du groupe de Lie SO(3) :

Comme on peut le voir, il y a bijection entre les vecteurs U et les matrices GU. L’ensemble so(3) est isomorphe à R3.

On remarquera par ailleurs que la matrice GU est aussi celle qui est associée au produit vectoriel dans R3 :

Il en découle les relations suivantes sur les générateurs associés aux rotations autour des 3 axes principaux :

Cette relation est celle qui définit les constantes de structure de so(3).

Remarque : En physique quantique, on utilise plutôt la notation :

Les matrices Lx, Ly, Lz associées aux rotations autour des axes Ox, Oy et Oz vérifient les relations :

Algèbre de Lie du groupe SU(2)

Tout élément de SU(2) peut s’écrire :

avec :

Les matrices antihermitiennes de trace nulle G_tilde sont donc les générateurs des matrices M du groupe de Lie SU(2). L’ensemble des matrices antihermitiennes de trace nulle G_tilde est l’algèbre de Lie du groupe SU(2) : 

Les matrices de Pauli sigmax, sigmay, sigmaz forment une base de su(2) :

A toute matrice G_tilde on peut donc faire correspondre un vecteur U de R3. L'algèbre de Lie su(2) est donc isomorphe à R3.

Remarque : les matrices de Pauli respectent les mêmes relations de commutation que les matrices Gx, Gy et Gz définie au paragraphe précèdent. Les algèbres su(2) et so(3) ont les mêmes constantes de structure : on dit qu’elles présentent un isomorphisme d’algèbre.  

Intéressons nous maintenant la matrice générée à  partir de G_tilde(U). On peut écrire cette matrice M(U) sous la forme : 

avec :

Rappelons que toute matrice de SU(2) peut aussi s’écrire sous la forme :

Il vient pour les composantes de M(U) :

Toute matrice du groupe SU(2) peut s’écrire à partir d’un vecteur unitaire u et d’un angle theta. C’est un résultat qui ne nous étonnera pas : nous l’avions déjà signalé au chapitre sur les groupes de Lie.

On notera une particularité des matrices de SU(2). L’angle theta utilisé pour exprimer les matrices M(u, theta) peut prendre ses valeurs entre 0 et 4pi. Il en découle les relatons suivantes : 

Une rotation de 360 degrés transforme M(u, theta) en son inverse. Il faut effectuer une rotation de 720 degrés pour revenir à la matrice initiale.

Algèbre de Lie et mécanique quantique

Les groupes et algèbres de Lie sont au cœur du formalisme utilisé en mécanique quantique. En physique, les relations d’invariance sont souvent associées à des symétries (théorème de Noether). Mathématiquement, les symétries présentent souvent une structure de groupe. Lorsque celui-ci est continu et dérivable, on a affaire à un groupe de Lie. La recherche des générateurs associés permet alors de définir une observable invariante dans toute symétrie de ce groupe (théorème d’Erhenfest).

Le groupe de Lie SU(2) a de nombreuses applications en physique : il est associé à la symétrie de rotation dans l’espace. Les équations d’un système ne changent pas si l’on opère une simple rotation du référentiel de coordonnées. En physique classique, cette symétrie se traduit par la conservation du moment cinétique. En mécanique quantique, il permet de construire une théorie complète du spin. Mais il faut pour cela définir un nouveau type de champ : le champ spinoriel.

Pour en savoir plus :

posts sur les groupes et algèbres de Lie

post sur les espaces vectoriels et les groupes de Lie

post sur les spineurs

post sur le théorème de Noether

groupes et algèbres de Lie sur Internet

index

[mamtajuyal1986]

IIT JAM 2020 Physics (PH) Syllabus | IIT JAM 2020 Physics (PH) Exam Pattern

IIT JAM 2020 Physics (PH) Syllabus | IIT JAM 2020 Physics (PH) Exam Pattern Physics (PH): The syllabus is a very important aspect while preparing for the examination. Therefore it is advised to all the appearing candidates that they should go through the Physics (PH) syllabus properly before preparing for the examination. Mathematical Methods: Calculus of single and multiple variables, partial derivatives, Jacobian, imperfect and perfect differentials, Taylor expansion, Fourier series. Vector algebra, Vector Calculus, Multiple integrals, Divergence theorem, Green's theorem, Stokes' theorem. First order equations and linear second order differential equations with constant coefficients. Matrices and determinants, Algebra of complex numbers. Mechanics and General Properties of Matter: Newton's laws of motion and applications, Velocity and acceleration in Cartesian, polar and cylindrical coordinate systems, uniformly rotating frame, centrifugal and Coriolis forces, Motion under a central force, Kepler's laws, Gravitational Law and field, Conservative and non-conservative forces. System of particles, Center of mass, equation of motion of the CM, conservation of linear and angular momentum, conservation of energy, variable mass systems. Elastic and inelastic collisions. Rigid body motion, fixed axis rotations, rotation and translation, moments of Inertia and products of Inertia, parallel and perpendicular axes theorem. Principal moments and axes. Kinematics of moving fluids, equation of continuity, Euler's equation, Bernoulli's theorem. Oscillations, Waves and Optics: Differential equation for simple harmonic oscillator and its general solution. Superposition of two or more simple harmonic oscillators. Lissajous figures. Damped and forced oscillators, resonance. Wave equation, traveling and standing waves in one-dimension. Energy density and energy transmission in waves. Group velocity and phase velocity. Sound waves in media. Doppler Effect. Fermat's Principle. General theory of image formation. Thick lens, thin lens and lens combinations. Interference of light, optical path retardation. Fraunhofer diffraction. Rayleigh criterion and resolving power. Diffraction gratings. Polarization: linear, circular and elliptic polarization. Double refraction and optical rotation. Electricity and Magnetism: Coulomb's law, Gauss's law. Electric field and potential. Electrostatic boundary conditions, Solution of Laplace's equation for simple cases. Conductors, capacitors, dielectrics, dielectric polarization, volume and surface charges, electrostatic energy. Biot-Savart law, Ampere's law, Faraday's law of electromagnetic induction, Self and mutual inductance. Alternating currents. Simple DC and AC circuits with R, L and C components. Displacement current, Maxwelll's equations and plane electromagnetic waves, Poynting's theorem, reflection and refraction at a dielectric interface, transmission and reflection coefficients (normal incidence only). Lorentz Force and motion of charged particles in electric and magnetic fields. Kinetic theory, Thermodynamics: Elements of Kinetic theory of gases. Velocity distribution and Equipartition of energy. Specific heat of Mono-, di- and tri-atomic gases. Ideal gas, van-der-Waals gas and equation of state. Mean free path. Laws of thermodynamics. Zeroth law and concept of thermal equilibrium. First law and its consequences. Isothermal and adiabatic processes. Reversible, irreversible and quasi-static processes. Second law and entropy. Carnot cycle. Maxwell's thermodynamic relations and simple applications. Thermodynamic potentials and their applications. Phase transitions and Clausius-Clapeyron equation. Ideas of ensembles, Maxwell-Boltzmann, Fermi-Dirac and Bose-Einstein distributions. Modern Physics: Inertial frames and Galilean invariance. Postulates of special relativity. Lorentz transformations. Length contraction, time dilation. Relativistic velocity addition theorem, mass energy equivalence. Blackbody radiation, photoelectric effect, Compton effect, Bohr's atomic model, X-rays. Wave-particle duality, Uncertainty principle, the superposition principle, calculation of expectation values, Schrodinger equation and its solution for one, two and three dimensional boxes. Solution of Schrodinger equation for the one dimensional harmonic oscillator. Reflection and transmission at a step potential, Pauli exclusion principle. Structure of atomic nucleus, mass and binding energy. Radioactivity and its applications. Laws of radioactive decay. Solid State Physics, Devices and Electronics: Crystal structure, Bravais lattices and basis. Miller indices. X-ray diffraction and Bragg's law; Intrinsic and extrinsic semiconductors, variation of resistivity with temperature. Fermi level. p-n junction diode, I-V characteristics, Zener diode and its applications, BJT: characteristics in CB, CE, CC modes. Single stage amplifier, two stage R-C coupled amplifiers. Simple Oscillators: Barkhausen condition, sinusoidal oscillators. OPAMP and applications: Inverting and non-inverting amplifier. Boolean algebra: Binary number systems; conversion from one system to another system; binary addition and subtraction. Logic Gates AND, OR, NOT, NAND, NOR exclusive OR; Truth tables; combination of gates; de Morgan's theorem. Related Articles: IIT JAM 2020 Syllabus Biotechnology (BT) Syllabus Biological Sciences (BL) Syllabus Chemistry (CY) Syllabus Geology (GG) Syllabus Mathematics (MA) Syllabus Mathematical Statistics (MS) Syllabus Physics (PH) Syllabus Read the full article

[drypauli]

Trois causes des problèmes relationnels

Résumé

Je vous propose de découvrir les 3 causes de vos problèmes relationnels. La médecine classique actuelle sépare la prise en charge du corps et de l’esprit, ce qui est une erreur car le corps influence l’esprit et vice versa. En effet, la cause originelle des douleurs physiques est très souvent liée au stress et aux émotions, notamment dans nos relations avec les autres.

Notre état de base est d’être en légère hypervigilance, notre système est un peu stressé, et nous ne pouvons accéder à un état sans stress qu’avec un effort conscient de relaxation pour créer un sentiment de sécurité. Or la qualité de nos relations avec les autres dépend de ces moments de relâchement que nous nous autorisons, il est bien connu que plus nous sommes stressés plus nous sommes irritables. Préservons donc des moments de relaxation dans nos journées.

Une autre cause des problèmes relationnels que nous rencontrons est liée aux « relations primordiales passées incomplètes ». Ce sont les relations que nous avons eues avec nos parents et les personnes proches dans notre petite enfance, qui ont pu causer de la colère ou de la frustration, parfois de manière traumatique. Nous projetons ces vieilles perceptions sur ce qui se passe aujourd'hui dans notre vie, souvent à tort. Il est donc important d’essayer de dissoudre ces sentiments de colère liés au passé.

La 3e cause est ce qu'on appelle l’enfant blessé ou l’ego. Cela prend en compte toutes les frustrations que nous avons vécues au cours de notre vie, d’une moquerie à l’école à un rejet amoureux, un mot dit de travers, etc. Nous avons développé à chaque fois un mécanisme de compensation qui nous permet de passer à travers. Aujourd'hui, quand une relation devient difficile à gérer ou se complique, nous avons tendance à réagir comme cet enfant blessé que nous avons été, nous ne réagissons pas de manière authentique. Quand cela vous arrive, sortez de la perception de victime qui nous rassure, et cherchez du soutien.

Transcription

Dans cet épisode, je vous propose de découvrir les 3 causes de vos problèmes relationnels.

Parce que la vie est bien trop magique pour être petite et que nous avons tous besoin d‘une prescription pour grandir en conscience et faire que nos rêves dévorent notre vie. Bonjour, je suis le Docteur Yannick Pauli, bienvenue à un nouvel épisode d’Une Grande Vie. Vous le savez, chaque semaine, je vous propose des stratégies pratiques, pragmatiques, pour grandir en conscience, qu’elle soit d’ordre physique, émotionnel, psychologique ou spirituel, parce que c'est cette conscience qui nous permet d’évoluer en tant qu’être humain et de vivre une vie pleinement vécue.

Cette semaine, j’avais envie de vous partager une notion par rapport au stress, et au stress créé par les relations que vous avez avec les autres, que ce soit au niveau du travail, au niveau de vos connaissances ou au niveau de vos amis, ou sur votre lieu professionnel.

Avant d’entrer dans ce partage de ce que je considère être les 3 causes les plus fréquentes des problèmes relationnels, j’aimerais vous donner un contexte sur ce message. Ça fait bientôt maintenant 20 ans que je suis en pratique en tant que chiropraticien, spécialisé dans les problématiques neurologiques et les problématiques liées au style de vie et au stress, et j’ai effectué plus de 100 000 consultations. Une des choses qui me frappent toujours dans le monde actuel et la manière dont la médecine se pratique, c'est cette séparation qu'on a entre le corps et l’esprit. On a cette notion même au travers des professions, si on prend les professions « classiques », où si vous avez un problème avec le corps, vous allez chez le médecin, spécialisé sur le corps, ou chez des spécialistes des différents organes du corps, et si vous avez un problème avec le psyché ou avec l’esprit, vous allez soit chez le psychiatre ou le psychologue, ou vous allez voir la personne qui vous suit si vous êtes croyant dans votre profession de foi, ça peut être le curé, le pasteur, l’imam, etc.

Donc on a vraiment divisé ce qui a à voir avec le corps et ce qui a à voir avec l’esprit. Mais en fait, cette division est complètement conceptuelle. Dans la réalité des choses, le corps influence l’esprit et l’esprit influence le corps. Au travers de ces 100 000 consultations, j’ai toujours été étonné du peu de gens qui ont vraiment pris conscience, je ne parle pas juste conceptuellement, mais qui ont vraiment incarné la notion que ce qui se passe dans leur corps va aussi être influencé par ce qui se passe au niveau émotionnel. Je dirais qu'il y a peut-être à peine 15-20% des gens qui font vraiment ce lien, alors qu’au niveau scientifique, dans les études qui sont faites, c'est très clair. Ce qui va se passer au niveau émotionnel va s’exprimer au travers du corps.

Pour une grande majorité des gens, leurs douleurs persistantes ne sont pas simplement dues à des problèmes physiques, mais sont dues au stress et aux émotions qu'ils ont dans leur vie. Si on remonte, si on ne reste pas au bas de la rivière sur les conséquences, mais qu'on essaie de comprendre ce qui se passe en haut de la rivière , quelles sont les causes vraiment fondamentales de ces problématiques qu'on trouve en bas, on va voir que dans cette dimension de problématique physique, de douleur physique, on va trouver des problèmes de stress, des problèmes émotionnels, et si on remonte dans ces problèmes émotionnels, on va très souvent, très souvent trouver à la base des problèmes relationnels, c'est-à-dire l’incapacité à développer de bonnes relations, des relations centrées, des relations basées sur la dignité des 2 individus, ou bien des relations où on va trouver des tensions, des problèmes de communication, on va trouver une personne qui domine l’autre, peut-être une personne avec une personnalité un peu narcissique et l’autre avec une personnalité un peu de victime, qu'on appelle souvent co-dépendante. Donc on trouve ces dynamiques de relation.

Aujourd'hui, je vous propose quelque chose inspiré des travaux d’un collègue qui était dans le collègue chiropratique que moi, le Dr Nima Rahmany, et des travaux du Dr. John Demartini, chiropraticien à la base devenu spécialiste du comportement humain. Donc 3 causes fondamentales à vos problèmes de relation.

Cause 1 : Neuro-matrice de défense

La première cause fondamentale, c'est que vous êtes en neuro-matrice de défense. Sur mes 20 ans de pratique, j’ai pu identifier que notre système nerveux peut être dans 5 modes différents, et notamment on a un mode de base, qui est le mode avec lequel on est livré « en sortie d’usine », et que j’appelle le mode par défaut.

On a longtemps cru que ce mode par défaut était une physiologie assez calme qui, lorsqu’un stress arrive, s’active, se met sous stress. Une fois que le stresseur disparaît, on retourne à la normale. Mais on sait désormais que ce n'est pas comme ça que ça fonctionne. On sait aujourd'hui que notre physiologie de base est une physiologie active de stress de basse intensité, c'est-à-dire que le système est toujours un peu hypervigilant. Si vous voulez vraiment vous relaxer, vous devez faire un effort conscient de créer un sentiment de sécurité, pour que le système contrôle cette réponse de stress de bas niveau. Si vous n’arrivez pas à créer suffisamment de plages de sécurité ou trop de stress, votre système va s’activer de plus en plus, au moins d’entrer dans un état de stress constant, ce que j’appelle cette neuro-matrice de la défense.

Vous l’avez déjà très certainement tous expérimenté dans la vie de tous les jours. Imaginez que vous avez un peu de tensions dans votre couple. Est-ce que, si vous avez une bonne nuit de sommeil, le jour suivant se passer mieux que si vous n’avez dormi que 2 heures ? On est bien d’accord que plus on est sous stress, plus on est fatigué, moins on se sent bien et plus on est réactif. On a même des expressions pour ça : être à fleur de peau, être sur les nerfs… Bien évidemment, si vous êtes à fleur de peau ou sur les nerfs, si vous êtes complètement stressé, dès le moment où l’autre personne va vous dire quelque chose, vous allez réagir automatiquement.

Donc la première des choses si vous voulez pouvoir avoir de meilleures relations, c'est de sortir de cette neuro-matrice de défense, donc d’apprendre à réguler votre système nerveux. Ça passe principalement par le corps physique. Que pouvez-vous faire pour sortir de cette neuro-matrice de défense ? C'est apprendre à réguler votre système nerveux, que ce soit en faisant de la respiration, que ce soit en faisant de la sophrologie, de la méditation de pleine conscience, etc. Vous pouvez utiliser aussi l’activité physique, recevoir des massages, faire régulièrement des séances de chiropratique ou d’ostéopathie pour réduire ces tensions. C'est absolument essentiel, c'est la base de tout travail que vous devez faire pour commencer d’améliorer vos relations, parce que plus vous allez être serein, plus vous allez être centré, moins vous serez réactif, mieux cela influencera votre communication. Donc peu importe si vous décidez de choisir une voie de soutien psychologique, cognitif, il faut que vous ayez en parallèle un travail sur le corps, parce que cette régulation du système nerveux en sortant de cette neuro-matrice de défense passe par un travail par le corps.

Cause 2 : Relations primordiales passées incomplètes

Deuxième raison, ce sont les relations primordiales passées incomplètes. Il s’agit des relations que vous avez eues avec votre père, avec votre mère, peut-être vos grands-parents, des gens proches de la famille dans les premières années de vie, et toutes les relations que vous avez eues par le passé, si vous avez été en couple avant d’être votre couple actuel. Toutes ces relations vont déterminer ce qui se passe dans le présent. Très souvent, on a développé au travers de ces relations, de par les perceptions qu'on a eues d’évènements qui se sont passés, peut-être traumatisants voire même très traumatisants, de la colère, du ressentiment, peut-être parce qu'on a fait des choses, de la culpabilité.

Il faut se rendre compte que ce que vous êtes en train de vivre dans votre relation actuelle n’a peut-être rien à voir avec ce qu'il se passe actuellement, mais a à voir avec ce qui a pu se passer dans des relations primordiales ou dans des relations passées. Si vous avez gardé de la colère ou du ressentiment par rapport à votre père, votre mère ou une autre personne, ou un ex dans votre couple, ces vieux schémas sont en train de rejouer dans votre relation actuelle. Une des problématiques est qu’en fait, vous répondez à la personne, pas par ce qu'il se passe dans le moment actuel, mais vous répondez sur la base de vieux schémas.

Imaginons que j’ai avec un problème de relation avec ma mère. Dans les moments de stress, si on est en neuro-matrice de défense, je vais potentiellement projeter ces vieux ressentiments, de colère, ces vieilles émotions sur mon époux/se, partenaire actuelle.

Donc c'est très important, si vous voulez sortir de ces dynamiques, on a dit d’abord passer sur le corps, faire un travail pour sortir de cette physiologie de défense, de cette neuro-matrice de la défense, puis de compléter ces relations, c'est-à-dire de dissoudre ces culpabilités, de dissoudre ces sentiments de colère ou de ressentiment du passé. Sans aller dans les détails sur comment on peut y travailler, mais c'est très important de rendre complet ces choses et de ne pas avoir ces vieux bagages émotionnels.

Cause 3 : Enfant blessé, Ego

Ce troisième élément peut être décrit de différentes manières, on pourrait l’appeler l’enfant blessé, l’ego, Jung l’appelait l’ombre, la partie sombre de nous-mêmes. C'est cette notion qu’au travers de notre existence, on a tous vécu un certain nombre de traumatismes. Certains psychologues pensent même que la naissance est une forme de séparation primordiale qui est un traumatisme duquel on ne guérit jamais vraiment. Et il y a toutes ces choses qui se sont passées : peut-être que vous avez eu l’impression que vos parents ne vous aimaient pas, peut-être que vous avez été abusé physiquement, peut-être même physiquement, peut-être que lorsque vous avez grandi à l’école, il y a des enfants qui se sont moqués de vous, peut-être qu’on vous a battu dans la cour d’école, peut-être qu’à l’âge de l’adolescence, vous avez été éperdument amoureux de cette fille ou de ce garçon, vous lui avez demandé s'il/elle voulait sortir avec vous, mais vous avez été rejeté et il/elle l’a dit à tout le monde, etc.

Tout ça, ce sont des blessures qui se créent et qui vont développer un certain nombre de mécanismes de compensation. Aujourd'hui, lorsque vous êtes dans une relation où cela devient difficile et conflictuelle, de plus est si vous êtes en stress, si vous avez ces relations primordiales incomplètes, vous n’allez pas fonctionner dans la relation à partir du vous authentique, mais vous allez réagir à partir du vous blessé.

Il faut se rendre compte que c'est toujours une dynamique, une danse entre les 2 personnes. Peut-être que pour les personnes qui ont eu des traumatismes violents, vous pensez que vous ne pouvez pas adhérer à ce que je dis, mais gardez en tête cette notion de danse, qu’il faut toujours 2 personnes. Il n'y a pas qu’un bourreau et une victime, les 2 jouent un rôle important. Il faut se rendre compte que dans cette dynamique, le but de cette dynamique est de vous permettre de reprendre votre pouvoir. Toutes ces dynamiques sont faites pour nous guérir. Maintenant, vous pouvez seulement avoir cette notion médicale, de la pathologie de la chose, mais si vous arrivez à prendre de la distance, des techniques et des processus existent pour ça pour vous permettre de voir l’ensemble de cette réalité, vous vous rendez compte que toutes ces différences, toutes ces personnes qu'on attire dans notre vie sont là pour nous faire grandir, nous faire apprendre quelque chose. Maintenant, la notion est : est-ce que vous allez juste rester dans cette notion de victime, que vous cherchez juste des thérapeutes qui vont vous valider dans votre sentiment de victime, ou est-ce que vous avez vraiment envie de trouver des solutions et les gens qui vont être là à la fois pour vous soutenir, mais aussi pour vous challenger, pour voir la magnificence de ce qui est en train de se passer, de comment l’univers fonctionne pour vous faire prendre conscience, pour vous faire reprendre votre pouvoir, pour pouvoir guérir de ces choses, c'est possible.

Vous devez vous rendre compte qu’indépendamment de ce qui s’est passé dans notre passé, même si c'est très traumatique, c'est familier pour nous. Tout ce qui est familier pour nous procure, malgré tout, un sentiment de sécurité, à un niveau parfois inconscient. Vous avez par exemple des enfants qui ont été maltraités et tout ce qu'ils connaissent, c'est cette maltraitance. Malgré tout, malgré la souffrance liée à ça, c'est quelque chose de familier et ça donne inconsciemment au système un sentiment de sécurité. Donc dans leur vie, ils vont commencer à attirer toujours les mêmes personnes qui continuent de les abuser parce que ça répète ce sentiment de familiarité et de sécurité.

Si vous voulez pouvoir casser ces schémas, il va falloir apprendre à danser avec cet ego, avec cet enfant blessé, de voir que ce qui se passe en ce moment est lié à ces vieux mécanismes, et qu'il y a des moyens de reconceptualiser les histoires que l’on se dit à soi-même, pour avoir une perception complètement différente des choses, qui nous permet d’aller de l’avant et qui n'est pas juste un boulet nous maintenant victime de nos histoires de vie, de notre passé, de nos antécédents.

Donc si vous avez des problèmes relationnels et que vous voulez vraiment aller au cœur du problème, n’oubliez pas ces 3 dimensions :

cette dimension du stress. C'est impossible de développer une bonne fondation relationnelle avec quelqu'un d’autre si vous n’allez pas bien, c’est fondamental. Souvenez-vous que dans les avions, on dit que si les masques à oxygène tombent, prenez d’abord soin de vous, mettez votre masque avant d’aider quelqu'un d’autre. Allez mieux vous-même, et ça passe absolument par un travail physique de régulation de votre système nerveux.

Ensuite, complétez ces relations primordiales, notamment avec vos parents ou d’autres personnes proches.

Enfin, prenez cette notion que très souvent, quand les choses deviennent difficiles, ce n'est pas le « vous » authentique qui réagit, et de même pour l’autre personne, ce n'est pas son « lui » authentique qui réagit, mais c'est ce petit enfant qui a été blessé à différents moments, et qui est en train de mettre en place, qui réagit avec les meilleures stratégies d’adaptation qu’il a à disposition pour faire face à ce moment, et qu'il a aussi besoin de faire un travail à ce niveau-là pour pouvoir intégrer ces expériences du passé.

Laissez-moi savoir si vous avez des questions, si cela vous parle. Nous, on se retrouve la semaine prochaine pour une nouvelle vidéo. D’ici là, souvenez-vous: émerveillez-vous, aimez la vie et contribuez chaque jour un petit peu plus.

[superojas]

Muchos escépticos afirman que la ciencia y la creencia en Dios es incompatible, pero no es algo tan cierto, acá una lista de grandes científicos creyentes de gran importancia. Durante el Renacimiento (XV y XVI), período esencialmente humanista y artístico, Leonardo da Vinci (padre precursor del helicóptero, el carro de combate, el submarino y el automóvil) o Nicolás Copérnico (Teoría del Heliocentrismo). Y del siglo XVII eran por ejemplo Galileo Galilei (padre de la astronomía moderna), Blaise Pascal  (autor del Principio, el Triángulo, el Teorema y la Apuesta que llevan su nombre) y Johannes Kepler (quien formuló leyes sobre el movimiento de los planetas sobre su órbita alrededor del Sol), entre otros. En los siglos XVIII y XIX se dio la Ilustración y la Revolución Industrial. Algunos creyentes científicos fueron Isaac Newton (Ley de la Gravitación Universal), Robert Boyle (Ley de Boyle), Gottfried Wilhelm Leibniz (cálculo infinitesimal y sistema binario), Carl von Linné (padre de la taxonomia moderna), Leonhard Euler (Número e Identidad de Euler y la Característica de Euler), Charles Coulomb (Ley de Coulomb), James Watt (máquina de vapor), Charles Bell (teléfono), Alessandro Volta (corriente eléctrica continua y pila eléctrica), André Marie Ampère (telégrafo eléctrico y el electroimán), Michael Faraday (padre del electromagnetismo y de la electroquímica), Samuel Morse(telégrafo Morse y Código Morse), James Clerk Maxwell (Teoría Electromagnética y Teoría Cinética de Gases), Gregor Mendel (Leyes de Mendel). Del siglo XX podemos destacar a William Thomson (Lord Kelvin) (padre de la escala de temperatura Kelvin), Louis Pasteur (pasteurización), Nikola Tesla(motor de corriente alterna entre otros muchísimos inventos), Guglielmo Marconi (radiotelegrafía sin hilos), Alexander Fleming (penicilina), Max Planck (padre de la física cuántica y de la Constante de Planck), Arthur Stanley Eddington (Límite de Eddington), Niels Bohr (padre del Modelo Atómico Bohr), Erwin Schrödinger (Ecuación y el Modelo Atómico de Schrödinger y Efecto Tunel), Werner Karl Heisenberg(Principio de Indeterminación de Heisenberg y Teoría de Matrices), Georges Lemaître (Teoría del Big Bang), John von Neumann (Teoría de Juegos), Wolfgang E. Pauli (Principio de Exclusión), Howard Hathaway (cerebro electrónico), etcétera. En la actualidad los ateos aseguran que todo esto es cosa del pasado, que el 90% de los grandes científicos de hoy día no cree en Dios aunque no publican sus nombres ni sus descubrimientos para probar cómo de grandes son. Deshagamos este mito citando unos cuantos cristianos vivos a principios de este siglo XXI: Arno Allan Penzias(radiación cósmica de fondo de microondas), William D. Philips(refrigeración mediante láser), Francis Collins (director del Proyecto Genoma Humano), Donald E. Kuth (análisis de algoritmos), Charles Hard Townes(estudio del láser y máser), Richard E. Smalley (fullerenos), etc. La lista de científicos creyentes de ayer, hoy y siempre podría ser mucho mayor pero baste con esta pequeña muestra. Y eso que hemos excluido a literatos, filósofos, humanistas, artistas, músicos, cineastas y otros intelectuales cristianos de gran talento. Fuente: «por qué deje de ser ateo», Josué Ferrer

[unpeudephysique]

Symétrie SU(2) et théorie générale du spin

La symétrie SU(2) est une propriété très générale en physique (voir le post sur les groupes de Lie). elle correspond à la symétrie de rotation dans l’espace. Les équations d’un système ne changent pas si l’on opère une simple rotation du référentiel de coordonnées. En physique classique, cette symétrie se traduit par la conservation du moment cinétique (théorème de Noether).

Nous allons voir comment on peut déduire des propriétés du groupe SU(2) les propriétés du spin des électrons au sein du nuage électronique. Nous avons exposé ces propriétés dans un post précédent consacré aux électrons. Dans ce post, ces propriétés étaient tirées du chapeau. Rappelons en quelques mots ces propriétés :

les différents états possibles d’un électrons sont caractérisés par trois nombres quantiques n, l, m ainsi que par son spin (+1/2, -1/2),

le nombre l correspond au moment cinétique orbital,

la projection du moment cinétique orbital sur un axe ne peut prendre que 2l+1 valeurs différentes,

ces trois nombres quantiques déterminent la fonction d’onde des électrons qui prend la forme d’une harmonique sphérique.

Par ailleurs, deux électrons ayant les mêmes nombres quantiques n, l, m ne peuvent pas avoir un spin identique.

Or, nous allons voir que ces propriétés sont directement liées aux propriétés du groupe SU(2) ! Pour parvenir à ce résultat, nous allons rechercher une représentation de SU(2) (au sens défini dans le post d’introduction sur les groupes) qui nous permettent de manipuler les vecteurs d’état psi(t) d’un système quantique et, si possible, de les décomposer sur une base de vecteurs propres. Comme nous l’avons dit dans le post sur le formalisme quantique, les vecteurs d’état d’un système appartiennent à un espace de Hilbert qui est un espace vectoriel sur le corps des complexes C.

Remarque : Plutôt que SU(2) nous utiliserons SL(2,C), groupe spécial linéaire des matrices 2 x 2 inversibles à valeurs complexes et de déterminant égal à 1 (les raisons de cette substitution importent peu, ces deux groupes ont des propriétés très similaires). Son algèbre de Lie est le groupe sl(2,C) constituée par les matrices 2x2 complexes de trace nulle. Les mathématiciens nous assurent qu’il y a bijection entre les représentations irréductibles de dimension finie de su(2) et celles de sl(2,C).

Un peu d’algèbre...

Soit Vn un espace vectoriel de dimension finie n sur C. Une représentation linéaire de sl(2,C) sur Vn peut, par définition, être décomposée sur une base de 3 matrices nxn qui vérifient les mêmes « équations de structure » que sl(2,C) et, donc, que su(2) :

(Voir les posts sur les algèbres de Lie.) Nous n’allons pas utiliser directement les matrices Jk mais plutôt les matrices suivantes : 

En se basant sur les constantes de structure des matrices de Pauli, il est facile de voir que e,f et h vérifient les équations qui suivent :

Puisqu’on s’intéresse aux représentations linéaires de sl(2,C) il n’est pas illégitime de faire l’hypothèse que l’opérateur h possède au moins une valeur propre que nous appellerons lambda. Cette valeur propre est associée à un sous-espace vectoriel de Vn de dimension d. Nous appellerons

avec k = 1…d les d vecteurs propres associées à lambda. Ces vecteurs propres présentent des propriétés tout à fait remarquables. Il est en effet facile de voir en utilisant les relations de commutation ci-dessus que :

Autrement dit :

le vecteur e_lambda_k est un vecteur propre de h avec la valeur propre lambda+1

le vecteur f_lambda_k est un vecteur propre de h avec la valeur propre lambda-1.

Il vient :

Vn étant de dimension finie, il existe une valeur entière P et une valeur entière Q telles que :

Des considérations sur la structure de sl(2,C) conduisent à montrer que :

On peut en déduire simplement que :

Le nombre j est donc nécessairement un entier ou un demi-entier. Les valeurs propres de h peuvent être représentées de la manière suivante :

ce qui conduit à l’existence de 2j+1 valeurs propres. Les valeurs des coefficients alpham s’expriment alors comme suit :

Le résultat auquel nous sommes parvenus devrait vous mettre la puce à l’oreille : 2j+1 valeurs propres telles que -j<m<j, on a déjà vu ça quelque part !

Remarque : On aurait pu, bien évidemment, choisir une autre décomposition par simple permutation des indices Jk. On obtiendrait un résultat identique, avec le même nombre de valeurs propres et la même formule pour alpham.

Application au moment cinétique d’une particule

Ce résultat est tout à fait remarquable. Il l’est encore plus si l’on s’intéresse à l’observable associée à l’opérateur h. Puisque l’opérateur h est associé à un groupe de symétrie, cette observable correspond à un invariant du système (théorème d’Erhenfest). Quel est cet invariant ? Il s’agit tout simplement du moment cinétique. On retrouve un résultat connu en mécanique classique puisque c’est l’invariant associé à la symétrie SO(3) par le théorème de Noether.

En physique quantique, le moment cinétique d’une particule selon un axe peut donc être décomposé sur les vecteurs propres associés à la matrice de Pauli correspondant à cet axe :

Il ne peut prendre que 2j+1 valeurs, j étant un nombre entier ou demi-entier. Cette propriété découle très directement de l’application de la théorie des groupes de Lie à la physique quantique. C’est elle qui permet d’expliquer les propriétés du spin d’un électron dans le nuage atomique.

Le développement qui précède nous montre toute la puissance des méthodes basées sur les symétries et des groupes de Lie. A posteriori, ça valait le coup de consacrer quelques minutes (ou quelques heures) sur le sujet, pas vrai ? Pour ceux qui ont séché, il n’est pas trop tard...

Bosons, fermions et principe d’exclusion de Pauli

Pourquoi s’arrêter en si bon chemin. La théorie a d’autres choses à nous apprendre. Comme nous l’avons vu plus haut, le spin d’une particule ne peut être qu’entier ou demi-entier. C’est un résultat fondamental de la physique quantique. Il est à la base de la partition des particules élémentaires en deux familles : les bosons (spin entier ou nul) et les fermions (spin demi-entier).

L’analyse des symétries du système va nous permettre de mieux caractériser ces deux familles. Intéresse-nous cette fois au groupe des permutations. Il est une autre propriété des particules quantiques qui est le principe d’indiscernabilité et qui stipule qu’il est impossible de différencier deux particules de même nature. Soient donc deux particules de même nature, appelées p1 et p2 et P12 l’opérateur qui les permute. Le hamiltonien H du système constitué par ces deux particules commute avec P12 puisqu’elles sont indiscernables. Les vecteurs propres de H sont donc également des vecteurs propres de P12. Une double permutation ramène à la situation initiale :

On en déduit que les valeurs propres de P12 sont +1 et -1.

Ceci signifie que la fonction d’onde de la paire de particules p1, p2 est soit symétrique, soit antisymétrique. Une analyse plus poussée montre que la solution symétrique correspond à une particule ayant un spin entier et la solution antisymétrique a une particule de spin demi-entier. Ceci induit une différence de comportement fondamentale entre bosons et fermions. Rien en effet n’empêche les bosons d’occuper le même état (on dit alors qu’ils forment un condensat). Cette configuration est par contre strictement interdite pour les fermions. Pour que deux fermions se retrouvent dans le même état à la même position, il faudrait en effet que :

ce qui entraîne automatiquement que :

La probabilité pour que deux particules de spin ½ occupe le même état quantique est donc nulle ! C’est le fondement théorique du principe d’exclusion de Pauli. C’est une propriété tout à fait essentielle pour nous : c’est cette propriété qui fait que la matière est matière, qu’elle a une certaine étendue spatiale, alors que le rayonnement, par exemple, peut concentrer un nombre indéfini de photons en un seul point !

Fonction d’onde et nuage électronique

La quantification du spin explique également la structure des atomes et, plus précisément l’organisation si particulière du nuage électronique. Comme on l’a vu dans le chapitre consacré à l’atome d’hydrogène, les électrons ne peuvent occuper qu’une série d’états quantiques correspondant à des niveaux d’énergie croissant caractérisés par un nombre appelé n. Pour chacun de ses niveaux (on parle de couches), il existe plusieurs sous-niveaux possibles (sous-couches), caractérisés cette fois par le nombre l, avec :

Un troisième niveau d’analyse conduit à une nouvelle quantification, avec le nombre m :

On reconnaît dans ces nombres l et m les nombres j et m utilisés dans le paragraphe précédent.

On peut aller plus loin en recherchant cette fois une représentation de SU(2) directement sur l’espace R3. Il est possible de trouver une telle représentation sur l’ensemble des polynômes harmoniques à coefficients complexes de degré l restreints à une sphère :

On voit toute la puissance des analyses menées à partir de la symétrie SU(2). Elles nous ont permis de retrouver les propriétés si déroutantes des électrons au sein du nuage électronique. Elles expliquent aussi la forme de leur fonction d’onde… et en prime elles fournissent une explication au sujet de principe d’exclusion de Pauli ! Que demander de plus...

Pour en savoir plus :

posts sur la mécanique quantique

post sur le formalisme quantique

post sur le spin

post sur les groupes de Lie

post sur les algèbres de Lie

post sur les spineurs

post sur les électrons d’un atome

index

[unpeudephysique]

Le spin, une propriété purement quantique

L’expérience de Stern et Gerlach

L’expérience de Stern et Gerlach joue un rôle particulier dans l’histoire de la physique quantique. En 1922, Niels Bohr multiplie les conférences et les séminaires pour rallier les scientifiques à sa vision de la matière. Sa théorie semi-classique d’un atome entouré d’électrons en orbite manque cependant de cohérence. Comment expliquer les niveaux d’énergie ainsi que les trois nombres quantiques qu’elle postule ? Pourquoi les électrons ne « tombent » ils pas sur le noyau. C’est à ce moment qu’intervient l’expérience montée par Otto Stern et Walther Gerlach. Elle met en évidence l’existence d’un moment cinétique intrinsèque des particules élémentaires (le spin), un moment cinétique dont les caractéristiques sont inexplicables dans le cadre de la physique classique. Elle montre surtout qu’on ne peut plus se contenter d‘un simple replâtrage de la théorie pour décrire le comportement des électrons au sein des atomes. Il va falloir au contraire revoir de fond en comble les bases de la physique. En ce sens, elle ouvre un immense chantier qui occupera les physiciens les plus brillants de leur génération pendant les dix années qui vont suivre.

L’expérience de Stern et Gerlach consiste à faire passer un faisceau d’atomes d’argent dans un champ magnétique orienté verticalement. Contre toute attente, ce faisceau est séparé en deux demi-faisceaux d’égale intensité déviés de manière symétrique. Or le moment magnétique orbital des atomes d’argent est supposé être nul, le faisceau ne devrait subir aucune déviation. Cette expérience montre au contraire que les atomes d’argent possèdent un moment cinétique intrinsèque en plus de leur moment cinétique orbital. Mais ce n’est pas tout : quelle que soit la direction dans laquelle on cherche à mesurer ce moment (c’est-à-dire quelle que soit l’orientation du champ magnétique transversal appliqué au dispositif), on trouve le même résultat ! Le faisceau est toujours séparé en deux demi-faisceaux d’intensité égale déviés symétriquement. Comme si ce moment cinétique ne pouvait prendre que deux valeurs quelle que soit sa direction et ce quelle que soit sa direction.

Si Wolfgang Pauli avait eu l’intuition qu’il était nécessaire de compléter le modèle de Bohr par un quatrième nombre qui ne peut prendre que deux valeurs différentes, il revient cependant à Samuel Goudsmit et George Uhlenbeck de donner en 1925 la première interprétation « quantique » de cette étrange propriété de l’électron.

Allons plus loin...

Poussons plus loin les investigations et intéressons-nous à un seul des deux demi-faisceaux. Si on lui applique à nouveau le même protocole (un champ magnétique transversal), on pourrait s’attendre à ce que tous les atomes de ce demi-faisceau réagissent de la même façon. Or ce n’est pas le cas. Si le champ appliqué est perpendiculaire au champ qui a servi à séparer en deux parties le faisceau initial, le demi-faisceau auquel on s’intéresse est à nouveau séparé en deux demi-faisceaux d’intensité égale déviés symétriquement. Si le champ fait un angle theta avec le champ initial, même déviation symétrique en deux demi-faisceaux mais cette fois l’intensité des deux demi-faisceaux diffère : elle vaut cos2(theta) pour l’un et sin2(theta) pour l’autre.

Un tel comportement est incompréhensible dans un cadre classique, voire semi-classique. Le spin est une grandeur physique de nature purement quantique. Ces propriétés ne peuvent être décrites qu’au travers du formalisme quantique  (voir le post consacré au formalisme quantique).

Quelle représentation du spin ?

Comme nous venons de le dire, le spin d’une particule ne peut prendre que deux valeurs lorsqu’on le mesure dans une direction donnée :

De prime abord, cette représentation vectorielle du spin dans l’espace euclidien R3 parait tout à fait adaptée. Problème : elle ne répond pas aux critères du formalisme quantique tels que nous les avons décrits. La représentation d’un objet quantique doit se faire dans une base orthogonale constituée à partir des vecteurs propres de l’opérateur correspondant à la propriété que l’on cherche étudier (voir le post sur le formalisme quantique). Les deux vecteurs + S et – S ci-dessus sont incontestablement les vecteurs propres de l’opérateur spin. Ce n’est pas le cas si on se place dans une représentation vectorielle dans R3. Celle-ci ne convient pas.

Reprenons le problème à la base… Comme nous l’avons vu, l’état d’un objet quantique (ici un atome d’argent) est décrit par une fonction d’onde |psi> qui est un vecteur dans un espace vectoriel complexe appelé espace de Hilbert. La dimension de cet espace est déterminée par le nombre d’états indépendants possibles de cet objet. Dans le cas du spin des atomes d’argent de l’expérience de Stern et Gerlach, cet espace est donc un espace complexe de dimension 2.

Appelons Hspin cet espace. Supposons que nous mesurions le spin dans la direction de l’axe Oz. Les deux états de spin possibles |+z> et |-z> forment donc une base de cet espace. Ce qui revient à dire que les deux vecteurs |+z> et |-z> sont deux vecteurs orthogonaux de l’espace Hspin. La correspondance entre la représentation du moment cinétique de l’atome d’argent dans R3 et son vecteur d’état dans Hspin est donnée par le tableau qui suit : 

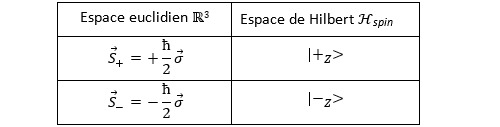
Mesure du spin dans une autre direction

Supposons maintenant que nous cherchions à mesurer le spin après avoir effectué une rotation du dispositif de mesure d’un angle theta autour de l’axe Oy. Dans l’espace euclidien R3, cette rotation peut être représentée par une matrice réelle de dimension 3x3 que nous appellerons Ry(theta). Quel sera le résultat de la mesure et comment cela se traduit-il dans l’espace des fonctions d’onde de spin Hspin ?

Pas de surprise côté mesure. Comme nous l’avons indiqué plus haut, la mesure du spin ne peut prendre que deux valeurs :

Si par exemple l’angle theta vaut pi/2 (mesure dans la direction de l’axe Ox), le résultat obtenu est parfaitement aléatoire, la probabilité de trouver l’une ou l’autre valeur est identique et égale à 50%. Le cas où l’angle theta est quelconque est plus intéressant. Comme nous l’avons indiqué, la probabilité de trouver l’une ou l’autre valeur en fonction de la mesure préalable dans la direction de l’axe Oz n’est plus égale à 50%. Elle dépend de la valeur de l’angle theta :

Qu’est-ce que ce résultat nous dit au sujet de la fonction d’onde de spin ? Les vecteurs |+Stheta> et |-Stheta> forment une base de l’espace Hspin au même titre que |+z> et |-z> . On peut donc décomposer la fonction d’onde d’une particule quelconque sur ces vecteurs propr

La probabilité de trouver l’une ou l’autre des valeurs est donnée par le carré du coefficient lambda correspondant. Dans le cas qui nous intéresse, on peut donc écrire :

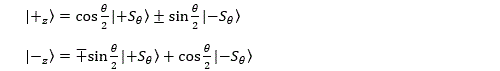
(La seule connaissance de la probabilité ne permet pas de déterminer le signe des coefficients.) On peut exprimer ceci en disant qu’à la rotation Ry(theta) dans R3 correspond un opérateur Ay(theta) agissant sur Hspin défini comme suit :

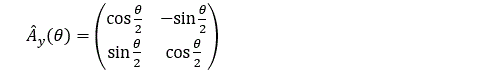
L’opérateur Ay(theta) a toutes les caractéristiques d’une rotation… mais à y regarder de plus près cette correspondance est très particulière :

la rotation Ry(theta) agit sur l’espace euclidien R3, espace vectoriel à trois dimensions réelles,

l’opérateur Ay(theta) agit sur l’espace Hspin, qui est un espace vectoriel complexe à deux dimensions complexes,

mais surtout Ry(theta) opère une rotation d’angle theta alors que Ay(theta) opère une rotation d’angle theta/2. 

Spineurs et algèbre de Lie

Pour ce qui concerne l’opérateur Ay(theta) on est en terrain connu (voir le post consacré aux espaces vectoriels et aux groupes de Lie). C’est une matrice 2x2 complexe. Elle fait partie d’un groupe appelé SU(2). Le groupe SU(2) est le groupe spécial unitaire des matrices 2x2 à coefficients complexes de déterminant 1 :

ce qui revient à écrire :

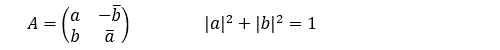
SU(2) est un groupe de Lie. Il joue un rôle très important en mécanique quantique car il est associé aux symétries sphériques. A chaque rotation d’un angle theta autour d’un vecteur unitaire u on peut en effet faire correspondre une matrice de SU(2) :

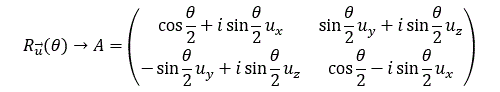
Mais que peut-on dire de l’espace de Hilbert Hspin sur lequel agissent les matrices de SU(2) ? Là, c’est moins évident, il va falloir s’accrocher… L’espace Hspin est un espace spinoriel. La théorie des spineurs a été introduite par le mathématicien français Elie Cartan au début du XXème siècle. Les spineurs ont des propriétés assez déroutantes. (Nous aborderons les rudiments de la théorie des spineurs dans un post séparé.) Un spineur peut être associé à un « plan orienté ». On peut définir un plan orienté à partir de deux vecteurs unitaires orthogonaux : 

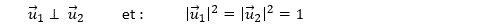
et du produit vectoriel de ces deux vecteurs. (L’ordre dans lequel on prend ces deux vecteurs est donc déterminant.) Il est facile de voir que cette définition est tout à fait adaptée au contexte du moment cinétique. La propriété la plus emblématique d’un spineur est qu’une rotation de 360 degrés le transforme en son inverse ! Il faut donc une rotation de 720 degrés pour revenir au spineur d’origine. 

Matrices de Pauli

Revenons au groupe SU(2). L’une des propriétés de SU(2) est la possibilité de générer les matrices de ce groupe à partir de 3 matrices élémentaires. Prenons par exemple le cas de l’opérateur Ay(theta). Un simple développement limité suffit à se convaincre qu’on peut l’écrire sous la forme suivante :

En fait, on peut montrer que toute matrice de SU(2) peut être générée à partir de matrices unitaires sigma :

avec :

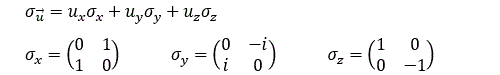
Les matrices sigmax, sigmay et sigmaz sont appelées matrices de Pauli, du nom du physicien Wolfgang Pauli qui est le premier à avoir établi une théorie complète du spin dans un cadre non-relativiste. Or, il est facile de voir que les vecteurs propres de ces matrices sigma sont précisément les vecteurs |+x>, |-x>, |+y>, |-y> et |+z> et |-z> correspondant aux opérateurs de mesure de spin dans les directions Ox, Oy et Oz ! 

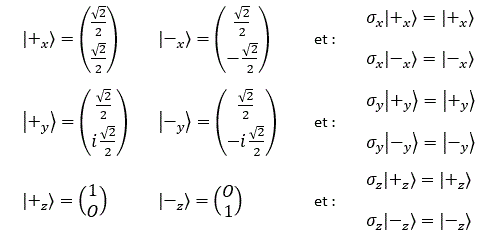
Les matrices de Pauli constituent donc une base qui permet de construire simplement une observable « spin » dans n’importe quelle direction de l’espace. 

Matrices de Pauli et symétrie de rotation

Dans la présentation qui précède, les matrices de Pauli semblent « sortir du chapeau ». Une présentation plus rigoureuse aurait permis de faire la liaison entre ces matrices et l’application d’un principe très général en physique, établi par la mathématicienne Emmy Noether au début du XXème siècle. Emmy Noether a en effet montré qu’à toute symétrie était associée la conservation d’une grandeur physique (théorème de Noether). C’est ainsi qu’à la symétrie de translation (les lois de la physique sont conservées dans toute translation du référentiel dans l’espace) est associée la conservation de la quantité de mouvement. De la même façon, à la symétrie de rotation dans l’espace (les lois de la physique sont conservées dans toute rotation du référentiel dans l’espace) est associée la conservation du moment cinétique. Or, comme nous l’avons dit plus haut, une rotation dans l’espace peut être représentée par une matrice du groupe SU(2) (que l’on appelle aussi d’ailleurs groupe de symétrie). Rien d’étonnant donc à ce que les opérateurs de mesure du spin puissent être directement déduits des matrices de Pauli puisque celle-ci forment une base à partir de laquelle on peut générer les matrices de ce groupe.

Remarque : Les matrices de Pauli ne commutent pas.  

Ceci signifie qu’il n’est pas possible de connaître simultanément la valeur de spin dans deux directions différentes. 

Pour en savoir plus :

post sur l'équation de Schrödinger 

post sur le formalisme quantique

post sur l’oscillateur harmonique quantique

post sur les espaces vectoriels et les groupes de Lie

post sur les algèbres de Lie

post sur les spineurs

post sur le théorème de Noether

post sur l’équation de Dirac

index

[unpeudephysique]

Et si on faisait un peu d’algèbre...

Que ceux qui sont allergiques aux mathématiques passent leur chemin… Pour les autres, nous allons faire quelques rappels sur les groupes et les espaces vectoriels pour pouvoir introduire la notion de groupe de Lie et d’algèbre de Lie , incontournable en physique quantique.

Groupe

Un groupe est un ensemble muni d’une loi interne : 

qui a les propriétés suivantes :

Le groupe est dit commutatif (ou abélien) si :

L’ensemble des entiers relatifs (appelé Z) est un groupe pour l’addition. Il en va de même pour l’ensemble R des nombres réels. L’ensemble des rotations forme aussi un groupe.

Espace vectoriel

Un espace vectoriel est un ensemble muni :

d’une loi de composition interne notée « + » appelée somme vectorielle et pour laquelle il est un groupe commutatif,

d’une loi de composition externe « o », associative et distributive, appelée produit par un scalaire.

K étant un ensemble ayant les propriétés d’un corps. Cette loi vérifie également les propriétés suivantes :

Dans ce qui précède, -u représente l’inverse de u par l’opération somme vectorielle.

L’ensemble R3 est un espace vectoriel sur le corps des réels R. L’ensemble des fonctions continues sur R3  à valeur réelle ou complexe est également un espace vectoriel sur R.

Représentation linéaire d’un groupe

On parle de représentation linéaire d’un groupe lorsque celui-ci agit sur un espace vectoriel et que cette action respecte la structure de l’espace vectoriel.

Soit E un espace vectoriel sur un corps (R ou C par exemple). Soit X_E l’ensemble des applications linéaires inversibles de E dans E. Une représentation linéaire de dans X_E associe à tout élément g de G une application linéaire T(g) de X_E.

Si E est un espace vectoriel de dimension n sur R alors X_E peut être identifié au groupe GL(n,R) des matrices inversibles n x n. Dans ce cas une représentation linéaire de G est une représentation qui associe à tout élément de G une matrice du groupe GL(n,R).

Même chose si l’on remplace le corps des réels par le corps des complexes C, dans ce cas X_E est le groupe des matrices complexes inversibles GL(n,C).

Groupe de Lie

Lorsqu’un groupe est une variété différentiable, que sa loi interne * est différentiable et que l’application inverse g à g-1 est également différentiable, ce groupe est un groupe de Lie. Le plus souvent, on identifie un groupe de Lie à sa représentation linéaire sur R (ou sur C), c’est-à-dire au groupe de matrices qui le représentent. 

Le groupe SO(2)

C’est le groupe des matrices orthogonales de dimension 2 et de déterminant 1. Le groupe des rotations dans R2 constituent l’une des représentations linéaires de ce groupe :

Le groupe SO(2) est un groupe de Lie. Il est commutatif. L’inverse de la matrice R(theta) est la matrice R(-theta). Il est possible d’écrire R(theta) sous la forme :

Si l’on remarque que G2 = -Id et que G2 = - G, un simple développement limité du second membre de l’équation ci-dessus suffit à le démontrer. On peut exprimer cette équation sous la forme suivante :

En ce sens, on peut dire que la matrice (considérée comme un élément d’un espace vectoriel) est un vecteur tangent au groupe SO(2) au point qui correspond à la matrice identité (c’est-à-dire tel que theta = 0).

Il existe une autre représentation de ce groupe, cette fois dans U(1). L’application définie comme suit :

est un isomorphisme. Un isomorphisme est une application bijective qui préserve la structure d’un ensemble et dont la réciproque préserve également la structure de cet ensemble. Les groupes SO(2) et U(1) sont isomorphes.

Le groupe SO(3)

C’est le groupe des matrices orthogonales de dimension 3 et de déterminant 1. Le groupe des rotations dans R3 est une représentation linéaire de ce groupe.

Une rotation dans R3 est caractérisée par un vecteur unitaire u et un angle theta appartenant à l’intervalle [-pi, pi [. On peut la représenter par un vecteur de R3 :

(Remarque : il ne s’agit pas d’une représentation linéaire.) L’extrémité de ce vecteur appartient à une boule centrée sur l’origine de R3 et de rayon pi. Cette représentation présente une particularité : deux points antipodaux du bord extérieur de cette boule représentent la même rotation alors qu’à toute rotation d’un angle inférieur à pi ne correspond qu’un point et un seul de la boule. Comme on l’a dit, cette représentation n’est pas une représentation linéaire. Elle nous donne par contre une indication sur la topologie de SO(3) : on peut en effet dire que SO(3) est compact.)

Le groupe SO(3) est un groupe de Lie. A la différence du groupe SO(2) il n’est pas commutatif : l’application de la rotation R1 suivie de la rotation R2 ne donne pas le même résultat que l’application de R2 suivi de R1.

Le groupe SU(2)

C’est le groupe des matrices 2x2 unitaires complexes de déterminant égal à 1.

Ceci revient à dire que :

Si on écrit a = x + iy  et b = z + it , il vient : 

C’est l’équation d’une hypersphère de rayon unité. Là encore il ne s’agit pas d’une représentation linéaire : c’est la topologie de l’hypersphère qui nous intéresse. Tout comme celle dans le cas précédent, elle est compacte.

Le groupe SU(2) et les quaternions

Le groupe SU(2) est souvent associé à la notion de quaternion. Cette notion a été introduite par William Rowan Hamilton pour représenter les rotations dans l’espace. Soit q le quaternion défini par : 

Les quaternions sont des nombres hypercomplexes. Au lieu de n’avoir qu’une seule composante imaginaire, ils en ont trois. Ou plutôt leur partie imaginaire est de nature vectorielle. On donne à la composante w de q le nom de composante scalaire de q et au triplet (x,y,z) le nom de composante vectorielle. Un quaternion q est dit unitaire si on peut le représenter sous la forme : 

Considérons maintenant un vecteur quelconque a appartenant à R3. On peut le représenter par un quaternion de composante scalaire nulle et de composante vectorielle égale à a: 

On peut montrer que la rotation de ce vecteur d’un angle theta autour de l’axe porté par le vecteur u s’écrit de manière simple dans l’espace des quaternions :

Il est facile de voir qu’il y a bijection entre l’ensemble des quaternions unitaires et SU(2) :

On écrit souvent la matrice en utilisant le formalisme suivant :

avec :

Ces matrices sont appelées matrices de Pauli.

Relation entre SU(2) et SO(3)

Comme on l’a vu, les groupes SU(2) et SO(3) sont tous deux associés aux rotations dans R3. Pour SO(3) la relation est directe : il y a isomorphisme entre le groupe des rotations dans R3 et SO(3). Dans le cas de SU(2) c’est un peu moins évident… La bijection entre l’ensemble des quaternions unitaires et le groupe SU(2) nous permet cependant d’établir une relation entre SU(2) et SO(3).

Pour cela nous allons introduire un nouveau type d’application T qui fait correspondre à un vecteur a de R3 une matrice de l’espace des matrices hermitiennes complexes MH(2,C) :

Au passage, on notera que la transformation inverse T-1 s’écrit comme suit :

Tr étant l’opérateur trace de la matrice.

Revenons à nos moutons… Considérons l’effet d’une rotation d’un vecteur a. Dans R3 on peut l’écrire de manière directe de la façon suivante :

Nous avons vu qu’il était également possible de représenter une rotation par un quaternion et qu’à tout quaternion on pouvait associer une matrice de SU(2) :

C’est ici qu’intervient l’application T définie plus haut. Nous avons vu qu’elle permettait d’associer à tout vecteur a de R3 une matrice de MH(2,C) :

C’est sur ces matrices de MH(2,C) que nous allons faire agir les matrices Q que nous avons définies en correspondance avec les rotations R(u,theta) :

Récapitulons. Première étape : à toute rotation dans R3 on fait correspondre une matrice dans SU(2) : 

Deuxième étape. A tout vecteur a de R3 on fait correspondre une matrice de l’espace des matrices hermitiennes complexes MH(2,C) :

Troisième étape. A toute rotation R(u,theta) on associe une application sur les matrices de MH(2,C) :

La boucle est bouclée… Nous avons bien défini une application qui fait correspondre à chaque élément du groupe SU(2) une rotation dans R3. C’est donc effectivement une application de SU(2) dans SO(3) :

On donne à ce type d’application le nom de morphisme de groupe. Dans le cas qui nous intéresse, ce morphisme n’est pas bijectif. On peut voir en effet que Q(u,theta) et Q(-u,-theta) ont tous deux la même transformée.

J’en vois qui hochent la tête… Le moins qu’on puisse dire, c’est que c’est plutôt tiré par les cheveux. L’espace R3, on connaît. Les rotations, on voit bien ce que c’est. Mais à quoi peut nous servir une application de l’espace des matrices hermitiennes complexes MH(2,C) dans lui-même ? Vous en connaissez beaucoup, vous, des matrices hermitiennes complexes ? Tout ça a un parfum d’inachevé. Si nous voulons tirer profit des propriétés des groupes de Lie en général et de SU(2) en particulier, il nous faut trouver une représentation plus commode et à laquelle nous pouvons raccrocher des objets physiques.

La théorie des spineurs va nous permettre de faire ce lien. Mais en attendant, nous allons continuer de creuser notre sillon et voir comment on peut générer les éléments d’un groupe de Lie à partir de son algèbre.

Pour en savoir plus :

posts sur les groupes et algèbres de Lie

post sur les notions de base des matrices

post sur les matrices (suite)

groupes et algèbres de Lie sur Internet

index