#elie cartan

[mrdirtybear]

Elie Joseph Cartan (1869-1951) was a French mathematician who is regarded as one of the most influential mathematicians of the twentieth century. I could name the areas of theoretical mathematics that were changed through his work but I would sound arch and incomprehensible if I did. Suffice to say he indirectly advanced quantum mechanics. He was also part of the pan-European effort in advancing scientific understanding in his day. In 1976 he had a lunar crater named after him. Find out more about him here.

[isomorphismes]

Once Euclidean geometry was no longer considered the only possibility for describing physical space, the question arose how the structure of space, or of spacetime, could be characterized in terms of symmetry structures on manifolds. The question was posed and discussed by Riemann (1854), taken up anew by Helmholtz at the end of the 1860s with ingenious conceptual insight but mathematically quite vague, even from the standpoint of contemporary mathematics. Helmholtz’s argument was refined by Lie (1886) and, independently, by Killing (1885). It acquired a prominent place in the broader discourse on mathematics and reality at the turn to the 20th century. In these considerations the possibility of “freely moving” rigid bodies as measuring devices was crucial.

Erhard Scholze, The problem of space in the light of relativity: the views of H. Weyl and E. Cartan

[unpeudephysique]

Le spin, une propriété purement quantique

L’expérience de Stern et Gerlach

L’expérience de Stern et Gerlach joue un rôle particulier dans l’histoire de la physique quantique. En 1922, Niels Bohr multiplie les conférences et les séminaires pour rallier les scientifiques à sa vision de la matière. Sa théorie semi-classique d’un atome entouré d’��lectrons en orbite manque cependant de cohérence. Comment expliquer les niveaux d’énergie ainsi que les trois nombres quantiques qu’elle postule ? Pourquoi les électrons ne « tombent » ils pas sur le noyau. C’est à ce moment qu’intervient l’expérience montée par Otto Stern et Walther Gerlach. Elle met en évidence l’existence d’un moment cinétique intrinsèque des particules élémentaires (le spin), un moment cinétique dont les caractéristiques sont inexplicables dans le cadre de la physique classique. Elle montre surtout qu’on ne peut plus se contenter d‘un simple replâtrage de la théorie pour décrire le comportement des électrons au sein des atomes. Il va falloir au contraire revoir de fond en comble les bases de la physique. En ce sens, elle ouvre un immense chantier qui occupera les physiciens les plus brillants de leur génération pendant les dix années qui vont suivre.

L’expérience de Stern et Gerlach consiste à faire passer un faisceau d’atomes d’argent dans un champ magnétique orienté verticalement. Contre toute attente, ce faisceau est séparé en deux demi-faisceaux d’égale intensité déviés de manière symétrique. Or le moment magnétique orbital des atomes d’argent est supposé être nul, le faisceau ne devrait subir aucune déviation. Cette expérience montre au contraire que les atomes d’argent possèdent un moment cinétique intrinsèque en plus de leur moment cinétique orbital. Mais ce n’est pas tout : quelle que soit la direction dans laquelle on cherche à mesurer ce moment (c’est-à-dire quelle que soit l’orientation du champ magnétique transversal appliqué au dispositif), on trouve le même résultat ! Le faisceau est toujours séparé en deux demi-faisceaux d’intensité égale déviés symétriquement. Comme si ce moment cinétique ne pouvait prendre que deux valeurs quelle que soit sa direction et ce quelle que soit sa direction.

Si Wolfgang Pauli avait eu l’intuition qu’il était nécessaire de compléter le modèle de Bohr par un quatrième nombre qui ne peut prendre que deux valeurs différentes, il revient cependant à Samuel Goudsmit et George Uhlenbeck de donner en 1925 la première interprétation « quantique » de cette étrange propriété de l’électron.

Allons plus loin...

Poussons plus loin les investigations et intéressons-nous à un seul des deux demi-faisceaux. Si on lui applique à nouveau le même protocole (un champ magnétique transversal), on pourrait s’attendre à ce que tous les atomes de ce demi-faisceau réagissent de la même façon. Or ce n’est pas le cas. Si le champ appliqué est perpendiculaire au champ qui a servi à séparer en deux parties le faisceau initial, le demi-faisceau auquel on s’intéresse est à nouveau séparé en deux demi-faisceaux d’intensité égale déviés symétriquement. Si le champ fait un angle theta avec le champ initial, même déviation symétrique en deux demi-faisceaux mais cette fois l’intensité des deux demi-faisceaux diffère : elle vaut cos2(theta) pour l’un et sin2(theta) pour l’autre.

Un tel comportement est incompréhensible dans un cadre classique, voire semi-classique. Le spin est une grandeur physique de nature purement quantique. Ces propriétés ne peuvent être décrites qu’au travers du formalisme quantique  (voir le post consacré au formalisme quantique).

Quelle représentation du spin ?

Comme nous venons de le dire, le spin d’une particule ne peut prendre que deux valeurs lorsqu’on le mesure dans une direction donnée :

De prime abord, cette représentation vectorielle du spin dans l’espace euclidien R3 parait tout à fait adaptée. Problème : elle ne répond pas aux critères du formalisme quantique tels que nous les avons décrits. La représentation d’un objet quantique doit se faire dans une base orthogonale constituée à partir des vecteurs propres de l’opérateur correspondant à la propriété que l’on cherche étudier (voir le post sur le formalisme quantique). Les deux vecteurs + S et – S ci-dessus sont incontestablement les vecteurs propres de l’opérateur spin. Ce n’est pas le cas si on se place dans une représentation vectorielle dans R3. Celle-ci ne convient pas.

Reprenons le problème à la base… Comme nous l’avons vu, l’état d’un objet quantique (ici un atome d’argent) est décrit par une fonction d’onde |psi> qui est un vecteur dans un espace vectoriel complexe appelé espace de Hilbert. La dimension de cet espace est déterminée par le nombre d’états indépendants possibles de cet objet. Dans le cas du spin des atomes d’argent de l’expérience de Stern et Gerlach, cet espace est donc un espace complexe de dimension 2.

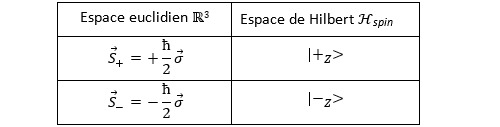
Appelons Hspin cet espace. Supposons que nous mesurions le spin dans la direction de l’axe Oz. Les deux états de spin possibles |+z> et |-z> forment donc une base de cet espace. Ce qui revient à dire que les deux vecteurs |+z> et |-z> sont deux vecteurs orthogonaux de l’espace Hspin. La correspondance entre la représentation du moment cinétique de l’atome d’argent dans R3 et son vecteur d’état dans Hspin est donnée par le tableau qui suit : 

Mesure du spin dans une autre direction

Supposons maintenant que nous cherchions à mesurer le spin après avoir effectué une rotation du dispositif de mesure d’un angle theta autour de l’axe Oy. Dans l’espace euclidien R3, cette rotation peut être représentée par une matrice réelle de dimension 3x3 que nous appellerons Ry(theta). Quel sera le résultat de la mesure et comment cela se traduit-il dans l’espace des fonctions d’onde de spin Hspin ?

Pas de surprise côté mesure. Comme nous l’avons indiqué plus haut, la mesure du spin ne peut prendre que deux valeurs :

Si par exemple l’angle theta vaut pi/2 (mesure dans la direction de l’axe Ox), le résultat obtenu est parfaitement aléatoire, la probabilité de trouver l’une ou l’autre valeur est identique et égale à 50%. Le cas où l’angle theta est quelconque est plus intéressant. Comme nous l’avons indiqué, la probabilité de trouver l’une ou l’autre valeur en fonction de la mesure préalable dans la direction de l’axe Oz n’est plus égale à 50%. Elle dépend de la valeur de l’angle theta :

Qu’est-ce que ce résultat nous dit au sujet de la fonction d’onde de spin ? Les vecteurs |+Stheta> et |-Stheta> forment une base de l’espace Hspin au même titre que |+z> et |-z> . On peut donc décomposer la fonction d’onde d’une particule quelconque sur ces vecteurs propr

La probabilité de trouver l’une ou l’autre des valeurs est donnée par le carré du coefficient lambda correspondant. Dans le cas qui nous intéresse, on peut donc écrire :

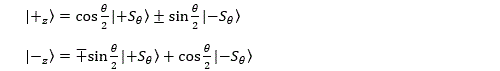
(La seule connaissance de la probabilité ne permet pas de déterminer le signe des coefficients.) On peut exprimer ceci en disant qu’à la rotation Ry(theta) dans R3 correspond un opérateur Ay(theta) agissant sur Hspin défini comme suit :

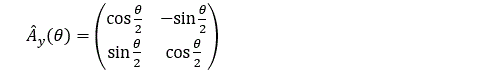
L’opérateur Ay(theta) a toutes les caractéristiques d’une rotation… mais à y regarder de plus près cette correspondance est très particulière :

la rotation Ry(theta) agit sur l’espace euclidien R3, espace vectoriel à trois dimensions réelles,

l’opérateur Ay(theta) agit sur l’espace Hspin, qui est un espace vectoriel complexe à deux dimensions complexes,

mais surtout Ry(theta) opère une rotation d’angle theta alors que Ay(theta) opère une rotation d’angle theta/2. 

Spineurs et algèbre de Lie

Pour ce qui concerne l’opérateur Ay(theta) on est en terrain connu (voir le post consacré aux espaces vectoriels et aux groupes de Lie). C’est une matrice 2x2 complexe. Elle fait partie d’un groupe appelé SU(2). Le groupe SU(2) est le groupe spécial unitaire des matrices 2x2 à coefficients complexes de déterminant 1 :

ce qui revient à écrire :

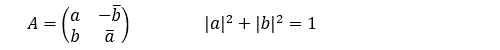
SU(2) est un groupe de Lie. Il joue un rôle très important en mécanique quantique car il est associé aux symétries sphériques. A chaque rotation d’un angle theta autour d’un vecteur unitaire u on peut en effet faire correspondre une matrice de SU(2) :

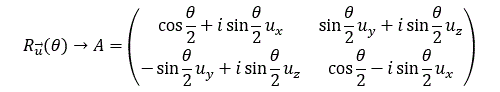
Mais que peut-on dire de l’espace de Hilbert Hspin sur lequel agissent les matrices de SU(2) ? Là, c’est moins évident, il va falloir s’accrocher… L’espace Hspin est un espace spinoriel. La théorie des spineurs a été introduite par le mathématicien français Elie Cartan au début du XXème siècle. Les spineurs ont des propriétés assez déroutantes. (Nous aborderons les rudiments de la théorie des spineurs dans un post séparé.) Un spineur peut être associé à un « plan orienté ». On peut définir un plan orienté à partir de deux vecteurs unitaires orthogonaux : 

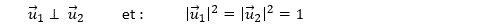
et du produit vectoriel de ces deux vecteurs. (L’ordre dans lequel on prend ces deux vecteurs est donc déterminant.) Il est facile de voir que cette définition est tout à fait adaptée au contexte du moment cinétique. La propriété la plus emblématique d’un spineur est qu’une rotation de 360 degrés le transforme en son inverse ! Il faut donc une rotation de 720 degrés pour revenir au spineur d’origine. 

Matrices de Pauli

Revenons au groupe SU(2). L’une des propriétés de SU(2) est la possibilité de générer les matrices de ce groupe à partir de 3 matrices élémentaires. Prenons par exemple le cas de l’opérateur Ay(theta). Un simple développement limité suffit à se convaincre qu’on peut l’écrire sous la forme suivante :

En fait, on peut montrer que toute matrice de SU(2) peut être générée à partir de matrices unitaires sigma :

avec :

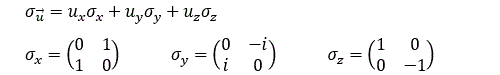
Les matrices sigmax, sigmay et sigmaz sont appelées matrices de Pauli, du nom du physicien Wolfgang Pauli qui est le premier à avoir établi une théorie complète du spin dans un cadre non-relativiste. Or, il est facile de voir que les vecteurs propres de ces matrices sigma sont précisément les vecteurs |+x>, |-x>, |+y>, |-y> et |+z> et |-z> correspondant aux opérateurs de mesure de spin dans les directions Ox, Oy et Oz ! 

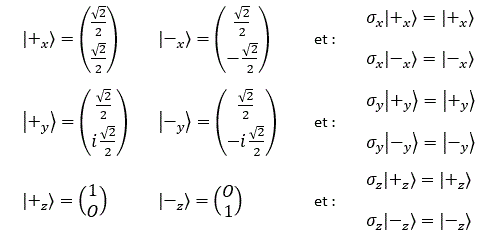
Les matrices de Pauli constituent donc une base qui permet de construire simplement une observable « spin » dans n’importe quelle direction de l’espace. 

Matrices de Pauli et symétrie de rotation

Dans la présentation qui précède, les matrices de Pauli semblent « sortir du chapeau ». Une présentation plus rigoureuse aurait permis de faire la liaison entre ces matrices et l’application d’un principe très général en physique, établi par la mathématicienne Emmy Noether au début du XXème siècle. Emmy Noether a en effet montré qu’à toute symétrie était associée la conservation d’une grandeur physique (théorème de Noether). C’est ainsi qu’à la symétrie de translation (les lois de la physique sont conservées dans toute translation du référentiel dans l’espace) est associée la conservation de la quantité de mouvement. De la même façon, à la symétrie de rotation dans l’espace (les lois de la physique sont conservées dans toute rotation du référentiel dans l’espace) est associée la conservation du moment cinétique. Or, comme nous l’avons dit plus haut, une rotation dans l’espace peut être représentée par une matrice du groupe SU(2) (que l’on appelle aussi d’ailleurs groupe de symétrie). Rien d’étonnant donc à ce que les opérateurs de mesure du spin puissent être directement déduits des matrices de Pauli puisque celle-ci forment une base à partir de laquelle on peut générer les matrices de ce groupe.

Remarque : Les matrices de Pauli ne commutent pas.  

Ceci signifie qu’il n’est pas possible de connaître simultanément la valeur de spin dans deux directions différentes. 

Pour en savoir plus :

post sur l'équation de Schrödinger 

post sur le formalisme quantique

post sur l’oscillateur harmonique quantique

post sur les espaces vectoriels et les groupes de Lie

post sur les algèbres de Lie

post sur les spineurs

post sur le théorème de Noether

post sur l’équation de Dirac

index

[lthmath]

Celebrating Cartan's birthday!!

Elie Cartan (1869-1951), French mathematician. Cartan was educated at Paris, and taught at many of the great universities of France. Cartan's most far-reaching work was the development of analysis of differentiable manifolds. This is a branch of topology which occupies a central place in mathematics and which has implications in fields such as analytical dynamics and general relativity. He reached these conclusions through his earlier study of Lie (continuous) groups. Cartan was largely overlooked for most of his life; only in his later years was he recognised as one of the most original and powerful mathematicians of the 20th Century.

[lookintomyeyeblog]

Bí ẩn cỗ máy ‘Quả chuông’ phản trọng lực của Đức quốc xã

Die Glocke (Quả chuông) là một siêu vũ khí bí mật thuộc dự án Wunderwaffe của Đức Quốc xã nhằm tạo ra một loại vũ khí với sức mạnh có thể thay đổi cục diện Thế chiến II.

Vũ khí đi trước thời đại

Thiết bị này được mô tả bởi nhà báo người Ba Lan - nhà văn Igor Witkowski trong cuốn sách có tên ‘Prawda o Wunderwaffe’ được xuất bản năm 2000 sau đó được phổ biến bởi nhà báo quân sự - nhà văn Nick Cook, cũng như của Joseph P. Farrell và các tác giả liên kết nó với chủ nghĩa huyền bí của Đức Quốc xã và nghiên cứu về năng lượng tự do.

[caption id="attachment_657940" align="alignnone" width="527"] Mô phỏng thiết bị Die Glocke của Đức quốc xã (Ảnh: Look4ward)[/caption]

Witkowski đã tìm hiểu chi tiết về Die Glocke sau khi có được thông tin về cuộc thẩm vấn sĩ quan cận vệ Jakob Sporrenberg từ cơ quan tình báo Ba Lan.

Sĩ quan này mô tả chi tiết về một thí nghiệm được thực hiện trong một căn cứ bí mật có tên là Der Riese, nằm trong dãy núi Owl, gần mỏ Wenceslaus ở Sudetes (gần biên giới Séc).

Theo bài báo của Patrick Kiger đăng trên Tạp chí Địa lý Quốc gia, Die Glocke đã trở thành một chủ đề gây tranh cãi và có rất nhiều người quan tâm. Thiết bị bí ẩn này cũng đã được nhiều tác giả mô tả như một chiếc máy có thể du hành thời gian của Đức quốc xã.

[caption id="attachment_657963" align="alignnone" width="488"] Nhà văn Igor Witkowski (Ảnh: Wikipedia)[/caption]

‘Quả chuông’ được nói đến như là một thứ vũ khí kỳ diệu, huyền bí, dựa trên công nghệ vượt xa mọi thứ mà nhân loại có thể sản xuất.

Tuy nhiên, khả năng có một thiết bị bí mật với công nghệ vượt trội tại thời điểm đó là rất hiếm, rất có thể nhiều người đã viết về đề tài này dựa trên trí tưởng tượng phong phú của mình.

Một số người trong số họ như Jan Van Helsing, Norbert-Jürgen Ratthofer và Vladimir Terziski cảm thấy không có vấn đề gì khi pha trộn giữa thực tế và hư cấu trong một hỗn hợp gồm những đề tài như vũ khí huyền bí, chủ nghĩa bí truyền của Đức Quốc xã, các xã hội bí mật và vật thể bay không xác định UFO để rồi một hiện tượng bắt đầu lan rộng nhanh chóng trong những năm 50.

'Quả chuông' là thiết bị như thế nào?

'Quả chuông' được các nhà khoa học Đức quốc xã phát triển dưới sự kiểm soát của lực lượng SS tại một cơ sở có tên là Der Riese gần mỏ Wenceslaus gần biên giới Séc.

'Quả chuông' được mô tả như là một thiết bị "làm bằng kim loại cứng và nặng", có đường kính khoảng 2,7 m và chiều cao từ 3,7 m đến 4,6 m, có hình dạng tương tự một quả chuông lớn.

[caption id="attachment_657972" align="alignnone" width="577"] 'Quả chuông' nhìn từ các góc độ khác nhau (Ảnh: Jeff Rense)[/caption]

Theo cuộc phỏng vấn của Cook với Witkowski, thiết bị này có hai xi lanh quay ngược, có thể "chứa đầy một chất tương tự như thủy ngân có màu tím".

Chất lỏng kim loại này có tên mã là "Xerum 525" và được "lưu trữ trong một bình thủy cách nhiệt cao 1m được bọc trong một lớp chì."

Người ta nói rằng các thí nghiệm đã sử dụng các chất bổ sung dưới dạng Leichtmetall (kim loại nhẹ), "bao gồm cả thori và berili peroxit".

Witkowski mô tả rằng khi 'Quả chuông' được kích hoạt, tầm ảnh hưởng của nó là từ 150 m đến 200 m.

Nhà báo Ba Lan giải thích rằng mục tiêu của Die Glocke là tạo ra lực đẩy phản kháng - đó là lý do tại sao nó được thắt chặt với mặt đất bằng các dây xích lớn.

[caption id="attachment_657975" align="aligncenter" width="316"] 'Quả chuông' khi hoạt động được cột lại bởi các sợi dây xích lớn (Ảnh: perpendicularity.org)[/caption]

Witkowski giải thích rằng khi thiết bị được kích hoạt, nó có thể gây ra những hậu quả chết người đối với những sinh vật sống trong bán kính 150 đến 200 mét: đông máu trong hệ thống tuần hoàn, sự phân hủy các mô hữu cơ...

Hơn nữa, năm trong số bảy thành viên của nhóm nghiên cứu - do nhà vật lí Walther Gerlach – đã chết không rõ nguyên nhân sau các cuộc thử nghiệm.

Witkowski nói trong cuốn sách của mình rằng một nhà khoa học người Pháp tên là Elie Cartan đã có những bước đi quan trọng trong lĩnh vực chống lại lực hấp dẫn sau Thế chiến thứ nhất, mặc dù sự phản trọng lực được tạo ra bởi thiết bị của ông quá yếu để có một ứng dụng thực tiễn. Die Glocke có thể đã được dựa trên công nghệ của Cartan.

[caption id="attachment_657932" align="alignnone" width="500"] The Henge - Một trong những kết cấu bí ẩn nhất còn sót lại sau thế chiến II được cho là nơi thử nghiệm 'Quả Chuông' (Ảnh: imensidao-oculta.blogspot.com)[/caption]

Dựa trên bằng chứng bên ngoài, Witkowski tuyên bố rằng những tàn tích của một cấu trúc bê tông có biệt danh là "The Henge" - gần vùng mỏ Wenceslas có thể đã phục vụ trong các thí nghiệm về "phản trọng lực" được tạo ra với 'Quả chuông'.

Dù 'Quả chuông' có thực sự tồn tại hay không vẫn là một trong những bí mật lớn nhất của Đức quốc xã và ít nhất nó đã không kịp hoàn thiện để xuất hiện trên chiến trường, nếu không, phe Đồng Minh có thể đã phải hứng chịu những tổn thất nặng nề và lịch sử thế giới có thể đã đi theo một hướng khác tồi tệ hơn nhiều những gì chúng ta thấy.

Nhật Quang

from Đại Kỷ Nguyên - Feed - http://bit.ly/2QlrcaI via IFTTT

[beatyroseflower]

Bí ẩn cỗ máy ‘Quả chuông’ phản trọng lực của Đức quốc xã

Die Glocke (Quả chuông) là một siêu vũ khí bí mật thuộc dự án Wunderwaffe của Đức Quốc xã nhằm tạo ra một loại vũ khí với sức mạnh có thể thay đổi cục diện Thế chiến II.

Vũ khí đi trước thời đại

Thiết bị này được mô tả bởi nhà báo người Ba Lan - nhà văn Igor Witkowski trong cuốn sách có tên ‘Prawda o Wunderwaffe’ được xuất bản năm 2000 sau đó được phổ biến bởi nhà báo quân sự - nhà văn Nick Cook, cũng như của Joseph P. Farrell và các tác giả liên kết nó với chủ nghĩa huyền bí của Đức Quốc xã và nghiên cứu về năng lượng tự do.

[caption id=“attachment_657940” align=“alignnone” width=“527”] Mô phỏng thiết bị Die Glocke của Đức quốc xã (Ảnh: Look4ward)[/caption]

Witkowski đã tìm hiểu chi tiết về Die Glocke sau khi có được thông tin về cuộc thẩm vấn sĩ quan cận vệ Jakob Sporrenberg từ cơ quan tình báo Ba Lan.

Sĩ quan này mô tả chi tiết về một thí nghiệm được thực hiện trong một căn cứ bí mật có tên là Der Riese, nằm trong dãy núi Owl, gần mỏ Wenceslaus ở Sudetes (gần biên giới Séc).

Theo bài báo của Patrick Kiger đăng trên Tạp chí Địa lý Quốc gia, Die Glocke đã trở thành một chủ đề gây tranh cãi và có rất nhiều người quan tâm. Thiết bị bí ẩn này cũng đã được nhiều tác giả mô tả như một chiếc máy có thể du hành thời gian của Đức quốc xã.

[caption id=“attachment_657963” align=“alignnone” width=“488”] Nhà văn Igor Witkowski (Ảnh: Wikipedia)[/caption]

‘Quả chuông’ được nói đến như là một thứ vũ khí kỳ diệu, huyền bí, dựa trên công nghệ vượt xa mọi thứ mà nhân loại có thể sản xuất.

Tuy nhiên, khả năng có một thiết bị bí mật với công nghệ vượt trội tại thời điểm đó là rất hiếm, rất có thể nhiều người đã viết về đề tài này dựa trên trí tưởng tượng phong phú của mình.

Một số người trong số họ như Jan Van Helsing, Norbert-Jürgen Ratthofer và Vladimir Terziski cảm thấy không có vấn đề gì khi pha trộn giữa thực tế và hư cấu trong một hỗn hợp gồm những đề tài như vũ khí huyền bí, chủ nghĩa bí truyền của Đức Quốc xã, các xã hội bí mật và vật thể bay không xác định UFO để rồi một hiện tượng bắt đầu lan rộng nhanh chóng trong những năm 50.

‘Quả chuông’ là thiết bị như thế nào?

'Quả chuông’ được các nhà khoa học Đức quốc xã phát triển dưới sự kiểm soát của lực lượng SS tại một cơ sở có tên là Der Riese gần mỏ Wenceslaus gần biên giới Séc.

'Quả chuông’ được mô tả như là một thiết bị “làm bằng kim loại cứng và nặng”, có đường kính khoảng 2,7 m và chiều cao từ 3,7 m đến 4,6 m, có hình dạng tương tự một quả chuông lớn.

[caption id=“attachment_657972” align=“alignnone” width=“577”] 'Quả chuông’ nhìn từ các góc độ khác nhau (Ảnh: Jeff Rense)[/caption]

Theo cuộc phỏng vấn của Cook với Witkowski, thiết bị này có hai xi lanh quay ngược, có thể “chứa đầy một chất tương tự như thủy ngân có màu tím”.

Chất lỏng kim loại này có tên mã là “Xerum 525” và được “lưu trữ trong một bình thủy cách nhiệt cao 1m được bọc trong một lớp chì.”

Người ta nói rằng các thí nghiệm đã sử dụng các chất bổ sung dưới dạng Leichtmetall (kim loại nhẹ), “bao gồm cả thori và berili peroxit”.

Witkowski mô tả rằng khi 'Quả chuông’ được kích hoạt, tầm ảnh hưởng của nó là từ 150 m đến 200 m.

Nhà báo Ba Lan giải thích rằng mục tiêu của Die Glocke là tạo ra lực đẩy phản kháng - đó là lý do tại sao nó được thắt chặt với mặt đất bằng các dây xích lớn.

[caption id=“attachment_657975” align=“aligncenter” width=“316”] 'Quả chuông’ khi hoạt động được cột lại bởi các sợi dây xích lớn (Ảnh: perpendicularity.org)[/caption]

Witkowski giải thích rằng khi thiết bị được kích hoạt, nó có thể gây ra những hậu quả chết người đối với những sinh vật sống trong bán kính 150 đến 200 mét: đông máu trong hệ thống tuần hoàn, sự phân hủy các mô hữu cơ…

Hơn nữa, năm trong số bảy thành viên của nhóm nghiên cứu - do nhà vật lí Walther Gerlach – đã chết không rõ nguyên nhân sau các cuộc thử nghiệm.

Witkowski nói trong cuốn sách của mình rằng một nhà khoa học người Pháp tên là Elie Cartan đã có những bước đi quan trọng trong lĩnh vực chống lại lực hấp dẫn sau Thế chiến thứ nhất, mặc dù sự phản trọng lực được tạo ra bởi thiết bị của ông quá yếu để có một ứng dụng thực tiễn. Die Glocke có thể đã được dựa trên công nghệ của Cartan.

[caption id=“attachment_657932” align=“alignnone” width=“500”] The Henge - Một trong những kết cấu bí ẩn nhất còn sót lại sau thế chiến II được cho là nơi thử nghiệm 'Quả Chuông’ (Ảnh: imensidao-oculta.blogspot.com)[/caption]

Dựa trên bằng chứng bên ngoài, Witkowski tuyên bố rằng những tàn tích của một cấu trúc bê tông có biệt danh là “The Henge” - gần vùng mỏ Wenceslas có thể đã phục vụ trong các thí nghiệm về “phản trọng lực” được tạo ra với 'Quả chuông’.

Dù 'Quả chuông’ có thực sự tồn tại hay không vẫn là một trong những bí mật lớn nhất của Đức quốc xã và ít nhất nó đã không kịp hoàn thiện để xuất hiện trên chiến trường, nếu không, phe Đồng Minh có thể đã phải hứng chịu những tổn thất nặng nề và lịch sử thế giới có thể đã đi theo một hướng khác tồi tệ hơn nhiều những gì chúng ta thấy.

Nhật Quang

from Đại Kỷ Nguyên - Feed - http://bit.ly/2QlrcaI via http://bit.ly/2QlrcaI https://www.dkn.tv from Đại Kỷ Nguyên http://bit.ly/2VuCIo4 via IFTTT

[daikynguyen]

Bí ẩn cỗ máy ‘Quả chuông’ phản trọng lực của Đức quốc xã

Die Glocke (Quả chuông) là một siêu vũ khí bí mật thuộc dự án Wunderwaffe của Đức Quốc xã nhằm tạo ra một loại vũ khí với sức mạnh có thể thay đổi cục diện Thế chiến II.

Vũ khí đi trước thời đại

Thiết bị này được mô tả bởi nhà báo người Ba Lan - nhà văn Igor Witkowski trong cuốn sách có tên ‘Prawda o Wunderwaffe’ được xuất bản năm 2000 sau đó được phổ biến bởi nhà báo quân sự - nhà văn Nick Cook, cũng như của Joseph P. Farrell và các tác giả liên kết nó với chủ nghĩa huyền bí của Đức Quốc xã và nghiên cứu về năng lượng tự do.

[caption id="attachment_657940" align="alignnone" width="527"] Mô phỏng thiết bị Die Glocke của Đức quốc xã (Ảnh: Look4ward)[/caption]

Witkowski đã tìm hiểu chi tiết về Die Glocke sau khi có được thông tin về cuộc thẩm vấn sĩ quan cận vệ Jakob Sporrenberg từ cơ quan tình báo Ba Lan.

Sĩ quan này mô tả chi tiết về một thí nghiệm được thực hiện trong một căn cứ bí mật có tên là Der Riese, nằm trong dãy núi Owl, gần mỏ Wenceslaus ở Sudetes (gần biên giới Séc).

Theo bài báo của Patrick Kiger đăng trên Tạp chí Địa lý Quốc gia, Die Glocke đã trở thành một chủ đề gây tranh cãi và có rất nhiều người quan tâm. Thiết bị bí ẩn này cũng đã được nhiều tác giả mô tả như một chiếc máy có thể du hành thời gian của Đức quốc xã.

[caption id="attachment_657963" align="alignnone" width="488"] Nhà văn Igor Witkowski (Ảnh: Wikipedia)[/caption]

‘Quả chuông’ được nói đến như là một thứ vũ khí kỳ diệu, huyền bí, dựa trên công nghệ vượt xa mọi thứ mà nhân loại có thể sản xuất.

Tuy nhiên, khả năng có một thiết bị bí mật với công nghệ vượt trội tại thời điểm đó là rất hiếm, rất có thể nhiều người đã viết về đề tài này dựa trên trí tưởng tượng phong phú của mình.

Một số người trong số họ như Jan Van Helsing, Norbert-Jürgen Ratthofer và Vladimir Terziski cảm thấy không có vấn đề gì khi pha trộn giữa thực tế và hư cấu trong một hỗn hợp gồm những đề tài như vũ khí huyền bí, chủ nghĩa bí truyền của Đức Quốc xã, các xã hội bí mật và vật thể bay không xác định UFO để rồi một hiện tượng bắt đầu lan rộng nhanh chóng trong những năm 50.

'Quả chuông' là thiết bị như thế nào?

'Quả chuông' được các nhà khoa học Đức quốc xã phát triển dưới sự kiểm soát của lực lượng SS tại một cơ sở có tên là Der Riese gần mỏ Wenceslaus gần biên giới Séc.

'Quả chuông' được mô tả như là một thiết bị "làm bằng kim loại cứng và nặng", có đường kính khoảng 2,7 m và chiều cao từ 3,7 m đến 4,6 m, có hình dạng tương tự một quả chuông lớn.

[caption id="attachment_657972" align="alignnone" width="577"] 'Quả chuông' nhìn từ các góc độ khác nhau (Ảnh: Jeff Rense)[/caption]

Theo cuộc phỏng vấn của Cook với Witkowski, thiết bị này có hai xi lanh quay ngược, có thể "chứa đầy một chất tương tự như thủy ngân có màu tím".

Chất lỏng kim loại này có tên mã là "Xerum 525" và được "lưu trữ trong một bình thủy cách nhiệt cao 1m được bọc trong một lớp chì."

Người ta nói rằng các thí nghiệm đã sử dụng các chất bổ sung dưới dạng Leichtmetall (kim loại nhẹ), "bao gồm cả thori và berili peroxit".

Witkowski mô tả rằng khi 'Quả chuông' được kích hoạt, tầm ảnh hưởng của nó là từ 150 m đến 200 m.

Nhà báo Ba Lan giải thích rằng mục tiêu của Die Glocke là tạo ra lực đẩy phản kháng - đó là lý do tại sao nó được thắt chặt với mặt đất bằng các dây xích lớn.

[caption id="attachment_657975" align="aligncenter" width="316"] 'Quả chuông' khi hoạt động được cột lại bởi các sợi dây xích lớn (Ảnh: perpendicularity.org)[/caption]

Witkowski giải thích rằng khi thiết bị được kích hoạt, nó có thể gây ra những hậu quả chết người đối với những sinh vật sống trong bán kính 150 đến 200 mét: đông máu trong hệ thống tuần hoàn, sự phân hủy các mô hữu cơ...

Hơn nữa, năm trong số bảy thành viên của nhóm nghiên cứu - do nhà vật lí Walther Gerlach – đã chết không rõ nguyên nhân sau các cuộc thử nghiệm.

Witkowski nói trong cuốn sách của mình rằng một nhà khoa học người Pháp tên là Elie Cartan đã có những bước đi quan trọng trong lĩnh vực chống lại lực hấp dẫn sau Thế chiến thứ nhất, mặc dù sự phản trọng lực được tạo ra bởi thiết bị của ông quá yếu để có một ứng dụng thực tiễn. Die Glocke có thể đã được dựa trên công nghệ của Cartan.

[caption id="attachment_657932" align="alignnone" width="500"] The Henge - Một trong những kết cấu bí ẩn nhất còn sót lại sau thế chiến II được cho là nơi thử nghiệm 'Quả Chuông' (Ảnh: imensidao-oculta.blogspot.com)[/caption]

Dựa trên bằng chứng bên ngoài, Witkowski tuyên bố rằng những tàn tích của một cấu trúc bê tông có biệt danh là "The Henge" - gần vùng mỏ Wenceslas có thể đã phục vụ trong các thí nghiệm về "phản trọng lực" được tạo ra với 'Quả chuông'.

Dù 'Quả chuông' có thực sự tồn tại hay không vẫn là một trong những bí mật lớn nhất của Đức quốc xã và ít nhất nó đã không kịp hoàn thiện để xuất hiện trên chiến trường, nếu không, phe Đồng Minh có thể đã phải hứng chịu những tổn thất nặng nề và lịch sử thế giới có thể đã đi theo một hướng khác tồi tệ hơn nhiều những gì chúng ta thấy.

Nhật Quang

from Đại Kỷ Nguyên - Feed - http://bit.ly/2QlrcaI via http://bit.ly/2QlrcaI https://www.dkn.tv

[isomorphismes]

The Lie algebra E₆ may be defined as the algebra of endomorphisms of a 27-dimensional complex vector space MC which annihilate a particular cubic polynomial. This raises a natural question: what is this polynomial? If we choose a basis for MC consisting of weight vectors {Xw } (for some Cartan subalgebra of E₆ ), then any invariant cubic polynomial must be a linear combination of monomials where ∑w + w′ + w″ = 0. The problem is then to determine the coefficients of these monomials. Of course, the problem is not yet well-posed, since we still have a great deal of freedom to scale the basis vectors Xw . If we work over the integers instead of the complex numbers, then much of this freedom disappears. The Z-module M then decomposes as a direct sum of 27 weight spaces which are free Z-modules of rank 1. The generators of these weight spaces are well-defined up to a sign. Using a basis for M consisting of such generators, a little bit of thought shows that the invariant cubic polynomial may be written as a sum where ∑w,w′,w″ = ±1. The problem is now reduced to the determination of the signs w,w′,w″. However, this problem is again ill-posed, since the Xw are only well-defined up to a sign.

Jacob Lurie

[arxt1]

Pseudo-Conformal Field Theory. (arXiv:1704.00321v2 [hep-th] UPDATED)

The lorentzian CR-structure (LCR-structure) is a special 4-dimensional totally real CR-structure, which contains two correlated 3-dimensional CR-structures. It is defined by explicit Cartan relations and characterized by the "left" and "right" CP3 points with two spinors and two Newman complex trajectories. Using a gauge field action, which depends on this LCR-structure and not the metric, a 4-dimensional pseudo-conformal field theory (PCFT) is formulated. It is invariant under the two Cartan infinite dimensional Lie algebras of the contained 3-dimensional CR-structures, in complete analogy to the 2-dimensional CFT. These algebras do not assume central charges. "Open" and "closed" LCR-manifolds are defined in analogy to the 2-dimensional string theory. The states and transition amplitudes of the PCFT model are defined using the path-integral formalism as functional integrations over the LCR-structures, where a summation over the structure relative invariants has to be considered in addition to the ordinary summation over the topological invariants of the LCR-manifolds. The gauge field propagator in the sector of the "open" degenerate LCR-structure is computed and found to be confining. Using the Elie Cartan list of automorphisms of the 3-dimensinal CR-structures, the automorphisms of the LCR-structures are investigated. The Poincar\'e group is an automorphism of the degenerate LCR-structure which is considered as the vacuum. The "left" and "right" spinors of the vacuum LCR-structure transform under the corresponding non-equivalent conjugate representations of the Lorentz group. The electron-positron with electromagnetic and gravitational radiations is identified as the Kerr-Newman LCR-manifold and the general phenomenological framework is outlined.

from gr-qc updates on arXiv.org http://ift.tt/2oCYfue