#quaternion

[poppiesandpromises]

[blake447]

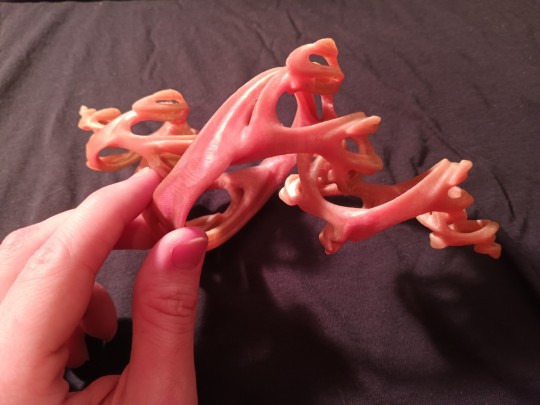
I realized I hadn't shared this here yet! Here's my 3D printed Quaternion Julia Set! See I first learned of these things reading about it from a pretty well known graphics programmer Inigo Quilez. Theirs are a lot prettier! But yeah, if you're familiar with Julia Sets and the Mandelbrot set already, this is basically that but we use 4D complex numbers called quaternions instead of the regular old complex numbers.

The original shaders I used to render them were unity CG/HLSL implementations, but this particular one is from a GLSL implementation over on my shadertoy you can find here: https://www.shadertoy.com/view/tdt3W8 It isn't exactly the same one that I've printed here (I've long lost the exact seed) but it is reasonably close. The way I printed it was I stole some marching cube code for blender and just plugged in the SDF function derived by Inigo Quilez, tweaked the values and eventually got a mesh I can print!

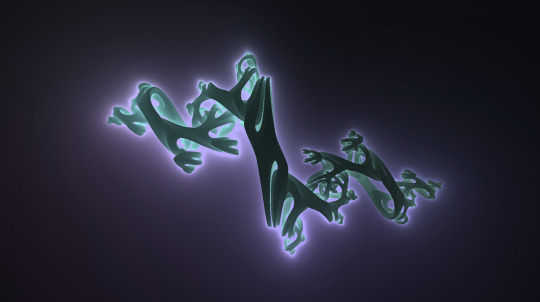
This uh, isn't the one I used lol. It did take a few tries to get one that was both visually interesting and also printable. In fact i wasn't even using the marching cube algorithm at first. I was using Poisson Surface Reconstruction with a python script that casted points to form a point cloud. Basically I was attempting to create a mesh like you would with photogrammetry, just with an abstract object rather than an actual thing or place.

The results were, well not good lol.

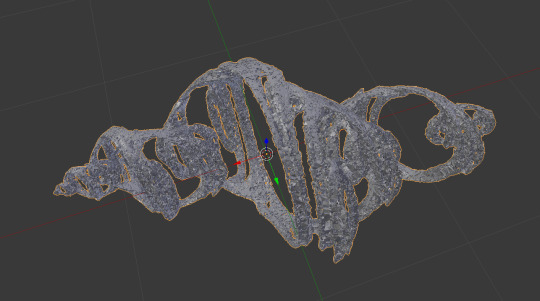
*Continues digging through box* I know its around here some where, I should have the one that works. Okay this still isnt it but this one is using the same method, I just wanted to use this for a vrchat world instead of using it for 3D printing. It gets the point across lol

But yeah. 3D printing is really cool if you're into a bit of math

[fastfouriertransfem]

Hi

actual announcement

new tag system !

#real - posts that are the limit of an infinite sequence of rationals

#imaginary - posts that square to a nonpositive real

#complex - posts representable by the sum of a real and an imaginary

#rational - posts representable by the division of an integer by a nonzero integer

#integer - posts that are an equivalence class of ordered pairs of naturals with the equivalence relation being the difference of the two but that's circular so do a thing with addition and stuff to define the relation without using negative numbers or anything yeahg

#natural - something something axiomatic (0 is natural btw)

#quaternion - something something rotation

#octonion - something that is not commutative or associative

#sedenion -

#transfinite - finite but trans (better way of saying infinite)

#art - art is a number post now (just take the binary of the image or whatever) (this reminds me of https://en.wikipedia.org/wiki/Illegal_number)

ok real tag system:

#real - posts that are so true so real (copyright held by Rosemi Lovelock, clipped by RandomVtubers_foreveryone on Aug 18, 2022)

#imaginary - random stuff

#complex - idk

#rational - stuff i wanna look at / be reminded of later

#integer - stuff related to computers and stuff ig

#natural - will come up with this later

#quaternion - will come up with this later

#octonion - ninomae ina'nis or something

#sedenion - idk

#transfinite - /trans(?!gender)/

#art - art (includes visual, auditory, written, combination, etc) (i will retroactively tag this later (i already tagged some) (when i do, i will move these parentheticals to the changelog post))

changelog: https://www.tumblr.com/fastfouriertransfem/734227254388883456/hi-changelog

[mathhombre]

Quaternion Games

Was reading Jim Propp's excellent expository piece on quaternions and it had links to three math games I wanted to remember.

Block'n'Roll (connection is with rotations)

Groupdoku

Hamilternion card game - practice with multiplication, I'd like to develop this one.

[dateaweirdboysuggest]

Date a boy who is compact, doesn't suffer from gimbal lock, and can easily be interpolated.

[takinbreak]

I love the fact that it’s commonly believed the writer (and mathematician!) Lewis Carroll could have done a math diss on quaternions, their unintuitive multiplication and their non-commutative nature in the Mad Hatter scene in “Alice in Wonderland”.

“Why, you might just as well say that I see what I eat is the same thing as I eat what I see !”

All credits to 3Blue1Brown on Youtube (Video: “Visualising quaternions (4d numbers) with stereographic projection”)

[livelifelater]

Things normally happen once but the 4th feeling makes them annoyingly reverberating. Used some of q’s and fractal techniques I use a lot on my page @gnarly_gens for photo edition this time #lofi #lofiphotography #darkphotography #quaternion #digitalart #digitalphotography #glitchart #glitch #pixelart #abstract #abstractart #delusion #outsiderart #noisephotography #psychedelicart #darkart #badqualitypic #badphotoshop #ghostly #creepy #creepyart #ａｅｓｔｈｅｔｉｃ https://www.instagram.com/p/Co7wRWxuuRk/?igshid=NGJjMDIxMWI=

[highlyentropicmind]

This is a reference to the discovery of the quaternions, which allow us to rotate things in 3 dimensions

You see, we have algorithms that can rotate vectors in 2D, they are really simple and a child could discover them by themselves if they tried hard enough

But rotating vectors in 3D is a different beast entirely. People tried to find this algorithm for centuries and they couldn't. Not even Euler, blessed by Athena, Saraswati and all the goddesses of wisdom could figure it out

Then a guy called William Hamilton tried to solve it. He studied what everyone else had done and tried to see what they had missed, but he couldn't, months went by, this was consuming his whole life. He stopped talking to his wife and kids and thinking all day about this

Finally his wife Helen was like "Babe, chill, let's go on a mental health walk". He agreed and as they walked he could feel his mind clearing out, letting go of the problem, and then as they passed over a wooden bridge the solution finally came to him. He had figured it out, but he didn't have pen or paper nor anything he could use

Desperate to not forget the solution he took a pocket knife (which he apparently always carried with him) and he carved the solution on the bridge itself. This is what he wrote:

i^2=j^2=k^2=-1

And I know what you are thinking. How does this help us rotate objects in 3D?

Well, this is what Hamilton discovered:

When you rotate a object in 2D the axis of rotation comes out of the page, it is in 3 dimensions, not two. Similarly to rotate an object in 3 dimensions we need an axis of rotation in 4 dimensions

But then, you can't just have four number and call it a day, you need these dimensions to have the correct relationship between them, and that's what that formula is explaining. Three numbers, i, j and k, all of which become -1 when they are squared. Three different kinds of imaginary numbers

From this one formula you can deduce all the relationship between these dimensions and then you can finally rotate objects in 3D

In fact every time you play a 3D video game your computer is rotating objects using quaternions. This is what the graphics card does all day

Also this has important connections to physics. When Einstein discovered Relativity he saw that he needed a "metric", a mathematical object that tells you how distances are measured in different spaces, and he found that the metric of spacetime was simply (-1,1,1,1). In other words, the quaternions

In a very real sense, the reason E=mc^2 is a consequence of the quaternions, a consequence of the fact that you need at least 4 numbers to define a rotation in 3D

Moral of the story: ALWAYS carry around a pocket knife

"what do I do if I have theories" will always be the fucking funniest reddit post

[noelements-setempty]

What if we had three square roots of -1? Haha, ijk.

[wolframcarbide]

[endofunktor]

All numbers are imaginary. Some are useful.

So, @lipshits-continuous (I like your blog very much!) was bringing to my attention someone who was, let's say, a little frustrated about having to learn "imaginary numbers". You know. They're not even real.

I don't want to write about that person specifically, I don't know them at all.

But.

My siblings in crisis.

There are no "real" numbers in this world. The act of counting is already an abstraction. If you have an apple and a pear, then counting them as two pieces of fruit is an act of forgetting all the properties that distinguish them and remembering only those that unite them. Same goes for two apples of course.

So the number 2 is already entirely imaginary. Made up. Nonsense.

This gets worse very quickly, by the way. You can't have negative apples! Sure, you can have positive fractions of apples, but I can assure you: Two halves of an apple do rarely make one apple, except when they are the two halves of the same apple. And even then: Having them cut up makes it impossible to rejoin them. Think about that.

Now you know where this is going, because let's talk about the so-called ""real"" numbers. Nasty little things. Have a look at the irrational numbers. First, there are comparatively tame irrationals: Algebraic numbers. These arise as roots of integer polynomials. You know, like our favorite, the square root of 2, the positive zero of X^2 - 2.

Did you know that the Pythagoreans believed that everything was in integer relation to each other. (For example: the lengths of a rectangular triangle could be 3-4-5, meanging one cathetus is 4/5, the other 3/5 the length of the hypotenuse.) And that when someone found out that sqrt(2) was indeed not in integer relation to, say, 1, they had him murdered? That didn't change the fact that they were wrong though. (This story is not true, of course, like all good stories. You could say: it is imaginary, but nonetheless an interesting tale to tell!)

And now, the non-algebraic, so called transcendent numbers. Like pi. We know (the abstract concept of) pi well enough to calculate the circumference of the observable universe up to the accuracy of a neutrino (or so they say, I'm not a physicist). We don't have to know it any better. We could quit at however many digits we know and that would be pi. Perfectly rational. Because if we are looking for """real""" numbers only, why should we ever even concern ourself with those nasty things?

Did you know that transcendent numbers make the vast majority of real line? Of course you do! Rationals are countable, integer polynomials are countable and thus are their roots. The real line is famously uncountable, so must be the transcendent numbers.

So. Our so called """"real"""" numbers are mostly non-precisely calculable numbers. (Arbitrarily precise, but not precise.)

Do you know what kind of numbers are used in electrical engineering? Me neither because I'm not an electrical engineer. That's right, complex numbers! Actual engineers have to actually work with the actually imaginary square roots of negative one.

Maybe Numbers aren't a thing of this world.

Maybe Abstraction is a thing of our worldview.

And maybe we can learn to cherish abstract math the way we learn to cherish abstract art: Not always a true representation of reality, but a thing of interest and beauty in itself.

[stanwixbuster]

fuck with me

[shwoo]

I figured out what calculations to do to transfer animations from the Bugsnax player rig to an NPC rig, and put a few onto the Filbo model I modified into the Journalist, but I'm not sure what to do with it now. I've got their idle animation, their walking animation, their crouching animation, their crouching and walking animation, some jumping stuff, and their on fire animation, but maybe there's some others I can add? A lot of the tool using animations clip through their body, so they don't look as good from a third person perspective.

Their face almost never moves because the player doesn't have a face to animate, which is also a problem. I guess I could... learn to actually animate. Or steal another character's face animation, like I did with the default expression. This model can do expressions, but that's because expression animations are the same for every character, so I just used the ones from Filbo's animation file.

I think their shoulders are a bit janky still too. I should see if I can fix that. And I'm not totally happy with some of the eye colours.

Heheheh, look at 'em go. They don't know they're trapped in Blender for the foreseeable future.

[jackiebranc]

"The Peculiar Math That Could Underlie the Laws of Nature", Natalie Wolchover, QUANTA MAGAZINE

[vermillioncrown]

long external meeting today w ppl that are ex-lab members (previous supe + a senpai)

i was doing derivations during downtime and my ex-supe joked upon seeing my Chaotic Papers (as denoted by current supe) "it's like a beautiful mind"

but then the topic got into computational fluid dynamics regarding someone's thesis and their use of quaternions and he immediately made a face and declared "that's definitely not a beautiful mind 😬"

[silverbridge-harbor]

favorite bridge and metal?

bridge: this part in this live version of this song where they take the normal bridge and replace it with the destruction of the universe and slowly reconstruct the void into a wall of sound:

metal: everything clutch has ever done:

hmmmmmm or im the mountain:

...or grim reefer by cloud:

ooouuugghhh i cannot decide on one

as recompense, have this actual answer: broom bridge, in ireland, where william hamilton figured out quaternions and did math graffiti:

i² = j² = k² = ijk = -1

and naquadah from stargate sg1 is pretty sicc