#mathblr
Explore tagged Tumblr posts
Text

oh no , the dog is drinking the wave equation
#what the dog doin#haha#hahaha#ha ha funny#relatable#relatable memes#dank memes#funny memes#litterally me#meme#shitpost#dog#doggo#dogs of tumblr#mathblr#mathematics#memes#animals#what da dog doin
58K notes
·
View notes
Text
thanks tumblr I too simp for mathematics

59 notes
·
View notes
Photo
This is the best horf I have ever seen. It's awful. I love it.
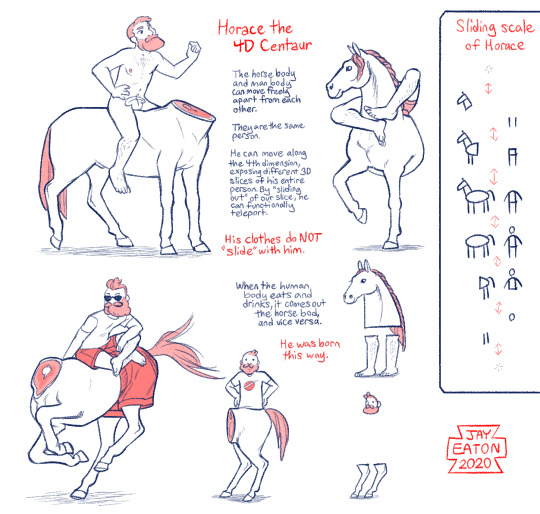
Ok so, I finally found a way to combine my obsessions with upsetting centaurs and 4-dimensional geometry, and his name is Horace. I will be taking questions now
PATREON | STORE
15K notes
·
View notes
Text
The maths fandom is wild. “Real” and “imaginary” numbers? I think you mean canon and non-canon. You guys seriously go “this is my number oc his name is i and he is the square root of -1” when in numbers canon lore it’s actually impossible to square root a negative but sure whatever. “Complex numbers”? I think you mean a character x oc ship. “f(x) = 3x - 5”? That is self-insert fanfiction.
#(spoiler for the maths finale) 7 eats 9#mathblr#math memes#shitpost#locus other time#this is a joke don’t get too worried about it. I just wanted an excuse to say imaginary numbers are OCs#i would go more in depth but alas. as I’m making this I’m 16 so I haven’t learned all the fun maths lore yet#math#to reiterate: I am aware this is an oversimplification and not how maths works and nothing in maths is canon!#I am not trying to say square rooting negative numbers is stupid or impossible or saying imaginary numbers are a lie or anything like that#I just wanted to have a bit of fun with using fandom terms for numbers (and play off the stereotype of people who police “canon”)#no hate to mathematicians or the field of maths. You guys are cool. Sorry if it came off that way
7K notes
·
View notes
Text
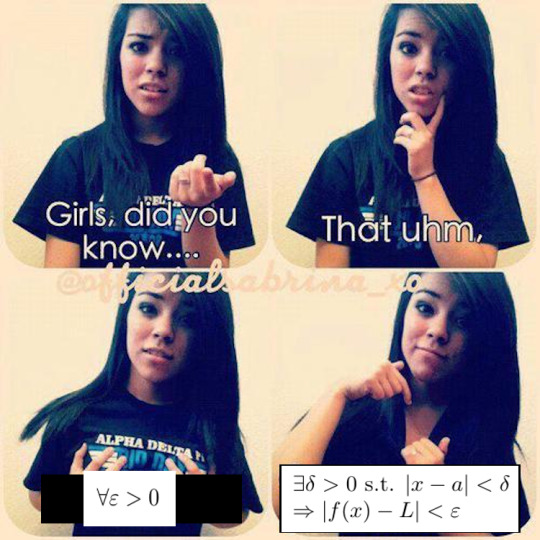
276 notes
·
View notes
Text
As a mathematician, this really pisses me off for two reasons
1. π is just about the sexiest thing there is, how dare approximately half the population choose anything else.
2. INFINITY IS NOT A NUMBER, IT IS A CONCEPT ok numbers are concepts to INFINITY IS A DIFFERENT CONCEPT THAN NUMBERS
Anyway I'm normal now

3K notes
·
View notes
Text

This full binary tree branches out over 8 levels 🌿✨, stitched with stem stitch and dotted with French knot leaves. Who knew recursion could look so cute? Template in my blog description if you want to stitch your own!
#Also PSA that I have a tiktok and youtube now#I'm posting timelapses of making the pieces (starting with this one)#If you want some more maths embroidery on your respective feeds#math#math art#mathblr#embroidery#craft#fibre arts#science craft#yarnblr#fiber craft#math embroidery#threadedtheorems
88 notes
·
View notes
Text
You all like bijective functions, but just wait until the trijective functions drop. Those are the real deal.
54 notes
·
View notes
Text
I do so love revolving door integrals. It gets even more fun and magical when you have something like \int e^x sin(3x) dx instead. (I'll let you cast that particular spell yourself; it's not that much harder.)
okay so we did this in class today Y'all wanna know the dumb ass solution to integrating e^x cos(x)?
first, you integrate by parts twice:
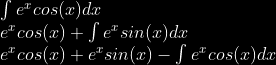
then, you set the entire integral equal to it like this:
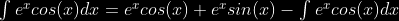
then, you move the entire fucking integral over to the left hand side of the equation:
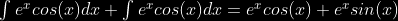
and then you can simplify to this:
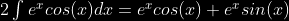
and then this:
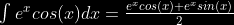
and boom you solved it.
the integral sign NEVER GOES AWAY and yet it's solved. what the hell man
851 notes
·
View notes
Text
The cool thing about doing math professionally is that you can work anywhere - on your walks, in the shower, as you fall asleep - just by rotating problems in your head. What's not so cool is that this drives you insane
2K notes
·
View notes
Text
A circle inscribed in a square covers 79% of the square.

A ball inscribed in a cube fills 52% of the cube.
A 4-ball inscribed in a hypercube fills 31% of the hypercube.
A 5-ball inscribed in a 5-cube fills 16% of the 5-cube.
⋮
A 9-ball inscribed in a 9-cube fills it up less than 1% of the way, yet there’s no room to fit a second ball of the same size without intersecting the first.
⋮
In dimensions 23 and up, you can fit a little cube in the corner of the diagram, such that the cube has a larger volume than the ball!

That's especially disconcerting because the 23-cube has 8,388,608 corners. Even if you inscribe the little red cubes in all eight million corners, your big cube will still be 99.5% empty space.
5K notes
·
View notes
Text
"not malicious" SEEMS PRETTY MALICIOUS TO ME!!
Look, I know this response isn’t malicious and simply an attempt at connection, but it’s still funny and incredibly frustrating that one of the most common responses a to “oh I’m doing/enjoy [math related thing]“ is “Oh man I HATE math” despite being an insanely wild response. Like, can you imagine this in a slightly different context?
“Hey, so what are your plans this weekend?”
“Oh, I’m just gonna hang out with my best friend”
“Neat, who is it?”
“David!”
“God, I HATE David, can’t STAND him!”
Like, in almost any other context this becomes hostile. What, you expecting me to shit on something I love with you??? Really?
I just genuinely don’t know what people expect to come of this response.
256 notes
·
View notes
Text
God, I love ∩ and ∪ being resized versions of ∧ and ∨. Very intuitive game design
25 notes
·
View notes
Text
do you guys ever see those accounts on instagram where they're like "i'm doing a phd in math at this extremely prestigious school" and then proceed to really slowly and dramatically prove theorems from undergrad analysis like the cauchy schwartz inequality or rolle's theorem? do we think they make money doing this? because there's certainly quite a lot of views on those videos? should we all be doing this? it probably takes them like 5 minutes max to edit that content
20 notes
·
View notes
Text
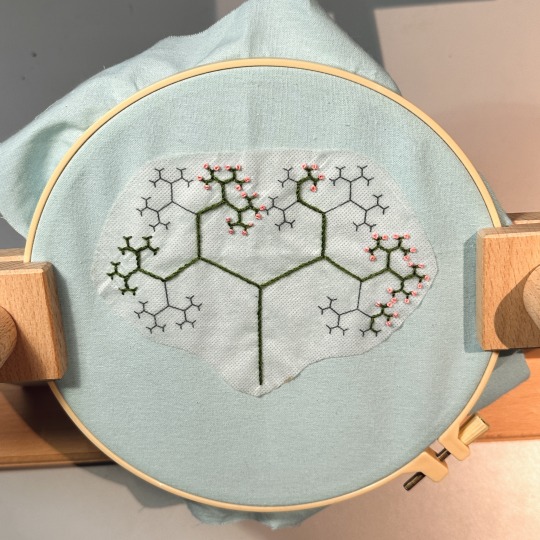
Work in progress of a binary tree.
#embroidery#fiber craft#math art#math embroidery#math#craft#mathblr#science craft#yarnblr#threadedtheorems
76 notes
·
View notes