#sierpinski carpet

[rlyehtaxidermist]

You're actually making a good point, I'll give it some thought. Thank you.

Although I was being generally nihilistic about the concept of having a discussion in the first place, when you're an insane freak with fringe ideas, the only thing you can do is petty acts of malice and plotting the demise of the human race if you're in a good headspace. I wrote what I did because I liked your blog, but I was so disappointed to see you supporting mainstream ideas about morality. What is your favorite fractal?😔

Aesthetically, the Burning Ship.

In general, Cantor's ternary set and its close relatives are too useful as counterexamples to not take the top spot.

[violetfractal]

You can generate Sierpiński carpet (the 2D analog of Menger sponge) at home! I started with addition modulo 3 and some conditional formatting in Excel.

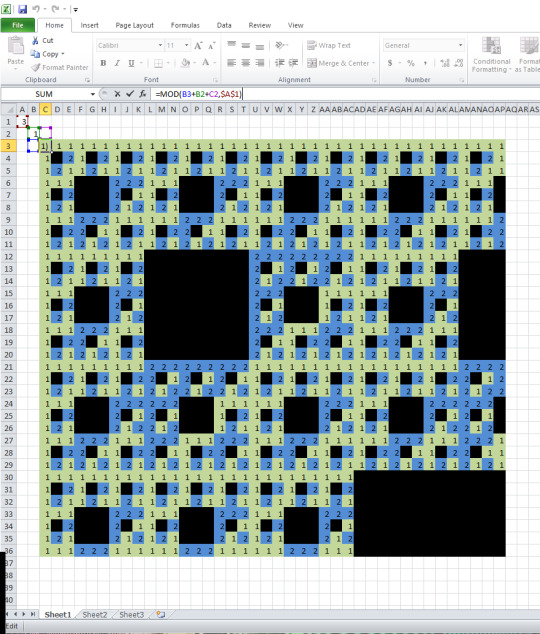
I left the modulus configurable. Powers of 2 produce simple tessellations instead of fractals, so the first viable fractal is A1=3. Here’s the modulus 3 image at 729x729 resolution:

This is the standard sierpinski carpet. But starting with modulus 5, higher primes are going to give us some trippy Menger-analogs with intricate self-similar geometry. Let’s dive in:

Modulus 5

Modulus 7

Not all composite numbers are duds! Mod 9 is beautiful with its single order 3 subgroup.

But Mod 15 is not so much a fractal as a self-similar glitch. The subgroups of order 3 and 5 are all jumbled together!

Modulus 17

Modulus 19

Modulus 23

Modulus 29 with 707281 cells. (That’s 29 to the fourth power!) And that’s the limit, because Excel is running garbage collection nonstop trying to compute any more of the image. Excel 2010 was limited to 2GB of ram and we are out. I call this collection of renders “seafloor”.

Original Date May 7th, 2023 11:16pm

[michaelrotonal]

just learned about the Delannoy numbers. they're like Pascal's Triangle but they don't believe in even numbers. the equivalent of the "odd numbers make sierpinski triangle" is "numbers not divisible by 3 make the sierpinski carpet"

[operator-report]

putting this under a readmore because it got long but it's about the signalis x the substance fanart. spoilers for both

one of the things i liked best about the substance despite it being honestly pretty shallow is that it is extremely about labor and it makes the connection between work under capitalism and age discrimination really fucking clear. obviously elisabeth gets fired from her job for being "too old" and that's why she takes the substance but the clone it creates is just a person who "can do" her old job! sue has the whole wide world open to her and she picks elisabeth's shitty fitness instructor gig! not even, like, elisabeth's red carpet oscar roles! and meanwhile, elisabeth cannot conceive of a life for herself outside of work, she shuts herself in her apartment and watches infomercials (grasping at being a consumer?) instead of, as other people have pointed out, enjoying her now-abundant free time. the substance creates "a better version of yourself" and that version is a worker!

and i think if signalis' political analysis were slightly better, it could pull off a similar theme. one of the most chilling things about the replikas is that they're very explicitly mass produced worker copies who are killed the second they stop being predictably useful as workers. again, we have cloning technology used to make workers who only have personhood to the extent that they are workers. the "corruption" in sierpinski is ariane hijacking the worker reproduction process to instead replicate the promise, and so falke, instead of being the ultimate expression of the state's labor power, reproduces both the roles of ariane and elster.

signalis screws up though by calling this relationship between labor and personhood and technology "communism." and so conversely i do think that the barbie-esque aesthetics (and, tbh, themes) actually serve the substance well.

but yeah sue is a replika soooooo true tumblr user shardikart-blog

[mahogakko]

from "Generating a Sierpinski carpet" question answered by user Mr.Wizard on Stack Exchange

[is-this-plural]

we're personally fond of the sierpinski carpet

the Mandelbrot Fractal (beloved)

FRACTALS MENTIONS 💯💯💯💯💯 WOOOO FRACTALS ‼️‼️‼️‼️‼️‼️ NO. ONE FRACTALS FAN 🔥🔥🔥🔥🔥🔥🔥yeah plural

[crazyskirtlady]

~Adjust perceptions~

s h i f t s h i f t

[isomorphismes]

ℂ→ℂ

[tunastudy]

Fourth-iteration Sierpinski Carpet

a doodle by moi (don’t worry, this was on graph paper, I’m not superhuman)

[z-arcane]

Sierpinski carpet addition

RENDERING FRACTALS

Written in Python using numpy, pyplot, and numba for the jit compiler.

[mathysphere]

My mom does a lot of very involved cross stitch projects that take a long time (she recently finished a pattern made from a photo of Denali that took a year and a half) BUT the project she just started is a Sierpinski carpet on a tote bag, planned out as 2^9 9x9 squares, which I thought y’all might appreciate.

Omg that's incredible! That's a dream project right there-- I've daydreamed about making a Sierpinski carpet cross-stitch before, but the sheer repetition of even a medium-sized one intimidates me.

Tell your mom she's a legend! With good taste! That kind of year-long piece is just incredible.

[thespamman24]

THINGS THAT ARE FORBIDDEN IN MY NEW RELIGION:

1.Saying mean things to children

2.Giving dogs the name “Wet Beef”

3.Vacuuming your front yard

4.Giving cats the name “Dry Beef”

5.Tattooing the name of all your body parts onto yourself

6.Discussing the Coastline Paradox

7. Giving yourself tattoos at all. That’s very dangerous.

8.Naming your right elbow “Beef”, then tattooing the word “beef” on that elbow

9. Naming your left elbow “bell pepper” then tattooing the word “bell pepper” on that elbow

10. Having a ridiculously small tongue.

11. Forcing a four legged creature to dance.

12. Messing up a crime scene by pouring salt and butter all over it

13. Messing up a child by pouring salt and butter all over them

14. Marrying one of your elbows. The other one will get jealous. Marrying both of your elbows is fine, but divorce is not recommended because then you won’t be able to use your arms well.

15. Pretending that a lizard is something other than a lizard (a kangaroo, a rock, another kangaroo)

16. Challenging an alternate version of yourself to a boxing match, and then falling in love with your alternate self. This will destroy the universe.

17. Calculating the exact geometric configurations of Gabriels Horn

18. Giving trees the power to smell things. This will make them too powerful. They will then be able to smell each other, all in love, and marry. And, when the trees go on their honeymoons, their will be no one left to give us any oxygen.

19. Any discussion or conversation of other concepts related to fractal geometry including (but not limited to), Sierpinskis Traingle, the Koch Snowflake, the Picard Horn, the Pseudosphere, the shape of the universe, The Mandelbrot Set, self-similiarity, non-differential functions, measure theory, infinite recursion, the Hausdorff-Besicovitch Demension, a Julia Set, the Sierpinski Carpet, a finite subdivision rule, and the Topological Dimension.

20. Naming your children “Bell Peppers and Beef”

[epikulupu]

[ ⭘ ] ​ SIERPICARPETAN ! ╰┈➤ ​ ​ a gender related to the sierpinski carpet fractal. ╰┈➤ ​ ​ sier + pi + car + pet + an ╰┈➤ ​ ​ from 'sierpinski' and 'carpet', and the suffix 'en'. ╰┈➤ ​ ​ requested by no one, coined by us. ​ [ ⭘ ]

[spankymerve]

A Sierpeniski carpet, if you will

sends you a pixelated dick pic

[altsoph]

In Scotland, there is such a phenomenon as tartans. These are textile patterns, unique for districts, clans, families, etc. (examples in Fig.A); historically, they play a role similar to the coat of arms; they are used to create kilts, scarves, etc. The first tartan found, Falkirk, dates back to ~250 AD, and now there are a lot of them — more than 3000 are currently registered in the official register.

They look pretty different but could be simply parameterized by generator codes like G106R26B4Y44 or G24K8G2K8, so it's easy to generate them, and there is already a twitter bot alltartans for it (Fig.C). On the other hand, these patterns are similar to unfinished fractals, so there are attempts to draw hyperbolic tartans (Fig. C). The square of the Cantor set is also called Cantor Tartan (and is similar to the Sierpinski carpet, Fig.D); for some reason, someone is trying to define a calculus on it.

Also, while writing this post, I discovered a strange carpet sect, Triangle Frenzy.

[mathhombre]

Sierpinski Carpet

A doodle for Sophia Wood’s #mathober, with four generations, on the theme of iterate. See all the themes here.