#mathart

[mathhombre]

Radial Tessellation derived from a square.

More Ghee Beom Kim magic!

[ozachou]

Computational Drawing CLXIV

[shonk]

Phase

(source code)

[elkement]

Reality and Imagination for real

Real and imaginary part of complex function 1/z - "Reality and Imagination" - for the first time drawn traditionally on paper, therefore I call it: "Reality and Imagination for real".

I picked the colors intuitively, but now I see: Red pill versus blue pill :-)

Geometric drawing - axonometry, creating the "3D view" from the view from above - "cloverleaf-like", placed in the center of the drawing - and from the side - where circles become just lines. Graphite pencil, watercolor pencils, ballpoint pens.

The contour lines of these functions are actually just circles whose radii decrease reciprocally with height, and which are aligned along one point of the circumference. The towers of reality and imagination can be rotated into one another. I also often call them "trumpets" - it's 4 trumpets, two blue and two red ones, each opening up to an infinite circle.

[regolo54]

[daily-public-domain]

Day 364: "Broken glass 1"

link

–This image is part of the public domain, meaning you can do anything you want with it! (you could even sell it as a shirt, poster or whatever, no need to credit it!)–

[eccentricstylist]

Winter Daylight Mandala

[coffeenuts]

[olbaid-st]

Deep Mandelbrot Set #158 Mag=9.72e+1774

Magnification = 9.72e+1774 = 2^5896.382 Max iteration = 1,132,860

[kaleidoscopevisualart]

[mathhombre]

Running in Circles

One more of these.

[ozachou]

Computational Drawing CXCIV

[shonk]

+

(source code)

[elkement]

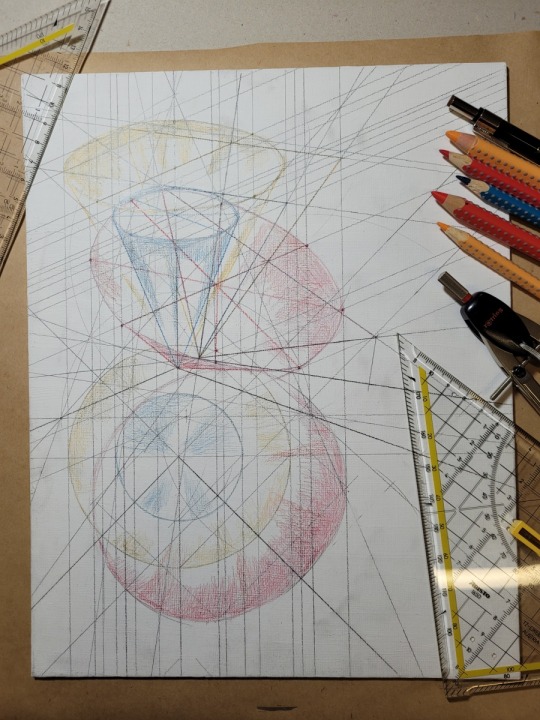
Physics of the gyroscope - "meditated upon geometrically":

Poinson's construction, prolate gyroscope.

Work in progress, first three stages:

The three cones in an axonometric projection, the red/violet one dances around the blue one and its axis traces out the yellow one.

Now I am stained-glass-i-fying it!

Graphite pencil construction, watercolor pencils, watercolor markers, black ballpoint pen on gessoed and sanded canvas board.

[regolo54]

[daily-public-domain]

Day 257: When Claude met Vincent

link

link

link

link

link

–These images are part of the public domain, meaning you can do anything you want with them! (you could even sell them as a shirt, poster or whatever, no need to credit them!)–