#prime number theorem

[math1089]

Mathematical Beauties of the Number 142587

There are some mysteries that the human mind will never penetrate. To convince ourselves we have only to cast a glance at tables of primes and we should perceive that there reigns neither order nor rule.Leonhard Euler Welcome to the blog Math1089 – Mathematics for All. I’m glad you came by. I wanted to let you know I appreciate your spending time here on the blog very much. I do appreciate your…

[karcatgirl-vantas]

system of mathematical notation where concatenation always means multiplication and each prime number has a unique one digit symbol. so counting to ten looks like "2, 3, 22, 5, 23, 7, 222, 33, 25". the advantages of this system would be making multiplication and division trivial, as well as accurately representing the true form and identity of every positive integer according to the fundamental theorem of arithmetic. the disadvantages to this system would be everything

[swuumi]

Nerd Reader x Nerd Nanami = smart power couple

you and kento were sitting at a corner table on a café, your eyes glued on your notebook, fingers fiddling with your pen.

“you’re so focused, working on how to divide zero now?” kento chuckles as he leans back.

“haha, very funny. if could divide zero, i’d be solving the world’s fundamental problems, not this stupid equation.” you huff.

you were preparing for an upcoming exam and you thought about inviting kento to study with you.

because why not, right?

“there’s beauty in the paradox of diving by zero, maybe you should just stop looking for the answer and let the question be.” he shruggs.

“so, you’re saying that i should just stop solving and just appreciate it? will that get me a passing grade?” you look at him, eyebrows furrowed.

“pretty much. though, to be fair, i get it. numbers don’t offer room for interpretation. but language—language is fluid. it can mean whatever you want it to mean... have you thought about math as a language?” kento suggests taking his drink and sipping a little.

“sure, math is a language. but it’s a language about rules. it’s all about structure and logic.” you refute, looking back at your messy math notes.

“if you look at it this way, math is a kind of poetry. just like a metaphor works in finding the unexpected connection between two things—math finds connections between numbers. patterns show up and suddenly something new appears where there was nothing before.” setting his cup down as he looked at you.

“you’re starting to sound like those motivational quotes that you find imprinted on the side of a coffee cup. you have a point, though i don’t think i’m gonna start writing sonnets about theorems anytime soon...” you laugh softly, scribbling nonsense on your notebook.

“i’ll take that as a win. i think you could give shakespeare a run for his money if you ever wrote a poem about prime numbers.”

“‘shall i compare thee to an irrational number? thou art infinite and never repeating…’” you say sarcastically.

“hey, don’t knock it until you try it. you could write a whole epic poem on pythagoras and his theorem, i guarantee it would have a bigger following than every other poems.” kento leans back on the chair again.

“yeah, yeah. you’re distracting me! go read whatever shenanigans you’re reading, you’re making me lose focus!” you lightly slap his shoulders.

nothing could beat moments like this, just you and him—throwing playful banters against one another.

and you did end up passing your test! but you’re not sure if you’re still gonna invite kento anytime soon knowing that he’s just gonna go off and talk about things that you really can’t comprehend...

who are you kidding? of course you’d invite him either way...

an: english isn’t my first language so this made my head hurt, i think i drained my brain juice and idrk how i’d portray this type of trope so i just went w it 😿 + i believe that kento is a english literature poem stuff kind of guy and becomes a yapper when that’s the topic, you can’t change my mind .

[dorothytheexplorothy]

you've been waiting a while for a new maths update - and it's finally here!

improvements include:

in gender selection screen, added "sumtraction" option

fixed bug where positive divergent sums evaluated to negative numbers

added new 2-dimensional version of off-by-1 errors - off-by-[1,1]

changed the discrete maths server to a PvP zone (note: computer science is still PvNP)

the category theory DLC is now (co)free!

to prevent confusion with function graphs, all voiced lines pronounce "graph theory" with a soft g

fixed "vacuously true" glitch

integrals can now disobey fundamental theorem of calculus when unhappy. they become happy again if fed logarithmic functions

hyperbolic geometry no longer exaggerates as a rhetorical device (note: spherical geometry left the same as before)

rebalanced primes so that 4k+1's and 4k+3's alternate in Thue-Morse pattern. added an uncomputable 4k+2 prime

hot combinatorial games now distribute their temperature according to the laws of thermodynamics; cold games are now superconductive

added demo of "finitist hardcore" gamemode. as of now only two levels are available

subtraction is now associative

recursion is now recursive

added a nontrivial linear, associative, commutative binary operation on the positive reals, over which addition is distributive

exponentiated liner logic, so that additive logic is multiplicative and multiplicative logic is exponential

fixed "negative probability" glitch

redesigned the Tits Building and the Cox-Zucker Machine

fixed trigonometry

increased hitboxes for infinitesimals

added lootboxes

[bubbloquacious]

What mathematical operators would you think make for the best fuck marry kill discussion

FMK: addition, multiplication, exponentiation

FMK: powers, roots, logarithms

FMK: group operation, inversion, unit element

FMK: polynomials, differential operators, continuous maps

FMK: greater than, less than, equal

FMK: one, two, three

FMK: numerator, denominator, quotient

FMK: rings, integral domains, fields

FMK: categories, functors, natural transformations

FMK: reflexivity, transitivity, antisymmetry

FMK: fundamental theorem of algebra, fundamental theorem of calculus, fundamental theorem of arithmetic

FMK: prime numbers, composite numbers, units

FMK: algebraic geometry, algebraic topology, algebraic number theory

FMK: compact Hausdorff spaces, abelian groups, algebraically complete fields

FMK: axiom of choice, well-ordering theorem, Zorn's lemma

[simplydnp]

who's hand is in this picture?

A Mathematically Rigorous Proof That I Spent Too Long Writing

welcome to university math: dnp hand edition

(no, don't leave, you'll be fine i promise)

to begin, we need a statement to prove. we have two options:

- the hand is dan's hand

- the hand is phil's hand

now, for most proofs in university math, you are told a true statement, and you must show why it is true using logic rules, definitions, and theorems. but, we do not know which of these statements are true, so we have to find out.

to prove that a statement is true, we must show that it is always true for the situation presented. to show a statement is false, we must present a single instance where the statement is false (also known as a counter example).

a quick not scary math example:

definition: a prime number is only divisible by 1 and itself.

statement: all prime numbers are odd

(this is false, because 2 is a prime number and it is even. you don't even need to check if there's any others, all you need is one single case where it isn't true to disprove it)

so now that we have a little background on proofs and how to prove and disprove them, we go back to our two statements.

the thing with this situation is, one of them must be true (unless you're gung-ho on someone else holding dan's face while phil takes a picture on his phone of dan in his glasses, in which case, i applaud your commitment, but in actuality this proof will cover that option too)

the full statement we have is: dan is touching his face or phil is touching dan's face

now, because this is Real Life and we have a picture where a hand is touching dan's face, we know already that one of these options is true (as mentioned above) but! using symbolic logic you could also come to this conclusion.

this type of statement is an 'or' statement, and if you're curious, you can look into 'truth-tables' and see why, but at least one of the options must be true.

back to the proof at hand (bah-duhm-tss)

okay. now, proofs also must be 'general' in order to mean anything, really. these are statements of truth of the universe, not just for individuals. so, we will prove this generally.

we have 2 people involved, so individual 1 (dan, the owner of the face and potential face toucher) will be labelled as 'D' , and individual 2 (phil, the possible face toucher who does not own the face) will be labelled as 'P'. thus, this can be true for any such D and any such P.

so with our 'or' statement, in order to prove it, we pick one of the options and say that it is not true, and we have to show then that the other is true.

step 1: let's assume this is not P's hand. (assumption)

step 2: thus, it must be D's hand. (what we take from our assumption)

step 3: now, if it is D's hand, we look at what a hand on one's own face is capable of appearing like. (a definition or true fact about step 2)

the position in the given photo shows the hand with a thumb on the cheek, and a finger on the forehead. so, we find an example of a person with their fingers in the same position (or close to) and see if this supports our claim.

consider:

now, with this image, you can clearly see how the subject's right hand has the thumb on the temple and index finger on the top of their head, however, it is a close enough position for our case.

from the view of the camera, the closest finger to the camera is the edge of the pinkie. in fact, it will always be the closest finger to the camera in this position, assuming the subject has all fingers and no additional appendages.

step 4: we now compare this to our photo (we verify if this holds to our claim or contradicts it)

in our photo, the closest appendage to the camera is the edge of the thumb.

step 5: thus, it cannot be the case that D is touching their own face. (what the evidence says)

step 6: as we assumed it was not P's hand and have shown it cannot be D's hand, and as this is an 'or' statement both of these claims cannot be false, we can therefore conclude it must be P's hand. (our conclusion: re-stating the statement and assumptions and conclusion)

step 7: we verify that P is true (optional step but in beginner proofs you generally show why your case works)

to do this, i will show a picture of a person touching another's face, and compare it to our image.

consider:

now, this image is not exactly the same, similar to above. however, P's left thumb is on the cheek, with their index on D's temple. the closest appendage to the camera (if it were in a similar perspective as our original) would be the edge of the thumb.

comparing it to our original:

our comparison holds.

thus, we can conclude that the true claim in this statement is that P must be touching D's face, which, in particular means that:

phil is touching dan's face in the image

thank you for partaking in phannie mathematics. we now know. i am not sorry.

bonus:

phil has a hitchhikers thumb and dan doesn't so why was this necessary at all 🤡

[positivelyprime]

Merry christmas to all who celebrate!

Among the people celebrating christmas some 400 years ago was Pierre de Fermat, who proved his *christmas theorem* this day!

Fermat's christmas theorem, better known as the two squares theorem, says that a prime number p can be expressed as a sum of two squares, i.e. p = a² + b², if and only if p is 1 mod 4.

Look at this jolly fellow

[rbrooksdesign]

"tDMT-#4," digital, Sept. 2024, Reginald Brooks

The original DMT (Divisor Matrix Table) reveals ALL natural numbers and their divisors.

The truncated DMT -- tDMT -- is based on the original DMT, only filtered to reveal just those ODDs in Column 1 that are the Running Sums (∑) of the Row 1, i.e. 1-3-7-15-31-...

Why? The tDMT reveals ONLY those Rows that are "container" Rows -- i.e. based on the ∑s of the Exponential Power of 2 (seen as the Butterfly Fractal 1 sequence in Row 1 -- and these contain ALL possible Mersenne Prime-Perfect Number (Mp-PN) candidates.

Yes, that's a lot to swallow up front. One is simply taking the DMT and redacting out every Row except those beginning with 1-3-7-15-31-...

Why, again? The tDMT gives a simpler view of the key numbers informing the Mp-PNs!

The Mp-PNs are the rarest gems of the Primes!

Notice the numerical entanglement of the basic Butterfly Fractal 1:

1. The TOP Row -- the BF1 -- increases as the Exponential Power of 2;

2. The PNs only fall under the 2, 4, 8, 16, 64 and 4096 Column headers marked in BOLD;

3. These Column Headers of the BF1 Row equal the "x" value in the PN=xz simplification of the Euclid-Euler Theorem -- PN=2ᵖ⁻¹ (2ᵖ -1), where p=prime, x=2ᵖ⁻¹ , and z=Mp=2ᵖ -1;

4. Column 1 -- ODDs -- follows the same pattern spacing as the BF1 header Row, only it is in the form of the Running Sums (∑) of that BF1;

5. The PNs fall at the intersection of these two Row and Column patterns (BOLD).

Interactive DMT and tDMT for TES (Teachers, Educators and Students) ---here.

[michaelrotonal]

cool math thing i'm wondering about

are there infinitely many primes of the form n^2+1?

you'd think you could figure it out easily but no

list of thoughts on this:

numbers of the form n^2+1 cannot be divisible by numbers that are 3 mod 4.

each prime of the form 1 mod 4 only has 2 values of n where n^2+1 is divisible by it

this is isomorphic to "are there infinitely many gaussian primes of the form n+i?"

each individual prime factor only blocks out at most half of the n values, but every n value hits some prime factor. i feel like there's no way that at some point every n value hits two prime factors.

there are two ways to prove that for any prime, there's a n^2+1 that doesn't include any primes up to it.

way one is by picking an appropriate remainder for each prime, and using the chinese remainder theorem to find an n that works

the other way is just multiplying all the primes up to it and taking that as your n

if you're reading this, i'd like to invite you to reblog with any of your own thoughts you may have on this problem that are not already there

every prime that is 4n+1 can be written as a sum of two squares, but the question is how often is one of those squares 1?

sums of two squares are nice because you can multiply together two of them and make another new one of them

how is this conjecture not on wikipedia yet though. it seems like such a simple thing to ask

[janmisali]

while we're yelling about primes. i have never stopped being mad about 1 not being a prime. i don't understand it and no one has explained it in a way that makes any sense.

oh I know this one!

so, historically, one was considered to be a prime number, though not universally. if wikipedia is to be believed, publications as recent as 1956 included one in lists of primes.

the problem was that there's a lot of really important theorems about primes that are only true if you ignore one. the biggest is a theorem so important that it's literally called "The Fundamental Theorem of Arithmetic", that every integer greater than one has a unique prime factorization. if one is counted as a prime number, this is no longer true (you can multiply any number by one arbitrarily many times and get the same number), so older definitions of the Fundamental Theorem of Arithmetic would refer to "prime numbers greater than one".

and this context of primes as the components of a number's prime factorization is like, The context in which mathematicians care about prime numbers. it is the reason studying prime numbers is even a thing anyone does. so, if one were considered a prime number (as it once was), the word "prime" would basically only ever be used in A) lists of prime numbers and B) the phrase "prime number greater than one".

so, in a sense, you're right, it would make more sense if one were classified as a prime number. but the purpose of the words and symbols used in math is to describe the properties that mathematical objects have, and just in terms of practicality, "an integer which isn't evenly divisible by anything other than one or itself" just isn't as useful of a definition as "an integer which is only divisible by two factors, one and itself".

[prime-factorizer]

what is a prime factor

i like your funny numbers but i dont know what they mean :(

First of all, we'll only be talking about positive whole numbers, so no decimals, fractions, complex numbers, etc. This is also just going to be an introduction because this topic is more complicated/nuanced than you might expect, and I don't know/understand a lot of it

With that out of the way prime number is a number that you can't get to by multiplying other numbers: 24 isn't prime because you can write it as 6×4, but 23 is prime because the only way to get to 23 (only using multiplication) is 1×23. If you're interested, I encourage you to try finding a few prime numbers. It can be a fun exercise if you haven't tried it before. I'll put all of the ones less than 100 under the cut

A prime factor is just a prime number that divides another number. You can divide 24 by 3, and 3 is prime, so 3 is a prime factor of 24

Also, if you can get to a number by multiplying other numbers, then it's a composite number. Also also, 0 and 1 are weird so just don't worry about them <3

The thing that makes this blog work though is what's known as the fundamental theorem of arithmetic (ftoa):

Like I said, you can write 24 as 6×4, but you might notice that neither 6 nor 4 are prime. If you rewrite 6 as 2×3 and 4 as 2×2, then you can then write 24 as 2×3×2×2. Now all of the numbers are prime!

But you'll notice you can also write 24 as 8×3, then write 8 as 2×4 to get 2×4×3, then write 4 as 2×2 to get 2×2×2×3. Now that all of the numbers are prime, you'll notice that they're the same as when we started with 6×4 (three 2s and one 3)

What the ftoa says is, no matter how you break down a number like this, you'll always end with the same prime numbers at the end (in this case, three 2s and one 3)

The only thing I do differently from this process is use exponents to make it shorter. In this case, you can rewrite 2×2×2 as 2³. So, when I say 24 is 2³×3, I've "factorized" 24, and 2 and 3 are its prime factors. Of course, I don't usually do this by hand or in my head; I just give the number to a computer and it does it for me (it can be fun to do it yourself though, so sometimes I'll do it in my head for the smaller numbers)

Prime numbers and the ftoa play a pretty big role in math, and there's a ton of unsolved problems related to them, which is why you'll see people make a big deal out of them

Prime numbers under 100 and other notes under the cut:

0 and 1 aren't considered prime or composite. There's probably a more sophisticated answer to why, but I like to justify the decision by saying they ruin the ftoa:

Prime numbers under 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 97

0 is divisble by every number, so it's not prime but you also can't factorize it, so it isn't composite. 1 isn't prime because if it was then you could add as many ×1s as you wanted to a factorized number, ruining the uniqueness of its factorization, and, once again, it also can't be composite because you can't factorize it

Also, like I said, this is only an introduction and I don't understand most of the more complicated/nuanced definitions. If you wanna learn about those though, I recommend TheGrayCuber's videos:

[talonabraxas]

Monas Hieroglyphica (The Hieroglyphic Monad)

Written by John Dee and published in Antwerp in 1564, the Monas Hieroglyphica (‘Hieroglyphic Monad’) was conceived in 12 days, a period, so claimed the author, of Divine Revelation. It presents Dee’s unified glyph, the Monad, by way of 24 theorems, each demonstrating a variety of mathematical, geometric, cabalistic, and cosmological principles gleaned from the ancient world. Highly influential, the titular glyph was later adopted into Rosecrutianism by way of the works of Paracelcian alchemist Heinrich Khunrath, with whom Dee was acquainted.

Chiefly a work of alchemy, it is perhaps best understood as a preeminent form of ‘diagrammatic alchemy’. The inception of the Diagram, a visual representation of information to accompany text, goes back to antiquity, but saw great use thanks to the printing technology of the 15th century. Dee took this a step further, with elaborate frontispieces brimming with cryptic symbolism. In theorem 18 he states, "it is not Aesop but Oedipus who prompts me," hinting at the presence of riddles within the text (just as Oedipus was challenged by the Sphinx).

Though still a devout Christian, Dee’s thinking was heavily informed by Pythagorean, Hermetic, and Neo-Platonic traditions which each posited that the universe was comprised of linguistic and numerical laws. Thus the symbols and images of Dee’s Monas were not mere representations of processes, but the manifestation of Truth itself. As such, meditative study of this truth would work the necessary alchemical transformation upon its student.

Given closer inspection, we see the Monad is a composite of other symbols. Indeed, it was designed such that all associated symbols, be they cosmological, alchemical, metallurgical, and chiefly, numerological, could be formulated, along with their governing principles. Together they form the ‘Unit’, or Monad; a key scientific concept of the many-in-one.

At the base we have the double crescent of Aries, the celestial fire of transformation; next the Solar Cross, the four elements, the cardinal directions, the Crucifixion, and the Hermetic mystery of the ‘quaternary in the ternary’, the ‘4 in the 3’. Dee believed in the Holy Trinity, but also that all creation was embodied in the number 4, the Trinity plus One (the One being manifest reality). Though seemingly mystical and arbitrary, the 4 in the 3 was a mathematical principle describing a Platonic solid called the Cuboctahedron, a shape made up of 8 triangles and 4 squares. This structure provides great supporting strength at little cost to weight, and was popularized in the 20th century by American architect Buckminster Fuller in the development of high-rise construction cranes as well as Geodesic Domes such as the one at Epcot, Florida.

Moving up, we have the point and the circle, two basic principles of geometry from which all others follow. Together they become the Sun with the Earth at its centre (a pre-Copernican worldview), over which we have the horned Moon. These horns combine with the circle to present the Earth sign of Taurus, as well as symbolising the alchemical wedding of the Active (Sun) and Passive (Moon). Joined with the circle and cross we find the symbol for Mercury, that the ancient Greeks called Stilbon (the God of the Wandering Star), which they considered the prime planet and metal. All seven classical planets, and the metals of the ancient world, are also revealed.

Considered as a whole, we can view the Monad as the alchemical process, with the transformative, Promethean fire of Aries at the base, and silver (the Moon) and gold (the Sun) at the top, forming the Cornucopian horns of wisdom. It also has an anthropomorphic aspect of a contemplative, kneeling figure. This finds a natural comparison in the spiritual concept of the Kundalini, the upward progression of energy points through the body, from the root through to the Divine light of revelatory experience; as well as in the Buddhist practice of meditation, in which fiery Desire fades with the awakening to our true, wise nature.

Despite Dee’s somewhat tarnished reputation as a magician and necromancer, even his critic, the pious Andrestius Babius, capitulated to recognising the Monad’s importance as a standardising tool that transcended language; a true, universal, scientific notation. That it so keenly marries Science with Spiritual wisdom presents an opportunity of revelatory understanding for those who would still take the time to study it.

[aedesluminis]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

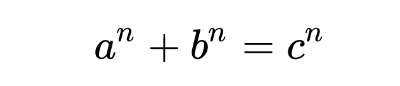
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[worlds-smallest-epsilon]

oh youre a math phd? Name 5 equations

1. The functional equation for the completed L-function associated with a modular form.

2. The Analytic Class Number Formula

3. 196883 + 1 = 196884

4. Chinese Remainder Theorem (gives an “equality” of rings)

5. Prime Number Theorem (gives an asymptotic equality of two functions)

(Can you tell what kind of mathematician I am from this? I feel like it’s pretty obvious lmao)

[a-lesson-you-never-asked-for]

Prime Numbers

A prime number is a number such that it has no factors except 1 and itself. These are often regarded as the building blocks of numbers, and are incredibly important from both:

a theoretical point of view, where problems such as the Riemann Hypothesis and Twin Prime conjecture revolve around the structure of primes

the application standpoint in music theory (Queen's famous song We Will Rock You has a beat that relies on prime numbers), and more relevantly, cryptography.

How do we get prime numbers

To say that a number x is a factor of another number y means that you can split y into equal groups, each group containing x things. So for example, if you wanted to divide 91 watermelons amongst your 13 friends, you can give them each 7 watermelons and everyone gets happy.

Another way of writing this is that 10 is a multiple of 2, or that 10 is divisible by 2.

With primes, you can't do this except by dividing them into groups of 1. For example, 2 is prime because you can only divide it into 2 equally sized groups. You can only divide 11 into 11 equally sized groups.

As a result, prime numbers have some very interesting properties, some of which are unknown. One very easy way to calculate them is by using the Sieve of Eratosthenes. The idea is that you start at 2 and remove every multiple of 2 except itself. So block out 4, 6, 8, 10, 12, and so on. Then you move onto the next unblocked number, which is 3. You go ahead and do the same, remove 6, 9, 12, 15, and so on. Notice that in the next step, 4 is blocked, so we go to 5, and block out 10, 15, 20, and so on. This process is very slow but it's certain. It tells you what the primes are with absolute certainty. Here's a picture to illustrate the idea. This excludes all the even numbers.

The atoms of natural numbers

Primes are regarded as the building blocks of numbers. This is due to the following theorem.

--------------

Fundamental Theorem of Arithmetic

Any integer n can be decomposed uniquely in products of powers of primes.

Examples

--------------

10 = 2 × 5

15 = 3 × 5

24 = 2³ × 3

There are many important theorems that come about due to primes, and almost all of them have to do with a topic called modular arithmetic.

Where to from here...

This is probably the extent to which you need to know about primes. Most of the ideas used will be introduced, as mentioned before, on an ad hoc basis. We will focus more on the code building aspects in our next parts, talking about binary and ISBN codes, before moving onto some more complicated examples of encrypting information.

[max1461]

So... ok, it's been a long time since I've thought about this, so forgive me if I get any details wrong. The natural numbers under addition are the free commutative monoid on one generator. And the fundamental theorem of arithmetic says that every natural can be represented uniquely as a product of primes. In other words: let M be the monoid of infinite sequences of naturals with finite support, under componentwise addition; then there is an isomorphism of monoids from M to (N, ×) given by (a_i)_{i \in N} ⟼ ∏_{i \in N}p(i)^{a_i}, where p(i) is the ith prime. Uh. Basically just take your sequence of naturals and interpret them as powers in a prime factorization. Anyway this is an isomorphism so M ≃ (N, ×). Well guess what: M is another way of describing the free commutative monoid on countably infinitely many generators. So the fundemental theorem of arithmetic is basically saying "ok, if you take the free commutative monoid on one generator and define a new operation on the same set that is comparable with it in this specific way, you get the free monoid on infinite generators".

This is kind of slick, I think. I mean free objects are sort of... right at the edge between combinatorics and algebra, right? And so are the natural numbers. It's like algebra is an emergent property of combinatorics, or is a the generalized form of one. And these things all sit right on the boundary. So it's unsurprising they'd be closely related. But it also says something about the naturals, you know... the axioms of a commutative monoid are sort of "all there is to know" about N. If you're like "make me a monoid!" it's canonically gotta be free, right? And then how many generators will you pick? Well two really natural answers are "1" and "countably infinite"—and those are both alternate ways of specifying N.

I don't know.