#prime numbers

[karpholmes]

(Mathematician here)

Quite possibly the funniest targeted ad I’ve ever gotten

[lord-of-the-noodles]

[xponentialdesign]

Prime Parallax

[teetering-dinosaur]

pls reblog for sample size it’s important to society that we know which numbers are superior once and for all

[keysnocar]

Little Bee doodles from my Prime Numbers AU..

Haven’t worked on this au in so long I been busy w my other one lol…

[noelements-setempty]

Stop asking me for my phone number you bitch ass websites. The only 'two factor' things that interest me are the beautiful prime numbers 💙

[shadowyyyidk]

this is prolly silly and people probs do wayyy more math but i absolutely love euclid's proof for an infinite number of primes. why's it so simple but so nice lol

[superrealmathtricks]

Super real math trick!

Can’t figure out if a number is prime or not? No worries! Just see if YOU can divide it into a whole number with any other number! If YOU can’t divide it, it’s a Prime Number!

[microqwavve]

im mkaing a list.. contact me for details

[positivelyprime]

Eisenstein primes (and integers)

You've heard of integer primes, but have you heard of different kind of primes? One of the most beautiful pictures in mathematics I've recently seen is this:

This is a picture displaying the Eisenstein primes and the rest of the post will be me explaining where this comes from.

Firstly, to understand what Eisenstein primes are, we need to know what Eisenstein integers are! An Eisenstein integer is a complex number of the form z = a + b w where a,b are integers and w = e^(2/3 pi i). Normally a small letter omega is used instead of w. Notice that w is a third root of unity, i.e. w³ = 1.

Appending this complex w to the regular integers has some consequences. In particular, we can now view the eligible numbers on the complex plane to get this picture:

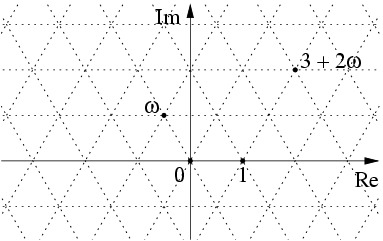
The Eisenstein integers correspond exactly to places where two dotted lines cross. As such, where normally one can view integers as laying on a 1-d line, we can now view Eisenstein integers as laying on a 2-d lattice!

Now one may start to wonder if, just like in the integers, one can have Eisenstein integers which are not divisible by other Eisenstein integers. In more mathematics: We call a number p an Eisenstein prime if p cannot be written as a*b where a,b are Eisenstein numbers which are not +-1, +-w, +-w² (the units in this system).

It turns out that some regular primes are still primes in the Eisenstein integers. For example, 2 can still not be decomposed. However, 3 can! We may write 3 = -(1+2w)(1+2w) which means that 3 is not an Eisenstein prime. One may investigate this further (using abstract algebra) to arrive at the picture at the top of this post. The 6-fold rotational symmetry is due to the Eisenstein integers having 6 units.

Of course a natural question is why take a third root of unity and not an nth root? This is a very interesting question and leads to the study of (integer rings of) cyclotomic fields! This concludes fun math fact tuesday

[positiveintegers]

727

[incognitopolls]

We ask your questions so you don’t have to! Submit your questions to have them posted anonymously as polls.

[kiwikiwikiwiii]

My dumb ass really just happened to crochet a prime fucking number in the round so now I've got el zilcho factors to work with for broomstick lace like wtf are the chances

[uchicagomagazine]

Web exclusive: What do UChicago mathematicians think of the Apple TV+ show Prime Target? We asked, so you don’t have to.

[fionaapplerocks]

Co-incidence or ???

FTBC was released on April 17 -- 17 is a prime number The Idler Wheel was released on June 19 -- 19 is a prime number Tidal was released on July 23 -- 23 is a prime number Extraordinary Machine was released on Oct 3rd -- 3 is a prime number Fiona's Birthday is September 13 -- 13 is a prime number When The Pawn was released on November 9, which is NOT a prime number, but it was the 313th day of the year. -- 313 is a prime number

primes (1 in 3 of days in the month) 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31

[keysnocar]

we repost just so i can move his etching

@ghotstx HERE im sorry for clickbaiting you here :)

Also I can’t make this up, I literally mixed up ur username w another person so..welcome.? Haha

@ghostbny

Anyway, I'm FINALLY getting time to add to my TF Prime Numbers AU, starting with a little Orion ref/doodle sheet. This mostly helps me get to know what kind of character I'd like this version of him to be. (and ngl the plot has been whooping me idk what's happening or why sometimes :() )

This is Orion! Or, as the other bots know him,"37." (I’ll explain it later gng)

Here, he’s been with the autobots for around four vorns, (since he was just over 13 vorns old.) 

His Weapon isn't the familiar star saber or Zeta Prime's Axe. This choice involves his 'childhood', as does his design. I kept his lovable boxyness (well i love it) but made him less detailed, with less armor in general- though specifically around the joints. This is mostly because I wanted him to be a smaller bot, with an emphasis on his agility and flexibility, rather than being a heavy hitter. (at least in his youth.)

The Matrix also has a bit of change in its functionality, use, and importance to the plot.

Both of which I'll expand on in a separate post.

DON'T BE MISTAKEN by my choices in drawing him, he's never without the face mask unless alone.

-------------------------------------------------

The little doodles I have of him are more so to solidify his personality while he's this age range, but this is dependent on what’s going on around him as well. His age has proven to complicate some of my plot, but since he’d bonded with the Matrix at 13, it made sense to me that he’d been gradually reformatted in that short span of time between that and joining the autobots by the Matrix . So he appears much older. (I’ll explain it later gang Ik it’s weird but its important hshgjfhd)

Since taking up residence in the main Autobot Outpost on Cybertron, Orion, or "37" works mostly in solo reconnaissance, scouting territories, or pathfinding for small teams on other kinds of missions. When on base. He focuses on compiling the small amount of data the Autobot faction has managed to gather or receive on any prominent threats.

He ‘moved in’ with the Autobots around an earth year after the ‘ Fall of Gold.’ (as many bots had not-so-fondly begun calling it.) This event being the night that Decepticon forces raided, and then destroyed the large informational hubs of Iacon. This included but was not limited to the Senate Hall, Multiple high class Universities, and the Records tower. To many this marked the true beginning of the war- as the attack and largely successful destruction of such a profound city solidified the danger of the rapidly growing Decepticon movement.  After Iacon fell, the other strongholds of the planet have been slow, but surely following.

In his free time, he’s always reading, thinking, filing, sorting, polishing, solving- 'doing' something. there isn't a spare second he's not busying his mind, or if he can't at least manage that, his servos. 

Orion is not social in the SLIGHTEST with new bots. (this being all of his Autobot peers)  It 100% creeps everyone else out when he attempts to be. (he's got these large, piercing, non-emotive optics that seem to stare past and yet into anyone who's got his attention- and WOW is it an alarming, unreadable, gaze to be caught in if you don't know him well.)

The rare moment or two he does find himself in a conversation about something other than strategy or information he'd gathered- others find his conversation.. lacking at most. It's not that he isn't interested, not at all. It's more so that any personal information he dares to give away may end up doing more harm to his goals among the autobots than good. It sure is a lot easier to keep your origins to yourself, if everyone's too intimidated or put off to speak with you.

It's mostly because of this, that he prefers quietly watching and taking things in, over putting himself into a conversation. It's simply how he's accustomed to and has been taught how to function. Observing and compiling, interpreting and mimicking.

(That being said he is still a ‘teenager’ so it sort of sucks trying to keep himself isolated.)

His more reclusive behavior tends to keep other bots from bothering him. His quietly observant posture and constantly active tendencies often leave the others assuming he's got no time for- or interest in talking.

 He sees all of this as a good thing, the first few vorns of living with the bots, as he’s committed to putting all of his focus on figuring out this weird matrix thing. More importantly, keeping the fact that it forced its way onto his spark and won’t come off-  a secret. (Not to mention he can’t afford to be distracted by bots he doesn’t entirely trust.)

But considering Commander Magnus and Medical Officer Ratchet have already been looking at him as if trying to remember something they’d once known- he might not be able to make that last.

…let's hope no one puts the pieces together on where he came from before he can figure out how to explain it.

Admittedly, this style has a different feel than the ones I'm accustomed to creating in- and trying to keep the characters to a consistent level of both simplistic and shapey is already proving to be a fun challenge. I’ve been working on this idea for a while, and I have a lot of other little details or broad stories to fill in. PLEASE I can talk and brainstorm about this all day. I've already got a google doc and MAD plotholes.

(Vorn = 83ish earth years, which I use interchangeably with an earth year for easier understanding, because of the long lifespans.)