#cyclic permutation

[math1089]

Mathematical Beauties of the Number 142587

There are some mysteries that the human mind will never penetrate. To convince ourselves we have only to cast a glance at tables of primes and we should perceive that there reigns neither order nor rule.Leonhard Euler Welcome to the blog Math1089 – Mathematics for All. I’m glad you came by. I wanted to let you know I appreciate your spending time here on the blog very much. I do appreciate your…

[canmom]

Music theory notes (for science bitches) - part 2: pentatonics and friends

or, the West ain't all that.

Hello again everyone! I'm grateful for the warm reception to the first music theory notes post (aka 'what is music? from first principles'). If you haven't read it, take a look~

In that stab at a first step towards 'what is music', I tried to distinguish between what's a relatively universal mathematical structure (nearly all musical systems have the octave) and what's an arbitrary convention. But in the end I did consciously limit myself, and make a beeline for the widely used 12TET tuning system and the diatonic scales used in Western music. I wanted to avoid overwhelming myself, and... 👻 it's all around us...👻

But! But but but. This is a series on music theory. Not just one music theory. The whole damn thing. I think I'm doing a huge disservice to everyone, not least me, if that's where we stop.

Today, then! For our second installation: 'Music theory notes (for science bitches)' will take a quick look through some examples that diverge from the diatonic scale: the erhu, Japanese pentatonic scales, gamelan, klezmer, and blues.

Also since the first part was quite abstract, we'll also having a go at using the tools we've built so far on a specific piece, the Edo-period folk song Sakura, Sakura.

Sound fun? Let's fucking gooooo

The story so far

To recap: in the first post we started by saying we're gonna be looking at tonal music, which isn't the only type of music. We introduced the idea of notes and frequencies by invoking the magic name of Fourier.

We said music can be approximated (for now) as an idealised pressure wave, which we can divide into brief windows called 'notes', and these notes are usually made of a strong sine wave at the 'fundamental frequency', plus a stack of further sine waves at integer multiples of that frequency called 'overtones'.

Then, we started constructing a culturally specific but extremely widespread system of creating structure between notes, known as '12 Tone Equal Temperament' or 12TET. The main character of this story is the interval, which is the ratio between the fundamental frequencies of two notes; we talked about how small-integer ratios of frequencies tend to be especially 'consonant' or nice-sounding.

We introduced the idea of the 'octave', which is when two notes have a frequency ratio of 2. We established the convention treating notes an octave apart as deeply related, to the point that we give them the same name. We also brought in the 'fifth', the ratio of 1.5, and talked about the idea of constructing a scale using small-integer ratios.

But we argued that if you try and build everything with those small-integer ratios you can dig yourself into a hole where moving around the musical space is rife with complications.

As a solution to this, I pulled out 'equal temperament' as an approximation with a lot of mathematical simplicity. Using a special irrational ratio called the "semitone" as a building block, we could construct the Western system of scales and modes and chords and such, where

a 'scale' is kind of like a palette for a piece of music, defined by a set of frequency ratios relative to a 'root' or 'tonic' note. this can be abstract, as in 'the major scale', or concrete, as in 'C major'.

a 'mode' is a cyclic permutation of an abstract scale. although it may contain the same notes, moving them around can change the feeling a lot!

a 'chord' is playing multiple notes at the same time. 'Triad' chords can be constructed from scales. There are other types which add or remove stuff from the triads. We'll come back to this.

I also summarised how sheet music works and the rather arbitrary choices in its construction, and at the end, I very briefly talked about chord notation.

There's a lot of ways to do this...

I recently watched a video by jazz musician and music theory youtuber Adam Neely, in which he and Philip Ewell discuss how much "music theory" is treated as synonymous with a very specific music theory which Neely glosses as "the harmonic style of 18th-century European composers". He argues, pretty convincingly imo, that 'music theory' pedagogy is seriously weakened by not taking non-white/Western models, such as Indian classical music theories, as a foil - citing Anuja Kamat's channel on Indian classical music as a great example of how to do things differently. Here's her introductory playlist on Indian classical music concepts, which I will hopefully be able to lean on in future posts:

There's two big pitfalls I wanna avoid as I teach myself music theory. I like maths a lot, and if I can fit something into a mathematical structure it's much easier for me to remember it - but I gotta be really careful not to mathwash some very arbitrary conventions and present them as more universal than they are. Music involves a lot of mathematics, but you can't reduce it to maths. It's a language for expressing emotion, not a predicate to prove.

One of the big goals of this series is to get straight in my head what has a good answer to 'why this way?', and what is just 'idk it's the convention we use'. And if something is an arbitrary convention, we gotta ask, what other conventions exist? Humans are inventive little buggers after all.

I also don't want to limit my analytical toolbox to a single 'hammer' of Western music theory, and try and force everything else into that frame. The reasons I'm learning music theory are... 1. to make my playing and singing better, and be more comfortable improvising; 2. to learn to compose stuff, which is currently a great mystery. How do they do it? I do like Western classical music, but honestly? Most of the music I enjoy is actually not Western. I want to be able to approach that music on its own terms.

For example, the erhu... for erhuample???

The instrument family I'm learning, erhu/zhonghu, is remarkably versatile - there are no frets (or even a soundboard!) to guide you, which is both a challenge and a huge freedom. You can absolutely play 12TET music on it, and it has a very beautiful sound - here is an erhu harmonising with a 12TET-tuned piano to play a song from the Princess Mononoke soundtrack, originally composed by Joe Hisaishi as an orchestral piece for the usual Western instruments...

This performance already makes heavy use of a technique called (in English) 'vibrato', where you oscillate the pitch around as you play the note (which means the whole construction that 'a note has a fixed pitch defined by a ratio' is actually an abstraction - now a note's 'frequency' represents the middle point a small range of pitches!). Vibrato is very common in Western music too, though the way you do it on an erhu and the way you do it on a violin or flute are of course a little different. (We could do an aside on Fourier analysis of vibrato here but I think that's another day's subject).

But if you listen to Chinese compositions specifically for Erhu, they take advantage of the lack of fixed pitch to zip up and down like crazy. Take the popular song Horse Racing for example, composed in the 1960s, which seems to be the closest thing to the 'iconic' erhu piece...

This can be notated in 12TET sheet music. But it's also taking full advantage of some of the unique qualities of the erhu's long string and lack of frets, like its ability to glide up and down notes, playing the full range of 'in between' frequencies on one string. The sheet music I linked there also has a notation style called 简谱 jiǎnpǔ which assigns numbers to notes. It's not so very different from Western sheet music, since it's still based on the diatonic major scale, but it's adjusted relative to the scale you're currently playing instead of always using C major. Erhu music very often includes very fast trills and a really skilled erhu/zhonghu player can jump between octaves with a level of confidence I find hard to comprehend.

I could spend this whole post putting erhu videos but let me just put one of the zhonghu specifically, which is a slightly deeper instrument; in Western terms the zhonghu (tuned to G and D) is the viola to the erhu's violin (tuned to D and A)...

To a certain degree, Chinese music is relatively easy to map across to the Western 12-tone chromatic scale. For example, the 十二律 shí'èr lǜ system uses essentially the same frequency ratios as the Pythagorean system. However, Chinese music generally makes much heavier use of pentatonic scales than Western music, and does not by default use equal temperament, instead using its own system of rational frequency ratios. correction: with the advent of Chinese orchestras in the mid-20thC, it seems that Chinese instruments now usually are tuned in equal temperament.

I would like my understanding of music theory to have a 'first class' understanding of Chinese compositions like Horse Racing (and also to have a larger reference pool lmao). I'm going to be starting formal erhu lessons next month, with a curriculum mostly focused on Chinese music. If I have interesting things to report back I'll be sure to share them!

Anyway, in a similar spirit, this post we're gonna try and do a brief survey of various musical constructs relevant to e.g. Japanese music, Klezmer, Blues, Indian classical music... I have to emphasise I am not an expert in any of these systems, so I can't promise to have the most elegant form of presentation for them, just the handles I've been able to get. I will be using Western music theory terms quite a bit still, to try and draw out the parallels and connections. But I hope it's going to be interesting all the same.

Let's start with... pentatonic scales!

Pentatonic scales

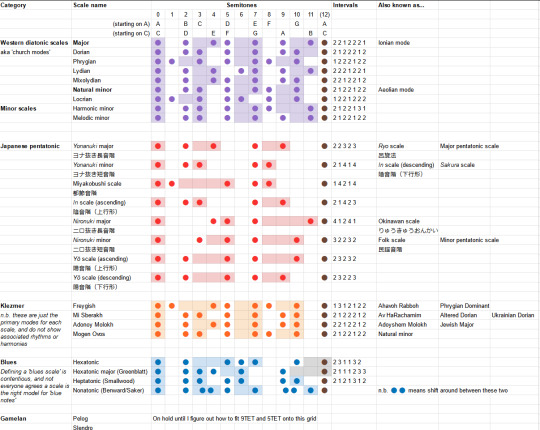
In the previous post we focused most of our attention on the diatonic scale. Confusingly, a "diatonic" scale is actually a type of heptatonic scale, meaning there are 7 notes inside an octave. As we've seen, the diatonic scale is constructed on top of the 12-semitone system.

Strictly defined, a 'diatonic' scale has five intervals of two semitones and two intervals of one semitone, and the one-semitone intervals are spread out as much as possible. So 'diatonic scales' includes the major scale and all its cyclic permutations (aka 'modes'), including the natural minor scale, but not the other two minor scales we talked about last time!

However, whoever said we should pick exactly 7 notes in the octave? That's rather arbitrary, isn't it?

After all, in illustration, a more restricted palette can often lead to a much more visually striking image. The same is perhaps even more true in music!

A pentatonic scale is, as the name suggests, a scale which has five notes in an octave. Due to all that stuff we discussed with small-number ratios, the pentatonic scales we are about to discuss can generally be mapped quite easily onto the 12-tone system. There's some reason for this - 12TET is designed to closely approximate the appealing small-number frequency ratios, so if another system uses the same frequency ratios, we can probably find a subset of 12TET that's a good match.

Of course, fitting 12TET doesn't mean it matches the diatonic scale, necessarily. Still, once you're on the 12 tone system, there's enough diatonic scales out there that you can often define a pentatonic scale in terms of a delta relative to one of the diatonic scale modes. Like, 'shift this degree down, delete that degree'.

Final caveat: I'm not sure if it's strictly correct to use equal temperament in all these examples, but all the sources I find define these scales using Western music notation, so we'll have to go with that.

Sakura, sakura and the yonanuki scale

Let's start with Japanese music. Here's the Edo-period folk song Sakura, Sakura, which is one of the most iconic pieces of Japanese music¸ especially abroad:

This uses the in scale, also known as the sakura pentatonic scale, one of a few widely used pentatonic scales in Japanese folk music, along with the yo scale, insen scale and iwato scale... according to English-language sources.

Finding the actual Japanese was a bit difficult - so far as I can tell the Japanese wiki page for Sakura, Sakura never mentions the scale named after it! - but eventually I found a page for pentatonic scales, or 五音音階 goon onkai. So we can finally determine the kanji for this scale is 陰音階 in onkai or 陰旋法 in senpou. [Amusingly, the JP wiki article on pentatonic scales actually leads with... Scottish folk songs and gamelan before it goes into Japanese music.]

However, perhaps more pertinent is this page: ヨナ抜き音階 which introduces the terms yonanuki onkai and ニロ抜き音階 nironuki onkai. This can be glossed as 'leave out the fourth (yo) and seventh (na) scale' and 'leave out the second (ni) and sixth (ro) scale', describing two procedures to construct pentatonic scales from a diatonic scale.

Let's recap major and minor. Last time we defined them using semitone intervals from a root note (the one in brackets is the next octave):

position: 1, 2, 3, 4, 5, 6, 7, (8) major: 0, 2, 4, 5, 7, 9, 11, (12) minor: 0, 2, 3, 5, 7, 8, 10, (12)

From here we can construct some pentatonic scales. Firstly, here are your yonanuki scales - the ones that delete the fourth and seventh:

major: 0, 2, 4, 7, 9, (12) minor: 0, 2, 3, 7, 8, (12)

Starting on C for the major and A for the minor (the ones with the blank key signature), this is how you notate that in Western sheet music. As you can see, we have just deleted a couple of steps.

The first one is the 'standard' major pentatonic scale in Western music theory; it's also called the ryo scale in traditional Japanese music (呂旋法 ryosenpou). The second one is a mode (cyclic permutation) of a scale called 都節音階 miyakobushi, which is apparently equivalent to the in scale.

In terms of gaps between successive notes, these go:

major: 2, 2, 3, 2, 3 - very even minor: 2, 1, 4, 1, 4 - whoah, huge intervals!

The miyakobushi scale, for comparison, goes...

miyakobushi (absolute): 0, 1, 5, 7, 8, (12) miyakobushi (deltas): 1, 4, 2, 1, 4

JP wikipedia lists two different versions of the 陰旋法 (in scale), for ascending and descending. Starting on C, one goes C, D, Eb, G, A; the other goes C, D, Eb, G, Ab. Let's convert that into my preferred semitone interval notation:

in scale (absolute, asc): 0, 2, 3, 7, 9, (12) in scale (relative, asc): 2, 1, 4, 2, 3 in scale (absolute, desc): 0, 2, 3, 7, 8, (12) in scale (relative, desc): 2, 1, 4, 1, 4

So we see that the 'descending form' of the in scale matches the minor yonanuki scale, and it's a mode (cyclic permutation) of the miyakobushi scale.

We've talked a great deal about the names and construction of the different type of scales, but beyond the vague gesture to the standard associations of 'major upbeat, minor sad/mysterious' I don't think we've really looked at how a scale actually affects a piece of music.

So let's have a look at the semitone intervals in Sakura, Sakura in absolute terms from to the first note...

sakura, sakura, ya yoi no so ra-a wa 0, 0, 2; 0, 0, 2; 0, 2, 3, 2, 0, 2-0, -4

and in relative terms between successive notes:

sa ku ra, sa ku ra, ya yo i no so ra-a wa 0, 0, +2; -2, 0, +2; -2, +2, +1, -1, -2, +2, -2, -4

If you listen to Sakura, Sakura, pay attention to the end of the first line - that wa suddenly drops down a huge distance (a major second - for some reason I miscalculated this and thought it was a tritone) and that's where it feels like damn, OK, this song is really cooking! It catches you by surprise. We can identify these intervals as belonging to the in/yoyanuki minor scale, and even starting on its root note.

Although its subject matter is actually pretty positive (hey, check it out guys, the cherry blossoms are falling!), Sakura, Sakura sounds mournful and mysterious. What makes it sound 'minor'? The first phrase doesn't actually tell you what key we're in, that jump of 2 semitones could happen in major or minor. But the second phrase, introduces the pattern of going up 2, then up 1, from the root note - that's the minor scale pattern. What takes it beyond just 'we're in minor'? That surprise tritone move down. According to the rough working model that 'dissonant notes create tension, consonant notes resolve it', this creates a ton of tension. This analysis is bunk, there isn't a tritone. It's a big jump but it's not that big a jump.

How does it eventually wrap up? The final phrase of Sakura, Sakura goes...

i za ya, i za ya, mi ni yu - u ka nn 0, 0, 2; 0, 0, 2; -5, -4, 2, 0, -4, -5 0, 0, +2; -2, 0, +2; -5, +1, +4, -2, -4, -1

Here's my attempt to try and do a very basic tonal/interval analysis. We start out this phrase with the same notes as the opening bars, but abruptly diverge in bar 3, slowing down at the same time, which provides a hint that things are about to come to a close. The move of -5 down is a perfect fourth; in contrast to the tritone major second we had before, this is considered a very consonant interval. (A perfect fourth down is also equivalent to going up a fifth and then down an octave. So we're 'ending on the fifth'.) We move up a little and down insteps of 4, 2, and 1, which are less dramatic. Then we come back down and end on the fifth. We still have those 4-steps next to 1 steps which is the big flag that says 'whoah we're in the sakura pentatonic scale', but we're bleeding off some of the tension here.

Linguistically, the song also ends on the mora ん, the only mora that is only a consonant (rather than a vowel or consonant-vowel), and that long drawn-out voiced consonant gives a feeling of gradually trailing away. So you could call it a very 'soft' ending.

Is this 'tension + resolution' model how a Japanese music theorist would analyse this song? It seems to be a reasonably effective model when applied to Japanese music by... various music theorist youtubers, but I don't really know! That's something I want to find out more about.

Something raised on the English wiki is the idea that the miyakobushi scale is divided into two groups, spanning a fourth each, which is apparently summarised by someone called Koizumi Fumio in a book written in 1974:

Each group goes up 1 (a semitone or minor second), then 4 (major third), for a total of 5 (perfect fourth). The edges of these little blocks are considered 'nucleus' notes, and they're of special importance.

Can we see this in action if we look at Sakura, Sakura? ...ehhhh. I admit, the way I think of the song is shaped by the way I play it on the zhonghu; I think of the first two two-bar phrases as the 'upper part' and the third phrase as the 'lower part', and neither lines up neatly with these little groups. Still. I suspect Koizumi Fumio, author of Nihon no ongaku, knows a little more about this than I do, so I figure it's worth a mention.

Aside: on absorbing a song

Sakura, Sakura is kinda special to me because it's like the second piece I learned to play on zhonghu (after Twinkle, Twinkle Little Star lmao). I can't play it well, but I am proud that I have learned to play it at least recognisably.

The process of learning to play it involved writing out tabs and trying out different ways of moving my hand. I transcribed Sakura Sakura down to start on F, since that way the open G string of the zhonghu could be the lowest note of the piece, and worked out a tab for it using a tab system I cooked up with my friend. Here's what it looks like. The system counts semitones up from the open string, and it uses an underline to mark the lower string.

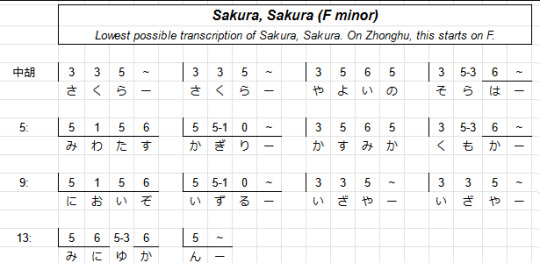
(Also, credit where it's due - I would never have made any progress learning about music if not for my friend Maki Yamazaki, a prodigiously multitalented self-taught musician who can play dozens of instruments, and also the person who sold me her old zhonghu for dirt cheap, if you're wondering why a white British girl might be learning such an unusual instrument. You can and should check our her music here! Maki has done more than absolutely anyone to make music comprehensible to me, and a lot of this post is inspired by discussing the previous post with her.)

When you want to make a song playable on an instrument, you have to perform some interpretation. Which fingers should play which notes? When should you move your hand? How do you make sure you hit the right notes? At some point this kind of movement becomes second nature, but I'm at the stage, just like a player encountering a new genre of videogame, where I still don't have the muscle memory or habituation to how things work, and each of these little details has to be worked out one by one. But this is great, because this process makes me way more intimately familiar with the contours of the song. Trying to analyse the moves it makes like the above even more so.

More Japanese scales

So, to sum up what we've observed, the beautiful minor sounds of Sakura Sakura come from a pentatonic scale which can be constructed by taking the diatonic scale and blasting certain notes into the sea, namely the fourth and the seventh of the scale. But what about the nironuki scale? Well, this time we delete the second and the sixth. So we get, in absolute terms:

major nironuki (abs): 0, 4, 5, 7, 11, (12) major nironuki (rel): 4, 1, 2, 4, 1 minor nironuki (abs): 0, 3, 5, 7, 10, (12) minor nironuki (rel): 3, 2, 2, 3, 2

Hold on a minute, doesn't that look rather familiar? The major nironuki scale is a permutation, though not a cyclic permutation, of the minor yonanuki scale. And the minor nironuki scale is a cyclic permutation (mode) of the major one.

Nevertheless, these scales have names and significance of their own. The major one is known as the 琉球音階 ryūkyū onkai or Okinawan scale. The minor one is what Western music would call a 'minor pentatonic scale'. It also mentions a couple of other names for it, like the 民謡音階 minyou onkai (folk scale).

We also have the yō scale, which like the in scale, comes in ascending and descending forms. You want these too? Yeah? Ok, here we go.

yō scale (asc, abs): 0, 2, 5, 7, 10, (12) yō scale (asc, rel): 2, 3, 2, 3, 2 yō scale (desc, abs): 0, 2, 5, 7, 9, (12) yō scale (desc, rel): 2, 3, 2, 2, 3

The yō scale is what's called an anhemitonic pentatonic scale, which is just a fancy way of saying it doesn't have semitones. (The in scale in turn is hemitonic). The ascending form is also called the 律戦法 ritsusenpou. Here's the complete table of all the variants I've found so far.

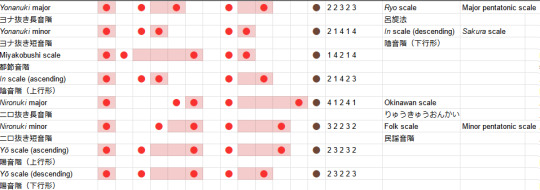
So, in summary: Japanese music uses a lot of pentatonic scales. (In a future post we can hopefully see how that applies in modern Japanese music). These pentatonic scales can be constructed by deleting two notes from the diatonic scales. In general, you land in one of two zones: the anhemitonic side, where all the intervals between successive notes, are 2 and 3, and the hemitonic side, where the intervals are spicier 1s and 4s and a lone 2. From there, you can move between other pentatonic scales by cyclic permutations and reversal.

If you analyse Japanese music from a Western lens, you might well end up interpreting it according to one of the modes of the major scale. In fact, the 8-bit music theory video I posted last time takes this approach. This isn't wrong per se, it's a viable way to getting insight into how the tune works if you want to ask the question 'how does this conjure emotions and how do I get the same effects', but it's worthwhile to know what analytical frame the composers are likely to be using.

Gamelan - when 12TET won't cut it

Gamelan is a form of Indonesian ensemble music. I do not at this time know a ton about it, but here's a performance:

However, if you're reading my blog then it's likely that if know gamelan from anywhere, it's most likely the soundtrack to Akira composed by Shōji Yamashiro.

This blends traditional gamelan instrumentation and voices with modern synths to create an incredibly bold and (for most viewers outside Indonesia!) unfamiliar sound to accompany the film's themes of psychic awakening and evolution. It was an inspired choice, adding a lot to an already great film.

'A gamelan' is the ensemble; 'gamelan' is also the style of music. There are many different types of gamelan associated with different occasions - some gamelans are only allowed to form for special ceremonies. Gamelan is also used as a soundtrack in accompaniment to other art forms, such as wayang kulit and wayang wong (respectively, shadow puppetry and dance).

Since gamelan music evidently uses quite a bit of percussion, and so far we've been focused on the type of music played on strings and wind instruments - a brief comment on the limitations of our abstractions. Many types of drums don't fit the 'tonal music' frame we've outlined so far, creating a broad frequency spectrum that's close to an enveloped burst of white noise rather than a sharply peaked fundamental + overtones. There's a ton to study in drumming, and if this series continues you bet I'll try to understand it.

But there are tonal percussion instruments, and a lot of them are to be found in gamelan, particularly in the metalophone family (e.g. the ugal or jegogan). The Western 'xylophone' and 'glockenspiel' also belong to this family. Besides metalophones, you've got bells, steel drums, tuning forks etc. Tuning a percussion instrument is a matter of adjusting the shape of the metal to adjust the resonant frequency of its normal modes. I imagine it's really fiddly.

In any case, the profile of a percussion note is quite different from the continual impulse provided by e.g. a violin bow. You get a big burst across all frequencies and then everything but the resonant mode dies out, leaving the ringing with a much simpler spectrum.

Anyway, let's get on to scales and shit. While I have the Japanese wikipedia page on pentatonic scales open, that it mentions a gamelan scale called pelog (written ᮕᮦᮜᮧᮌ᮪, ꦥꦺꦭꦺꦴꦒ꧀ or ᬧᬾᬮᭀᬕ᭄ in different languages) meaning 'beautiful'. Pelog is not strictly one scale, but a family of tunings which vary across Indonesia. Depending on who you ask, it might in some cases be reasonably close to a 9-tone equal temperament (9TET), which means a number of notes can't be represented in 12TET - you have that 4 12TET semitones would be equivalent to 3 9TET semitones. From this is drawn a heptatonic scale, but not one that can be mapped exactly to any 12TET heptatonic scale. Isn't that fun!

To represent scales that don't exactly fit the tuning of 12TET, there's a logarithmic unit of measure called the 'cent'. Each 12TET semitone contains 100 cents, so in terms of ratios, a cent is the the 1200th root of 2. In this system, a 9TET semitone is 133 cents. Some steps in the pelog heptatonic scale would then be two 9TET semitones, and others one 9TET semitone. However, this system of 'semitones' does not seem to be how gamelan music is actually notated - it's assumed you already have an established pelog tuning and can play within that. So it's a little difficult for me to give you a decent representation of a gamelan scale that isn't approximated by 12TET.

From the 7-tone pelog scale, whatever it happens to be where you live, you can further derive pentatonic scales. These have various names, like the pelog selisir used in the gamelan gong kebyar. I'm not going to itemise them here both because I haven't actually been able to find the basic pelog tunings (at least by their 9TET approximation).

Another scale used in gamelan is called slendro, a five tone scale of 'very roughly' equal intervals. Five is coprime with 12, so there's no straightforward mapping of any part of this scale to the 12-tone system. But more than that, fully even scales are quite rare in the places we've looked so far. (Though apparently within slendro, you can play a note that's deliberately 'out of place', called 'miring'. This transforms the mood from 'light, cheerful and busy' to one appropriate to scenes of 'homesickness, love missing, sadness, death, languishing'.)

The Western musical notation system is plainly unsuited for gamelan, and naturally it has its own system - or rather several systems. In one method, the seven tones of the pelog are numbered 1 through 7, and a subset of those numbers are used to enumerate slendro tuning. You can write it on a grid similar to a musical staff.

But we could wonder with this research - is the attempt to map pélog to 'equal temperament' an external imposition? Presented with a tuning system with seven intervals that are not consistently equal temperament, averaging them to construct an equal temperament hypothesis on that basis, and finally attempting to prove that gamelan players 'prefer' equal temperament... well, they do at least bother to ask, but I'm not entirely convinced that 9TET or 5TET is the right model. Unfortunately, most of the literature I'm able to find on gamelan music theory with a cursory search is by Western researchers.

There's a fairly long history of Western composers taking inspiration from gamelan, notably Debussy and Saty. And of course, modern Indonesian composers such as I Nyoman Windha have also been finding ways to combine gamelan with Western styles. Here's a piece composed by him (unfortunately not a splendid recording):

Klezmer - layer 'em up

If you've known me for long enough you might remember the time I had a huge Daniel Kahn and the Painted Bird phase. (I still think he's great, I just did that thing where I obsessively listen to one small set of things for a period). And I'd also listen to old revolutionary songs in Yiddish all the time. Because of course I did lmao. Anyway, here's a song that combines both: Kahn's modern arrangement of Arbetlose Marsch in English and Yiddish:

That's a style of music called klezmer, developed by Ashkenazi Jews in Central/Eastern Europe starting in the late 1500s and 1600s. It's a blend of a whole bunch of different traditions, combining elements from Jewish religious music with other neighbouring folk music traditions and European music at large. When things really kicked off at the end of the 19th century, klezmer musicians were often a part of the Jewish socialist movement (and came up with some real bangers - the Tsar may have been shot by the Bolsheviks but tbh, Daloy Politsey already killed him). But equally there's a reason it sounds insanely danceable: it was very often used for dances.

The rest of the 20th century happened, but klezmer survived all the genocides and there are lots of different modern klezmer bands.

The defining characteristics of klezmer per Wikipedia are... ok, this is quite long...

Klezmer musicians apply the overall style to available specific techniques on each melodic instrument. They incorporate and elaborate the vocal melodies of Jewish religious practice, including khazones, davenen, and paraliturgical song, extending the range of human voice into the musical expression possible on instruments.[21] Among those stylistic elements that are considered typically "Jewish" in Klezmer music are those which are shared with cantorial or Hasidic vocal ornaments, including dreydlekh ("tear in the voice"; plural of dreidel)[22][23] and imitations of sighing or laughing ("laughter through tears").[24] Various Yiddish terms were used for these vocal-like ornaments such as קרעכץ (Krekhts, "groan" or "moan"), קנײטש (kneytsh, "wrinkle" or "fold"), and קװעטש (kvetsh, "pressure" or "stress").[10] Other ornaments such as trills, grace notes, appoggiaturas, glitshn (glissandos), tshoks (a kind of bent notes of cackle-like sound), flageolets (string harmonics),[22][25]pedal notes, mordents, slides and typical Klezmer cadences are also important to the style.[18]

So evidently klezmer will be relevant throughout this series, but for now, since we're trying to flesh out the picture of 'how is tuning formed', let's take a look at the notes.

So it's absolutely possible to fit klezmer into the 12TET system. But we're going to need to crack open a few new scales. Though the Wikipedia editors enumerating this list caution us: "Another problem in listing these terms as simple eight-note (octatonic) scales is that it makes it harder to see how Klezmer melodic structures can work as five-note pentachords, how parts of different modes typically interact, and what the cultural significance of a given mode might be in a traditional Klezmer context."

With that caution in mind, let's at least see what we're given. First of all we have the Freygish or Ahavoh Rabboh scale, one of the most common pieces, good friend of the Western phrygian but with an extra semitone. Then there's Mi Sbererakh or Av HaRachamim which is a mode of it, that's popular around Ukraine. Adonoy Molokh or Adoyshem Molokh is the major scale but you drop the seventh a semitone. Mogen Ovos is the same as the natural minor at least on the interval level.

Which means, without the jargon, here are the semitones (wow wouldn't it be nice if you had tables on here?):

position: 1, 2, 3, 4, 5, 6, 7, (8) freygish: 0, 1, 4, 5, 7, 8, 10, (12) deltas: 1, 3, 1, 2, 1, 2, 2 mi sberakh: 0, 2, 3, 6, 7, 9, 10, (12) deltas: 2, 1, 3, 2, 2, 1, 2 adonoy m.: 0, 2, 4, 5, 7, 9, 10, (12) deltas: 2, 2, 1, 2, 2, 1, 2 mogen o.: 0, 2, 3, 5, 7, 8, 10, (12) deltas: 2, 1, 2, 2, 1, 2, 2

...that's a big block of numbers to make your eyes glaze over huh. Maybe this 'convert everything to semitone deltas' thing isn't all it's cracked up to be... or maybe what I need to do is actually visualise it somehow? Some kinda big old graph showing all the different scales we've worked out so far and how they relate to each other? ...hold your horses...

[It seems like what I've done is reinvent something called 'musical set theory', incidentally.]

OK, having enumerated these, let's return to the Wikipedian's caution. What is a pentachord? Pretty simple, it's a chord of five notes. Mind you, some people define it as five successive notes of a diatonic scale.

In klezmer, you've got a bunch of different instruments playing at once creating a really dense sound texture. Presumably one of the things you do when you play klezmer is try and get the different instruments in your ensemble to hit the different levels of that pentachord. How does that work? Well, if we consult the sources, we find this scan of a half-handwritten PDF presenting considerably more detail on the modes and how they're played. The scales above are combined with a 'motivic scheme' presenting different patterns that notes tend to follow, and a 'typical cadence'. Moreover, these modes can have 'sub-modes' which tend to follow when the main mode gets established.

To me reading this, I can kind of imagine the process of composing/improvisation within this system almost like a state machine. It's not just that you have a scale, you have a certain state you're in in the music (e.g. main mode or sub-mode), and a set of transitional moves you can potentially make for the next segment. That's probably too rigid a model though. There's also a more specific aspect discussed in the book that a klezmer musician needs to know how to move between their repertoire of klezmer pieces - what pieces can sensibly follow from what.

Ultimately, I don't want to give you a long list of stuff to memorise. (Sure, if you want to play klezmer, you probably need to get familiar with how to use these modes, but that's between you and your klezmer group). Rather I want to make sure we don't have any illusion that the Western church modes are the only correct way to compose music.

Blues - can anyone agree?

Blues is a style of music developed by Black musicians in the American south in the late 1800s, directly or indirectly massively influential on just about every genre to follow, but especially jazz. It's got a very characteristic style defined by among other elements use of 'blue notes' that don't fit the standard diatonic scale. According to various theorists, you can add the blue notes to a scale to construct something called the 'blues scale'. According to certain other theorists, this exercise is futile, and Blues techniques can't be reduced to a scale.

So for the last part of today's whirlwind tour of scales, let's take a brief look at the blues...

There are a few different blues scales. The most popular definition seems to be a hexatonic scale. We'll start with the minor pentatonic scale, or in Japanese, the minor nironuki scale - which is to say we take the minor diatonic scale and delete positions 2 and 6. That gives:

minor nironuki (abs): 0, 3, 5, 7, 10, (12) minor nironuki (rel): 3, 2, 2, 3, 2

Now we need to add a new note, the 'flat fifth degree' of the original scale. In other words, 6 semitones above the root - the dreaded tritone!

hexatonic blues (abs): 0, 3, 5, 6, 7, 10, (12) hexatonic blues (rel): 3, 2, 1, 1, 3, 2

Easy enough right? Listen to that, it does sound kinda blues-y. But hold your horses! Moments after defining this scale, we read...

A major feature of the blues scale is the use of blue notes—notes that are played or sung microtonally, at a slightly higher or lower pitch than standard.[5] However, since blue notes are considered alternative inflections, a blues scale may be considered to not fit the traditional definition of a scale.

So, if you want to play blues, it's not enough to mechanically play a specific scale in 12TET. You also gotta break the palette a little bit.

There's also a 'major blues' heptatonic scale which goes 0, 2, 3, 4, 7, 9, according to one guy called Dan Greenblatt.

But that's not the only attempt to enumerate the 'blues scale'. Other authors will give you slightly longer scales. For example, if you ask Smallwood:

heptatonic blues (abs): 0, 2, 3, 5, 6, 9, 10, (12) heptatonic blues (rel): 2, 1, 2, 1, 3, 1, 2

which isn't quite a mode of any of those klezmer scales we saw previously, but nearly!

If you ask Benward and Saker, meanwhile, a Blues scale could actually be nonatonic scale, where you add flattened versions of a couple of notes to the major scale.

nonatonic blues (abs): 0, 2, 3/4, 5, 7, 9, 10/11, (12)

There's also an idea that you should play notes in between the semitones, i.e. quarter tones, which would be a freq ratio of the 24th root of 2 if you're keeping score at home.

The upshot of all this is probably that going too far formalise the blues is probably not in the spirit of the blues, but if you want to go in a blues-y direction it will probably mean insert an extra, flattened version of a note to one of your scales. Muck around and see what works, I guess!

Of course, there's a lot more to Blues than just tweaking a scale. For example, 'twelve bar blues' is a specific formalised chord progression that is especially universal in Jazz. What it means for chords to 'progress' is a whole subject, and I think that's the next thing I'll try to understand for post 3. Hopefully we'll be furnished with a slightly broader model of how music works as we go there though.

To wrap up, here's the spreadsheet showing all the 12TET scales encountered so far in this series in a visual way. There's obviously plenty more out there, but this is not ultimately a series about scales. It's all well and good to have a list of what exists, but it's pointless if we don't know how to use it.

Phew

Mind you even with all this, we haven't covered at all some of the most complex systems of tonal music - I've only made the vaguest gesture towards Indian classical music, Chinese music, Jazz... That's way beyond me at the moment. But maybe not forever.

Next up: I'm going to try and finally wrap my head around chords and make sense of what it means for them to 'progress', have 'movement' etc. And maybe render a bit more concrete the vague stuff I said about 'tension' and 'resolution'.

(Also: I definitely know I have friends on here who are very widely knowledgeable about music theory. If I've made any major mistakes, please let me know! At some point I hope to republish this series with nicer formatting on canmom.art, and it would be great to fix the bugs by then!)

[xyymath]

Why the Number 7 is Everywhere: Cultural and Mathematical Significance

The number 7 has long captured human imagination—not just as a symbol of luck or mysticism, but also as a profound and pervasive number in mathematics and culture. From ancient myths to modern probability theory, the number 7 seems to appear everywhere, woven into the fabric of our world.

Cultural Significance

In culture, 7 holds a near-universal place of importance. Think of the Seven Wonders of the World, one of the earliest examples of human categorization. Across different cultures, the number appears in the Seven Deadly Sins, the Seven Chakras, and the seven days of the week. These recurring appearances suggest an innate human tendency to group things into manageable, meaningful sets, with 7 striking the right balance between complexity and simplicity. Even the seven colors of the rainbow or the seven notes in a musical scale speak to its symbolic completeness.

But what makes 7 so special in the human mind? It might be related to cognitive biases—our brains tend to favor things in clusters, and 7 is often the number that feels just right. Psychologist George Miller's famous theory of "The Magical Number Seven" suggests that 7 is the optimal number of items we can hold in our working memory, further solidifying its importance.

Mathematical Significance

While cultural significance can be arbitrary, the mathematical characteristics of 7 reveal its deeper properties and importance. 7 is a prime number, meaning it is divisible only by itself and 1. Prime numbers are the building blocks of all natural numbers, playing an essential role in number theory. As an odd prime, 7 also introduces us to the first of the Sophie Germain primes, an intriguing class of primes with particular properties used in cryptography.

In probability theory, 7 makes an appearance in the context of randomness. The famous seven-sided die from various games like Dungeons and Dragons relies on the fact that 7 is the first prime number greater than 6 (the number of sides on a standard die). Mathematically, the probabilities associated with rolling a 7 are interestingly statistically significant in certain games. For example, in a two-dice roll, the number 7 has the highest probability of appearing, giving it a role in games of chance, which enhances its allure.

Moreover, modular arithmetic (a fundamental concept in number theory) often deals with systems that involve 7. For example, 7 mod 3 equals 1. This cyclic behavior, known as congruences, underlies many cryptographic algorithms.

7 in Geometry and Combinatorics

In geometry, consider the heptagon, a 7-sided polygon. Though not as common as the triangle or pentagon, the heptagon still holds significance in various geometric studies, particularly when exploring regular polygons. A regular heptagon can be constructed by dividing a circle into 7 equal parts, and it has intrigued mathematicians, especially in the realm of constructible polygons.

Combinatorics also reveals the number 7’s importance. In the study of permutations and combinations, the number 7 appears frequently when exploring set theory. For example, the number of ways to arrange 7 distinct objects in a sequence is 7! (7 factorial), which equals 5,040 possible arrangements. This highlights the number's mathematical elegance in the context of permutation theory.

The Golden Ratio, Fibonacci, and 7's Appearance

One of the most fascinating mathematical aspects of 7 involves its connection to the Fibonacci sequence and the Golden Ratio. Although 7 doesn't directly appear in the Fibonacci sequence (which begins 1, 1, 2, 3, 5, 8…), the ratio between consecutive Fibonacci numbers approaches the Golden Ratio, which is roughly 1.618. Interestingly, the Fibonacci sequence often appears in natural patterns such as the arrangement of leaves or the branching of trees—processes that, in turn, shape the world around us.

In the context of music, the number 7 takes center stage through the musical scale. The diatonic scale, the basis for much of Western music, consists of 7 distinct pitches, and the octave is seen as a return to the starting note after 12 semitones. This inherent mathematical structure plays a pivotal role in harmony and rhythm, reinforcing 7’s symbolic resonance as the “perfect” number in the realm of sound.

[reductionisms]

if the gintama “human” = gintoki = perpetually becoming human. then why not the permutation group composed of permutations of gintoki (including himself inside it as most composed identity) and the whole group itself is what it is to be human. cyclically connecting others inside of you and making you in the process, eternally…

[as-if-and-only-if]

so, coding challenge! what’s the quickest way (in a real, normal computer—ok, a very quick way) to generate all and only all length-N sequences of bits such that:

among all bit sequences equivalent to each other under cyclic permutation, only the lexicographically minimal one is generated.

For example:

if N = 4, we only want to wind up with

0000

0001 (equivalent to: 0010, 0100, 1000)

0011 (equivalent to: 0110, 1100, 1001)

0101 (equivalent to: 1010)

0111 (equivalent to: 1110, 1101, 1011)

1111

They don’t need to be generated in lexicographic order, though. Output order is irrelevant.

Also, I’m willing to sacrifice lexicographic minimality for simply generating a single element of each equivalence class if need be—the core of the problem is generating these representatives without redundancy!

If somehow it happens to be convenient, we can even exclude ones that are periodic (like 0000 and 0101, i.e. with nontrivial stabilizer under the cyclic permutation action) if we like. (Doing so is technically better for my application, but only very very slightly, so it’s not necessary in practice.)

Bonus points for an approach that is lazy and parallelizable, e.g. one that bijectively maps integers up to some known quantity to sequences directly; it would be good to sample randomly from things here. Even more bonus points if you can specify N, k, i, and get out the i’th bit sequence of length N (not necessarily in any particular order) that has exactly k 1’s in it! But speed is more important than both of these.

N should be able to be, like, pretty big. At least 25.

Does this problem have a name? Has someone figured this out already?

Note: this is equivalent to generating all lists of integers that sum to N and, similarly, choosing a representative from each orbit-under-cyclic-permutations which is lexicographically maximal among those in the orbit: just look at all runs of the form 0…01 for nonzero bit sequences after rotating the sequence at hand so that it ends with a 1 (e.g. 100011010 ↦ 010001101 = (01)(0001)(1)(01) ↦ [2,4,1,2]; we would not generate this one, and instead generate [4,1,2,2]). (fun exercise: prove this makes sense!)

[disorderofsevenstars]

Gender and Divinity

At one end of the gender spectrum lies the Feminine, associated with Black and darkness, the Earth and mundane matters, collectivity, interconnection, receptivity, cyclicality, synthesis, and heterogeneity. At the other end lies the Masculine, associated with White and illumination, the Heavens and spiritual matters, individuality, separation, exclusivity, linearity, analysis, and homogeneity. These two extremes, Yin and Yang, interact to create a multitude of permutations which lie somewhere in between the purely Feminine and the purely Masculine. Everything that exists as part of what we usually call "reality" is located somewhere in this intermediate space. The extremes themselves are conceptual, and do not exist in material reality, as they are characterized by a purity which cannot be found in Nature.

Sleeping, dreaming, and Death-as-a-state (in contrast with Death-as-a-process) fall within the domain of the Feminine, as do gravity and magnetism, Zero and the even numbers, the elements of Water and Earth, the Moon, and the Cosmic Void or World Egg. Femininity denotes a state of rest, stability, and equilibrium. It promotes slowness and longevity, regeneration and even immortality, characteristic of oceanic or cold environments and the organisms that live there, shielded from the mutagenic properties of solar radiation. The influence of the Feminine on human societies manifests through tribalism, collectivism, and egalitarianism, giving rise to social structures such as animist and polytheistic religions, cults, clans, matrilineal descent systems, polygamy and polyamory, democracy, communism, hedonism, mysticism, subcultures and countercultures. It is driven by the Dionysian impulse to shed the Ego, losing the Self within something larger, like a drop of rain falling into the ocean. The Moon is a mirror; it does not generate its own light.

Femininity is the original and final state of all things. It is prominent in small children and the elderly, more so in non-human animals (especially large and slow-moving animals, those animals which are more primordial or lower on the food chain, as well as small animals with collectivistic tendencies such as ants), even more so in plants, and still more so in rocks, soil, and water. In animals, it is highly oriented toward the senses of touch, taste, and smell. During the course of our evolution, we developed eyes, learned to hunt, learned to walk on land, learned to stand upright, became taller, acquired language and logic, mastered the use of tools and fire, and lost our fur; some of us also lost our melanin. The development of an embryo into an infant, into a child, into an adult, involves a loss of plasticity; bones harden and fuse, the percentage of water in the body decreases, and neural pathways become more rigid. All of these traits indicate a process of Masculinization.

The Masculine is the domain of awareness, alertness, problem-solving, and conflict. It governs changes, transitions, and boundaries. Masculinity is a property of electricity, odd numbers, prime numbers, the elements of Fire and Air, the Sun, and the Axis Mundi. It is dynamic and always in motion, striving to reach the Feminine rest-state, like an arrow flying towards a target, or a key inserted into a lock. The influence of the Masculine on human societies manifests through individualism and inequality, giving rise to colonialism, capitalism, competition, war, monotheism, monogamy, patriarchy, the nation-state, asceticism, and scientific thought. Driven by the Apollonian impulse towards separation and clarity, it prioritizes facts over feelings.

Unable to coexist and seeing plurality as a threat, Masculinity seeks to dominate the Other and propagate the Self, often through violent means; Western culture, Christianity, and Islam are examples of this. Monotheism and patriarchy have a mutual affinity, and in many cases, one promotes the other. The god of a monotheistic religion is usually male. The Sun is the central axis around which all bodies in the Solar System revolve. This tendency of the Masculine to see itself as superior lies behind the association of Light with Good, and Darkness with Evil. Humans, considered as a whole, lean towards Masculinity, and serve as a Masculine counterpart to the natural environment of Earth.

The supreme divinity is like a polygon with an infinite number of sides: simultaneously circular and linear. Fate arises from the interconnection of individual wills, a product of emergent complexity, many individual entities inadvertently working together in a larger system. "GOD" can be described as genderless, or a perfect balance of all possible genders. It has the Feminine quality of Being, and the Masculine quality of Unity. It is an all-pervasive energy field of pure universal consciousness, which can be channeled into various manifestations that possess genders and other specific attributes, like white light being split by a prism into its spectral components. These facets of divinity are conceptualized in every pantheon of deities, in the 12 signs of the Zodiac, in the 22 Major Arcana or 22 letters of the Hebrew Alphabet, in Kabbalah as the 10 Sefirot, in Christianity as the Holy Trinity, in the Tzolk'in as the 20 Naguales, and in Chinese cosmology as the Ba Gua (Eight Trigrams) and 64 Hexagrams of the I Ching.

[3/16/2024]

[shimyereh]

Spring, spring! How many variations On fleeting youth can poets write? I sift through years of permutations — Their words are passionate but trite, An iconography of yearning. In well-worn phrases, brightly burning With uninventive ardor, they Reiterate each old cliché Of meadows, nightingales, and roses. And yet — they struggle to define: Is time a circle, or a line? Spring’s cyclical return exposes A loophole, letting some conclude That even youth may be renewed.

[excludedmiddle]

Back on the horse (a little)

Let's write up a codeforces problem!

A couple important nuances - this problem revolves around fixed points - namely, array elements where the index of the element matches the value of the element (indexing from 1, which codeforces inexplicably loves to do).

My first instinct is that we can conceptualize this as a directed graph. Each permutation of the array is a different node on the graph, and each fixed point transformation is a directed edge from the previous state to the shifted state.

In this model, what we're looking for is a path through the graph with k edges. This could be a cycle or it could be a non-cyclic path, but there are only n nodes in the graph (they are shifts, not true permutations) so either way our answer is bounded.

This alone can get you the solution - construct the graph, find the connections, run DFS - but that solution is slow and annoying to implement.

The missing insight that gets you to a nice solution is that after such a transformation, the fixed point that you used to transform the array must be the last element, simply because of how fixed points work. Then all we have to do is check that element.

Egor has a very nice implementation here:

[starseedfxofficial]

Genetic Algorithm Secrets for AUD/CAD Traders The Genetic Code of Currency: Why AUD/CAD is the Perfect Lab Rat You ever notice how some traders treat the Australian Dollar Canadian Dollar pair like that drawer full of tangled wires? Too complex, too random, too "I'll deal with it later"? Here's the twist: AUD/CAD isn't random. It’s just misunderstood. And when paired with the hidden weapon of genetic algorithms, it becomes a predictable beast—once you decode its DNA. If you've ever felt like your trades are more "Darwin Awards" than "Darwinian survival," this guide will flip your Forex evolution on its head. So, let’s break the genetic code of the market, one optimized allele at a time. The Hidden Pattern Most Traders Ignore The AUD/CAD pair is what we in the underground call a "cyclical chameleon"—it thrives on macroeconomic rhythms (think oil prices, mining cycles, and labor force dynamics), yet traders often treat it with the same RSI rules they use on EUR/USD. Mistake #1: Assuming AUD/CAD trends like a momentum-based pair. Truth: AUD/CAD often operates like a reversion-to-mean machine, especially during Asian and early European sessions. And here’s where genetic algorithms (GAs) flex their computational biceps. Genetic Algorithms 101 (Without the PhD Pain): - Think of a GA as a matchmaking app for trading rules—only it doesn’t swipe left on bad strategies. It evolves them. - Inspired by natural selection, GAs simulate thousands of strategy "mutations" and keep the best performers. - Unlike traditional backtesting, GAs don’t just optimize a few parameters. They test entire logic trees. Now imagine running 50,000 strategy variations on AUD/CAD over the past 10 years. GAs do this while you're still brewing your morning coffee. Why Most Optimization Tools Are Trapped in 2005 Let’s be real. Most traders use optimization like seasoning—"a little more of this indicator, a little less of that... boom, flavor." The problem? That’s curve-fitting, not evolution. Genetic algorithms don’t just tweak RSI from 14 to 16. They rebuild your entry/exit framework, test moving average crossovers, custom candlestick patterns, and exotic risk models all in one go. You’re not just seasoning. You’re Gordon Ramsay-ing your trading strategy. Case Study: The Mutation That Outperformed In a StarseedFX backtest (2024), a genetic algorithm evolved a strategy for AUD/CAD that: - Used a 7-period Williams %R + 21-day OBV divergence - Only traded during overlapping Tokyo-London hours - Applied a variable stop-loss based on daily ATR percentile - Avoided Friday entries entirely Result? 18.4% annualized return with a max drawdown of only 4.6%—beating most institutional strategies by a country mile. The Weird (But Effective) Filters GAs Uncovered Here’s where it gets juicy. Through thousands of generations, GAs found hidden relationships between AUD/CAD movement and: - Canadian Crude Inventories (weekly) - Australian Building Approvals YoY - NYMEX front-month oil contract volatility spikes - Unemployment deviation between RBA and BoC forecasts Who looks at this stuff? Genetic algorithms do. And now, so can you. Step-by-Step: Evolve Your Own AUD/CAD Strategy with GAs - Gather Raw Data: Download at least 5 years of AUD/CAD 1-hour data. - Collect Fundamentals: Pull weekly economic data like crude stocks, approvals, and CPI surprises. - Choose a Platform: Use software like StrategyQuant, MQL5 Optimizer, or Python libraries (e.g., DEAP). - Define Your Chromosomes: Create logic blocks like entry signals, stop-loss rules, time filters, and indicators. - Run the GA Simulation: Let the algorithm generate and test thousands of permutations. - Select for Fitness: Choose strategies with low drawdown, high Sharpe ratio, and consistency across years. - Walk-Forward Test: Validate on out-of-sample data. - Deploy & Monitor: Automate it. Tweak as needed. Let it evolve over time. Pro Tip: Only trust a strategy that survived both 2020’s chaos and 2022’s inflation hammer. The Expert Angle "Genetic algorithms provide a frontier for truly adaptive trading systems. Unlike neural nets, they don’t just fit—they innovate." — Dr. Ernest Chan, Author of Quantitative Trading "We’re seeing retail traders outperform funds using GA-powered optimizations. It’s a new arms race, and the smart money is adapting fast." — Paul Kavanaugh, Former Forex Strategist, Barclays Capital The Underground Advantage (You Won’t Hear on YouTube) The majority of trading education is built on ancient frameworks: MACD this, Bollinger that. Meanwhile, quietly in forums and Python subreddits, underground quants are crafting genetic strategies that adapt like bacteria in a petri dish. And AUD/CAD? It’s the ideal test subject. Oil-sensitive. Politically stable. Low noise-to-signal ratio. If you’re not using GAs on this pair, you’re basically trying to catch kangaroos with a fishing net. Before You Go, Remember This Genetic algorithms aren’t magic. They’re disciplined chaos. They require clean data, smart boundaries, and regular mutation control. But they give back something no static system can: a strategy that evolves with the market. So the next time your AUD/CAD setup fails, ask yourself: “Am I optimizing… or just overfitting?” Because while others chase lagging indicators, you could be running evolutionary experiments that would make Darwin blush. Elite Takeaways - Genetic algorithms evolve trading strategies far beyond traditional optimization. - AUD/CAD’s cyclical nature makes it an ideal candidate for GA-based strategies. - GAs found hidden edge in macroeconomic factors like crude oil volatility and unemployment forecast gaps. - Real-world GA strategies can achieve lower drawdowns and higher returns than many institutional models. - Use software or Python libraries to create your own GA frameworks and adapt over time. Want More Alpha? Level up your edge with StarseedFX’s premium tools: - Forex News Today: Stay two steps ahead with real-time insights. - Free Forex Courses: Learn the secrets they don’t teach on YouTube. - Community Membership: Trade with insiders, not followers. - Free Trading Plan: Your custom roadmap to Forex evolution. - Smart Trading Tool: Automate, optimize, and dominate. —————– Image Credits: Cover image at the top is AI-generated Read the full article

[literaturereviewhelp]

Group action   Consider a necklace with four colored beads with the possibility of each bead being green or blue. The necklace can be flipped over and the beads are able to rotate around the necklace. The necklace may have 16 different arrangements. However, the rotation of the beads may yield similar arrangements. Flipping the beads also results in similar necklace arrangements for different flip modes. These operations are called necklace rigid motions. Each necklace rigid motion permutes the elements of the necklace to affect the arrangement (Po? lya and Tarjan et al., 2010). The rigid motions are represented by permutations of S or X. the S permutations are commonly used as they represent the four vital elements, which is advantageous over the X elements that are 16 in number. Suppose X represents a finite set like a set of beads and G a group of permutations of the finite set X or a symmetry group that is finite and acts on X. Therefore, G represents a particular group of permutations of the set of beads. If the beads make up an necklace with n number of beads, the rotational symmetry is relevant and G is the cyclic group, C. supposing that the set of colors of the finite beads is denoted Y, YX denotes the set of colored arrangements of the beads (Po?lya and Tarjan et al., 2010). This means Y is a function of X with the number of colors found by |Y| =t. representing elements of G as permutations of X requires a notation that is much more extensive. A 900 anticlockwise rotation of G, the permutation (1)(2,3,4,5)(6,7,8,9)(10,11)(12,13,14,15)(16) on X could be denoted by writing ?2. In comparison, the use of the four-value system will illustrate the rigid motion as (1234). According to the theorem, the number of orbits of G of colored arrangements is calculated using: . Suppose S is a collection of objects and R a set of elements like bead colors. Describing R as colors of S means the assignment of unique colors to each of the elements of S. this relation is interpreted as ; f : S > R. if the value of |S| is n and |R| is m the total distinct colorings will be mn . for a set Y and group G, an action of G on Y creates the relationship G ? Y > Y. this satisfies two properties of the theory illustrated below. 1. (g1g2)(y) = g1(g2(y)) for all g1, g2 € G and y € Y 2. e(y) = y for all y € Y, where e represents the identity element in G Burnside’s theorem This theorem is applied in the counting of the patterns when a group is acting on a set of colorings. The focus lies in the count of the number of orbits when the group is acting on the set. Supposing a group G is acting on a set of elements Y. for each element ? € G in the set, it is fixed by ? as Fix(?). Generally this implies Fix(?) = {y € Y | ?(y) = y}. Applying the specifics of a necklace similar to the one in the previous theorem, the rigid motions of a square, G, that are acting on the set X, a sequence is developed (Po?lya and Tarjan et al., 2010). The enumeration relies on the on the notation ? Read the full article

[pigeon-playlists]

Monthly Music Diary #2

A project for myself, so I can remember the music I enjoy.

Even just on this second MMD, I'm realising that I'm wildly inconsistent when it comes to listening to things. Which to be fair I already knew, but the way I veer wildly between listening to whole albums when I'm working vs having one of my comfort shows on a rewatch (Gossip Girl, Gilmore Girls, 90210, The Bold Type etc) on repeat is so intensely cyclical.

I went through a week or so of having background TV on instead of listening to stuff, but finally got back to music a few days ago, mostly via the route of listening to Daily Mixes and realising the only thing i wanted to listen to was Clairo.

So it's weird that the first thing I want to talk about is...not Clairo.

--

Luna Li - When A Thought Grows Wings

This whole album is gorgeous, and Would You Be My... is my absolute favourite. Sweet, longing, a little bit haunting. I love Luna's voice so much; it really scratches my brain nicely. Her vocals are breathy in a way that just doesn't irritate me the wyay it does with some people.

--

Amon Tobin - Permutation

When I don't know what, or can't decide what to listen to, I listen to Amon Tobin. Two albums I always come back to are Permutation and his Splinter Cell: Chaos Theory OST. Both are absolute favourites of mine, and my three favourite tracks from him are 'Fast Eddie' from Permutation, 'El Cargo' (AKA the Cargo Suite) from Chaos Theory, and 'Chocolate Lovely' from Supermodified.

As an album, I listen to Supermodified less often than the other two, but it still crops up sometimes mostly so I can listen to 'Chocolate Lovely' in context.

--

SIMS 2 SOUNDTRACKS

I've been feeling nostalgic for the Sims on its 25th anniversary, but particularly Sims 2, which was the first game I was ever truly obsessed with and have never got over.

Some of the individual expansion pack OSTs are on Spotify, but I had to go to YouTube to find the Open for Business one. Then I found out very suddenly that Open for Business has Simlish covers of Kajagoogoo's 'Too Shy' and Howard Jones' 'Things Can Only Get Better'??? Genuinely how did I never know this.

Jk, I know why - it's because I only ever put my Sims' radio on Shopping or Rock when I was a kid. I was sort of obsessed with the Simlish Flaming Lips cover, as well as that Steadman cover I can never ever remember the name of.

Just imagining Howard Jones in his studio singing in Simlish is very funny to me. He's so great.

Having listened to the soundtracks from all four main Sims games, I feel pretty dedicated to the Sims 2 soundtrack more than any other. It's such a comfort to me, and reminds me of spending evenings after school and weekends as a kid just absorbed in my little dolls, snuggled up with a duvet around me.

--

Heterotic - Weird Drift

I've had this album on my 'to listen' playlist for a long time, and finally decided to do it when I was cleaning up my messy Spotify. It wasn't quite what I was expecting - I came across it on a recommended list on μ-ziq's record label, I'm pretty sure? So I think I was expecting some rbasive Squarepusher-type thing (which I do enjoy, but can't listen to for long periods of time because it makes me fight-y lol). But I did really enjoy it - particularly Sultana and Shoe Soul. I thought the vocals were a bit OTT at points, but in general the whole was very pretty and vibe-y.

--

Neutral Milk Hotel - In The Aeroplane Over The Sea

This is another one I meant to listen to for a looooong time. I...can't quite tell how I feel about it? I liked it in parts, and a couple of songs I explicitly enjoyed, but it feels like maybe it was one of those things you really had to be there for at the time. I think were a couple of points where I was definitely not enjoying it, but by the time Oh Comely came on I'm pretty sure I was into it. We'll see if I ever pick this album up again, I guess.

--

Masayoshi Takanaka - On Guitar

Sometimes I am in a bad mood, and I listen to Masayoshi Takanaka, and the bad mood goes away. That's all I have to say, really.

--

Onra - Nobody Has To Know

Goose told me to listen to this, and when I did I was surprised by how much it didn't strike me? Not bad at all by any means, but when she was listening to it, it sounded 100% my type of thing. But then when it came to listening to it myself, it didn't quite hit the same. I liked this one, though:

--

MINNIE - Her

10/10 no notes, loved this whole album, love this for her. Pleasantly surprised all the way through.

--

Luna Li - When A Thought Grows Wings

I am so in love with this album, it's become my current "I don't know what to listen to" album, which is actually more of a compliment than it sounds because I'm really picky with what I listen to and am completely mood-led. Like I could have my favourite album on but if I'm not in the correct mood or...idk the weather isn't right, it's not staying on. So basically I'm saying Luna Li is good for all moods and weathers and that's really quite impressive.

--

...and after this I got into a mood where I wanted to have the TV on in the background while I'm working again, and didn't really listen to anything properly for the rest of February.

[infriga]

I finally finished Saint's campaign, Rubicon sucked a lot but other than that I quite enjoyed it.

I have a few theories based on Saint's ending. My main one is that Saint isn't the Triple Affirmative (it's been pretty much confirmed that Saint and Sliver of Straw weren't involved with each other or otherwise had anything to do with each other and that Saint wasn't even around at the same time as Straw), but IS the closest it's possible to get without actually being the Triple Affirmative itself. I think the Triple Affirmative would be someone or something that managed to ascend, like fully ascend, and then figure out how to come back afterwards. I think Saint got to the edge of ascending, but then wanted to share what they were witnessing/experiencing with others to help them ascend as well, and refused to ascend since they didn't think they would be able to ascend first and then come back. But as a result they became an echo, but unlike other echoes they aren't tied to a specific location. And I think that's where their campaign starts, with them as an echo.

But the thing is, I don't think they're stuck repeating the same actions or memories over and over again, It's implied that their experience is cyclical, but not that their experience is the same every single time. I think every time they ascend creatures, then go back to the void sea through Rubicon, they're refusing to ascend again and returning, but each time they return it's a new timeline. They're essentially going through and ascending every individual version of each creature in each timeline, but since by nature there are an endless number of timelines, they can never reach an end to this task, they're stuck endlessly ascending every individual version of everyone. I think they may even be guiding the spirits of those they forcibly ascended through Rubicon by getting rid of the guardians, and that's why if you ascend the iterators they appear near the end to speak to you before vanishing. That's why you have to start a new campaign after finishing and can't continue the old one like you can with all the other slug cats, but you can smuggle an item from the previous campaign in your stomach if you go to the void sea with it, which as far as I can tell is intentional and something that only Saint can do. No two playthroughs will be the same, and you can never go back to a previous playthrough, so each playthrough is like a new timeline, similar but not exactly the same.

I based this theory largely on the fact that it seems like Saint ISN'T the real Triple Affirmative, and dialogue from Pebbles and Moon, where they talk about time collapsing in on itself, how Saint is real even if the events around them are like a dream, how they sense the various versions of themselves, even referring to them as permutations, etc. I think echos are themselves outside of time, extending through each timeline like a dream of one version of a person who once failed to ascend, but in Saint's case they're referred to as real while those around them are the ones dreaming, as if everyone else is an echo of someone who hasn't ascended yet. Ripples upon ripples. So by ascending creatures Saint is essentially waking them up from said dream, and helping them pass on to the next stage or whatever comes after ascension. But as a result they are unable to ever finish ascending themselves, even if they can physically make it back to the void sea and force their way past the guardians, they will always refuse to finish ascending because they feel duty bound to continue to the next permutation and ascend the next batch. Maybe that's what their echo is tied to, not a place but a choice.

Presumably, the difference between what Saint has become and a true Triple Affirmative, is that a true Triple Affirmative would be able to be easily applied "at scale", aka they could ascend every version of someone in every timeline at the same time. And based on the iterator dialogue in Rubicon, I think it makes sense that the Triple Affirmative would be someone/thing that made it past ascension and then somehow came back. They'd have the completed knowledge of how ascension truly works, while Saint's knowledge is still incomplete because they didn't make it all the way over to the other side before returning. So they are essentially a failed Triple Affirmative.

I feel like when The Watcher comes out it may shed some light on whether this theory has any ground to stand on in regards to the existence of multiple alternative timelines, so I guess we'll see. Or maybe it'll just make things even less clear, or do it's own separate thing, you never know with Rain World lol.

[iit-jam]

IIT JAM Syllabus 2025: A Comprehensive Guide

The IIT JAM (Joint Admission Test for Masters) is one of the most competitive exams for students aspiring to pursue postgraduate studies in esteemed institutions like IITs and IISc. Mathematics, being a core subject, attracts candidates with strong analytical and problem-solving skills. To excel in this exam, a thorough understanding of the IIT JAM Mathematics Syllabus 2025 is essential. This blog outlines the syllabus in detail and provides tips to help candidates prepare effectively.

Overview of IIT JAM Mathematics Syllabus 2025

The IIT JAM Mathematics Syllabus 2025 is crafted to test the candidates' knowledge of fundamental mathematical concepts covered at the undergraduate level. The syllabus is broad, covering topics such as calculus, linear algebra, differential equations, and numerical analysis. Each section focuses on key areas that are crucial for advanced studies and professional applications.

Key Topics in the Syllabus

1. Sequences and Series

This section includes the convergence of sequences and series, tests for convergence (such as comparison, ratio, and root tests), and the study of power series and their radius of convergence.

2. Differential Calculus

Candidates must understand single-variable calculus concepts like limits, continuity, and differentiability. Topics also include Taylor series, mean value theorem, and indeterminate forms. For multivariable calculus, partial derivatives, maxima, minima, saddle points, and the method of Lagrange multipliers are essential.

3. Integral Calculus

This section covers definite and indefinite integrals, improper integrals, and special functions like beta and gamma functions. The application of double and triple integrals is also emphasized.

4. Linear Algebra

A critical area of the syllabus, it focuses on vector spaces, subspaces, linear transformations, rank, nullity, eigenvalues, eigenvectors, and matrix diagonalization. Understanding the solution of systems of linear equations is vital.

5. Real Analysis

This section involves the properties of real numbers, limits, continuity, differentiability, and Riemann integration. Candidates must also be familiar with sequences, Cauchy sequences, and uniform continuity.

6. Ordinary Differential Equations (ODEs)

This includes first-order ODEs, linear differential equations with constant coefficients, systems of linear ODEs, and Laplace transform techniques for solutions.

7. Vector Calculus

Important topics include gradient, divergence, curl, line integrals, surface integrals, and volume integrals, along with Green’s, Stokes’, and Gauss divergence theorems.

8. Group Theory

The basics of groups, subgroups, cyclic groups, Lagrange’s theorem, permutation groups, and homomorphisms are covered.

9. Numerical Analysis

This section focuses on numerical solutions for non-linear equations, numerical integration and differentiation, interpolation methods, and error analysis.

Tips for Preparing the Syllabus

Understand the Weightage: Review past papers to prioritize high-scoring topics like Linear Algebra, Real Analysis, and Differential Calculus.

Strategize Your Study Plan: Divide the syllabus into manageable sections, set achievable goals, and stick to a consistent schedule.

Practice Regularly: Solve previous years’ papers and mock tests to familiarize yourself with the question patterns and improve speed.

Strengthen Fundamentals: Focus on core concepts by revisiting undergraduate textbooks and seeking clarity on challenging topics.

Leverage Online Resources: Utilize tutorials, study materials, and practice tests available online to supplement your preparation.

Conclusion

The IIT JAM Mathematics Syllabus 2025 is extensive yet well-structured, providing a clear framework for aspirants to plan their preparation. By mastering the syllabus and practicing diligently, candidates can confidently tackle the exam and achieve their dream of joining top postgraduate programs. Dedicate time, stay consistent, and focus on strengthening your mathematical foundations to excel in IIT JAM Mathematics 2025.

[geopolicraticus]

Friday 11 October 2024

Grand Strategy Newsletter

The View from Oregon – 310

Permutation of Cyclicality and Linearity

…in which I discuss linear and cyclical history, reductivist formulations of history, Nietzsche’s eternal return, inter-definability of permutations, temporal iterations, uniqueness in time, repetition, plate tectonics, and the supercontinent cycle…

Substack: https://geopolicraticus.substack.com/p/permutations-of-cyclicality-and-linearity

Medium: https://jnnielsen.medium.com/permutations-of-cyclicality-and-linearity-1dead7293ef4

Reddit:

[russian--wind]

My last three days in New orleans.

If I could visualize time, I often see the threads of a chaotic attractor, zipping through an invisible ether like a craft in an asteroid belt. Trajectories. People think that the immaterial and intangible have no limitations or structure, which is where the concept of the "butterfly effect" comes from, as well as the common pitfall of FOMO and feeling like you have no control over the events around you. But time like all good things has a tight order to it. Most paths circle back around. Sometimes you run into a dead end. It's like in a game, where what you're really playing with is the higher order but the effects are only visible in the tangible. So you have to abstract a level out, and mastery comes when you don't get too rigid about it, and kind of just flow with it. Often eventspace is like water. For instance, all the houses I visited to potentially move in have all been in the same neighborhood. And they're all dead ends now. I would've ended up here no matter which set of paths I took, and it would have ended in some permutation of what happened. For an intuitive life experience fills in your calibration of what navigating through time, making decisions, and manipulating (in the same way you manipulate a ball in a game) events around you can look like.

When I was 20, I was fascinated by mathematics. I threw it away like the suicidal protagonist of Cormac McCarthy's swan song, Stella Maris. Alicia, like me at 20, is a brilliant math prodigy, who, afflicted with hallucinations and the belief that her brother whom she's in love with is dead, commits suicide at 20. I lived, but I threw away the math until the underlying emotion beneath it resurfaced in New Orleans this year. Did I tell you that Alicia's brother, who was in love with her, ends up drifting in New Orleans a decade after her death? As a salvage diver? And that the other day, the mailman walked into my workplace and handed me an anonymous postcard with a quote from Cormac's The Road? And that I'm currently in a round of interviews with the institute where he holed up in the last two decades of his life and wrote those books, the same institute that studies the complex systems phenomena I was entranced with as a 20 year old?

I could feel in the patterns of dynamical systems and wave flows, the shapes of fractal geometry, and scaling theory, the shape of the universe around us expressed in some gestalt way -- that's what drew me to those topics.

Synchronicities point to some trajectories that are so dense in our personal life path that they are inescapable. Not in a doom-y way, more in a way that engenders faith. Your destiny won't leave you. You can't miss your destiny because you went down the wrong aisle at the grocery store. Gravity doesn't work like that and even the intangible is ruled by physical laws.

So! Free from FOMO, what will you do? How will you meet the universe halfway?

Time is also a wave, and I think about it less like this. There are cycles that repeat themselves with different periodic frequencies. Astrology is really a study of time. I wonder if people struggle with mixing the music of the spheres (the zodiac) with the cyclical nature of time. How do you know when exactly it stops being Aries and starts being Gemini? I don't know, the same way you know it stops being a fourth and starts being a fifth? Or that there is a fourth and a fifth? We don't expect order to arise out of chaos, much less a geometric, harmonious, implicitly beautiful order.

My last three days in New Orleans. I understand this time's coming to an end. I'm taking it all in. Old decision points are returning to me, magnifying. The job interview. Camp. Timelines I didn't take in 2018 are being offered to me once more. Like a promised reunion, or just the second verse. Neutral Milk Hotel's In the Aeroplane Over the Sea spinning through my head, through the galaxies, the half decade separating me from when I dreamed of this city and didn't know it was a real place. I sat in Jackson Square and played the song again and I could feel myself on the couch reaching for a place, reaching for the song, reaching for myself. I connected the two times and felt them click. Magic. Ever have a vision and then you're in the vision?

[canmom]

aaah tysm! you're one of the most knowledgeable people I know when it comes to music theory, so I was hoping you'd read this and like it ^^'

That's fascinating about the historical context to the church modes! I fully admit I skimmed right over all the parts of the wiki article on medieval church modes to understand the version of the idea used in modern day composition, but evidently that's very reductive ^^'

I've had someone else talk to me a bit about modes and mode progressions, so for the next part I definitely want to build a much stronger understanding of the idea than just 'oh it's cyclic permutations'.

Music Theory Notes (for science bitches) 1: chords & such

This is one of these series where I use my blog as a kind of study blog type thing. If you're knowledgeable about music theory, it will be very basic. But that's kind of the problem, I've really struggled to absorb those basics!

When I was a teenager I learned to play violin and played in orchestras. I could read music, and play decently enough, but I didn't really understand music. I just read what was on the page, and played the scales I had to play for exams.

Lately I've been trying to learn music again. This time my instruments are zhonghu, voice, and DAWs. At some point I might get my violin back too. But really, I'm a total beginner again, and this time I want to do it properly.

For a long time when I tried to learn about music I would get overwhelmed with terminology and jargon and conventions. I might watch videos on composition and they'd be interesting but a lot of it would just fly over my head, I'd just have to nod along because I had no idea what all the different types of chord and such were. I tried to learn from sites like musictheory.net, but I found it hard to figure out the logical structure to fit it all into.

I feel like I'm finally making a bit of headway, so it's time to take some notes. The idea here is not just to answer the what, but also to give some sense of why, a motivation. So in a sense this is a first attempt at writing the introduction to music theory I wish I'd had. This is going to assume you know a little bit about physics, but basically nothing about music.

What is music? From first principles.

This is impossible to answer in full generality, especially since as certain people would be quick to remind me, there's a whole corner of avant-garde composers who will cook up counterexamples to whatever claim you make. So let's narrow our focus: I'm talking about the 'most common' type of music in the society I inhabit, which is called 'tonal music'. (However some observations may be relevant to other types of music such as noise or purely rhythmic music.)

Music is generally an art form involving arranging sound waves in time into patterns (in the sense that illustration is about creating patterns on a 2D surface with light, animation is arranging illustrations in time, etc.).

Physically, sound is a pressure wave propagating through a medium, primarily air. As sound waves propagate, they will reflect off surfaces and go into superposition, and depending on the materials around, certain frequencies might be attenuated or amplified. So the way sound waves propagate in a space is very complicated!

But in general we've found we can pretty decently approximate the experience of listening to something using one or two 'audio tracks', which are played back at just one or two points. So for the sake of making headway, we will make an approximation: rather than worry about the entire sound field, we're going to talk about a one-dimensional function of time, namely the pressure at the idealised audio source. This is what gets displayed inside an audio editor. For example, here's me playing the zhonghu, recorded on a mic, as seen inside Audacity.

A wrinkle that is not relevant for this discussion: The idealised 'pressure wave' is a continuous real function of the reals (time to pressure). By contrast, computer audio is quantised in both the pressure level and time, and this is used to reconstruct a continuous pressure wave by convolution at playback time. (Just like a pixel is not a little square, an audio sample is not a constant pressure!) But I'm going to talk about real numbers until quantisation becomes relevant.

When the human eye receives light, the cone cells in the eye respond to the frequencies of EM radiation, creating just three different neural signals, but with incredibly high sensitivity to direction. By contrast, when the human ear receives sound, it is directed into an organ called the cochlea which is kind of like a cone rolled up into a spiral...

Inside this organ, the sound wave moves around the spiral, which has a fascinatingly complex structure that means different frequencies of wave will excite tiny hairs at different points along the tube. In effect, the cochlea performs a short-time Fourier transform of the incoming sound wave. Information about the direction of the incoming wave is given by the way it reflects off the shape of the ear, the difference between ears, and the movement of our head.

So! In contrast to light, where the brain receives a huge amount of information about directions of incoming light but only limited information of the frequency spectrum, with sound we receive a huge amount of information about the frequency spectrum but only quite limited information about its direction.

Music thus generally involves creating patterns with vibration frequencies in the sound wave. More than this, it's also generally about creating repeating patterns on a longer timescale, which is known as rhythm. This has something to do with the way neurons respond to signals but that's something I'm not well-versed in, and in any case it is heavily culturally mediated.

All right, so, this is the medium we have to play with. When we analyse an audio signal that represents music, we chop it up into small windows, and use a Fourier transform to find out the 'frequencies that are present in the signal'.

Most musical instruments are designed to make sounds that are combinations of certain frequencies at integer ratios. For example here is a plot of the [discrete] Fourier transform of a note played on the zhonghu:

The intensity of the signal is written in decibels, so it's actually a logarithmic scale despite looking linear. The frequency of the wave is written in Hertz, and plotted logarithmically as well. A pure sine wave would look like a thin vertical line; a slightly wider spike means it's a combination of a bunch of sine waves of very close frequencies.

The signal consists of one strong peak at 397Hz and nearby frequencies, and a series of peaks at (roughly) integer multiples of this frequency. In this case the second and third peaks are measured at 786Hz, and 1176Hz. Exact integer ratios would give us 794Hz and 1191Hz, but because the first peak is quite wide we'd expect there to be some error.

Some terminology: The first peak is called the fundamental, and the remaining peaks are known as overtones. The frequency of the fundamental is what defines this signal as a particular musical note, and the intensities of the overtone and widths of the peaks define the quality of the note - the thing that makes a flute and a violin playing the same fundamental frequency sound different when we listen to them. If you played two different notes at the same time, you'd get the spectrums of both notes added together - each note has its own fundamental and overtones.

OK, so far that's just basic audio analysis, nothing is specific to music. To go further we need to start imposing some kind of logical structure on the sound, defining relationships between the different notes.

The twelve-tone music system

There are many ways to do this, but in the West, one specific system has evolved as a kind of 'common language' that the vast majority of music is written in. As a language, it gives names to the notes, and defines a space of emotional connotations. We unconsciously learn this language as we go through the process of socialisation, just as we learn to interpret pictures, watch films, etc.

The system I'm about to outline is known as 12-tone equal temperament or "12TET". It was first cooked up in the 16th century almost simultaneously in China and Europe, but it truly became the standard tuning in the West around the 18th century, distilled from a hodgepodge of musical systems in use previously. In the 20th century, classical composers became rather bored of it and started experimenting with other systems of tonality. Nevertheless, it's the system used for the vast majority of popular music, film and game soundtracks, etc.

Other systems exist, just as complex. Western music tends to create scales of seven notes in an octave, but there are variants that use other amounts, like 6. And for example classical Indian music uses its own variant of a seven-note scale; there are also nuances within Western music such as 'just intonation' which we'll discuss in a bit; really, everything in music is really fucking complicated!

I'll be primarily discussing 12TET because 1. it's hard enough to understand just one system and this one is the most accessible; 2. this has a very nice mathematical structure which tickles my autismbrain. However, along the way we'll visit some variants, such as 'Pythagorean intervals'.

The goal is to try and not just say 'this is what the notation means' but explain why we might construct music this way. Since a lot of musical stuff is kept around for historical reasons, that will require some detours into history.

Octaves

So, what's the big idea here? Well, let's start with the idea of an octave. If you have two notes, let's call then M and N, and the frequency of N is twice the frequency of M... well, to the human ear, they sound very very closely related. In fact N is the first overtone of M - if you play M on almost any instrument, you're also hearing N.

Harmony, which we'll talk about in a minute, is the idea that two notes sound especially pleasant together - but this goes even further. So in many many music systems around the world, these two notes with frequency ratio of 2 are actually identified - they are in some sense 'the same note', and they're given the same name. This also means that further powers of 2, of e.g. 4, 8, 16, and so on, are also 'the same note'. We call the relationship between M and N an octave - we say if two notes are 'an octave apart', one has twice the frequency of the other.

For example, a note whose fundamental frequency is 261.626Hz is known as 'C' in the convention of 'concert pitch'. This implies an infinite series of other Cs, but since the human ear has a limited range of frequencies, in practice you have Cs from 8.176Hz up through 16744.036. These are given a series of numbers by convention, so 261.626Hz is called C4, often 'middle C'. 523.251Hz is C5, 1046.502Hz is C6, and so on. However, a lot of the time it doesn't matter which C you're talking about, so you just say 'C'.

But the identification of "C" with 261.626Hz * 2^N is just a convention (known as 'concert pitch'). Nothing is stopping you tuning to any other frequency: to build up the rest of the structure you just need some note to start with, and the rest unfolds using ratios.

Harmony and intervals

Music is less about individual notes, and more about the relationship between notes - either notes played at the same time, or in succession.

Between any two notes we have something called an interval determined by the ratio of their fundamental frequencies. We've already seen one interval: the octave, which has ratio 2.

The next interval to bring up is the 'fifth'. There are a few different variants of this idea, but generally speaking if two notes have a ratio of 1.5, they sound really really nice together. Why is this called a 'fifth'? Historical reasons, there is no way to shake this terminology, we're stuck with it. Just bear with me here, it will become semi-clear in a minute.

In the same vein, other ratios of small integers tend to sound 'harmonious'. They're satisfying to hear together. Ratios of larger integers, by contrast, feel unsatisfying. But this creates an idea of 'tension' and 'resolution'. If you play two notes together that don't harmonise as nicely, you create a feeling of expectation and tension; when you you play some notes that harmonise really well, that 'resolves' the tension and creates a sense of relief.

Building a scale - just intonation

The exact 3:2 integer ratio used in two tuning systems called 'Pythagorean tuning' and 'just intonation'. Using these kinds of integer ratios, you can unfold out a whole series of other notes, and that's how the Europeans generally did things before 12TET came along. For example, in 'just intonation', you might start with some frequency, and then procede in the ratios 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, and at last 2 (the octave). These would be given a series of letters, creating a 'scale'.

What is a scale? A scale is something like the 'colour palette' for a piece of music. It's a set of notes you use. You might use notes from outside the scale but only very occasionally. Different scales are associated with different feelings - for example, the 'major scale' generally feels happy and triumphant, while a 'minor scale' tends to feel sad and forlorn. We'll talk a lot more about scales soon.

In the European musical tradition, a 'scale' consists of seven notes in each octave, so the notes are named by the first seven notes of the alphabet, i.e. A B C D E F G. A scale has a 'base note', and then you'd unfold the other frequencies using the ratios. An instrument such as a piano would be tuned to play a particular scale. The ratios above are one definition of a 'major scale', and starting with C as the base note, the resulting set of notes is called 'C Major'.

All these nice small-number ratios tend to sound really good together. But it becomes rather tricky if you want to play multiple scales on the same instrument. For example, say your piano is tuned in just intonation to C Major. This means, assuming you have a starting frequency we'll call C, you have the following notes available in a given octave:

C, D=(9/8)C, E=(5/4)C, F=(4/3)C, G=(3/2)C [the fifth!], A=(5/3)C, B=(15/8)C, and 2C [the start of the next octave].

Note: the interval we named the 'fifth' is the fifth note in this scale. It's actually the fifth note in the various minor scales too.

But now suppose you want to play with some different notes - let's say a scale we'll call 'A major', which has the same frequency ratios starting on the note we previously called A. Does our piano have the right keys to play this scale?

Well, the next note up from A would be (9/8)A, which would be (9/8)(5/3)C=(15/8)C - that's our B key, so far so good. Then (5/4)A=(5/4)(5/3)C=(25/12)C and... uh oh! We don't have a (25/12)C key, we have 2C, so if we start at A and go up two keys, we have a note that is slightly lower frequency than the one we're looking for.

What this means is that, depending on your tuning, you could only approximate the pretty integer ratios for any scale besides C major. (25/12) is pretty close to 2, so that might not seem so bad, but sometimes we'd land right in between two notes. We can approximate these notes by adding some more 'in between' piano keys. How should we work out what 'extra' keys to include? Well, there were multiple conventions, but we'll see there is some logic to it...

[You might ask, why are you spending so long on this historical system that is now considered obsolete? Well, intervals and their harmonious qualities are still really important in modern music, and it makes most sense to introduce them with the idea of 'small-integer ratios'.]

The semitone

We've seen if we build the 'major scale' using a bunch of 'nice' ratios, we have trouble playing other scales. The gap above may look rather haphazard and arbitrary, but hold on, we're working in exponential space here - shouldn't we be using a logarithmic scale? If I switch to a logarithmic x-axis, we suddenly get a rather appealing pattern...

All the gaps between successive notes are about the same size, except for the gap between E and F, and B and C, which are about half that size. If you try to work that out exactly, you run into the problems we saw above, where C to D is 9/8 or 1.125, but D to E is 10/9 or 1.11111... Even so, you can imagine how people who were playing around with sounds might notice, damn, these are nice even steps we have here. Though you might also notice places where, in this scheme, it's not completely even - for example G to A (ratio 10/9) is noticeably smaller than A to B (ratio 9/8).

We've obliquely approached the idea of dividing the octave up into 12 steps, where each step is about the size of the gap between E and F or B and C. We call each of these steps a 'semitone'. Two semitones make a 'whole tone'. We might fill in all the missing semitones in our scale here using whole-number ratios, which gives you the black keys on the piano. There are multiple schemes for doing this, and the ratios tend to get a bit uglier. In the system we've outlined so far, a 'semitone' is not a fixed ratio, even though it's always somewhere around 1.06.

The set of 12 semitones is called the 'chromatic scale'. It is something like the 'colour space' for Western music. When you compose a piece, you select some subset of the 12 semitones as your 'palette' - the 'scale of' a piece of music.

But we still have a problem here, which is the unevenness of the gaps we discussed above. This could be considered a feature, not a bug, since each scale would have its own 'character' - it's defined by a slightly different set of ratios. But it does add a lot of complication when moving between scales.

So let's say we take all this irregularity as a bug, and try to fix it. The solution is 'equal temperament', which is the idea that the semitone should always be the exact same ratio, allowing the instrument to play any scale you please without difficulty.

Posed like this, it's easy to work out what that ratio should be: if you want 12 equal steps to be an octave, each step must be the 12th root of 2. Which is an irrational number that is about 1.05946...

At this point you say, wait, Bryn, didn't you just start this all off by saying that the human ear likes to hear nice simple integer ratios of frequencies? And now you're telling me that we should actually use an irrational number, which can't be represented by any integer ratio? What gives? But it turns out the human ear isn't quite that picky. If you have a ratio of 7 semitones, or a ratio of 2^(7/12)=1.4983..., that's close enough to 1.5 to feel almost as good. And this brings a lot of huge advantages: you can easily move ('transpose') between different scales of the same type, and trust that all the relevant ratios will be the same.

Equal temperament was the eventual standard, but there was a gradual process of approaching it called stuff like 'well-tempered' or 'good temperament'. One of the major steps along the way was Bach's collection 'the well-tempered klavier', showing how a keyboard instrument with a suitable tuning could play music in every single established scale. Here's one of those pieces:

Although we're using these irrational numbers, inside the scale are certain intervals that are considered to have certain meanings - some that are 'consonant' and some that are 'dissonant'. We've already mentioned the 'fifth', which is the 'most consonant' ratio. The fifth consists of 7 semitones and it's roughly a 1.5 ratio in equal temperament. Its close cousin is the 'fourth', which consists of 5 semitones. Because it's so nice, the fifth is kind of 'neutral' - it's just there but it doesn't mean a lot on its own.

For the other important intervals we've got to introduce different types of scale.

The scale zoo

So, up above we introduced the 'major' scale. In semitones, the major scale is intervals of 2, 2, 1, 2, 2, 2, 1. This is also called a 'mode', specifically the 'Ionian mode'. There are seven different 'modes', representing different permutations of these intervals, which all have funky Greek names.

The major scale generally connotes "upbeat, happy, triumphant". There are 12 different major scales, taking the 12 different notes of the chromatic scale as the starting point for each one.

Next is the minor scale, which tends to feel more sad or mysterious. Actually there are a few different minor scales. The 'natural minor' goes 2, 1, 2, 2, 1, 2, 2. You might notice this is a cyclic permutation of the major scale! So in fact a natural minor scale is the same set of notes as a major scale. What makes it different?

Well, remember when we talked about tension and resolution? It's about how the notes are organised. Our starting note is the 'root' note of the scale, usually established early on in the piece of music - quite often the very first note of the piece. The way you move around that root note determines whether the piece 'feels' major or minor. So every major scale has a companion natural minor scale, and vice versa. The set of notes in a piece is enough to narrow it down to one minor and one major, but you have to look closer to figure out which one is most relevant.

The 'harmonic minor' is almost the same, but it raises the second-last note (the 7th) a semitone. So its semitone intervals are 2, 1, 2, 2, 1, 3, 1.

The 'melodic minor' raises both the 6th and 7th by one semitone. So its semitone intervals are 2, 1, 2, 2, 2, 2, 1.

If you talk about a 'minor scale' unqualified, you mean the natural minor. It's also the 'Aeolian mode' in that system of funky Greek names I mentioned earlier.

So that leads to a set of 24 scales, a major and minor scale for every semitone. These are the most common scale types that almost all Western tonal music is written in.

But we ain't done. Because remember I said there were all those other "modes"? These are actually just cyclic permutations of the major scale. There's a really nerdy Youtube channel called '8-bit music theory' that has a bunch of videos analysing them in the context of videogame music which I'm going to watch at some point now I finally have enough background to understand wtf he's talking about.

And of top of that you have all sorts of other variants that come from shifting a note up or down a semitone.

The cast of intervals

OK, so we've established the idea of scales. Now let's talk intervals. As you might guess from the 'fifth', the intervals are named after their position in the scale.

Let me repeat the two most common scale modes, in terms of number of semitones relative to the root note:

position: 1, 2, 3, 4, 5, 6, 7, 8 major: 0, 2, 4, 5, 7, 9, 11, 12 minor: 0, 2, 3, 5, 7, 8, 10, 12

So you can see the fourth and fifth are the same in both. But there's a difference in three places: the third, the sixth, and the seventh. In each case, the minor is down a semitone from the major.

The interval names are... not quite as simple as 'place in the scale', but that's mostly how it works. e.g. the 'major third' is four semitones and the 'minor third' is three.

The fourth and fifth, which are dual to each other (meaning going up a fifth takes you to the same note as going down a fourth, and vice versa) are called 'perfect'. The note right in between them, an interval of 6 semitones, is called the 'tritone'.

(You can also refer to these intervals as 'augmented' or 'diminished' versions of adjacent intervals. Just in case there wasn't enough terminology in the air. See the table for the names of every interval.)

So, with these names, what's the significance of each one? The thirds, sixths and sevenths are important, because they tell us whether we're in minor or major land when we're building chords. (More on that soon.)

The fifth and the octave are super consonant, as we've said. But the notes that are close to them, like the seventh, the second and even more so the tritone, are quite dissonant - they're near to a nice thing and ironically that leads to awkward ratios which feel uncomfy to our ears. So generally speaking, you use them to build tension and anticipation and set up for a resolution later. (Or don't, and deliberately leave them hanging.)

Of course all of these positions in the scale also have funky Latin names that describe their function.

There's a lot more complicated nuances that make the meaning of a particular interval very contextual, and I certainly couldn't claim to really understand in much depth, but that's basically what I understand about intervals so far.

Our goofy-ass musical notation system

So if semitones are the building block of everything, naturally the musical notation system we use in the modern 12TET era spaces everything out neatly in terms of semitones, right?

Right...?

Lmao no. Actually sheet music is written so that each row of the stave (or staff, the five lines you write notes on) represents a note of the C major scale. All the notes that aren't on the C major scale are represented with special symbols, namely ♯ (read 'sharp') which means 'go up a semitone', and ♭ (read 'flat') which means 'go down a semitone'. That means the same note can be notated in two different ways: A♯ and B♭ are the same note.

The above image shows the chromatic scale, notated in two different ways. Every step is exactly one semitone.

Since a given scale might end up using one of these 'in between' notes that has to be marked sharp or flat, and you don't want to do that for every single time that note appears. Luckily, it turns out that each major/minor scale pair ends up defining a unique set of notes to be adjusted up or down a semitone, called the 'key signature'. So you can write the key signature at the beginning of the piece, and it lasts until you change key signature. For example, the key of 'A♭ major' ends up having four sharps:

There is a formula you can use to work out the set of sharps or flats to write for a given key. (That's about the point I checked out on musictheory.net.)

There is some advantage to this system, which is that it very clearly tells you when the composer intends to shift into a different scale, and it saves space since with the usual scales there are no wasted lines. But it's also annoyingly arbitrary. You just have to remember that B to C is only a semitone, and the same for E to F.

What are those weird squiggly symbols? Those are 'clefs'. Each one assigns notes to specific lines. The first one 𝄞 is the 'treble clef', the second one 𝄢 is the 'bass clef'. Well, actually these are the 'G-clef' and the 'F-clef', and where they go on the stave determines note assignment, but thankfully this has been standardised and you will only ever see them in one place. The treble clef declares the lines to be E G B D F and the bass clef G B D F A.

There is also a rarer 'C-clef' which looks like 𝄡. This is usually used as the 'Alto clef' which means F A C E G.

This notation system seems needlessly convoluted, but we're rather stuck with it, because most of the music has been written in it already. It's not uncommon for people to come up with alternative notations, though, such as 'tabs' for a stringed instrument which indicate which position should be played on each string. Nowadays on computers, a lot of DAWs will instead use a 'piano roll' presentation which is organised by semitone.

And then there's chords.

Chords! And arpeggios!

A chord is when you play 3 or more notes at the same time.

Simple enough right? But if you wanna talk about it, you gotta have a way to give them names. And that's where things get fucking nuts.

But the basic chord type is a 'triad', consisting of three notes, separated by certain intervals. There are two standard types, which you basically assemble by taking every other note of a scale. In terms of semitones, these are:

Major triad: 0 - 4 - 7 Minor triad: 0 - 3 - 7

Then there's a bunch of variations, for example:

Augmented: 0 - 4 - 8 Diminished: 0 - 3 - 6 Suspended: 0 - 2 - 7 (sus2) or 0 - 5 - 7 (sus4) Dominant seventh: 0 - 4 - 7 - 10 Power: 0 - 7

There is a notation scheme for chords in pop, jazz, rock, etc., which starts with a root note and then adds a bunch of superscripts to tell you about any special features of a chord. So 'C' means the C Major triad (namely C,E,G) and 'Cm' or 'c' means the C Minor triad (namely C,E♭,G).

In musical composition, you usually tend to surround the melody (single voice) with a 'chord progression' that both harmonises and creates a sense of 'movement' from one chord to another. Some instruments like guitar and piano are really good at playing chords. On instruments that can't play chords, they can still play 'arpeggios', which is what happens if you take a chord and unroll it into a sequence of notes. Or you play in an ensemble and harmonise with the other players to create a chord together. Awww.

Given a scale, you can construct a series of seven triad chords, starting from each note of the scale. These are generally given scale-specific Roman numerals corresponding to the position in the scale, and they're used to analyse the progression of chords in a song. I pretty much learned about this today while writing this post, so I can't tell you much more than that.

Right now, that's about as far as I've gotten with chords. On a violin, you can play just two strings at the same time after all - I never had much need to learn about them so it remains a huge hole in my understanding of music. I can't recognise chords by ear at all. So I gotta learn more about them.

As much as I wrote this for my own benefit... if you found this post interesting, let me know. I might write more if people find this style of presentation appealing. ^^'