#multicomparison

[phoenixlionme]

Terry Crews and his roles as a protective, attentive, hard-working, caring father in most of his iconic roles

[phoenixlionme]

Adding some I think of myself and ones that were mentioned in reblog or comments about the post:

"Nice characters are boring" to YOU. I love characters who no matter what, will always have genuine love for humanity in their heart. Characters who dance and laugh and sing with sincerity. Characters who believe in others, and are willing to extend a helping hand to people when no one gave them the same luxury. Characters who have gone through so much but believe, no matter what, that humanity and life is something beautiful and worth protecting

[alineonfire]

MODULE II_Week 1_ ANOVA test_Duration of sleep and happiness

I continue the course with my topic:  'Could the quality of sleep impact happiness?

From the AddHealth code, I focus on variables [H1GH51]: ‘How many hours do you sleep ?’ and [H1FS11]: ‘Do you feel happy ?’

Before continuing with the analysis of variance, I first went back to the fundamentals and managed my variables : Setting variables as numeric, studying the frequency distribution and managing the ‘Refused’ or ‘Don’t know’ response as NAN for both variables.

Code:

I reduce the duration of sleep from 1 to 10 hours for [H1GH51] and check the result by an univariate representation :

[H1FS11]‘Were you happy ? with  0=never or rarely; 1=sometimes; 2=a lot of the time; 3=most of the time or all of the time; 6=Refused; 8=Dont know')

Now that the data are cleaned and managed, I can proceed with analysis of variance. The response variable [H1GH51] is quantitative and the explanatory variable [H1FS11] is categorical with several level of response.

The hypothesis Ho : There is NO relationship between the happiness and duration of sleep and all means are equal ; The alternative H1 is then, There IS a relationship between the happiness and duration of sleep. 

I run the ANOVA tests on Python and ask for mean and standard deviation for [H1GH51] (hours of sleep)

And the results are :

The p-Value is 6.96E-20 << 0.05 This would allow us to reject the null hypothesis and say that the duration of sleep and happiness could be linked. But as the explanatory variable [H1FS11] has more than two levels, before concluding, I need to conduct a post hoc test, the TukeyHSD for multicomparison of the means.

And results:

This is very interesting: The ANOVA test revealed a very low p-Value, meaning that duration of sleep and happiness are significantly associated. The postHoc comparisons revealed that in fact, only subjects who responded 0-Never or rarely and 1-sometimes to the question ‘Did you feel happy’ have a different mean . The others means are statistically similar. While this, of course remains statistical, one piece of advice is that if you want to feel happy, sleep more! 😊

[eden2023]

ANOVA

DataSet: Salary Data based on Experience,Age,Gender,Job Title and Education Level

Issue of the problem:

HO: There is diference in salaly between genders HA: There is a difference is salary between genders

CODE

#Libaries

import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt

import scipy.stats as stats import statsmodels.api as sm import statsmodels.formula.api as smf import statsmodels.stats.multicomp as pairwise import statsmodels.stats.multicomp as multicomparison

#main code

data = pd.read_excel('Salary_Data.xlsx') print(data)

boxplt = sns.boxplot(x='Gender', y='Salary', data=data, color=('magenta')).set_title("Gender vs Salary")

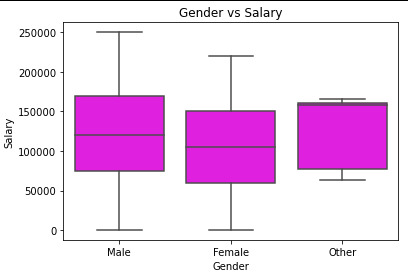
mediangender = data.groupby('Gender').median() print(mediangender)

meangender = data.groupby('Gender').mean() print(meangender)

model = smf.ols(formula='Salary ~ C(Gender)',data=data) res = model.fit() print(res.summary())

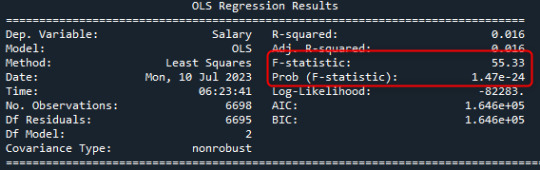
After verifying the p-value < 0.05 with ANOVA, it is necessery to verify which group is different. ANOVA can not give this information. For that we performe a POST HOC TEST which conducts a post hoc comparisions. From serveral choices, for thsi dataset, I sused the tukey. Tukey -> conduct a tukey honest significant difference test mc=multicomparison.MultiComparison((data['Salary']),data['Gender']) result = mc.tukeyhsd(0.05) print(result.summary())

By analysing the data:

->P-value for the difference in means between Female and Male: 0.001

->P-value for the difference in means between Female and Other: 0.4072

->P-value for the difference in means between Male and Other: 0.9

Thus, we would conclude that there is a statistically significant difference between the means of Female and Male, but not a statistically significant difference between the means of Female and Other, Male and Others.

[phoenixlionme]

Could you imagine a friendship between these trio of loving, sensitive men who give off big bro vibes?

[phoenixlionme]

Mama Odie from Disney's The Princess and the Frog

Luz Noceda from Disney's The Owl House

Prudence Night from the Chilling Adventures of Sabrina

Black Witches

Black Witches

Tabby || The Craft: Legacy

Nynaeve al'Meara || Wisdom || The Wheel of Time

Calypso || Sea Goddess/Witch || Pirates of The Carribean

Jada Sheilds || Whitelighter-Witch || Charmed (2018)

Leta Lestrange || Fantastic Beasts: Crimes of Grindelwald

Eulalie Hicks || Fantastic Beasts: Secrets of Dumbledore

Fringilla Vigo || The Witcher

Seraphina Picquery || Fantastic Beasts and Where to Find Them

Kaela Danso || Charmed (2018)

Macy Vaughn and Maggie Vera || Charmed (2018)

[cjdathw1]

Assignment 1

Assignment 1

This assignment is aim to test differences in the mean number of cigarettes smoked among young adults of 5 different levels of health condition. The data for this study is from  U.S. National Epidemiological Survey on Alcohol and Related Conditions (NESARC). The response variable “NUMCIGMO_EST” is the number cigarettes smoked in a month based on the young adults age 18 to 25 who have smoked in the past 12 month.  NUMCIGMO_EST is created as follows:  1. “USFREQMO” is converted to number of days smoked in the past month, 2. multiplying new “USFREQMO”  and “S3AQ3C1" which is cigarettes/day.  The explanatory variable in the test is column “S1Q16”, which is described as “SELF-PERCEIVED CURRENT HEALTH”, with values from 1 (excellent) to 5 (poor).  Since this is a C->Q test, thus I ran ANOVA using OLS model to calculate F-statistic and p-value,

Here is the output from the OLS output:

=========================================================================== Dep. Variable:           NUMCIGMO_EST   R-squared:                       0.031 Model:                            OLS                    Adj. R-squared:                0.025 Method:                 Least Squares             F-statistic:                        5.001 Date:                Mon, 22 Mar 2021            Prob (F-statistic):        0.000567 Time:                               19:54:15            Log-Likelihood:              -4479.1 No. Observations:                   629            AIC:                                   8968. Df Residuals:                           624           BIC:                                    8991. Df Model:                                     4                                         Covariance Type:            nonrobust                 ��                       ===========================================================================                                   coef      std err               t      P>|t|      [0.025      0.975] ----------------------------------------------------------------------------------- Intercept              315.4803     22.538     13.997     0.000     271.220     359.741 C(S1Q16)[T.2.0]    15.4845     30.537      0.507      0.612     -44.483      75.452 C(S1Q16)[T.3.0]    89.5654     31.530      2.841      0.005      27.648     151.482 C(S1Q16)[T.4.0]   119.1863     50.173      2.376      0.018      20.658     217.715 C(S1Q16)[T.5.0]   348.8054    115.867     3.010      0.003     121.268     576.342 =========================================================================== Omnibus:                      346.462   Durbin-Watson:                       2.001 Prob(Omnibus):                0.000   Jarque-Bera (JB):             4387.366 Skew:                                2.167   Prob(JB):                                  0.00 Kurtosis:                          15.191   Cond. No.                                 10.7 ===========================================================================

With F-statistic is 5.001 and p-value is 0,000567,  I can safely reject the null hypothesis and conclude that there is an association between number of cigarettes smoked and the health conditions.  To determine which levels of health conditions are different from the others, I perform a post hoc test using the Tukey HSDT, or Honestly Significant Difference Test (this is implemented by calling “MultiComparison” function).  The following shows the result of the Post Hoc Pair Comparison:

 Multiple Comparison of Means - Tukey HSD, FWER=0.05   ======================================================= group1 group2 meandiff p-adj      lower        upper      reject -------------------------------------------------------   1.0     2.0        15.4845    0.9      -68.0574   99.0263   False   1.0     3.0         89.5654 0.0374     3.3073  175.8234    True   1.0     4.0       119.1863 0.1236   -18.0761  256.4488  False   1.0     5.0       348.8054 0.0227    31.8177  665.7931    True   2.0     3.0         74.0809 0.1025    -8.4764   156.6383  False   2.0     4.0       103.7019 0.2205   -31.2657  238.6694  False   2.0     5.0       333.3209 0.0328    17.3202  649.3216    True   3.0     4.0         29.621    0.9      -107.0445  166.2864   False   3.0     5.0       259.24 0.1668       -57.4896  575.9697   False   4.0     5.0       229.619 0.3295    -104.6237  563.8618  False -------------------------------------------------------

In the last column, we can determine which health level of groups smoke significantly different mean number of cigarettes than the others by identifying the comparisons in which we can reject the null hypothesis, that is, in which reject equals true.

Python script for the homework:

import numpy import pandas import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi

data = pandas.read_csv('nesarc.csv', low_memory=False)

data['S3AQ3B1'] = pandas.to_numeric(data['S3AQ3B1'], errors="coerce")           data['S3AQ3C1'] = pandas.to_numeric(data['S3AQ3C1'], errors="coerce")           data['CHECK321'] = pandas.to_numeric(data['CHECK321'], errors="coerce")        

#subset data to young adults age 18 to 25 who have smoked in the past 12 months sub1=data[(data['AGE']>=18) & (data['AGE']<=25) & (data['CHECK321']==1)]

#SETTING MISSING DATA sub1['S3AQ3B1']=sub1['S3AQ3B1'].replace(9, numpy.nan) sub1['S3AQ3C1']=sub1['S3AQ3C1'].replace(99, numpy.nan)

#recoding number of days smoked in the past month recode1 = {1: 30, 2: 22, 3: 14, 4: 5, 5: 2.5, 6: 1} sub1['USFREQMO']= sub1['S3AQ3B1'].map(recode1)                                  

#converting new variable USFREQMMO to numeric sub1['USFREQMO']= pandas.to_numeric(sub1['USFREQMO'], errors="coerce")

sub1['NUMCIGMO_EST']=sub1['USFREQMO'] * sub1['S3AQ3C1']                        

sub1['NUMCIGMO_EST']= pandas.to_numeric(sub1['NUMCIGMO_EST'], errors="coerce")

sub1['S1Q16']=sub1['S1Q16'].replace(9, numpy.nan) sub3 = sub1[['NUMCIGMO_EST', 'S1Q16']].dropna()

''' By running an analysis of variance, we're asking whether the number of cigarettes smoked differs for different health conditions. ''' model2 = smf.ols(formula='NUMCIGMO_EST ~ C(S1Q16)', data=sub3).fit() print (model2.summary())

print ('means for numcigmo_est by major depression status') m2= sub3.groupby('S1Q16').mean() print (m2)

print ('standard deviations for numcigmo_est by major depression status') sd2 = sub3.groupby('S1Q16').std() print (sd2)

mc1 = multi.MultiComparison(sub3['NUMCIGMO_EST'], sub3['S1Q16']) res1 = mc1.tukeyhsd() print(res1.summary())

1 note

[dpikablog]

Week 1 Assignment – Running an Analysis of variance (ANOVA)

 Objective:

The assignment of the week deals with Analysis of variance. Given a dataset some form of Statistical Analysis test to be performed to check and evaluate its Statistical significance.

Before getting into the crux of the problem let us understand some of the important concepts

Hypothesis testing - It is one of the most important Inferential Statistics where the hypothesis is performed on the sample data from a larger population. Hypothesis testing is a statistical assumption taken by an analyst on the nature of the data and its reason for analysis. In other words, Statistical Hypothesis testing assesses evidence provided by data in favour of or against each hypothesis about the problem.

There are two types of Hypothesis

Null Hypothesis – The null hypothesis is assumed to be true until evidence indicate otherwise. The general assumptions made on the data (people with depression are more likely to smoke)

Alternate Hypothesis – Once stronger evidences are made, one can reject Null hypothesis and accept Alternate hypothesis (One needs to come with strong evidence to challenge the null hypothesis and draw proper conclusions).In this case one needs to show evidences such that there is no relation between people smoking and their depression levels

Example:

The Null hypothesis is that the number of cigarettes smoked by the person is dependent on the person’s depression level. Based on the p-value we make conclusions either to accept the null hypothesis or fail to accept the null hypothesis(accept alternative hypothesis)

 Steps involved in Hypothesis testing:

1.     Choose the Null hypothesis (H0 ) and alternate hypothesis (Ha)

2.     Choose the sample

3.     Assess the evidence

4.     Draw the conclusions

 The Null hypothesis is accepted/rejected based on the p-value significance level of test

If p<= 0.05, then reject the null hypothesis (accept the alternate hypothesis)

If p > 0.05 null hypothesis is accepted

 Wrongly rejecting the null hypothesis leads to type one error

 Sampling variability:

The measures of the sample (subset of population) varying from the measures of the population is called Sampling variability. In other words sample results changing from sample to sample.

 Central Limit theorem:

As long as adequately large samples and an adequately large number of samples are used from a population,the distribution of the statistics of the sample will be normally distributed. In other words, the more the sample the accurate it is to the population parameters.

 Choosing Statistical test:

Please find the below tabulation to identify what test can be done at a given condition. Some of the statistical tools used for this are

Chi-square test of independence, ANOVA- Analysis of variance, correlation coefficient.

Explanatory variables are input or independent variable And response variable is the output variable or dependent variable.

Explanatory            Response        Type of test

Categorical             Categorical         Chi-square test 

Quantitative            Quantitative        Pearson correlation

Categorical             Quantitative        ANOVA

Quantitative            Categorical         Chi-square test   

ANOVA:

Anova F test, helps to identify, Are the difference among the sample means due to true difference among the population or merely due to sampling variability.

F = variation among sample means / by variations within groups

Let’s implement our learning in python.

The Null hypothesis here is smoking and depression levels are unrelated

The Alternate hypothesis is smoking and depression levels are related.

# importing required libraries

import numpy as np

import pandas as pd

import statsmodels.formula.api as smf

 data = pd.read_csv("my_data...nesarc.csv",low_memory=False)

 #setting variables you will be working with to numeric

data['S3AQ3B1'] = data['S3AQ3B1'].convert_objects(convert_numeric=True)

#data['S3AQ3B1'] = pd.to_numeric(data.S3AQ3B1)

data['S3AQ3C1'] = data['S3AQ3C1'].convert_objects(convert_numeric=True)

#data['S3AQ3C1'] = pd.to_numeric(data.S3AQ3C1)

data['CHECK321'] = data['CHECK321'].convert_objects(convert_numeric=True)

#data['CHECK321'] = pd.to_numeric(data.CHECK321)

 #subset data to young adults age 18 to 25 who have smoked in the past 12 months

sub1=data[(data['AGE']>=18) & (data['AGE']<=25) & (data['CHECK321']==1)]

 #SETTING MISSING DATA

sub1['S3AQ3B1']=sub1['S3AQ3B1'].replace(9, np.nan)

sub1['S3AQ3C1']=sub1['S3AQ3C1'].replace(99, np.nan)

 #recoding number of days smoked in the past month

recode1 = {1: 30, 2: 22, 3: 14, 4: 5, 5: 2.5, 6: 1}

sub1['USFREQMO']= sub1['S3AQ3B1'].map(recode1)

 #converting new variable USFREQMMO to numeric

sub1['USFREQMO']= sub1['USFREQMO'].convert_objects(convert_numeric=True)

 # Creating a secondary variable multiplying the days smoked/month and the number of cig/per day

sub1['NUMCIGMO_EST']=sub1['USFREQMO'] * sub1['S3AQ3C1']

 sub1['NUMCIGMO_EST']= sub1['NUMCIGMO_EST'].convert_objects(convert_numeric=True)

 ct1 = sub1.groupby('NUMCIGMO_EST').size()

print (ct1)

print(sub1['MAJORDEPLIFE'])

 # using ols function for calculating the F-statistic and associated p value

The ols is the ordinary least square function takes the response variable NUMCIGMO_EST and its explanatory variable MAJORDEPLIFE, C is indicated to specify that it’s a categorical variable.

model1 = smf.ols(formula='NUMCIGMO_EST ~ C(MAJORDEPLIFE)', data=sub1)

results1 = model1.fit()

print (results1.summary())

 Inference – Since the p value is greater than 0.05, we accept the null hypothesis that the sample means are statistically equal. And there is no association between depression levels and cigarette smoked.

 sub2 = sub1[['NUMCIGMO_EST', 'MAJORDEPLIFE']].dropna()

 print ('means for numcigmo_est by major depression status')

m1= sub2.groupby('MAJORDEPLIFE').mean()

print (m1)

 print ('standard deviations for numcigmo_est by major depression status')

sd1 = sub2.groupby('MAJORDEPLIFE').std()

print (sd1)

 Since the null hypothesis is true we conclude that the sample mean and standard deviation of the two samples are statistically equal. From the sample statistics we infer that the depression levels and smoking are unrelated to each other

Till now, we ran the ANOVA test for two levels of the categorical variable(MAJORDEPLIFE, 0,1) Lets now look at the categorical variable(ETHRACE2A,White, Black, American Indian, Asian native and Latino) having five levels and see how the differences in the mean are captured.

The problem here is, The F-statistic and ‘p’ value does not provide any insight as to why the null hypothesis is rejected when there are multiple levels in categorical Explanatory variable.

The significant ANOVA does not tell which groups are different from the others. To determine this we would need to perform post-hoc test for ANOVA

 Why Post-hoc tests for ANOVA?

Post hoc test known as after analysis test, This is performed to prevent excessive Type one error. Not implementing this leads to family wise error rate, given by the formula

FWE = 1 – (1 – αIT)C

Where:

αIT = alpha level for an individual test (e.g. .05),

c = Number of comparisons.

 Post-hoc tests are designed to evaluate the difference between the pair of means while protecting against inflation of type one error.

 Let’s continue the code to perform post-hoc test.

 # Importing the library

Import statsmodels.stats.multicomp as multi

 # adding the variable of interest to a separate data frame

sub3 = sub1[['NUMCIGMO_EST', 'ETHRACE2A']].dropna()

# calling the ols function and passing the explanatory categorical and response variable

model2 = smf.ols(formula='NUMCIGMO_EST ~ C(ETHRACE2A)', data=sub3).fit()

print(model2.summary())

print ('means for numcigmo_est by major depression status')

m2= sub3.groupby('ETHRACE2A').mean()

print(m2)

print('standard deviations for numcigmo_est by major depression status')

sd2 = sub3.groupby('ETHRACE2A').std()

print(sd2)

# Include required parameters  in the MultiComparison function and then run the post-hoc TukeyHSD test

mc1 = multi.MultiComparison(sub3['NUMCIGMO_EST'], sub3['ETHRACE2A'])

res1 = mc1.tukeyhsd()

print(res1.summary())

[phoenixlionme]

I would like a story exploring this “proof” with it being thoroughly debunked by using the above characters or rather, expies of them

collage of female characters that people have used to “prove” that there are too many masc women in media

[panickypeachboy]

Measure me!

Send in “Measure me!” and I’ll compare the heights of our muses using this generator | Accepting!

(quiet sobbing because can’t edit the multicomparison generator)

//Look at this adorable fam!!//

[jon-ting-data-manage-vis]

Running an ANOVA

Having selected the GapMinder data set and a research question, managed my variables of interest, namely oil consumption per person, residential electricity consumption per person and urban population, and visualized their relationship graphically, we are now ready to test these relationships statistically. 

The analysis of variance (ANOVA) assesses whether the means of two or more groups of categorical variables are statistically different from each other. Since all of the variables chosen are quantitative, they are categorised for the purpose of running the test. Post hoc paired comparisons were also carried out  in instances where the original statistical test was significant for explanatory  variables with more than two levels of categories.

The codes written for this program are shown below:

#############################################

# Import required libraries import pandas as pd import numpy as np import seaborn as sns import matplotlib as mpl import matplotlib.pyplot as plt import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi

# Bug fix for display formats and change settings to show all rows and columns pd.set_option('display.float_format', lambda x:'%f'%x) pd.set_option('display.max_columns', None) pd.set_option('display.max_rows', None)

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Report facts regarding the original dataset print("Facts regarding the original GapMinder dataset:") print("---------------------------------------") print("Number of countries: {0}".format(len(raw_data))) print("Number of variables: {0}\n".format(len(raw_data.columns))) print("All variables:\n{0}\n".format(list(raw_data.columns))) print("Data types of each variable:\n{0}\n".format(raw_data.dtypes)) print("First 5 rows of entries:\n{0}\n".format(raw_data.head())) print("=====================================\n")

# Choose variables of interest # var_of_int = ['country', 'incomeperperson', 'alcconsumption', 'co2emissions', # 'internetuserate', 'oilperperson', 'relectricperperson', 'urbanrate'] var_of_int = ['oilperperson', 'relectricperperson', 'urbanrate'] print("Chosen variables of interest:\n{0}\n".format(var_of_int)) print("=====================================\n")

# Code out missing values by replacing with NumPy's NaN data type data = raw_data[var_of_int].replace(' ', np.nan) print("Replaced missing values with NaNs:\n{0}\n".format(data.head())) print("=====================================\n")

# Cast the numeric variables to the appropriate data type then quartile split numeric_vars = var_of_int[:] for var in numeric_vars: data[var] = pd.to_numeric(data[var], downcast='float', errors='raise') print("Simple statistics of each variable:\n{0}\n".format(data.describe())) print("=====================================\n")

# Create secondary variables to investigate frequency distributions print("Separate continuous values categorically using secondary variables:") print("---------------------------------------") data['oilpp (tonnes)'] = pd.cut(data['oilperperson'], 4) oil_val_count = data.groupby('oilpp (tonnes)').size() oil_dist = data['oilpp (tonnes)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4)  # Variable range is extended by 0.1% elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

data['urbanr (%)'] = pd.cut(data['urbanrate'], 4) urb_val_count = data.groupby('urbanr (%)').size() urb_dist = data['urbanr (%)'].value_counts(sort=False, dropna=True, normalize=True) urb_freq_tab = pd.concat([urb_val_count, urb_dist], axis=1) urb_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of urban population:\n{0}\n".format(urb_freq_tab)) print("=====================================\n")

# Code in valid data in place of missing data for each variable print("Number of missing data in variables:") print("oilperperson: {0}".format(data['oilperperson'].isnull().sum())) print("relectricperperson: {0}".format(data['relectricperperson'].isnull().sum())) print("urbanrate: {0}\n".format(data['urbanrate'].isnull().sum())) print("=====================================\n")

print("Investigate entries with missing urbanrate data:\n{0}\n".format(data[['oilperperson', 'relectricperperson']][data['urbanrate'].isnull()])) print("Data for other variables are also missing for 90% of these entries.") print("Therefore, eliminate them from the dataset.\n") data = data[data['urbanrate'].notnull()] print("=====================================\n")

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

null_oil_data = data[data['oilperperson'].isnull()].copy() oil_map_dict = data.groupby('urbanr (%)').median()['oilperperson'].to_dict() print("Median values of oilperperson corresponding to each urbanrate group:\n{0}\n".format(oil_map_dict)) null_oil_data['oilperperson'] = null_oil_data['urbanr (%)'].map(oil_map_dict) data = data.combine_first(null_oil_data) data['oilpp (tonnes)'] = pd.cut(data['oilperperson'], 4) print("Replace oilperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("=====================================\n")

# Investigate the new frequency distributions print("Report the new frequency table for each variable:") print("---------------------------------------") oil_val_count = data.groupby('oilpp (tonnes)').size() oil_dist = data['oilpp (tonnes)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

urb_val_count = data.groupby('urbanr (%)').size() urb_dist = data['urbanr (%)'].value_counts(sort=False, dropna=True, normalize=True) urb_freq_tab = pd.concat([urb_val_count, urb_dist], axis=1) urb_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of urban population:\n{0}\n".format(urb_freq_tab)) print("=====================================\n")

# Run ANOVA print("ANOVA results:") print("-------------------------------------") model1 = smf.ols(formula='relectricperperson ~ C(Q("oilpp (tonnes)"))', data=data) m1, std1 = data[['relectricperperson', 'oilpp (tonnes)']].groupby('oilpp (tonnes)').mean(), data[['relectricperperson', 'oilpp (tonnes)']].groupby('oilpp (tonnes)').std() mc1 = multi.MultiComparison(data['relectricperperson'], data['oilpp (tonnes)']) print("relectricperperson ~ oilpp (tonnes)\n{0}".format(model1.fit().summary())) print("Means for relectricperperson by oilpp status:\n{0}\n".format(m1)) print("Standard deviations for relectricperperson by oilpp status:\n{0}\n".format(std1)) print("MultiComparison summary:\n{0}\n".format(mc1.tukeyhsd().summary()))

model2 = smf.ols(formula='relectricperperson ~ C(Q("urbanr (%)"))', data=data) m2, std2 = data[['relectricperperson', 'urbanr (%)']].groupby('urbanr (%)').mean(), data[['relectricperperson', 'urbanr (%)']].groupby('urbanr (%)').std() mc2 = multi.MultiComparison(data['relectricperperson'], data['urbanr (%)']) print("relectricperperson ~ urbanr (%)\n{0}".format(model2.fit().summary())) print("Means for relectricperperson by urbanr status:\n{0}\n".format(m2)) print("Standard deviations for relectricperperson by urbanr status:\n{0}\n".format(std2)) print("MultiComparison summary:\n{0}\n".format(mc2.tukeyhsd().summary()))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

All variables: ['country', 'incomeperperson', 'alcconsumption', 'armedforcesrate', 'breastcancerper100th', 'co2emissions', 'femaleemployrate', 'hivrate', 'internetuserate', 'lifeexpectancy', 'oilperperson', 'polityscore', 'relectricperperson', 'suicideper100th', 'employrate', 'urbanrate']

Data types of each variable: country                 object incomeperperson         object alcconsumption          object armedforcesrate         object breastcancerper100th    object co2emissions            object femaleemployrate        object hivrate                 object internetuserate         object lifeexpectancy          object oilperperson            object polityscore             object relectricperperson      object suicideper100th         object employrate              object urbanrate               object dtype: object

First 5 rows of entries:       country   incomeperperson alcconsumption armedforcesrate  \ 0  Afghanistan                              .03        .5696534   1      Albania  1914.99655094922           7.29       1.0247361   2      Algeria  2231.99333515006            .69        2.306817   3      Andorra  21943.3398976022          10.17                   4       Angola  1381.00426770244           5.57       1.4613288  

 breastcancerper100th      co2emissions  femaleemployrate hivrate  \ 0                 26.8          75944000  25.6000003814697           1                 57.4  223747333.333333  42.0999984741211           2                 23.5  2932108666.66667  31.7000007629394      .1   3                                                                     4                 23.1         248358000  69.4000015258789       2  

   internetuserate lifeexpectancy     oilperperson polityscore  \ 0  3.65412162280064         48.673                            0   1  44.9899469578783         76.918                            9   2  12.5000733055148         73.131  .42009452521537           2   3                81                                               4  9.99995388324075         51.093                           -2  

 relectricperperson   suicideper100th        employrate urbanrate   0                     6.68438529968262  55.7000007629394     24.04   1   636.341383366604  7.69932985305786  51.4000015258789     46.72   2   590.509814347428   4.8487696647644              50.5     65.22   3                     5.36217880249023                       88.92   4   172.999227388199  14.5546770095825  75.6999969482422      56.7  

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Replaced missing values with NaNs:      oilperperson relectricperperson urbanrate 0              NaN                NaN     24.04 1              NaN   636.341383366604     46.72 2  .42009452521537   590.509814347428     65.22 3              NaN                NaN     88.92 4              NaN   172.999227388199      56.7

=====================================

Simple statistics of each variable:       oilperperson  relectricperperson  urbanrate count     63.000000          136.000000 203.000000 mean       1.484085         1173.179199  56.769348 std        1.825090         1681.440430  23.844936 min        0.032281            0.000000  10.400000 25%        0.532542          203.652103  36.830000 50%        1.032470          597.136444  57.939999 75%        1.622737         1491.145233  74.209999 max       12.228645        11154.754883 100.000000

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person:                  value_count  frequency oilpp (tonnes)                           (0.0201, 3.0814]           58   0.920635 (3.0814, 6.13]              3   0.047619 (6.13, 9.18]                1   0.015873 (9.18, 12.229]              1   0.015873

Frequency table of residential electricity consumption per person:                        value_count  frequency relectricpp (kWh)                             (-11.155, 2788.689]             122   0.897059 (2788.689, 5577.377]             10   0.073529 (5577.377, 8366.0662]             3   0.022059 (8366.0662, 11154.755]            1   0.007353

Frequency table of urban population:               value_count  frequency urbanr (%)                           (10.31, 32.8]           42   0.206897 (32.8, 55.2]            51   0.251232 (55.2, 77.6]            68   0.334975 (77.6, 100]             42   0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Investigate entries with missing urbanrate data:     oilperperson  relectricperperson 43            nan                 nan 71            nan            0.000000 75            nan                 nan 121           nan                 nan 134           nan                 nan 143           nan                 nan 157           nan                 nan 170           nan                 nan 187      2.006515         1831.731812 198           nan                 nan

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

Investigate entries with missing relectricperperson data:    oilperperson  relectricperperson  urbanrate oilpp (tonnes)  \ 0            nan                 nan  24.040001            NaN   3            nan                 nan  88.919998            NaN   5            nan                 nan  30.459999            NaN   8            nan                 nan  46.779999            NaN   12           nan                 nan  83.699997            NaN  

  relectricpp (kWh)     urbanr (%)   0                NaN  (10.31, 32.8]   3                NaN    (77.6, 100]   5                NaN  (10.31, 32.8]   8                NaN   (32.8, 55.2]   12               NaN    (77.6, 100]  

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

Replace relectricperperson NaNs based on their quartile group's median:   oilperperson  relectricperperson  urbanrate    oilpp (tonnes)  \ 0           nan           59.848274  24.040001               NaN   1           nan          636.341370  46.720001               NaN   2      0.420095          590.509827  65.220001  (0.0201, 3.0814]   3           nan         1741.486572  88.919998               NaN   4           nan          172.999222  56.700001               NaN  

    relectricpp (kWh)     urbanr (%)   0  (-11.155, 2788.689]  (10.31, 32.8]   1  (-11.155, 2788.689]   (32.8, 55.2]   2  (-11.155, 2788.689]   (55.2, 77.6]   3  (-11.155, 2788.689]    (77.6, 100]   4  (-11.155, 2788.689]   (55.2, 77.6]  

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

Replace oilperperson NaNs based on their quartile group's median:   oilperperson  relectricperperson  urbanrate    oilpp (tonnes)  \ 0      0.079630           59.848274  24.040001  (0.0201, 3.0814]   1      0.359173          636.341370  46.720001  (0.0201, 3.0814]   2      0.420095          590.509827  65.220001  (0.0201, 3.0814]   3      2.087848         1741.486572  88.919998  (0.0201, 3.0814]   4      0.844574          172.999222  56.700001  (0.0201, 3.0814]  

    relectricpp (kWh)     urbanr (%)   0  (-11.155, 2788.689]  (10.31, 32.8]   1  (-11.155, 2788.689]   (32.8, 55.2]   2  (-11.155, 2788.689]   (55.2, 77.6]   3  (-11.155, 2788.689]    (77.6, 100]   4  (-11.155, 2788.689]   (55.2, 77.6]  

=====================================

Report the new frequency table for each variable: --------------------------------------- Frequency table of oil consumption per person:                  value_count  frequency oilpp (tonnes)                           (0.0201, 3.0814]          198   0.975369 (3.0814, 6.13]              3   0.014778 (6.13, 9.18]                1   0.004926 (9.18, 12.229]              1   0.004926

Frequency table of residential electricity consumption per person:                        value_count  frequency (-11.155, 2788.689]             189   0.931034 (2788.689, 5577.377]             10   0.049261 (5577.377, 8366.0662]             3   0.014778 (8366.0662, 11154.755]            1   0.004926

Frequency table of urban population:               value_count  frequency (10.31, 32.8]           42   0.206897 (32.8, 55.2]            51   0.251232 (55.2, 77.6]            68   0.334975 (77.6, 100]             42   0.206897

=====================================

ANOVA results: ------------------------------------- relectricperperson ~ oilpp (tonnes)                            OLS Regression Results                             ============================================================================== Dep. Variable:     relectricperperson   R-squared:                       0.350 Model:                            OLS   Adj. R-squared:                  0.340 Method:                 Least Squares   F-statistic:                     35.72 Date:                Mon, 10 Aug 2020   Prob (F-statistic):           1.63e-18 Time:                        02:21:51   Log-Likelihood:                -1721.6 No. Observations:                 203   AIC:                             3451. Df Residuals:                     199   BIC:                             3464. Df Model:                           3                                         Covariance Type:            nonrobust                                         ============================================================================================================                                               coef    std err          t      P>|t|      [95.0% Conf. Int.] ------------------------------------------------------------------------------------------------------------ Intercept                                  830.4105     83.731      9.918      0.000       665.298   995.523 C(Q("oilpp (tonnes)"))[T.(3.0814, 6.13]]  5618.9698    685.364      8.199      0.000      4267.462  6970.477 C(Q("oilpp (tonnes)"))[T.(6.13, 9.18]]    7532.1579   1181.164      6.377      0.000      5202.953  9861.362 C(Q("oilpp (tonnes)"))[T.(9.18, 12.229]]   634.4268   1181.164      0.537      0.592     -1694.778  2963.631 ============================================================================== Omnibus:                      141.891   Durbin-Watson:                   1.778 Prob(Omnibus):                  0.000   Jarque-Bera (JB):             1183.713 Skew:                           2.690   Prob(JB):                    9.12e-258 Kurtosis:                      13.536   Cond. No.                         14.3 ==============================================================================

Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Means for relectricperperson by oilpp status:                  relectricperperson oilpp (tonnes)                       (0.0201, 3.0814]          830.410461 (3.0814, 6.13]           6449.380371 (6.13, 9.18]             8362.568359 (9.18, 12.229]           1464.837280

Standard deviations for relectricperperson by oilpp status:                  relectricperperson oilpp (tonnes)                       (0.0201, 3.0814]         1108.687744 (3.0814, 6.13]           4128.518555 (6.13, 9.18]                     nan (9.18, 12.229]                   nan

MultiComparison summary:           Multiple Comparison of Means - Tukey HSD,FWER=0.05           =======================================================================     group1          group2      meandiff    lower      upper    reject ----------------------------------------------------------------------- (0.0201, 3.0814] (3.0814, 6.13] 5618.9698  3843.1866   7394.753   True (0.0201, 3.0814]  (6.13, 9.18]  7532.1579  4471.7516  10592.5642  True (0.0201, 3.0814] (9.18, 12.229]  634.4268  -2425.9795 3694.8331  False (3.0814, 6.13]   (6.13, 9.18]  1913.1881  -1611.7745 5438.1507  False (3.0814, 6.13]  (9.18, 12.229] -4984.543  -8509.5056 -1459.5804  True  (6.13, 9.18]   (9.18, 12.229] -6897.7311 -11214.911 -2580.5512  True -----------------------------------------------------------------------

relectricperperson ~ urbanr (%)                            OLS Regression Results                             ============================================================================== Dep. Variable:     relectricperperson   R-squared:                       0.320 Model:                            OLS   Adj. R-squared:                  0.310 Method:                 Least Squares   F-statistic:                     31.26 Date:                Mon, 10 Aug 2020   Prob (F-statistic):           1.33e-16 Time:                        02:21:51   Log-Likelihood:                -1726.1 No. Observations:                 203   AIC:                             3460. Df Residuals:                     199   BIC:                             3473. Df Model:                           3                                         Covariance Type:            nonrobust                                         ======================================================================================================                                         coef    std err          t      P>|t|      [95.0% Conf. Int.] ------------------------------------------------------------------------------------------------------ Intercept                            127.4246    185.907      0.685      0.494      -239.176   494.025 C(Q("urbanr (%)"))[T.(32.8, 55.2]]   211.0778    251.045      0.841      0.401      -283.973   706.128 C(Q("urbanr (%)"))[T.(55.2, 77.6]]   905.2163    236.449      3.828      0.000       438.949  1371.484 C(Q("urbanr (%)"))[T.(77.6, 100]]   2271.6658    262.912      8.640      0.000      1753.214  2790.117 ============================================================================== Omnibus:                      196.152   Durbin-Watson:                   2.055 Prob(Omnibus):                  0.000   Jarque-Bera (JB):             4118.605 Skew:                           3.766   Prob(JB):                         0.00 Kurtosis:                      23.741   Cond. No.                         5.26 ==============================================================================

Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Means for relectricperperson by urbanr status:               relectricperperson urbanr (%)                       (10.31, 32.8]          127.424568 (32.8, 55.2]           338.502319 (55.2, 77.6]          1032.640869 (77.6, 100]           2399.090332

Standard deviations for relectricperperson by urbanr status:               relectricperperson urbanr (%)                       (10.31, 32.8]          344.180664 (32.8, 55.2]           313.532440 (55.2, 77.6]          1103.424927 (77.6, 100]           2194.876709

MultiComparison summary:       Multiple Comparison of Means - Tukey HSD,FWER=0.05       ===============================================================    group1       group2     meandiff   lower     upper   reject --------------------------------------------------------------- (10.31, 32.8] (32.8, 55.2]  211.0778 -439.3829  861.5385 False (10.31, 32.8] (55.2, 77.6]  905.2163  292.5745  1517.858  True (10.31, 32.8] (77.6, 100]  2271.6658 1590.4579 2952.8737  True (32.8, 55.2] (55.2, 77.6]  694.1385  115.8783 1272.3986  True (32.8, 55.2] (77.6, 100]   2060.588 1410.1273 2711.0487  True (55.2, 77.6] (77.6, 100]  1366.4495  753.8078 1979.0913  True ---------------------------------------------------------------

#############################################

Model Interpretation for ANOVA:

When examining the association between residential electricity consumption per person (quantitative response) and binned oil consumption per person (categorical explanatory), the ANOVA test revealed that among countries with the relevant data available, the subgroups of countries with intermediate oil consumption per person (3.08-6.13 and 6.13-9.18 litres) reported significantly greater consumption of residential electricity per person (m=6449.380371, s.d.=±4128.518555 and m=8362.568359) compared to the subgroups with the lowest oil consumption per person (m=830.4105, s.d.=± 1108.687744), F(3, 199) =35.72, p <0001.

On the other hand, when examining the association between residential electricity consumption per person (quantitative response) and binned urban population (categorical explanatory), the ANOVA test revealed that among countries with the relevant data available, the subgroups of countries with higher urban population (55.2-77.6 and 77.6-100%) reported significantly greater consumption of residential electricity per person (m=1032.640869, s.d.=±1103.424927 and m=2399.090332, s.d.=± 2194.876709) compared to the subgroups with lowest urban population (m=127.424568, s.d.=±344.180664), F(3, 199) =31.26, p <0001.

#############################################

Model Interpretation for post hoc ANOVA:

ANOVA revealed that among countries with the relevant data available, the oil consumption per person (collapsed into 4 ordered categories, which is the categorical explanatory variable) and residential electricity consumption per person (quantitative response variable) were significantly associated, F(6, 196)= 35.72, p=1.63e-18. Post hoc comparisons of mean residential electricity consumption by pairs of oil consumption per person categories revealed that other than the comparisons between the group with lowest and highest consumption (i.e. 0.02-3.08 and 9.18-12.23 litres) and the 2 intermediate groups (i.e. 3.08-6.13 and 6.13-9.18 litres), all other comparisons were statistically significant.

Additionally, ANOVA also revealed that among countries with the relevant data available, the urban population (collapsed into 4 ordered categories, which is the categorical explanatory variable) and residential electricity consumption per person (quantitative response variable) were significantly associated, F(6, 196)= 31.26, p=1.33e-16. Post hoc comparisons of mean residential electricity consumption by pairs of urban population categories revealed that other than the comparisons between the 2 subgroups with the lowest urban population (i.e. 10.3-32.8 and 32.8-55.2%), all other comparisons were statistically significant.

[jcvallier]

Data Analysis Tools - Week 1

(gapminder dataset)

Model Interpretation for ANOVA:

Using income per person variable, I put the bottom 1/3, middle 1/3, and top 1/3 percentile into a 3,2,1 values, respectively.  This variable is the income percentile group or perc_group.

When examining the association between employment rate and income percentile group, an Analysis of Variance (ANOVA) there is a significant difference between the top, middle, and bottom, with the mean and standard deviation for top percentile is a Mean=57.34% /  s.d. ±7.51%, for the middle percentile is a Mean=55.22% /  s.d. ±9.46%, and bottom percentile is a Mean=64.39% / s.d. ±11.53%, F score=13.66, p value = 3.27e-06.  Since the p value is less than 0.05 there is a significant difference between the means and we reject the null hypothesis.

The degrees of freedom can be found in the OLS table as the DF model and DF residuals 2 and 163, respectively. 

 OLS Regression Results                             ============================================================================== Dep. Variable:             employrate   R-squared:                       0.144 Model:                            OLS   Adj. R-squared:                  0.133 Method:                 Least Squares   F-statistic:                     13.66 Date:                Mon, 04 Sep 2017   Prob (F-statistic):           3.27e-06 Time:                        23:47:31   Log-Likelihood:                -609.75 No. Observations:                 166   AIC:                             1226. Df Residuals:                     163   BIC:                             1235. Df Model:                           2                                         Covariance Type:            nonrobust                                         ======================================================================================                         coef    std err          t      P>|t|      [95.0% Conf. Int.] -------------------------------------------------------------------------------------- Intercept             57.3386      1.274     45.020      0.000        54.824    59.854 C(perc_group)[T.2]    -2.1145      1.826     -1.158      0.249        -5.720     1.491 C(perc_group)[T.3]     7.0541      1.817      3.881      0.000         3.465    10.643 ============================================================================== Omnibus:                        0.415   Durbin-Watson:                   1.951 Prob(Omnibus):                  0.813   Jarque-Bera (JB):                0.460 Skew:                          -0.118   Prob(JB):                        0.794 Kurtosis:                       2.894   Cond. No.                         3.68 ==============================================================================

Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Model Interpretation of post hoc ANOVA results:

ANOVA analysis p value was significant, but to determine which of the means are significantly different I ran a Post hoc test, using ‘Tukey Honest Sigificant Difference’.  

Multiple Comparison of Means - Tukey HSD,FWER=0.05 ============================================ group1 group2 meandiff lower   upper  reject --------------------------------------------  1      2    -2.1145  -6.434  2.2049 False  1      3     7.0541  2.7549 11.3534  True  2      3     9.1687  4.8112 13.5261  True --------------------------------------------

When compared with employment rate, there is a difference between top and bottom income percentiles.  There is also a difference between middle and bottom income percentiles.   

Related Code:

import pandas as pd

data = pd.read_csv('GapminderData.csv')

# select the variables of interest df1 = data[['country','lifeexpectancy','employrate','femaleemployrate','DevelCountry','incomeperperson','perc_group']]

# new variable  - earningpower (lifeexpectancy * incomeperperson) - this is not an average lifetime income but an indication of earning power potential over ones lifetime

df1['earningpower'] = df1['lifeexpectancy'] * df1['incomeperperson']

# new variable - unemployment (100 - 'employrate') - this is the percentage of the population who does not hold a job

df1['unemployment'] = 100 - df1['employrate']

# new variable - femaleunemployment (100 - 'femaleemployrate') - this is the percentage of females who does not hold a job

df1['femaleunemployment'] = 100 - df1['femaleemployrate']

# how many NAs do we have in employrate

print(df1['employrate'].value_counts(dropna=False))

# drop countries that does not have employrate variable

df1 = df1[pd.notnull(df1['employrate'])]

# did we remove the NAs in employrate variable?

print(df1['employrate'].value_counts(dropna=False))

# how many NAs do we have in lifeexpectancy

print(df1['lifeexpectancy'].value_counts(dropna=False))

# drop contries that have NAs in lifeexpenctancy

df1 = df1[pd.notnull(df1['lifeexpectancy'])]

# did we remove the NAs in lifeexpectancy

print(df1['lifeexpectancy'].value_counts(dropna=False))

df1.dropna(inplace=True)

#%%

df4 = df1[['employrate','perc_group']]

#%%

import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi

model = smf.ols(formula='employrate ~ C(perc_group)',data=df4) results = model.fit() print(results.summary())

#%%

df5=df4.groupby('perc_group').mean() df6=df4.groupby('perc_group').std()

print(df5,df6)

#%%

mc = multi.MultiComparison(df4['employrate'],df4['perc_group']) result2 = mc.tukeyhsd() print(result2.summary())

[phoenixlionme]

I picked Detective Conan.

[phoenixlionme]

Great Fictional Characters who are constantly looked down upon and/or underestimated but still CHOOSE to be kind

[glennbergthings-blog]

Wesleyan Course 2 -Data Analysis Tools - Week 1 Assignment

Week 1 - Hypothesis Testing and ANOVA

Background

My research project uses the Gapminder data set and I am exploring the relationship between Breast Cancer rates and Life expectancy. The research shows that this should be a positive relationship. The research also shows that the Breast Cancer reporting rates in developing countries tends to be under reported – indicating that we may have data quality issues. The less developed countries have the lower Life Expediencies.

The below graph shows an scatter plot of the data I am analyzing. As we can see (fig1) the correlation between higher Breast cancer rates and Life Expectancy is more observant at the higher Life expediencies and less correlated at the lower Life expediencies

                                fig1

I have chosen to use Python for all my coding. I will review my results by showing my Null Hypothesis, my P test and my ANOVA/Tukey test. At the end of the summary, I will show all the code used to generate my results

Hypothesis testing

To provide analysis using a multitude of tests. I have run two different relationship analysis.

Relationship 1

This relationship compares two quantitative relationships of the explanatory variable being Life Expectancy and the Response variable being breast Cancer rates. This a quantitative to Quantitative relationship. We will use the Pearson Correlation Test to check our Null Hypotheses.  My Null Hypothesis is that there is no relationship between the Breast Cancer rates and Life Expectancy. If our P value is P > 0.05 then we can reject the Null Hypothesis.

Relationship 2

My second test involves categorizing life Expectancy into 4 groups based upon the Min and Max values of the life Expectancy. This will turn my explanatory variable of Life Expectancy into a quantitative variable and leaves my Response variable of Breast Cancer Rates as a quantitative variable. Our Null Hypothesis will be that all the population means are equal between the groups. Our Alternative Hypothesis is that they are not equal. I will perform a ANOVA test to see if we can reject the Null Hypothesis test. Since our Categorical variable has 4 groups, I will perform a post hoc Tukey test to see which groups are actually different

P-test for Relationship 1

Since my observations are all quantitative, the simple P test is used. My results are as below in Output 1:

                                                Output 1

As we can see the P test (or the Prob (F-Statistic)) = 5.50e-21 shows that there is a strong set of evidence to reject the null hypothesis and that there is indeed a correlation between Breast Cancer rates and Life expectancy

ANOVA /Tukey test – Relationship 2

To perform an ANOVA and Tukey test, I broke my data up into 4 categories based upon Life expectancy. These 4 categories were based upon dividing the minimum and Maximum life expectancy values into 4 equal length categories. The summary of he data split into categories is as follows in Table 1:

                                             Table 1

The Null Hypothesis that we are testing is that there is no relationship between the 4 age categories of Life Expectancy

Results seen in Output 2:

                                          Output 2

The P test shows a value of 1.06e-26 and the F statistic is 60.91. With these values, I can safely reject the Null Hypothesis.

This test however does not show if just some of the means are not equal on the Null hypothesis. By looking at the data of the means and standard deviations of our 4 categorical groups, we get the following results as seen in Output 3:

                           Output 3

Based upon these results, it does seem that Categories 1 and 2 of Life Expectancy seem to generate an overlap – thus they do not seem statistically significant from each other. In order to further test this I will perform a Tukey test.

The Tukey Test results are seen in Output 4:

                                         Output 4

The Tukey results indicate that we cannot reject the Null Hypothesis between Category 1 and 2, but that we can between all other category comparisons.

Based upon these test, we have further confirmed the relationship between higher Life Expectancy and higher Breast Cancer rates. The results of our test also reinforce what we see on the scatter plots, as well as what our research indicated – Countries with lower life Expectancies who have lower Breast Cancer rates are under reporting and the data may not be of very good quality. The categorization of our data shows that the relationship at lower levels of Life Expectancy is not that strong or may not even exist. From this we must start considering if we should be including this data in our research. More to come in this area as the tests and course move forward.

Python Code Used to Perform All Tests

#1- These commands load the pandas, numpy, matplot and statistics libraries

#I am also creating my dataframe of relevant variables - County, Life Expectancy

#and Breast Cancer rates

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from matplotlib import style

import seaborn

import statsmodels.formula.api as smf

import statsmodels.stats.multicomp as multi

 gm_data = pd.read_csv('gapminder.csv', low_memory = False)

#2- This converts the Life expectancy and breast cancer rates

# to numeric from string. In order to do math calculations we need the

#data to be in a numeric form. In this case since there are numbers after

#the decimal, I am converting the data to a float format

gm_data["lifeexpectancy"] = pd.to_numeric(gm_data["lifeexpectancy"],errors='coerce')

gm_data["breastcancerper100th"] = pd.to_numeric(gm_data["breastcancerper100th"],errors='coerce')

 #3 - This pulls out the relevant columns we are looking to analyze from the

#gapminder data sets. For My project I am interested in only 3 variables

#Country, Life expectancy and Breast cancer rates. I am calling this

#new dataframe sub_data_set

sub_data_set = gm_data[['country','lifeexpectancy','breastcancerper100th']].copy()

#4 - This creates Bolean values for our Nan variables

 print("Corelation of a Q to Q set of variables - Looking at the P test")

test1 = sub_data_set.copy()

test1 = test1.dropna()

model1 = smf.ols(formula='breastcancerper100th ~ lifeexpectancy', data=test1)

results1 = model1.fit()

print (results1.summary())

  #'1-Lower_qtr_Life_Expectency','2-Lower-Middle_qtr_Life_Expectency',

#'3-Upper-Middle_qtr_Life_Expectency','4-Upper_qtr_Life_Expectency

print('life Expectancy Categorization')

sub_le = sub_data_set.copy()

bins = [0, 56, 66, 76, 84]

group_namesle = ['1','2','3','4']

categories = pd.cut(sub_le['lifeexpectancy'], bins, labels=group_namesle)

sub_le['categories'] = pd.cut(sub_le['lifeexpectancy'], bins, labels=group_namesle)

categories

print(pd.value_counts(sub_le['categories']))

 #Testing a Quantitative to Categorical relationship

print("Creating a quantitative set of variables to perform a ANOVA Test")

test3 = sub_le

test3 = test3.dropna()

test3['categories'] = pd.to_numeric(test3['categories'],errors='coerce')

model3 = smf.ols(formula='breastcancerper100th ~ C(categories)', data=test3)            

results3 = model3.fit()

print (results3.summary())

 #Calculating the mean and standard deviation of our categories

 print("Mean")

m1 = test3.groupby('categories').mean()

print(m1)

 print("Standard Deviation")

sd1 = test3.groupby('categories').std()

print(sd1)

 #Multicomparison Tukey test for the  categorical data

print('Performing a Tukey test')

mc1 = multi.MultiComparison(test3['breastcancerper100th'],test3['categories'])

res1 = mc1.tukeyhsd()

print(res1.s

[phoenixlionme]

I was inspired by this Twitter post.