jon-ting-data-manage-vis - Tumblr blog

jon-ting-data-manage-vis · 4 years ago

Text

Writing about My Data

The dataset used for this project included one year of numerous country-level indicators of health, wealth and development. It was put together from different resources by GapMinder. For the purpose of this assignment, I will only discuss about the variables investigated so far, namely residential electricity consumption per person, oil consumption per person and urban population. The study actually included a lot more variables than what is described in this post as my data analytic sample mainly consists of the country development part.

Sample

For all 3 variables, the sample is obtained from The World Bank (https://data.worldbank.org/). The data were provided by both Organisation for Economic Co-operation and Development (OECD) and non-OECD member governments. Despite the fact that there are only 195 countries in the world in 2020, the number of participant countries in this dataset is 213. The study population is the countries in the whole world. My analytic sample included only the countries that have their percentage of urban population recorded (N=203). The sample thus represented non-institutionalized population of the whole world. The level of analysis studied is at the group level as the values were averaged across the whole countries.

Procedure

The data were collected by GapMinder for the purpose of fighting devastating ignorance with a fact-based worldview that everyone can understand.

Data on oil and residential electricity consumption were collected by the World Bank annually (the data were collected for every year since 1960, and similarly for urban population) through questionnaires completed by OECD member governments (the data were collected at the OECD member countries). World Bank population estimates are used to calculate per capita data. The energy data are compiled by the International Energy Agency (IEA). IEA data for economies that are not members of the OECD are based on national energy data adjusted to conform to annual questionnaires completed by OECD member governments. Data for combustible renewables and waste are often based on small surveys or other incomplete information and thus give only a broad impression of developments and are not strictly comparable across countries. The IEA reports include country notes that explain some of these differences.

Data on electric power production and consumption were collected from national energy agencies by the IEA and adjusted to meet international definitions. Data were reported as net consumption as opposed to gross consumption. Net consumption excludes the energy consumed by the generating units. For all countries except the United States, total electric power consumption is equal total net electricity generation plus electricity imports minus electricity exports minus electricity distribution losses. The IEA makes these estimates in consultation with national statistical offices, oil companies, electric utilities, and national energy experts.

Urban population data were calculated using World Bank population estimates and urban ratios from the United Nations World Urbanization Prospects. To estimate urban populations, UN ratios of urban to total population were applied to the World Bank's estimates of total population.

Measures

The oil consumption is actually measured in energy used (kg of oil equivalent per capita), which refers to the use of primary energy before transformation to other end-use fuels (such as electricity and refined petroleum products). It includes energy from combustible renewables and waste - solid biomass and animal products, gas and liquid from biomass, and industrial and municipal waste. Biomass is any plant matter used directly as fuel or converted into fuel, heat, or electricity. All forms of energy - primary energy and primary electricity - are converted into oil equivalents. A notional thermal efficiency of 33 percent is assumed for converting nuclear electricity into oil equivalents and 100 percent efficiency for converting hydroelectric power. The scale is between 0.02-12.23 tonnes per capita. This quantitative variable was binned into 4 categories for some of the analyses to be carried out. However, the quantitative column was maintained for some other analyses.

Electric power consumption measures the production of power plants and combined heat and power plants less transmission, distribution, and transformation losses and own use by heat and power plants. It includes consumption by auxiliary stations, losses in transformers that are considered integral parts of those stations, and electricity produced by pumping installations. Where data are available, it covers electricity generated by primary sources of energy - coal, oil, gas, nuclear, hydro, geothermal, wind, tide and wave, and combustible renewables. Neither production nor consumption data capture the reliability of supplies, including breakdowns, load factors, and frequency of outages. The scale recorded went from 0-11155 kWh per capita. This quantitative variable was binned into 4 categories for some of the analyses to be carried out. However, the quantitative column was maintained for some other analyses.

Urban population refers to people living in urban areas as defined by national statistical offices. Countries differ in the way they classify population as "urban" or "rural." The population of a city or metropolitan area depends on the boundaries chosen. Aggregation of urban and rural population may not add up to total population because of different country coverage. There is no consistent and universally accepted standard for distinguishing urban from rural areas, in part because of the wide variety of situations across countries. Most countries use an urban classification related to the size or characteristics of settlements. Some define urban areas based on the presence of certain infrastructure and services. And other countries designate urban areas based on administrative arrangements. Because of national differences in the characteristics that distinguish urban from rural areas, the distinction between urban and rural population is not amenable to a single definition that would be applicable to all countries. Estimates of the world's urban population would change significantly if China, India, and a few other populous nations were to change their definition of urban centers. Because the estimates of city and metropolitan area are based on national definitions of what constitutes a city or metropolitan area, cross-country comparisons should be made with caution. The scale is between 0-100%. This quantitative variable was binned into 4 categories for some of the analyses to be carried out. However, the quantitative column was maintained for some other analyses.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Testing a Potential Moderator

Following previous visualizations and assessments done on the GapMinder dataset, the conclusion obtained seems to indicate that the oil consumption per person is significantly related to the residential electricity consumption per person. It would thus be interesting to test for a potential moderator between the variables. Urban population is chosen for this purpose.

The codes written for this program are shown below:

#############################################

# Import required libraries import pandas as pd import numpy as np import seaborn as sns import matplotlib as mpl import matplotlib.pyplot as plt import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi import scipy.stats

# Bug fix for display formats and change settings to show all rows and columns pd.set_option('display.float_format', lambda x:'%f'%x) pd.set_option('display.max_columns', None) pd.set_option('display.max_rows', None)

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Report facts regarding the original dataset print("Facts regarding the original GapMinder dataset:") print("---------------------------------------") print("Number of countries: {0}".format(len(raw_data))) print("Number of variables: {0}\n".format(len(raw_data.columns))) print("All variables:\n{0}\n".format(list(raw_data.columns))) print("Data types of each variable:\n{0}\n".format(raw_data.dtypes)) print("First 5 rows of entries:\n{0}\n".format(raw_data.head())) print("=====================================\n")

# Choose variables of interest # var_of_int = ['country', 'incomeperperson', 'alcconsumption', 'co2emissions', # 'internetuserate', 'oilperperson', 'relectricperperson', 'urbanrate'] var_of_int = ['oilperperson', 'relectricperperson', 'urbanrate'] print("Chosen variables of interest:\n{0}\n".format(var_of_int)) print("=====================================\n")

# Code out missing values by replacing with NumPy's NaN data type data = raw_data[var_of_int].replace(' ', np.nan) print("Replaced missing values with NaNs:\n{0}\n".format(data.head())) print("=====================================\n")

# Cast the numeric variables to the appropriate data type then quartile split numeric_vars = var_of_int[:] for var in numeric_vars: data[var] = pd.to_numeric(data[var], downcast='float', errors='raise') print("Simple statistics of each variable:\n{0}\n".format(data.describe())) print("=====================================\n")

# Create secondary variables to investigate frequency distributions print("Separate continuous values categorically using secondary variables:") print("---------------------------------------") data['oilpp (tonnes)'] = pd.cut(data['oilperperson'], 4) oil_val_count = data.groupby('oilpp (tonnes)').size() oil_dist = data['oilpp (tonnes)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 2) elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

data['urbanr (%)'] = pd.cut(data['urbanrate'], 4) urb_val_count = data.groupby('urbanr (%)').size() urb_dist = data['urbanr (%)'].value_counts(sort=False, dropna=True, normalize=True) urb_freq_tab = pd.concat([urb_val_count, urb_dist], axis=1) urb_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of urban population:\n{0}\n".format(urb_freq_tab)) print("=====================================\n")

# Code in valid data in place of missing data for each variable print("Number of missing data in variables:") print("oilperperson: {0}".format(data['oilperperson'].isnull().sum())) print("relectricperperson: {0}".format(data['relectricperperson'].isnull().sum())) print("urbanrate: {0}\n".format(data['urbanrate'].isnull().sum())) print("=====================================\n")

print("Investigate entries with missing urbanrate data:\n{0}\n".format(data[['oilperperson', 'relectricperperson']][data['urbanrate'].isnull()])) print("Data for other variables are also missing for 90% of these entries.") print("Therefore, eliminate them from the dataset.\n") data = data[data['urbanrate'].notnull()] print("=====================================\n")

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 2) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

null_oil_data = data[data['oilperperson'].isnull()].copy() oil_map_dict = data.groupby('urbanr (%)').median()['oilperperson'].to_dict() print("Median values of oilperperson corresponding to each urbanrate group:\n{0}\n".format(oil_map_dict)) null_oil_data['oilperperson'] = null_oil_data['urbanr (%)'].map(oil_map_dict) data = data.combine_first(null_oil_data) data['oilpp (tonnes)'] = pd.cut(data['oilperperson'], 4) print("Replace oilperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("=====================================\n")

# Investigate the new frequency distributions print("Report the new frequency table for each variable:") print("---------------------------------------") oil_val_count = data.groupby('oilpp (tonnes)').size() oil_dist = data['oilpp (tonnes)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

urb_val_count = data.groupby('urbanr (%)').size() urb_dist = data['urbanr (%)'].value_counts(sort=False, dropna=True, normalize=True) urb_freq_tab = pd.concat([urb_val_count, urb_dist], axis=1) urb_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of urban population:\n{0}\n".format(urb_freq_tab)) print("=====================================\n")

# Testing for moderator effect print("Testing for moderator effect:") print("-------------------------------------") print("Urban population as moderator:") urb1 = data[data['urbanr (%)'] == '(10.31, 32.8]'] urb2 = data[data['urbanr (%)'] == '(32.8, 55.2]'] urb3 = data[data['urbanr (%)'] == '(55.2, 77.6]'] urb4 = data[data['urbanr (%)'] == '(77.6, 100]'] print('Association between relectricperperson and oilperperson for urbanr (%) (10.31, 32.8]:\n{0}\n' .format(scipy.stats.pearsonr(urb1['relectricperperson'], urb1['oilperperson']))) print('Association between relectricperperson and oilperperson for urbanr (%) (32.8, 55.2]:\n{0}\n' .format(scipy.stats.pearsonr(urb2['relectricperperson'], urb2['oilperperson']))) print('Association between relectricperperson and oilperperson for urbanr (%) (55.2, 77.6]:\n{0}\n' .format(scipy.stats.pearsonr(urb3['relectricperperson'], urb3['oilperperson']))) print('Association between relectricperperson and oilperperson for urbanr (%) (77.6, 100]:\n{0}\n' .format(scipy.stats.pearsonr(urb4['relectricperperson'], urb4['oilperperson'])))

print("\nBivariate graphs:") print("-------------------------------------") sns.regplot(x='oilperperson', y='relectricperperson', data=urb1) plt.xlabel("Oil consumption per person (tonnes)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot for urbanr (%) (10.31, 32.8]") plt.show() sns.regplot(x='oilperperson', y='relectricperperson', data=urb2) plt.xlabel("Oil consumption per person (tonnes)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot for urbanr (%) (32.8, 55.2]") plt.show() sns.regplot(x='oilperperson', y='relectricperperson', data=urb3) plt.xlabel("Oil consumption per person (tonnes)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot for urbanr (%) (55.2, 77.6]") plt.show() sns.regplot(x='oilperperson', y='relectricperperson', data=urb4) plt.xlabel("Oil consumption per person (tonnes)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot for urbanr (%) (77.6, 100]") plt.show()

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

All variables: ['country', 'incomeperperson', 'alcconsumption', 'armedforcesrate', 'breastcancerper100th', 'co2emissions', 'femaleemployrate', 'hivrate', 'internetuserate', 'lifeexpectancy', 'oilperperson', 'polityscore', 'relectricperperson', 'suicideper100th', 'employrate', 'urbanrate']

Data types of each variable: country object incomeperperson object alcconsumption object armedforcesrate object breastcancerper100th object co2emissions object femaleemployrate object hivrate object internetuserate object lifeexpectancy object oilperperson object polityscore object relectricperperson object suicideper100th object employrate object urbanrate object dtype: object

First 5 rows of entries: country incomeperperson alcconsumption armedforcesrate \ 0 Afghanistan .03 .5696534 1 Albania 1914.99655094922 7.29 1.0247361 2 Algeria 2231.99333515006 .69 2.306817 3 Andorra 21943.3398976022 10.17 4 Angola 1381.00426770244 5.57 1.4613288

breastcancerper100th co2emissions femaleemployrate hivrate \ 0 26.8 75944000 25.6000003814697 1 57.4 223747333.333333 42.0999984741211 2 23.5 2932108666.66667 31.7000007629394 .1 3 4 23.1 248358000 69.4000015258789 2

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

relectricperperson suicideper100th employrate urbanrate 0 6.68438529968262 55.7000007629394 24.04 1 636.341383366604 7.69932985305786 51.4000015258789 46.72 2 590.509814347428 4.8487696647644 50.5 65.22 3 5.36217880249023 88.92 4 172.999227388199 14.5546770095825 75.6999969482422 56.7

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Replaced missing values with NaNs: oilperperson relectricperperson urbanrate 0 NaN NaN 24.04 1 NaN 636.341383366604 46.72 2 .42009452521537 590.509814347428 65.22 3 NaN NaN 88.92 4 NaN 172.999227388199 56.7

=====================================

Simple statistics of each variable: oilperperson relectricperperson urbanrate count 63.000000 136.000000 203.000000 mean 1.484085 1173.179199 56.769348 std 1.825090 1681.440430 23.844936 min 0.032281 0.000000 10.400000 25% 0.532542 203.652103 36.830000 50% 1.032470 597.136444 57.939999 75% 1.622737 1491.145233 74.209999 max 12.228645 11154.754883 100.000000

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count ��frequency oilpp (tonnes) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of residential electricity consumption per person: value_count frequency relectricpp (kWh) (-11.155, 5577.377] 132 0.970588 (5577.377, 11154.755] 4 0.029412

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Investigate entries with missing urbanrate data: oilperperson relectricperperson 43 nan nan 71 nan 0.000000 75 nan nan 121 nan nan 134 nan nan 143 nan nan 157 nan nan 170 nan nan 187 2.006515 1831.731812 198 nan nan

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

Investigate entries with missing relectricperperson data: oilperperson relectricperperson urbanrate oilpp (tonnes) \ 0 nan nan 24.040001 NaN 3 nan nan 88.919998 NaN 5 nan nan 30.459999 NaN 8 nan nan 46.779999 NaN 12 nan nan 83.699997 NaN

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

Replace relectricperperson NaNs based on their quartile group's median: oilperperson relectricperperson urbanrate oilpp (tonnes) \ 0 nan 59.848274 24.040001 NaN 1 nan 636.341370 46.720001 NaN 2 0.420095 590.509827 65.220001 (0.0201, 3.0814] 3 nan 1741.486572 88.919998 NaN 4 nan 172.999222 56.700001 NaN

relectricpp (kWh) urbanr (%) 0 (-11.155, 5577.377] (10.31, 32.8] 1 (-11.155, 5577.377] (32.8, 55.2] 2 (-11.155, 5577.377] (55.2, 77.6] 3 (-11.155, 5577.377] (77.6, 100] 4 (-11.155, 5577.377] (55.2, 77.6]

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

Replace oilperperson NaNs based on their quartile group's median: oilperperson relectricperperson urbanrate oilpp (tonnes) \ 0 0.079630 59.848274 24.040001 (0.0201, 3.0814] 1 0.359173 636.341370 46.720001 (0.0201, 3.0814] 2 0.420095 590.509827 65.220001 (0.0201, 3.0814] 3 2.087848 1741.486572 88.919998 (0.0201, 3.0814] 4 0.844574 172.999222 56.700001 (0.0201, 3.0814]

=====================================

Report the new frequency table for each variable: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (tonnes) (0.0201, 3.0814] 198 0.975369 (3.0814, 6.13] 3 0.014778 (6.13, 9.18] 1 0.004926 (9.18, 12.229] 1 0.004926

Frequency table of residential electricity consumption per person: value_count frequency (-11.155, 5577.377] 199 0.980296 (5577.377, 11154.755] 4 0.019704

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Testing for moderator effect: ------------------------------------- Urban population as moderator: Association between relectricperperson and oilperperson for urbanr (%) (10.31, 32.8]: (0.01366522, 0.93155224561464989)

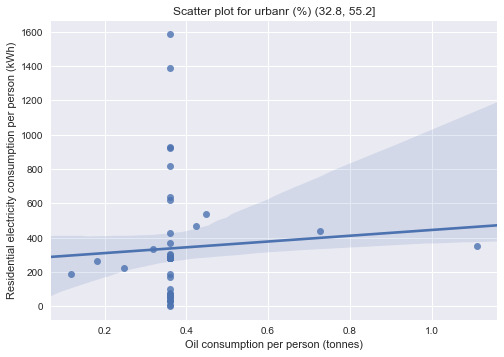
Association between relectricperperson and oilperperson for urbanr (%) (32.8, 55.2]: (0.0682716, 0.63405606539354642)

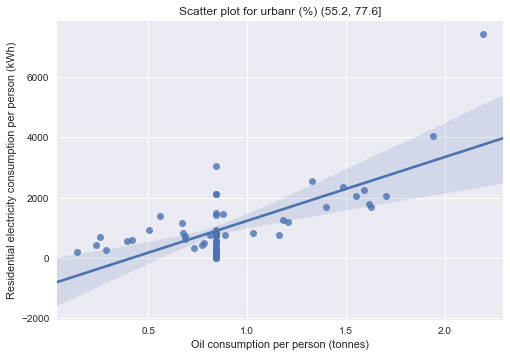
Association between relectricperperson and oilperperson for urbanr (%) (55.2, 77.6]: (0.71694803, 6.1341947698015476e-12)

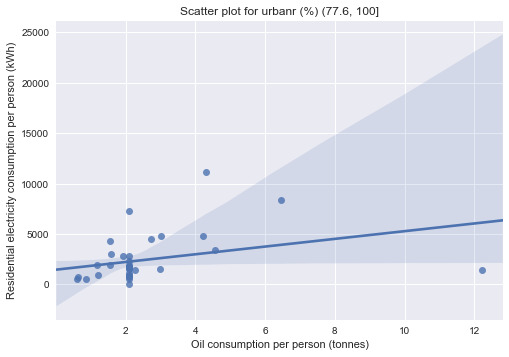
Association between relectricperperson and oilperperson for urbanr (%) (77.6, 100]: (0.32389528, 0.036392765827368875)

Bivariate graphs: -------------------------------------

#############################################

The data are separated into 4 groups according to the urban population quartile they belong to. Since both of the explanatory and response variables in this experiment are quantitative, correlation coefficients are computed for the test.

The test showed that only correlation coefficients between residential electricity consumption per person and oil consumption per person for country subgroups with higher urban population (>55.2%) are statistically significant (p=6.1341947698015476e-12 and p=0.036392765827368875 respectively). This means that the finding from the previous assessments that oil consumption per person is strongly correlated with residential electricity consumption is only applicable to countries with relatively high urban population (i.e. urban population is acting as a moderator between the 2 variables in question).

The scatter plots confirmed the findings as the regression lines for the subgroups with lower urban population are relatively flat compared to those with higher urban population. The oil consumption per person was most correlated to residential electricity consumption per person for subgroup with urban population between 55.2-77.6%.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Generating Correlation Coefficients

Having selected the GapMinder data set and a research question, managed my variables of interest, namely oil consumption per person, residential electricity consumption per person and urban population, visualized their relationship graphically, and tested them statistically, I would like to assesses the degree of linear relationship between the variables. Correlation coefficients are employed for these purposes. Since the variables chosen are all quantitative, no modification is required to be done prior to the computation.

The codes written for this program are shown below:

#############################################

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Generate correlation coefficients print("Generate correlation coefficients:") print('Association between relectricperperson and oilperperson:\n{0}\n'.format(scipy.stats.pearsonr(data['relectricperperson'], data['oilperperson']))) print('Association between relectricperperson and urbanrate:\n{0}\n'.format(scipy.stats.pearsonr(data['relectricperperson'], data['urbanrate'])))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (tonnes) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of residential electricity consumption per person: value_count frequency relectricpp (kWh) (-11.155, 5577.377] 132 0.970588 (5577.377, 11154.755] 4 0.029412

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

=====================================

Frequency table of residential electricity consumption per person: value_count frequency (-11.155, 5577.377] 199 0.980296 (5577.377, 11154.755] 4 0.019704

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Generate correlation coefficients: Association between relectricperperson and oilperperson: (0.60319066, 1.6756086041748473e-21)

Association between relectricperperson and urbanrate: (0.5264625, 7.1877698842960214e-16)

#############################################

The correlation coefficient between residential electricity consumption per person and oil consumption per person was found to be 0.60 while the correlation coefficient between residential electricity consumption per person and urban population was 0.52. Both of the values indicated that there is a moderate positive linear relationship between the 2 explanatory variables and the response variable, with the former being slightly stronger. Both p-values indicated that the results are statistically significant.

Squaring the coefficients give coefficient of determination of 0.36 and 0.27 respectively, meaning that about 36% and 27% of the variance in the residential electricity consumption per person could be explained by the oil consumption per person and urban population respectively, which is not a great deal.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Running a Chi-Square Test of Independence

In addition to the analysis of variance (ANOVA), chi-square test of independence were also carried out. It compares the frequencies of one categorical variable for different values of a second categorical variable. Since all of the variables chosen are quantitative, they are categorised for the purpose of running the test. Post hoc paired comparisons were also carried out in instances where the original statistical test was significant for explanatory variables with more than two levels of categories. The null hypothesis proposed wasthat oil consumption per person is not related to residential electricity consumption per person .

The codes written for this program are shown below:

#############################################

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) # Variable range is extended by 0.1% elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

# Run Chi-Square Test for Independence print("Chi-square test for independence results:") print("-------------------------------------") ct1 = pd.crosstab(data[['relectricpp (kWh)', 'oilpp (tonnes)']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'oilpp (tonnes)']]['oilpp (tonnes)']) colpct1 = ct1 / ct1.sum(axis=0) cs1 = scipy.stats.chi2_contingency(ct1) print("Contingency table of observed counts:\n{0}\n".format(ct1)) print("Column percentages:\n{0}\n".format(colpct1)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs1))

print("Post hoc chi-square test for independence results:") print("-------------------------------------") recode1 = {'(0.0201, 3.0814]': '(0.0201, 3.0814]', '(3.0814, 6.13]': '(3.0814, 6.13]'} data['COMP1v2']= data['oilpp (tonnes)'].map(recode1) recode2 = {'(0.0201, 3.0814]': '(0.0201, 3.0814]', '(6.13, 9.18]': '(6.13, 9.18]'} data['COMP1v3']= data['oilpp (tonnes)'].map(recode2) recode3 = {'(0.0201, 3.0814]': '(0.0201, 3.0814]', '(9.18, 12.229]': '(9.18, 12.229]'} data['COMP1v4']= data['oilpp (tonnes)'].map(recode3) recode4 = {'(3.0814, 6.13]': '(3.0814, 6.13]', '(6.13, 9.18]': '(6.13, 9.18]'} data['COMP2v3']= data['oilpp (tonnes)'].map(recode4) recode5 = {'(3.0814, 6.13]': '(3.0814, 6.13]', '(9.18, 12.229]': '(9.18, 12.229]'} data['COMP2v4']= data['oilpp (tonnes)'].map(recode5) recode6 = {'(6.13, 9.18]': '(6.13, 9.18]', '(9.18, 12.229]': '(9.18, 12.229]'} data['COMP3v4']= data['oilpp (tonnes)'].map(recode6)

ct2 = pd.crosstab(data[['relectricpp (kWh)', 'COMP1v2']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP1v2']]['COMP1v2']) colpct2 = ct2 / ct2.sum(axis=0) cs2 = scipy.stats.chi2_contingency(ct2) print("Contingency table of observed counts:\n{0}\n".format(ct2)) print("Column percentages:\n{0}\n".format(colpct2)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs2))

ct3 = pd.crosstab(data[['relectricpp (kWh)', 'COMP1v3']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP1v3']]['COMP1v3']) colpct3 = ct3 / ct3.sum(axis=0) cs3 = scipy.stats.chi2_contingency(ct3) print("Contingency table of observed counts:\n{0}\n".format(ct3)) print("Column percentages:\n{0}\n".format(colpct3)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs3))

ct4 = pd.crosstab(data[['relectricpp (kWh)', 'COMP1v4']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP1v4']]['COMP1v4']) colpct4 = ct4 / ct4.sum(axis=0) cs4 = scipy.stats.chi2_contingency(ct4) print("Contingency table of observed counts:\n{0}\n".format(ct4)) print("Column percentages:\n{0}\n".format(colpct4)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs4))

ct5 = pd.crosstab(data[['relectricpp (kWh)', 'COMP2v3']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP2v3']]['COMP2v3']) colpct5 = ct5 / ct5.sum(axis=0) cs5 = scipy.stats.chi2_contingency(ct5) print("Contingency table of observed counts:\n{0}\n".format(ct5)) print("Column percentages:\n{0}\n".format(colpct5)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs5))

ct6 = pd.crosstab(data[['relectricpp (kWh)', 'COMP2v4']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP2v4']]['COMP2v4']) colpct6 = ct6 / ct6.sum(axis=0) cs6 = scipy.stats.chi2_contingency(ct6) print("Contingency table of observed counts:\n{0}\n".format(ct6)) print("Column percentages:\n{0}\n".format(colpct6)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs6))

ct7 = pd.crosstab(data[['relectricpp (kWh)', 'COMP3v4']]['relectricpp (kWh)'], data[['relectricpp (kWh)', 'COMP3v4']]['COMP3v4']) colpct7 = ct7 / ct7.sum(axis=0) cs7 = scipy.stats.chi2_contingency(ct7) print("Contingency table of observed counts:\n{0}\n".format(ct7)) print("Column percentages:\n{0}\n".format(colpct7)) print('chi-square value, p value, expected counts:\n{0}\n'.format(cs7))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (tonnes) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of residential electricity consumption per person: value_count frequency relectricpp (kWh) (-11.155, 2788.689] 122 0.897059 (2788.689, 5577.377] 10 0.073529 (5577.377, 8366.0662] 3 0.022059 (8366.0662, 11154.755] 1 0.007353

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

relectricpp (kWh) urbanr (%) 0 (-11.155, 2788.689] (10.31, 32.8] 1 (-11.155, 2788.689] (32.8, 55.2] 2 (-11.155, 2788.689] (55.2, 77.6] 3 (-11.155, 2788.689] (77.6, 100] 4 (-11.155, 2788.689] (55.2, 77.6]

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

=====================================

Frequency table of residential electricity consumption per person: value_count frequency (-11.155, 2788.689] 189 0.931034 (2788.689, 5577.377] 10 0.049261 (5577.377, 8366.0662] 3 0.014778 (8366.0662, 11154.755] 1 0.004926

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Chi-square test for independence results: ------------------------------------- Contingency table of observed counts: oilpp (tonnes) (0.0201, 3.0814] (3.0814, 6.13] (6.13, 9.18] \ relectricpp (kWh) (-11.155, 5577.377] 196 2 0 (5577.377, 11154.755] 2 1 1

oilpp (tonnes) (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 1 (5577.377, 11154.755] 0

Column percentages: oilpp (tonnes) (0.0201, 3.0814] (3.0814, 6.13] (6.13, 9.18] \ relectricpp (kWh) (-11.155, 5577.377] 0.989899 0.666667 0.000000 (5577.377, 11154.755] 0.010101 0.333333 1.000000

oilpp (tonnes) (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 1.000000 (5577.377, 11154.755] 0.000000

chi-square value, p value, expected counts: (65.992259276178885, 3.0767136281290661e-14, 3, array([[ 1.94098522e+02, 2.94088670e+00, 9.80295567e-01, 9.80295567e-01], [ 3.90147783e+00, 5.91133005e-02, 1.97044335e-02, 1.97044335e-02]]))

Post hoc chi-square test for independence results: ------------------------------------- Contingency table of observed counts: COMP1v2 (0.0201, 3.0814] (3.0814, 6.13] relectricpp (kWh) (-11.155, 5577.377] 196 2 (5577.377, 11154.755] 2 1

Column percentages: COMP1v2 (0.0201, 3.0814] (3.0814, 6.13] relectricpp (kWh) (-11.155, 5577.377] 0.989899 0.666667 (5577.377, 11154.755] 0.010101 0.333333

chi-square value, p value, expected counts: (4.7694176614631161, 0.028969623086921414, 1, array([[ 1.95044776e+02, 2.95522388e+00], [ 2.95522388e+00, 4.47761194e-02]]))

Contingency table of observed counts: COMP1v3 (0.0201, 3.0814] (6.13, 9.18] relectricpp (kWh) (-11.155, 5577.377] 196 0 (5577.377, 11154.755] 2 1

Column percentages: COMP1v3 (0.0201, 3.0814] (6.13, 9.18] relectricpp (kWh) (-11.155, 5577.377] 0.989899 0.000000 (5577.377, 11154.755] 0.010101 1.000000

chi-square value, p value, expected counts: (15.917145519824091, 6.617651278198667e-05, 1, array([[ 1.95015075e+02, 9.84924623e-01], [ 2.98492462e+00, 1.50753769e-02]]))

Contingency table of observed counts: COMP1v4 (0.0201, 3.0814] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 196 1 (5577.377, 11154.755] 2 0

Column percentages: COMP1v4 (0.0201, 3.0814] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 0.989899 1.000000 (5577.377, 11154.755] 0.010101 0.000000

chi-square value, p value, expected counts: (24.24939432395016, 8.4633693191566959e-07, 1, array([[ 1.96010050e+02, 9.89949749e-01], [ 1.98994975e+00, 1.00502513e-02]]))

Contingency table of observed counts: COMP2v3 (3.0814, 6.13] (6.13, 9.18] relectricpp (kWh) (-11.155, 5577.377] 2 0 (5577.377, 11154.755] 1 1

Column percentages: COMP2v3 (3.0814, 6.13] (6.13, 9.18] relectricpp (kWh) (-11.155, 5577.377] 0.666667 0.000000 (5577.377, 11154.755] 0.333333 1.000000

chi-square value, p value, expected counts: (0.0, 1.0, 1, array([[ 1.5, 0.5], [ 1.5, 0.5]]))

Contingency table of observed counts: COMP2v4 (3.0814, 6.13] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 2 1 (5577.377, 11154.755] 1 0

Column percentages: COMP2v4 (3.0814, 6.13] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 0.666667 1.000000 (5577.377, 11154.755] 0.333333 0.000000

chi-square value, p value, expected counts: (0.44444444444444442, 0.50498507509384571, 1, array([[ 2.25, 0.75], [ 0.75, 0.25]]))

Contingency table of observed counts: COMP3v4 (6.13, 9.18] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 0 1 (5577.377, 11154.755] 1 0

Column percentages: COMP3v4 (6.13, 9.18] (9.18, 12.229] relectricpp (kWh) (-11.155, 5577.377] 0.000000 1.000000 (5577.377, 11154.755] 1.000000 0.000000

chi-square value, p value, expected counts: (0.0, 1.0, 1, array([[ 0.5, 0.5], [ 0.5, 0.5]]))

#############################################

Model Interpretation for Chi-Square Tests :

When examining the association between residential electricity consumption per person (categorical response) and oil consumption per person (categorical explanatory), a chi-square test of independence revealed that among countries with the relevant data available, those with lower oil consumption per person were more likely to have higher residential electricity consumption per person compared to those higher oil consumption per person, X2=65.99, 3 df, p=0.0001. Residential electricity consumption per person and oil consumption per person are thus significantly associated. Since the explanatory variable has 4 categories, a post hoc test need to be conducted to identify in what way the residential electricity consumption per person are not equal across the different categories of oil consumption per person.

############################################

Model Interpretation for post hoc Chi-Square Tests results:

A Chi Square test of independence revealed that among countries with the relevant data available, residential electricity consumption per person (binary categorical variable) and oil consumption per person (collapsed into 4 ordered categories) were significantly associated, X2=65.99, 3 df, p=0.0001.

The adjusted Bonferroni p-values were compared for the post hoc test. The comparisons of residential electricity consumption per person by pairs of oil consumption per person revealed that lower residential electricity consumption per person were seen among those countries with lower oil consumption per person (less than 3.08 tonnes). In comparison, prevalence of low residential electricity consumption per person was statistically similar among the groups with higher oil consumption per person.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Running an ANOVA

The analysis of variance (ANOVA) assesses whether the means of two or more groups of categorical variables are statistically different from each other. Since all of the variables chosen are quantitative, they are categorised for the purpose of running the test. Post hoc paired comparisons were also carried out in instances where the original statistical test was significant for explanatory variables with more than two levels of categories.

The codes written for this program are shown below:

#############################################

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

# Run ANOVA print("ANOVA results:") print("-------------------------------------") model1 = smf.ols(formula='relectricperperson ~ C(Q("oilpp (tonnes)"))', data=data) m1, std1 = data[['relectricperperson', 'oilpp (tonnes)']].groupby('oilpp (tonnes)').mean(), data[['relectricperperson', 'oilpp (tonnes)']].groupby('oilpp (tonnes)').std() mc1 = multi.MultiComparison(data['relectricperperson'], data['oilpp (tonnes)']) print("relectricperperson ~ oilpp (tonnes)\n{0}".format(model1.fit().summary())) print("Means for relectricperperson by oilpp status:\n{0}\n".format(m1)) print("Standard deviations for relectricperperson by oilpp status:\n{0}\n".format(std1)) print("MultiComparison summary:\n{0}\n".format(mc1.tukeyhsd().summary()))

model2 = smf.ols(formula='relectricperperson ~ C(Q("urbanr (%)"))', data=data) m2, std2 = data[['relectricperperson', 'urbanr (%)']].groupby('urbanr (%)').mean(), data[['relectricperperson', 'urbanr (%)']].groupby('urbanr (%)').std() mc2 = multi.MultiComparison(data['relectricperperson'], data['urbanr (%)']) print("relectricperperson ~ urbanr (%)\n{0}".format(model2.fit().summary())) print("Means for relectricperperson by urbanr status:\n{0}\n".format(m2)) print("Standard deviations for relectricperperson by urbanr status:\n{0}\n".format(std2)) print("MultiComparison summary:\n{0}\n".format(mc2.tukeyhsd().summary()))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (tonnes) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

=====================================

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

ANOVA results: ------------------------------------- relectricperperson ~ oilpp (tonnes) OLS Regression Results ============================================================================== Dep. Variable: relectricperperson R-squared: 0.350 Model: OLS Adj. R-squared: 0.340 Method: Least Squares F-statistic: 35.72 Date: Mon, 10 Aug 2020 Prob (F-statistic): 1.63e-18 Time: 02:21:51 Log-Likelihood: -1721.6 No. Observations: 203 AIC: 3451. Df Residuals: 199 BIC: 3464. Df Model: 3 Covariance Type: nonrobust ============================================================================================================ coef std err t P>|t| [95.0% Conf. Int.] ------------------------------------------------------------------------------------------------------------ Intercept 830.4105 83.731 9.918 0.000 665.298 995.523 C(Q("oilpp (tonnes)"))[T.(3.0814, 6.13]] 5618.9698 685.364 8.199 0.000 4267.462 6970.477 C(Q("oilpp (tonnes)"))[T.(6.13, 9.18]] 7532.1579 1181.164 6.377 0.000 5202.953 9861.362 C(Q("oilpp (tonnes)"))[T.(9.18, 12.229]] 634.4268 1181.164 0.537 0.592 -1694.778 2963.631 ============================================================================== Omnibus: 141.891 Durbin-Watson: 1.778 Prob(Omnibus): 0.000 Jarque-Bera (JB): 1183.713 Skew: 2.690 Prob(JB): 9.12e-258 Kurtosis: 13.536 Cond. No. 14.3 ==============================================================================

Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Means for relectricperperson by oilpp status: relectricperperson oilpp (tonnes) (0.0201, 3.0814] 830.410461 (3.0814, 6.13] 6449.380371 (6.13, 9.18] 8362.568359 (9.18, 12.229] 1464.837280

Standard deviations for relectricperperson by oilpp status: relectricperperson oilpp (tonnes) (0.0201, 3.0814] 1108.687744 (3.0814, 6.13] 4128.518555 (6.13, 9.18] nan (9.18, 12.229] nan

MultiComparison summary: Multiple Comparison of Means - Tukey HSD,FWER=0.05 ======================================================================= group1 group2 meandiff lower upper reject ----------------------------------------------------------------------- (0.0201, 3.0814] (3.0814, 6.13] 5618.9698 3843.1866 7394.753 True (0.0201, 3.0814] (6.13, 9.18] 7532.1579 4471.7516 10592.5642 True (0.0201, 3.0814] (9.18, 12.229] 634.4268 -2425.9795 3694.8331 False (3.0814, 6.13] (6.13, 9.18] 1913.1881 -1611.7745 5438.1507 False (3.0814, 6.13] (9.18, 12.229] -4984.543 -8509.5056 -1459.5804 True (6.13, 9.18] (9.18, 12.229] -6897.7311 -11214.911 -2580.5512 True -----------------------------------------------------------------------

relectricperperson ~ urbanr (%) OLS Regression Results ============================================================================== Dep. Variable: relectricperperson R-squared: 0.320 Model: OLS Adj. R-squared: 0.310 Method: Least Squares F-statistic: 31.26 Date: Mon, 10 Aug 2020 Prob (F-statistic): 1.33e-16 Time: 02:21:51 Log-Likelihood: -1726.1 No. Observations: 203 AIC: 3460. Df Residuals: 199 BIC: 3473. Df Model: 3 Covariance Type: nonrobust ====================================================================================================== coef std err t P>|t| [95.0% Conf. Int.] ------------------------------------------------------------------------------------------------------ Intercept 127.4246 185.907 0.685 0.494 -239.176 494.025 C(Q("urbanr (%)"))[T.(32.8, 55.2]] 211.0778 251.045 0.841 0.401 -283.973 706.128 C(Q("urbanr (%)"))[T.(55.2, 77.6]] 905.2163 236.449 3.828 0.000 438.949 1371.484 C(Q("urbanr (%)"))[T.(77.6, 100]] 2271.6658 262.912 8.640 0.000 1753.214 2790.117 ============================================================================== Omnibus: 196.152 Durbin-Watson: 2.055 Prob(Omnibus): 0.000 Jarque-Bera (JB): 4118.605 Skew: 3.766 Prob(JB): 0.00 Kurtosis: 23.741 Cond. No. 5.26 ==============================================================================

Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. Means for relectricperperson by urbanr status: relectricperperson urbanr (%) (10.31, 32.8] 127.424568 (32.8, 55.2] 338.502319 (55.2, 77.6] 1032.640869 (77.6, 100] 2399.090332

Standard deviations for relectricperperson by urbanr status: relectricperperson urbanr (%) (10.31, 32.8] 344.180664 (32.8, 55.2] 313.532440 (55.2, 77.6] 1103.424927 (77.6, 100] 2194.876709

MultiComparison summary: Multiple Comparison of Means - Tukey HSD,FWER=0.05 =============================================================== group1 group2 meandiff lower upper reject --------------------------------------------------------------- (10.31, 32.8] (32.8, 55.2] 211.0778 -439.3829 861.5385 False (10.31, 32.8] (55.2, 77.6] 905.2163 292.5745 1517.858 True (10.31, 32.8] (77.6, 100] 2271.6658 1590.4579 2952.8737 True (32.8, 55.2] (55.2, 77.6] 694.1385 115.8783 1272.3986 True (32.8, 55.2] (77.6, 100] 2060.588 1410.1273 2711.0487 True (55.2, 77.6] (77.6, 100] 1366.4495 753.8078 1979.0913 True ---------------------------------------------------------------

#############################################

Model Interpretation for ANOVA:

When examining the association between residential electricity consumption per person (quantitative response) and binned oil consumption per person (categorical explanatory), the ANOVA test revealed that among countries with the relevant data available, the subgroups of countries with intermediate oil consumption per person (3.08-6.13 and 6.13-9.18 litres) reported significantly greater consumption of residential electricity per person (m=6449.380371, s.d.=±4128.518555 and m=8362.568359) compared to the subgroups with the lowest oil consumption per person (m=830.4105, s.d.=± 1108.687744), F(3, 199) =35.72, p <0001.

On the other hand, when examining the association between residential electricity consumption per person (quantitative response) and binned urban population (categorical explanatory), the ANOVA test revealed that among countries with the relevant data available, the subgroups of countries with higher urban population (55.2-77.6 and 77.6-100%) reported significantly greater consumption of residential electricity per person (m=1032.640869, s.d.=±1103.424927 and m=2399.090332, s.d.=± 2194.876709) compared to the subgroups with lowest urban population (m=127.424568, s.d.=±344.180664), F(3, 199) =31.26, p <0001.

#############################################

Model Interpretation for post hoc ANOVA:

ANOVA revealed that among countries with the relevant data available, the oil consumption per person (collapsed into 4 ordered categories, which is the categorical explanatory variable) and residential electricity consumption per person (quantitative response variable) were significantly associated, F(6, 196)= 35.72, p=1.63e-18. Post hoc comparisons of mean residential electricity consumption by pairs of oil consumption per person categories revealed that other than the comparisons between the group with lowest and highest consumption (i.e. 0.02-3.08 and 9.18-12.23 litres) and the 2 intermediate groups (i.e. 3.08-6.13 and 6.13-9.18 litres), all other comparisons were statistically significant.

Additionally, ANOVA also revealed that among countries with the relevant data available, the urban population (collapsed into 4 ordered categories, which is the categorical explanatory variable) and residential electricity consumption per person (quantitative response variable) were significantly associated, F(6, 196)= 31.26, p=1.33e-16. Post hoc comparisons of mean residential electricity consumption by pairs of urban population categories revealed that other than the comparisons between the 2 subgroups with the lowest urban population (i.e. 10.3-32.8 and 32.8-55.2%), all other comparisons were statistically significant.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Creating Graphs for My Data

To better present my findings, I carried on with the processed GapMinder data to generate univariate distribution graphs and bivariate scatterplots of my variables of interest, namely oil consumption per person, residential electricity consumption per person, and urban population. Note that only scatterplots were presented for bivariate graphs as all 3 variables chosen are quantitative instead of categorical.

The codes written for this program are shown below:

#############################################

# Import required libraries import pandas as pd import numpy as np import seaborn as sns import matplotlib as mpl import matplotlib.pyplot as plt

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Create secondary variables to investigate frequency distributions print("Separate continuous values categorically using secondary variables:") print("---------------------------------------") data['oilpp (litre)'] = pd.cut(data['oilperperson'], 4) oil_val_count = data.groupby('oilpp (litre)').size() oil_dist = data['oilpp (litre)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

null_oil_data = data[data['oilperperson'].isnull()].copy() oil_map_dict = data.groupby('urbanr (%)').median()['oilperperson'].to_dict() print("Median values of oilperperson corresponding to each urbanrate group:\n{0}\n".format(oil_map_dict)) null_oil_data['oilperperson'] = null_oil_data['urbanr (%)'].map(oil_map_dict) data = data.combine_first(null_oil_data) data['oilpp (litre)'] = pd.cut(data['oilperperson'], 4) print("Replace oilperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("=====================================\n")

# Investigate the new frequency distributions print("Report the new frequency table for each variable:") print("---------------------------------------") oil_val_count = data.groupby('oilpp (litre)').size() oil_dist = data['oilpp (litre)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

# Visualize the data mpl.rcParams['axes.titlesize'] = 15 mpl.rcParams['axes.labelsize'] = 12 print("Univariate graphs:") print("-------------------------------------") sns.distplot(data['oilperperson'], kde=False) plt.xlabel("Oil consumption per person (litres)") plt.ylabel("Number of countries") plt.title("Distribution of oil consumption per person") plt.show() sns.distplot(data['relectricperperson'], kde=False) plt.xlabel("Residential electricity consumption per person (kWh)") plt.ylabel("Number of countries") plt.title("Distribution of residential electricity consumption per person") plt.show() sns.distplot(data['urbanrate'], kde=False) plt.xlabel("Urban population (%)") plt.ylabel("Number of countries") plt.title("Distribution of urban population") plt.show()

print("\nBivariate graphs:") print("-------------------------------------") sns.regplot(x='oilperperson', y='relectricperperson', data=data) plt.xlabel("Oil consumption per person (litres)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot of oil vs residential electricity consumption per person") plt.show() sns.regplot(x='urbanrate', y='relectricperperson', data=data) plt.xlabel("Urban population (%)") plt.ylabel("Residential electricity consumption per person (kWh)") plt.title("Scatter plot of urban population vs residential electricity consumption per person") plt.show()

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (litre) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

Investigate entries with missing relectricperperson data: oilperperson relectricperperson urbanrate oilpp (litre) \ 0 nan nan 24.040001 NaN 3 nan nan 88.919998 NaN 5 nan nan 30.459999 NaN 8 nan nan 46.779999 NaN 12 nan nan 83.699997 NaN

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

Replace relectricperperson NaNs based on their quartile group's median: oilperperson relectricperperson urbanrate oilpp (litre) \ 0 nan 59.848274 24.040001 NaN 1 nan 636.341370 46.720001 NaN 2 0.420095 590.509827 65.220001 (0.0201, 3.0814] 3 nan 1741.486572 88.919998 NaN 4 nan 172.999222 56.700001 NaN

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

Replace oilperperson NaNs based on their quartile group's median: oilperperson relectricperperson urbanrate oilpp (litre) \ 0 0.079630 59.848274 24.040001 (0.0201, 3.0814] 1 0.359173 636.341370 46.720001 (0.0201, 3.0814] 2 0.420095 590.509827 65.220001 (0.0201, 3.0814] 3 2.087848 1741.486572 88.919998 (0.0201, 3.0814] 4 0.844574 172.999222 56.700001 (0.0201, 3.0814]

=====================================

Report the new frequency table for each variable: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (litre) (0.0201, 3.0814] 198 0.975369 (3.0814, 6.13] 3 0.014778 (6.13, 9.18] 1 0.004926 (9.18, 12.229] 1 0.004926

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Univariate graphs: -------------------------------------

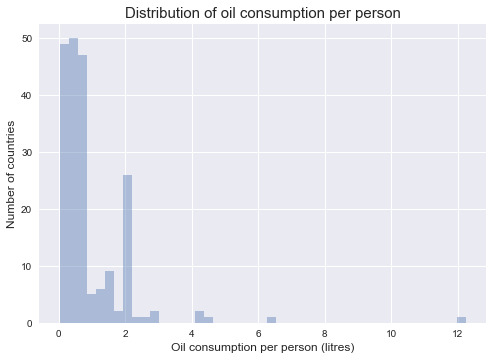
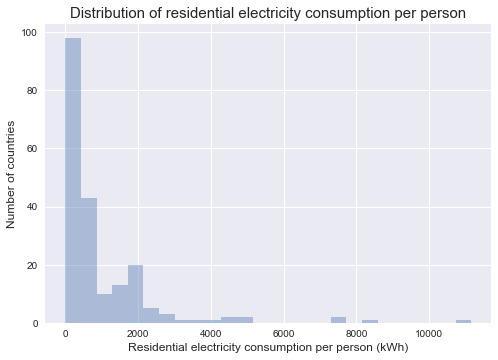
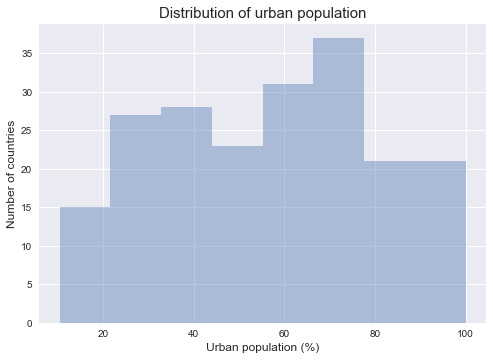
Bivariate graphs: -------------------------------------

#############################################

The distribution histograms allow us to visualize the conclusion I made in earlier posts regarding the distribution of the variables, that is, both of the consumption variables are strongly rightly-skewed and the urban population is roughly normally distributed.

The distribution of oil consumption per person centers around 0.25 litre while the center of residential electricity consumption per person is around 125 kWh. Most of the values are concentrated below 3 litres for oil consumption and below 5000 kWh for electricity consumption. The spread of the data is thus wider for electricity consumption compared to oil consumption. The urban population seems to be bimodal with a rather even spread according to the visualization, yet the data points are relatively scarce for a definitive conclusion to be made regarding this issue.

In attempt to answer the research question generated at the beginning of the project, we can see from the scatterplots that both oil consumption per person and urban population are positively associated with residential electricity consumption per person. The uncertainty of the regression line in the first plot increases drastically as the oil consumption as the number of data points in this region is extremely scarce. The country with the maximum oil consumption per person could very well be an outlier that might have influenced the gradient of the regression line greatly.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Making Data Management Decisions

As a continuation of the previous post, this post outlines the steps taken to manage the processed GapMinder data further before displaying the new frequency tables of three variables of interest, namely oil consumption per person, residential electricity consumption per person, and urban population.

The codes written for this program are shown below:

#############################################

# Import required libraries import pandas as pd import numpy as np

# Bug fix for display formats to avoid run time errors pd.set_option('display.float_format', lambda x:'%f'%x)

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Create secondary variables to investigate frequency distributions print("Separate continuous values categorically using secondary variables:") print("---------------------------------------") data['oilpp (litre)'] = pd.cut(data['oilperperson'], 4) oil_val_count = data.groupby('oilpp (litre)').size() oil_dist = data['oilpp (litre)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

null_elec_data = data[data['relectricperperson'].isnull()].copy() print("Investigate entries with missing relectricperperson data:\n{0}\n".format(null_elec_data.head())) elec_map_dict = data.groupby('urbanr (%)').median()['relectricperperson'].to_dict() print("Median values of relectricperperson corresponding to each urbanrate group:\n{0}\n".format(elec_map_dict)) null_elec_data['relectricperperson'] = null_elec_data['urbanr (%)'].map(elec_map_dict) data = data.combine_first(null_elec_data) data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4) print("Replace relectricperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("-------------------------------------\n")

null_oil_data = data[data['oilperperson'].isnull()].copy() oil_map_dict = data.groupby('urbanr (%)').median()['oilperperson'].to_dict() print("Median values of oilperperson corresponding to each urbanrate group:\n{0}\n".format(oil_map_dict)) null_oil_data['oilperperson'] = null_oil_data['urbanr (%)'].map(oil_map_dict) data = data.combine_first(null_oil_data) data['oilpp (litre)'] = pd.cut(data['oilperperson'], 4) print("Replace oilperperson NaNs based on their quartile group's median:\n{0}\n".format(data.head())) print("=====================================\n")

# Investigate the new frequency distributions print("Report the new frequency table for each variable:") print("---------------------------------------") oil_val_count = data.groupby('oilpp (litre)').size() oil_dist = data['oilpp (litre)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=====================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=====================================

Separate continuous values categorically using secondary variables: --------------------------------------- Frequency table of oil consumption per person: value_count frequency oilpp (litre) (0.0201, 3.0814] 58 0.920635 (3.0814, 6.13] 3 0.047619 (6.13, 9.18] 1 0.015873 (9.18, 12.229] 1 0.015873

Frequency table of urban population: value_count frequency urbanr (%) (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

=====================================

Number of missing data in variables: oilperperson: 150 relectricperperson: 77 urbanrate: 10

=====================================

Data for other variables are also missing for 90% of these entries. Therefore, eliminate them from the dataset.

=====================================

relectricpp (kWh) urbanr (%) 0 NaN (10.31, 32.8] 3 NaN (77.6, 100] 5 NaN (10.31, 32.8] 8 NaN (32.8, 55.2] 12 NaN (77.6, 100]

Median values of relectricperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 59.848274, '(32.8, 55.2]': 278.73962, '(55.2, 77.6]': 753.20978, '(77.6, 100]': 1741.4866}

-------------------------------------

Median values of oilperperson corresponding to each urbanrate group: {'(10.31, 32.8]': 0.079630107, '(32.8, 55.2]': 0.35917261, '(55.2, 77.6]': 0.84457392, '(77.6, 100]': 2.0878479}

=====================================

Frequency table of urban population: value_count frequency (10.31, 32.8] 42 0.206897 (32.8, 55.2] 51 0.251232 (55.2, 77.6] 68 0.334975 (77.6, 100] 42 0.206897

#############################################

After the data management step, all missing data in the dataset are dealt with. The 10 countries missing the data for urbanrate are discarded while the missing values for both oil and residential electricity consumption per person are imputed to be the median of subgroups calculated based of the quartile that they belong to in the urbanrate variable. It could be seen that the frequency distribution of the 2 consumption variables have not changed much except that the first quartiles are more populated.

0 notes

jon-ting-data-manage-vis · 4 years ago

Text

Running My First Program

This post outlines the steps taken to process the GapMinder raw data to display the frequency tables of three variables of interest, namely oil consumption per person, residential electricity consumption per person, and urban population.

The codes written for the purpose mentioned above are shown below:

#############################################

# Import required libraries import pandas as pd import numpy as np

# Bug fix for display formats to avoid run time errors pd.set_option('display.float_format', lambda x:'%f'%x)

# Read in the GapMinder dataset raw_data = pd.read_csv('./gapminder.csv', low_memory=False)

# Report facts regarding the original dataset print("Facts regarding the original GapMinder dataset:") print(" --------------------------------------------------------------------------- ") print("Number of countries: {0}".format(len(raw_data))) print("Number of variables: {0}\n".format(len(raw_data.columns))) print("All variables:\n{0}\n".format(list(raw_data.columns))) print("Data types of each variable:\n{0}\n".format(raw_data.dtypes)) print("First 5 rows of entries:\n{0}\n".format(raw_data.head())) print("=========================================\n")

# Replace missing values with NumPy's NaN data type data = raw_data[var_of_int].replace(' ', np.nan) print("Replaced missing values with NaNs:\n{0}\n".format(data.head())) print("=========================================\n")

# Investigate frequency distribution of each variable data['oilpp (litre)'] = pd.cut(data['oilperperson'], 4, labels=['< 3.09', '3.09-6.13', '6.14-9.18', '> 9.18']) oil_val_count = data.groupby('oilpp (litre)').size() oil_dist = data['oilpp (litre)'].value_counts(sort=False, dropna=True, normalize=True) oil_freq_tab = pd.concat([oil_val_count, oil_dist], axis=1) oil_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of oil consumption per person:\n{0}\n".format(oil_freq_tab))

data['relectricpp (kWh)'] = pd.cut(data['relectricperperson'], 4, labels=['< 2788.7', '2788.7-5577.4', '5577.5-8366.1', '> 8366.1']) elec_val_count = data.groupby('relectricpp (kWh)').size() elec_dist = data['relectricpp (kWh)'].value_counts(sort=False, dropna=True, normalize=True) elec_freq_tab = pd.concat([elec_val_count, elec_dist], axis=1) elec_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of residential electricity consumption per person:\n{0}\n".format(elec_freq_tab))

data['urbanr (%)'] = pd.cut(data['urbanrate'], 4, labels=['< 32.9', '32.9-55.2', '55.3-77.6', '> 77.6']) urb_val_count = data.groupby('urbanr (%)').size() urb_dist = data['urbanr (%)'].value_counts(sort=False, dropna=True, normalize=True) urb_freq_tab = pd.concat([urb_val_count, urb_dist], axis=1) urb_freq_tab.columns = ['value_count', 'frequency'] print("Frequency table of urban population:\n{0}\n".format(urb_freq_tab)) print("=========================================\n")

# Report number of missing data for each variable print("Number of missing data in oilperperson {0}".format(data['oilperperson'].isnull().sum())) print("Number of missing data in relectricperperson: {0}".format(data['relectricperperson'].isnull().sum())) print("Number of missing data in urbanrate: {0}".format(data['urbanrate'].isnull().sum()))

#############################################

The output of the program is as follow:

#############################################

Facts regarding the original GapMinder dataset: --------------------------------------------------------------------------- Number of countries: 213 Number of variables: 16

internetuserate lifeexpectancy oilperperson polityscore \ 0 3.65412162280064 48.673 0 1 44.9899469578783 76.918 9 2 12.5000733055148 73.131 .42009452521537 2 3 81 4 9.99995388324075 51.093 -2

=========================================

Chosen variables of interest: ['oilperperson', 'relectricperperson', 'urbanrate']

=========================================

Frequency table of oil consumption per person: value_count frequency oilpp (litre) < 3.09 58 0.920635 3.09-6.13 3 0.047619 6.14-9.18 1 0.015873 > 9.18 1 0.015873

Frequency table of residential electricity consumption per person: value_count frequency relectricpp (kWh) < 2788.7 122 0.897059 2788.7-5577.4 10 0.073529 5577.5-8366.1 3 0.022059 > 8366.1 1 0.007353

Frequency table of urban population: value_count frequency urbanr (%) < 32.9 42 0.206897 32.9-55.2 51 0.251232 55.3-77.6 68 0.334975 > 77.6 42 0.206897

=========================================

Number of missing data in oilperperson: 150 Number of missing data in relectricperperson: 77 Number of missing data in urbanrate: 10

#############################################

In summary, the frequency distributions of both oil and residential electricity consumption per person are heavily skewed to the right. The frequency tables clearly showed that most of the data points reside within the first quartile of the distributions. As for urban population, the data seems to be normally distributed as the intermediate values (second and third quartiles) are more populated compared to the more extreme values.

Missing data is found in all three variables, with the oil consumption per person suffering the most from it. Among 213 countries, record of this particular variable is not found for 150 of them, which means the data is only available for around 30% of the countries. The condition of residential electricity consumption per person is slightly better, with about 36% of the data missing for the variable.

0 notes