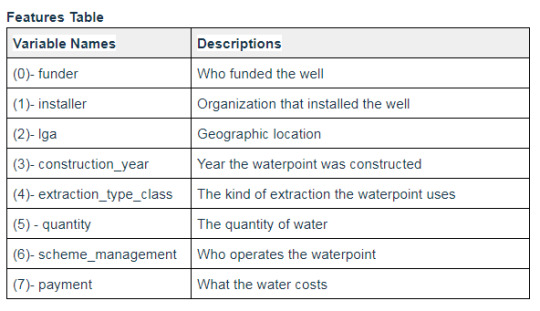
Text
Data Analysis Capstone - Week 3
This week I am discussing my analysis of Tanzania water wells. Analysis
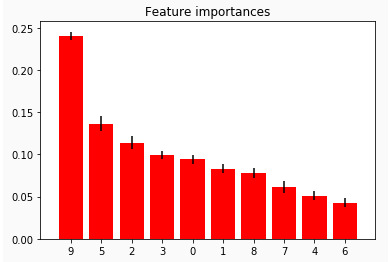
After using the random forest algorithm, the following 10 variables were ranked for importance using the scikit-learn feature importance function (use the feature table to reference each variable name and description), see chart below. The top four variables were: (9) gps_height, (5) quantity, (2) lga, (3) construction_year.
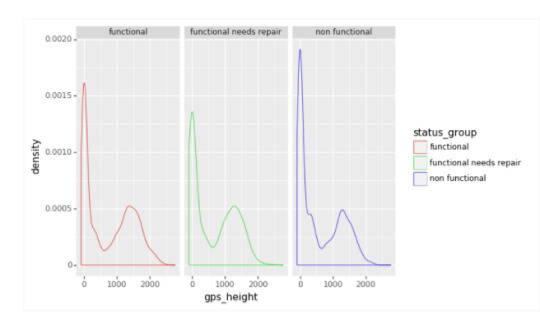
Gps_height variable :
The following is a density plot of of gps_height. The target variables of functional, functional needs repair, and nonfunctional all have similar plots, with a spike at zero and another near 1500 meters(units assumed).
This indicates that gps_height alone is not sufficient to determine between the target variables.Given that gps_height is the most important feature, there is probably a strong relationship with other variables in the dataset.
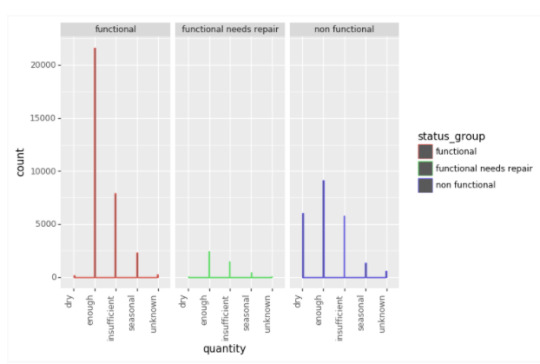
Quantity variable :
For the quantity variable there is more non functional dry wells than functional dry or functional needs repair dry. It is also of note that non functional enough is the largest count for functional, functional needs repair, and non functional. It is important to note, it is twice more likely to be functional when the quantity is functional enough versus non-functional enough.
Lga variable:
Lga Is a geographical territory. No one region had more non functionals in the top ten, see table below.

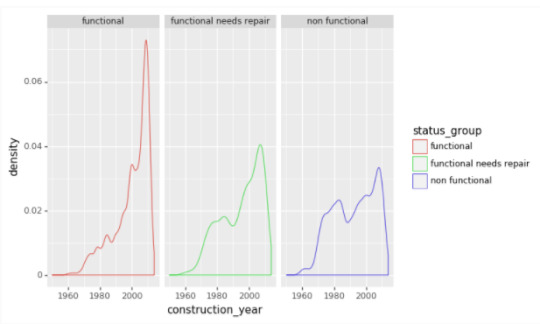
Construction_Year variable -
The range of dates included 1960 through 2013 (excluding nulls 20,710). This variable revels that the vast majority of wells were set up in the last decade. It is interesting to see that there are more significant spikes in functional needs repair and non functional repair around 1980.
0 notes
Text
Data Analysis - Capstone Week 2
Methods
Sample:
Data was collected from 2002 to 2013 by Taarifa and the Tanzanian Ministry of Water on water pumps in through out Tanzanian. The data collected was designed to understand which waterpoints will fail and where they can improve maintenance operations and ensure that clean, potable water is available to local communities. The wells are classified into three categories: functional, functional needs repair, and not functional.
Variables:
The following variables were selected to train and test the model.
The following are the target variables, were ‘not functional’ is the key target to be predicted for feature importance.

Statistical Analyses:
Training & Test Split with cross validation
After the key variables were selected above, the remaining dataset was split into a training set and a test set. The dataset training to test split was 75% and 25%, respectively.
A 10 k-fold cross validation was done with on 8 features with the sequential feature selection greedy algorithm. This was done to observe which features contributed to the overall accuracy score.
Random Forest Algorithm Explained:
Random Forest is an ensemble approach with decision trees. The ensemble method takes a group of weak learners and together form a strong learner.
Therefore, a decision tree which, in ensemble terms, corresponds to our weak learner, and takes your target data entered at the top and then gets traverses down the tree where it is bucketed into smaller and smaller sets until your target cannot be split any further.
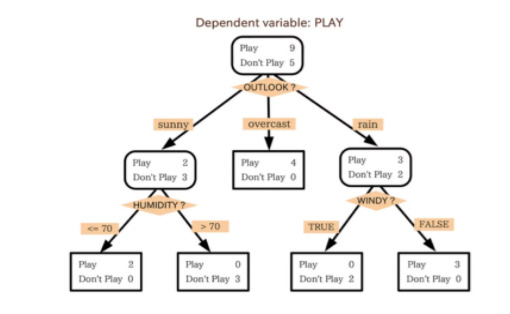
In the example below, the tree advises us, based upon weather conditions, whether to play ball. For example, if the outlook is sunny and the humidity is less than or equal to 70, then it’s probably OK to play. See diagram below..
As shown in diagram below, random forest is a collection of the decision trees where the data are randomly shuffled into subsets and decision trees are formed for each random split.
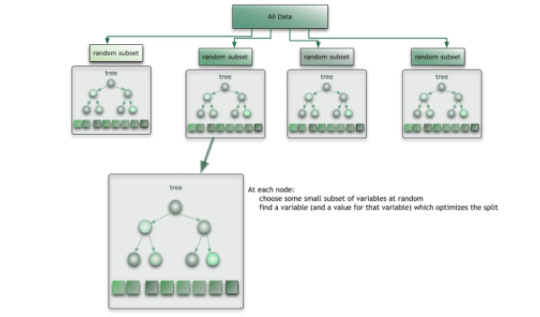
Once the trees have been split, a majority vote of the mode is used for categorical predictor and mean for quantitative. The result is a predictive model, that due to the ensemble method, creates a stronger predictive model that avoids overfitting the data due to its randomness.
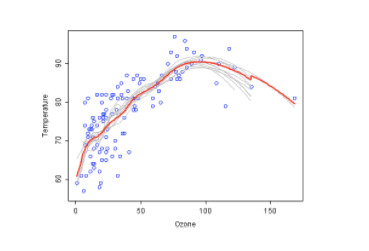
See the example below, where each decision tree is shown as a gray curve. Each gray curve (a weak learner) is a fair approximation to the underlying data. The red curve (the ensemble “strong learner”) can be seen to be a much better approximation to the underlying data.
Random forests can be used to rank the importance of variables in a regression or classification problem in a natural way, where features which produce large values for this score are ranked as more important than features which produce small values.
This method of determining variable importance has some drawbacks. For data including categorical variables with different number of levels, random forests are biased in favor of those attributes with more levels. Using additional unbiased trees or training on a balanced data set can help with this problem.
How Random Forest is being applied to the dataset :
When setting the parameters of random forest, 125 trees were selected for a robust generalized score. Additionally, class weight was selected as ‘balanced’ as the key target of ‘not functional’ was under-represented in the training set and additional weight for predication would be given to the other categories of ‘functional’, and ‘functional needs repair’ if left unadjusted.
Source: http://blog.citizennet.com/blog/2012/11/10/random-forests-ensembles-and-performance-metric
0 notes
Text
Data Analysis - Capstone Week 1
In the preparation of writing a data analysis paper for this capstone. This week we are asked to provide a (1) project title, (2) a research question with my motivation for answering the question, and (3) potential implications of answering the research question.
(1) Project Title: Identifying the best predictors which may cause water pumps to fail in Tanzania using a random forest machine learning algorithm.
(2) Research Question: Can a random forest machine learning algorithm predicts which water pumps will fail in Tanzania, to improve improve maintenance operations that provide clean, potable water for local communities? I plan on using the this method to best identify possible factors.
(3) Implications for research question: By answering this question, this could lead to an improved maintenance schedule that could decrease the amount of water pump failures, and lead to more potable clean water for local communities.
0 notes
Text
Machine Learning for Data Analysis - Week 4
This week we focused on K-means unsupervised learning algorithm. K-means clustering aims to partition n observations into k - clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster. These clusters are not labeled and need the user to examine closely the related variables to understand the characteristics.
I did this assignment on red wine quality dataset found in UCI machine learning data set repository.
I didn’t have any N/A values to manage:
angeIndex: 1599 entries, 0 to 1598 Data columns (total 12 columns): fixed acidity 1599 non-null float64 volatile acidity 1599 non-null float64 citric acid 1599 non-null float64 residual sugar 1599 non-null float64 chlorides 1599 non-null float64 free sulfur dioxide 1599 non-null float64 total sulfur dioxide 1599 non-null float64 density 1599 non-null float64 pH 1599 non-null float64 sulphates 1599 non-null float64 alcohol 1599 non-null float64 quality 1599 non-null int64 dtypes: float64(11), int64(1)
Looking at the elbow method for electing how many k clusters, it looks like between 2 and 4 looks optional. I ran a Turkey HSD test for 3 and 4 clusters. with the best results for 3 clusters.
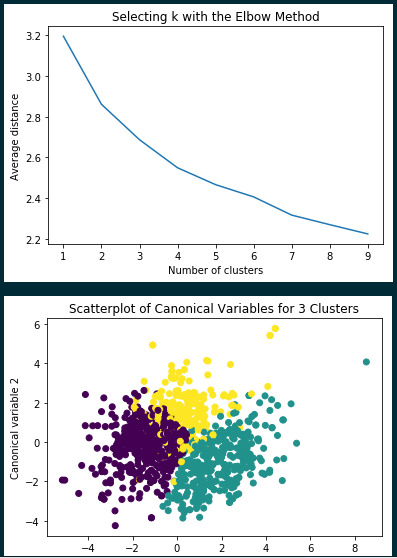
Clustering variable means by cluster index fixed acidity volatile acidity citric acid \ cluster 0 852.964981 -0.613198 0.523980 -0.766575 1 735.110787 0.972455 -0.724979 1.044456 2 710.416031 -0.000537 0.037230 0.174129
residual sugar chlorides free sulfur dioxide total sulfur dioxide \ cluster 0 -0.213666 -0.157534 -0.246837 -0.351623 1 0.006391 0.270782 -0.473441 -0.497666 2 0.489412 0.020018 1.046380 1.276995
density pH sulphates alcohol quality cluster 0 -0.384480 0.590419 -0.315140 -0.005503 -0.187766 1 0.368134 -0.734856 0.576452 0.413372 0.570021 2 0.385615 -0.199118 -0.121968 -0.521363 -0.447425
Here cluster 1 has the best quality with the highest alcohol, sulphates, and fixed acidity. Cluster 0 is close to the mean quality and has the second highest alcohol (near average), however other qualities vary. Cluster 2 has the lowest quality and the lowest alcohol, but also vary in other qualities.
Running a post hoc test again we can see the clusters rejected the null hypthesis and the means and standard deviations vary.
means for alcohol by cluster alcohol_y cluster 0 -0.060487 1 0.422731 2 -0.513167 standard deviations for alcohol by cluster alcohol_y cluster 0 0.949251 1 1.045772 2 0.728444 Multiple Comparison of Means - Tukey HSD,FWER=0.05 ============================================= group1 group2 meandiff lower upper reject --------------------------------------------- 0 1 0.4832 0.3003 0.6661 True 0 2 -0.4527 -0.6481 -0.2573 True 1 2 -0.9359 -1.1472 -0.7246 True
In summary, it looks like I was able to determine three categories of wine: high quality, middle quality, and low quality using K-means analysis. This allowed me to understand the characteristics of each category and to perhaps predict whether a bottle of wine will be high quality. Here is my code:
@author: jcvall """
from pandas import Series, DataFrame import pandas as pd import numpy as np import matplotlib.pylab as plt from sklearn.model_selection import train_test_split from sklearn import preprocessing from sklearn.cluster import KMeans
#%% """ Data Management """ #%cd /Users/jcvall/Google Drive/Education/Python & Data Science/Mac - Python data = pd.read_csv("winequality-red.csv",sep=";")
# subset clustering variables data.info()
# preprocess dataframe
clustervar = data
# standardize clustering variables to have mean=0 and sd=1
clustervar['fixed acidity']=preprocessing.scale(clustervar['fixed acidity'].astype('float64')) clustervar['volatile acidity']=preprocessing.scale(clustervar['volatile acidity'].astype('float64')) clustervar['citric acid']=preprocessing.scale(clustervar['citric acid'].astype('float64')) clustervar['residual sugar']=preprocessing.scale(clustervar['residual sugar'].astype('float64')) clustervar['chlorides']=preprocessing.scale(clustervar['chlorides'].astype('float64')) clustervar['free sulfur dioxide']=preprocessing.scale(clustervar['free sulfur dioxide'].astype('float64')) clustervar['total sulfur dioxide']=preprocessing.scale(clustervar['total sulfur dioxide'].astype('float64')) clustervar['density']=preprocessing.scale(clustervar['density'].astype('float64')) clustervar['pH']=preprocessing.scale(clustervar['pH'].astype('float64')) clustervar['sulphates']=preprocessing.scale(clustervar['sulphates'].astype('float64')) clustervar['alcohol']=preprocessing.scale(clustervar['alcohol'].astype('float64')) clustervar['quality']=preprocessing.scale(clustervar['quality'].astype('float64'))
# split data into train and test sets clus_train, clus_test = train_test_split(clustervar, test_size=.3, random_state=111)
# k-means cluster analysis for 1-9 clusters from scipy.spatial.distance import cdist clusters=range(1,10) meandist=[]
for k in clusters: model=KMeans(n_clusters=k) model.fit(clus_train) clusassign=model.predict(clus_train) meandist.append(sum(np.min(cdist(clus_train, model.cluster_centers_, 'euclidean'), axis=1)) / clus_train.shape[0])
#%%
""" Plot average distance from observations from the cluster centroid to use the Elbow Method to identify number of clusters to choose """
plt.plot(clusters, meandist) plt.xlabel('Number of clusters') plt.ylabel('Average distance') plt.title('Selecting k with the Elbow Method') plt.show()
# Interpret 3 cluster solution model3=KMeans(n_clusters=5) model3.fit(clus_train) clusassign=model3.predict(clus_train) # plot clusters
from sklearn.decomposition import PCA pca_2 = PCA(2) plot_columns = pca_2.fit_transform(clus_train) plt.scatter(x=plot_columns[:,0], y=plot_columns[:,1], c=model3.labels_,) plt.xlabel('Canonical variable 1') plt.ylabel('Canonical variable 2') plt.title('Scatterplot of Canonical Variables for 3 Clusters') plt.show()
#%% """ BEGIN multiple steps to merge cluster assignment with clustering variables to examine cluster variable means by cluster """ # create a unique identifier variable from the index for the # cluster training data to merge with the cluster assignment variable clus_train.reset_index(level=0, inplace=True) # create a list that has the new index variable cluslist=list(clus_train['index']) # create a list of cluster assignments labels=list(model3.labels_) # combine index variable list with cluster assignment list into a dictionary newlist=dict(zip(cluslist, labels)) newlist # convert newlist dictionary to a dataframe newclus=DataFrame.from_dict(newlist, orient='index') newclus # rename the cluster assignment column newclus.columns = ['cluster']
# now do the same for the cluster assignment variable # create a unique identifier variable from the index for the # cluster assignment dataframe # to merge with cluster training data newclus.reset_index(level=0, inplace=True) # merge the cluster assignment dataframe with the cluster training variable dataframe # by the index variable merged_train=pd.merge(clus_train, newclus, on='index') merged_train.head(n=100) # cluster frequencies merged_train.cluster.value_counts()
#%%
""" END multiple steps to merge cluster assignment with clustering variables to examine cluster variable means by cluster """
# FINALLY calculate clustering variable means by cluster clustergrp = merged_train.groupby('cluster').mean() print ("Clustering variable means by cluster") print(clustergrp)
#%%
# validate clusters in training data by examining cluster differences in alcohol using ANOVA # first have to merge alcohol with clustering variables and cluster assignment data alcohol_data=data['alcohol'] # split alcohol data into train and test sets alcohol_train, alcohol_test = train_test_split(alcohol_data, test_size=.3, random_state=123) alcohol_train1=pd.DataFrame(alcohol_train) alcohol_train1.reset_index(level=0, inplace=True) merged_train_all=pd.merge(alcohol_train1, merged_train, on='index') sub1 = merged_train_all[['alcohol_y', 'cluster']]
import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
alcoholmod = smf.ols(formula='alcohol_y ~ C(cluster)', data=sub1).fit() print (alcoholmod.summary())
print ('means for alcohol by cluster') m1= sub1.groupby('cluster').mean() print (m1)
print ('standard deviations for alcohol by cluster') m2= sub1.groupby('cluster').std() print (m2)
mc1 = multi.MultiComparison(sub1['alcohol_y'], sub1['cluster']) res1 = mc1.tukeyhsd() print(res1.summary())
0 notes
Text
Machine Learning for Data Analysis - Week 3
This week we studied lasso regression. A regression algorithm that selects the best variable for better predictability. Lasso Regression is able to achieve this goal by forcing the sum of the absolute value of the regression coefficients to be less than a fixed value, which forces certain coefficients to be set to zero, effectively choosing a simpler model that does not include those coefficients.
I used the red wine data set where I am predicting the highest quality of wine, based on wine characteristics.
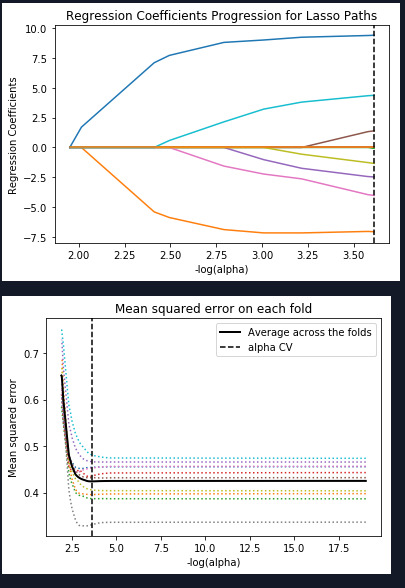
As you can see above the mean squared error is close to each fold with the exception of one that is very low MSE. The training and test MSE are within .02 and the R square test is also within .02 of the training. The lasso regression model has an R square of .34 in the test which means these variables can explain approximately 34% of the variable qualities of wine.
training data MSE 0.41434260704 test data MSE 0.432483541099 training data R-square 0.362115137182 test data R-square 0.340279344086
In summary the model shows us that the there is a relationship with Sulphates and Alcohol and red wine quality with other factors playing a lesser role.
Code:
#from pandas import Series, DataFrame import pandas as pd import numpy as np import matplotlib.pylab as plt from sklearn.cross_validation import train_test_split from sklearn.linear_model import LassoLarsCV import os
#Load the dataset os.chdir('C:/Users/10040207/myproject/Upload') data = pd.read_csv("winequality-red.csv",sep=';')
#%%
#select predictor variables and target variable as separate data sets target = data['quality'] data.drop('quality',axis=1,inplace=True) predvar= data #%% # standardize predictors to have mean=0 and sd=1 predictors=predvar from sklearn import preprocessing predictors['fixeed acidity']=preprocessing.scale(predictors['fixed acidity'].astype('float64')) predictors['volatile acidity']=preprocessing.scale(predictors['volatile acidity'].astype('float64')) predictors['citric acid']=preprocessing.scale(predictors['citric acid'].astype('float64')) predictors['residual sugar']=preprocessing.scale(predictors['residual sugar'].astype('float64')) predictors['chlorides']=preprocessing.scale(predictors['chlorides'].astype('float64')) predictors['free sulfur dioxide']=preprocessing.scale(predictors['free sulfur dioxide'].astype('float64')) predictors['total sulfur dioxide']=preprocessing.scale(predictors['total sulfur dioxide'].astype('float64')) predictors['density']=preprocessing.scale(predictors['density'].astype('float64')) predictors['pH']=preprocessing.scale(predictors['pH'].astype('float64')) predictors['alcohol']=preprocessing.scale(predictors['alcohol'].astype('float64'))
#%% # split data into train and test sets pred_train, pred_test, tar_train, tar_test = train_test_split(predictors, target, test_size=.3, random_state=111)
# specify the lasso regression model model=LassoLarsCV(cv=10, precompute=False).fit(pred_train,tar_train) #%% # print variable names and regression coefficients dict(zip(predictors.columns, model.coef_))
#%% # plot coefficient progression m_log_alphas = -np.log10(model.alphas_) ax = plt.gca() plt.plot(m_log_alphas, model.coef_path_.T) plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k', label='alpha CV') plt.ylabel('Regression Coefficients') plt.xlabel('-log(alpha)') plt.title('Regression Coefficients Progression for Lasso Paths') #%% # plot mean square error for each fold m_log_alphascv = -np.log10(model.cv_alphas_) plt.figure() plt.plot(m_log_alphascv, model.cv_mse_path_, ':') plt.plot(m_log_alphascv, model.cv_mse_path_.mean(axis=-1), 'k', label='Average across the folds', linewidth=2) plt.axvline(-np.log10(model.alpha_), linestyle='--', color='k', label='alpha CV') plt.legend() plt.xlabel('-log(alpha)') plt.ylabel('Mean squared error') plt.title('Mean squared error on each fold') #%%
# MSE from training and test data from sklearn.metrics import mean_squared_error train_error = mean_squared_error(tar_train, model.predict(pred_train)) test_error = mean_squared_error(tar_test, model.predict(pred_test)) print ('training data MSE') print(train_error) print ('test data MSE') print(test_error)
# R-square from training and test data rsquared_train=model.score(pred_train,tar_train) rsquared_test=model.score(pred_test,tar_test) print ('training data R-square') print(rsquared_train) print ('test data R-square') print(rsquared_test)
0 notes
Text
Machine Learning for Data Analysis - Week 2
I continued with the red wine dataset this week to see if random forest can do a better job than decision trees. I was able to get a marginal improvement from 0.978 for decision trees to 0.987 for random forest. I used the quality variable as the target variable, where 1 is the highest rating and 0 is all other ratings. The goal was to develop a random forest model that can pick the best quality wine. Random Forest features ranking are as follows (higher the number the better).
Features Rankfixed acidity0.065315 (9)volatile acidity0.109250 (3)citric acid0.104638 (4)residual sugar
0.0977009( 5)
chlorides0.059328 (10)free sulfur dioxide0.053690 (11)total sulfur dioxide0.072195 (7)density0.067850 (8)ph
0.093891 (6)
sulphates0.113916 (2)alcohol
0.162228 (1)
Summary -
The most important five features are Alcohol, sulphates, volatile acidity, Citric acid, and residual sugar. The confusion matrix is as follows:
Confusion Matrix::
[[632 0] [ 7 1]]
The model correctly identified 632 that were correct classified as 0, 1 correctly classified as 1. Seven classified incorrectly when they indicate 0 but should have been 1. Overall the model may need more examples but seems to do a good job.

Here is the code:
from pandas import Series, DataFrame import pandas as pd import numpy as np import os import matplotlib.pylab as plt from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import classification_report import sklearn.metrics # Feature Importance from sklearn import datasets from sklearn.ensemble import ExtraTreesClassifier %matplotlib inline
print(wine.dtypes) print(wine.describe())
#Split into training and testing sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.4,random_state=111)
col = X.columns
# fit an Extra Trees model to the data model = ExtraTreesClassifier() model.fit(X_train,y_train) # display the relative importance of each attribute features = model.feature_importances_ print(features)
pd.DataFrame(features,index=col,columns=['Features Rank'])
""" Running a different number of trees and see the effect of that on the accuracy of the prediction """
trees=range(25) accuracy=np.zeros(25)
for idx in range(len(trees)): classifier=RandomForestClassifier(n_estimators=idx + 1) classifier=classifier.fit(X_train,y_train) predictions=classifier.predict(X_test) accuracy[idx]=sklearn.metrics.accuracy_score(y_test, predictions) plt.cla() plt.plot(trees, accuracy)
0 notes
Text
Machine Learning for Data Analysis
I went to the UCI website to get an additional data set for the assignment. I choose red wine quality data. A created a new variable for the where there is a 1 if it is the highest quality (8) or 0 if it is below 8.
My variables are as such:
fixed acidity X1 volatile acidity X2 citric acid X3 residual sugar X3 chlorides X4 free sulfur dioxide X5 total sulfur dioxide X6 density X7 pH x8 sulphates X9 alcohol X10 quality �� X11 Highest_Q X12
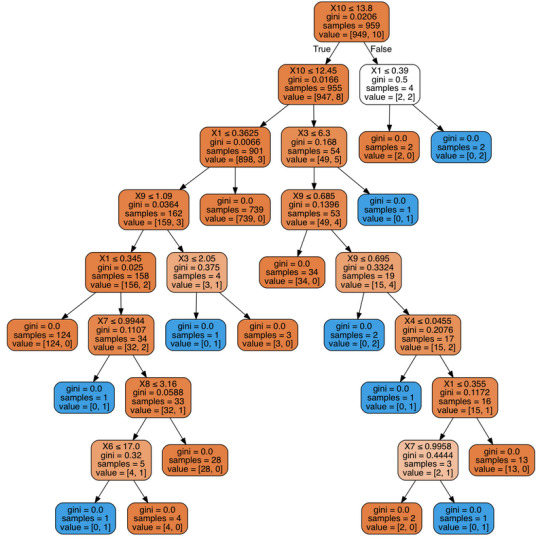
Decision Tree:
My Code:
import pandas as pd import matplotlib.pyplot as plt import numpy as np import os from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier from sklearn.metrics import classification_report import sklearn.metrics
wine = pd.read_csv('winequality-red.csv',sep=";")
wine['Highest_Q'] = wine['quality'].apply(lambda x: 0 if x < 8 else 1)
wine['quality'] = wine['quality'].astype('float64') wine['Highest_Q'] = wine['Highest_Q'].astype('float64') y = wine['Highest_Q'] wine.drop('quality',axis=1,inplace=True) wine.drop('Highest_Q',axis=1,inplace=True) X = wine
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.4,random_state=111)
classifier = DecisionTreeClassifier() classifier = classifier.fit(X_train,y_train)
predictions = classifier.predict(X_test)
sklearn.metrics.confusion_matrix(y_test,predictions)
sklearn.metrics.accuracy_score(y_test,predictions)
from sklearn.externals.six import StringIO from IPython.display import Image from sklearn.tree import export_graphviz import pydotplus dot_data = StringIO() export_graphviz(classifier, out_file=dot_data, filled=True, rounded=True, special_characters=True) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) Image(graph.create_png())
Summary:
My decision tree will give the key elements as to what makes great wine. For example if alcohol is less than 12.45 and fixed acidity is less than .36 and citric acid is less than 2.05. Then it classifies as an 8 (highest wine) 35 percent of the time.
0 notes
Text
Regression Modeling - Week 4
This week I tested to see if I certain variables were important to the developed countries. I used life expectancy, employment rate, female employment rate, and income per person.
I first checked to see if there were any confounding relationships among the variables. It seems that income per person is a confounder for life expectancy and female employment rate where my p-values went from 0.05 to 0.15 for female employment. Life expectency went from 0.0 to 0.37 after adding income per person. see below.
Logit Regression Results before income per person variable added. ============================================================================== Dep. Variable: DevelCountry No. Observations: 166 Model: Logit Df Residuals: 162 Method: MLE Df Model: 3 Date: Wed, 18 Oct 2017 Pseudo R-squ.: 0.4786 Time: 18:43:56 Log-Likelihood: -39.274 converged: True LL-Null: -75.327 LLR p-value: 1.511e-15 ==================================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------------ Intercept -29.9497 7.088 -4.225 0.000 -43.842 -16.058 employrate -0.1755 0.084 -2.085 0.037 -0.340 -0.011 femaleemployrate 0.1314 0.068 1.939 0.052 -0.001 0.264 lifeexpectancy 0.4229 0.092 4.594 0.000 0.243 0.603 =============================================================
Logit Regression Results after income per person added ============================================================================== Dep. Variable: DevelCountry No. Observations: 166 Model: Logit Df Residuals: 161 Method: MLE Df Model: 4 Date: Wed, 18 Oct 2017 Pseudo R-squ.: 0.5935 Time: 18:41:47 Log-Likelihood: -30.624 converged: True LL-Null: -75.327 LLR p-value: 1.760e-18 ==================================================================================== coef std err z P>|z| [0.025 0.975] ------------------------------------------------------------------------------------ Intercept -1.6280 6.810 -0.239 0.811 -14.975 11.719 employrate -0.2039 0.072 -2.838 0.005 -0.345 -0.063 femaleemployrate 0.0752 0.052 1.442 0.149 -0.027 0.177 lifeexpectancy 0.0751 0.084 0.890 0.374 -0.090 0.240 incomeperperson 0.0002 5.17e-05 3.680 0.000 8.89e-05 0.000 =============================================================
After removing female employment rate and life expectancy, I get the following results.
Logit Regression Results ============================================================================== Dep. Variable: DevelCountry No. Observations: 166 Model: Logit Df Residuals: 163 Method: MLE Df Model: 2 Date: Wed, 18 Oct 2017 Pseudo R-squ.: 0.5684 Time: 19:06:14 Log-Likelihood: -32.509 converged: True LL-Null: -75.327 LLR p-value: 2.538e-19 =================================================================================== coef std err z P>|z| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 3.4351 2.232 1.539 0.124 -0.940 7.810 employrate -0.1433 0.048 -2.984 0.003 -0.237 -0.049 incomeperperson 0.0002 4.16e-05 5.624 0.000 0.000 0.000 =================================================================================== Odds Ratio Intercept 31.034682 employrate 0.866494 incomeperperson 1.000234 dtype: float64 Lower CI Upper CI Odds Ratio Intercept 0.390663 2465.424885 31.034682 employrate 0.788658 0.952011 0.866494 incomeperperson 1.000153 1.000316 1.000234
The odds the country being a developed country shown insignificant for income per person with an odds ratio of 1 (OR=1.00, 95% CI = 1.00-1.00, p=0.0001). Employment rate had an odds ratio of less than one. So lower employment rate is slight more probable with developed countries than non-developed countries (OR= 0.87, 95% CI=0.78-0.95, p=0.003).
0 notes
Text
Regression Modeling - Week 3
For week three, I ran a multiple regression to determine if female employment rate and whether it is a developed country can predict life expectancy. Though I knew these variables would not have a strong r square score, I wanted to see what I can learn from this relationship.
OLS Regression Results ============================================================================== Dep. Variable: lifeexpectancy R-squared: 0.295 Model: OLS Adj. R-squared: 0.286 Method: Least Squares F-statistic: 34.07 Date: Sat, 14 Oct 2017 Prob (F-statistic): 4.35e-13 Time: 23:58:47 Log-Likelihood: -587.22 No. Observations: 166 AIC: 1180. Df Residuals: 163 BIC: 1190. Df Model: 2 Covariance Type: nonrobust ========================================================================================= coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------------- Intercept 67.4903 0.715 94.434 0.000 66.079 68.902 C(DevelCountry)[T.1] 12.1850 1.741 7.001 0.000 8.748 15.622 norm_femaleemployrate -0.2029 0.045 -4.538 0.000 -0.291 -0.115 ============================================================================== Omnibus: 18.222 Durbin-Watson: 1.734 Prob(Omnibus): 0.000 Jarque-Bera (JB): 20.716 Skew: -0.836 Prob(JB): 3.17e-05 Kurtosis: 3.445 Cond. No. 39.6 ==============================================================================
Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Both variables, developed countries and female employment rate are significant with a p value of 0.00.
The coefficients give a developed country a 12.19 increase in life expectancy and for each female employment%, a decrease of life expectancy of -0.20 in years. The regression equation is life y = 67.49 + 12.19(x1) + -0.20(x2).
The null hypothesis would be rejected and we would say there is a relationship with developed countries and female employment with a r square score of 0.29.
There is no confonding variables in my analysis.
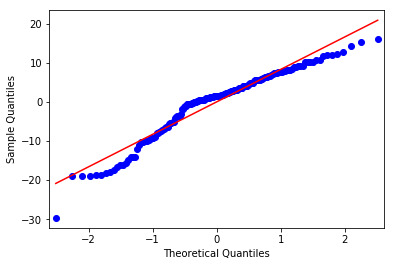
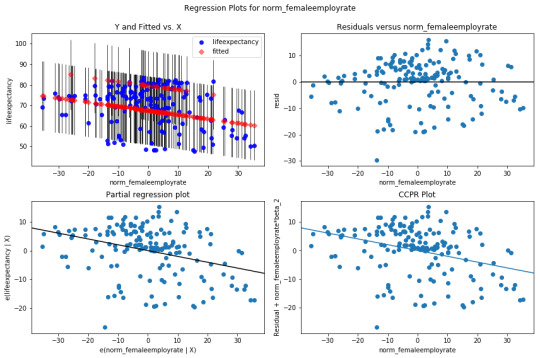
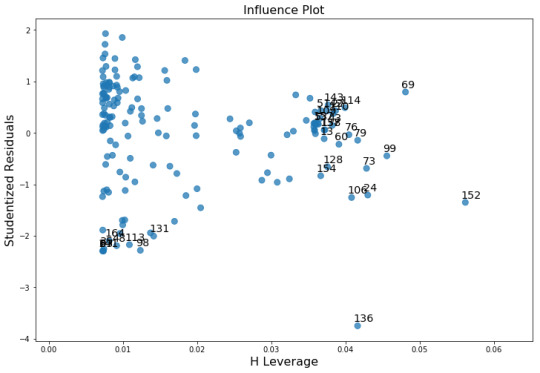
There is a non-linear relationship at the outer quartiles. There is a poor linear fit in the residuals and an outlier (almost 4 standard deveations from the mean) that should be removed from the analysis and re-run.
0 notes
Text
Regression Modeling - Week 3
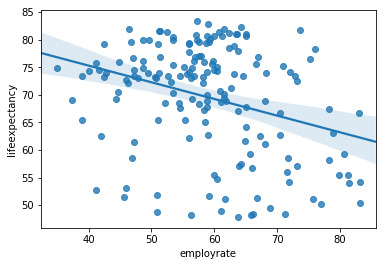
For this week I used the Gapminder data set variables life expectancy and empoyment rate. I used a regression analysis to determine if employment rate is associated with life expectancy.
I adjusted the employment rate variable by subtracting each observation by the mean of approximately 58.99. This normalized the variable by centering the mean to zero.
The regression analysis gave me a p-value of zero and a formula of y=-.03x+69.54. The r squared is .10
This means that for every 1 point increase in employment rate decreases life expectancy by .03.
This model has a negative trend showing employment rate to be significant, but I would not consider this to be a robust model, as the r-squared is a weak score of.10 and the residuals are not linear.
Program and Output:
import warnings import statsmodels.api as sm import statsmodels.formula.api as smf import seaborn as sns warnings.filterwarnings("ignore")
df2 = df1[['lifeexpectancy','employrate']] df2['norm_employrate'] = df2['employrate'] - df2['employrate'].mean() df2['norm_employrate'].mean() df2['trans_employrate'] = np.exp(df2['employrate'])
modelname = smf.ols(formula='lifeexpectancy ~ norm_employrate', data = df2).fit() print(modelname.summary())
print('average life exp:' , df2['lifeexpectancy'].mean()) print('average employ rate:' , df2['employrate'].mean())
sns.regplot(x='employrate',y='lifeexpectancy', data=df2) OLS Regression Results ============================================================================== Dep. Variable: lifeexpectancy R-squared: 0.099 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 17.94 Date: Sun, 08 Oct 2017 Prob (F-statistic): 3.79e-05 Time: 15:24:51 Log-Likelihood: -607.59 No. Observations: 166 AIC: 1219. Df Residuals: 164 BIC: 1225. Df Model: 1 Covariance Type: nonrobust =================================================================================== coef std err t P>|t| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 69.5456 0.734 94.694 0.000 68.095 70.996 norm_employrate -0.3021 0.071 -4.235 0.000 -0.443 -0.161 ============================================================================== Omnibus: 11.183 Durbin-Watson: 1.772 Prob(Omnibus): 0.004 Jarque-Bera (JB): 12.051 Skew: -0.639 Prob(JB): 0.00242 Kurtosis: 2.669 Cond. No. 10.3 ==============================================================================
Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. average life exp: 69.54557228915664 average employ rate: 58.9879518766265
average norm employ rate: 9.16000876220852e-15
0 notes
Text
Regression - Week 1
Source: Gapminder.com
Sample
We have decided to include the following entities:
192 UN members (as of April 2008)
51 other entities listed in the “List of countries” in Wikipedia (2008-05-13). These include the Vatican, dependent territories, special entities and disputed territories. We have excluded the two “sub-dependencies” Ascension Island and Tristan da Cunha, although they are listed by Wikipedia.
4 French overseas territories (Guadeloupe, Martinique, Reunion and French Guyana), although they are considered an integral part of France
10 former states
2 ad-hoc areas: “Serbia excluding Kosovo” and “the Channel Islands”. The latter is the collective name of the two dependent territories Guernsey and Jersey.
In spetember 2012 we added the new UN state “South Sudan” to our country list. The new number of UN members are hence 193. This gives a total of 193+51+4+10+2=260 countries and territories. Our goal is to have data for all these entities for at least two indicators (one of them being population), from 1800 onwards. However, most indicators will only have data for a selection of these entities.
Procedure
The main purpose of this observational data is to produce graphical presentations that display the magnitude of health and wealth disparities in the contemporary world. Therefore, we have also included rough estimates for countries and territories for which reliable data was not available for 2006. These estimates can only be taken as an indication of the order of magnitude for the indicator. Furthermore, we have not been able to make sure that every single observation is based on the best estimates available. Hence we discourage the use of this data set for statistical analysis and advise those who require more exact data to investigate the available data more carefully and look for additional sources, when appropriate.
Variables
The main analysis performed used income per person to predict employment rate. The income per person comes from 2010 Gross Domestic Product per capita in constant 2000 US$. The inflation but not the differences in the cost of living between countries has been taken into account. Employment rate is 2007 total employees age 15+ (% of population) Percentage of total population, age above 15, that has been employed during the given year.
0 notes
Text
Data Analysis Tools- Week 4
This week we have learned about moderators and how they act as a third variable that affects the strength of the relationship between a dependent and independent variable.
This week I picked income per person to explain female employment rate as my two variables. I also chose developed countries and non-developed countries as my moderator.
When looking at the income per person and female employment rate, I have an r square of 0.00.
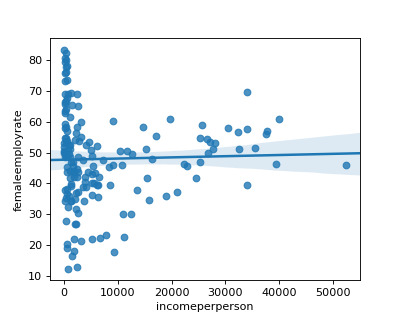
Now, I introduce the moderator of developed countries to find if income per person can explain the female employment rate in this subgroup.
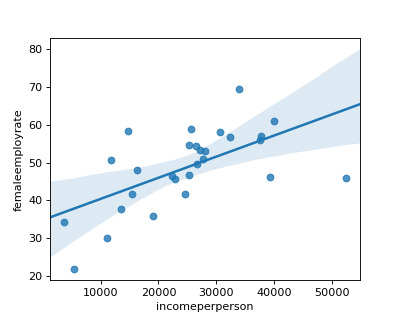
I found that in developed countries, there is a positive relationship between higher income per person and higher female employment rate. This is reflected in the higher r square score of 0.37.
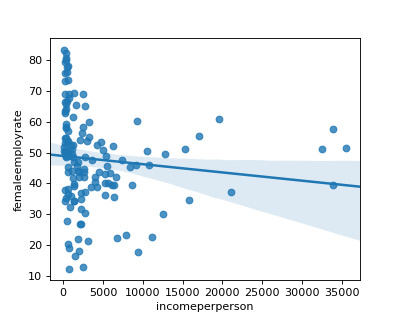
I found that in non developed countries, there is a negative relationship between income per person and higher female employment rate. But, this is reflected in the lower r square score of 0.13.
Code:
#import libraries import pandas as pd from scipy.stats import pearsonr import matplotlib.pyplot as plt import seaborn as sns
# import data data = pd.read_csv('GapminderData.csv')
# select the variables of interest df1 = data[['country','lifeexpectancy','employrate','femaleemployrate','DevelCountry','incomeperperson']]
# new variable - earningpower (lifeexpectancy * incomeperperson) - this is not an average lifetime income but an indication of earning power potential over ones lifetime
df1['earningpower'] = df1['lifeexpectancy'] * df1['incomeperperson']
# new variable - unemployment (100 - 'employrate') - this is the percentage of the population who does not hold a job
df1['unemployment'] = 100 - df1['employrate']
# new variable - femaleunemployment (100 - 'femaleemployrate') - this is the percentage of females who does not hold a job
df1['femaleunemployment'] = 100 - df1['femaleemployrate']
# how many NAs do we have in employrate
print(df1['employrate'].value_counts(dropna=False))
# drop countries that does not have employrate variable
df1 = df1[pd.notnull(df1['employrate'])]
# did we remove the NAs in employrate variable?
print(df1['employrate'].value_counts(dropna=False))
# how many NAs do we have in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
# drop contries that have NAs in lifeexpenctancy
df1 = df1[pd.notnull(df1['lifeexpectancy'])]
# did we remove the NAs in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
reg = sns.regplot(x='incomeperperson',y='femaleemployrate',data = df1)
fig = reg.get_figure() fig.savefig('ploy.png')
# run scipy stats pearson correlation (R correlation, P Value) x = df1['incomeperperson'] y = df1['femaleemployrate']
pearsonr(x,y)
0.02836*0.02836
df2 = df1[df1['DevelCountry']==1] df3 = df1[df1['DevelCountry']==0]
reg1 = sns.regplot(x='incomeperperson',y='femaleemployrate',data = df2)
fig = reg1.get_figure() fig.savefig('ploy1.png')
x = df2['incomeperperson']
y = df2['femaleemployrate']
pearsonr(x,y)
0.60528 * 0.60528
reg2 = sns.regplot(x='incomeperperson',y='femaleemployrate',data = df3)
fig = reg2.get_figure() fig.savefig('ploy2.png')
x = df3['incomeperperson'] y = df3['femaleemployrate']
pearsonr(x,y)
-0.11386 * -0.11386
0 notes
Text
Data Analysis Tools - Week 3
This week I used life expectancy to explain the employment rate in developed countries vs non-developed countries.
My Code:
#import libraries import pandas as pd from scipy.stats import pearsonr import seaborn as sns
#import data data = pd.read_csv('GapminderData.csv')
#Visualization of life expectancy and employment rate sns.regplot(x='lifeexpectancy',y='employrate', data=data)
# run scipy stats pearson correlation (R correlation, P Value) x = data['lifeexpectancy'] y = data['employrate']
pearsonr(x,y)
# life expectancy to explain employment rate in developed countries dev = data[data['DevelCountry'] == 1] sns.regplot(x='lifeexpectancy',y='employrate', data=dev)
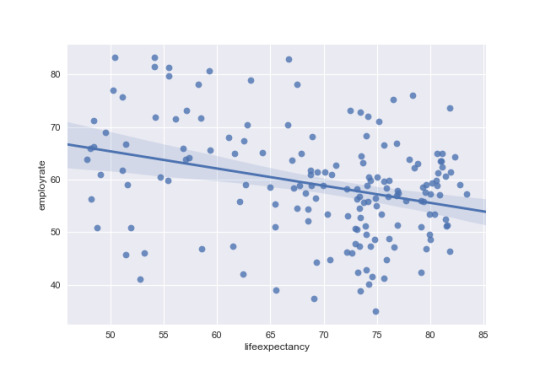
# run scipy stats pearson correlation (R correlation, P Value) x = dev['lifeexpectancy'] y = dev['employrate']
pearsonr(x,y)
rsquare = (-.3140)*(-.3140)
# life expectancy to explain employment rate in developed countries dev = data[data['DevelCountry'] == 1]
regfig2 = sns.regplot(x='lifeexpectancy',y='employrate', data=dev)
# run scipy stats pearson correlation (R correlation, P Value) x = dev['lifeexpectancy'] y = dev['employrate']
pearsonr(x,y)
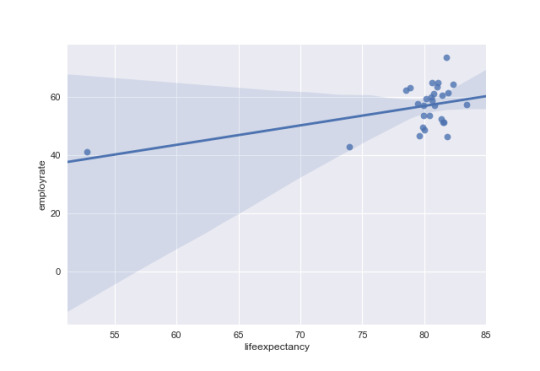
rsquare = (.4872)*(.4872)
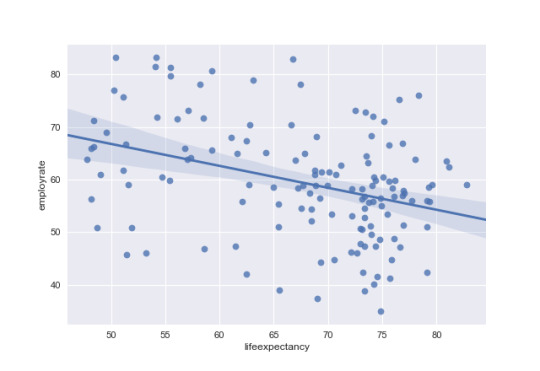
# life expectancy to explain employment rate in non-developed countries nondev = data[data['DevelCountry'] == 0] regfig3 = sns.regplot(x='lifeexpectancy',y='employrate', data=nondev)
# run scipy stats pearson correlation (R correlation, P Value) x = nondev['lifeexpectancy'] y = nondev['employrate']
pearsonr(x,y)
rsquare = (-.3648)*(-.3648)
## Summary of Correlation (Developed vs. Non-Developed Countries)
Looking at all countries the R correlation life expectancy has a negative relationship with employment rate of -0.31 and a p value of less than .05. This means there is a significat relationship where employment rate decreases as life expectancy increases. There is also an r square of .099 which means life expectancy can explain approxamatly 10% of the variance.
Then, Looking at developed countries the R correlation life expectancy has a positive relationship with employment rate of 0.49 and a p value of less than .05. This means there is a significat relationship where employment rate increaes as life expectancy increases. There is also an r square of .237 which means life expectancy can explain approxamatly 24% of the variance.
Finally, Looking at non-developed countries the R correlation life expectancy has a negative relationship with employment rate of -0.36 and a p value of less than .05. This means there is a significat relationship where employment rate decreases as life expectancy increases. There is also an r square of 0.133 which means life expectancy can explain approxamatly 13% of the variance.
0 notes
Text
Data Analysis Tools - Week 2
Model Interpretation for Chi-Square Tests:
For this test I needed to create two new variables perc_group & perc_lifeexp. Where perc_group is three groups( by percentile 0-33%,34-66%,67-100%) from income per person variable. Perc_lifeexp is three groups (by percentile 0-33%,34-66%,67-100%) from life expectancy variable.
When examining the association between life expectancy and income per person, a chi-square test of independence revealed that higher income percentile have longer life spans. The top income percentile has a life expectancy of 76-83 years old, 83% of the time. The middle income percentile has a life expectancy of 68-75, 63% of the time . The bottom life expectancy is 47-67, 78% of the time. X2 =136.9, 2 df, p=1.285e-28.
Model Interpretation for post hoc Chi-Square Test results:
A Chi Square test of independence revealed the null hypothsysis can be rejected between life expectancy and income per person.
Post hoc comparisons of rate adjusted for the Bonferroni adjustment is .05/3 = .02. When comparing this with the pvalue = 1.285e-28 this post hoc evaulation confirms we are correct in rejecting the null hypothsysis
perc_lifeexp 1 2 3 perc_group 1 46 10 1 2 8 35 11 3 1 11 43 perc_lifeexp 1 2 3 perc_group 1 0.836364 0.178571 0.018182 2 0.145455 0.625000 0.200000 3 0.018182 0.196429 0.781818 Chi Square value, p value, excpected counts (136.92436043046089, 1.2852905779637279e-28, 4, array([[ 18.88554217, 19.22891566, 18.88554217], [ 17.89156627, 18.21686747, 17.89156627], [ 18.22289157, 18.55421687, 18.22289157]]))
Code
import pandas as pd
# import data data = pd.read_csv('GapminderData.csv')
# select the variables of interest df1 = data[['country','lifeexpectancy','employrate','femaleemployrate','DevelCountry','incomeperperson','perc_group','perc_lifeexp']]
# new variable - earningpower (lifeexpectancy * incomeperperson) - this is not an average lifetime income but an indication of earning power potential over ones lifetime
df1['earningpower'] = df1['lifeexpectancy'] * df1['incomeperperson']
# new variable - unemployment (100 - 'employrate') - this is the percentage of the population who does not hold a job
df1['unemployment'] = 100 - df1['employrate']
# new variable - femaleunemployment (100 - 'femaleemployrate') - this is the percentage of females who does not hold a job
df1['femaleunemployment'] = 100 - df1['femaleemployrate']
# how many NAs do we have in employrate
print(df1['employrate'].value_counts(dropna=False))
# drop countries that does not have employrate variable
df1 = df1[pd.notnull(df1['employrate'])]
# did we remove the NAs in employrate variable?
print(df1['employrate'].value_counts(dropna=False))
# how many NAs do we have in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
# drop contries that have NAs in lifeexpenctancy
df1 = df1[pd.notnull(df1['lifeexpectancy'])]
# did we remove the NAs in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
df1.dropna(inplace=True)
sht3.range('A1').expand('table').value = df1
print(df1['lifeexpectancy'].max()) print(df1['lifeexpectancy'].min())
CROSS = pd.crosstab(df1['perc_group'],df1['perc_lifeexp'])
print(CROSS)
#%%
colsum = CROSS.sum(axis=0) colpct = CROSS/colsum print(colpct)
#%%
print('Chi Square value, p value, ecpected counts') gchi1 = sci.stats.chi2_contingency(CROSS) print(chi1)
0 notes
Text
Data Analysis Tools - Week 1
(gapminder dataset)
Model Interpretation for ANOVA:
Using income per person variable, I put the bottom 1/3, middle 1/3, and top 1/3 percentile into a 3,2,1 values, respectively. This variable is the income percentile group or perc_group.
When examining the association between employment rate and income percentile group, an Analysis of Variance (ANOVA) there is a significant difference between the top, middle, and bottom, with the mean and standard deviation for top percentile is a Mean=57.34% / s.d. ±7.51%, for the middle percentile is a Mean=55.22% / s.d. ±9.46%, and bottom percentile is a Mean=64.39% / s.d. ±11.53%, F score=13.66, p value = 3.27e-06. Since the p value is less than 0.05 there is a significant difference between the means and we reject the null hypothesis.
The degrees of freedom can be found in the OLS table as the DF model and DF residuals 2 and 163, respectively.
OLS Regression Results ============================================================================== Dep. Variable: employrate R-squared: 0.144 Model: OLS Adj. R-squared: 0.133 Method: Least Squares F-statistic: 13.66 Date: Mon, 04 Sep 2017 Prob (F-statistic): 3.27e-06 Time: 23:47:31 Log-Likelihood: -609.75 No. Observations: 166 AIC: 1226. Df Residuals: 163 BIC: 1235. Df Model: 2 Covariance Type: nonrobust ====================================================================================== coef std err t P>|t| [95.0% Conf. Int.] -------------------------------------------------------------------------------------- Intercept 57.3386 1.274 45.020 0.000 54.824 59.854 C(perc_group)[T.2] -2.1145 1.826 -1.158 0.249 -5.720 1.491 C(perc_group)[T.3] 7.0541 1.817 3.881 0.000 3.465 10.643 ============================================================================== Omnibus: 0.415 Durbin-Watson: 1.951 Prob(Omnibus): 0.813 Jarque-Bera (JB): 0.460 Skew: -0.118 Prob(JB): 0.794 Kurtosis: 2.894 Cond. No. 3.68 ==============================================================================
Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Model Interpretation of post hoc ANOVA results:
ANOVA analysis p value was significant, but to determine which of the means are significantly different I ran a Post hoc test, using ‘Tukey Honest Sigificant Difference’.
Multiple Comparison of Means - Tukey HSD,FWER=0.05 ============================================ group1 group2 meandiff lower upper reject -------------------------------------------- 1 2 -2.1145 -6.434 2.2049 False 1 3 7.0541 2.7549 11.3534 True 2 3 9.1687 4.8112 13.5261 True --------------------------------------------
When compared with employment rate, there is a difference between top and bottom income percentiles. There is also a difference between middle and bottom income percentiles.
Related Code:
import pandas as pd
data = pd.read_csv('GapminderData.csv')
# select the variables of interest df1 = data[['country','lifeexpectancy','employrate','femaleemployrate','DevelCountry','incomeperperson','perc_group']]
# new variable - earningpower (lifeexpectancy * incomeperperson) - this is not an average lifetime income but an indication of earning power potential over ones lifetime
df1['earningpower'] = df1['lifeexpectancy'] * df1['incomeperperson']
# new variable - unemployment (100 - 'employrate') - this is the percentage of the population who does not hold a job
df1['unemployment'] = 100 - df1['employrate']
# new variable - femaleunemployment (100 - 'femaleemployrate') - this is the percentage of females who does not hold a job
df1['femaleunemployment'] = 100 - df1['femaleemployrate']
# how many NAs do we have in employrate
print(df1['employrate'].value_counts(dropna=False))
# drop countries that does not have employrate variable
df1 = df1[pd.notnull(df1['employrate'])]
# did we remove the NAs in employrate variable?
print(df1['employrate'].value_counts(dropna=False))
# how many NAs do we have in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
# drop contries that have NAs in lifeexpenctancy
df1 = df1[pd.notnull(df1['lifeexpectancy'])]
# did we remove the NAs in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
df1.dropna(inplace=True)
#%%
df4 = df1[['employrate','perc_group']]
#%%
import statsmodels.formula.api as smf import statsmodels.stats.multicomp as multi
model = smf.ols(formula='employrate ~ C(perc_group)',data=df4) results = model.fit() print(results.summary())
#%%
df5=df4.groupby('perc_group').mean() df6=df4.groupby('perc_group').std()
print(df5,df6)
#%%
mc = multi.MultiComparison(df4['employrate'],df4['perc_group']) result2 = mc.tukeyhsd() print(result2.summary())
0 notes
Text
Data Management and Visualization - Week 4
I have selected the following variables to visualize (python: .describe() function):
lifeexpectancy employrate femaleemployrate DevelCountry \ count 166.000000 166.000000 166.000000 166.000000 mean 69.545572 58.987952 47.963855 0.168675 std 9.936253 10.327332 14.618138 0.375597 min 47.794000 34.900002 12.400000 0.000000 25% 62.725000 51.575001 39.250001 0.000000 50% 73.129000 58.850000 48.450001 0.000000 75% 76.844750 64.975000 56.150001 0.000000 max 83.394000 83.199997 83.300003 1.000000
incomeperperson earningpower unemployment femaleunemployment count 166.000000 1.660000e+02 166.000000 166.000000 mean 7604.543086 5.943488e+05 41.012048 52.036145 std 10812.642619 8.776830e+05 10.327332 14.618138 min 103.775857 5.022440e+03 16.800003 16.699997 25% 609.437746 3.884985e+04 35.025000 43.849999 50% 2507.859649 1.723875e+05 41.150000 51.549999 75% 9209.272098 7.000834e+05 48.424999 60.749999 max 52301.587180 4.182192e+06 65.099998 87.600000
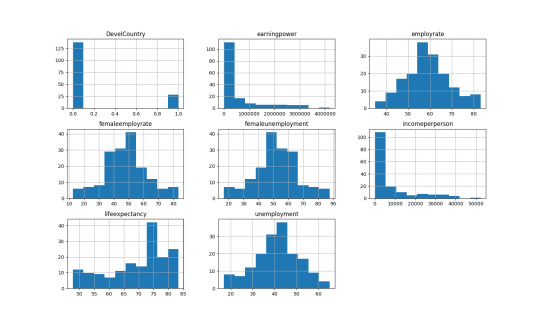
I needed to remove the NAs to perform the histogram analysis.
The first graph, DevelCountry or ’Developed Countries’, is a categorical variable indicated by 1 or 0. Here 28 or 16.87% are developed countries out of 166.
Earningspower and incomperperson is basically the equivalent. Over 126 of the 166 have income equal to or less than $10,000. The highest income per person is Luxenberg of $52,301.
Employment rate and unemployment rate are the inverse of each other. The average employment rate is 59.0% with a standard deviation of 10.3%.
Female employment rate and female unemployment rate are the inverse of each other, as well. The average female employment rate is 48.0% with a standard deviation of 14.6%.
Life expectancy average is 69.5 years with a standard deviation of 9.9 years.
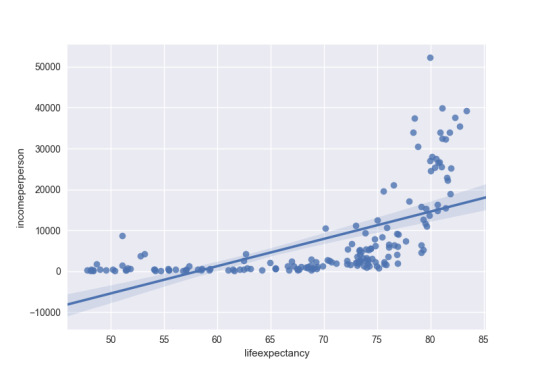
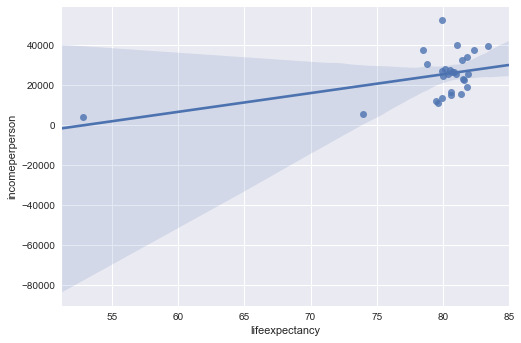
The first bivariate graph is income per person vs. life expectancy as a scatter plot. This looks like an “L” on its back, where you have countries with similar incomes, but a wide difference in life expectancy. The spike toward the higher end of the plot are related to the developing countries who center around 80 years of life expectancy and much higher income per person. You can confirm this in the second graph, which is only developing countries. There is a developing country with low income and low life expectancy, South Africa.
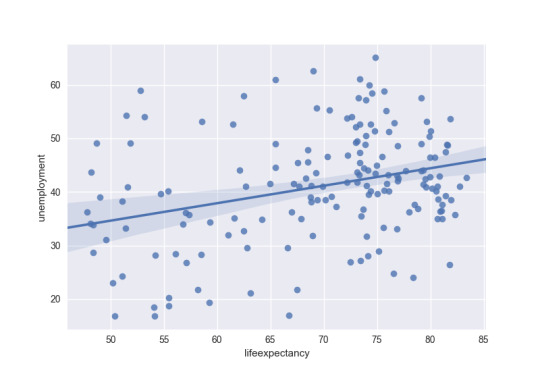
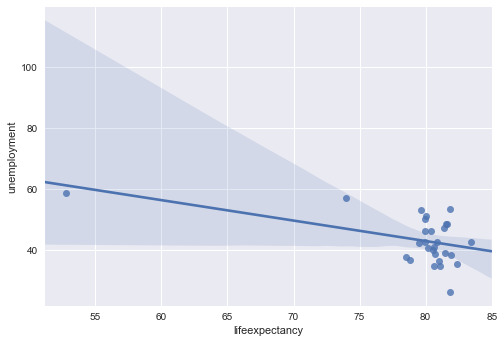
The third and four graph is unemployment and life expectancy. The data is widely spread around with no real relationship between the two variables.
0 notes
Text
Data Management and Visualization - Week 3
I added three new varaibles for my week 3 assignment: earningpower, unemployment, and femaleunemployment.
Earning Power was added to represent potential earnings over ones lifetime and not represented of an average earnings over ones lifetime. The unemployment rate and female unemployment rate was created as a more intuitive way of viewing the data.
Since my analysis is on how unemployment is associated with life expectancy, I managed these two variables by dropping any ‘NAs’ that existed as I could not infer an average by country, nor would I want to do so. I left the ‘NAs’ for income per person and earning power as these are more of my secondary variables and not my primary variables. When I use these columns in any calculation I will manage them according at that time.
Here is my code:
# import libraries import pandas as pdf import numpy as np
# import data data = pd.read_csv('GapminderData.csv')
# select the variables of interest df1 = data[['country','lifeexpectancy','employrate','femaleemployrate','DevelCountry','incomeperperson']]
# new variable - earningpower (lifeexpectancy * incomeperperson) - this is not an average lifetime income but an indication of earning power potential over ones lifetime
df1['earningpower'] = df1['lifeexpectancy'] * df1['incomeperperson']
# new variable - unemployment (100 - 'employrate') - this is the percentage of the population who does not hold a job
df1['unemployment'] = 100 - df1['employrate']
# new variable - femaleunemployment (100 - 'femaleemployrate') - this is the percentage of females who does not hold a job
df1['femaleunemployment'] = 100 - df1['femaleemployrate']
# how many NAs do we have in employrate
print(df1['employrate'].value_counts(dropna=False))
# drop countries that does not have employrate variable
df1 = df1[pd.notnull(df1['employrate'])]
# did we remove the NAs in employrate variable?
print(df1['employrate'].value_counts(dropna=False))
# how many NAs do we have in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
# drop contries that have NAs in lifeexpenctancy
df1 = df1[pd.notnull(df1['lifeexpectancy'])]
# did we remove the NAs in lifeexpectancy
print(df1['lifeexpectancy'].value_counts(dropna=False))
# completed managed dataset
print(df1)
Here is my output:
NaN 35 59.900002 3 47.299999 3 58.900002 3 61.500000 3 65.000000 3 53.500000 3 55.900002 3 54.500000 2 60.400002 2 59.000000 2 66.000000 2 58.200001 2 57.500000 2 48.700001 2 56.799999 2 63.799999 2 51.200001 2 61.000000 2 53.400002 2 50.900002 2 83.199997 2 56.000000 2 78.199997 2 51.000000 2 48.599998 2 42.400002 2 70.400002 2 58.400002 2 46.000000 2 .. 57.599998 1 57.200001 1 61.299999 1 54.599998 1 56.400002 1 73.099998 1 79.800003 1 46.200001 1 46.799999 1 41.599998 1 63.200001 1 55.400002 1 44.799999 1 73.199997 1 37.400002 1 41.200001 1 49.599998 1 71.599998 1 44.200001 1 57.099998 1 61.700001 1 62.299999 1 46.400002 1 71.699997 1 57.299999 1 38.900002 1 45.700001 1 55.599998 1 75.199997 1 50.500000 1 Name: employrate, Length: 140, dtype: int64 55.900002 3 59.900002 3 47.299999 3 61.500000 3 53.500000 3 65.000000 3 58.900002 3 48.700001 2 50.900002 2 66.000000 2 58.200001 2 60.400002 2 59.000000 2 54.500000 2 63.799999 2 61.000000 2 51.200001 2 53.400002 2 57.500000 2 56.799999 2 83.199997 2 56.000000 2 59.099998 2 78.199997 2 51.000000 2 48.599998 2 42.400002 2 70.400002 2 58.400002 2 46.000000 2 .. 34.900002 1 41.200001 1 61.299999 1 53.099998 1 54.599998 1 73.099998 1 79.800003 1 46.200001 1 46.799999 1 41.599998 1 63.200001 1 55.400002 1 44.799999 1 73.199997 1 57.599998 1 37.400002 1 49.599998 1 71.599998 1 44.200001 1 57.099998 1 61.700001 1 62.299999 1 46.400002 1 71.699997 1 57.299999 1 38.900002 1 45.700001 1 55.599998 1 75.199997 1 50.500000 1 Name: employrate, Length: 139, dtype: int64 NaN 2 73.979 2 72.974 2 50.239 1 54.675 1 70.349 1 75.850 1 79.158 1 72.477 1 68.846 1 75.901 1 72.150 1 76.640 1 50.411 1 54.116 1 73.235 1 80.934 1 73.339 1 67.185 1 75.181 1 79.120 1 62.095 1 81.126 1 51.093 1 64.986 1 80.557 1 65.437 1 80.414 1 72.640 1 78.531 1 .. 73.403 1 74.044 1 74.941 1 67.017 1 48.196 1 76.835 1 51.088 1 77.005 1 73.131 1 81.097 1 75.620 1 76.652 1 72.231 1 78.371 1 74.156 1 53.183 1 76.072 1 48.673 1 49.025 1 69.042 1 65.493 1 74.825 1 68.823 1 67.852 1 81.618 1 75.632 1 51.610 1 66.618 1 76.848 1 63.125 1 Name: lifeexpectancy, Length: 175, dtype: int64 72.974 2 73.979 2 50.239 1 81.126 1 70.349 1 75.850 1 79.158 1 72.477 1 68.846 1 75.901 1 72.150 1 54.675 1 48.132 1 50.411 1 76.640 1 73.235 1 80.934 1 73.339 1 67.185 1 75.181 1 79.120 1 54.116 1 51.093 1 70.563 1 83.394 1 65.438 1 65.437 1 80.414 1 72.640 1 78.531 1 .. 74.847 1 73.403 1 74.044 1 74.941 1 67.017 1 48.196 1 76.835 1 51.088 1 81.097 1 75.620 1 76.652 1 76.848 1 79.499 1 72.231 1 78.371 1 74.156 1 53.183 1 76.072 1 48.673 1 49.025 1 69.042 1 65.493 1 74.825 1 68.823 1 67.852 1 81.618 1 75.632 1 51.610 1 66.618 1 63.125 1 Name: lifeexpectancy, Length: 174, dtype: int64 country lifeexpectancy employrate femaleemployrate \ 0 Afghanistan 48.673 55.700001 25.600000 1 Albania 76.918 51.400002 42.099998 2 Algeria 73.131 50.500000 31.700001 4 Angola 51.093 75.699997 69.400002 6 Argentina 75.901 58.400002 45.900002 7 Armenia 74.241 40.099998 34.200001 9 Australia 81.907 61.500000 54.599998 10 Austria 80.854 57.099998 49.700001 11 Azerbaijan 70.739 60.900002 56.200001 12 Bahamas 75.620 66.599998 60.700001 13 Bahrain 75.057 60.400002 30.200001 14 Bangladesh 68.944 68.099998 53.599998 15 Barbados 76.835 66.900002 60.299999 16 Belarus 70.349 53.400002 48.599998 17 Belgium 80.009 48.599998 41.700001 18 Belize 76.072 56.799999 38.799999 19 Benin 56.081 71.599998 58.200001 21 Bhutan 67.185 58.400002 39.900002 22 Bolivia 66.618 70.400002 61.599998 23 Bosnia and Herzegovina 75.670 41.200001 34.900002 24 Botswana 53.183 46.000000 38.700001 25 Brazil 73.488 64.500000 53.299999 26 Brunei 78.005 63.799999 55.500000 27 Bulgaria 73.371 47.299999 42.099998 28 Burkina Faso 55.439 81.300003 75.800003 29 Burundi 50.411 83.199997 83.300003 30 Cambodia 63.125 78.900002 73.400002 31 Cameroon 51.610 59.099998 49.000000 32 Canada 81.012 63.500000 58.900002 33 Cape Verde 74.156 55.900002 43.599998 .. ... ... ... ... 179 Spain 81.404 52.500000 41.700001 180 Sri Lanka 74.941 55.099998 39.200001 181 Sudan 61.452 47.299999 27.900000 182 Suriname 70.563 44.700001 30.400000 183 Swaziland 48.718 50.900002 47.099998 184 Sweden 81.439 60.700001 56.700001 185 Switzerland 82.338 64.300003 57.000000 186 Syria 75.850 44.799999 16.700001 188 Tajikistan 67.529 54.599998 50.099998 189 Tanzania 58.199 78.199997 76.099998 190 Thailand 74.126 72.000000 65.000000 191 Timor-Leste 62.475 67.300003 54.700001 192 Togo 57.062 63.900002 48.400002 194 Trinidad and Tobago 70.124 61.500000 50.500000 195 Tunisia 74.515 41.599998 21.400000 196 Turkey 73.979 42.799999 21.900000 197 Turkmenistan 64.986 58.500000 53.900002 199 Uganda 54.116 83.199997 80.000000 200 Ukraine 68.494 54.400002 49.400002 201 United Arab Emirates 76.546 75.199997 37.299999 202 United Kingdom 80.170 59.299999 53.099998 203 United States 78.531 62.299999 56.000000 204 Uruguay 77.005 57.500000 46.000000 205 Uzbekistan 68.287 57.500000 52.599998 207 Venezuela 74.402 59.900002 45.799999 208 Vietnam 75.181 71.000000 67.599998 209 West Bank and Gaza 72.832 32.000000 11.300000 210 Yemen, Rep. 65.493 39.000000 20.299999 211 Zambia 49.025 61.000000 53.500000 212 Zimbabwe 51.384 66.800003 58.099998 DevelCountry incomeperperson earningpower unemployment \ 0 0 NaN NaN 44.299999 1 0 1914.996551 1.472977e+05 48.599998 2 0 2231.993335 1.632279e+05 49.500000 4 0 1381.004268 7.055965e+04 24.300003 6 0 10749.419240 8.158917e+05 41.599998 7 0 1326.741757 9.849863e+04 59.900002 9 1 25249.986060 2.068151e+06 38.500000 10 1 26692.984110 2.158235e+06 42.900002 11 0 2344.896916 1.658757e+05 39.099998 12 0 19630.540550 1.484461e+06 33.400002 13 0 12505.212540 9.386037e+05 39.599998 14 0 558.062877 3.847509e+04 31.900002 15 0 9243.587053 7.102310e+05 33.099998 16 0 2737.670379 1.925924e+05 46.599998 17 1 24496.048260 1.959904e+06 51.400002 18 0 3545.652174 2.697249e+05 43.200001 19 0 377.039699 2.114476e+04 28.400002 21 0 1324.194906 8.896603e+04 41.599998 22 0 1232.794137 8.212628e+04 29.599998 23 0 2183.344867 1.652137e+05 58.799999 24 0 4189.436587 2.228068e+05 54.000000 25 0 4699.411262 3.453503e+05 35.500000 26 0 17092.460000 1.333297e+06 36.200001 27 0 2549.558474 1.870637e+05 52.700001 28 0 276.200413 1.531227e+04 18.699997 29 0 115.305996 5.812691e+03 16.800003 30 0 557.947513 3.522044e+04 21.099998 31 0 713.639303 3.683092e+04 40.900002 32 1 25575.352620 2.071910e+06 36.500000 33 0 1959.844472 1.453342e+05 44.099998 .. ... ... ... ... 179 1 15461.758370 1.258649e+06 47.500000 180 0 1295.742686 9.710425e+04 44.900002 181 0 523.950151 3.219778e+04 52.700001 182 0 2668.020519 1.882635e+05 55.299999 183 0 1810.230533 8.819081e+04 49.099998 184 1 32292.482980 2.629868e+06 39.299999 185 1 37662.751250 3.101076e+06 35.699997 186 0 1525.780116 1.157304e+05 55.200001 188 0 279.180453 1.885278e+04 45.400002 189 0 456.385712 2.656119e+04 21.800003 190 0 2712.517199 2.010680e+05 28.000000 191 0 369.572954 2.308907e+04 32.699997 192 0 285.224449 1.627548e+04 36.099998 194 0 10480.817200 7.349568e+05 38.500000 195 0 3164.927693 2.358346e+05 58.400002 196 1 5348.597192 3.956839e+05 57.200001 197 0 2062.125152 1.340093e+05 41.500000 199 0 377.421113 2.042452e+04 16.800003 200 0 1036.830725 7.101668e+04 45.599998 201 0 21087.394120 1.614156e+06 24.800003 202 1 28033.489280 2.247445e+06 40.700001 203 1 37491.179520 2.944220e+06 37.700001 204 0 9106.327234 7.012327e+05 42.500000 205 0 952.827261 6.506572e+04 42.500000 207 0 5528.363114 4.113213e+05 40.099998 208 0 722.807559 5.434140e+04 29.000000 209 0 NaN NaN 68.000000 210 0 610.357367 3.997414e+04 61.000000 211 0 432.226337 2.118990e+04 39.000000 212 0 320.771890 1.648254e+04 33.199997 femaleunemployment 0 74.400000 1 57.900002 2 68.299999 4 30.599998 6 54.099998 7 65.799999 9 45.400002 10 50.299999 11 43.799999 12 39.299999 13 69.799999 14 46.400002 15 39.700001 16 51.400002 17 58.299999 18 61.200001 19 41.799999 21 60.099998 22 38.400002 23 65.099998 24 61.299999 25 46.700001 26 44.500000 27 57.900002 28 24.199997 29 16.699997 30 26.599998 31 51.000000 32 41.099998 33 56.400002 .. ... 179 58.299999 180 60.799999 181 72.100000 182 69.600000 183 52.900002 184 43.299999 185 43.000000 186 83.299999 188 49.900002 189 23.900002 190 35.000000 191 45.299999 192 51.599998 194 49.500000 195 78.600000 196 78.100000 197 46.099998 199 20.000000 200 50.599998 201 62.700001 202 46.900002 203 44.000000 204 54.000000 205 47.400002 207 54.200001 208 32.400002 209 88.700000 210 79.700001 211 46.500000 212 41.900002 [176 rows x 9 columns]
0 notes