#identity theorem

[falseandrealultravival]

A Theorem in Logistics(identity theorem)

"Arthur Wellington=Lao Tzu

In Logistics"

Q.E.D.

By Rei Morishita

[therighthandofvengeance]

[omegaphilosophia]

The Philosophy of Invariance

The philosophy of invariance examines the concept of constancy or unchanging nature within various contexts, including science, mathematics, ethics, and metaphysics. This philosophical exploration seeks to understand what remains constant amidst change and why such constancies are significant for our comprehension of reality, knowledge, and truth.

Key Concepts in the Philosophy of Invariance

Definition of Invariance:

Concept: Invariance refers to properties or principles that remain unchanged under specific transformations or conditions.

Argument: Identifying invariances helps in understanding the fundamental nature of systems and theories, providing a stable foundation for analysis and interpretation.

Invariance in Science and Mathematics:

Physical Laws: Many physical laws, such as the laws of motion and conservation laws, are considered invariant under transformations like time shifts or spatial rotations.

Symmetry: Invariance is closely related to symmetry in physics and mathematics. For example, the invariance of physical laws under certain symmetries leads to conservation laws according to Noether's theorem.

Mathematical Constants: Constants like π (pi) and e (Euler's number) are examples of invariance in mathematics, holding the same value across various contexts.

Invariance in Metaphysics:

Universal Principles: In metaphysics, invariance pertains to principles or truths that remain constant across possible worlds or different contexts.

Identity and Change: Philosophers explore how identity can persist over time despite changes, focusing on the invariant core that defines an entity.

Ethical Invariance:

Moral Principles: The idea that certain ethical principles are invariant, holding true regardless of cultural or situational differences.

Universal Ethics: This approach argues for the existence of universal moral truths that apply to all rational beings.

Theoretical Debates and Implications

Role of Invariance in Scientific Theories:

Concept: Invariance as a criterion for the validity and robustness of scientific theories.

Argument: Scientific theories that exhibit invariance under transformation are often considered more fundamental and reliable.

Philosophical Implications of Mathematical Invariance:

Concept: The philosophical significance of invariant mathematical properties and structures.

Argument: The constancy of mathematical truths supports the notion of an objective mathematical reality, independent of human perception.

Ethical Relativism vs. Invariant Ethics:

Concept: The debate between ethical relativism, which denies invariant moral principles, and invariant ethics, which upholds them.

Argument: While ethical relativism emphasizes cultural and contextual differences, invariant ethics seeks universal moral truths applicable to all.

Metaphysical Invariance and Identity:

Concept: The persistence of identity amidst change and the metaphysical basis for invariance.

Argument: Philosophers debate whether there are essential properties that remain invariant to preserve identity through change.

The philosophy of invariance explores the concept of constancy across different domains, from science and mathematics to ethics and metaphysics. By understanding what remains unchanged amidst transformations, this philosophical inquiry provides insights into the fundamental nature of reality, the stability of scientific theories, and the universality of ethical principles.

[karcatgirl-vantas]

system of mathematical notation where concatenation always means multiplication and each prime number has a unique one digit symbol. so counting to ten looks like "2, 3, 22, 5, 23, 7, 222, 33, 25". the advantages of this system would be making multiplication and division trivial, as well as accurately representing the true form and identity of every positive integer according to the fundamental theorem of arithmetic. the disadvantages to this system would be everything

[leporellian]

i genuinely really think that, besides my “musicals are what you get if you make operas not autistic” theorem (another thing for another day), there is One massive thing that stands in the way of me liking (modern) musicals and it’s the relationship they have to their texts vs operas.

with an opera, it’s kind of established that part of the big game is that every production is a negotiation and not a reproduction. it’s a conversation. there is no one “canon” version of an opera and it’s the audience expectation that every production will differ somehow. this especially kicks in when we’re dealing with operas that have harmful ideas either explicitly (madama butterfly) or implicitly (die meistersinger von nurnberg) because you can turn those works into ruminations on themselves. you’re dissecting the animal but the animal is conscious and fully consenting and marvels at your work as you go.

with a musical, meanwhile, there is usually a dedicated version you are looking at and an insistence on a CANONICAL way things are Meant to be interpreted. there is One Accepted Concept and branching into reinterpretations counts as “headcanons” or another modern fan term. a musical is not seen as “sociological/anthropological record of multiple time periods” but as “Content”

musicals have two problems. 1) they don’t have the gap in time that allows for that kind of retrospective look (which is fair that’s not a them issue), and 2) they have a fandom cultivated around them and are seen as Content. they also are so “concurrent” with our time (and also very fast) that they don’t have a sense of Allowing for reinterpretation. sure, you’ll have your regional/student productions that’ll do some minor detail like a character acting slightly differently or a silent interaction included- but you aren’t going to have your deconstructed heathers that pulls apart how it’s kind of immediately fallen apart in a post-2018 world, or a lion king performed as if it was a brand new text without any regard for the details of either the original film or julie taymor’s stage treatment. god forbid you start deconstructing your musical! that’ll make the fans sad!

and until we get to the de-fandomization of musicals and acknowledge them as sociological texts and not Content(TM), we aren’t going to get there. but alas that culture is baked into musicals, especially as the shows see shorter and shorter long-term visions as the machine of broadway grows hungrier for money and so brand identity and imposition of ‘fandom culture’ grow stronger with it.

(this is also why i’m so fascinated with chess the musical, which is a musical that doesn’t work So Much that nearly every new production is some extensive revision or another (usually making it somehow more incomprehensible in the process). the idea of “musicals can be reinterpreted” is there! we’re getting there! but it’s Not Quite. and i find that Fascinating from a dramaturgical context.)

Anyway if i had my way every new musical revival would be like the daniel fish oklahoma over and over and over FOREVER!!!! YOUR BRAND IS DEAD AND BOW TO THE NEBULOUS CONCEPT OF REGIETHEATRE AS YOUR NEW KINGGGGG

[canisvesperus]

Calculus is significantly easier if you’re SUPER sharp on your trig and your algebra skills. If you know your identities and your theorems and you’re good at factoring and playing with numbers in general— you have a lot less to think hard about and trip up on while you’re working on the actual calculus itself, which can be surprisingly straightforward as long as you’ve trained yourself to see the patterns, stay organized, and think a few moves ahead.

[lipshits-continuous]

A Short Intro to Category Theory

A common theme in mathematics is to study certain objects and the maps between that preserve the specific structure of said objects. For example, linear algebra is the study of vector spaces and linear maps. Often we have that the identity maps are structure preserving and the composition of maps is also structure preserving. In the case of vector spaces, the identity map is a linear map and the composition of linear maps is again a linear map. Category theory generalises and axiomatises this common way of studying mathematical objects.

I'll introduce the notion of a category as well as the notion of a functor, which is another very important and ubiquitous notion in category theory. And I will finish with a very powerful result involving functors and isomorphisms!

Definition 1:

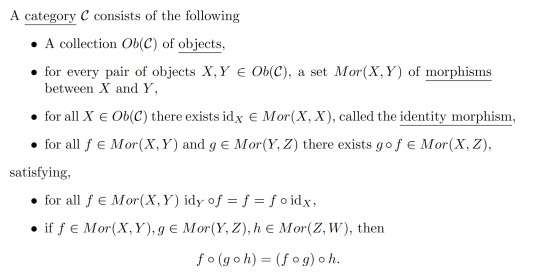
We call the last property the associative property.

Here are some examples:

Examples 2:

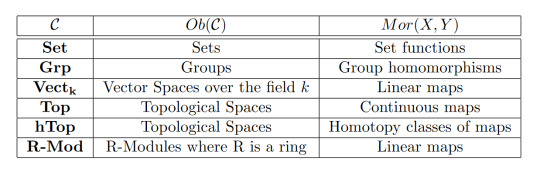
Note that whilst all of these examples are built from sets and set functions, we can have other kinds of objects and morphisms. However the most common categories are those built from Set.

Functors:

In the spirit of category theory being the study of objects and their morphisms, we want to define some kind of map between categories. It turns out that these are very powerful and show up everywhere in pure maths. Naturally, we want a functor to map objects to objects and morphisms to morphisms in a way that respects identity morphisms and our associative property.

Definition 3:

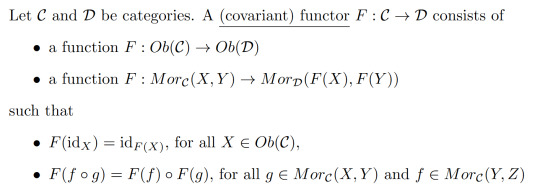
Example 4:

For those familiar with a some topology, the fundamental group is another exmaple of a covariant functor from the category of based spaces and based maps to Grp.

We also have another kind of functor:

Defintion 5:

It may seem a bit odd to introduce at first since all we've done is swap the directions of the morphisms, but it turns out that contravariant functors show up a lot!

This example requires a little bit of knowledge of linear algebra.

Example 6:

In fact, this is somewhat related to example 5! We can produce a contravariant functor Mor(-,X) is a similar way. For V and W vector spaces over k, we have that Mor(V,W) is a vector space over k. In particular, V*=Mor(V,k). So really this -* functor is just Mor(-,k)!

Isomorphisms

Here we generalise the familiar notion of isomorphisms of any algebraic structure!

Definition 7:

For a category of algebraic objects like Vectₖ, isomorphism are exactly the same as isomorphisms defined the typical way. In Top the isomorphisms are homeomorphisms. In Set the isomorphisms are bijective maps.

Remark:

So if f is invertible, we call it's right (or left) inverse, g, the inverse of f.

Isomorphisms give us a way to say when two objects of a category are "the same". More formally, being isomorphic defines an equivalence relation.

Lemma 8:

A natural question one might as is how do functors interact with isomorphisms? The answer is the very important result I hinted at in the intro!

Theorem 9:

Remark: In general, the converse is not true. That is F(X) isomorphic to F(Y) does not imply X is isomorphic to Y. An example of this is the fundamental groups of both S² and ℝ² are isomorphic to the trivial group but these spaces are not homeomorphic.

Taking the negation of Theorem 9 gives us a very powerful result:

Corollary 10:

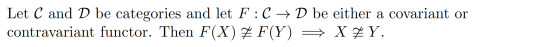
This means that if we can find a functor such that F(X) and F(Y) aren't isomorphic, we know that X and Y are not isomorphic. This is of particular importance in algebraic topology where we construct functors from Top or hTop to a category of a given algebraic structure. This gives us some very powerful topological invariants for telling when two spaces aren't homeomorphic or homotopy equivalent. (In fact, this is where category theory originated from!)

[joehills]

The year is 1994.

Several furious vampires emerge from the theatre fuming that the Greek play of καθορισμός δασικών εκτάσεων (a comedy about how a single Greek vampire inspired the construction of trojan horse, the conception of the pythagorean theorem, and the composition of the friezes on the Parthenon... and after all that, later went on to drink Hemlock in Socrates' place due to a case of mistaken identity), has never been retold so poorly.

[sirenjose]

The Proof of Azoth's Theorem - (Concept Art) Analysis

(About Philosopher's Stone, Stibnite, Maria's Axiom, Philemon's Altar, Azoth, and a few of the symbols on each of their outfits)

Philosopher’s stone: the goal of turning base metals like iron into precious metals like gold or silver. It was also said to provide the elixir of life, which could cure any illness or bring longevity. It was considered the most pure and perfect of all substances.

Stibnite: an ore that is the primary source of antimony

Described in Basil Valentine's 1st Key (the image Fool's Gold is holding). This depicts purifying gold using melted stibnite.

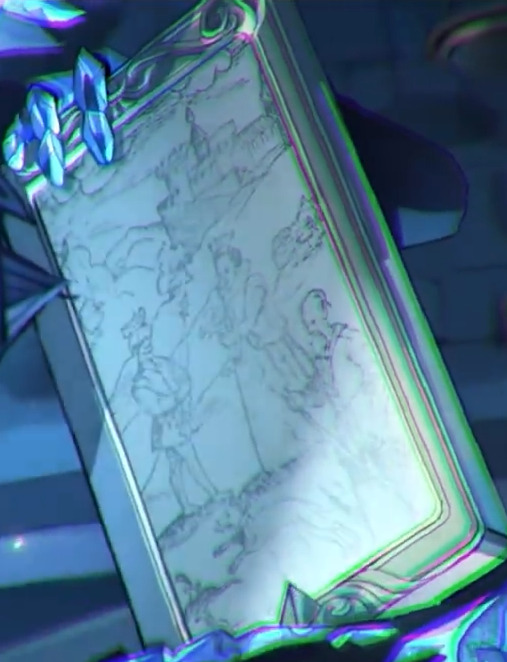
Impure gold dissolves in melted stibnite. Metals besides gold are turned into sulfides and rise to the surface, while a white allow of antimony and gold sink to the bottom. Roasting this alloy causes the antimony to evaporate, leaving only the purified gold behind.

In the image of the First Key, stibnite is likened to a hungry wolf in the First Key due to how quickly stibnite dissolves (devours) metals.

In German, stibnite is called “spießglanz”, which means “spear shine” due to its shiny “spear” like crystals, thus why the First Key says “on account of his name, is subject to bellicose Mars”, as a spear is a weapon and all weapons are subject to Mars (the god of war).

This is like what is described by Nicholas Flamel, where silver is combined with mercury and antimony then distilled and cohobated (repeatedly distilling a liquid then pouring the distillate back onto the residue to extract more of the desired substance) to produce red power.

Maria’s Axiom: “1 becomes 2, 2 becomes 3, and out of the 3rd comes the 1 as the 4th” (also described as “1 becomes 2, 2 becomes 3, and by means of the 3rd and 4 thachieving unity, thus 2 are but 1”)

Carl Jung uses this as a metaphor to describe the process of “individuation”. This refers to the process of self-discovery to become our true, unique self.

This involves finding your identity outside of the roles and expectations imposed by the outside (society, others, etc…). The goal here being to achieve a sense of “wholeness” and “unity” with yourself.

1 is the 1st matter, or prima materia, containing everything you need. This is then divided (into opposites), with each element purified by itself then united again (reconciliation of opposites) into a complete whole more perfect than the starting matter, the philosopher’s stone.

Philemon’s altar: may refer to Jung’s Philemon, which is based on Philemon and Baucis from Ovid’s Metamorphosis and Goethe’s Faust.

With Ovid, Jupiter and Mercury are disguised knocking on houses but not shown kindness until they meet Philemon and Baucis, an old, poor couple. They let them live while killing everyone else (the wicked), with the couple’s house being transformed into a temple.

With Goeth, Faust is building a city on land reclaimed from the sea and asks the devil Mephistopheles to move Philemon and Baucis, but Faust is horrified to see the demon burn their house down with the couple still inside. Faust then decides he needs to atone for his crime.

Philemon was a figure in a dream of Jung's, a wise old man that represented superior insight and wisdom. For Jung, Philemon symbolized the “artifax” or skilled alchemist, with the goal to purify and perfect materials (transform base materials into noble ones like gold).

On a spiritual level, the goal of the artifax is to purify and perfect the human soul, achieving enlightenment (becoming a higher/whole human being).

Over Jung’s gate he put the inscription: “Philemon’s Shrine – Faust’s Repentance”. This involved integrating the moral questions raised by with the spiritual goal of alchemy via the opposing figures of Philemon and Faust (so acknowledge necessity of confronting evil on the path to individuation, atoning for Faust’s crime, and affirming the goal represented by Philemon).

Azoth: Considered to be a universal cure or Elixir of Life that could be created by the philosopher’s stone.

It is also essential agent of transformation in alchemy.

As the Universal Life Force, it's the energy responsible for the drive towards physical/spiritual perfection

Azoth is called Prima Materia in Latin. This was the first matter, the starting material required for the creation of the philosopher’s stone. It is the primitive formless base of all matter similar to chaos, the quintessence or aether.

It is the 1st matter at the beginning as well as its perfected essence (philosopher’s stone).

It relates to unity, wholeness, and synthesis of opposites

Alchemy Symbols:

Philosopher’s Stone:

triangle = fire

triangle in a circle = Wheel of Fire (Ignis Rotae)

entwined snakes = likely Hermes Caduceus (Hermes as Hermes Trismegistus was closely associated with alchemy)

Stibnite

upside down triangle = water

hexagram?() = represented the reconciliation/union of opposites (fire and water)

Philemon:

- triangle with a line through it = air

Maria's Axiom:

- downward triangle with a line through it = earth

- symbols on her dress and floor for Mercury/Quicksilver, Venus/Copper, Moon/Silver, Saturn/Lead, Jupiter/Tin, Mars/Iron, and Sun/Gold

There were several bits that looked like they could be symbols but I haven't been able to identify them yet (I've already spent so long working to identify everything. I'll try to add more if I identify them later).

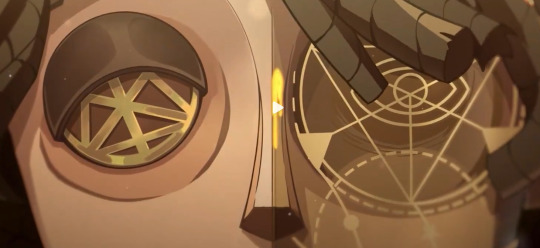
Also I did notice/wonder how that shadow thing has eyes that appear around it could relate to Hunter Norton's weapon, which almost looks like an eye. Matthias also might have something on his boots but it's hard to be sure.

[city-of-ladies]

Mathematician, physician and philosopher (1776-1831), Sophie Germain was a genius who fought hard to be heard a recognized.

A self-taught prodigy 

The daughter of a silk merchant, Sophie was born in Paris to a relatively wealthy family. When the French Revolution broke out in 1789, her father became a member of the Constituent Assembly. Amidst the chaos, Sophie found solace in her father's library and discovered mathematics.

Fascinated by the subject, she learned everything she could, studying at night. Her parents disapproved. Mathematics was thought to be too complex for women who had to focus first and foremost on their home.

Sophie's parents tried to stop her by putting out the fire in her room at night and confiscating her clothes and candles after nightfall. Sophie's thirst for knowledge was stronger. According to her obituary, she studied “at night in a room so cold that the ink often froze in its well, working enveloped with covers by the light of a lamp”. She even taught herself Latin to read the essential works.

Sophie impresses

The École Polytechnique was founded in 1974 with to train a new elite of engineers, mathematicians and scientists. Being a woman, Sophie couldn’t attend. She learned that a student named Leblanc wasn’t able to go to class. She wrote to the school, pretending to be him, and managed to obtain lecture notes. She was also able to complete and submit assignments. 

This promising student impressed mathematician Joseph-Louis Lagrange who found her answers brilliant. The self-taught Sophie had gained the admiration of one of the most renowned mathematicians of her time.

Lagrange's desire to meet her forced Sophie to reveal her real identity. Lagrange was at first surprised to learn that his correspondent was a woman. He nonetheless became Sophie’s mentor, introducing her to a new world and opportunities.

Sophie made major contributions to number theory. She worked on Fermat's last theorem, making major observations and creating her own theorem. This would be one of her major contributions to mathematics.

In 1804, she began a correspondence with another mathematician, Carl Friedrich Gauss, whose work she admired. He was similarly impressed by her intelligence:

“But how to describe to you my admiration and astonishment at seeing my esteemed correspondent Monsieur Leblanc metamorphose himself into this illustrious personage who gives such a brilliant example of what I would find it difficult to believe. A taste for the abstract sciences in general and above all the mysteries of numbers is excessively rare: one is not astonished at it: the enchanting charms of this sublime science reveal only to those who have the courage to go deeply into it. But when a person of the sex which, according to our customs and prejudices, must encounter infinitely more difficulties than men to familiarize herself with these thorny researches, succeeds nevertheless in surmounting these obstacles and penetrating the most obscure parts of them, then without doubt she must have the noblest courage, quite extraordinary talents and superior genius.”

An incomplete recognition

Sophie was also interested in physics. In 1811, she entered a contest held by the French Academy of Sciences, but her lack of formal education turned against her. She didn't give up and won the contest in 1816 with her Memoir on the vibrations of Elastic Plates. She kept working on the theory of elasticity and published several more memoirs. Her work would prove pivotal in the field.

This prize also meant official recognition for Sophie. In 1823, she became the first woman to be allowed at the Academy of Sciences' sessions. Though respected as an equal collaborator by some, she still felt like a “foreigner” in the scientific community.

Sophie Germain died at the age of 55, on June 27, 1831, after a battle with breast cancer. Carl Friedrich Gauss had convinced the university of the University of Gottingen to give her an honorary degree but Sophie was dead before she could receive it.

Her death certificate designated her as a "rentière-annuitant" (a single woman with no profession) instead of a mathematician. 

Today, a street in Paris, schools in France and a crater on Venus are named in her honor. She appeared on a French postal stamp released in 2016.

Feel free to check out my Ko-Fi if you like what I do! Your support would be greatly appreciated.

Further reading 

Alkalay-Houlihan Coleen, “Sophie Germain and special cases of Fermat’s last theorem”

Boyé Anne,, “Sophie Germain, une mathématicienne face aux préjugés de son temps”

“Biographies of women mathematicians : Sophie Germain”

Lamboley Gilbert, “Math’s hidden woman”

Koppe Martin, “Sophie Germain, une pionnière enfin reconnue”

[otakusparkle]

Identity V 6th Anniversary Global Event Begin

Truth and Inference 6th Anniversary Global Even

Title : "Azoth's theorem proof"

Season 32 Essence 3

S-Tier

- Night Watch (Ithaqua)

A-Tier

- Fool's Gold (Norton Campbell)

- Puppeteer (Matthias Czernim)

S-Tier Costume and A-Tier Accessories of The Mind's Eye (Helena Adams) will be available in shop for limited time

The will be event tasks to finish to get many free bonuses such as B-Tier Costume and Accessories!

In addition, all this items will be reprinted back to the game for limited time!

There will be new furniture and dishes too!

The Ripper and Grave Keeper S-Tier Costume and A-Tier Accessories set will also be reprinted back to the game for limited time!

In addition, there will be limited time public map for 6th Anniversary!

There will be special price for recharge

There will also be free 10x essence for the anniversary essences!

[bubbloquacious]

Hydrogen bomb vs. coughing baby: graphs and the Yoneda embedding

So we all love applying heavy duty theorems to prove easy results, right? One that caught my attention recently is a cute abstract way of defining graphs (specifically, directed multigraphs a.k.a. quivers). A graph G consists of the following data: a set G(V) of vertices, a set G(A) of arrows, and two functions G(s),G(t): G(A) -> G(V) which pick out the source and target vertex of an arrow. The notation I've used here is purposefully suggestive: the data of a graph is exactly the same as the data of a functor to the category of sets (call it Set) from the category that has two objects, and two parallel morphisms from one object to the other. We can represent this category diagrammatically as ∗⇉∗, but I am just going to call it Q.

The first object of Q we will call V, and the other we will call A. There will be two non-identity morphisms in Q, which we call s,t: V -> A. Note that s and t go from V to A, whereas G(s) and G(t) go from G(A) to G(V). We will define a graph to be a contravariant functor from Q to Set. We can encode this as a standard, covariant functor of type Q^op -> Set, where Q^op is the opposite category of Q. The reason to do this is that a graph is now exactly a presheaf on Q. Note that Q is isomorphic to its opposite category, so this change of perspective leaves the idea of a graph the same.

On a given small category C, the collection of all presheaves (which is in fact a proper class) has a natural structure as a category; the morphisms between two presheaves are the natural transformations between them. We call this category C^hat. In the case of C = Q, we can write down the data of such a natural transformations pretty easily. For two graphs G₁, G₂ in Q^hat, a morphism φ between them consists of a function φ_V: G₁(V) -> G₂(V) and a function φ_A: G₁(A) -> G₂(A). These transformations need to be natural, so because Q has two non-identity morphisms we require that two specific naturality squares commute. This gives us the equations G₂(s) ∘ φ_A = φ_V ∘ G₁(s) and G₂(t) ∘ φ_A = φ_V ∘ G₁(t). In other words, if you have an arrow in G₁ and φ_A maps it onto an arrow in G₂ and then you take the source/target of that arrow, it's the same as first taking the source/target in G₁ and then having φ_V map that onto a vertex of G₂. More explicitly, if v and v' are vertices in G₁(V) and a is an arrow from v to v', then φ_A(a) is an arrow from φ_V(v) to φ_V(v'). This is exactly what we want a graph homomorphism to be.

So Q^hat is the category of graphs and graph homomorphisms. This is where the Yoneda lemma enters the stage. If C is any (locally small) category, then an object C of C defines a presheaf on C in the following way. This functor (call it h_C for now) maps an object X of C onto the set of morphisms Hom(X,C) and a morphism f: X -> Y onto the function Hom(Y,C) -> Hom(X,C) given by precomposition with f. That is, for g ∈ Hom(Y,C) we have that the function h_C(f) maps g onto g ∘ f. This is indeed a contravariant functor from C to Set. Any presheaf that's naturally isomorphic to such a presheaf is called representable, and C is one of its representing objects.

So, if C is small, we have a function that maps objects of C onto objects of C^hat. Can we turn this into a functor C -> C^hat? This is pretty easy actually. For a given morphism f: C -> C' we need to find a natural transformation h_C -> h_C'. I.e., for every object X we need a set function ψ_X: Hom(X,C) -> Hom(X,C') (this is the X-component of the natural transformation) such that, again, various naturality squares commute. I won't beat around the bush too much and just say that this map is given by postcomposition with f. You can do the rest of the verification yourself.

For any small category C we have constructed a (covariant) functor C -> C^hat. A consequence of the Yoneda lemma is that this functor is full and faithful (so we can interpret C as a full subcategory of C^hat). Call it the Yoneda embedding, and denote it よ (the hiragana for 'yo'). Another fact, which Wikipedia calls the density theorem, is that any presheaf on C is, in a canonical way, a colimit (which you can think of as an abstract version of 'quotient of a disjoint union') of representable presheaves. Now we have enough theory to have it tell us something about graphs that we already knew.

Our small category Q has two objects: V and A. They give us two presheaves on Q, a.k.a. graphs, namely よ(V) and よ(A). What are these graphs? Let's calculate. The functor よ(V) maps the object V onto the one point set Hom(V,V) (which contains only id_V) and it maps A onto the empty set Hom(A,V). This already tells us (without calculating the action of よ(V) on s and t) that the graph よ(V) is the graph that consists of a single vertex and no arrows. The functor よ(A) maps V onto the two point set Hom(V,A) and A onto the one point set Hom(A,A). Two vertices (s and t), one arrow (id_A). What does よ(A) do with the Q-morphisms s and t? It should map them onto the functions Hom(A,A) -> Hom(V,A) that map a morphism f onto f ∘ s and f ∘ t, respectively. Because Hom(A,A) contains only id_A, these are the functions that map it onto s and t in Hom(V,A), respectively. So the one arrow in よ(A)(A) has s in よ(A)(V) as its source and t as its target. We conclude that よ(A) is the graph with two vertices and one arrow from one to the other.

We have found the representable presheaves on Q. By the density theorem, any graph is a colimit of よ(V) and よ(A) in a canonical way. Put another way: any graph consists of vertices and arrows between them. I'm sure you'll agree that this was worth the effort.

[a-fox-studies]

October 6, 2023 • Friday

Exams in 2 months! Classes are going at a faster rate than usual, and I realised I was slowly falling behind again.

I got in 3 hours 21 minutes of focus today, 40 minutes of which was spent in the uni library tackling calculus. A calculus rant under the cut!

Things I did today:

30 minutes of Duolingo

Continued with Physics module 4.

Exercise problems of differential calculus module 2.

🎧 - New Romantics — Taylor Swift

So far what I understood about calculus is that it needs a lot of analysis. What I do is:

I first look at the problem, and see if I can simplify it (using trigonometric identities or theorems)

Then I recollect and write down the list of formulae that seem suitable for that problem.

Once I get an idea, I start working on the solution.

Since I'm pretty new to the subject, one problem takes almost thirty minutes for me to solve — and that's okay. I've set aside an hour for calculus everyday, so it gives me time to analyse one type of problem everyday. This way there is consistency, and I don't lose touch.

[your-bigender-big-brother]

Ok so I don't know if this is crazy or not but here we go!

is it possible for you to make a system of genders based on the concept of a theorem?

The definition if you need:

Theorem

a general proposition not self-evident but proved by a chain of reasoning; a truth established by means of accepted truths.

For example: in my own personal experience I don't necessarily FEEL nonbinary specifically, but I accept that I am through a process of deductive reasonings based on my own experiences. So my nonbinary identity is based on a theorem of what my gender actually is. If that makes any sense? (⁠T°T⁠)

I'm honestly just a bit confused on how to go about naming this system of genders and how to even go about making flags for this.

If you do take this on I'd like to encompass a lot of different existing genders with their own separate labels, to be inclusive as possible, man, woman, masc, fem, androgyne, centrigender, nonbinary genders, agender, bigender, multigender, genderfluid, genderflux, xenogender, maverique, ect

This would just be a pretty big undertaking so I wanted to know if you think you can do it, I know it'd be a lot especially with the amount of other projects you've been working on, but if you could it'd be so awesome!!

This certainly is a huge project and while I'm not sure what to name the terms, I would like to pass along some flag ideas that people can take and come up with a name for.

Here is the general flag for this group of genders based on theorem:

I made a handful of flags for specific identities to show off how the flag can be edited. Here are agender, nonbinary, masculine, feminine, and epicene. Maybe they can also have a corresponding gender symbol in the center?

This is the Photoshop file for the general theorem flag that can be downloaded and used. I know for sure that it can be opened and edited in Paint Tool SAI, so maybe it works that way for other programs?

Anyway, I hope someone can come grab this and do something fun with it because it's a really cool idea! - 💙💚

[aedesluminis]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

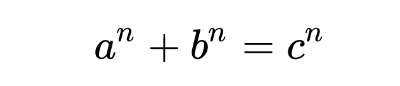
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[sophieinwonderland]

Hi sophie, thank you so much for that....uh....riveting(?) response. As always you have completely cherry picked something (this whole thing apparently). I gave you a source for the information bias, that I mentioned because I have read your entire blog (has legitimately taken weeks, my god girl gtfo the internet and see some sun!) and other blogs surrounding you and your....uh opinions on this whole endo shit. Also you are wrong, which is ironic because I was meaning to comment if YOU had made it through grade school. I'm actually a psychologist with a specialized degree in dissociative disorders and applied behavioral therapy and currently writing my dissertation on the matter. Identity disturbances among a select few things do have a correlation if not cause of someone developing a lesser dissociative disorder. In my statement about outdated sources, I put in a little note (might have forgotten this because yk I have a life unlike you) that a source can be 100 years old and still he credible AS LONG AS there aren't any current sources/studies that prove the theorem/case study wrong. That was literally the catch. This isn't a gotcha. All you've down is managed to show how much you cherrypick things. I'm not saying ALL of your information is wrong, I'm literally saying that you actively seek out sources/studies whatever to fit whatever niche ridiculous shit you are on that day.

Had to dumb this response down because apparently you don't have the intellect that you portray. Your words are empty, the little backing you do have is untrustworthy because of YOU. You lie so damn much that nobody knows if the 'sources' you give are even true. Nobody has time to look through hundreds of pages of a random ass theory or search relentlessly on Google to find whatever information you painstakingly plugged into the search engine. For the love of God, woman play with your own damn fantasy characters and world but don't make it other people's problem. Like do what YOU want on YOUR time but you literally do not have to post this shit. You spend day after day after day on this godforsaken website. I can smell the dirty dishes and unwashed armpits from here. Get a life that isn't grooming minors into thinking they have a serious dissociative disorder.

Hi! I see you found my post!

I'm gonna need to break this down point by point, aren't I?

As always you have completely cherry picked something (this whole thing apparently).

I literally screenshotted every paragraph you wrote.

How is that cherrypicking?

Are you just using this as a buzzword now? Do you actually understand what this means?

I gave you a source for the information bias

Sorry, I forgot. You sourced something that has absolutely no relevancy and isn't being debated. That statistical biases can exist in research. Good for you, I guess. Congrats on sourcing something that absolutely nobody is disputing.

that I mentioned because I have read your entire blog (has legitimately taken weeks, my god girl gtfo the internet and see some sun!) and other blogs surrounding you and your....uh opinions on this whole endo shit.

My ENTIRE blog?

I mean, yeah, over the course of three years, including reblogs, I've apparently made 11,000 posts

Which averages out to about 10-11 posts per day. I'll admit, that be a bit excessive. (Again though, a huge number of these are reblogs. I'd wager that only about half of these are actually my posts as opposed to posts I'm sharing.)

But if you read all of those posts, which were created over three years, within a span of weeks... I'm really not sure that you've got much of a leg to stand on to tell other people to get off the internet and see some sun. 😛

I'm actually a psychologist with a specialized degree in dissociative disorders and applied behavioral therapy and currently writing my dissertation on the matter.

But apparently found time to spend weeks reading my entire blog, and still think only .edu and .gov sources are valid. Yeah... forgive me for being skeptical...

Identity disturbances among a select few things do have a correlation if not cause of someone developing a lesser dissociative disorder.

Yeah, the correlation part is something we agree on. The "causing someone to develop a dissociative disorder" is something that you're going to need to back up with a source.

In my statement about outdated sources, I put in a little note (might have forgotten this because yk I have a life unlike you) that a source can be 100 years old and still he credible AS LONG AS there aren't any current sources/studies that prove the theorem/case study wrong.

You did NOT include any such note. I would think someone who allegedly read through the 11,000 posts on my blog would be able to reread the paragraph they wrote to confirm if they actually posted this or not. It wouldn't have even taken much more time than you did writing in parentheses that you may have forgot it.

What you actually said was that a source isn't reputable if it's more than a certain number of years old.

"In addition to that, yes a source being x number of years ago is considered not reputable especially if in that time other sources vastly state and give anecdotal evidence to discrediting that."

You ltierally said it was about the number of years.

If you wanted to argue that what makes a source outdated isn't the age of the source in years at all, but whether the source has been disputed by later research, then fine.

We would be in agreement.

But if that's what you want to argue, and I present sources affirming endogenic plurality a real psychological phenomenon, then the burden of proof is on you to provide later sources that would challenge it.

If you cannot, then there is no basis for claiming the source is outdated.

That was literally the catch. This isn't a gotcha. All you've down is managed to show how much you cherrypick things.

Okay, I think I got it! I "cherrypicked" by not reading the note that only existed in your mind. 🤣🙄

I'm not saying ALL of your information is wrong, I'm literally saying that you actively seek out sources/studies whatever to fit whatever niche ridiculous shit you are on that day.

"Your problem is that you seek out studies and sources to back up your arguments. You need to stop doing that."

🤔

Your words are empty, the little backing you do have is untrustworthy because of YOU.

Is that how that works? 😲

I quote a peer reviewed academic paper published by reputable publishers like the American Psychiatric Association and Oxford University Press, and the papers become less trustworthy because I posted them?

You lie so damn much that nobody knows if the 'sources' you give are even true.

Do you actually have examples of me lying, or are we employing circular reasoning?

"She claims to be an endogenic systems which is a lie therefore any sources she provides to prove endogenic systems exist are lies."

Nobody has time to look through hundreds of pages of a random ass theory or search relentlessly on Google to find whatever information you painstakingly plugged into the search engine.

You had time to read through my 11,000 posts?

But not to read any of the articles I've directly linked to? And screenshotted so that people could read the quotes parts without having to click on the external links I provide?

I mean, had you clicked on those, you might have actually learned something, which might have been good for you if you actually are studying psychology.

When you've claimed to read through my entire blog, and yet haven't read the sources I've linked to countless times, it starts to seem like maybe it's not a time issue but an avoidance issue.

That you can cling to your worldview as long as you don't have to challenge it.

I'm going to ignore most of the personal attacks and ad hominems that come after this because they don't really warrant a response. It's just the flailings of someone who knows they've lost on matters of facts, and are desperately flinging insults to see if any touch a nerve. It's sad more than anything.

Except for this one...

Get a life that isn't grooming minors into thinking they have a serious dissociative disorder.

Because I do want to remind people, again, that the "grooming minors" line is rooted in queerphobia, and is the same rhetoric that homophobes and transphobes have targeted LGBTQ people with for decades, and has ramped up considerably over the past few years.

Know where your talking points are coming from!

I'll end by saying this. Your original post was in response to a post of mine about the lengths sysmeds will go to in order to make up reasons to dismiss psychological research into endogenic plurality, and professional opinions that endogenic plurality is real.

You've given me a new one to add to the list which is apparently that sources are invalid just because pro-endos post them.

Call pro-endos liars, then say the sources posted by liars aren't valid because they're liars.

This is both circular reasoning and an ad hominem.

But more than anything, it's closed-minded cowardice. It's you making up any excuses to not challenge or re-evaluate your worldview or opinions.