#algebra elemental

[ibrahimacademia]

Domina suma de monomios y polinomios

[bubbloquacious]

Jacobson's Basic algebra 1 gives such a nice argument for why algebraic numbers have minimum polymials, making it a corollary of the fact that polynomial rings over fields are principal ideal domains. Consider a field extension E/F (i.e. a field E that contains a field F). For any u ∈ E we have in E the subring F[u] and the subfield F(u). These are defined as the smallest subring and subfield of E respectively that contain both F and u. If E = F(u) for some u ∈ E, then E/F is called a simple field extension.

Let F(u)/F be an arbitrary simple field extension. Consider the polynomial ring F[X]. By the universal property of polynomial rings (which is essentially what one means when they say that X is an indeterminate), there is a unique ring homomorphism F[X] -> F(u) that sends any a ∈ F to itself and that sends X to u (you can think of this homomorphism as evaluation of a polynomial at u). If the kernel of this homomorphism is the zero ideal, then F[u] is isomorphic to F[X], so u is transcendental over F. If the kernel is non-zero, then by definition there are non-zero polynomials p ∈ F[X] such that p(u) = 0 in F(u), so u is algebraic over F. Because F[X] is a principal ideal domain, there is a polynomial p that generates the kernel. In other words, p divides all polynomials q such that q(u) = 0 in F(u). Two polynomials (over a field) generate the same ideal if and only if they differ by a constant factor, so there is a unique monic minimum polynomial in F[X] for u.

[jucomx]

Surprising absolutely noone except undergraduate math students, it turns out math actually is only about numbers in the end!

[seeleybooth]

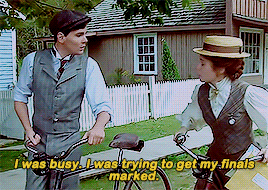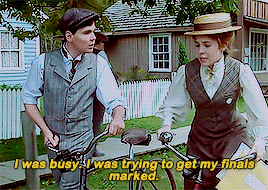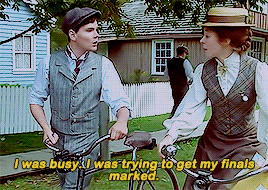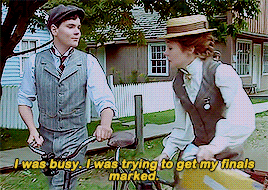
"Don't get up on your high horse with me, Anne Shirley."

"Marilla pessimistically expected more trouble since Anne had again begun to go to school. But none developed. Perhaps Anne caught something of the “model” spirit from Minnie Andrews; at least she got on very well with Mr. Phillips thenceforth. She flung herself into her studies heart and soul, determined not to be outdone in any class by Gilbert Blythe. The rivalry between them was soon apparent; it was entirely good-natured on Gilbert’s side; but it is much to be feared that the same thing cannot be said of Anne, who had certainly an unpraiseworthy tenacity for holding grudges. She was as intense in her hatreds as in her loves. She would not stoop to admit that she meant to rival Gilbert in schoolwork, because that would have been to acknowledge his existence which Anne persistently ignored; but the rivalry was there and honors fluctuated between them. Now Gilbert was head of the spelling class; now Anne, with a toss of her long red braids, spelled him down. One morning Gilbert had all his sums done correctly and had his name written on the blackboard on the roll of honor; the next morning Anne, having wrestled wildly with decimals the entire evening before, would be first. One awful day they were ties and their names were written up together. It was almost as bad as a take-notice and Anne’s mortification was as evident as Gilbert’s satisfaction. When the written examinations at the end of each month were held the suspense was terrible. The first month Gilbert came out three marks ahead. The second Anne beat him by five. But her triumph was marred by the fact that Gilbert congratulated her heartily before the whole school. It would have been ever so much sweeter to her if he had felt the sting of his defeat.

Mr. Phillips might not be a very good teacher; but a pupil so inflexibly determined on learning as Anne was could hardly escape making progress under any kind of teacher. By the end of the term Anne and Gilbert were both promoted into the fifth class and allowed to begin studying the elements of “the branches”—by which Latin, geometry, French, and algebra were meant. In geometry Anne met her Waterloo.

“It’s perfectly awful stuff, Marilla,” she groaned. “I’m sure I’ll never be able to make head or tail of it. There is no scope for imagination in it at all. Mr. Phillips says I’m the worst dunce he ever saw at it. And Gil—I mean some of the others are so smart at it. It is extremely mortifying, Marilla.

“Even Diana gets along better than I do. But I don’t mind being beaten by Diana. Even although we meet as strangers now I still love her with an inextinguishable love. It makes me very sad at times to think about her. But really, Marilla, one can’t stay sad very long in such an interesting world, can one?”

Anne of Green Gabes (1908) by L.M. Montgomery - CHAPTER XVII - A New Interest in Life

[ghostly-bat]

It's the fact that Jon was in space for like 7+ years, came back, and then they just send him to college like what?? I highly doubt he was being taught at anything educational when he was up there. Algebra?? He doesn't know what that is. His reading and writing skills? When you're in 5th grade you're being taught reading comprehension skills, improving writing mechanics including proper grammar, punctuation, and spelling, understanding basic parts of speech, writing different types of paragraphs (narrative, informative), and learning to analyze text elements like theme and point of view. You think he was keeping up with any of that while he was being imprisoned in a volcano? No! He wasn't! Damian is over here, yelling at him, using words he doesn't understand, that's nothing new but it's still pisses him off cus he feels like he probably should know some of those words are by now.

My boy left with a 5th grade education, spent 7 years trapped in space, came back with that same 5th grade education plus trauma and they send him to college. Absolutely insane.

[depezblob]

So what's up with dividing by zero anyways - a ramble on algebraic structures

Most everyone in the world (at least in theory) knows how to add, subtract, multiply, and divide numbers. You can always add two numbers, subtract two numbers, and multiply two numbers. But you must **never** divide by zero... or something along those lines. There's often a line of logic that leads to dividing by zero leading to "infinity," whatever infinity means, unless you're doing 0/0, whatever that means either. Clearly this is a problem! We can't have such inconsistencies in our fundamental operations! Why aren't our top mathematicians working on this?

So, that might be a bit of an exaggeration: division by zero isn't really a problem at all and is, for all intents and purposes fairly well understood, but to see why we'll have to take a crash course through algebra (the field of math, not the grade school version). Sorry for those of y'all who have seen fields and projective space before, not much to gain out of this one.

Part I: In the beginning, we had a Set.

As is true with most things in math, the only structure we start with is a set. A set isn't useful for much; all we can do with a single set is say what elements are and aren't in the set. Once you have more than one set, you start getting interesting things like unions or intersections or functions or Cartesian products, but none of those are _really_ that useful (or at least necessary) for understanding algebraic structures at the level we need, so a single set is what we start with and a single set there will be. The story then goes as follows: on the first day the lord said "Let there be an operation!" and it was so. If you want to be a bit of a nerd, a (binary) operation on a set A is formally a map * : A x A -> A, but for our purposes we just need to know that it matches the standard operations most people know (i.e. addition, subtraction, multiplication, but not division) in that for any two numbers a and b, we can do a * b and get another number. Of course, once again this is not very helpful on its own, and so we need to impose some more conditions on this operation for it to be useful for us. Not to worry though, these conditions are almost always ones you know well, if not by name, and come rather intuitively.

The first structure we'll discuss is that of a monoid: a set with an operation that is associative and has an identity. Associativity simply means that (a * b) * c = a * (b * c), and an identity simply means that we have some special element e such that a * e = e * a = a. For two simple examples and one nonexample, we have the natural numbers (with 0) under addition is a monoid: 0 + a *= *a *+ 0 = *a, and any two natural numbers add to another natural number; the integers under multiplication is a monoid: 1 * a = a * 1 = a, and any two integers multiply to another integer; and the integers under subtraction is not a monoid, since subtraction is not associative (a - (b - c) =/= (a-b) - c). In both of these examples, the operation is commutative: in other words, a * b = b * a for every a and b. There are plenty of examples of operations that are not commutative, matrix multiplication or function composition probably being the most famous, but for the structures we're going to be interested in later operations are almost always commutative, so we can just assume that from the start.

Of course, you might wonder where subtraction comes from, if it doesn't fit into a monoid structure (and in particular isn't associative). Not to worry! We can simply view subtraction as another type of addition, and our problems go away. In particular, we add the condition that for every a, we have an inverse element a⁻ ¹ (or -a if our operation is addition) such that a * a⁻ ¹ = a⁻ ¹ * a = e. For fans of universal algebra, just as a binary operation can be thought of as a function, the inverse can be thought of as a function i : A -> A that sends each element to its inverse. This forms a structure we know as a group. While none of the above examples form a group, one of them can be naturally extended to a group: if we simply add negative whole numbers to natural numbers, we get the group of integers over addition, where for any integer a, we have its inverse -a where a + -a = 0. In particular, the subtraction a - b is just a + -b = -b + a, where -b is the additive inverse of b. As we will soon see, division can also be thought of in a similar way, where a/b = a * /b = /b * a where /b is the multiplicative inverse of b. As a side note, the examples above are very specific types of monoids and groups which turn out to be quite far from the general ideas that monoids and groups are trying to encapsulate. Monoids show up often in computer science as they're a good model for describing how a list of commands affects a computer, and groups are better thought of as encapsulating symmetries of an object (think of the ways you can rotate and reflect a square or a cube).

Part II: So imagine if instead of one operation, we have... two...

If you've ever taken introductory algebra, you've probably never heard of monoids and only done groups. This is partially because monoids are much less mathematically interesting than groups are and partially because monoids are just not as useful when thinking about other things. For the purposes of this post, however, the logical steps from Set -> Monoid -> Group are surprisingly similar to the steps Group -> Ring -> Field, so I've chosen to include it regardless.

Just as we started from a set and added an operation to make a monoid, here we start from an additive group (i.e. a group where the operation is addition) and add another operation, namely multiplication, that acts on the elements of the group. Just like in the monoid, we will impose the condition that multiplication is associative and has an identity, namely 1, but we also impose the condition that multiplication meshes nicely with addition in what you probably know as the distributive properties. What we end up with is a ring, something like the integers, where you can add, subtract, and multiply, but not necessarily divide (for example, 2 doesn't have a multiplicative inverse in the integers, as a * 2 = 1 has no solutions). Similarly, when we add in multiplicative inverses to every nonzero element, we get a field, something like the rational numbers or the real numbers, where we can now divide by every nonzero number. In other words, a ring is an additive group with a multiplicative monoid, and a field is an additive group with a subset that is a multiplicative group (in particular the subset that is everything except zero). For those who want to be pedantic, multiplication in a ring doesn't have to be commutative, but addition is, and both addition and multiplication are commutative in a field. A full list of the conditions we impose on the operations of a monoid, group, ring, and field can be found here).

So why can't we have a multiplicative inverse to 0 in a field? As it turns out, this is because 0 * a = 0 for every a, so nothing times 0 gets you to 1. There is technically a structure you can have if 0 = 1, but it turns out there's only the one single element 0 in that structure and nothing interesting happens, so generally fields specifically don't allow 0 = 1. Then, what if instead we relaxed the condition that 0 * a = 0? Similarly, it turns out that this isn't one of the fundamental conditions on multiplication, but rather arises from the other properties (a simple proof is a * 0 = a * (0 + 0) = a * 0 + a * 0 implies 0 = a * 0 - a * 0 = a * 0 + a * 0 - a * 0 = a * 0). If we were to relax this condition, then we lose some of the other nice properties that we built up. This will be a recurring theme throughout the rest of this post, so be wary.

Part III. We can't have everything we want in life.

While all the structures so far have been purely algebraic and purely algebraically motivated, the simplest way to start dividing by zero is actually "geometric," with several different ways of constructing the same space. The construction we'll use is as follows: take any field, particularly the real numbers or the complex numbers. We can always take the cartesian product of a field K with itself to form what's called affine space K^2, which is the set of ordered pairs (a,b) for a, b in K. As a side note, the product of groups, rings, or fields has a natural definition of addition or whatever the underlying group operation is by doing it componentwise, i.e. (a,b) * (c,d) = (a * c, b * d), but our operations will not coincide with this, as you'll see soon. This affine space is a plane - in fact, when we do this to the real numbers, we get the Cartesian plane - within which we can construct lines, some of which we get by considering the set of points (x, y) satisfying the familiar equation y = mx + b for some 'slope' m and 'intercept' b. In particular, we want to characterize all the lines through the origin. This gives us all the lines of the form y = mx, as well as one additional line x = 0. This is the basic construction of what we call the projective line, a space characterizing all the lines through the origin of affine 2-space. The geometric picture of this space is actually a circle: the bottom point representing the number 0; the left and right halves representing negative and positive numbers, repsectively; and the top point representing the number "infinity."

There are a few ways of describing points on the projective line. The formal way of doing so is by using what are called homogenous coordinates. In other words, for any nonzero point (a,b) in affine space, it is surely true that we can find a line through the origin and (a,b). In particular, if a is not zero, then this line takes the form y = (b/a) x where the slope is b/a. Furthermore, any two points (a,b) and (c,d) can actually sit on the same line, in particular whenever c = ka and d = kb for some number k. Thus, we can define homogenous coordinates as the set of points [a : b] for a, b in our field where [a : b] = [ka : kb] by definition, and the point [0 : 0] is not allowed as it doesn't specify any particular line (after all, every line passes through the origin). As is alluded to above, however, this means that whenever a =/= 0, we can take k = 1/a to get [a : b] = [1 : b/a], in other words characterizing each line by its slope. Furthermore, whenever a = 0, we can take k = 1/b to get [0 : b] = [0 : 1]. In other words, the projective line is, as we informally stated above, equivalent to the set of slopes of lines through the origin plus one other point representing the vertical line, the point at "infinity." Since slopes are just numbers in a field, we can add, subtract, multiply, and divide them as we normally do with one exception: the slope of the lines containing [a : b] for any a =/= 0 is b/a, so clearly the line with infinite slope consisting of points [0 : b] implies that b/0 should be infinity. Voila! We can divide by zero now, right? Well... there are two loose ends to tie down. The first is what infinity actually means in this case, since it is among the most misunderstood concepts in mathematics. Normally, when people bandy about phrases such as "infinity isn't a number, just a concept" or "some infinities are different from others" they are usually wrong (but well meaning) and also talking about a different kind of infinity, the ones that arise from cardinalities. Everything in math depends on the context in which it lies, and infinity is no different. You may have heard of the cardinal infinity, the subject of Hilbert's Hotel, describing the size of sets and written primarily with aleph numbers. Similarly, you may also have heard of the ordinal infinity, describing the "place" in the number line greater than any natural number. Our infinity is neither of these: it is to some extent an infinity by name only, called such primarily to take advantage of the intuition behind dividing by zero. It's not "greater" than any other number (in fact, the normal ordering of an ordered fields such as the real numbers breaks down on the projective line), and this is a consequence of the fact that if you make increasingly negative and increasingly positive slopes you end up near the same place: a vertical line. In other words, "negative infinity" and "positive infinity" are the same infinity.

The second loose end is that defining our operations this way is actually somewhat algebraically unsound, at least with respect to the way we think about operations in groups, rings, and fields. As mentioned above, the operation of addition can be lifted to affine space as (a,b) + (c,d) = (a+c,b+d). However, this same operation can't really be used for homogenous coordinates, since [1, 0] = [2, 0] as they lie on the same line (the line with slope 0), but [1, 0] + [1, 1] = [2, 1] while [2, 0] + [1, 1] = [3, 1], and [2, 1] and [3, 1] are not the same line, as they have slopes 1/2 and 1/3, respectively. Dividing by zero isn't even needed to get weirdness here. Luckily, we can simply define new operations by taking inspiration from fractions: b/a + d/c = (bc + ad)/ac, so we can let [a : b] + [c : d] equal [ac : bc + ad] (remembering that homogenous coordinates do to some extent just represent the slope). Luckily, multiplication still works nicely, so we have [a : b] * [c : d] = [ac : bd]. Unluckily, with these definitions, we no longer get a field. In particular, we don't even have an additive group anymore: [a : b] + [0 : 1] = [0 : a] = [0 : 1], so anything plus infinity is still infinity. In other words, infinity doesn't have an additive inverse. Furthermore, despite ostensibly defining infinity as 1/0, the multiplicative inverse of 0, we have that [1 : 0] * [0 : 1] = [0 : 0], by our rules, which isn't defined. Thus, 0 still doesn't have a multiplicative inverse and 0/0 still doesn't exist. It seems like we still haven't really figured out how to divide by zero, after all this. (Once again, if you want to read up on the projective line, which is a special case of projective space, which is a special case of the Grassmannian, in more depth.)

Part IV: I would say wheels would solve all our problems, if not for the fact that they just make more problems.

At this point, to really divide by zero properly, we're going to need to bite the bullet and change what dividing really means. Just as we can think of subtraction as adding the additive inverse (i.e. a - b = a + -b where -b was a number), we can start thinking of division as just multiplying by... something, i.e. a/b = a * /b, where /b is something vaguely related to the multiplicative inverse. We can already start doing this in the projective line, where we can define /[a : b] = [b : a], and it works nicely as [a : b] * [b : a] = [ab : ab] = [1 : 1] whenever neither a nor b is zero. This lets us rigorize the statements 1/infinity = 0, infinity/0 = infinity, and 0/infinity = 0, but doesn't really help us do 0/0 or infinity/infinity. Furthermore, note that because 0/0 =/= 1, /[a : b] isn't really the multiplicative identity of [a : b], it's just the closest we can get.

Enter the wheel! If 0/0 is undefined, then we can simply... define it. It worked so nicely for adding in infinity, after all - the picture of the point we added for infinity is taking a line and curling it up into a circle, and I like circles! Surely adding another point for 0/0 would be able to provide a nice insight just as turning a line into the projective line did for us.

So here's how you make a wheel:

You take a circle.

You add a point in the middle.

Yeah that's it. The new point, usually denoted by ⊥, is specifically defined as 0/0, and really just doesn't do anything else. Just like for infinity, we still have that a + ⊥ = ⊥ and a * ⊥ = ⊥ for all a (including infinity and ⊥). It doesn't fit into an order, it doesn't fit in topologically, it is algebraically inert both with respect to addition and multiplication. It is the algebraic formalization of the structure that gives you NaN whenever you fuck up in a calculator and the one use of it both inside and outside mathematics is that it lets you be pedantic whenever your elementary school teacher says "you can't divide by zero" because you can go "yeah you can it's just ⊥ because i've been secretly embedding all my real numbers into a wheel this whole time" (supposing you can even pronounce that).

Part V: So what was the point of all this anyways

The wheel is charming to me because it is one of the structures in mathematics where you can tell someone just asked a question of "what if this was true," built some space where it was, and just started toying with it to see what happens. It's a very human and very beautiful thing to see someone go against conventional knowledge and ask "what breaks when you allow 0/0" even if conventional knowledge does tend to be right most of the time. In this sense, perhaps the uselessness of the wheel is the point, that even despite how little ⊥ does from a mathematical lens, some people still took the time to axiomatize this system, to find a list of conditions that were both consistent and sufficient to describe a wheel, and genuinely do actual work seeing how it fits in within the universe of algebraic structures that it stays in.

While a wheel may not be used for much (it might be describable in universal algebra while a field isn't, though I'm not too well versed in universal algebra so I'm not actually entirely sure), every other structure discussed above is genuinely well studied and applicable within many fields inside and outside of math. For more viewpoints on what the projective line (and in general the projective sphere) is used for, some keywords to help you on your way are compactification of a set if you care about the topological lens, the real projective line or the Riemann Sphere if you care more about the analysis side, or honestly the entirety of classical algebraic geometry if that's your thing.

Another structure that might be interesting to look at is the general case of common meadows, an algebraic structure (M, 0, 1, +, -, *, /) where the condition of / being involutive (i.e. /(/x) is not always x) is relaxed, unlike a wheel where it is always involutive. Note that these structures are called meadows because the base structure they worked on is a field (get it? not our best work I promise mathematicians are funnier than this). These structures are at the very least probably more interesting than wheels, though I haven't checked them out in any amount of detail either so who knows, perhaps there isn't much of substance there either.

[maths-terms-identifier]

Group

Group Theory, Abstract Algebra

A group is a pair (G,•) where G is a set and a binary operation •:G×G->G such that:

There exists e∈G such that e•g=g•e=g for all g∈G, called the identity of G

For all g∈G, there exists h∈G such that g•h=h•g=e, called the inverse of g

For all f,g,h∈G f•(g•h)=(f•g)•h, that is • is associative

Sumbitted by @anon. Anon added: apparently, sociologists say 3, psychologists say 1 + blorbo. Let's settle this!

[xyymath]

Why the Number Zero Changed Everything

Zero: a concept so foundational to modern mathematics, science, and technology that we often forget it wasn’t always there. Its presence in our world today seems obvious, but its journey from controversial abstraction to indispensable tool has shaped entire civilizations.

1. The Birth of Zero: A Revolutionary Idea

The concept of zero didn't exist in many ancient cultures. For example, the Greeks, despite their advancements in geometry and number theory, rejected the idea of a placeholder for nothingness. The Babylonians had a placeholder symbol (a space or two slashes) for zero, but they didn't treat it as a number. It wasn't until Indian mathematicians in the 5th century, like Brahmagupta, that zero was truly conceptualized and treated as a number with its own properties.

Zero was initially used as a place-holder in the decimal system, but soon evolved into a full-fledged number with mathematical properties, marking a huge leap in human cognition.

2. The Birth of Algebra

Imagine trying to solve equations like x + 5 = 0 without zero. With zero, algebra becomes solvable, opening up entire fields of study. Before zero’s arrival, solving equations involving unknowns was rudimentary, relying on geometric methods. The Indian mathematician Brahmagupta (again) was one of the first to establish rules for zero in algebraic operations, such as:

x + 0 = x (additive identity)

x × 0 = 0 (multiplicative property)

These properties allowed algebra to evolve into a system of abstract thought rather than just arithmetic, transforming the ways we understand equations, functions, and polynomials.

3. Calculus and Zero: A Relationship Built on Limits

Without zero, the foundation of calculus—limits, derivatives, and integrals—wouldn’t exist. The limit concept is intrinsically tied to approaching zero as a boundary. In differentiation, the derivative of a function f(x) is defined as:

f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}

This limit process hinges on the ability to manipulate and conceptualize zero in infinitesimal quantities. Similarly, integrals, which form the backbone of area under curves and summation of continuous data, rely on summing infinitely small quantities—essentially working with zero.

Without the concept of zero, we wouldn’t have the means to rigorously define rates of change or accumulation, effectively stalling physics, engineering, and economics.

4. Zero and the Concept of Nothingness: The Philosophical Impact

Zero is more than just a number; it’s an idea that forces us to confront nothingness. Its acceptance was met with philosophical resistance in ancient times. How could "nothing" be real? How could nothing be useful in equations? But once mathematicians recognized zero as a number in its own right, it transformed entire philosophical discussions. It even challenged ideas in theology (e.g., the nature of creation and void).

In set theory, zero is the size of the empty set—the set that contains no elements. But without zero, there would be no way to express or manipulate sets of nothing. Thus, zero's philosophical acceptance paved the way for advanced theories in logic and mathematical foundations.

5. The Computing Revolution: Zero as a Binary Foundation

Fast forward to today. Every piece of digital technology—from computers to smartphones—relies on binary systems: sequences of 1s and 0s. These two digits are the fundamental building blocks of computer operations. The idea of Boolean algebra, where values are either true (1) or false (0), is deeply rooted in zero’s ability to represent "nothing" or "off."

The computational world relies on logical gates, where zero is interpreted as false, allowing us to build anything from a basic calculator to the complex AI systems that drive modern technology. Zero, in this context, is as important as one—and it's been essential in shaping the digital age.

6. Zero and Its Role in Modern Fields

In modern fields like physics and economics, zero plays a crucial role in explaining natural phenomena and building theories. For instance:

In physics, zero-point energy (the lowest possible energy state) describes phenomena in quantum mechanics and cosmology.

In economics, zero is the reference point for economic equilibrium, and the concept of "breaking even" relies on zero profit/loss.

Zero allows us to make sense of the world, whether we’re measuring the empty vacuum of space or examining the marginal cost of producing one more unit in economics.

7. The Mathematical Utility of Zero

Zero is essential in defining negative numbers. Without zero as the boundary between positive and negative values, our number system would collapse. The number line itself relies on zero as the anchor point, dividing positive and negative values. Vector spaces, a fundamental structure in linear algebra, depend on the concept of a zero vector as the additive identity.

The coordinate system and graphs we use to model data in statistics, geometry, and trigonometry would not function as we know them today. Without zero, there could be no Cartesian plane, and concepts like distance, midpoint, and slope would be incoherent.

[max1461]

I don't typically feel at home with "nerds" (in the sense of "programmer type guys"), because I feel there is something important about the world that very often they cannot see, and I am going to try to articulate what it is.

First, a digression.

My extended family is... well, most of them are not really evangelicals (insofar as they're Christian at all, they're not very good Christians and they mostly don't seem to care), but culturally they're part of the vulgar evangelical milieu; the sort of people to whom prosperity gospel megachurch pastors appeal. Years ago when I was about to start college, my uncle came to visit, and I told my him that I was going to study math. He's a smart guy, and started telling me about how he was always good at math in school, and telling me stories about the various times he'd used math (meaning, basically, elementary algebra) to great effect in his various business ventures. That's what he understands: business, making money... to put it less charitably (though I say this with considerable affection): scheming. So he tried to speak the language of making money to me about it. When he asked me what I wanted to do with my math degree (by implication: what sort of scheming was I looking to get involved in) I said something to the effect of "there are all kinds of job opportunities you have with a math degree, but that's not really why I'm studying it—I really just want to understand math at a deeper level". I remember the look on his face when I said that very clearly. It was utter bafflement. Not because he hated math or something, but because I genuinely don't think the concept of "wanting to understand something at a deeper level for its own sake" had ever occurred to him. The inherent appeal of understanding the world is, I think, not something which exists (or exists very strongly) in his emotional landscape. He is blind to that part of the human experience which drives scientists to be scientists.

Well, that's alright. He's a schemer and not a scientist by nature. Some people are that way. I like my uncle well enough, and I enjoyed talking to him on that visit. But he's not someone I would try to share my love of math or linguistics with; on both accounts I don't think there is anything I could say to make him get it.

Why do I bring all this up? Well, one way in which I relate to programmer type guys is that we both like math, and I think we like for basically the same reason. And I think most programmer type guys will have met someone like my uncle, someone who seems like they fundamentally cannot see the appeal in this thing which drives you so strongly, this thing which is so great a part of your emotional landscape. I'm sure a lot of you will know the exact feeling I had during the above interaction. You are so fascinated by these questions about how the world works, and how it can be rationally understood, and this other guy basically seems like he just... can't even comprehend what it's like to be motivated by that. It's so completely foreign to him, and his perspective is thus completely foreign to you.

We are all, sometimes, this uncle.

Part of why I am interested in linguistics is because I have this deep urge to explore the world (by this I mean principally: the human world). I have this desire to travel, to talk to people, to see and experience different places and different ways of doing things. I want to go to various places and see what they look like, and meet the people there and hear what they have to say, and so on and so forth. There is an "openness to experience" element to this, but that is very insufficient to characterize the thing I am trying to articulate; for instance, I have little interest in psychedelics or other prototypical "high openness to experience" type activities. To me, there is an ineffable vibe that every place seems to have (a "place" in this sense could be as large as a country or a small as a particular bar), and the vibes of nested places are like layers on top of one another that make being in the world feel like an extremely rich experience. Learning languages and learning about languages gives me this window into other places, which is extremely appealing, and furthermore I can access it to some degree from my own home, which is nice. Of course doing this from my bedroom is not enough, I want to actually go, to wander around, and in those times when I've gotten the chance to do so I have felt that it was very much everything I had imagined it to be.

When I try to talk to programmer type nerds about this aspect of myself, I often feel much the same as when I was trying to talk to my uncle about wanting to study math. They just don't seem to have any sort of reference for what I'm talking about, these emotions have never occurred to them in any significant way, and they can't figure out how to relate. I believe this is, in essence, the source of my frequent abrasions with rattumb, and why I have basically bounced off of coding for cultural reasons time and time again in my life, even though conceptually it's exactly the sort of thing that interests me. For reasons of nature or nurture, programmer guy personality traits rarely co-occur with wanderluster personality traits, they just don't seem to go together. And so in spaces like, well, this one, I'm just left feeling like nobody can quite relate to what I am getting at a good chunk of the time, and the consequence of this is that I feel emotionally impoverished. That's not anybody's fault for being a different sort of guy than me, and I'm sure there's stuff about which I'm the confused uncle (in fact, I know there is: the appeal of psychedelics, meditation, and other "transcendence" based activities is one of these things for me). Idk, just thought that was something worth expressing.

[bubbloquacious]

What mathematical operators would you think make for the best fuck marry kill discussion

FMK: addition, multiplication, exponentiation

FMK: powers, roots, logarithms

FMK: group operation, inversion, unit element

FMK: polynomials, differential operators, continuous maps

FMK: greater than, less than, equal

FMK: one, two, three

FMK: numerator, denominator, quotient

FMK: rings, integral domains, fields

FMK: categories, functors, natural transformations

FMK: reflexivity, transitivity, antisymmetry

FMK: fundamental theorem of algebra, fundamental theorem of calculus, fundamental theorem of arithmetic

FMK: prime numbers, composite numbers, units

FMK: algebraic geometry, algebraic topology, algebraic number theory

FMK: compact Hausdorff spaces, abelian groups, algebraically complete fields

FMK: axiom of choice, well-ordering theorem, Zorn's lemma

[legallyschrodingers]

Goodluck soldier🫡

Guys today’s the day…

I’m asking my history teacher if he has a favorite marshal✊

Wish me luck🤞

[originalcrime]

for the soft prompts - 27, buddie.

Evan!! thank you for the prompt! 😍 sorry in advance the actual musical element is blink and you’ll miss it 😬😳 but it is soft!

27. humming/singing

“We’re not getting extra pepperoni,” Eddie says firmly. Buck and Chris both start to protest, but he cuts them off. “It’s a racket! A dollar fifty and this place gives you something like five extra pieces. The regular amount is plenty.”

“Fine, Ebenezer, you win,” Buck says fondly. Eddie’s always been more or less a live-below-your-means guy, but ever since selling the house in Texas he’s been more frugal than ever. It’s fine, Buck loves him (he loves him!), even when he’s being a penny pincher about pepperoni. “Chris, you want any other toppings?”

“No other toppings,” Eddie pronounces.

“What.” Buck says.

“Dad!” Chris groans.

“What?” Eddie says. He gestures toward the fridge. “We’ve got veggies. We’ve got a sauté pan. We can pull the rest together ourselves.”

Chris scoffs. “The point of ordering pizza is you don’t have to pull anything together yourself.”

Buck thinks the kid makes a good point, but Eddie ignores him entirely, tossing Buck his phone. “Make the call, babe. Just two medium pepperonis. Pickup. We don’t need to pay for delivery.” Which is crazy talk, frankly, but he called Buck ‘babe,’ so how is Buck not supposed to do as he asks?

By the time he’s done placing the order, Chris has put his headphones back on and is bent over his homework, chewing his pencil eraser thoughtfully as he flips pages in his algebra textbook. Eddie is chopping up an orange bell pepper, tongue between his teeth in concentration as he precision cuts perfectly even strips.

There’s another cutting board sitting out, next to an onion and a carton of mushrooms. Buck sidles up next to him, grabs a handful of champignons, and gets to work himself. Eddie shoots him a soft smile, just about making the extra effort worth it.

Up close, Buck can hear that Eddie’s cheerily humming something under his breath—hey mambo, mambo italiano—which is so delightfully dorky Buck could cry. Shit. He should’ve taken the onion.

“When did they say it’d be ready by?” Eddie asks, flicking on the burner.

“Twenty, twenty-five minutes,” Buck tells him. “I’ll go get em, if you’re watching the stove?”

“I can make the drive,” Eddie says. “Since it was my idea.”

“Babe,” Buck says, just for the small joy of seeing Eddie flush at the pet name, too. “You think picking up a couple pizzas on a Thursday night isn’t the least I’d do for you?”

Eddie grins at him, biting the inside of his cheek. He makes a furtive head gesture toward Chris, oblivious over at the kitchen table. “For us,” he says. He looks at Buck carefully. “All of us.”

All of us. Isn’t that something? Buck leans in to give Eddie a soft, dry peck, and goes to find his keys so he can pick up family dinner. For their family.

send me soft prompts!

accepting buddie and wincest

[kata4a]

so if you have some group G, there's a fairly straightforward argument that every product is unique, i.e., there is no a, x and y such that x ≠ y y but ax = ay

(because, assume there are. then:

x = (a⁻¹a)x = a⁻¹(ax) = a⁻¹(ay) = (a⁻¹a)y = y

but x ≠ y by assumption)

now this proof obviously relies on the associative property of groups. but does it need such a property? well, yes, because consider the finite group G = {e, a, b} with the following multiplication table:

ee = e; ea = a; eb = b; ae = a; aa = e; ab = b; be = b; ba = b; bb = e;

by inspection, we can see that the operation is closed, that there is exactly one identity, e, and that every element has a unique inverse (itself). every group axiom except associativity holds, and indeed, we see that every product is not unique: eb = ab = b, despite e ≠ a

in other words, a loop is guaranteed to have unique products if it is associative, which further implies that if you can find two products ax = ay then the operation must not be associative

but can we prove this more directly?

as it turns out, yes! in fact the algebraic manipulations are quite similar to the proof at the beginning of this post. first, let there be a, x, y such that x ≠ y but ax = ay

then,

a⁻¹(ax) = a⁻¹(ay) (a⁻¹a)x ≠ (a⁻¹a)y

therefore, if a⁻¹(ax) = (a⁻¹a)x then a⁻¹(ay) ≠ (a⁻¹a)y, and vice versa—either way we've found some a, b and c such that a(bc) ≠ (ab)c

so, the natural next question to me is, if you have a non-associative loop, can you always find some a, x and y such that x ≠ y y but ax = ay? I think this is equivalent to asking: is every multiplication table where no element appears twice in the same row or column associative? and I'm pretty sure the answer to that is yes but it would be really cool to have a constructive proof where you go from a(bc) ≠ (ab)c to gx = gy

[mathematical-cheese]

Tell me about math's. Anything. I'm so curious

Okay! I will tell you about one way we can test for holes in a topological space!

I will first clarify what I mean by a loop because it's important to be precise and they are the star of this show! A loop in a topological space X is continuous map from the interval [0,1] to X which starts and ends at the same point.

To motivate our test we shall look at two examples!

First imagine a plane (ℝ²). Intuitively this has no holes. If we consider a loop in the plane we can imagine shrinking this loops down to a point. This is sort of like placing a rubber band on a table and squishing it down as close as you can (except rubber bands have a physical limitation. Even if you can keep squishing it, you'd eventually make a black hole). It's important to point out that the loop lives in the space rather than on top of it like a rubber band on a table.

Now imagine an annulus (see picture)

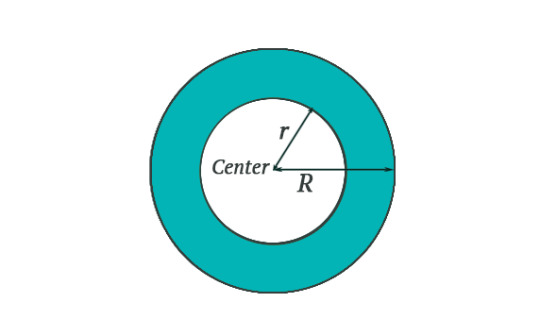
This obviously has a hole in the middle. Now we can consider loops in an annulus. We can think about two kinds of loops!

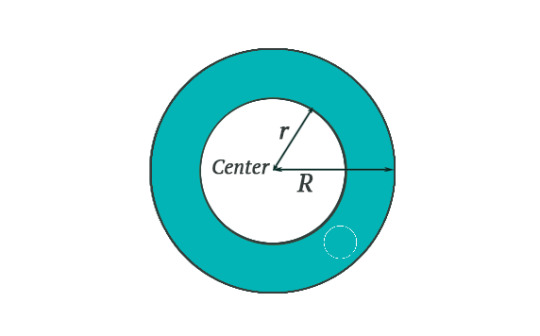
The first kind doesn't go around the hole and we can still shrink these to a point. The other kind goes around the hole and when we try to shrink it, it snags on the hole.

So the idea is that we can find the presence of a hole in a space by shrinking loops to see whether they can be made into a point or not. We can adapt the rubber band analogy by adding the extra rule that the rubber band must always touch the table at all its points. So if we were to cut a hole into the table, we would no longer be able to shrink the rubber band.

Let's try another example! We shall look at a torus. This is the surface of a ring doughnut (that is, it doesn't have anything on this inside).

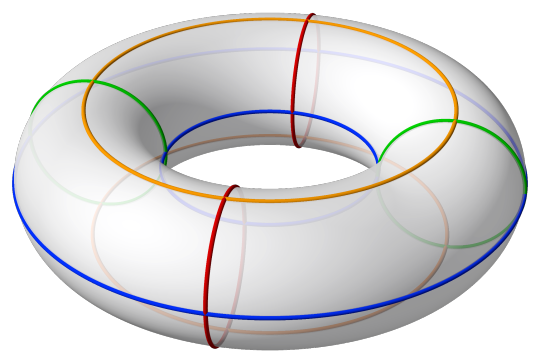
First consider the red and green loops. All we can do with these is move them around the tube. We can't shrink them. Similar, we can't shrink the orange and blue loops. We also can't deform a blue/orange loop into a green/red loop and vice versa! So a torus must have some holes!

One thing that might seem weird is that holes can have different dimensions! The part of our space which bounds the hole can have a different dimension which means the hole is fundamentally different. In this context the dimension of a space is to do with what the space locally looks like. That is, if you were to zoom in closely the space would sorta look like a flat Euclidean space, i.e. a line or a plane or 3D space etc. For example, the torus is 2 dimensional since locally it looks like a plane. A circle is 1 dimensional since locally it looks like a line. Another way to think of this is how many different independent directions could you walk if you lived in that space. Another example is the sphere, think the surface of the earth. This is two dimensional because we only require two numbers to describe positions on it!

The reason I bring this up is our test can't always detect the presence of holes! This is because our test is great at picking up on 1 dimensional holes, but it doesn't always detect higher dimensional holes. A good example here is the sphere. We can always shrink a loop on a sphere but it's fairly easy to see that the sphere bounds a region that isn't a part of the sphere itself. There is a 2 dimensional hole in the sphere.

One more neat thing we can do with loops in spaces is we can use them to define a nice algebraic structure! By algebraic structure, I mean anything that involves a set and an operation between elements of that set which produces another element of that set. An example of this is the integers with addition. We can add two integers to get another integer. The integers have some nice properties. There is an element 0 such that 0+n=n+0=n. We can also take inverses, i.e. we for any integer n there exists another integer m such that n+m=0. We also have a property called associativity. This is the rule that says (n+m)+k=n+(m+k). This makes the integers what's called a group!

We can make a group using loops in a topological space! We first pick a basepoint which every loop will start at. Then we define out operations on the loops to be concatenation. That is, given two loops f and g, we define f*g to be the loop we get by first going around f then going around g. We also have the added rule that we consider loops that can be deformed into each other to be the same. The identity element is the constant loop, i.e. the loop e such that e(t)=x for all values of t, where x is our basepoint. The group that we get is called the fundamental group (kinda pompous but it really is important!).

We can see an example of this using the annulus from earlier! We can consider an anticlockwise loop around the hole to correspond to the number 1. We can get successive positive numbers by going around this loop the right number of times! We get negative numbers using clockwise loops! (Equally we can make clockwise loops correspond to positive numbers and anticlockwise to negative numbers).

The fundamental group turns out to be a very powerful tool! It turns out that if topological spaces have different fundamental groups they can't be the same space (strictly speaking, they can't be homeomorphic or even homotopy equivalent). And we can prove some useful results using fundamental groups too!

This is all formalised in the area of maths called Algebraic Topology (the area I hope to do research in!). Making this all rigorous is no easy task (I have written a few formal posts about it on my maths blog!)

This was a lot longer than I had planned originally haha. I've been writing for about an hour and a half. I hope you find it interesting!

[maths-terms-identifier]

Module

Abstract Algebra

Let R be a ring, then a left R-module, M is an Abelian group (M,+) along with an operation ·:R×M->M such that for all r,s∈R and x,y∈M we have

r·(x+y)=r·x+r·y,

(r+s)·x=r·x+s·x

(r·s)·x=r·(s·x)

1·x=x

+ is called addition and · is called scalar multiplication

trying to learn tech is so fucking hard there's so much jargon. "what gooble are you using" "what's a gooble" "you use the gooble to respink your matrix" "what does respink mean and what is a matrix" "respinking means unpiling a component to change it back to its base spink. a matrix connects your device's AKD to your networks z jamper" how does anyone understand any of this

[louquorice]

AVATAR: TLA/LOK universe “sequel AU” concept

AU takes place several avatar cycles after Korra

In the year 2000, the world has undergone a massive transformation and is a far cry from the one known in the days of the Four Nations. The once-divided nations of the Water Tribes, Earth Kingdom, Fire Nation, and Air Nomads have united under a single banner, forming [unnamed country], a progressive society that has largely abandoned its ancient traditions. Bending—once revered as an essential skill—is now in a regulatory grey area (regulated; either licensed, suspended, or exiled), seen as irrelevant in the age of technology. The Avatar, once the world's protector, is now nothing more than a forgotten relic of history, their role reduced to a mere tradition. It is a society where the ancient traditions have been abandoned in favor of rapid technological advancement.

When Sozin's Comet unexpectedly returns years ahead of its predicted path, it brings with it a cosmic anomaly that disrupts the natural balance of all four elements. The comet’s influence creates global chaos:

Fire becomes uncontrollable, causing wildfires and spontaneous flames.

Earthquakes rattle cities, weakening infrastructures.

Water floods coastal cities and causes unpredictable tides.

Air storms destroy weather patterns, leading to violent, erratic tempests.

The comet’s arrival also shatters the delicate peace between the coexisting physical world and Spirit World, awakening once-dormant spirits and causing widespread spiritual disturbances.

The Avatar, the latest in the Waterbender line and is no one but just a typical high schooler in every way, is ill-prepared for such a crisis. A world-saving hero that no one expects because they’ve been ignored their whole life. Someone who prefers to have an Algebra test rather than deal with a world-ending crisis. Untrained and inexperienced, they are thrust into a world where bending is forbidden and the Avatar’s spiritual connection is weak. With the balance of the world in jeopardy, the Avatar embarks on a journey to rediscover bending, reconnect with lost traditions, and confront the growing chaos.

(Excerpt from lore written by burymenot)

Note: This is a concept developed by my digital arts class, in collaboration with myself, that we got way too invested in, and so we must release this hyperfixation in public lol

Team Avatar

Zen, 17 (Avatar from the Water tribe)

He is the incarnation following the unscrupulous air nomad Avatar Khando, widely reviled for being a menace to society. He led a renegade faction of the Freedom Fighters, who were more extremist in their methods. This unflattering reputation further soured the reception towards the next Avatar. (written by clygerdoodles, who is a friend I roped into this AU lol)

Zen is the titular Avatar, master of Four elements & meant to bring balance to the world. He is in his last year of high school, living a typical teenage life in a quiet neighborhood together with his parents and pet (otter-platypus) Shin, content with a life of mediocrity ever since his unceremonious announcement as the Avatar. When called to fulfill his traditional duty, he reluctantly accepts the responsibility, having feelings of doubt bothering him every now and again.

Thrust into a chaotic world that suddenly needs an Avatar after some cycles of indifference, he faces many challenges that questions his principles and world views, hardwired by history and his own upbringing. While he strives hard to exceed the expectations placed upon him despite his unpreparedness, deep down all he wants is to live a normal life like others. (Written by jnzn.art)

Jia Zhang, 17 (Avatar’s bestfriend)

With one parent being a famous Mover star, and the other being a top socialite, Jia’s parents barely spend time with her and as such, she is spoiled rotten, if only to prevent her from complaining about them on social media and ruining their reputation.

Daughter of extremely wealthy and successful parents, Jia is someone used to getting what she wants. Besides her snobbish personality, she is also loud and catty, which makes most of her classmates dislike her. She has an unbridled obsession with Avatar lore and became notorious for her many product orders from Avatarland, always looking forward when she will receive her next parcel. Born an earthbender, she instead appropriates waterbender customs, all because the current Avatar is from the water tribe.

As the self-appointed bestfriend of the Avatar, she is ever supportive of him and he is one of the few people she acts cordial with. She accompanies Zen on his training journey across the world, oftentimes paying for the group’s expenses with no questions asked. Always feels unappreciated and useless, as her ideas are usually shot down or talked over by others and isn’t assigned in serious roles in the team dynamic. (Written by kuramaru)

The Twins (Children of current head of the White Lotus)

Kyna, 18 (potentially talented airbender)

Bubbly and down to earth, Kyna is the more approachable one between the twins. Unlike her brother, she prefers to go out with friends and traveling to different Air Temples. At home, she dutifully fulfills her responsibilities in the household, leading her to be considered the “favored child.” Despite that, she has a close relationship with Kai, and loves to pester him, much to his annoyance, but would sometimes help him in his tech endeavors.

Trying to live up to her namesake, she learned airbending at a very young age but has yet to master it. Touted as talented, yet plagued by laziness. She wants to earn her master tattoos yet spends more time reading scrolls or watching documentaries about the art rather than practicing it. When presented with the opportunity by her father to accompany the Avatar on his training journey, she jumps on the chance, relishing on the thought of traveling the world. (Written by Mikay C)

Kai, 18 (tech savvy non-bender)

Kai is someone who is not interested with his Father’s work in the White Lotus nor in his sister’s involvement with Team Avatar. In fact, he aims to graduate from high school and finally pursue a degree in Robotics Engineering. Deeming their duty to the Avatar more important, his father convinced him through bribery, buying him tech he so badly wants just as long as he tags along with the Team. Also, he cares too much about his sister to leave her alone.

His personality consists of him being distant most of the time, always appearing cool and mysterious, but is actually emotionally repressed and easily irritated. He is tech savvy and a self-identified gamer, preferring to shut himself in his room studying robotics and tinkering, or play games the whole day. (Written by KeziartS)

(The students assigned these roles didn’t fulfill some of their requirements, hence the minimal art from them directly 😔)

Zhihan, 21 (Lost heir to the Fire Nation throne)

She is the heir to the Fire Nation royal family, their lineage difficult to trace when the monarchy collapsed after the relatively short reign of Iroh II. The fact is revealed to her by her Uncle Ikigai, whom she doesn’t have the best relationship with, believing him to be her father’s killer. Ultimately, her ‘princess’ status is something she doesn’t have it in her to really care about.

A college drop-out who opted to be a cast member in Avatarland, a theme park located at an old Fire Nation temple. Along with her cousin Zar, they live in poverty, being overworked and underpaid in their jobs as performers, so they would often stage scams on unsuspecting tourists in order to get by. Self-serving and ignorant to a fault, but not without morals. She mostly comes off as friendly and endearing, and uses that natural charm to commit petty theft or lie her way out of trouble. Never having formal combat training in Firebending, she is at the very least, aware of the basics, and mostly uses it in her performances akin to party tricks.

Somewhat apologetic for causing a rift between two members of Team Avatar, she leads them to her uncle Ikigai, one of the firebending masters listed to help train Zen. Consequently, she is forced to accompany them the rest of the way, acting as the ‘legal guardian’ for Team Avatar, but only after striking an agreement with them that she is to be compensated.

(The character was supposed to be one-off, like the Cabbage guy, but my students kept adding roles and traits to her and since I go along with what they say, she eventually became a fleshed out character I got attached to 😭)

Enola Baolan, 19 (Book 1 antagonist)

She is branded as the child of traitors, a title she inherited through no fault of her own, but because the United Republic of Nations’ leaders labeled her parents as such, for their groundbreaking invention on technology capable of mimicking bending abilities to a certain extent.

Enlian, who uses “Enola” as an alias, is a non-bender with a troubled past, born in Ba Sing Se to earthbending parents who specialize in metalbending. After her parents were “banished” by the government for their inventions, she is orphaned at a very young age. She lived with many foster families, enduring both kindness and neglect. She worked odd jobs through the years, such as a mechanic at Teo’s workshop and as a courier at Kuruk Express, earning enough wage for modest living conditions.

Once she discovers the truth about her parent’s disappearance, she finds their hidden laboratory, collecting their notes and working prototypes, and vows vengeance against their oppressors. Though she cannot bend, she compensates for it with sheer tenacity and tactical ingenuity, paired with utilizing her parent’s prized invention, the Earth Gauntlets, makes her a force to be reckoned with.

Initially masquerading as a bender of all elements, she acts as the foil to the Avatar. She challenges Zen’s views, who believes himself a beacon of balance, but for Enola, he is the enduring symbol of a flawed system. (Written by burymenot)