#ask panda

[mathematical-cheese]

Tell me about math's. Anything. I'm so curious

Okay! I will tell you about one way we can test for holes in a topological space!

I will first clarify what I mean by a loop because it's important to be precise and they are the star of this show! A loop in a topological space X is continuous map from the interval [0,1] to X which starts and ends at the same point.

To motivate our test we shall look at two examples!

First imagine a plane (ℝ²). Intuitively this has no holes. If we consider a loop in the plane we can imagine shrinking this loops down to a point. This is sort of like placing a rubber band on a table and squishing it down as close as you can (except rubber bands have a physical limitation. Even if you can keep squishing it, you'd eventually make a black hole). It's important to point out that the loop lives in the space rather than on top of it like a rubber band on a table.

Now imagine an annulus (see picture)

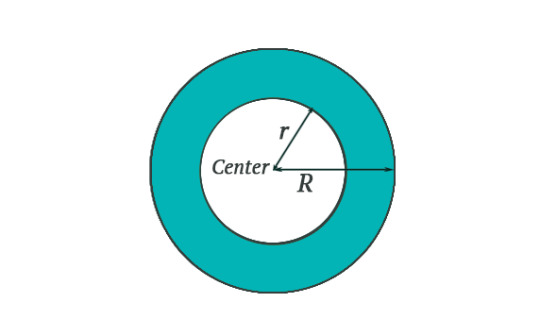
This obviously has a hole in the middle. Now we can consider loops in an annulus. We can think about two kinds of loops!

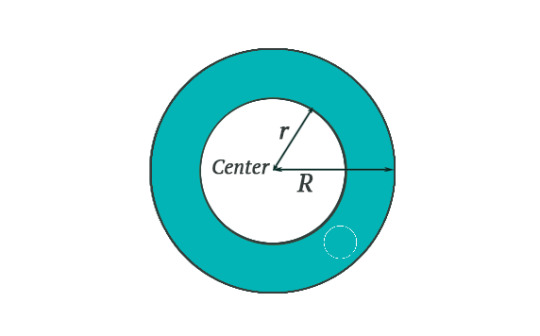
The first kind doesn't go around the hole and we can still shrink these to a point. The other kind goes around the hole and when we try to shrink it, it snags on the hole.

So the idea is that we can find the presence of a hole in a space by shrinking loops to see whether they can be made into a point or not. We can adapt the rubber band analogy by adding the extra rule that the rubber band must always touch the table at all its points. So if we were to cut a hole into the table, we would no longer be able to shrink the rubber band.

Let's try another example! We shall look at a torus. This is the surface of a ring doughnut (that is, it doesn't have anything on this inside).

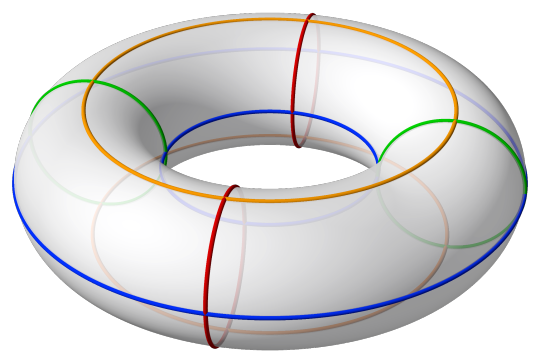
First consider the red and green loops. All we can do with these is move them around the tube. We can't shrink them. Similar, we can't shrink the orange and blue loops. We also can't deform a blue/orange loop into a green/red loop and vice versa! So a torus must have some holes!

One thing that might seem weird is that holes can have different dimensions! The part of our space which bounds the hole can have a different dimension which means the hole is fundamentally different. In this context the dimension of a space is to do with what the space locally looks like. That is, if you were to zoom in closely the space would sorta look like a flat Euclidean space, i.e. a line or a plane or 3D space etc. For example, the torus is 2 dimensional since locally it looks like a plane. A circle is 1 dimensional since locally it looks like a line. Another way to think of this is how many different independent directions could you walk if you lived in that space. Another example is the sphere, think the surface of the earth. This is two dimensional because we only require two numbers to describe positions on it!

The reason I bring this up is our test can't always detect the presence of holes! This is because our test is great at picking up on 1 dimensional holes, but it doesn't always detect higher dimensional holes. A good example here is the sphere. We can always shrink a loop on a sphere but it's fairly easy to see that the sphere bounds a region that isn't a part of the sphere itself. There is a 2 dimensional hole in the sphere.

One more neat thing we can do with loops in spaces is we can use them to define a nice algebraic structure! By algebraic structure, I mean anything that involves a set and an operation between elements of that set which produces another element of that set. An example of this is the integers with addition. We can add two integers to get another integer. The integers have some nice properties. There is an element 0 such that 0+n=n+0=n. We can also take inverses, i.e. we for any integer n there exists another integer m such that n+m=0. We also have a property called associativity. This is the rule that says (n+m)+k=n+(m+k). This makes the integers what's called a group!

We can make a group using loops in a topological space! We first pick a basepoint which every loop will start at. Then we define out operations on the loops to be concatenation. That is, given two loops f and g, we define f*g to be the loop we get by first going around f then going around g. We also have the added rule that we consider loops that can be deformed into each other to be the same. The identity element is the constant loop, i.e. the loop e such that e(t)=x for all values of t, where x is our basepoint. The group that we get is called the fundamental group (kinda pompous but it really is important!).

We can see an example of this using the annulus from earlier! We can consider an anticlockwise loop around the hole to correspond to the number 1. We can get successive positive numbers by going around this loop the right number of times! We get negative numbers using clockwise loops! (Equally we can make clockwise loops correspond to positive numbers and anticlockwise to negative numbers).

The fundamental group turns out to be a very powerful tool! It turns out that if topological spaces have different fundamental groups they can't be the same space (strictly speaking, they can't be homeomorphic or even homotopy equivalent). And we can prove some useful results using fundamental groups too!

This is all formalised in the area of maths called Algebraic Topology (the area I hope to do research in!). Making this all rigorous is no easy task (I have written a few formal posts about it on my maths blog!)

This was a lot longer than I had planned originally haha. I've been writing for about an hour and a half. I hope you find it interesting!

[confusedpandabear]

Me too Cloud. Me too. twitter(.)com/TylorHepnerArt/status/1747310968063864875

Me every day until 29 Feb:

[rjhpandapaws]

Hey yall, im getting drunk tonight so ask me anything!!

[cryptidtrashpan]

Hi hello. I would apologize for the huge spam of likes I just gave you, but I'm not sorry cause I think your art is very good and very cool and I just wanted to tell you that.

Also I think the daily sketches you do are awesome cause I know I could not keep up with that lmao

That's all. I just wanted to tell you that you're awesome, your art is awesome, your brain is awesome. I hope you have a really good day (:

Here's a picture of my cat sitting in the bathtub if you ever need cheering up

AAAAAHHHHHH you made my day with how sweet this is!!

i hope you are having a great day and i love your cat give smooch on head for me~

[tiredpandaportfolio]

DMC Questions Anon here!

Take every character you wish to and tell me what you think is the most emotionally devastating situation they could be put in and how they would react to it.

[crawls out of the ground] I have been busy.

===

Well, easy. I am in the process of writing something, about that. Dante gets to feel the sting of the consequences of his feud with Vergil.

The whole DMC5 thing killed a lot of people. There is nowhere to hide from that fact. Dante and Vergil and even Nero cannot hide from that fact forever. Vergil may not care, and Nero may try to cope, but I believe Dante will start to buckle. He has been weathering so much all these years and using shitty humour to cope with what he's seen and what he's done.

But what happens when he can't take anymore?

What if, he had some connection completely separate from his family nonsense, that he wanted to keep separate from the problems so they wouldn't taint it? A witch he's gotten very fond of. A witch, who lives in a quiet, near-constant state of being a cornered animal because demons want to literally eat her and unscrupulous humans wouldn't bat an eye at murder and dark rituals just to gain power off her life.

She gets to see exactly what the trees do, she gets to find out that the trees are particularly after witches because their blood runs thick with power. She sees a lot of people die horribly. She nearly dies. She hasn't seen Dante in months by the time they finally see each other again and she's a very different creature now. She's terrified of him. She has no patience for his jokes and his light-hearted attitude. She doesn't use jokes to cope and her trauma is too fresh and too deep.

She's angry. She blames him--she blames all of them. She doesn't want to fight, she doesn't want revenge, she just wants to never see them again because she's terrified one day Dante, or Nero or Vergil, will snap and give in to the demonic urge to acquire more power, and she will be a prime target.

Because they've had a taste of the power the trees distilled from blood and she's scared it's like an addiction they can't help. She does not want to be a rabbit in a den of wolves. So she angrily curses them and flees. Whatever she and Dante had is over.

And he blames himself, because that's what Dante does. He bottles it all up, blaming himself and trying to forget it, but he can't. It's not fair. He got his brother back, he has a family again... but it's not complete. He feels as though the cost of achieving all that was losing her. It's not fair. He's been living with guilt and grief for years.

His time with her was a reprieve; a welcome break from his life of quiet suffering, hidden under his humour and weary pretending that all is well. She really made him feel happy. And now, she's gone. He scared her away. Her words have hurt. Her presence has hurt, because he spoiled her. She went from friend, ally and love to a victim of his idiotic feud with Vergil. But he can't blame Vergil-- he had as much of a hand in this as Vergil. And he can't bear to start another round of fighting over that.

So he bottles it up until it starts to crack him. He can't fight against the dread any longer. Any joy he got from Vergil being back has been marred. He can't ignore the blame anymore. He blames himself for everything and it will destroy him.

[rjhpandapaws]

I write for Hades, Legend of Zelda, The Magnus Archives, Welcome to Night Vale, and about my various OCs (Iori, Hallian, Hazel, Blayke, Wryn, Astor, and Ziur (he is new and half Shiekah and half Hylian)

Just send me the Number of the Prompt, the Prompt itself and who you want me to write about

One Liner Prompt list #13

1- “Don’t look at me, I was still dead at the time.”

2- “….Aren’t you a little young, to be here?”

3- “Everyone is entitled to their own opinion, I just wish you had kept yours to yourself.”

4- “I don’t know how to tell you this, but yelling at someone to, stop panicking, isn’t going to stop them from panicking.”

5- “It’s not your fault. Sometimes you can do everything right, and things will still go wrong…. This just happened to be one of those times.”

6- “…..I’m going to pretend I didn’t see that.”

7- “Why am I the one who always ends up getting targeted by the creep of the week?!”

8- “Fuck…. I knew I should have bought those light up sneakers.”

9- “None of this, seems healthy.”

10- “….Should I be concerned?”

11- “I said pass it to me, not throw it in my general direction!”

12- “It is my deep pleasure, to inform you that I am not the one in charge here.”

13- “Quick! You hide the equipment, I’ll hide the grenades!”

[thoughtfulbearpanda]

Hi could you do a reading on taylor swift and travis kelce's relationship? please

AoW rx, 7oP, wheel of Fortune

I'm getting that one person is trying to leave the relationship. To them the relationship has lost it's luster, like it's no longer fun for that person and they want but the person is procrastinating. They don't want don't want to end part ways just yet. If these 2 are PR, then they're contract may have reached it's expiration date and that would explain the energies here.

[sonadowcentral]

SONIC!

On a scale of 1 - 10, how much do you trust Ruby?

all he can do is hope she comes around and make things right.

[grizzly-bear-official]

Got any fat & lazy bears chilling, not ripping someone apart?

Show plz...

here are some straight up vibing bears

[mathematical-cheese]

Bro...aroaces are literally the most represented everywhere. And you're still complaining. Go ask aroallos and aceallos about being recognised lol

The post wasn't even about representation, it's about the fact that even in aspec spaces there is a tendency to leave out the aro part of aroace and just viewing those people as asexual where being aro is an afterthought. Do you not see how that is also harmful for both aroallos and alloaces?

In the case of aroallos it's the fact that they're forgotten about because they aren't asexual and therefore their identity isn't even at the forefront of most people's minds when discussing aspec stuff. Their aroness is erased because it is not accompanied by asexuality.

In the case of alloaces there is the underlying assumption that romantic attraction isn't felt because there is still the assumption that aroace and asexual are the same thing. The fact they do feel romantic attraction is erased by the fact they're asexual.

The underlying issue here is that there isn't a great understanding of how different attractions interact with each other and the different labels we have to describe different experiences, even within the aspec community.

I made the post because an irl aspec group that I'm in were talking about the aroace character in the new series of Heartstopper and almost all of them referred to him as asexual. I have not watched Heartstopper (romance stuff doesn't interest me) but I was informed that there's actually a stronger focus on romantic attraction, i.e. the aro part in his aroace identity. As well as a consistent feeling that my aroness was erased when I identified as aroace and is ultimately one of the reasons I dropped the ace part of the label.

[confusedpandabear]

Not to be left out, have an annoyed protective Cloud too😒: twitter(.)com/hermitage777/status/1627284332909068288

I loooooove the way he holds her 🥺

[rjhpandapaws]

Its my birthday week! Ask me anything you would like!!!

I will answer anything except when my birthday actually is, those who need to know, know

[habken]

hi habs! i was curious if you had a sona or something of that sorts?

Imagine a guy on a fishing trip with one of those “women want me fish fear me” hats

[tiredpandaportfolio]

I want you ask me about Sparda boy hcs. I don't do Y-N/reader answers well, I'm more comfortable answering regarding hcs about my ficverse, but I'm still willing to try! I'm looking for excuses to practice. Ask this account!

[bluepandadraws-log]

Remember folks, if you hate a ship REALLY BAD I insist blocking tags; it's in the Account Settings under Content you See, you can add tags to filter so you can't see them.

I say this cuz I WAS gonna rant about a ship I've grown to really not like, but I held back and blocked tags instead. I hate yucking up anyone's yum and ship wars are pointless lol

[thoughtfulbearpanda]

Could you do a reading on kendall jenner and bad bunny's relationship? please

Hello. So I got the AoC (clarified by 10oc rx), 5oC (clarified by emperor), and the 6oS (clarified by the 9oW & KoP). The knight of cups rx popped out and the is Pisces and Aquarius energy, BB is a Pisces. The 5oC is Scorpio so that is Jenner's energy. From I gathered BB may be trying to reach out to Jenner with the possibility of rekindling their relationship, however I don't think it was a stable relationship. It could have been toxic, they're relationship could have been on/off. Jenner knows that and I believe she is exhausted by the constant back and forth. It's like she knows if she gets back with him they'll be fine for awhile, then he'll probably cheat or hurt her feelings in some way, then they'll call it off -wash, rinse, repeat. *The knight of cups rx can indicate a cheater/flirt/homewrecker.

I do see Jenner rejecting BB's offer and focusing on herself instead. Choosing to move forward, move on. She'll focus on getting her bag instead of entertaining him. She may have her eyes set on someone else, someone more stable and financially secure or who will bring more financial security to her (maybe another PR relationship who knows). This person that she may be moving towards will probably be a Taurus or an Aries (*doesn't necessarily have to be these signs, but some who is financially successful - like a CEO or something)