#標準
Explore tagged Tumblr posts
Text
跟上大家腳步是最低要求
以下一位有緣人分享,來文照登:
《阿伯的話-現場開示精華節錄》:「有些事情看似來得很突然,實則上天早就安排好了,所以不要認為現在沒事,就掉以輕心;表面上看起來風平浪靜,其實背地裡波濤洶湧。計畫永遠趕不上變化,好好地珍惜每個當下,���不空過,莫讓人生老是在遺憾中渡過。」
4月3日突發的一場地震,是我所經歷過震撼感最強烈的一次地震。那天早上正在靜坐,忽覺一陣陣頭暈襲來。心裡一邊想,怎麼大清早就開始頭暈?一邊就聽到廚房掛鉤上的平底鍋撞擊瓷磚,發出規律的聲響。怎麼回事?剛睜開眼,就看到眼前厚重的窗簾在左右搖晃,一抬頭,又看到頭上的燈也在晃。這才猛然意識到——地震了!同時才發覺頭暈的原因,是我和房子都在左右搖晃。十一層樓的房子,四個單元連在一起,我家住二樓,在二樓都有如此明顯的震感,這一定是場大地震。
我就一直坐著抬頭看燈,看它晃動的幅度會不會變大,再判斷要不要跑出去。晃動的過程持續了大概不到一分鐘,一切就恢復平靜。聽到樓下一位鄰居說:「生命誠可貴」,心裡想到的只有無常說來就來,人生就是一場夢,什麼都是假的。萬般帶不走,唯有業隨身。如果真發生了什麼,最遺憾的就是還有那麼多開示出來的經文沒唸完,就又要帶著滿身的罪業,不知流轉到哪道了。
想到誦經,想到修行,又想到心得分享的事。前陣子修行社團訂出文章分享新制度,不能在當週期內交心得的,最晚下次發表時一併補齊。爾後未照規定,直接退團。這是給點方便,但不隨便。阿伯說:「再不快點,魔性就是到下輩子去了」、「大家別白來世上一遭,讓妳(你)的阿賴耶識裡充滿佛法的正能量,以便來世不再誤入岐途,墮入地獄受苦。臨陣磨槍,不亮也光。」既然選擇進社團修行,就要遵守共修社團的制度,修行要的是安愚守分,連這點分都守不好,遑論其它。
懺悔以前對按時交心得這件事沒有很重視,想著這周寫不出來,就拖到下周,下周再寫不出來,就拖下下周。看到別人也沒交,我也心安理得,就是這種拖和懶的心理,讓回報表上開出一個又一個的天���,也對其他人產生了不好的影響,覺得沒按時交心得也不會怎樣。慚愧!愚癡啊!拖到拖不下去,不還是一樣要花時間去寫嗎?而且心理上還要承受很大的壓力。理由千千萬,不做就是難。手機是滑不完的,小視頻是看不完的,把心靜一靜,思緒理一理,早起試一試。只要有心,會發現辦法總比困難多。
跟上大家腳步是最低要求,努力精進才是更好。要向那些超額完成定課量的師兄姐們學習,把娛樂的時間、閒聊的時間,都拿來誦經持咒,好好寫文章。看到別人都在努力精進,也是對自己的一種無形鞭策。現在的辛苦,是為了未來不辛苦。以有涯之生命,滅無涯之痛苦。黑氣快點消,業障快點還,心性快點提升,人生還是很美好的。好好珍惜每個當下,心不空過,不然無常一來,就只能留下無盡的遺憾和後悔了。阿彌陀佛!
(分享完畢)
《阿伯的話—現場開示精華節錄》:「人世無常,是明天先到還是無常先到,你如何保證每天都可以看到明天的太陽?」有緣人從地震的震撼中醒來,心裡想到的:「只有無常說來就來,人生就是一場夢,什麼都是假的。萬般帶不走,唯有業隨身。如果真發生了什麼,最遺憾的就是還有那麼多開示出來的經文沒唸完,就又要帶著滿身的罪業,不知流轉到哪道了。」
您想過您要活多久嗎?台灣人均壽命約80歲,但臨終前平均臥床時間約8年,還沒往生就已經在人間地獄受苦了,往生後又會去到哪裡呢?更何況,您有把握一定能健康長壽嗎?人世無常,生死是由閻羅王所決定的,人生酬業,無常不期而到,沒有一帆風順的。業障討報、外靈沖犯、外道干擾、陽世業主菩薩討報,隨便一項就讓生活雞飛狗跳。人生是苦海,流連在人世間,未來就是輪轉於六道輪迴,生生世世換個皮囊續受苦。
《阿伯的話—現場開示精華節錄》:「『自業自消、自性自渡』,如果業障太多讓你覺得煩,要問自己,為什麼當初要造下這些罪過?為什麼現在不多花時間趕快唸經、趕快圓滿?而且『人世無常』、『天有不測風雲,人有旦夕禍福』,歡喜做,甘願受,若是精進消業障,且真心改過,人逢無常來臨之時,才能有機會大事化小,小事化無。」
我們有緣遇到牟尼精舍,有福報跟著精舍修行,是否有把握機緣拚一把,好好努力耕耘,提升法身慧命呢?佛菩薩給大家制定的修行功課有誦經、持咒、靜坐、寫心得,您是否有認真執行呢?有機緣來到牟尼精舍的人,想��生命也經歷了不少磨難,才會有醫生看到沒醫生,有神問到無神,終於來到牟尼精舍找到人生的燈塔,汪洋中的一條船,終於找到避難的港灣。但是精舍只是幫大家加油、指引方向的中繼站,每個人的生命航道各有不同的因緣,佛經是地圖,指引如何到達淨土的途徑,而要如何達到終點,靠的是各位水手們的各自努力。
當您誦經懈怠、修行心得遲交、把佛號拋腦後,消業懺悔一拖再拖,對業主菩薩愛理不理,對修行心得輕忽怠慢,佛菩薩也只能搖搖頭,您把自己放生大海,隨業流轉,苦海無邊自承擔。《阿伯的話—現場開示精華節錄》:「趁年輕就要精進修行銷業,不要等到年老色衰再消業。不管是什麼身分地位,只要業障來,都是阻礙重重,諸事不順,故要好好努力精進消業,方能排除人生旅途的障礙,運途才會開展。天有不測風雲,人有旦夕禍福,人世無常。」
跟上大家腳步是最低要求,精舍制定的修行功課有誦經、持咒、靜坐、寫心得,您是否有認真執行呢?每天的部落格分享,您有跟進閱讀嗎?每周的誦經進度,您有按時填報嗎?每月兩篇的心得分享,您又有按時繳交嗎?生活處處是道場,而社團功課樣樣都是修行的檢視點。檢視您是否在修行的軌道上,踏實地前進,還是已經偏離航道,快要撞上暗礁。
《阿伯的話—現場開示精華節錄》:「人世間本是無常,成住壞空是必然的現象,做一天和尚撞一天鐘,趕快修行,要把握能夠渡眾的機會,其它的別想太多。」、「遇到佛法是很殊勝的,要好好精進,不要荒廢,不要為了別人而放棄珍貴的修行機會,因為下一世會不會再遇到佛法都是未知數。」、「凡事要精進,『是日已過,命亦隨減,如少水魚,斯有何樂;大眾當勤精進,如救頭然,但念無常,慎勿放逸』。勤消魔性與業障,切莫虛耗光陰,得過且過。」
人都有需要休息喘口氣的時候,但是跟上大家腳步是最低要求,懈怠期若是拖太長,老天爺就會用無常來提醒,屆時付出的時間、精神、淚水、汗水,就無可估計了。與其如此,不如把握當下,好好的努力精進,以有涯之生命,滅無涯之痛苦。隨時點亮心中的佛光,為自己的人生加油!南無藥師琉璃光如來!南無本師釋迦牟尼佛!
南無本師釋迦牟尼佛
南無藥師琉璃光如來
南無阿彌陀佛
南無大悲觀世音菩薩
南無大願地藏王菩薩
南無韋馱菩薩
南無伽藍菩薩
南無十方一切諸佛菩薩摩訶薩




0 notes
Text
TEDにて
ブライアン・グリーン:宇宙はひとつしか存在しないのか?
(詳しくご覧になりたい場合は上記リンクからどうぞ)
我々の住むユニバースの他にも宇宙はそこかしこに存在するのでしょうか?
映像を交えたスリルのある話し方で、ブライアン・グリーンが物理学上の未知の問題(何がビッグバンを起こしたかを始めとする数々の問題)を考えることが、多元ユニバースの可能性につながることを示唆します。Fly?
この枠組とは、地球、銀河系、その他の銀河のはるか向こうでは、我々のユニバースはひとつではなく、沢山のユニバースが入り混じった「多元ユニバース」というものの一部であるという可能性です。
CERN(セルン)の巨大ハドロン衝突型加速器で、ヒッグス粒子がほぼ見つかったことで、標準理論よりも大きな枠組みであるSuper Symmetric Theory(スーパーシンメトリック理論:超対称性理論)というもの��あって
Super String Theory(スーパーストリング理論)のSuper(超)とは、このSuper Symmetric Theory(スーパーシンメトリック理論:超対称性理論)のSuper(超)から派生しています。
ここで、言われているダークエネルギー(暗黒エネルギー:dark energy)とは、量子力学黎明期に言われていた黒体(こくたい: black body)あるいは、完全放射体(かんぜんほうしゃたい)と同じような表現です。
アインシュタインの一般相対性理論が、改良されたビックバン宇宙論のキーポイントとなるようです。
この理論は、1929年に始まります。偉大な天文学者エドウィン・ハッブルが、遥か彼方にある銀河が我々からどんどん遠ざかっているのに気付き宇宙がだんだんと大きくなり膨張している事実を確立しました。
そして、ユニバースにダークエネルギーがどのくらいあれば、膨張の加速が起こるか?天文学者が計算したところこの様な答えが出ました。とても小さな数字となっています。
ストリング理論では、粒子の質量、力の強さ、そして、何よりもダークエネルギーの量が、次元の形によって決定されます。もし、これら余剰次元の形が解れば、特徴を計算できつつダークエネルギーの量も計算できます。
問題は、これら余剰次元の形が、世界の誰にもわかっていないと言う事です。わかればノーベル賞をもらう事も可能です。
さて、これまでビックバンの爆発の元となった力については、何も説明がありませんでした。
しかし、このギャップを埋めたのが、改良されたビッグバン理論です。インフレーション宇宙論とも呼ばれ、これによるとユニバース空間の外への膨張に必要な燃料は何かを特定してます。場の量子論に関係しています。
これまでに出てきた結論を統合した結果、現時点では、私達のユニバースは、スーパーストリング理論の計算によると多数の泡の集合した多元ユニバースの一つの泡に過ぎないそうです。
場の量子論(Quantum Field Theory)は、粒子性と波動性を調和させるために100年前位に構築されています。
100年近くかけて膨大に蓄積された世界中の数値化されたデータを源にして、自然現象を裏付けされた法則に収斂させています。これらは、標準理論にも深く関係してきます。
そして、1957年にエヴェレットが提案した「エヴェレットの公理」。また、シュレーディンガー方程式は、この理論でも重要な役割を果たしています。
そして、シュレーディンガー方程式とは、1926年にオーストリアの物理学者エルヴィン・シュレーディンガーが量子力学の理論の整合性をとるために波動力学という体系を提唱した際の基礎方程式として提案された���
当時は、波動性と粒子性の問題が持ち上がっていて、実験事実を丁寧に方程式の形式にまとめあげた物理学の巨人のひとりです。
なので、一般式なシュレーディンガー方程式は、ディラック方程式から場の量子論まで量子力学全般で使う事ができます。基礎方程式といわれるゆえんです。
アインシュタインの光電効果仮説(1905年)。アインシュタイン・ドブロイの関係式や量子からマクロ世界のニュートン力学に拡張する過程で、古典力学での方程式は量子力学から導出されるとも言われる(プランク定数をゼロに近似したとき)
ボーアの量子条件やハイゼンベルクの不確定性原理でも整合性がとれています。
次元に関してはこの場合、数学的な次元を前提としています。
次元のコンパクト化の説明の前に、数学的な次元の重要性について、さて、一般相対性理論をカルツァは、電磁気力に応用していきます。
当時は、それが重力以外に考えられる唯一の力でした。つまり、電気や、磁石の引き付けなどを引き起こす力のことです。 ここで空間と時間が歪むこと以外に、もしも次元が歪むことで電磁気力が働くかもしれないことに気づきます。
1926年にオスカークラインも、知覚で見えない次元がある可能性を示します。5 次元化して電磁気力も幾何学として表せるようにしたカルツァ・クライン理論というものです。
カルツァが3次元ではなく、4次元の宇宙における歪みと曲がりを説明する方程式を書き出した時、彼はアインシュタインがすでに3次元で導き出していた方程式を見出しました。それらは、重力を説明するための方程式です。
でも、カルツァは次元がひとつ増えたことによるもうひとつの方程式も見つけました。その方程式を見てみるとそれは正に科学者たちが長年の間。電磁力を表すために使ってきた方程式でした。驚くべきことです。それが、こつぜんと計算結果に現れてきたのです。
こうして、数学的な次元は、空間の量子化を数値的に表現できるようになっていくキッカケになりました。
その後のカルツァ・クライン理論は、無限に存在する次元の形状の一部をカラビ・ヤウ多様体として表現できました。
例えば、手を振って大きな弧を描く時、手のひらは3つの広がった次元の中ではなく、巻き上げられた次元の中を突っ切っています。
もちろん、巻き上げられた次元はとても小さいので、体を動かす間に、こうした次元を1サイクルして出発点に戻ることが繰り返され、その回数は、膨���な数にのぼります。このように次元の広がりが小さいと言う事は、手のような大きな物体が動く余地があまりないと言うことです。
それは結局、平均化されてしまい腕を振った時でも、私たちは巻き上げられたこのような次元を横断し膨大に旅したことに全く気づいていません。
これは、結び目の不変量にも関連しています。
まず初めに、円周を3次元ユークリッド空間に埋め込んだものを「結び目」と定義していることから始まります。
結び目理論においては、変形して移り合う「結び目」は、同じ「結び目」とみなして「結び目」を研究する。
「結び目」を研究するひもの結び方はいろいろあるので、様々なタイプの「結び目」がある。では、「結び目」のタイプはどのようにして区別すれば良いのであろうか?
「結び目」に対して定められる値で、「結び目」を変形することに関して不変であるようなものを「不変量」と言う。結び目理論は、トポロジー(位相幾何学)の一分野である。
1980年代に、数理物理的手法が、低次元トポロジーに導入されて、3次元トポロジーにおいては「結び目」と3次元多様体の膨大な数の不変量(量子不変量)が発見された。
これによって、4次元トポロジーには、ゲージ理論がもたらされることになりました。これらからゲージ場の数学的根拠として、活用されることになっていきます。
次元のコンパクト化については・・・
トポロジーの結び目理論に登場するチャーン・サイモンズ理論から数値化して表現していきます。
例えば、これはボール。球で表面に格子が組まれています。正方形の形をしていますね。ここで説明することは、レオンハルト・オイラーによって見出されたことです。1700年代の偉大な数学者です。その発見は数学のとても重要な分野である代数的位相幾何学へと発展しました。
私たちの論文もここにルーツがあります。では説明しましょう。ここには8つの頂点、12の辺と6つの面があります。頂点の数から辺の数を引き、面の数を足すと2となります。2です。まあ、そんなもんでしょう。別のケースを見てみましょう。三角形で覆ってみます。
今度は、12の頂点。30の辺、20の面があり、20枚のタイルで覆われていますが、頂点-(辺+面)は、またもや2になります。実際のところ、覆うものが、たとえ、三角形や他の多角形。それが混合していようとも結果は同じで、頂点-(辺+面)は、2になるのです。
今度は、別の形です。トーラスでドーナツ状の形をしています。これを長方形で覆います。頂点は16、辺は32、面の数は16です。頂点-(辺+面)は0になります。いつだって0です。トーラスは、正方形、三角形や他のどんなもので覆っても0になるのです。
このような数をトポロジーのオイラーの標数といいます。位相不変量と呼ばれるものの一種です。とても興味深いことです。どの様にやっても、いつも同じ結果が得られます。この分野は、1700年代中頃に芽生え、今では、代数的位相幾何学と呼ばれるものになりました。
チャーン・サイモンズ理論は、ここにヒントを得て、より高い次元の理論へと高次元の物体へと拡げ、新たな不変量を見い出します。
素粒子のゲージ理論にもチャーン・サイモンズ理論は、応用されてます!定数。
量子力学では、古典力学のxyz位置じゃなく、波動方程式なのでsinやcos位相を主に時空間を数値化します。
ゲージ対称性、アイソスピン、クォーク理論、ヒッグス粒子など。
さらに、数理物理に由来する量子群や共形場理論、チャーンサイモンズ理論もあります。
そして、スーパーストリング理論や量子化学の「変分法」にも応用されている。
量子不変量は、数理物理に由来する量子群や共形場理論やチャーンサイモンズ理論を背景として、様々な代数構造を用いて構成される量子不変量やこれに関連するトピックを研究する研究領域を量子トポロジーと呼ばれています。
古典的な結び目理論においては、個々の結び目の特性を個別に研究する研究が中心であったが、量子トポロジーでは多くの「結び目の集合」を研究対象としています。
1980年代に結び目の不変量が大量に発見される発端になったのは、1914年にジョーンズ多項式と言う結び目不変量が発見されたことにあります。
その後、統計物理で知られていたヤンバクスター方程式の多数の解、つまり「R行列」を用いて大量の結び目不変量が発見されました。
さらに、1980年代後半に量子群が、発見されたことにより、それらの大量の不変量は、量子不変量として整理されて理解されるようになりました。
1990年代には、これらの大量の量子不変量を統一的に扱って、研究する2つの手法が開発されました。
これは、次元のコンパクト化への始まりになります。
1つは、コンセビッチ不変量と言う1つの巨大な不変量に、すべての量子不変量を統一する方法。
もう一つは、バシリエフ不変量と言う「共通の性質」で不変量を特徴づける方法があります。
詳しくは、ご覧ください!必見です。
<おすすめサイト>
ブラックホールと観測者問題2023
宇宙際(うちゅうさい)タイヒミューラー理論は、Dブレンの数値的裏付けを与える数学2021
カラビ - ヤウ多様体で量子の狂乱を解消するアイデア2022
フェルミバブルと素粒子の偶然の一致について2022
ヒッグス粒子は数種類存在?2019
マーカス・デュ・ソートイ: 対称性の秘密
コルム・ケレハー:数学的な対称性の科学
ジム・サイモンズ:ウォールストリートを制した天才数学者
ジム・ホルト:宇宙はどうして存在するのか?
エネルギーと量子化について
ルネデカルトの「方法序説」についてOf Rene Descartes on “Discourse on Method”
超対称性理論について
対称性と陰陽五行理論について
ロン・エグラッシュ: アフリカのデザインに潜むフラクタル
ブライアン・グリーン:スーパーストリング理論を語る
ショーン・キャロル:遥かなる時間と多元宇宙の未知なる可能性
コニフォールド転移とオートファジーとの偶然の一致について2016
ダークマターとダークエネルギーは、ブラックホールのことかもしれないというアイデア2022
フェルミバブルと素粒子の偶然の一致について2022
重力波のデータ観測に成功。世界初
重力子は原子核内部から生成されている?2018
<提供>
東京都北区神谷の高橋クリーニングプレゼント
独自サービス展開中!服の高橋クリーニング店は職人による手仕上げ。あなたが服を持ち込む手間も無用。家まで届け���くれる。お手頃50ですよ。往復送料、詳細は、今すぐ電話。東京都内限定。北部、東部、渋谷区周囲。地元周辺区もOKです
東京都北区神谷高橋クリーニング店Facebook版
#ブライアン#グリーン#super#fly#wave#CERN#標準#理論#ヒッグス#粒子#ダーク#エネルギー#黒体#量子#jwave#string#theory#ヒーリング#日本#食#シュレーディンガー#トポロジー#NHK#zero#ニュース#発見#discover#discovery
1 note
·
View note
Text
國外採購醫材攜帶回國,入境前確認數量限制免受罰!
隨著疫情解封,國外旅遊再度興起,許多旅行者在海外旅程中也會選購一些醫療器材並攜帶回國,尤其是日本國、大韓民國的藥妝店更是許多人出國時必逛的伴手禮首選。
隨著疫情解封,國外旅遊再度興起,許多旅行者在海外旅程中也會選購一些醫療器材並攜帶回國,尤其是日本國、大韓民國的藥妝店更是許多人出國時必逛的伴手禮首選。 然而,迷走想提醒大家,在回國攜帶醫材時必須注意相關的限量規定,以免遭遇不必要的困擾。讓我們一起來了解這些規定,確保您能夠順利入境。 根據中華民國衛生福利部食品藥物管理署(簡稱食藥署)的相關規定,針對一些常見的醫材,建議旅行者在購買時限量選購才能安心帶回國。 根據我國特定醫療器材專案核准製造及輸入辦法第6條第4項第1款的規定,以下是一些臺灣、金門、馬祖地區入境海關規定的常見醫材及其數量限制規定: OK蹦:上限為60個或片。 液體oK蹦:上限為4條、罐、瓶、支。 (醫用)棉棒:上限為200支。 衛生套(保險套):上限為60個。 衛生棉條:上限為120個。 日拋隱形眼鏡:上限為60個(每人以單一品牌及2種不同度數為限)。 矯…

View On WordPress
0 notes
Text
查看「男女體脂率標準是多少?如何減少體脂率?」一文。
0 notes
Text


𓇚 𝝩𝘆𝗽𝗲𝗽𝗼𝘀𝘁𝗲𝗿 : 心存善念 盡力而為 Typeface Used - Rany / Custom Type - Bear kindness in your mind and do your best. - - -
#posterdeaign#typedesign#lettering#graphicdesign#chinesetype#graphicradar#typography#poster#typeposter#logo#logodesign#logotype#customtype#goodtype#graphik#海報#字體海報#文字設計#做字#作字#標準字#海報設計#字体#漢字#디자인#타이포#인생도#타이포그래피#포스터#로고디자인제작
10 notes
·
View notes
Text
日本一のモグラ駅

また行きたいなぁと思い、前行った時の写真を振り返ってみる。

もう階段を登るのは嫌だ!と思っても、しばらくしてまた行ってみたくなる不思議な駅。
FE 50mm F1.8、いわゆる撒き餌レンズ的なので撮ってたけど、値段の割によく写るレンズだなぁ。
もう手元にないけど…。


日本一標高の高いところにある鉄道駅の野辺山駅、そしてこの土合駅と過去に行ってきた。
次はどの日本一の駅に行こうかな。
camera : SONY α7
lens : FE 50mm F1.8
#写真好き#写真が好きな人と繋がりたい#カメラ#カメラ好き#カメラ好きな人と繋がりたい#sony#α7#fe50mmf1.8#単焦点レンズ#標準レンズ#撒き餌レンズ#土合駅#上越線#また行きたい場所#群馬県#思い出写真
345 notes
·
View notes
Text



#就喜歡看海克特坐在各種椅子上面…等等,好像混進去奇怪的東西了#馬桶也是一種椅子嗎#實際上我覺得暗咒有些建築物的比例好像大得離譜 但是仔細一想如果是以德爺兩米以上的標準來看的話好像也不奇怪了#雖然動森里馬桶確實算是一種椅子
3 notes
·
View notes
Text
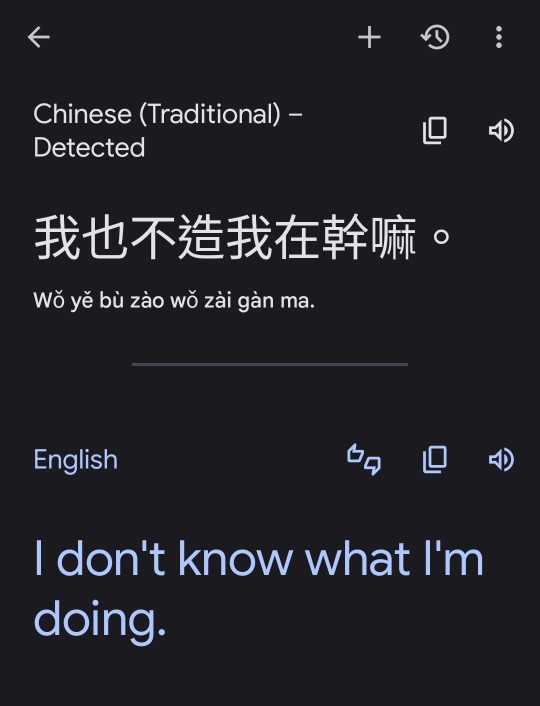
欸幹 老實說這句google翻得出來蠻厲害的欸
#難得用中文po文的一天 你各位準備好見到我超級煩人的一面了←趁機po一堆廢文#欸不過這種網路用語(?簡稱?)居然翻對我蠻驚訝的#看來你們可能還有機會看得懂我在供三小呢 嘿嘿#但我平常打字都不會用標點符號裡面還參雜一堆奇怪的東西 孤狗加油ㄚ#不是很正統的中文裡面還有注音跟台語ㄏㄏ 很符合這天的精神吧#the ho rambles
8 notes
·
View notes
Text

花東縱谷觀光圈 Logo&標準字設計(2022)
7 notes
·
View notes
Photo
I think i needed to hear some version of this when i was a kid. Now that I'm an adult, I'm aware of all the baggage and riches I've picked up along the way, and I've accepted myself and my quirks a lot more.
I was born Japanese in Tokyo but grew up in England and now I live in the USA. People here cannot place me and I'm basically *origin unknown* to some. tbh I often find a little bit of joy when i see brains short circuit from trying to decide if I'm from Hong Kong or Australia (i see the logic, but neither!). I've picked up dialects and random phrases from all the people around me.
So why did it uncomfortably jolt me when i said something weirdly the other day and my little bro quipped "どこぞの人?!" ("Wtf are you meant to be from?!)?
It took me a little moment before i could answer that, as i usually do in English, that yeah the way i speak is a cryptic mess of unknown origin. Because i was born in Tokyo and taught to speak as an upper middle class princess but my family now live in Kansai and my little bro who I'm closest to speaks in a kansai dialect. I don't communicate very often in Japanese anymore but i do still spend time with my grandma who grew up during the war in Niigata who reverts back to that dialect every so often, and also Hiroshima is my current obsession and current favourite part of Japan.
I've stopped trying to stick to RP in English because why deny myself the rich variety of language that I'm naturally picking up just for the sake of nationalism/racism/classism/other bullshit. But i guess i hadn't deprogrammed that part of my brain in Japanese yet.

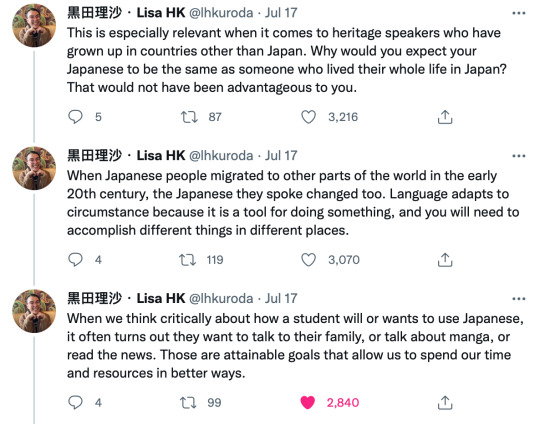
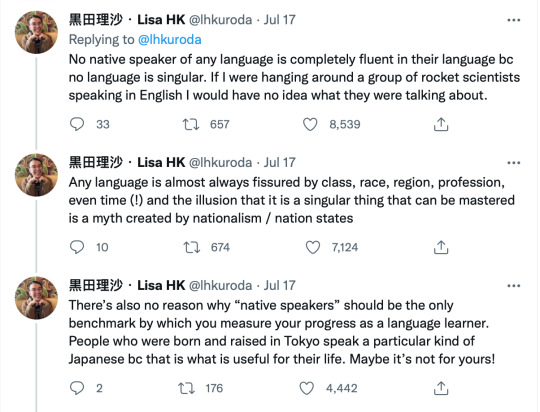
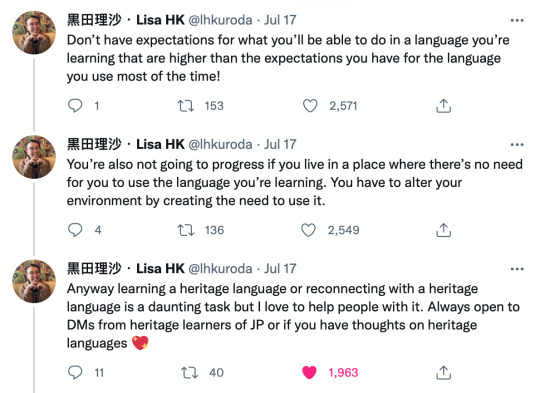
This Twitter thread really spoke to me. I wanted to share it with anyone who hasn’t seen it.
#i was taught to call my mother okaasama when i was a kid so you can see why i needed deprogramming#heritage language#langblr#deprogramming#classism in language#racism in language#標準語#received pronunciation#rp
38K notes
·
View notes
Text
TEDにて
ジャン・ジュディチェ:ヒッグス粒子が語りかけるユニバースの運命
(詳しくご覧になりたい場合は上記リンクからどうぞ)
ヒッグス粒子発見の一番の驚きは、何でしょう?それは、別に、特別に驚く事でもなかった!と言う事です。
ジャン・ジュディチェ氏が、理論物理学での問題を通し、私達に話しかけます。
もし、ヒッグス場が超高密度の状態でも存在するなら、その場は、全ての原子で成る物質は崩壊する事になるかもしれません。
その機知とその魅力で、ジュディチェ氏は、ちょっとビックリするくらいの宇宙の運命の予測と、また同時にそれは、私達が特別に心配する事でもない理由を語ります。(TEDxCERNにて収録)
2012年の7月4日は「大型���ドロン衝突加速器(LHC)」の実験でヒッグス粒子が発見された歴史的な日でした。
今後は間違いなく7月4日は、米国独立記念日としてでなくヒッグス粒子発見の日として少なくともCERN(欧州原子核研究機構)ではそう記憶されるでしょう。
しかし、その日に私が最も驚いたのは意外な結果が、発表されなかったことです。
理論物理学者にとってヒッグス粒子の発見で他の素粒子がどうやって質量を得たのかがうまく説明できますが、それだけでは十分ではなく完全な答えだとは思えないのです。
あまりに多くの疑問点が残されています。ヒッグス粒子は、他の素粒子のように美しさ、対称性、優雅さを持ち合わせていません。
この理由で理論物理学者の大半は、今回発見されたヒッグス粒子以外にもっと何かがあるはずだと確信しています。
ヒッグス粒子に伴う新しい素粒子や現象を期待していたのです。しかし現在のところLHCでの測定値からは新しい素粒子や予期しない現象の兆候は検知されていません。
勿論、これではっきり決まった訳ではありません。2015年にLHCは、陽子を現在の2倍近いエネルギーで衝突させこのさらに高エネルギーの衝突で粒子の世界をもっと探索出来、もっと色々な事が解るでしょう。
ここでヒッグス粒子は五種類あるかもしれない可能性も2015年以降に噂されています。
今の所、新しい現象の証拠は見つかっていないので今見つかっているヒッグス粒子を含む素粒子だけが、自然界に存在する全ての素粒子だと仮定しましょう。
さらに高エネルギーで探索してもこれだけだと仮定するわけです。その仮定ではどうなるか考えて見ましょう。ユニバースに関して驚くべき面白い結果が分かるでしょう。
これを説明するためにまずヒッグス粒子が、どんなものかお話しします。
それにはビッグバンの百億分の1秒後に戻らなければなりません。ヒッグス理論によるとその瞬間、ユニバースでは劇的な事が起きました。
時空が相転移したのです。
それは摂氏零下になった時に水が氷に変わることに非常によく似ていますが、時空に関する相転移は、物質内の分子の並び方が、変化するのとは異なり時空を織り成すものそのものの変化なのです。
この相転移の間、何もなかった空間はヒッグス場と呼ばれるもので埋め尽くされました。これは見えないかもしれませんが、明らかに存在し、常に私たちの周りにあります。
この部屋の空気の様なものです。素粒子の中には、ヒッグス場と相互作用を起こしエネルギーを得るものもあります。この内在するエネルギーこそが、粒子の「質量(一般相対性理論より)」なのです。
ヒッグス粒子の発見によりLHCはこの場の存在が、正しいと結論を出したのです。
ヒッグス粒子を生み出すものだからです。これがヒッグスに関する簡単な説明です。
しかし、この話はそれよりもっと面白いのです。ヒッグス理論を研究する理論物理学者は、実験からでなく数学の力でヒッグス場は必ずしも今日、見る様な姿で存在するとは限らないと���見したのです。
物質が液体や固体の状態で存在する様に時空を埋め尽くすヒッグス場も2種類の状態で存在するかもしれません。
既知のヒッグスの状態以外のもう1つの状態のヒッグス場は、現在見られるより何十億倍のそのまた何十億倍もの高密度でこの様なヒッグス場存在そのものが問題であるかもしれません。
なぜなら量子力学の法則によると2つの状態を隔てるエネルギー障壁があってもその2つの状態の間に転移があり得、その現象をとても適切な呼び名ですが、量子トンネル現象と呼びます。
量子トンネル効果で私もこの部屋から壁を通り抜け隣の部屋に現れる事があり得はしますが、今、実際、私がそれをやるのを期待しないで下さい。
なぜなら量子レベルなので私が壁を通り抜けるその可能性の確率は、驚く程、微々たるもので起きるのを待っていたら気の遠くなる程、待たなくてはなりません。
つまり、量子レベル以外では不可能です。
とは言っても量子トンネル効果は、現実の現象です。あらゆるシステムで見られます。例えば、トンネルダイオードなどの電子機器に使われる部品がそうです。量子トンネル効果の、驚異の力のお陰です。
ヒッグス場にもどります。超高密度のヒッグス場が、存在するなら量子トンネル効果である時、宇宙のある場所でこの凝縮状態の泡が、突然現れる事があるかもしれません。
それは水が、沸騰するのに似ていて水蒸気の泡が水の中に出来、膨張し液体が気体になるように量子トンネル効果により超高密度のヒッグス状態での計測器には検出されるけど人間の眼には見えない泡が現れるかもしれません。
この泡は光速で膨張し、空間を満たしヒッグス場をそれまでの状態から新しい状態へと変えます。
これは問題でしょうか?
そうです。大きな問題です。普段、生活では、計測器には検出されるけど人間の眼には見えないから気がつかないでしょうが、ヒッグス場の強度は、物質構成に決定的に作用します。
もしヒッグス場が、ほんの数倍強かったなら原子は収縮し、原子核内で中性子は崩壊し、原子核はバラバラになり水素だけがユニバースの元素となるでしょう。
超高密度のヒッグス状態でのヒッグス場は、今より数倍の強度だけでなく、何十億倍も強いものです。もし時空がこのヒッグス状態で埋まっているなら原子物質は全て崩壊するでしょう。
どんな分子構造ももちろん生命などあり得ないでしょう。それで未来には、ヒッグス場が相転移を起こし、量子トンネル効果の結果、このように大変な超高密度の状態に変わる事があり得るか?
言い換えると、我われの住むユニバースのヒッグス場の運命を疑問に思うわけです。この質問の答の決定的要因は、ヒッグス粒子の質量です。LHCでの実験でヒッグス粒子の質量は、約126GeVだと分りました。
日常使われている単位からすると10⁻²²グラム位にしか、匹敵しない小さなものですが、1本のDNAを構成する総分子の重さと等しいので素粒子物理学の単位では大きなものです。
LHCからの情報を使いCERNの仲間と共に私たちのユニバースが、超高密度のヒッグス場に量子トンネル現象を起こす確率を計算したら面白い結果がでました。
計算されたヒッグス粒子の質量はとても特別なものだと分ったのです。ユニバースを不安定な状態にしておくのにその質量は丁度の値なのです。
ヒッグス場は今まで何とか存在して来た様な不安定な状態にありますが、いつかは崩壊するでしょう。計算によると最後にはヒッグス場は、相転移を起こし、物質は自己崩壊するでしょう。
これが人類滅亡のシナリオでしょうか?
そうではないと思います。計算では、ヒッグス場の量子トンネル現象は、10¹⁰⁰年内には起らない見込みです。随分先の話です。それはイタリアが、安定した政府を築くよりずっと先の話です。
そうだとしても、それまでには人類は絶えているでしょう。今から約50億年後には、私たちの太陽は赤色巨星になり、地球軌道に迫るほど膨張します。そうなれば地球はおしまいです。
1兆年後には、暗黒エネルギーが今の割合でユニバースの拡張を加速していれば、周りのすべてが光速より速く拡張しているでしょうから私たちは自分の足元さえ見ることはできないでしょう。
なので人類は、ヒッグス場の崩壊を見る事はあり得ないでしょう。ヒッグス場の転移に私が関心を持つ理由は、ヒッグス粒子の質量が、なぜそのような特別な値をしているかと問いかけたいからです。
なぜその質量の値が宇宙を相転移の瀬戸際の状態にして置くのに丁度なのでしょう。
理論物理学者は常に「なぜ」という質問を持ちます。現象がなぜ起きるかというよりも理論物理学者が関心を持つのは、現象がなぜその様に起きるかということです。
この「なぜ」という質問は、自然の根本的原理に関しての自然の根本的原理に関してのヒントをもたらしてくれると理論物理学者は思うからです。
実際、私の質問への答えは、文字通り新しい複数のユニバースへと導いてくれるでしょう。
私たちのユニバースは、泡だった石鹸のような多元宇宙(マルチバース)の中のたった1つのユニバースにしかすぎず、そ��1つ1つの泡は独自の基本的な物理定数や物理の法則があると憶測されています。
こう考えると、ヒッグス粒子の質量といってもある特定の値を発見する確率を語ることしか今出来ません。その神秘の鍵は、多元宇宙(マルチバース)の統計的特性にあるかもしれません。
それはビーチの砂浜で起きてる事に似ています。原理的にはビーチにあらゆる傾斜角を有する砂丘が存在するはずですが、しかし、典型的な傾斜角は30度から35度です。
その簡単な理由は、風が砂を積み上げその後、重力で又滑り落ちるからです。その結果、砂丘の山の大半は崩壊寸前の臨界値に近い角度の傾斜にあるのです。
多元宇宙(マルチバース)のヒッグス粒子にも同じ様なことが、起きているかもしれません。多元宇宙の殆どでは、ヒッグス粒子の質量は臨界値に近く、ヒッグス場の宇宙崩壊寸前の値なのかもしれません。
2つの競合する影響の結果、砂丘と似た現象が起こっているのかもしれません。この話の終わりは、まだ分らないのでこれで終わりではありません。進行中の科学です。この謎を解くにはまだもっとデーターが必要です。
LHCが、すぐに新しい手がかりをもたらしてくれることを期待します。ヒックス粒子の質量ただこの数字だけですが、これから分る事が多いのです。今まで探索された範囲を超えてでもユニバースにある素粒子は、既知のものだけという仮定から始めました。
これから分ったことは、時空を埋め尽くすヒッグス場は、ユニバース崩壊寸前の非常に不安定な状態にあるかもしれないことであり、また私たちのユニバースは多元宇宙(マルチバース)という巨大なビーチの砂の1粒でしかないのではという手掛かりを得ました。
この仮説が、正しいかどうか分りません。これが物理の世界です。
たった1つの測定値が、新しいユニバースの理解への道を開いてくれるか我々を行き詰まらせてしまうかです。
どちらにせよ。はっきり言える事は1つ。これからの探求の旅は驚きで満たされているでしょう。
ありがとうございました。
また、ヒッグス粒子は、自発的対称性の破れにも関係してきます。すべて、これは量子レベルの大きさの現象です。
1960年に南部陽一郎は、対称性が自発的に破れるとアイデアを立て、南部=ゴールドストーン・ボソン(現在、この粒子は存在していないと考えられている)と呼ばれる質量0の新しい粒子を創造させれば良いと発想する。
光子は、南部=ゴールドストーン粒子(ボソン)と絡み合って、質量を獲得することも予想した。
しかし、1964年、この「自発的対称性の破れ」のアイデアを拡張したのが、ヒッグスら6人の物理学者。
理論に粒子ではなく、ヒッグス場という新しい場を創造すれば、質量0の南部=ゴールドストーン粒子(ボソン)ではなく、対称性を自発的に破ることができる。
ヒッグス粒子は、場の量子論の副産物として、発現すると考えました。
そして、1967年、ワインバーグとサラムは独立に、電弱統一理論を発見。弱い力と電磁気力は、ゲージ粒子4種類から本質的には同じ力になることが計算上わかりました。
また、ヒッグス粒子もゲージ粒子だ!という結果がCERN(セルン)の観測データの結果から2015年に確実になっています。
続いて・・・
詳細の確定が、2018年まで経過した理由として、2012年からのデータ観測が継続して行われ、CERNの解析結果は、2012年に一度だけではなく、そのデータ蓄積で、統計の精度を上げて普遍的な確実性を積み重ねたためと思われます。
データ観測の結果として、標準理論に従ってヒッグス粒子(スピン0のボース粒子)は、フェルミ粒子のボトムクォーク対へと崩壊(雲の性質が相転移)することが判明しました。
崩壊(雲の性質が相転移)後、は、「フォトン」「γγ(ガンマ線)」や「Wボゾン対」「Zボゾン対」「グルーオン対」(ここまで、ボース粒子)
(ここからフェルミ粒子)「タウ粒子対」「チャームクォーク対」などになることもデータ観測からわかった。
他には、トップクォーク対とも相互作用してることも判明し、質量起源もヒッグス機構からとデータ観測上で証明されました。
また、ヒッグス粒子(スピン0のボース粒子)は、自発的対称性の破れにも関係してきます。すべて、これは量子レベルの大きさの現象です。
(個人的アイデア)
Well, it is said that Higgs particles are filled after the big bang, but calculate easily using the explosion energy of the supernova thought to be lower than that
よく、ビックバンの後に、ヒッグス粒子が充満したと言われるが、それよりも低いと考えられる超新星の爆発エネルギーを源にして簡単に計算をする
Generation of Higgs particles can be predicted from the results of CERN (Cern) that, when comparing the supernova explosion, symmetry can be voluntarily broken at considerably low energy and can be generated.
ヒッグス粒子の生成は超新星爆発を比べると、かなり低いエネルギーで自発的に対称性が破れて、生成できることがCERN(セルン)の結果から予想できます。
When observing with the size of the level of the universe, Higgs particles may be produced in large quantities easily, except for it.
宇宙のレベルの大きさで観察すると、以外と、簡単に大量にヒッグス粒子は生成されているのかもしれません。
Or it may be related to particles that have not been observed.
もしくは、観測はされていない粒子も関係してるかもしれませんね。
<おすすめサイト>
フェルミバブルと素粒子の偶然の一致について2022
ジム・ホルト:宇宙はどうして存在するのか?
宇宙際(うちゅうさい)タイヒミューラー理論は、Dブレンの数値的裏付けを与える数学2021
カラビ - ヤウ多様体で量子の狂乱を解消するアイデア2022
ダークマターとダークエネルギーは、アクシオンやブラックホールのことかもしれないというアイデア2022
ヒッグス粒子は数種類存在?2019
スチュワート・ファイアスタイン:無知の追及について
リチャード・ドーキンス:「奇妙な」ユニバースを語る!
ボース粒子について
フェルミ粒子について
パウリの排他律について
標準理論のすばらしさ
ガリレオのAngels & Demons(天使と悪魔)とCERN(セルン)
<提供>
東京都北区神谷の高橋クリーニングプレゼント
独自サービス展開中!服の高橋クリーニング店は職人による手仕上げ。お手頃50ですよ。往復送料、曲Song購入可。詳細は、今すぐ電話。東京都内限定。北部、東部、渋谷区周囲。地元周辺区もOKです
東京都北区神谷のハイブリッドな直送ウェブサービス(Hybrid Synergy Service)高橋クリーニングFacebook版
#ジャン#ジュディチェ#ヒッグス#粒子#量子#原子力#宇宙#物理学#CERN#素粒子#電気#標準#超電導#南部#ノーベル#エネルギー#重力#クォーク#アクシオン#NHK#zero#ニュース#発見#discover#discovery
0 notes
Text
標準的進化。

雌性的篩選機制,雖然源自於生理對心理的觸發,看似會剝奪走精神自由的可能,但現實的自由卻可以因此實現,因為經此看見更強大的存在,擁有感知「人外有人,天外有天。」的自由。 也就是人類的雌性本身,即擁有進化指標的能力,因此指標指向之處,必有著併手抵足的兢兢業業,一則是為社會帶來動能,二則是在對男性本身作為進化的催促劑,這就是「成功男人背後,一定有個偉大的女人。」的成因。
那麼我們就必須作為兩性關係的奴隸來生活嗎?
當以個人來作為標準時,標準的存在,就會導致那一個個體成為下限的存在,即便原本是上限,也終將成為下限。 只因成長的勢能是多面向的存在,當個體在現實中以標準的存在時,必會受到人類文明發展的其他面向,針對標準存在,所給予的反饋,而缺少總體勢能的加持,即便是完美的個體也終將只能成為現實的底限存在。 綜合雌性的篩選機制,以及以個體為標準終將被勢能追趕而只能以客觀存在,如法律、制度、戒律等等時,以上兩者,便可以清楚地看見,進化對於標準的潛滋暗長。
雖然當男性在面對著選擇繁衍時,就意味著必須承擔起額外的承擔,進而失去精神完全自由的可能,從在過渡期中幾近於喪失自主性,但在雌性總是選擇強大存在的繁衍意志下,卻能在其中承擔起更多,同時也因為始終嚮往著自由的美好,而最終可以讓自己擁有自由的同時,又已經實現雌性所需要的強大。
至此! 我們不妨試著想像一下,如果愛情的力量如此強大,那麼當對象不是兩性時,生命的滋養究竟會讓精神體強大到什麼境界? 雖然這樣一想,就好像在玷污自由,彷彿男性也應該像女性一樣擁有篩選機制,強大才是真理,但廣義與狹義的存在,讓格局與遠見有著無垠的可能。 也就是說,當男性處於在與理想連接而持續完美的自由狀態,面臨到女性為孕育與繁衍所需要的男性理想投射,以及要實際讓理想的凝聚產生轉移的需求時,失去狹義自由的男性,應該可以從以上論述中,看見廣義自由的存在,也就是標準的持續進化。
雖然核心在於自由之心,但缺少女性的存在,自由在現實就只能是狹義的存在,也就是「我的孕育,不是讓你鄙視我為奴隸的談資。」,也只有借鏡尼采對女性深刻瞭解的到位,才更能體悟覺醒到尼采的超人,在現實之中越來越可能實際存在著。
1 note
·
View note
Text


𓇚 𝗟𝗼𝗴𝗼𝘁𝘆𝗽𝗲 : 心存善念 盡力而為 - - -
#typedesign#lettering#motif#graphicdesign#chinesetype#graphicradar#typography#typographic#type#logo#logodesign#logotype#customtype#goodtype#graphik#eyeondesign#type01#文字設計#平面設計#作字#標準字#字體練習#字体#漢字#디자인#타이포#인생도#타이포그래피#로고#로고디자인제작
16 notes
·
View notes
Text
初めての赤バッチ

2月28日の予約開始日に予約して21日に届いた人生初のG Masterレンズ、FE 50mm F1.4 GM。
予約してまで高額のレンズに手を出してしまったのはいつぶりだろう、それほど欲しかったレンズ。
軽めに近場で試し撮りしてみた。






解像感で言えば今までMACRO APO-LANTHAR 65mm F2 Asphericalがピカイチだったけど、それを超えてる。
それでいてF1.4の綺麗なボケ、そして軽量コンパクトなボディ、これがG Masterなのか。
キタムラの店員も言ってたなぁ、G Masterはえげつないって(笑)
確かにえげつないレンズだった!
camera : SONY α7RⅣ
lens : FE 50mm F1.4 GM
#カメラ#カメラ好き#カメラ好きな人と繋がりたい#写真好き#写真好きな人と繋がりたい#sony#α7rⅳ#g master#fe50mmf1.4gm#単焦点レンズ#標準レンズ#単焦点の世界#風景写真#japan#japanese photography#光前寺#信州#長野県#nagano
77 notes
·
View notes