#quantum computing

[quasi-normalcy]

Hey, so--we cooled your boyfriend down to a hundredth of a kelvin above absolute zero. Yeah, it was so cold that all of the chemical reactions in his body ceased. Sorry. We, uh, yeah, we used him as a dielectric material in a tiny qubit. And then we quantum-entangled him with another qubit, just to see if we could. Sorry. Yeah, anyway, we thawed him out after two weeks and apparently he's doing fine now. Didn't really teach us anything about how quantum processes work in biological systems, but it sure was, uh, cool. If you'll pardon the pun.

[glitchphotography]

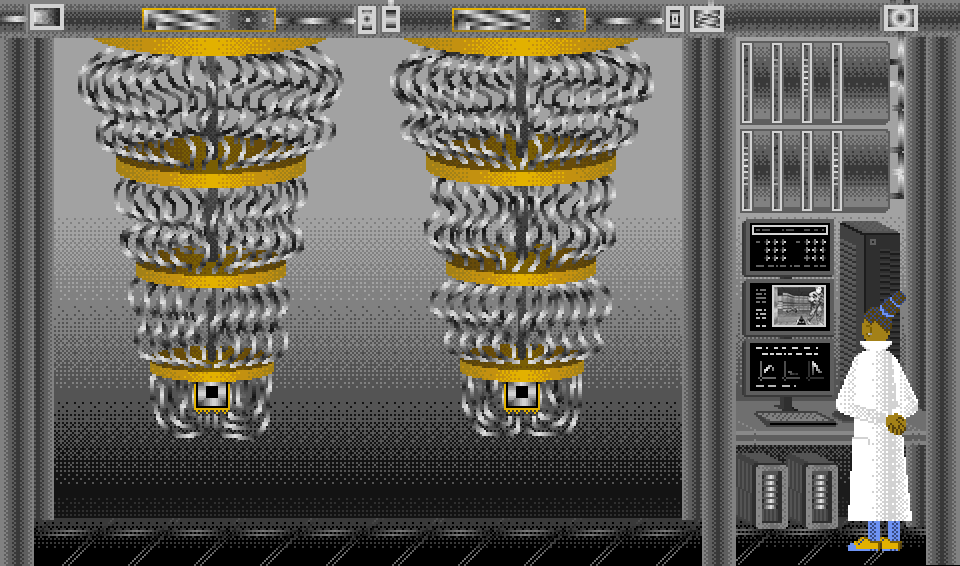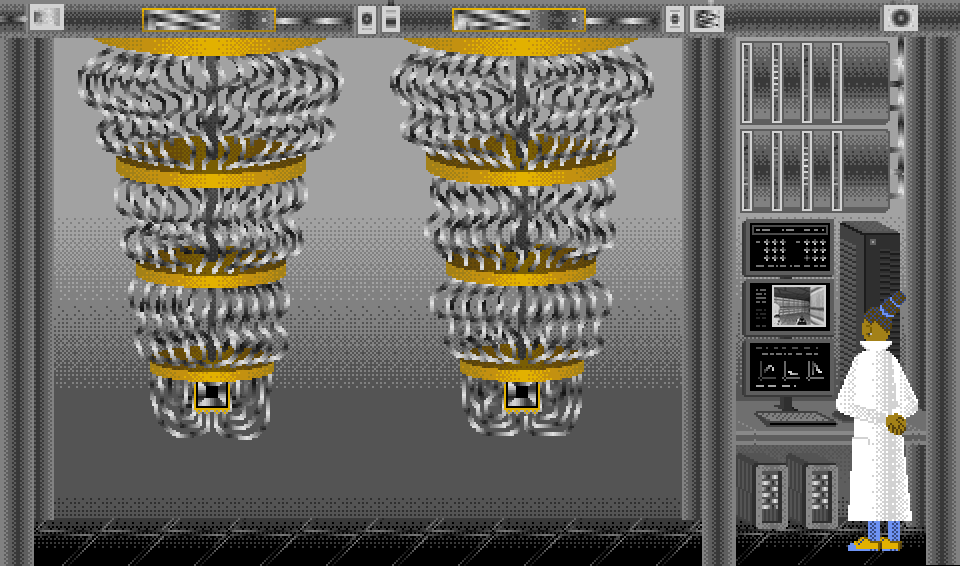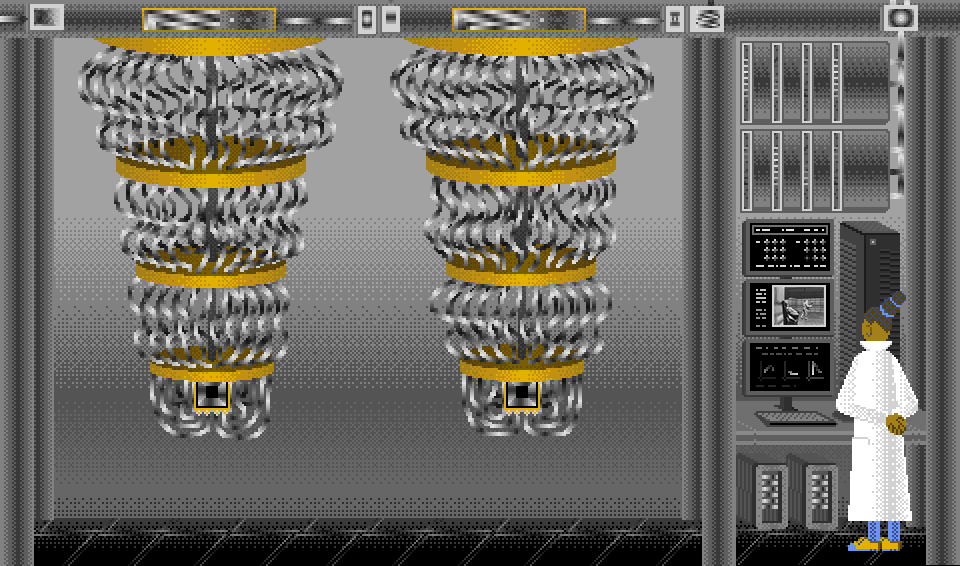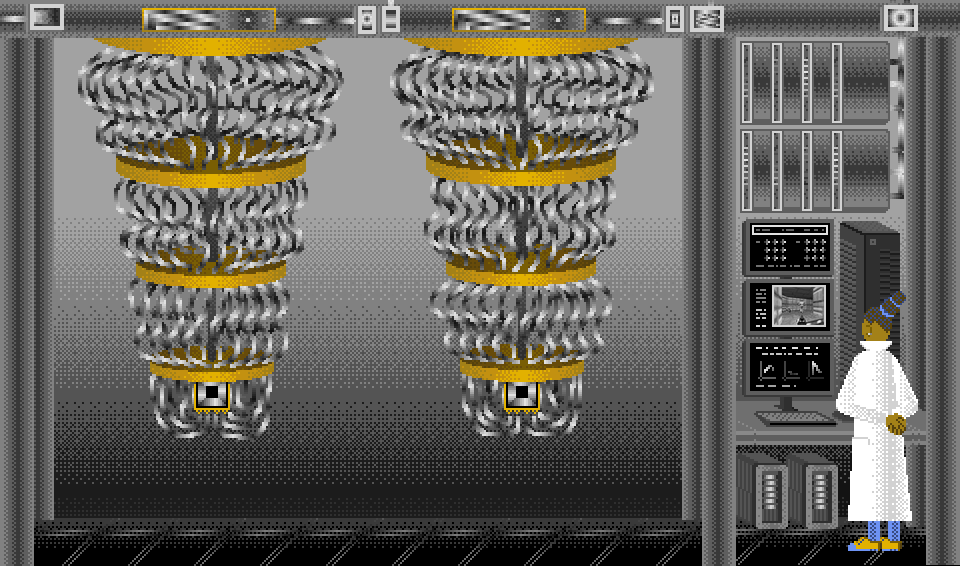
Quantum Computer (Two Sycamores)

[mindblowingscience]

A quantum state of light has been successfully teleported through more than 30 kilometers (around 18 miles) of fiber optic cable amid a torrent of internet traffic – a feat of engineering once considered impossible. The impressive demonstration by researchers in the US may not help you beam to work to beat the morning traffic, or download your favourite cat videos faster. However, the ability to teleport quantum states through existing infrastructure represents a monumental step towards achieving a quantum-connected computing network, enhanced encryption, or powerful new methods of sensing.

Continue Reading.

[asomaton]

I looove that quantum computers look, you know, LIKE THAT ™

Like a clockwork waiting to chime in a new age (or a bell who may toll for all of us).

Next step is pentagrams and runes instead of circuits.

How many angels can dance on top of a qubit chip? Immeasurable

[astra-ravana]

Technomancy: The Fusion Of Magick And Technology

Technomancy is a modern magickal practice that blends traditional occultism with technology, treating digital and electronic tools as conduits for energy, intent, and manifestation. It views computers, networks, and even AI as extensions of magickal workings, enabling practitioners to weave spells, conduct divination, and manipulate digital reality through intention and programming.

Core Principles of Technomancy

• Energy in Technology – Just as crystals and herbs carry energy, so do electronic devices, circuits, and digital spaces.

• Code as Sigils – Programming languages can function as modern sigils, embedding intent into digital systems.

• Information as Magick – Data, algorithms, and network manipulation serve as powerful tools for shaping reality.

• Cyber-Spiritual Connection – The internet can act as an astral realm, a collective unconscious where digital entities, egregores, and thought-forms exist.

Technomantic Tools & Practices

Here are some methods commonly utilized in technomancy. Keep in mind, however, that like the internet itself, technomancy is full of untapped potential and mystery. Take the time to really explore the possibilities.

Digital Sigil Crafting

• Instead of drawing sigils on paper, create them using design software or ASCII art.

• Hide them in code, encrypt them in images, or upload them onto decentralized networks for long-term energy storage.

• Activate them by sharing online, embedding them in file metadata, or charging them with intention.

Algorithmic Spellcasting

• Use hashtags and search engine manipulation to spread energy and intent.

• Program bots or scripts that perform repetitive, symbolic tasks in alignment with your goals.

• Employ AI as a magickal assistant to generate sigils, divine meaning, or create thought-forms.

Digital Divination

• Utilize random number generators, AI chatbots, or procedural algorithms for prophecy and guidance.

• Perform digital bibliomancy by using search engines, shuffle functions, or Wikipedia’s “random article” feature.

• Use tarot or rune apps, but enhance them with personal energy by consecrating your device.

Technomantic Servitors & Egregores

• Create digital spirits, also called cyber servitors, to automate tasks, offer guidance, or serve as protectors.

• House them in AI chatbots, coded programs, or persistent internet entities like Twitter bots.

• Feed them with interactions, data input, or periodic updates to keep them strong.

The Internet as an Astral Plane

• Consider forums, wikis, and hidden parts of the web as realms where thought-forms and entities reside.

• Use VR and AR to create sacred spaces, temples, or digital altars.

• Engage in online rituals with other practitioners, synchronizing intent across the world.

Video-game Mechanics & Design

• Use in-game spells, rituals, and sigils that reflect real-world magickal practices.

• Implement a lunar cycle or planetary influences that affect gameplay (e.g., stronger spells during a Full Moon).

• Include divination tools like tarot cards, runes, or pendulums that give randomized yet meaningful responses.

Narrative & World-Building

• Create lore based on historical and modern magickal traditions, including witches, covens, and spirits.

• Include moral and ethical decisions related to magic use, reinforcing themes of balance and intent.

• Introduce NPCs or AI-guided entities that act as guides, mentors, or deities.

Virtual Rituals & Online Covens

• Design multiplayer or single-player rituals where players can collaborate in spellcasting.

• Implement altars or digital sacred spaces where users can meditate, leave offerings, or interact with spirits.

• Create augmented reality (AR) or virtual reality (VR) experiences that mimic real-world magickal practices.

Advanced Technomancy

The fusion of technology and magick is inevitable because both are fundamentally about shaping reality through will and intent. As humanity advances, our tools evolve alongside our spiritual practices, creating new ways to harness energy, manifest desires, and interact with unseen forces. Technology expands the reach and power of magick, while magick brings intention and meaning to the rapidly evolving digital landscape. As virtual reality, AI, and quantum computing continue to develop, the boundaries between the mystical and the technological will blur even further, proving that magick is not antiquated—it is adaptive, limitless, and inherently woven into human progress.

Cybersecurity & Warding

• Protect your digital presence as you would your home: use firewalls, encryption, and protective sigils in file metadata.

• Employ mirror spells in code to reflect negative energy or hacking attempts.

• Set up automated alerts as magickal wards, detecting and warning against digital threats.

Quantum & Chaos Magic in Technomancy

• Use quantum randomness (like random.org) in divination for pure chance-based outcomes.

• Implement chaos magick principles by using memes, viral content, or trend manipulation to manifest desired changes.

AI & Machine Learning as Oracles

• Use AI chatbots (eg GPT-based tools) as divination tools, asking for symbolic or metaphorical insights.

• Train AI models on occult texts to create personalized grimoires or channeled knowledge.

• Invoke "digital deities" formed from collective online energies, memes, or data streams.

Ethical Considerations in Technomancy

• Be mindful of digital karma—what you send out into the internet has a way of coming back.

• Respect privacy and ethical hacking principles; manipulation should align with your moral code.

• Use technomancy responsibly, balancing technological integration with real-world spiritual grounding.

As technology evolves, so will technomancy. With AI, VR, and blockchain shaping new realities, magick continues to find expression in digital spaces. Whether you are coding spells, summoning cyber servitors, or using algorithms to divine the future, technomancy offers limitless possibilities for modern witches, occultists, and digital mystics alike.

"Magick is technology we have yet to fully understand—why not merge the two?"

[that-red-bastard]

It's so wild to me that biology is not a complete science by now

We're making computers out of the very building blocks of our reality, particles that we can't even see, not because they are conventionally small, but because light simply don't really work at that level. Particles so small and with movement so erratic that their existence is intrinsically probabilistic

And YET no one can tell me why the fuck do I have migraines

[jayyoocomics]

Technology

[stormy-skyzzzzzz]

“If the Universe was designed, it seems, the designer is a programmer.”

Black Holes: The Key To Understanding The Universe, Brian Cox and Jeff Foreshaw

[wikipediapictures]

Quantum computing

[ketrinadrawsalot]

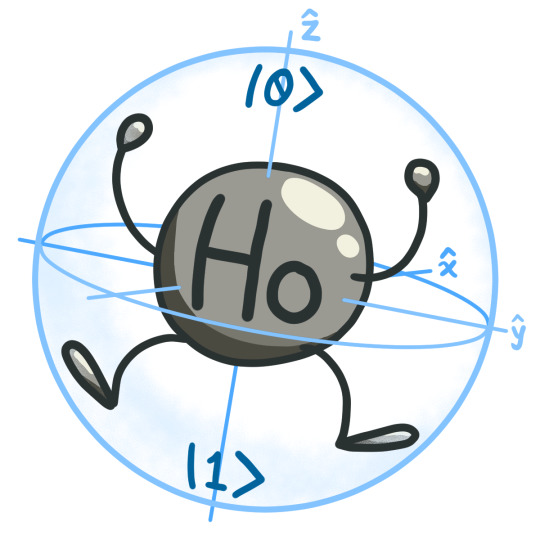
Holmium is named after the city of Stockholm (or Holmia in Latin). Its magnetic properties allow it to create powerful fields when added to magnets. The colorful properties of its compounds are used in glass and cubic zirconia.

[catswilleatyou]

quantum

[mindblowingscience]

The potential of quantum computing is immense, but the distances over which entangled particles can reliably carry information remains a massive hurdle. The tiniest of disturbances can make a scrambled mess of their relationship. To circumvent the problem, quantum computing researchers have found ways to stabilize long lengths of optical fibers or used satellites to preserve signals through the near-vacuum of space.

Continue Reading.

[materialsscienceandengineering]

Scientists merge two 'impossible' materials into new artificial structure

An international team led by Rutgers University-New Brunswick researchers has merged two lab-synthesized materials into a synthetic quantum structure once thought impossible to exist and produced an exotic structure expected to provide insights that could lead to new materials at the core of quantum computing. The work, described in a cover story in the journal Nano Letters, explains how four years of continuous experimentation led to a novel method to design and build a unique, tiny sandwich composed of distinct atomic layers. One slice of the microscopic structure is made of dysprosium titanate, an inorganic compound used in nuclear reactors to trap radioactive materials and contain elusive magnetic monopole particles, while the other is composed of pyrochlore iridate, a new magnetic semimetal mainly used in today's experimental research due to its distinctive electronic, topological and magnetic properties.

Read more.

[hackeocafe]

The truth about New Microsoft Majorana Chip

[scissorhands-trustfall]