#polyhedron net
Explore tagged Tumblr posts
Text
Colorful nets of Truncated Tetrahedron and Tetrahedron
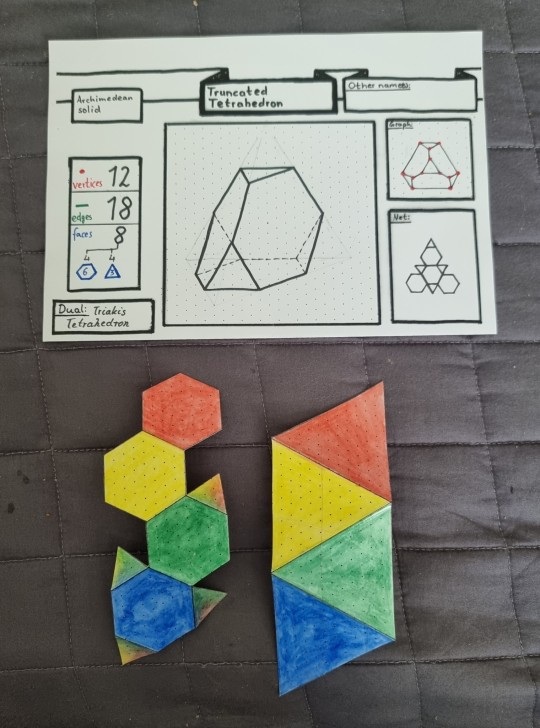




#truncated tetrahedron#tetrahedron#polyhedron#polyhedron net#polyhedra#geometry#visualized math#math#mathematics#knottys math#archimedean solid#shapes and colors#shapes#shape soup
26 notes
·
View notes
Text
Question for you: What kind of polyhedron will it fold into?

#It is rather easy if you remember the visualizations I made recently#i might post the solution (the photograph of the folded model) later#math#mathematics#math stuff#math art#polyhedron#polyhedra#polyhedron net#polyhedra net#math models#math crafts#my crafts#crafts#crafting#my art#art#i only made some minor mistakes in the sketch: i forgot to mark the cuts in the flaps#but this minor mistake only impacts the transfer of the sketch to a foil
49 notes
·
View notes
Text


Square antiprism box
Part I
(many thanks @queercus-books for finding out what that shape is called XD)
Over a year ago I saw this particular kind of box on the bookbinders fair in Leiden (NL). After having been recently reminded of them, I decided to give it a go and try to reverse engineer them from the pictures I found here (check out her other boxes, they are gorgeous!).
After staring at the original boxes for a bit, it was obvious they were not covered on the inside after gathering them. The pattern was visible in one consecutive pattern. It told me that a) the board was laminate with the patterned paper while still flat and b) the box was made from one piece, not single pieces glued together. For that the corners and edges needed to be scratched, but not cut through.

What stumped me in the beginning was what angle to pick for the walls. Naturally the base of each triangle had to be as long as the sides of the squares it connected to, but a too pointy angle at the tip resulted in long boxes that looked rather twisted than having that bulbous look I was looking for.
The solution (after some more staring and a few more paper models) was 'right angles'! Any square piece of board can be made into this box by marking out the center square and have the walls point away in right angles.

Next I cut away the parts that won't be needed (to make sure I don't cut one of the side walls off, I crossed them out). The net of polyhedrons for this box could look different than this and still give me this shape, but with the way the paper pattern is was not visibly interrupted I'm confident this is the net the Dutch bookbinder has used. (It also wastes the least material)

Now it was scratching the other lines just enough so they would bend nicely, but not get too weak to hold the structure and test assemble. Shallow cuts and test bending every now and then helps to get there (also a metal ruler to keep carving the same line)




Cutting the board half way through ended me up with those gaps though. I''m not sure how much they would show if I dressed them just like that, but I decided to not take the risk and reinforced them with a white paper just in case.


The white paper is really just a white strip of paper long enough to go all around the box and a bit wider than one of the triangles is high so I could have an overlap and reinforcement to the bottom too. Part of why I did this was also to see if covering the body would work as I thought it would. With the angled planes the strip of paper bends up and and down, but in the end it's still one straight strip of paper.
I let it dry a bit before adding another layer, this time with the patterned paper and turn in's on top and bottom. In hindsight I could have cut the turn ins to the inside at an wider angle to avoid them reaching onto the better visible part, but then. this is the first time I made this box so I take that as a lesson learned.


Now all it needs is a base and a lid and I'm done.
59 notes
·
View notes
Text
Still on my pathologic kick, anyway, character relationships we don't talk enough about but that make me insane, Artemy addition
Artemy and Capella
First off, just the fact that she can, has, and will psychically, unconsciously SOS him across town. We need to talk about that,
and like the fact it's unconscious, please image post-canon Capella accidentally summoning Artemy bc she and Khan had a fight. Giant, angry doctor on call at any moment against both their wills
Their first conversation where she tells him about curling up in her mother's coffin, "of course we're friends", presenting herself as still weak and coming into her powers vs. their conversation at the Cape, denying an emotional connection, "we're not friends", saying she can do it all on her own - I'm insane. I don't even think it's manipulation, I think she wants an adult who treats her like a child - not a reincarnation of her mother- but gets frightened at the possibility of losing even a drop of her control. The way she specifically denied seeing Artmey as a father.
Capella desperately wanting to be her mother and to have an adult's responsibilities as a Mistress and the children of the town's mother (the way she calls Artemy's list, "our children" - like they are both adults) vs. Artemy seeing how much Capella can resemble her (shitty) dad and being the one person reminding Capella she's not her mother and she is a child, and he'll treat her like one.
The role of the White Mistress based on Victoria's Tomb as "being" the town vs. Artemy specifically talking about the Town calling him - He'll always hear Capella's troubles and pain
And we're back to the psychic SOS thing, but like from a humorous standpoint she really could do the "projecting my period cramps meme"
Artemy and Khan
Okay this is shorter, because they don't interact much but their conversation after the House of Death where Khan gets mad at Artemy for letting him and Notkin go into the dangerous house makes me want to scream
Like not in a bad way - Khan has a point that it was irresponsible to let him and Notkin do that (as does Artemy in that he couldn't really stop them), but just ....
Super independent Peter Pan-meets-child dictator character's first response being "Why didn't you (an adult) stop me (a child)?" is wild
He gives very similar vibes to Capella in which they will loudly declared they don't see Artemy as a parental figures and don't want him to be one, while simultaneously desperately (and likely unconsciously) really wanting the safety net of an adult who will selflessly care for them - something they don't have due to their (1) weird families' expectations of them as future mistress/Kain, (2) their own hyper-competence and independence
Artemy and Andrey
This isn't as serious, I just think it's funny that Andrey has suggestive lines at Artemy in patho1 and patho2. Also is like genuinely pretty friendly with him in both (he'll give you Tyrwine for checking on Peter and he's outright help in his 1st Patho 1 sidequest)
Also just straight up, doesn't believe Artmey if he takes credit for destroying the Polyhedron
Like in fan depictions, I often see them not getting along, but I'm 99% sure Andrey's impression of Artemy is "My Hot and Helpful Weed (Twyr) dealer" - outside of Dankovsky, he's the Utopian who probably likes Artemy the most
Meanwhile Artemy gives off strong "i am choosing to barely register a word coming out of this man's mouth for my own sanity" vibes
Aspity and Dankovsky vs. Aspity and Artmey
Okay, mixing Pathologic 1 and Pathologic 2 here a bit which might not be fair as Aspity in general does seem more serious in Pathologic 2 (even for Daniil in the Marble Nest)
BUT the sheer whiplash of Aspity calling Daniil a prickly prick and monologuing suggestively about naked women at him in Patho1 vs.
Declaring herself Artemy's spiritual elder-sister/mother, keeping his inheritance safe, trying to save him from a cruel fate with Patches even at the cost of her life in Patho2
The whiplash is wild, I want to lock the three of them in a room and see what she does
Artemy and Taya
I love that being the co-ruler/enforcer/parental figure mix to one weird-magical little girl ruler who can magically communicate with him wasn't enough
Taya subconsciously yoinking Artemy into her dreams to play dolls or tell her stories - he hasn't slept in a week
Also I think it would be really interesting post-canon to look at how they are doing as the two big spiritual and political leaders of the Kin
#pathologic 2#artemy burakh#capella olgimskaya#khan pathologic#long post#andrey stamatin#aspity#taya tycheek#sorry not over capellas 'OUR kids' and artemy saying “YOU are one of my kids” and never will be#i could probably do another no artemy version bc the inter-character relations and what Clara and Dankovsky have going on is also wild
50 notes
·
View notes
Text
Polyhedron of the Day #63: Triakis tetrahedron


The triakis tetrahedron is a Catalan solid. It has 12 faces, 18 edges, and 8 vertices. It is also known as the kistetrahedron, as it is the Kleetope of the tetrahedron (i.e., this shape can be obtained by attaching triangular pyramids to each face of a tetrahedron). Its structure is similar to that of the net of the four-dimensional 5-cell. Its faces are all isosceles triangles. Its dual polyhedron is the truncated tetrahedron.
Triakis tetrahedron GIF and image created by Cyp using POV-Ray, distributed under a CC BY-SA 3.0 license.
8 notes
·
View notes
Note
Nothing could convince me that Daniil and a psychologist reader wouldn’t psychoanalyze eachother as a way of flirting nothing more romantic then listing off all the personality disorder symptoms your partner has over a candle lit dinner
But yeah being a psychologist stuck in the town during the events of the game(s) would be utter hell that would probably cause some form of sanity slippage after some point there’s neurosis everywhere in that town and sure maybe one fire is put out but oops there’s four more in its place so after awhile it’s gonna cause them to bang their head against a desk or two….maybe even a decent wall if one can’t find a proper desk!
I think a psychologist would really shine through and become crucial in the aftermath of the plague when the town is attempting to heal itself.
Whether you're with the utopians utop the tower or down behind the wall of soldiers watching the polyhedron comes crashing down, your importance becomes very apparent very fast.
The Stamatins who come to you mourning their tower, Aspity and Oyun struggling to come to terms with the death of mother earth, Maria who suddenly can't hear her mother's voice anymore, Stakh who's lost all direction in his life overnight.
You'd be more than encouraged to stay. Your presence would be demanded if anything. As the last plague cloud dissipates from the streets, the wounds are still too fresh in everyone's hearts.
And while the doctors in town can tell you a lot about how to stich cuts, heal broken bones, and cure illnesses, they can't help mend scarred minds.
A psychologist would be the safety net catching the afterfall of those two nightmarish two weeks.
10 notes
·
View notes
Text
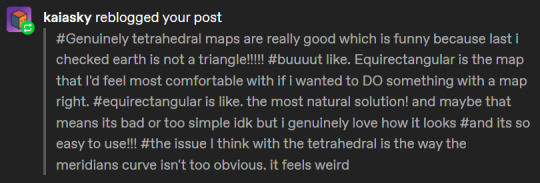
@kaiasky
Yeah, tetrahedral maps are great! I think it's mainly because when the map is centred on the north pole you sort of get three "prongs" of land extending from the centre (South America, Africa, and Australasia/Oceania), which then obviously fit into the three points of the Lee Tetrahedron's resulting triangle really well.
This manages to keep most of the land away from the distortion points at the centre of each side and at the corners, with the noticeable exceptions of the area around Myanmar & Bangladesh, Hawaii, and Antarctica.

I'll put the rest of this under a cut because it got quite long.
There are a couple of different ways to fix this, centring it on 65°N 30°E rather than the pole manages to put Antarctica back in one piece and now the only noticeable distortion is that Sri Lanka and southern India are way too big, (There are probably better options than this for the centre but I couldn't find them)
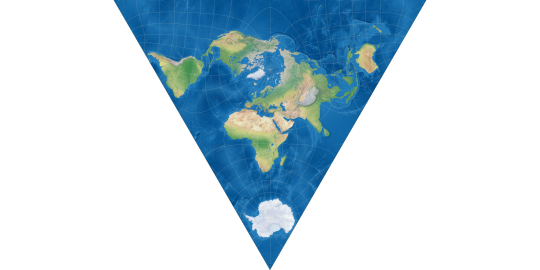
Of course, you might also notice that the three "prongs" are really closer to 90° apart than 120°, which is where the popularity of octahedral projections like Cahill's and Waterman's projections probably comes from, but I quite like the Peirce Quincuncial for this, and if you take the top octant and split and rotate it round, you get a layout very similar to the tetrahedron. The most noticeable distortion here is probably Papua New Guinea being slightly to big.
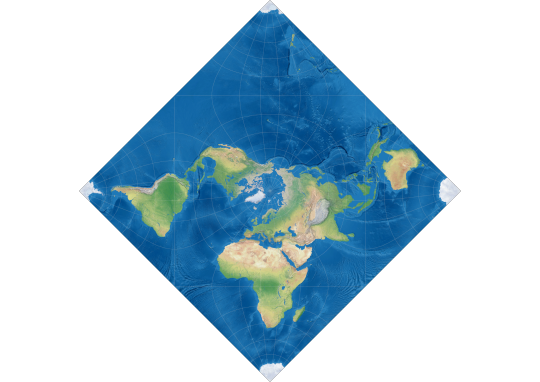
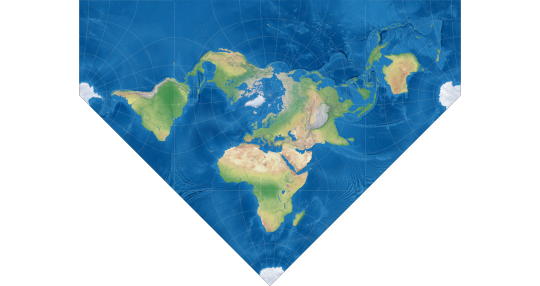
(And like in this post from last week, you can also move the bit of Antarctica at the bottom to get this)

A lot of people have tried to use Lee's Tetrahedron as a base and either rearrange it into a rectangle (Markley and CALM) or a half hexagon (Lee-Concialdi and Lee-Xarax), it's just a really good projection if you need something conformal with low area distortion.
The only oblique aspect rearrangement of the Peirce Quincuncial I've seen is Grieger's Triptychal (see the Markley and CALM link).
A polyhedral projection I really want to see is one based off a rhombic dodecahedron, a polyhedron with twelve rhombi for sides.
It's net isn't particularly pretty because the rhombi it uses don't tesselate, however this paper does a really interesting thing by compressing the net to squares rather than rhombi.
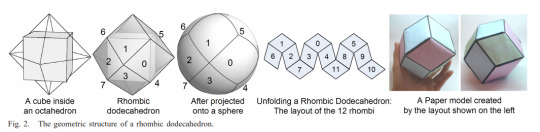

It's original use case is as replacement for cubemaps which can cause a loss of visual quality where the distortion is large, but I want to see what it would look like for a world map.
The projection they're using for each face (gnomonic I think) isn't conformal so you get discontinuities between face, but you might be able to change it so it is, sort of like how the Peirce Quincuncial uses right angle triangles for each octant rather than equilateral triangles like the Cahill while still maintaining conformality, but I don't know how I'd work out the maths for that, iirc Peirce did it with complex analysis.
38 notes
·
View notes
Text
Two Symmetrohedra Which Each Feature Four Regular Enneagons
This symmetrohedron has the following faces: four regular enneagons, four equilateral triangles, and twelve isosceles triangles with vertex angles of 43.5686 degrees. Its net is shown below. If this polyhedron is stellated once, the result is another symmetrohedron — one with four enneagonal faces, as well as twelve kites. The angles in the kites are 116.762, 99.8348, 43.5686, and 99.8348…
0 notes
Text
Yet I did noticed Something was wrong when I Draw a polyhedron net :)) Maybe it wasn't a Corner .. My (Not evil not twin sister) did drop the cube and told me later that she Had to repair Something. Crashed the whole cube and rebuild it Fittiing again which massively helped my perception 👍








he learned an evil trick
2K notes
·
View notes
Video
youtube
Pull up nets, cube, tetrahedron, octahedron, dodecahedron and icosahedron
I was reading a paper about pull up nets and it suggested that not all of the nets of a cube necessarily can be made to pull up.
Challenge accepted, I have made all eleven of the cube nets and depending on your definition of 'pull up' all of them can be made to pull up. I accept that not all of them do so elegantly but they do pull up into a cube. Given that there are many ways to loop thread through them improvements may be possible if there were an easy way to determine the most effective route.
When considering this, knowing which bit of the net end up where in the cube, that is to say which corners in the net end up in which vertices in the cube helps in choosing a thread route that pulls these together.
Tacked on to the end are the only two unique nets of the tetrahedron, one of the eleven nets of the octahedron and one each of the thousands of nets of the dodecahedron and the icosahedron. I may get round to the other ten nets of the octahedron but not the thousands of the dodeca and icosahedrons. The number of nets increases geometrically with the number of faces and side of the polyhedron I don’t know if there is a formula but it does get very silly very quickly.
These are card with sticky tape hinges and the eagle eyed will have seen that sometimes they flex the wrong way and yes the card came from pizza boxes, I eat a lot of pizza and always save the cardboard for making maquettes.
1 note
·
View note
Text
Icosahedron net - slightly colorful visualization


Currently I am obsessed with polyhedra nets - and crafting tiny models and creating visualizations.
For this one I created a template for the net that somehow reminds me of the cornu spiral - as this kind of net can be "coiled up" to fold the polyhedron.
Furthermore, I used 12 colors for the 12 vertices - in a gradient-like arrangement (it starts at red and gradually follows the route at orange, yellow, green, blue, violet, and ends at pink.)





#icosahedron#icosahedra#icosahedron net#math visualization#math#mathematics#math art#polyhedra#polyhedron#regular polyhedron#regular polyhedra#platonic solids#polyhedra net#polyhedra grid#geometry#math models#geometric#mathy art#math and art#coiling#coil#cornu spiral#spirals#spiral#coiling up the icosahedron net#coiling up#mathy stuffy#mathy#math is beautiful#STEM
21 notes
·
View notes
Text





Stella Users' Polyhedron Models
Fr. Magnus Wenninger | Ulrich Mikloweit | Tom Lechner | Piotr Pawlikowski | Kyle French | Sergey Kaliberda | Sebastián Naccas | Hamp Stevens | David Bodoh | Alex Doskey | Adam Stolicki | Giacomo Artoni | Richard Stratton | Marc Picquendar | Robert Rech | Linda Zurich | Karlos Alonso Mediavilla | Steve Waterman | Michael Barltrop | Keith Davison |
Here are some models made by people other than me, using measurements or nets generated by Stella4D, Great Stella or Small Stella.
If you have made models using Stella, please email me ([email protected]) some images, and I may include them here.
See also: What people have to say about Stella.
Models by Fr. Magnus Wenninger
Author of "Polyhedron Models", "Dual Models" and "Spherical Models"
0 notes
Text
Coiling up the polyhedron nets by pulling a thread:
Cube:


Truncated cube:


Cuboctahedron:


All three (aligned):


Inserting them like russian puppets:
Cuboctahdron inside truncated cube: (Left)
Truncated cube inside cube: (Right)



Drawing a truncated cube and a cuboctahedron from a cube....
As for understanding truncation: You can imagine having a cheese cube and just cutting of the vertices...
- - -- --- -----
Truncated cubes and cuboctahedra are Archimedian solids.
----- --- -- - -
I used isometric dot paper.
#polyhedra#polyhedron#archimedian solids#cube#truncated cube#polyhedron net#cuboctahedron#platonic solid#geometry#geometric models#math#mathy stuff#math stuff#knottys crafts#mathy crafts#mathematics#colorful math#pretty math#math passion#math joy
378 notes
·
View notes
Text
Polyhedron of the Day #14: Cube


The cube, also called a regular hexahedron, is a Platonic solid. It has 6 faces, 12 edges, and 8 vertices. It can also be seen as a square parallelpiped, equilateral cuboid, right rhombohedron, 3-zonohedron, or regular square prism. It is also a Hanner polytope. The dual of the cube is the octahedron. It is the only convex polyhedron whose faces are all squares. Its primary Schläfli symbol is {3,4}. The cube has three uniform colourings and eleven nets.
Cube GIF and image created by Cyp, distributed under a CC BY-SA 3.0 license.
#I'm sorry I missed yesterday! I will post two of these in one day at some point in the near future to make up for it.#daily polyhedron#math#mathematics#polyhedra#polyhedron#shape#shapes
7 notes
·
View notes
Text


I built some of my polyhedra
a Johnson solid is a strictly convex polyhedron each face of which is a regular polygon. There is no requirement that each face must be the same polygon, or that the same polygons join around each vertex. An example of a Johnson solid is the square-based pyramid with equilateral sides (J1)

Although there is no obvious restriction that any given regular polygon cannot be a face of a Johnson solid, it turns out that the faces of Johnson solids which are not uniform (i.e., not a Platonic solid, Archimedean solid, uniform prism, or uniform antiprism) always have 3, 4, 5, 6, 8, or 10 sides.
In 1966, Norman Johnson published a list which included all 92 Johnson solids (excluding the 5 Platonic solids, the 13 Archimedean solids, the infinitely many uniform prisms, and the infinitely many uniform antiprisms), and gave them their names and numbers. He did not prove that there were only 92, but he did conjecture that there were no others. Victor Zalgaller in 1969 proved that Johnson's list was complete.
As in any strictly convex solid, at least three faces meet at every vertex, and the total of their angles is less than 360 degrees. Since a regular polygon has angles at least 60 degrees, it follows that at most five faces meet at any vertex. The pentagonal pyramid (J2) is an example that has a degree-5 vertex.

A database of solids and polyhedron vertex nets of these solids is maintained on the Sandia National Laboratories Netlib server (https://netlib.sandia.gov/polyhedra/), but a few errors exist in several entries. Corrected versions are implemented in the Wolfram Language via PolyhedronData.
The following list summarizes the names of the Johnson solids and gives their images and nets.

252 notes
·
View notes
Text
The Lens of Human Perception
There’s a topic I’ve realized I haven’t discussed here, so I figure it’s time to write something about it. As usual, due to the length of this essay, the bulk of it is under the cut.
I’ve seen a lot of posts going around by people exploring nonhuman past lives, especially those which aren’t possible here/now (i.e., angels, dragons, etc.), and describing any memories they have in very human terms. Things like walking down streets, gathering in gardens or libraries, standing before a judge in court during a trial. I think this is the result of a lack of awareness of a phenomenon we all deal with, but which is rarely (if ever) discussed directly.
Every memory you have, from the broadest strokes to the finest detail, is filtered through the perception and understanding we have here/now. We’re experiencing three-dimensional space, with a (relatively) constant and linear flow of time, seeing the world by way of reflected light and hearing things by way of vibrations in the air around us. Unfortunately, because those things are the only way we’ve experienced reality in this lifetime, we are literally incapable of properly modeling other forms of reality in our minds. It’s a limitation of being here/now, and having the kinds of experiences we do.
A (slightly extended) example: It’s pretty common to be taught about nets of polyhedra in school these days. As a refresher for those who haven’t dealt with the concept in a while: Polyhedra (singular “polyhedron”) is a three-dimensional figure made up of flat planes joined at some angle. One of the most common polyhedra is the cube. Six flat faces, joined at right angles. A net of a polyhedron is a way of “unfolding” the faces of a polyhedron into a two-dimensional shape. That two-dimensional shape can then be folded through the third dimension to recreate the original polyhedron.
Nets aren’t limited to unfolding three-dimensional objects, however. Theoretically, you can create a one dimensional net of a two dimensional polygon (it’ll just be a line, but it counts). More significantly for this discussion, though, you can create three-dimensional nets of four-dimensional shapes. Some of you may be familiar with the concept of a hypercube (sometimes called a tesseract). In the same way that a cube can be thought of as being made of squares arranged in three dimensions, a hypercube can be thought of as being made of three-dimensional cubes arranged in four dimensions. (There are multiple ways of representing a hypercube in three dimensions, but all of them are by necessity inaccurate.) Now, I’d like you to take a moment, and try to imagine a proper four-dimensional hypercube, and how it unfolds into a three-dimensional net. Then try to imagine that three-dimensional net folding back into a four-dimensional hypercube.
It is, quite simply, impossible to do accurately. Our brains are simply incapable of truly visualizing four-dimensional space, and the way objects behave in four dimensions, because we’re limited to experiencing only three of them. Similarly, it is impossible to truly comprehend how reality functions outside of here/now, because we’re limited to experiencing only here/now. Brains are amazing things, however, and will try their hardest to fill in the gaps with something, even if that something is inaccurate.
When it comes to remembering nonhuman incarnations, this means that our brains will grab whatever feels closest to what you’re unable to understand, and use that to fill in the gap, regardless of if it actually fits or not. As a result, those kinds of memories are inherently unreliable, since they’re (in many ways) just our brain’s best guess about what actually happened.
I’ve taken to referring to this problem as “the lens of human perception”, since it occurs due to filtering things through the understanding we can have by perceiving the world the way humans do. Like any imperfect lens, it leads to our view of things being distorted, and because of the way brains work, we generally aren’t even aware that the distortion has occurred. And so we redefine things in terms of here/now without even realizing we’re redefining our own experiences.
Being aware of the lens of human perception can be helpful, however. It lets you consider the context of your memories, and figure out where the gaps in your understanding are getting filled in. You can then make an effort to explore those gaps, and refine your understanding to get a clearer picture of how things actually were. It’s difficult sometimes, and takes some work to do effectively, but it can be worlds better than getting caught up in misunderstandings about your own experiences.
So if you’re exploring memories and notice that things are very similar to the world around you, take some time and question things. Think about what it is that you might not be able to understand within those memories. Reflect on what unconscious associations you might have with the here/now things your brain is using to fill in the gap. Use those associations as a starting point to explore further, and refine your understanding into something more accurate to what you really experienced. You may not be able to remove the distortion from the lens completely, but you can at least compensate for it. With time and effort, it’ll help you be more certain about your experiences, and know that you have a clearer view of yourself. And believe me, it’s a great feeling when you get there.
#metaphysics#essay#angelkin#otherkin#alterhuman#There's also something to be said about the way expectations can skew things#But that's a separate discussion#I don't have my thoughts sorted enough to properly write on that one yet#If anyone else wants to in the meantime#Feel free to drop me a link
83 notes
·
View notes