#enneagon

[notreallyherehahaha]

A Polyhedron Featuring Twenty Regular Enneagons and Sixty Kites

I made this using Stella 4d, which you can try for free at this website.

[gorrus]

[yugiohcardsdaily]

QQ Enneagon

"If this card is in your hand or GY: You can reveal 1 Level 9 monster in your hand, except 'QQ Enneagon': Special Summon both this card and the revealed monster in Defense Position, also you cannot Special Summon from the Extra Deck for the rest of this turn, except Rank 9 or higher Xyz Monster. You can only use this effect of 'QQ Enneagon' once per turn. A Rank 9 or higher Xyz Monster that has this card as material gains this effect.

This card gains 900 ATK/DEF."

[squareallworthy]

Reverse unpopular opinion ask meme: Irregular polygons

Irregular polygons are awesome. You can do so much more with them, in so many areas, but I'm going to limit myself to talking about just two of them: tiling and triangle centers.

(Did you think I was going to be all snobby toward my irregular friends and give them only grudging approval? Heck no, I love those guys! And so by the rules of the meme I get to infodump about the things I love, so this may be long but you asked for it.)

Let's first talk about covering the plane with copies of a single shape -- a monohedral tiling. And for now, let's restrict ourselves to periodic tilings. All triangles and all non-self-intersecting quadrilaterals tile the plane periodically, so that's not very interesting. All you have to do is place one polygon and then make copies by rotating 180 degrees around the midpoints of the sides.

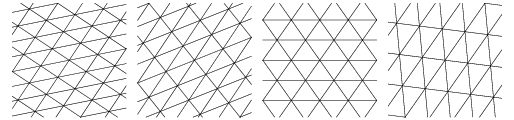
With five sides, things become more complicated, because regular pentagons don't tile by themselves, but there are fifteen ways an irregular pentagon can periodically tile the plane. Here are four of them that were discovered in 1976 and 1977 by Marjorie Rice, an amateur mathematician.

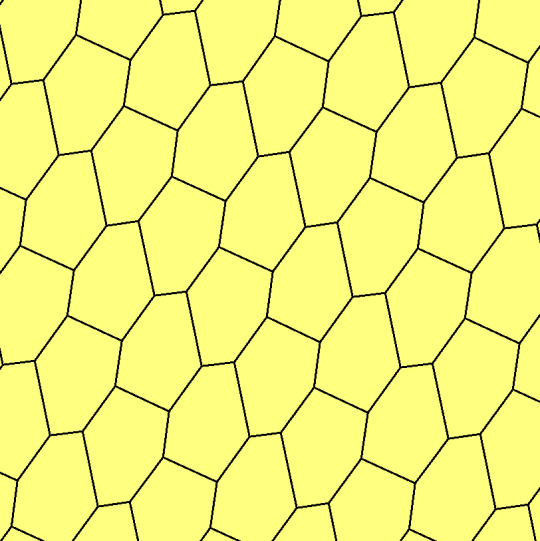
There are three types of monohedral periodic convex hexagonal tilings.

For polygons with seven or more sides, there are no monohedral periodic tilings using a convex prototile , but there are periodic tilings for nonconvex polygons of any size. Some of them are quite famous.

Most of Escher's work in his Regular Division of the Plane series uses shapes with curves as well as straight sides, so they don't show polygon tilings, strictly, but the patterns do point toward complex tilings that are visually pleasing.

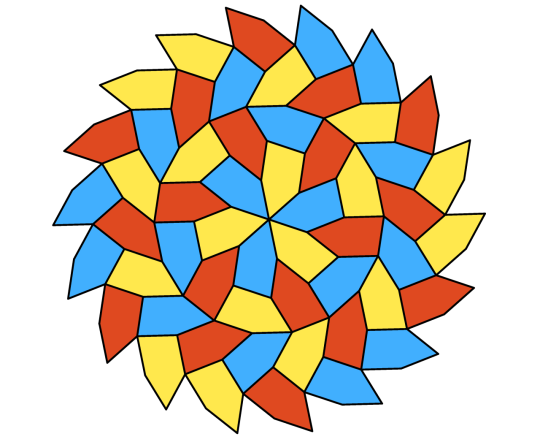
Irregulars can tile aperiodically, too. Here's a pentagon tiling with 6-fold rotational symmetry. It can be extended infinitely, and tilings can be constructed with pentagons for n-fold symmetry of any n>2.

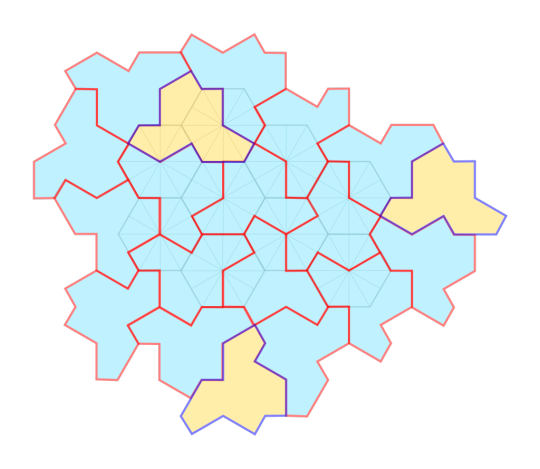
Going back to non-convex shapes, here's the Voderberg tile, an enneagon that forms a spiral tiling. Notably, one copy of the shape can be completely surrounded by two others.

And of course I can't go without mentioning the tiling news of the century: "Tile (1,1)", aka the Hat, aka the T-shirt, a tridecagon (and polykite) that can tile the plane but only aperiodically. IDK if you follow polygon news but this was huge.

Okay, enough about tilings. With tilngs it's pretty easy to get what's going on just by looking at them, but my next topic, triangle centers, requires a bit more explanation. Also there's a bit of jargon, but I will try to keep it simple.

Take an arbitrary triangle ABC. Where is its center? One way you might define it is to find the midpoint of each side and draw a line to it from the opposite vertex. Each line divides the triangle in half, and these three lines (the medians) all cross at a point, the centroid. This works for any triangle, no matter its shape. The point marks the center of gravity of the area of the triangle, and also the center of gravity of its vertices. Based on that, you could consider this the center of the triangle.

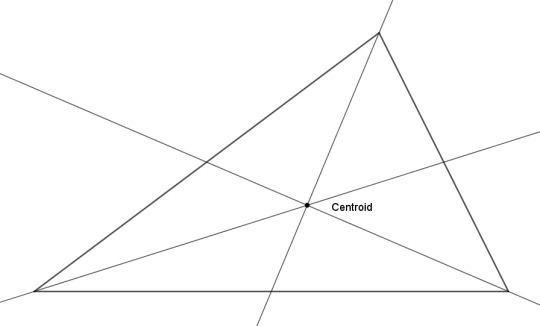
Or you could work with angles instead of sides. Draw lines from each vertex that divide the angles in half (the angle bisectors). These all meet at a point called the incenter, which marks the center of the largest circle that fits inside the triangle. To put it another way, it's the point that is equidistant from all three sides. That's another point you could call the center of the triangle.

Or, how about a circle around the triangle instead? From the midpoints of the sides, draw the perpendicular bisectors. Again, they all intersect at a point, the circumcenter, which is the center of the circle that passes through the vertices -- the point that is equidistant from all three of them. So you could also call that the center of the triangle.

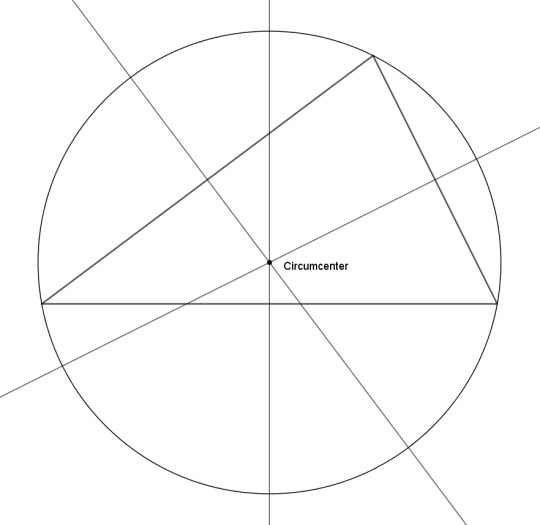
Or how about drawing perpendicular lines from the sides again, but having them pass through the opposite vertices (the altitudes)? They coincide at a point called the orthocenter. Isn't that neat? Yet another point we could call the center of the triangle.

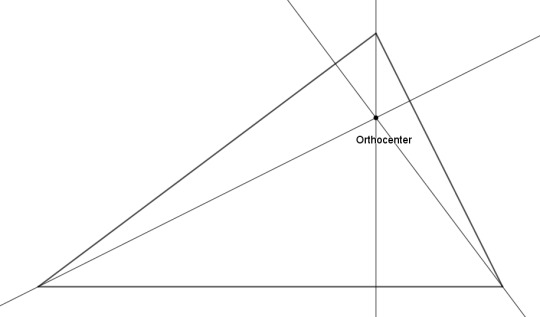
But wait -- can we? For an obtuse triangle, the circumcenter and the orthocenter are going to lie outside the triangle. (For the orthocenter of an obtuse triangle, you have to extend each side into a line, and draw the altitude as a perpendicular to that.) Being outside a thing is really not what we have in mind when we talk about the center of the thing. Should we care about that?

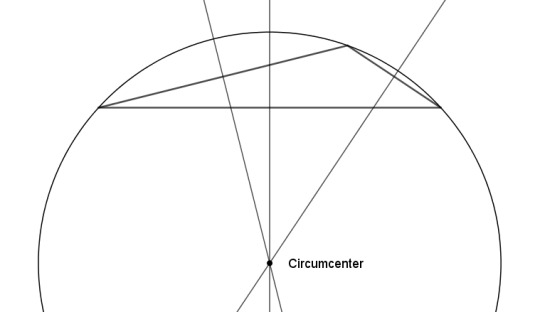
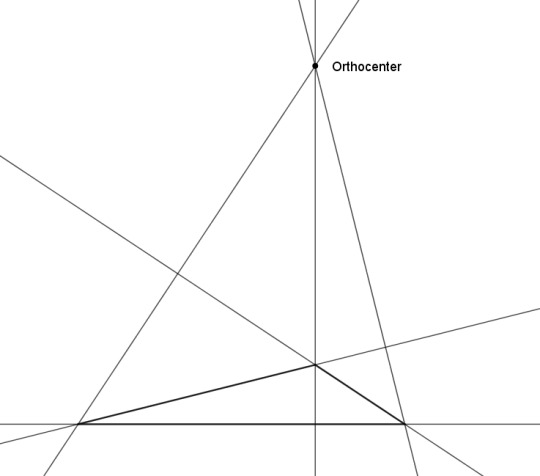
Maybe not. Check this out. We'll go back to the circumcircle, and draw tangents to it at the three vertices. The three tangents form the tangential triangle (in blue), which we'll call A'B'C', where A' is opposite A, and so on with B and C. Now draw the circle that passes through A, A', and the circumcenter, and do the analogous construction for B and C (in red). The three circles coincide in two places: the circumcenter and another point called the far-out point. And as the name suggests, this is usually well outside the triangle, even for acute triangles.

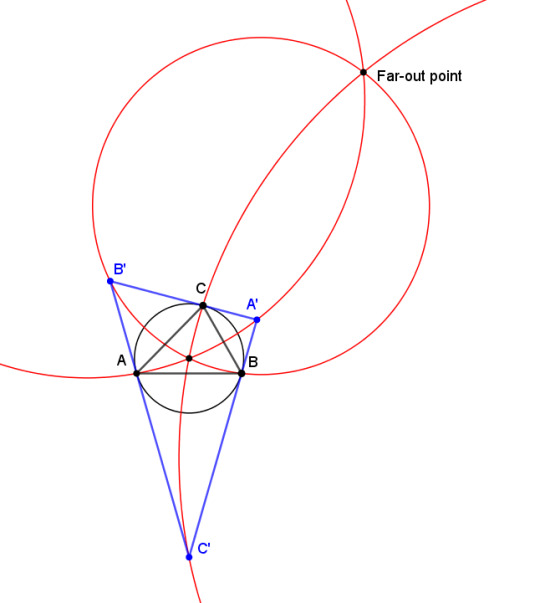
There's no reasonable way to call this point the center of the circle. But so what? I just love the fact that the three circles line up like that. I no longer care about finding "the" center of the triangle. I no longer care that "center" is rather a misnomer for many of these points. I just think it's neat that you can draw these constructions on ordinary aysmmetrical triangles and they keep all converging on one point. Want more? Reflect the medians across the angle bisectors, and they all meet at the symmedian point. Or connect the vertices of the tangential triangle with the intersections of the medians and the circumcircle. Those lines meet at the Exeter point. Or, from each vertex, draw the line that splits the perimeter of the triangle in half. These are called the splitters, and they meet at the Nagel point. And on and on and on.

You can simply wander around a triangle, connecting things that relate somehow to vertex A, then do the equivalent thing for B and C, and stumble upon new centers. And there are tens of thousands of these things, constructed with straightedge and compass or by other methods. And there are so many ways to enjoy these things. You can page through the enormous collection and get a kind of stamp-collecting satisfaction just looking at their variety and knowing that they exist. Or you can appreciate the proofs that show that the constructions really do specify a unique point. Or proofs that show that a point constructed to have one property has a surprisingly different property. Or you can notice that the points fall into certain families and appreciate the connections between them. (For instance, the centroid, circumcenter, orthocenter, far-out point, and Exeter point, among others, all happen to lie on the same line, the Euler line.) Or you can convert the points to trilinear coordinates, manipulate them algebraically, and get to know them that way.

But to appreciate them at all, you need to work with irregular triangles. Because here's the thing: in an equilateral triangle, all these points collapse to the same point. Everything simplifies to a single center, and the incredible wealth of invisible structure that teems inside every ordinary triangle is gone.

You have finally found "the" center, but at what cost? Symmetry is death. Only through asymmetry will the vast truth of the triangle be revealed to you.

And those are just a few of the reasons irregular polygons are cool!

[revenant-coining]

Digonlexic, Enneagonlexic, Gigagonlexic, and Hectogonlexic

[ IDs in alt text ! ]

Digonlexic: a gender connected to or best described by the word digon.

Enneagonlexic: a gender connected to or best described by the word enneagon.

Gigagonlexic: a gender connected to or best described by the word gigagon.

Hectogonlexic: a gender connected to or best described by the word hectogon.

Etymology: digon / enneagon / gigagon / hectogon; “lexic” a suffix for lexegenders

@lexegender-archival , @radiomogai , @oneofmanyarchives

[ID: an orange line divider with a star covered in flame in the middle. End ID]

[fleurelinathehybrid]

🪽[2]🪽

Of all the journeys he had experienced throughout his long life, Hermes had never been so anxious about making this trip ordered by his father Zeus.

Among all the times he almost got into trouble for carrying out his orders and duties imposed by the other gods, while fighting to stay alive and not be reprimanded in the process; it only made Hermes realize that, JUST this once, he wasn't going to get away unscathed after that.

He had, in advance, his equipment ready for anything he needed during his mission and for any situation. Hermes, of all the gods, was the most cautious about being prepared for a mission, whether it was war or not.

Now, he was beginning to lament about being prepared for the new mission of “non-kidnapping” the Shape giver’s daughter, Oneiros. Being powerful that, although it is difficult for him to admit it, made the feathers on the wings of his feet ruffle.

He could never forget the time he had given his son, the talented Orpheus, the lyre with which he was able to conquer the beautiful Eurydice and whom he would soon marry. He would never forget the day he received the news that she had died prematurely on their wedding day due to a snake bite, on which he would learn that he would be in charge of testifying how Orpheus would bring her back to the world of the living.

One of the pains she would feel the most would be seeing the poor boy crying because he would be forced to take her back to the underworld because he couldn't resist turning to see her.

He would never forget the pain he experienced, for which he had to inform his parents about the situation.

Just as it had also hurt him to learn of his death. He could never forget those sad dreams after he had to report his death to the muse Calliope, his mother.

That and other experiences linked to that have been added to the list of Hermes' worst experiences.

With his backpack ready, his winged sandals and nerves the weight of a feather, the messenger god and guide of thieves took flight and headed to the garden of the labyrinths of Potmos.

“Okay… may the wise Fates guide me in this”

[ 🪽🪽🪽 ]

[ 💛💛💛 ]

When Dream, Hob and Dawn arrived in the kingdom of Destiny, they expected anything but for the other siblings to welcome them with open arms.

Destiny, Death, Desire, Despair and Delirium were sitting on the sides of the enneagon table (which had always been a heptagonal table, when they had not met Hob and the fourth brother was present), awaiting the arrival of the third brother's new family. When they saw them pass from their kingdom to the place where the dinner would be held, some could not help but stand up to receive them.

—Brother! —Delirium exclaimed animatedly, after levitating up from her chair and flying to where her brother, brother-in-law and niece were.

—They arrived, and with the little star guest. —Desire speaks, while looking at them very mischievously, and then placing a small touch with their finger on Dawn's nose and making her smile. —Definitely, this dinner is going to be very special.

—It's nothing out of this world, my twin. — Despair speaks to her, as he approaches and attracts his niece's attention with small tickles on her feet— It's just a dinner like the others.

—With the only difference that we have one more guest in the family: the tender Dawn. —Death concludes, while she caressed her niece's hair, who couldn't stop smiling because of their displays of affection and attention.

—Well, we're not here to delay dinner any further. —Destiny finally speaks, attracting the attention of his other brothers and the guests. He goes ahead to approach them and caresses his little niece's blushing cheek— Welcome to my kingdom, brother. The only thing missing was you for dinner.

—Thank you for the invitation, brother. —Dream smiles gratefully at them, while holding his daughter and being hugged by Hob— It means a lot to us her first time being part of this, and in any future meeting.

—It's understandable. —he responds warmly, as he guides them to the table to start dinner. —Go take your seats, dinner will be served shortly.

Each Endless member took a seat at the huge table for the family reunion. Destiny was the first to sit down, on his left side sits Death, who on her side sits Dream, who on his side places Dawn sitting in a baby chair, who on her side sits Hob, who on his side is an empty chair (where the Prodigal used to sit), on the side of said chair sits Desire, who on their side sits Despair, who next to her sits Delirium to finally close the enneagon.

Once all the family members and guests are seated, the conversations begin and then flow. Delirium, being as always the youngest sister of the seven, goes ahead to levitate to be close to her niece and make her play with the butterflies and fish that she made appear with her powers. Dawn took this as the same fun she felt when she was in the Dreaming, so her obvious reaction was to laugh and enjoy the bright colors her aunt was showing her.

—Sister don't burden the girl with your fish. You're going to make her dizzy. —Desire calmly warns her, as they see her levitating near the little girl.

—But I can't help it! —she says a little euphorically, while levitating upside down— Besides, she likes them, doesn't she, little light?

Dawn smiles and nods in response, so tenderly melting the hearts of her parents and piblings present.

Delirium, levitating still face down, gives the girl a kiss on the forehead. —I'm glad you like it. —she says before flying back to her seat.

Suddenly, some walking shadows appeared, bringing with them a huge rounded tray with a lid that had a handle on the tip that was placed in the center of the table, implying that below that were the dishes served for dinner. As soon as the thin silhouette of the shadow lands, the magician takes the lid and removes it, eight saucers are immediately revealed, forming a pyramid of four saucers at the base, three in the middle and one small one at the tip; not forgetting that for drinks they had some bottles of wine and a bottle full of juice.

When they least expect it, each member at the table had their area of ​​the table served with their plate, their cutlery and their glass of wine; Dawn being the exception, with her saucer, her cutlery and her bottle with juice.

—Wow, this is a good dinner. —Hob spoke, surprised by the presentation.

—Is this what a good dinner is like for you? Wait until you see dessert, I think sweet Dawn will like it. —Desire tells him, while he was cutting the steak with the knife and fork.

—In fact, my brother is right, dessert is another topic. You'll see it when we finish dinner. —Destino informs them as soon as he takes the spoon for his dish. —You can start eating.

After that order, everyone continues to eat dinner. Each one enjoying their dish while they talked and saw sweet Dawn eating sweetly from her dish while her father Dream wiped her mouth with the napkin.

The family dinner was definitely going well.

[marsjake]

Ship Blueprint

I started off with my ship drawing, I scanned it in and converted it to solid black and white, to get that high contrast blueprint look.

I then made some geometrical Alien lettering, keeping in mind the idea of the star Enneagon and it's many forms, I used only 45 and 90 degree angles to make up my characters.

I then selected a pleasant blue colour and imported my space ship image into picsart, an easy to use mobile editing software which i am very familiar with. I needed to just include the line work, so I used the blend tool to eliminate the whites, just leaving the black outlines.

I then converted my image to negative, revealing a striking while outline in contrast to the blue background, the signiture look was beginning to take shape.

I then repeated this process with my alien text, putting it in the bottom left corner, almost like it were patent information or annotation.

I then used the blend tool to add a scratch worn texture and also imported a stock paper tear asset to give it a battle work or relic type look.

The end result, in my opinion looks really smart! I think maybe If I were to do this again, add more annotation.

[twice-star]

Enneagon

[theedgeofspirit]

“Before the Horizon” (4/9/2020, @theedgeofspirit)

[fyeahforsana]

© Enneagon | ❀ Do not edit.

[notreallyherehahaha]

Two Symmetrohedra, Both of Which Feature Eight Regular Enneagons

The first of these, shown above, also includes six squares, 24 isosceles trapezoids, and twelve rectangles among its faces. The second one, shown below, also includes among its faces six regular octagons, and twelve pairs of “bowtie” trapezoids. I made both of these models using Stella 4d, which you can try for free here. The starting point for making them was the enneagonal-faced polyhedron…

[forjihyo]

♡ enneagon | do not edit.

[nayeon-fy]

© Enneagon | Do not edit or remove logo

[fy-mina]

171109 Mini Fanmeeting © Enneagon | Do not edit or remove logo

[fy-myouimina]

171109 M Countdown Mini Fanmeeting © Enneagon1020 | Do not edit.

[fyeah-chaeyoung]

© enneagon | do not edit.