#now that's what i call topology

[more-mathematics-mor-lam]

An illustration by topologist A.T. Fomenko found in the Lev Sabinin book ‘Mirror Geometry of Lie Algebras, Lie Groups and Homogeneous Spaces’.

[simlicious]

CC Creation Tutorial: Smooth Seams in Blender

In this tutorial, I will show you how to make your mesh seams smooth inside Blender (no Milkshape required!) and walk you through the process step by step. We will make a perfectly smooth mesh and transfer the normal data from that mesh to our main mesh using the Data Transfer modifier.

I am using Blender 3.6 in this tutorial (though you should be able to follow along using other versions as well)

You do not need to have much previous knowledge to follow this tutorial, but I assume you know some basics in Blender like how to select, things, navigate around, etc, and know how to import the meshes and put them into Blender.

For this tutorial, I exported the Sims 3 afbodyEP4DressPromBigBow mesh with TSR Workshop. You can use any clothing mesh you like though, and works on any meshes, not just Sims 3 ones.

This is our mesh. You can already tell that it has the dreaded seams on the neck and the rest of the body.

First, we need to make a copy of the mesh (in Object mode, select the mesh and hit Ctrl+D Shift+D to duplicate it, then hit Esc to stop it from moving around).

Rename the mesh (I added Seamless to the mesh name).

Make sure the original mesh is hidden (click the eye symbol) and select the Seamless mesh.

Press the Tab key to go into Edit Mode.

Now we select the parts that we want to have smooth seams. Let's select everything that is skin (you can select a litte piece of the mesh and then press Ctrl+L to select the entire piece)!

Now, press M and in the menu, choose By Distance. (in older versions, this is called Remove Doubles).

This will remove all double vertices at the seams on the selection we made.

It will show you how many vertices it removed. The skin looks nice and smooth!

Let's switch back to our original mesh: Make sure you deactivate the eye on the Seamless mesh and activate the eye again on the main mesh. Then, select the main mesh.

Now, let's add a data modifier to our main mesh. Click the blue wrench icon in the vertical list of the properties panel and then onto Add Modifier, then choose Data Transfer from the list.

As the source, we choose our Seamless mesh.

Also toggle on Face Corner Data and click the Custom Normals button.

Hold on, there is a message saying that we should enable Auto Smooth in Object Data Properties. Let's do that next! (if the message does not appear for you, maybe Auto Smooth is already on).

Click the green inverted triangle button and in the Normals section, toggle on Auto Smooth.

Now we can switch back to the modifier tab by clicking the blue wrench icon again.

But hang on, what happened to our mesh? There are now black spots over the dress and shadows on the legs!

This is due to the Data transfer modifier's Mapping setting. If we change it to Topology, our mesh goes back to normal again. Phew!

Now that the normals look good, we can start the transfer of our new smooth normals from the seamless mesh to our main mesh. To do that, we hit the Generate Data Layers button. This button works destructively, so you cannot undo what it did, just FYI.

Note: On newer versions of Blender, Generate Data Layers may not be enough to transfer the normals and you may need to apply the modifier instead.

You can toggle the modifier's visuals on and off with the little screen icon to see the results after you click Generate Data Layers to see if it stuck. If it did not (and you see the seams of your base mesh when toggling it off), try to apply it instead.

I switched from textured to solid shading because the differences are just more noticeable in this mode. This is how our mesh looks now with the modifier turned off.

Because we clicked the transfer button, the normals have been permanently applied to our mesh. The skin is smooth now, and so is the dress (even though we did not smooth that one, hmm...)

If we toggle the modifier back on, suddenly the dress has seams again! What's going on there? I'm not exactly sure why, but Auto Smooth seems to be doing some smoothing on the dress mesh as well.

I am not sure if this is normal behavior or not, but let's pretend that this did not happen and the modifier in fact did not smooth the dress.

Maybe we just forgot to smooth some areas on the Seamless mesh that we noticed only later on. That's no problem. We simply modify our Seamless mesh again!

So let's swap back to the seamless mesh and select it (remember to click the eye icons so only the Seamless mesh is visible).

Let's select the main dress parts and press M -> merge by distance on them. We cannot smooth the whole dress all at once, because then that would remove some seams that we want (like those for the backfaces and the middle section of the dress where the bow is attached).

If we remove the wrong seams, we ruin our normals and will have black splotches.

Now, let's select the backfaces and areas we left out before and repeat this process: M -> merge by distance.

Look at how perfect our Seamless mesh is looking now! Now, let's transfer those beautiful normals to our main mesh.

Select the main mesh and toggle the eye icons again, to hide our Seamless mesh and reveal our main mesh.

Once again, we will use the Generate Data Layers button in our Data Transfer modifier. If you have previously applied the modifier, just add the modifier again to the main mesh and use the settings shown here.

And that's it, you are done! You have a perfectly smoothed mesh that you can export now.

Final Note: it is best to transfer the normals at the very end of your meshing process because any action that recalculates the normals can reset our custom-made smooth normals again.

Of course, you can simply use the Generate Data Layers button again to re-add them, but it saves you time to only do this step at the end.

I almost forgot to say: You still have to use Mesh Toolkit to fix the seams on the edges of your mesh and do the usual shenanigans.

[mathematical-cheese]

Tell me about math's. Anything. I'm so curious

Okay! I will tell you about one way we can test for holes in a topological space!

I will first clarify what I mean by a loop because it's important to be precise and they are the star of this show! A loop in a topological space X is continuous map from the interval [0,1] to X which starts and ends at the same point.

To motivate our test we shall look at two examples!

First imagine a plane (ℝ²). Intuitively this has no holes. If we consider a loop in the plane we can imagine shrinking this loops down to a point. This is sort of like placing a rubber band on a table and squishing it down as close as you can (except rubber bands have a physical limitation. Even if you can keep squishing it, you'd eventually make a black hole). It's important to point out that the loop lives in the space rather than on top of it like a rubber band on a table.

Now imagine an annulus (see picture)

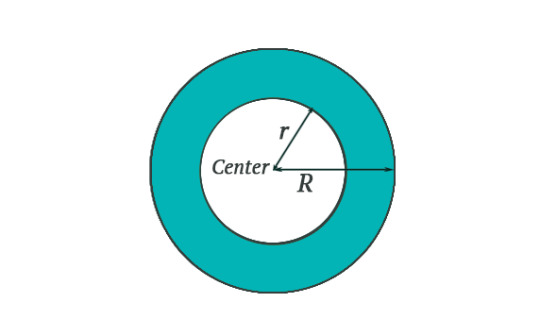
This obviously has a hole in the middle. Now we can consider loops in an annulus. We can think about two kinds of loops!

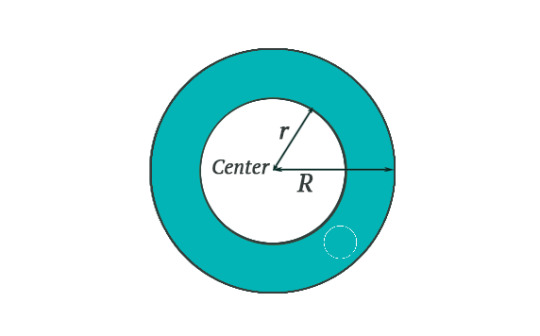
The first kind doesn't go around the hole and we can still shrink these to a point. The other kind goes around the hole and when we try to shrink it, it snags on the hole.

So the idea is that we can find the presence of a hole in a space by shrinking loops to see whether they can be made into a point or not. We can adapt the rubber band analogy by adding the extra rule that the rubber band must always touch the table at all its points. So if we were to cut a hole into the table, we would no longer be able to shrink the rubber band.

Let's try another example! We shall look at a torus. This is the surface of a ring doughnut (that is, it doesn't have anything on this inside).

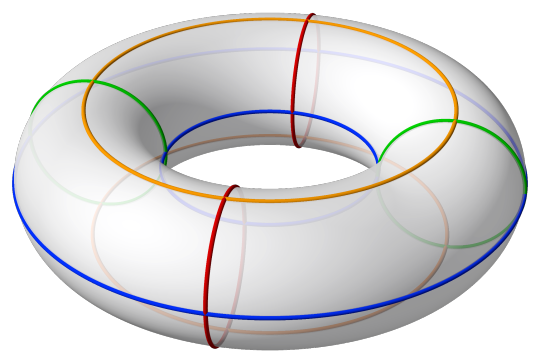
First consider the red and green loops. All we can do with these is move them around the tube. We can't shrink them. Similar, we can't shrink the orange and blue loops. We also can't deform a blue/orange loop into a green/red loop and vice versa! So a torus must have some holes!

One thing that might seem weird is that holes can have different dimensions! The part of our space which bounds the hole can have a different dimension which means the hole is fundamentally different. In this context the dimension of a space is to do with what the space locally looks like. That is, if you were to zoom in closely the space would sorta look like a flat Euclidean space, i.e. a line or a plane or 3D space etc. For example, the torus is 2 dimensional since locally it looks like a plane. A circle is 1 dimensional since locally it looks like a line. Another way to think of this is how many different independent directions could you walk if you lived in that space. Another example is the sphere, think the surface of the earth. This is two dimensional because we only require two numbers to describe positions on it!

The reason I bring this up is our test can't always detect the presence of holes! This is because our test is great at picking up on 1 dimensional holes, but it doesn't always detect higher dimensional holes. A good example here is the sphere. We can always shrink a loop on a sphere but it's fairly easy to see that the sphere bounds a region that isn't a part of the sphere itself. There is a 2 dimensional hole in the sphere.

One more neat thing we can do with loops in spaces is we can use them to define a nice algebraic structure! By algebraic structure, I mean anything that involves a set and an operation between elements of that set which produces another element of that set. An example of this is the integers with addition. We can add two integers to get another integer. The integers have some nice properties. There is an element 0 such that 0+n=n+0=n. We can also take inverses, i.e. we for any integer n there exists another integer m such that n+m=0. We also have a property called associativity. This is the rule that says (n+m)+k=n+(m+k). This makes the integers what's called a group!

We can make a group using loops in a topological space! We first pick a basepoint which every loop will start at. Then we define out operations on the loops to be concatenation. That is, given two loops f and g, we define f*g to be the loop we get by first going around f then going around g. We also have the added rule that we consider loops that can be deformed into each other to be the same. The identity element is the constant loop, i.e. the loop e such that e(t)=x for all values of t, where x is our basepoint. The group that we get is called the fundamental group (kinda pompous but it really is important!).

We can see an example of this using the annulus from earlier! We can consider an anticlockwise loop around the hole to correspond to the number 1. We can get successive positive numbers by going around this loop the right number of times! We get negative numbers using clockwise loops! (Equally we can make clockwise loops correspond to positive numbers and anticlockwise to negative numbers).

The fundamental group turns out to be a very powerful tool! It turns out that if topological spaces have different fundamental groups they can't be the same space (strictly speaking, they can't be homeomorphic or even homotopy equivalent). And we can prove some useful results using fundamental groups too!

This is all formalised in the area of maths called Algebraic Topology (the area I hope to do research in!). Making this all rigorous is no easy task (I have written a few formal posts about it on my maths blog!)

This was a lot longer than I had planned originally haha. I've been writing for about an hour and a half. I hope you find it interesting!

[proof-by-intimidation]

CGWH spaces

As I was reading May's book and was about to enter the realms of homotopy theory, I was stopped by a chapter on point-set topology. I didn't entirely understand the point of this detour but the author insisted that one would truly appreciate it later. But, my curiosity didn't let me be, so I read around it and here's what I found.

1. What is happening?

So, apparently, for various reasons, the category of topological spaces (Top) is not nice enough to work with in homotopy theory (I will try to give a couple of reasons). For a lot of results in homotopy theory, there are these weird topological spaces which don't satisfy them meaning we would have to impose additional conditions every time in the hypotheses.

Instead of doing that, topologists proposed considering a full subcategory of Top which is not too restrictive but also gets rid of these pathological spaces. So, what do we want this subcategory to satisfy?

2. Some Pathologies that arise

2.1 Product of CW complexes

CW complexes are the most important kind of spaces studied in homotopy theory. Essentially, any space can be reduced to a CW complex. I won't go into the construction of CW complexes here, but the issue with the product of CW complexes is that the natural CW decomposition (arising from the CW complex structure of the components) doesn't necessarily coincide with the categorical product of the CW complexes in Top.

So, one motivation could be to find a subcategory (which, of course, contains all CW complexes) where the CW product of CW complexes coincides with the product in that category.

2.2 Mapping spaces and adjoints

Another important class of spaces studied in homotopy theory is the set of continuous functions between two spaces X and Y (denoted as U(X,Y)). There is a conventional topology on this set (I don't know why it's the chosen one) called the compact-open topology. With this, we have a couple of important maps

which are not continuous for all spaces.

Moreover, we have the following adjoint map

which is a bijection for sure, but not necessarily a homeomorphism with our chosen topology on the mapping spaces.

With these motivations in mind, let's list down the axioms for the subcategory.

3. The Category of Spaces

After a long search and coordinated efforts, topologists came up with the category of compactly generated weak Hausdorff spaces which satisfies all the axioms and provides a suitable framework to do homotopy theory.

4. The category of Compactly generated spaces

When I read the first part of this chapter in May's book, which was a bunch of (seemingly arbitrary) topological definitions, I thought I was screwed. Am I supposed to go back to these definitions every time I work with 'spaces' now? Well, not really.

At the categorical level, it's quite elegant and makes your life so much easier. Sure, you might want to think about the topology once in a while (like showing every cofibration is a closed embedding) but a lot of meaningful work can be done using the categorical properties of these spaces (I hope so).

I am not going to intimidate you by listing down the definitions (although it is amazing to me how people came up with this shit) but I do think it is worthwhile to go through the technical constructions at least once. I found the blog post by Dongryul Kim (which I have linked in the end) served this purpose.

Notes : In May's book however, he considers the category of compactly generated spaces as his category of interest. This category is not closed under colimits (which is why one had to add the weak Hausdorff part) but he claims that all the colimits that he will be considering in his book are in CG spaces.

I also think in the axioms, we just want it to be closed under small limits and colimits. Not sure about this.

References

Peter May's A concise course in Algebraic Topology

Jeffery Strom's Modern Classical Homotopy Theory

Dongryul Kim's blog post : link

[reductionisms]

circle, line

A circle and a line look different, right?

What about now?

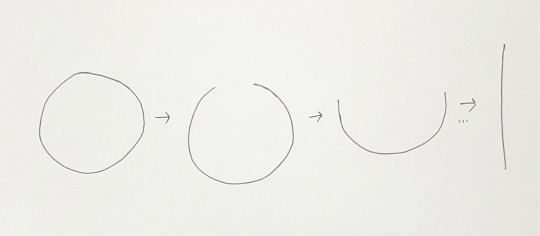
Time in gintama is a useless subject. Unfortunately, it is also a prerequisite to the gintama-human ontology. Thus, with a heavy heart, I look at lines, loops, and other unlikely time-mechanics in order to construct a gintama time for the gintama-human. 

Throughout this pseudoscientific inquiry, I locate gintama time– which I eventually call [time], for lack of better notation– in my thematic abuse of two mathematical concepts: irrationality and uncountable infinity. To give away the end, [time] is an uncountable infinity born in irrationality. Which, even to its own creator, makes little sense. 

Finally, this is my defense of the gintama time loop. Why? Well, I like loops and loop-like things, and, after all, we want good things to last, to repeat. So this turns out to be a love letter to algebraic topology. Sorry time loop fiction.

Onto more interesting things.

preliminary time notes

To think about time in gintama, I bracket [real world time] from [the narrative structure of gintama, which follows a time] and [time as characters in gintama experience it, i.e. personal time]. The latter two time-categories reflect [real world time] because gintama is written by an author, who, by virtue of existing, lives in [real world time]. That is, while narrative is fun because you can play with reality to make something new (e.g., time loop, time travel, non-chronological narratives in general), creation still requires building blocks, which are ultimately some sort of known assumption, that inevitably require some understanding of actual Time. 

All this to say I look at [narrative time] and [personal time] through philosophies about [real world time], which themselves are not especially real; in other words, my methodology is kind of shit. 

the situation– personal time

Otae announces the whole of gintama in chapter one.

This is gintama’s genetic code. 

To speak of time here is to note a few things:

1. amanto possess advanced technology;

2. humans are forced to throw away their physical swords;

3. the sword of the soul. 

The sword is a tool*; later chapters tell us that it “carries the soul”. So the sword represents, or, rather, is, something irreplaceable to humanity, that relates to the soul and personhood. This much is corroborated by the plot cycle. 

With contrast to the sword, time appears impersonal. We conceive of time, at least scientifically, as the movement between past to present, present to future, stretching infinitely before and after, where our existence does not matter to its flow. 

But would “time” exist without anyone to observe it?

Alternatively, how can “time” be experienced as time– as a movement– without anything to measure it? 

The human must “create” “time”, if only because it would not be “time” without a person to observe and call it as such. What this person perceives, they conceptualize as movement (measurement); and thus there must be a prior position to reference, or, in the least, a default– a memory. 

So “time” requires the present to be given by a prior; that is, for “time” to be experienced, the human who observes it needs already given into a past. The past itself (“knowledge” of the histories that make us who we are, “knowledge” of the tools that allow us to intend various things)– i.e., its inherent “given-ness” to us– depends upon it outliving those who live it. Thus various contexts, with their technologies, arts, and writing (though these are not really separable), function also to contain the essential past-as-memory for those who use and engage with them. 

Alright, great, but what does this have to do with the dick-and-balls manga? Nothing, really, except for everything. The amanto (with futuristic technology, in futuristic contexts**) force humans to give up their swords. It would be ridiculous to talk about what the “sword” means here. Suffice to say that it carries (an assumed) cultural-historical weight, an (idealized) memory. We would expect that its dispossession disrupts temporality. And it does– hence the “time loop”.

People love to talk about cyclical time in gintama. It is the same situations, over and over again; that no one ages, injuries heal by the next chapter, and, more than serial-typical regressions, that there is a sense that things won’t work, that important change won’t last, that life “just gets worse and worse”. Time as lasting change– or what we like to call “linear time”– doesn’t feel like it exists.

To return to chapter one. Here the central conflict is not actually between amanto and human; it is between Shinpachi and Otae. Their dying father tells them that even if they give up their physical swords (memory, past), they are not to lose the sword in their soul (?unknown). Sword-less Shinpachi resents him. Rather than “cling to the past”, he tries to adapt to the “linear time” of the amanto: he works in modern food service, gives up on the dojo, and, most importantly, opposes Otae.  

What does Otae do? We might expect her to inverse Shinpachi, that is, to “embrace” cyclicality, which would be to give up. She doesn’t. Otae tries to adjust, to make a living and survive, but, unlike her brother, she does so also to protect the “thing she can never take back”. This, as Shinpachi points out, is ridiculous, unrealistic, and makes no sense. And yet it is Otae who is thematically vindicated in the end.

From the first chapter, then, we can construct a sense of [personal time (to the characters)]. Again, for change to exist, there must be a prior form; that is, a certain sort of time is what makes change (technological, political, situational advancement) possible. Further, the self is involved in the process of time. Thus when the self is not whole (lacks the sword), time, and thereby change, becomes cyclical. So “time”, to the amanto, advances, because they can work with their external “selves” (technology, worlds, knowledge-memory) to “make change”. But time, to humanity, loops back on itself, is stopped, because humanity is bereft of its self and can only return to the starting point. 

We notice that humans still live in a world where time progresses– where time goes on without them. There is a split between the time of the self and the time of the world. Shinpachi decides to do away with memory and join the world-time, the “linear time”, that is, the time of futuristic technology and change; but his sister, who goes along with this and drags the past with her, does much better. 

For a more thorough application of this thought, please rewatch the monkey hunter arc. 

*It is also (obviously) a dick. **This reveals some connection between the concepts of “tool”, “context”, and time. Though I say so inverse-facetiously, since nothing about gintama can be taken as if it were serious.

time loop– narrative time 

So what about infinity?

Personal time is not infinity. In a first sense, it simply is not infinite– characters die. In a second sense, even considering that memory can be (haphazardly) preserved beyond a lifetime, especially in a story, humanity as a whole is finite– there comes a point, eventually, where no one is left to do the remembering. And in a third sense, personal time is still a string of pasts that were once presents, into futures that will be presents; though this finite string might divide into an infinite number of presents, its divisibility renders it still essentially patterned, which is to say that it is not really “infinity”– it is still mathematically countable.

I mentioned a dysfunction of personal time into cyclical (“un-change-able”) personal time. This is associated with sword-less-ness, equivalently memory-loss, equivalently not being a whole self. The fun of stories is that “character” can be projected into the structure of the story itself; it would make sense for cyclical personal time to have some correspondence to, or at least effect on, narrative time, that is, narrative structure. 

At this point I should be more general about the time loop. 

The time loop is thought to stand opposed to “linear time” in the stagnation-change, lack-presence, circle(hole)-line([censored]) dichotomy. Specifically, the time loop is opposed to “linear time” in the sense that nothing (usually) changes in a time loop. Or, more exactly, change is slow, nothing gets “better” in any real sense. Again, only where time flows “linearly" can we build off of what is prior, can we intend and achieve a future, can we change for the better (or so we assume). Thus the time loop carries a sort of moral condemnation in its very structure— a karmic debt, if you will.

Characters in plots get thrown into time loops because something has gone wrong. Whether or not they are the direct cause, the character must “figure something out”, “learn a lesson”, that is, address the problem that created the time loop, which will almost always be related to a step within the story of their self-development, in order to escape it. The point of the story is to escape it. This is just how stories go.

Then the gintama narrative “time loop” is barely a time loop. It repeats itself, sure, and no one ages, but that’s because no one should age in a wsj serial and sorachi tried to be funny about it. Still, some lingering sense of futility, or maybe just the sheer repetition of the same event for 16 years of serialization, weighs on anyone who reads it. This kind of feels like time loop fiction; there should be a point to the plot cycles. What are they trying to force Gintoki to do, to show us in his character? What are they aiming for, what is driving the “time loop” in the first place?

Takasugi is driving the time loop. 

(More specifically, Takasugi’s crushed eye-ball (soul), his eyelid; inaccessible past (memory), is driving the time loop.)

Another clarification. Personal time is time as experienced by the person; it is pure interiority. Thus, while the world moves on– personal time is time as movement– the person may not. 

For the person to move on, they must be able to make change, that is, from a prior form, give birth to the next form. This is because only the person can observe, know, and experience “time”, which itself is a movement (a change in position) from past to present, present to future, that is defined by the person. So change and time-as-movement, within personal time, look synonymous.

Further, movement in personal time requires the given past– the memory, from before me, passed down to me by people and places and things and contexts that I outlive– to be held by me, to be part of the “I”, and thus for my bodily self and my non-embodied self to generate personal time together. In gintama, I locate “memory” as the sword. But gintama’s sword is also part of the Self; so personal time in which the Self can move is only born out of a whole self. Equivalently, personal time is not the Self, but it is intimately related to a change that can only be wrought by the Self, which is to say, both my body and my given memory are necessary to the movement of personal time. 

In any case, “gin-tama” is about Gin-toki, and, quite literally, his soul, so we would suspect that narrative time is a projection of Gintoki’s personal time. But narrative time cycles weirdly, and Gintoki still has his sword. Alternatively: if Gintoki was not already a Self, that is, if he had to learn some lesson to become a Self through the time loop, how could he have saved any of the endless roster of villains that conveyor-belts around him? So maybe Gintoki holds his sword without remembering– except that he doesn’t, and the story makes this clear (“I haven’t lost a single thing”). He does, however, seem to possess a slightly different personal time. He and his sword remind antagonists of what they’ve forgotten, and these antagonists sometimes move forward with him into the next cycle. In other words, there is some sort of movement, a change, in the narrative, in the structure, associated with each loop. 

But cycles stay cycles, up to a very particular moment.

At which point I revert to the most obvious advantage of narrative time: it interacts with the readers. Gintoki “is” a Self (in the sense that an electron is both a wave and a particle), who carries his sword, who remembers, who hasn’t lost a single thing. Yet the time around him repeats the same events, over and over again. Why? Well, in part for the above: every gintama villain needs to learn the same lesson. But every gintama villain is also Gintoki, and even if he remembers, we don’t. To risk being redundant, we, as readers, have no idea what actually happened to him until chapter 519, when it is fished (unwillingly, I think) out of Takasugi’s eyelid. 

Then narrative time functions in several senses. It relates to Gintoki’s personal time, but indirectly; more generally it looks like a projection of the Losers’ personal times, where a Loser is one who has lost their sword. Still every Loser is also Gintoki, and every lost sword is lost memory, and even if Gintoki hasn’t forgotten anything– and even if Gintoki carries his past, his sword, with him– we, the readers, don’t. Surely enough, historical time in gintama only begins after chapter 519. The revelation must precede it. 

So the gintama time loop is driven forward by whatever it takes for this memory to be revealed. Each iteration brings us closer, but there is no lesson for Gintoki to learn that would speed this up; the heart of it is that he is waiting, he has to wait, for memory to return, for his past to come back to him, and this past is exactly Takasugi. 

Why? Takasugi is the past (his eye, his eyelid, is the past); his eye is therefore Gintoki’s sword, the sword of the soul we need for time to move on. But 10 years jump before Takasugi can make the approach, and even then only from behind. Worse, it takes hundreds more chapters for him to work up the resolve to face Gintoki head on. So if Gintoki somehow constrains the world to cyclical time, equally so does Takasugi. 

In short, narrative time cannot move until Takasugi’s eye becomes Gintoki’s sword. Thus half of the loop is about Gintoki always standing up again, always waiting for Takasugi to face him, and the other half of the loop, that is, its motivation, is about Takasugi working up the guts, or whatever he does throughout the series, to finally come at Gintoki* face to face. Yes, I’m equating circles and lines, which is silly. But I did this in the beginning anyways. Rewatch the final.

So why does this matter? Readers well-versed in gintama sword theo-ontology may recognize that the sword which is memory is identical to the sword of the human. This is partly because I’ve defined personal time to require the whole Self (the human) to move, which itself requires both the sword-as-memory and its human wielder. It is also because I’ve equated Takasugi to memory instead of treating him like a character (sorry Takasugi). Nevertheless, creation of the human sword (the memory-sword) is now essential to creating time, and creating time is now equivalent to completing the Self, that is, to becoming “human”. Put another way, Shouyou isn’t killed until Gintoki kills him in 519. 

More specifically, Gintoki killing Shouyou undoubtedly completes (undoes) his humanity**. It is also the only way for anyone in gintama to have a future, because it creates, gives birth, to time, the time of the series. Further, its revelation births time in the present just as its actuality births time in the past: the Gintoki who swings his human sword, who cries, in Takasugi’s eye, is the one who swings it at him now. Gintama doesn’t actually timeskip until Gintoki kills Utsuro in silver soul.  

Then the movement of time, both personal and narrative, requires three things:

1. a memory-sword (the human sword) (the sword of the soul);

2. a human to wield it;

3. and a decision on how to swing

I have discussed one and two to exhaustion. Now we turn to three.

*Gintoki is always Takasugi, in every case. The inverse holds as well. **It also completes Shouyou’s, but that is for later.

in defense of the time loop

Birthing time looks like an escape from the time loop. 

This is where the division between time, self, and change becomes essential. Why does the time loop, in many treatments, depress its readers? For the same reason that any tragedy is depressing: fate, un-change-ability, specifically, un-change-ability of things we want to change. 

The time loop is a “literalization” of tragedy. The person trapped in the time loop, at best, loses the ability to determine their future, accomplish their projects, do what they want and have it last, that is, to find lasting (exterior) meaning (this is all exterior). At worst, this person carries their incapacity into a loop that is the same tragedy, over and over again, which they are helpless to prevent or change in any way.

This setup is not exclusive to the time loop– other variations could be immortality, reincarnation, oracles, endless linear eternity, et cetera. In every instance, though, the tragedy is that people cannot change the things that matter. And while the time loop usually removes external change to provoke internal change in its protagonist, gintama characters also struggle with the impossibility of changing themselves.

More generally, though, real time isn’t actually cyclical or linear. We move through time, changing form, towards our death– and so the common thought of time is “linear time”, which is really about “linear change” and an inability to “go back”. But time is only known to us, only countable, because of its cyclicality. There are 60 seconds to a minute; 60 minutes to an hour; 24 hours to the day; and then this repeats the next minute, the next hour, the next day; and then the next month, and then the next season, and then the next year; and then it repeats all over again. Time is only measurable, knowable, existent to us because it repeats. If it wasn’t known beforehand, how could we measure the present, the future, against it? And for it to be knowable, it has to be familiar; and for it to be familiar, we must have encountered it before; and here is the inherent repetition– we can’t stop the cyclicality or flow of time anymore than we can avoid our deaths. Real time makes possible our “change” just as it is unchangeable, just as its existence is conditioned on unchangeability.

Gintama is a story, and story time works differently than real time, so maybe in the story we can separate “linear time” (change-ability) from “cyclical time”, from “time loop” (un-change-ability). Even still, what happens after you escape a time loop? Equivalently, what happens after you escape the tragedy? In the usual time loop– at least the usual time loop in our minds– the loop is escaped into linear time, or, more appropriately, it is escaped into the time where linear change is possible. But why is “linear time” the happy ending? Even granted that it exists (which is questionable), what makes linearity better than repetition, that is, why do people love “linear change”?

The Joui 4 lived “linear time” during the war. They fought enemies, and won. They progressed towards something, and believed in it, too; they were the main characters of a power-scaling, battle-shounen manga. And yet, their linear time ended, or more accurately, was never “linear”. Shouyou’s death, if anything, only proved the inherent impossibility of their shounen dreams. So narrative time twists into defeatist cycles, and Takasugi is doomed forever to repeat, and this is probably more accurate to the condition of the actual world they inhabit, because, most importantly, time was always like this, linear change as linear time never existed. 

But again, the tragedy was never about the time loop. From its inception, the tragedy has always been about intentionality versus ruination, “I” as capable actor versus “I” as acted upon, and the utter inability of anyone to change any of this. We want out of the time loop because we can’t do anything; we want out because we can’t act out of ourselves to make external change in any way that lasts. Ultimately, we want out of the time loop because we discover that our intentionality actually means jackshit. The world does what I don’t want it to, and traps me in this; I cannot act, and yet it acts on me. My despair at the exterior world which rivets me to itself quickly translates to despair in, at, my self. I can’t make change, so what does being [x person] matter, so this is my fault, so there’s no point in changing myself, so I can’t change myself in any way that matters, because even if I do everything right, there’s no meaningful effect on the world that holds me captive, et cetera. Thus everyone wants out of the tragedy, the time loop.

Including gintama villains, who usually try to get out of it by killing themselves. This never works. 

The time loop is tragic because it makes its inhabitants absolutely passive to it and acts on them eternally. The gintama cast is supposedly full of “losers”; its villain of the week, while beating Gintoki, calls him a masterless dog, a ghost, the one who lost, along with the rest of the samurai, et cetera; and the loser here is inherently passive against a winning actor. Nevermind that Gintoki never fought for the Romantic Japan that lost to the amanto– his loss is even more infinite for the narrowness of its scope. 

And yet, you’re not supposed to kill yourself.

Escaping the time loop– or, more generally, the tragedy– never guarantees linear time, because we always have to end the book on the happily ever after. So what really happens after you escape the time loop– is linear time actually a relief? Either things start going wrong, which isn’t the linear time ideal, or you achieve every dream, you make possible every impossibility, and come to the end of the infinite series by continuing on within it infinitely. Is that really “happy”? 

Alternatively: the cycles of narrative time drive towards the birth of a new time. But the tragedy of the cycles is intentionality/ruination, and the cycles can’t be escaped into their “opposite”. Gintoki, a human, with a human sword, kills Shouyou, and thereby brought forth a new time. And yet, this new time was still cyclical. 

Then what’s the solution– killing yourself? Takasugi, repetition Personified, asks this to Gintoki the entire series. Why won’t you stay down?, [Why are you crying?], [Why can’t I comfort you?], Why keep living in this world? Villainy aside, he does have a point– if you look carefully, living in the gintama world is incredibly, incredibly stupid. 

Gintoki says: no matter how many times I fall, no matter how many times I fight the same fight over and over again, no matter if it never ends, I will always stand up.

This is the height of stupidity. 

[time]

So narrative cycles aim at the revelation of Gintoki’s memory, which would identify sword with eye, tool with wielder, that is, complete the “human”, and thereby give birth to a new (non-linear) time. 

Here we get to mathematical infinity. 

Mathematical infinity is not a number, or even properly a concept. It’s more like a sign at the edge of a cliff that says, there’s a cliff here, here’s the end of the world– except that this sign also signifies whatever, and everything, that might lie beyond the cliff, which cannot really be called “essence”, or even be said to exist in the first place. In other words, infinity is a marker for a point of no return, that in of itself is nothing.

Some things are said to be “infinite”. Usually, these are patterns. A line is infinite, as is a parabola; but these infinities are predictable, that is, countable, because patterns are rules. Their comprehensibility allows us to treat them like fancy numbers. 

Conversely, some functions decompose into situations that are entirely ungraspable. This edge of knowledge, where it devolves into paradox and nonsense, looks like uncountable infinity. 

Uncountable infinity is the infinity whose name itself means nothing. It signifies to something that is, by axiom, impossible impossibility, ungraspable. When infinity “interacts” with the mathematical world– or, rather, when we push far enough to reach it– we come to paradox, chaos, and unintelligibility. Certainly, science could advance sufficiently to reconcile the mysteries of particle physics; but the fun of mathematical concepts is that you can define them in any way you like, even if they’re fake. And uncountable infinity is, by my definition, the “thing” that is always uncountable. 

So gintama narrative cycles aim at something, while those in cyclical personal times suffer for them. Cycles, better, change-less-ness, correspond to sword-less-ness, to lack of memory, and historical time only “restarts” when Takasugi brings us the past. Et cetera, et cetera, et cetera. 

This doesn’t mean our new time won’t be cyclical.

In the end, “time” is associated with sense of Self. This is an unavoidable relation, because time is a human word, in a human language, that describes what is ultimately only known to us as human experience. But “Self” is (itself) a problematic concept. After all, what determines one’s Self? Relatedly, who, and/or what, and/or where, and/or why, gets to possess Selves at all?

Within concepts of Self is often embedded an instinct towards differentiation. The (western philosophical) impulse is to originate this difference in agency: that is, through my free determination of my Will, my Projects, my Actions, and et cetera, I differentiate “I” from “other” and thereby constitute Me. Needless to say, concepts of “agency” are inextricably linked to “change”. Thus, in this particular conception, “time” is bound to “Self”, is bound to “agency”, is bound to “change”, and to invoke any one is to invoke the other three. 

Here, “knowing” (as agency) finds itself imperiled. That is, though the “unknowable” would strip agents of acting-ability, “knowing” would also consign existence, life, the universe, et cetera, to determinism. In both cases, “(un)-knowledge” renders the agent passive. Thus someone might long for an unknowable magic in order to undo determinism, just as they might long for the knowledge to successfully determine their life; yet the one who longs for agency could find agency a disappointment, a not-agency. Equally, if the time loop embodies both desires before they collapse into paradox (I can continue into the unknown future if I escape; something is tying me down, my knowledge is insufficient to escape), “linear time” does so as well. 

But now we return to infinity, to irrationality, to uncountability, in short, to paradox. The bulk of the previous 5000 words has been to determine that the dichotomy is false. To be straight, knowing and not knowing, agent and non-agent, the linear and the cyclical, are not separable from each other. Their binary is an illusion, and the suggestion of one carries within it the absence of the other; they are synonymous at the exact and every moment they are not. Clearly, this is not not-knowing, and not knowing, and not not-either of them at the same time. I call this uncountable infinity, the mathematically irrational. 

The mathematically irrational is paradox. Consider: we can graph, and look at, certain functions, and yet never grasp their value (put x(sin(1/x)) into desmos). Similarly, we know exactly what “pi” is– the ratio of a circle’s circumference to its diameter– and we can define it, use it, find it in every instance. And yet, pi is an irrational number, because its decimals trail off into uncountable infinity. Knowing and not-knowing, united in the same action: irrationality is knowing in not-knowing, not-knowing in knowing, and also neither. 

I will be ridiculous and find this paradox in gintama. I want to claim, in the first place, that the self never generated time at all; in the second, that this is never irreducible to agent/acted, knowing/unknown; and in the third, that time is generated by [time]. To do so, we must investigate the moment of its birth, in 519.

the cliff—519

Tools, given memory, etc., together with the persons who hold them, produce an actor-self, a time of possible change (a “linear” time). It is in 519 that Takasugi finally faces the camera.  

Now Gintoki grasps the sword (memory, Takasugi). This should give us “linear” time. 

But 519 is not so willing. Where we hope for capable agency, we find none. Instead linear/cyclical, active/passive, presence/distance, collapse into irrationality.

Take the archetypical moment. To Takasugi’s why, Gintoki says he’ll stand up. Specifically, he says, too bad– I (you) won’t fall. 

Standing up is what Gintoki (a person, with a sword) does. It is how he defeats each suicidal villain, kills Shouyou, and kills Shouyou and Takasugi all over again. This is what the “time loop” would require of him. 

Gintama antagonists, those paragons of rationality, tell us that it is irrational. 

Otae is also irrational. Her irrationality doesn’t fix anything (⇔escape cyclical time, make change), and she knows so herself– “If I’ll suffer either way, I’d rather suffer protecting it.” 518 chapters later, Gintoki says: “I won’t fall until you [Takasugi] fall, until you stop, no matter how many times it takes, I’ll stand up again… even if I have to walk over my teacher’s corpse, even if I have to walk over your corpse, I’ll protect his disciple, our companion, Shoka Sonjuku’s Takasugi Shinsuke, his soul.” 

So Gintoki stand(ing)s up until something– until Takasugi stops, until time is born– in order to protect Takasugi’s soul. This might look like an “end” to the cycle, but it doesn’t feel like one. “Even if I have to walk over your corpse”? 

Alternatively, “saving” Takasugi should be the change that the cycles want to make, that would break them in any normal work of time loop fiction. It is “agency” (capable action, material change) at its purest. But Gintoki says he will stand up and kill Takasugi and stand up again. No matter how many times the same thing repeats, no matter if time never moves on, no matter if he is forced to kill the very person he’s trying to protect, Gintoki will stand up. How could Gintoki possibly care about escaping any cycle, when he is the one “perpetuating it”?

So gintama is not actually about escaping the time loop, which is the rational thing to do. Gintama is about, do you have the strength to keep living in the time loop, even if it never ends?, or, do you have the strength to kill your teacher and your friend, and lose everything all over again?, or, do you have the strength to eternally suffer for the thing that can never be taken back? In short: forget the capable actor– gintama is about being foolish, and irrational, and embracing the time loop by standing up. 

If we look to chapter one, [standing up] is [protecting the thing that can’t be taken back]. Neither can be appropriately confined to cyclical or linear time. Otae says she’ll suffer either way, and Gintoki says he stands up to protect what Shouyou held precious, Takasugi’s soul. 

Otae protects a thing that cannot be taken back. This is the past. Gintoki acts for– and this is also a protecting– the past. Takasugi is, in a literal sense, pierced by this past every moment of his life. 

The past that we can recover, that we can fully integrate into ourselves, is the past that can be used to generate the future in “time”. Thus “accepting” the past “to move on” – accepting, making entirely part of oneself, making entirely interior – because only then can the past become knowable, comprehensible, and usable. The person must accept their past to change things, i.e., to make linear time. Time, change, and agency coincide.

Yet Otae’s past “cannot be taken back”. Certainly, even the accepted past cannot be “returned” to. But Otae’s past is the past that pierces Takasugi’s eye– that is, the past whose “revelation”, whose self-same existence, drives the completion/generation of gintama time itself.

So this is the past that “cannot be taken back”, in more than the literal sense. Takasugi is scandalized by its distance, even as he dies satisfied; Gintoki, ever-silent, still loses his composure at its provocation, is emptied by it, cries in 519 (in all of gintama), in 703. It is a past that refuses total use or incorporation; instead it acts on those who carry it, even after person is reconciled to sword (to its memory).  

Its paradox in position. Though “the past” is always present (“I haven’t lost anything”, “how long will you keep looking at that crushed eye of yours”), it is simultaneously kept from us by an irreparable distance. Distance, of course, suggests space, which itself suggests a space that is surpassable. But this distance is not spatial– it is temporal. Gintoki carries the past, yet never reveals it to anyone, much less to us; in the end it is Takasugi who has to do the revealing, and even then only after 500 chapters. Further, its revelation actually increases the distance. We grow used to our proximity to Gintoki’s “point of view”, to our role, through him, as protagonist of the story; and here his defining moment is told not through his eyes, but through the eyes of the distant antagonist, whose breaking point is the discovery of the distance between him and Gintoki. Gintoki is reflected– more, revealed to have always been– across a distance that is unsurpassable. 

This distance is equally time, because Takasugi and Gintoki were separated always, and only, by “the 10 years”. Takasugi comes to Edo– there is nothing stopping him, spatially, no physical restriction or meaningful law imposed, from making the approach– and yet he cannot make it. Or so we assume. We only know its universal separation axiom: 10 years, a distance between two points that could never be overcome or recuperated. 

So the past is across an unsurpassable distance. In this sense, it cannot be taken back. It is simultaneously carried in, pierces, Takasugi’s eye, who struggles because he cannot reconcile it to himself. Just as it is always with him– “every time I look, the beast…”– it is also the one thing he cannot bear to see (your crying face). Though its revelation is necessary to New time, it is also what sent time into irregularity in the first place. And though it is irreparably distant, it pierces every moment of the present, which is to say: it degrades time, it makes things weird.

Its paradox in times. The cliff is pre-originary to everything by narrative position. Gintama narrative cycles press towards its revelation as first dilemma. It is before even the corpse field, before anything else. It drives each time Gintoki swings his sword and reenacts it. The very first moment that Shouyou finds Gintoki, is predated, predicated upon, generated, made possible by, the fact that Gintoki kills him with his sword. 

From this past, Gintoki is (in the verb sense). It is ahead of him (in 519) and behind him (before 1). For its sake he “acts” towards a “change” (stands up) that he knows is impossible (“if I have to walk over even your corpse”*). In other words, for sake of this past, Gintoki lives as if he belongs to a “linear” time, even as he knows he doesn’t. The past brings forth itself again.

Finally, its paradox in agency. What is burned onto Takasugi’s eyelid is a single moment he cannot recover or recuperate. Instead, this moment acts on him, it pierces him, against his will. This sort of past is not an empty concept, that could be filled with any given circumstance. Takasugi is tortured because the content matters– because what happens on the cliff that day, matters.

The cliff is not what Takasugi, Gintoki, Shouyou, or anyone else, wanted. Worse, it is not what they fought for: Takasugi to save Shouyou, Gintoki to protect Shouyou’s disciples (in an act that he knows will destroy them), Shouyou to protect his children. Instead Takasugi is stripped of agency, and the eye that would acquire it; in the present he acts on everything because he is, in every moment, acted on. Equally, just as Shouyou tries to protect his students, he destroys them, and Gintoki, who is forced (acted on) to choose (acts on) between two wrongs, two denials of his self** (of linearity), that is, two losses, is the classic agent paradox most of all.  

So the past cannot be taken back, and this not only in the sense that no one can return to it. The past cannot be taken back as a memory, nor can it be incorporated as part of the self, nor can it function as the essential memory that projects forward normal time, even as it is known at every single moment. It cannot be domesticated. 

Gintoki killing Shouyou, and crying, is unacceptable. It is distance itself, just as it is proximity; it is simultaneously known (Takasugi sees it), unknown (no one can reconcile it), and neither (we still move on). It should not have happened. It is irrationality itself. 

And yet, by virtue of being “a past”, in its relation to the present, in its position as driving force of the time of the entire series, it still is time. The human, with the human sword, who cuts off someone’s head, is [time] itself.

Clearly, this is something outside of normal time. The question becomes, who needs to be killed, and where, and why?

The one who gives birth to a future.

*–and he does. 

**“No need. They’ll never hold a sword again.”

the future

That Gintoki kills Shouyou is essential. 

The start of gintama’s “historical timeline” is the corpse field. Here the time that Gintoki sits in carries a heavy sense of eternity. The moment where Shouyou finds him could be forever; historical time is out of place. 

What breaks this time is very particular. It is not that person and sword = human = time in the automatic sense, because Gintoki, who holds a successful sword (“before meeting you, I never lost to an adult”), remains inhuman. Rather, Shouyou, a human (to Gintoki), must give his sword to Gintoki for time to start. This is also what makes Gintoki human. Gintoki, the human, had to be given his humanity– and thereby time– by someone else. 

Equivalently, it is not enough for gintama’s [being human] that the right person holds the right sword. Only a human can progress time, that is, give birth to the future, but reconciling self to past, sword to eye, escaping the time loop, is insufficient. That Shouyou finds Gintoki is predicated by the cliff; sword can only become eye through the cliff’s revelation (and the cliff happens concurrently); self and past are reconciled only after Gintoki kills Takasugi; and the Shimura dojo is restored only once the Shimura siblings kill their mentor. It isn’t enough just to hold the sword– you have to actually swing it. 

This swing must be something irrational, because everything else is just the natural extension of a person with a sword (it is the person and the sword). Further, the person must make the swing themselves. For it to be a swing they make, they need to choose it. So the swing is a decision made in irrationality. 

Swinging a sword at– beheading someone— who is clearly the irrational choice. What goes against the logic of the world, of time, of all the meaning you sought after? Gintoki fought to protect Shouyou’s disciples; but Takasugi tells us that he wanted to save Shouyou more than anyone. Narrative logic says that Shouyou’s disciples should die to save him, and the logic of their linear time– their humanities and their swords– is to rescue Shouyou and progress into the future. Gintoki swings against everything. And cries.

Gintoki stands up, is irrational, for the past that can never be taken back. This past completes his humanity (person, sword, swing) in the moment that it ruins it (he cries). Gintoki kills the one before him(先生) to make them the one behind (into the past); which itself is a loop, is a cycle, but also a line. It is a [being human] that gives birth to an irrational time. 

Gintoki kills Shouyou even though it changes nothing. How does this birth time? “Time” comes out of a self, but Gintoki loses his self; “time” is what renders change possible, but Gintoki cannot “save” Shouyou or Takasugi. Certainly Gintoki knows this, and kills Shouyou in spite of it. But how does this bring forth a future at all?

Gintoki does kill Shouyou for something, for some reason, and this is concretely the survival (into the future) of Shouyou’s disciples. Abstractly, though the purpose is less clear– “even if I have to walk over your corpse” – it is still what drives (is the purpose of) every instance that Gintoki, or anyone, stands up. 

Gintoki’s purpose is Shouyou’s purpose, and Shouyou dies to give birth to the “future” (a future that is born in irrationality). So when Utsuro comes to kill him, Shouyou sees also Gintoki, and smiles. Sakamoto calls this “hope”.

We are told that Shouyou gives birth to hope– his students– almost as if to invoke the analogy. Shouyou’s disciples– his “children” – are him, because he gave birth to them, and they are not him, because they have a futurity beyond his imagination. Equally, this future is knowable, because the child is you, and time repeats, just as it is not, because the child is not you, and you will not be there to see it. This is the substance of “hope”.

With regards to the structure of his world, his time, and perhaps even his own humanity, Gintoki makes the irrational choice: he stands up. But to stand up is actually for, to give birth to, the uncountable future. Sakamoto tells us that Gintoki “gives birth” to this future in every shounen-bond he ever makes. And here is the paradox, something more generative than irrational dilemma– Gintoki’s “descendants” inherit his soul to be in ways unimaginable to him. 

This future pierces every moment, and in the same moment it escapes. Take that Shouyou knows, and cannot know, what his disciples will be. Their possibility is imaginable, in the sense that he can delineate it– “I hope you all find your own bushidous” – but it is also uncountably infinite, because your child is not you and not beholden to your patterns. Equivalently, Otae’s happy memories end when her father dies, but she still keeps the sword of her soul, this unspeakable thing, that past, and it is her purpose in standing up. 

Gintoki, with the sword he has been given by a human, kills Shouyou. This gives birth to an uncountable future– uncountable because it is born in irrationality, beyond the possibilities and expectations of pattern, either linear or cyclic– that is an uncountable infinity, and this is [time].  [time] drives, again, pierces, every second of all of time, and in the same moment it escapes. It is also irreparably beyond the one who births it. This is why gintama had to end. 

So the human is constituted in the moment of death (⇔the moment of irrational swing), which is to release the future— [time]. In the same moment, humanity, and [time], escapes. But the moment of constitution (⇔ [time]) is what births the next instance of being human, that is, the rest of time. 

In the moment before Gintoki’s irrational swing, each [time] was truly infinite. Here possibility is as unthinkable as Gintoki’s heart; there is no better way I can describe this than an uncountable infinity. Gintoki did what he should have (not) (not) have done. Neither he, nor Shouyou, nor Takasugi, Katsura, Oboro, or anyone, could have imagined any possibility for the future that was to come. In its sheer impossibility, this was infinity: the past that cannot be taken back. 

But the past that cannot be taken back is also the sword of the soul. By definition, this generates an impossible impossibility, that slips away as soon as it is born; and as the uncountable, that is, the mother of all irrationality, and also its child, [time] has little to say about lines or circles, aside from that they are essentially the same. So gintama never cared about time loops or not: all that matters is if you follow [time] by standing up. 

When Gintoki recovers his sword (Takasugi’s eye, Takasugi), he does so amidst a wreckage that looks like pine trees, as Takasugi (the one who finally stood before him, who now will stand behind) dies in his arms. Here, we find that the “cycle” repeats: Gintoki stands up, and the sun rises.

This is the dawn of a new, impossible day.

I don’t think that’s so bad. 

[unnatural-transformations]

My Favorite Mathematical Proofs [2 of n]

For any convex polyhedron with V vertices, E edges and F faces it is always true that V-E+F=2. This result is known as Euler's formula, named after the prolific Swiss mathematician Leonard Euler. In more modern terminology, we can also express this fact by saying that a convex polyhedron has Euler characteristic equal to 2.

However, the story of this formula goes back to well before Euler, and it would be decades after Euler before any really satisfactory proofs were discovered.

Ancient Greek mathematicians had proved the existence of exactly five convex, regular polyhedron [also known as the Platonic solids]. Recall that these are:

The tetrahedron, which has 4 vertices, 6 edges and 4 [triangular] faces

The cube, which has 8 vertices, 12 edges and 6 [square] faces

The octohedron, which has 6 vertices, 12 edges and 8 [triangular] faces

The dodecahedron, which has 20 vertices, 30 edges and 12 [pentagonal] faces

The icosahedron, which has 12 vertices, 30 edges and 20 [triangular] faces

[The images above are from the Polytope Wiki and were created using Robert Webb's Stella Software, http://www.software3d.com/Stella.php]

In the 16th century, the Sicilian mathematician Francesco Maurolico observed that all five Platonic solids satisfy the equation V-E+F=2. A couple of centuries later, Euler -- who probably wasn't aware of Maurolico's earlier work -- discovered that the same formula seems to hold for convex polyhedron more generally [i.e. without the assumption of regularity]. However, Euler himself did not publish a convincing proof. (It feels a bit surprising that it took mathematicians this long to notice what now seems such an obvious fact. In fact, in the 17th century René Descartes had stated a result about the face angles of a polyhedron which implies Euler's formula, but Descartes doesn't seem to have explicitly recongized the connections between face angles and edges.)

Imre Lakatos' (excellent) book Proofs and Refutations uses a (deliberately very simplified) version of the history of attempts by mathematicians to investigate this formula as a way of discussing Lakatos's thoughts on the role of proof-attempts in developing mathematics. Rather than describe the actual history, Lakatos presents a discussion of Euler's claim in a classroom setting, with the various students (named Alpha, Beta, Gamma and so on) variously attempting to prove, falsify, defend or expand the scope of the original formula. Reading this book as a teenager made a huge impact on me, and I'd recommend it to anyone interested in the philosophy of mathematics who hasn't read it before (just don't take the historical footnotes too literally...).

I was particularly impressed by the final proof Lakatos presents (through the student named Epsilon), which is actually due to Henri Poincare (who is really the first mathematician to establish topology -- or 'analysis situ', as he called it -- as a branch of mathematics in its own right).

Epsilon's proof works by first translating the geometric definitions of polyhedron (or more generally any n-dimensional polytope) into purely combinatorial language. A polyhedron is a collection of objects called vertices, edges and faces, all of which can be related to each other in terms of incidence matrices. These incidence matrices let us translate our new combinatorial terms into the language of linear algebra. The vertices, edges and faces of our polyhedron become the basis of vector spaces over the field with two elements. The geometrically intuitive notion of a 'boundary' (of a given polygonal face, say) corresponds to a linear map between such vector spaces, which sends a given face to the sum of its boundary elements (a polygon is mapped to the formal sum of the edges that bound it, an edge is mapped to the sum of its two vertices, and so on).

Finally Euler's original claim about polyhedrons becomes a claim about the properties of this map, which we can prove directly using the rank-nullity theorem.

For the simplest possible example, consider the tetrahedron $P^T$.

(Obviously in any worked example like this when we can simply read off the number of faces, edges and vertices such a proof seems redundant. The point is that we can show that this approach will work for any convex polyhedron, or indeed convex polytope, not just a given one.)

The faces $F^T_i$, edges $E^T_j$ and vertices $V^T_k$ are related as shown in the Hasse diagram below.

We associate a vector space to each row of the diagram, with basis given by the number of nodes on that row. The boundary maps δn map each basis element to the [basis element corresponding to the] sum of the nodes incident to this element on the row below. This then extends linearly to a map defined on the whole vector space.

It can be checked directly from the diagram that the boundary maps are as given below:

Indeed, working over the field with two elements (so that addition is modulo 2), we can explicitly calculate the kernel and image of all four of these maps. The results are summarzied in the table below.

Note that the image of δn is always equal to the kernel of δn-1. Epsilon argues -- or asserts, anyway -- that this is necessarily true for any simply connected polyhedron [and in particular any convex polyhedron]. A polyhedron is simply connected if it contains no 'holes'; and a hole in a polyhedron would correspond exactly to an element of the kernal of δn that was not an element of the image of δn-1.

Assuming this to be true -- and noting that the images of both δ3 and δ0 are always one dimensional for any single polyhedron, we have, using the rank-nullity theorem and the fact that F, E and V are by definiton the dimensions of the vector spaces V2, V1 and V0:

The proof as presented in Proofs and Refutations is not quite as rigorous as Epsilon claims (and indeed the slightly longer version that appears in Coexter's Regular Polytopes suffers from some of the same flaws). Nonetheless, I found it pretty amazing when I first saw it. It would be a few more years before I knew anything about algebraic topology or category theory [even basic linear algebra was quite new to me at the time], and this idea of solving a problem in one mathematical field by transforming it into something that seemed to be completely unrelated kind of blew my mind at the time.

As always, more details below the cut, where I try to sketch a version of the proof that holds for n-dimensional convex polytopes.

We start by defining a convex polytopes, which are a generalization of two-dimensional polygons and three-dimensional polyhedra to any n dimensions.

This definition doesn't mention vertices explicitly, but these arise as particular points in the convex hull. For example, the tetrahedron is the convex hull of its four vertices in three dimensional space, while the (regular) pentagon is the convex hull of its five vertices in two dimensional space.

However note that two different sets may have the same convex hull. For example, if a and b are points and we add a new point 0.5a + 0.5b this clearly does not change the convex hull. More generally if any point p can be written as the convex combination of a set of points S then the convex hull of S ⨃ {p} is just the convex hull of S.

The vertices (or extreme points) of a convex set are exactly those elements that cannot be written as a convex combination of any other points.

Definition 1 also makes no explicit mention of 'faces' or 'edges' but these concepts can be recovered. It is conventional to use the more general term 'face' to refer to both edges and (two-dimensional) faces and their higher dimensional generalizations. (Some authors use 'facet' to specifically refer to the faces of codimension 1.)

[As @bubbloquacious pointed out in the replies, the version of this definition I stated originally didn't correctly define the dimension of a face. This definition has now been updated.]

The set of all faces has the structure of a particular type of partially ordered set. We recall some related terminology:

We can now introduce the face lattice of a polytope. This is a purely combinatorial object that (we claim) captures all the information about a convex polytope we will need for our proof of Euler's (generalized) formula.

See the texts by Grünbaum or Ziegler below for more details. The geometric properties of a polytope are often easier to reason about when translated into the languages of lattices. To begin to do this, we need a few more definitions.

The face lattice of a polytope has many of these properties. We will not use them all in the proof but list them anyway for background. The key property we want to make use of is the so-called diamond property.

For example, the dual of the face lattice of a cube is the face lattice of the octohedron while the dual of the face lattice of the dodecahedron is the face lattice of the icosohedron. The tetrahedron's face lattice is self-dual.

We will not prove Proposition 6 by the interested reader is again encouraged to check the references, particularly the book by Ziegler.

We will try to be a little more careful than Epsilon in establishing that the boundary maps have the properties we want. In words, we want to show that 'boundaries have no boundaries' and 'all cycles are boundaries'.

We just need one more result before stating our main theorem.

A proof of this result can be found in any linear algebra textbook.

Now we are ready to state and prove our result.

References & Further Reading

H. S. M. Coxeter, Regular Polytopes (Methuen, 1947)

Branko Grünbaum, Convex Polytopes (John Wiley & Sons, 1967)

Imre Lakatos, Proofs and Refutations (Cambridge University Press, 1976)

Richard Stanley, Enumerative Combinatorics Volume 1 (Wadsworth & Brooks/Cole, 1986)

Gunter M. Ziegler, Lectures on Polytopes (Springer-Verlag, 1995)

[blood-orange-juice]

I'm not a fan of bridging Genshin and Honkai, but the authors seem to be doing it anyway, so... blame Hoyo for this post.

tl;dr of Honkai lore

At the core of Honkai's cosmogony are two concepts. The Imaginary Tree — a tree of branching parallel universes, each twig of which is a timeline and each leaf a world. And The Sea of Quanta — a boundless place of entropy and chaos from which the Imaginary tree spawned.

Order and chaos, basically. They exist in constant conflict, the tree tries to consume the sea of quanta and the sea tries to flood and dissolve the tree.

When a world fails to persist it can "fall" from the tree into the sea of quanta, becoming an unstable fragmented version of itself called a bubble universe. A shadow of a proper world. Such a universe is eventually dissolved in the sea.

Bubbles universes can also be artificially created or spawned from someone's memories. Either way they are unstable. If I recall correctly, Genshin was confirmed to be a bubble universe in a Honkai 3rd easter egg.

Ether Anchors

There's a technology allowing to extend a bubble universe's lifespan, is called an Ether Anchor. An Ether Anchor holds together fragments of a bubble universe that follow a fixed set of laws.

It seems to be more of a place/space anomaly than an object (“a topological formation that exists between the dimensional manifolds”), if I understood Durandal's and Roland's lore correctly, but also can take the form of an object, if honkai wiki is to be believed.

(I think space anomalies are anchor points, not the anchor itself? the places where it sews fragments of reality together. I'm still figuring this part out)

Quotes from Durandal VN summary:

At the core of the Ether Anchor, space from different dimensions were cluttered together like vines

"There, he witnessed the endless possibilities of another ancient world. "

Tartaglia's character story 4

Readjusted her body composition with the Ether Anchor to turn herself into a weapon.

I think there was a guy in Genshin who constantly talks about turning himself into a weapon. I can't quite remember his name though...

 Synchronized themselves with the Ether Anchor, becoming the “Son of God” itself.

"The purpose of this line in the ritual scripture is to forsake the self and sink into the abyss, and in the abyss, to welcome rebirth as a holy infant."

Narcissenkreuz Ordo note

Another property of the Ether Anchor is that it allows bubble universes to interact with one another. 

Or maybe not exactly different bubble universes but rather fragments of the same bubble universe (or, since we are in a multiverse, these could be the same thing)?

"Unborn life, unfulfilled wishes, Tragic dreams at the edge of the universal darkness that could never come true."

Festering Desire description

Ok, this is getting too long and no one reads long posts. Maybe I'll continue in a separate post later. There are still the topics of the Abyss (and why it's not The Sea of Quanta), Descenders, whether the anchors need to be sustained in some way, Tsaritsa's goals, why does everyone who has seen the Abyss speaks of ultimate injustice, Alice and Hexenzirkel in general, what is Irminsul exactly, and, of course, Childe, why Childe's promise of a battle at the edge of the universe is more important than it might seem, what are world cycles, and why Childe's part of 4.2 story sucked so much (I now have a Lore Explanation. or maybe a copium overdose. probably both).

For now I'm calling it though. Whatever Khaenri'ahns messed up, it had to do something with Teyvat's Aether Anchor.

[bagalois]

100 days of productivity - 6/100

jan 22, 2025.

✔ went to class ✔ washed my dishes ✔ meal prepped! ✔ put away groceries ✔ troubleshooted an issue with my fridge to my landlord

(more under the cut - warning for very long and kind of negative)

today's the first day of classes (where i'm a student)! i'm taking combinatorics, group theory, and algebraic topology.

the profs for algtop and group theory were... okay, i guess. i dont doubt they are very knowledgeable about their field, and the lecture content was all fine and good, but the presentation i fear was not so good. my algtop professor waffled on about inconsequential things that only made sense to him for probably half of the entire lecture (random jokes and pedantic clarifications that depend entirely on your specialty that, frankly, while i understand their place, the slight difference in convention between algebraists and geometers doesn't mean very much to me as somebody who is not that familiar with either field). and the group theory prof, he spoke too quietly and the entire class could barely read his handwriting.

also, i fear that i've come down with a cold or a fever, so even though i got a lot done, i felt pretty bad all day. i felt okay this morning but i still wore a mask. another grad student asked me why i was wearing one, and i told them i was worried i got exposed to some sickness, since i was feeling under the weather.

i was started to overheat and get overstimulated just from my combo prof's voice .-. and she was the only good lecturer i had today! straightforward, concise, and had briefly humorous moments that didn't detract from the rest of the lecture.

overall i've been feeling less than great, but getting as much as i have done today makes me feel better. posting, cleaning, cooking - all these things help ground me in some semblance of reality.

(begin cw: us politics)

it's probably because i'm sick, but i can't deny that trump's inauguration -- specifically how a lot of people are panicking about it -- is weighing on me. i really hate how little i know about anything. palestine-israel was what got me to seriously think about politics for the first time. of course i remember what i learned in high school history class, and as an ethnically han chinese person i paid attention to BLM and stop asian hate, but i didn't really think critically. my history classes didn't seem relevant when i was taking them, but of course they're relevant; the history is the context for what i'm living now.

eventually i was going to grow up and fend for myself and the people i care about in this country. i never realized that somehow. i have been so naive and ignorant.

it seems that everybody else has long understood what has been going on, with everything. but now my friends are panicking and i don't know what i'm supposed to worry about or not. when news articles and social media become untrustworthy, you need to rely on yourself - your own knowledge and critical thinking. unfortunately, i forgot to do that growing up...

(acknowledgement and disclaimer) i'm in a better position than most. the fact that i'm just worried about being informed is nothing compared to the others currently losing/have lost their homes, jobs, reproductive care access, their dignity (transgender inmates being forced to detransition), etc. so i don't mean to say all this to mean i'm genuinely panicking about living in trump's america. i just have a fever and i'm more stressed than i should be about the weight of my privilege and resulting responsibility if i want to call myself an ally/leftist/whatever.

(/end cw)

in any case.... i like to finish these things on a positive note so i'll keep writing.

i have to teach tomorrow morning at 8:30am :/ last time i barely spent any time reviewing/teaching summation notation to the class. i just showed them the anatomy of the notation and did one example, but for some it's their first time seeing that, so i should be spending more time on it.

after teaching, well, i wanted to sit in on riemannian geometry but if i still feel shitty tomorrow then i might just go home... i have textbook chapters to read and review so that'll keep me occupied while im not at school.

i'm taking a couple mg of melatonin as i'm writing this sentence. i need to rest. bye~

[lipshits-continuous]

Topological Spaces 2: Topologies and Continuity

Welcome to the second post in my introductory series to topology! The goal today is to give the definition of both topological spaces and continuous maps between them. These definitions will be very familiar from the last post so I highly recommend reading it here.

I do make brief reference to some constructions from linear algebra and abstract algebra however these aren't necessary for understanding the post. They are merely inserted for futher emphasis for those who are familiar.

2.1: Topological Spaces

In the last post, we saw that open sets are potentially a structure that we wish to study. Our definition will be in terms of properties we wish open sets to have without invoking any notion of a distance between point. Fortunately, open sets in metric spaces have properties which fit this exactly in the form of Lemma 1.11. We shall use these to give our definition of a topological space!

Definition 2.1:

Remarks:

We can show by induction that finite intersections of open sets are open. This property is equivalent to (T3), but (T3) is usually an easier property to check.

We can have different topologies on the same set as we shall see in the examples!

Examples 2.2:

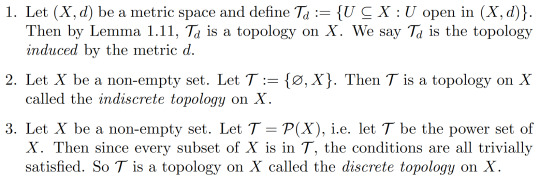
Remarks:

The topology on ℝ induced by the absolute value metric is called the standard topology on ℝ. Similarly, The topology induced by the Euclidean norm on ℝⁿ is called the standard topology on ℝⁿ.

The discrete topology is actually the same topology as the topology induced by the discrete metric. The proof involves showing that every singleton set (set that contains one element) is open in X with the discrete metric. Then use Lemma 1.11 to conclude that every set is open in X with the discrete metric.

Just like how some metrics can't be realised as the metric induced by a norm (and how some norms can't be realised as the norm induced by an inner product), not all topologies can be realised as the topology induced by a metric. A topology which can realised as the topology induced by a metric is called metrizable. The area of study dedicated to classifying metrizable spaces is called metrization theory and is very rich (and very much beyond the scope of these posts)

Both the indiscrete topology and the topology in 4) are non-metrizable. We shall see a proof of this in a future post.

One thing we may want to do is to make new topological spaces out of old ones. We don't yet have enough theory developed to do much but one easy construction we may do is putting a topology on subsets of our topology space:

Proposition 2.3:

2.2 Continuous Maps:

Now we have defined what a topology is, we may finally generalise the notion of continuity! Our guide will be Lemma 1.12.

Definition 2.4:

Remarks:

Continuity very much depends on the topology.

This really is a generalisation of continuity since Lemma 1.12 says that for metric spaces this notion is equivalent to our ε-δ definition (Definition 1.3)

We shall now see some examples in the form of the following proposition:

Proposition 2.5:

Now we shall define a special kind of continuous map: homeomorphisms. You may have heard of these from pop maths, especially in the context of a coffee mug and a donut being "the same" to a topologist.

Definition 2.6:

Remarks:

Not only are homeomorphisms bijections between the sets, they also induce a bijection between the topologies:

This means that in some sense the topologies on X and Y are the same!

More formally, one can show that ≅ is an equivalence relation on topological spaces. The proof relies on 1) and 2) from Proposition 2.5

Homeomorphisms are in this sense "topological space isomorphisms" since they preserve the important structure of topological spaces: the topology. This is analagous to how bijective linear maps are vector space isomorphisms and how bijective group homomorphisms are group isomorphisms.

Example 2.7:

In fact, we may show any open interval (a,b) is homeomorphic to ℝ by showing that (0,1) is homeomorphic to (a,b) via an affine map then using the fact that "being homeomorphic" is an equivalence relation.

One major goal of topology is to classify topological spaces up to homeomorphism. This is insurmountable if attempted all at once, even if one restricts to special topological spaces, and is still an active area of research. What is a more approachable goal is to find certain properties that topological spaces have which are invariant under homeomorphism. A vast majority of what follows in this series of posts can be seen as a hunt for these invariants whilst also generalising a lot of familiar concepts we have on ℝ with its standard topology.

[bubbloquacious]

Zariski topologies

So if you take kⁿ, the n-dimensional coordinate space over some field k, the Zariski topology on kⁿ is the topology whose closed sets are of the form

Z(S) = { x ∈ kⁿ : f(x) = 0 for all f ∈ S }

for some subset S ⊆ k[x₁,...,xₙ]. That is, the closed sets are the common zero loci of some set of polynomials over k in n variables, i.e. they are the solution sets for some system of algebraic equations. Such sets are called algebraic sets. If I is the ideal generated by S, then Z(S) = Z(I), so we can restrict ourselves to ideals.

Now if you take a commutative unital ring R, we let Spec R denote its prime spectrum, the set of prime ideals of R. We let Max R ⊆ Spec R be the subset consisting of the maximal ideals, the maximal spectrum. The Zariski topology on Spec R is the topology whose closed sets are of the form

Z(S) = { P ∈ Spec R : P ⊇ S }

for some subset S ⊆ R. A prime ideal P contains S if and only if it contains the ideal generated by S, so again we can restrict to ideals. What's the common idea here? Classically, if k is algebraically closed, then Hilbert's Nullstellensatz (meaning Zero Locus Theorem) allows us to identify the points of kⁿ with those of Max k[x₁,...,xₙ], by mapping a point (a₁,...,aₙ) to the maximal ideal (x₁ - a₁,...,xₙ - aₙ), and the Zariski topologies will agree along this identification. There's nothing very special about these algebraic sets though.

Let X be any (pre-)ordered set with at least one bottom element. For a subset Y ⊆ X, define the lower and upper sets associated to Y as

L(Y) = { x ∈ X : x ≤ y for all y ∈ Y }, U(Y) = { x ∈ X : x ≥ y for all y ∈ Y }.

We call a lower [upper] set principal if it is of the form L(x)= L({x}) [U(x) = U({x})] for some x ∈ X. If X is complete (any subset has at least one least upper bound and greatest lower bound), then any lower or upper set is principal. Note that ⋂ᵢ L(Yᵢ) = L(⋃ᵢ Yᵢ), so lower sets are closed under arbitrary intersections; they provide what's called a closure system on the power set of X. The lower closure of a set Y is the intersection of all lower sets containing Y. We have that Y ⊆ L(x) if and only if x ∈ U(Y), so the lower closure of Y is given by L(U(Y)). If the lower sets were furthermore closed under finite unions (including empty unions), then they would form the closed sets of a topology on X.

This is not generally true; first of all, note that any lower set contains the bottom elements of X, of which there is at least one, so the empty set is not a lower set. As for binary unions, generally we have L(Y₁) ∪ L(Y₂) ⊆ L(Y₁ ∩ Y₂), but this inclusion might be strict. This is something we can fix by restricting to a subset of X.

We say that p ∈ X is prime if p is not a bottom element and for all x, y such that for all z such that x ≤ z and y ≤ z we have p ≤ z, we have that p ≤ x or p ≤ y. That is, if p is smaller than every upper bound of x and y, then p is smaller than x or y. Furthermore, we say that p is a prime atom if it is a minimal prime element. Let P(X) and A(X) denote the sets of primes and prime atoms of X, respectively. For a subset Y ⊆ X, let the Zariski closed set associated to Y be given by

Z(Y) = L(Y) ∩ P(X) = { p ∈ P(X) : p ≤ y for all y ∈ Y }.

We again have ⋂ᵢ Z(Yᵢ) = Z(⋃ᵢ Yᵢ), so the Zariski closed sets are closed under arbitrary intersections. Note also that Z(X) = ∅, so the empty set is closed. Now let Y₁, Y₂ be subsets of X. We find that Z(Y₁) ∪ Z(Y₂) = Z(U(Y₁ ∪ Y₂)). Clearly if p is smaller than all of the elements of one Yᵢ, then it is smaller than every upper bound; the interesting part is the other containment.

Assume that p ∈ Z(U(Y₁ ∪ Y₂)), so p is smaller than every upper bound of Y₁ ∪ Y₂. If p is smaller than every element of Y₁ then we are done, so assume that there is some y ∈ Y₁ with p ≰ y. For every y' ∈ Y₂ we have that p is smaller than every upper bound of y and y', so because p is prime we get that it is smaller than y or y'. It is not smaller than y, so p ≤ y'. We conclude that p ∈ Z(Y₂), and we're done.

As before, the Zariski closure of a set of primes Q ⊆ P(X) is given by Z(U(Q)). Note however that for a point x ∈ X we have L(x) = L(U(x)), so the Zariski closure of a prime p is Z(p). It follows that A(X) is exactly the subspace of closed points of P(X).

So we have defined the Zariski topology on P(X). How can we recover the classical examples?

If X is the collection of algebraic subsets of kⁿ ordered by inclusion, then P(X) consists of the irreducible algebraic subsets, and we can identify kⁿ itself with A(X). Our Zariski topology coincides with the standard definition.

If X = R is a unital commutative ring, ordered by divisibility, then being prime for the ordering coincides with being either prime for the ring structure, or being equal to 0 if R is an integral domain. Note that this ordering is not generally antisymmetric; consider 1 and -1 in a ring of characteristic not equal to 2.

A more well-behaved version of the previous example has X = { ideals I ⊴ R }, ordered by reverse inclusion. Note that for principal ideals (r), (s) we have (r) ⊇ (s) if and only if r divides s. We have P(X) = Spec R and A(X) = Max R, and our Zariski topology coincides with the standard definition.

You can play the same game if X is the lattice of subobjects of any structure H. If H is a set (or a topological space) and X is its power set, then the primes and prime atoms are the same; the points. The Zariski topology is the discrete topology on H. If H is a vector space, then P(X) is empty, because any non-zero subspace V can be contained in the span of two subspaces that don't contain V. It seems that the sweet spot for 'interesting' Zariski topologies is somewhere in between the rigidity of vector spaces and the flexibility of sets.

If H is an affine space, then again the prime elements are exactly the points. The resulting Zariski topology has as closed sets the finite unions of affine subspaces of H.

An interesting one is if X is the set of closed sets of some topological space S (generalizing the first example). The prime elements are the irreducible closed sets, and if S is T1 (meaning all points are closed), then the points of A(X) can be identified with those of S. Then the Zariski topology on A(X) is the same as the topology on S, and the Zariski closure of an irreducible closed set is the set of all irreducible closed sets contained in it.

[vacuously-true]

seeing you post about lily and calling her a senior (??!!) made me realise that i've been following you for 6ish+ years and that

what do you mean grown up lily, she is a baby! im going to cry

in this time i have also grown up. 6 years ago I was just getting into math as a highschooler - a significant part of that was because of loving your posts about braids and topology and your and reals fractal memes. and now having just started a phd. (im technically not a mathematician - but i use category theory + its associates if that counts)

all that to say, ive really appreciated the lily posting, math posting, general posting, shit posting, and vibes over the years. you guys have been very inspiring in many ways, in particular for the idea that math can just be \fun\ for funs sake.

🥺🥺🥺 Thank you for sharing, it's so nice to hear from people who've let me be a little part in their lives for so long. I'm glad it's been valuable to you and I hope you stick around for another six years or more. 💚💚💚

[mathematical-cheese]

Why Straws Have One Hole: An Introduction to Homology Part 2

In this post I'll discuss simplicial complexes and how we can use them to make our test for holes simpler and motivate the definitions for simplicial homology! The post is more technical but I have tried to motivate each step.

Simplicial Complexes:

A common theme in topology is to build up our spaces from smaller, simpler spaces. One way of doing this is to use simplices! These are generalisations of triangles to all dimensions:

Image is taken from here

An n-simplex has n+1 verticies and is denoted by its vertices in square brackets: <e₀,...,eₙ>. A simplicial complex is made by gluing simplices together such that the intersection of two simplices is also a simplex that is included in the complex. We also require that any n vertices can define at most one n-simplex in the complex. If some vertices e₀,...,eₙ in a simplicial complex, K, define an n-simplex <e₀,...,eₙ> that is in K, we call <e₀,...,eₙ> an n-face of K.

An example of a simplicial complex is a square where each vertex of the square is a 0 simplex and each edge is a 1-simplex. If instead we considered a solid square, we wouldn't automatically get a simplicial complex because the 2 dimensional part isn't made up of 2-simplices. We fix this by adding an addition 1-simplex bewteen one pair of diagonal points which gives us a simplical complex with four vertices, five 1-simplices and two 2-simplices:

We can construct a great number of spaces using simplices! This construction is only up to homeomorphism but that's all we care about! A simplicial complex that is homeomorphic to a space is called a triangulation of that space. Importantly we can triangulate a straw:

This is the simplest triangulation because having fewer simplices would lead to us having different simplices described by the same vertices.

Simplicial Homology

So why do we care about triangulations? The key here is to notice that the boundary of an n-simplex is a simplicial complex made up of (n-1)-simplices. For example, the boundary of a 2-simplex is a simplicial complex made of three 1-simplices. The idea is to modify our test to only involve simplices because then we only have to check finitely many things! This is where things start to get a bit more technical but I will try my best to motivate each step!

Firstly, we need to introduce a convention in the way we describe simplices. We pick an order for the vertices in our complex to be listed, e.g. for the triangulation of the straw we could pick the order a,b,c,d,e,f. Then any time we write a simplex we must list the vertices in that order. For example, with the order above, <a,b,d> is how we describe the left most 2-simplex. The reason we need this is we are about to start thinking about simplices in a more abstract way and we need a systematic way of writing them.

Now for arguably the weirdest (but most powerful) step. We want a way to talk about the boundary of a simlicial complex as one object and we want a way to say when a particular simplicial complex has no boundary. The motivation for this is we want to talk find the analogue of a loop that we can use to test for holes, that is we want a one dimensional object that doesn't have a boundary. Since we eventually want to count things, it might be prudent to somehow assign numbers to things. As mentioned above, the boundary of an n-simplex can be thought of as the union of (n-1)-simplices and unions of sets are kind of similar to a kind of sum. The idea is to talk about "sums" of simplices. It doesn't really make sense to add simplices but we can sort of just fudge it. This fudging is known as "formal sums" and this is when we say "okay, we don't know what a sum of these things actually is but we study it anyway".

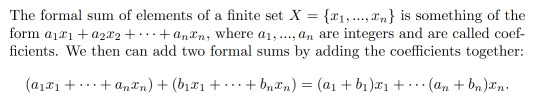
We say the elements of X generate these formal sums.

We then consider the set Cₙ(K) of all the formal sums of n-simplices in a simplicial complex K and we call it the nth simplicial chain group of K and we call elements of Cₙ(K) n-chains. We say that the rank of Cₙ(K) is the number of elements of X. Note that the sum or difference of two chains is again a chain.

The rank of C₂(K) is 1 and the rank of C₁(K) and of C₀(K) is 3.

We can now also give meaning to a simplex that is written in a different order to our chosen order. Given an ordered list of vertices, we can swap two elements around to get a different ordered list. If n is the number of swaps it takes to get an ordered list of vertices into our chosen order, we say that the simplex with vertices written in a different order is equal to the element of Cₙ(K) given by (-1)ⁿ times the simplex with the vertices written in our chosen order.

Now we want to figure out how to represent the boundary as a map from Cₙ(K) to Cₙ₋₁(K) since the boundary of an n-simplex is made up of (n-1)-simplices.

The full representation of this map is a bit detailed so I will stick to the case when n is less than or equal to 2 since that's all we need. The definition of this boundary map only depends on what it does to the simplices because it comes from considering their boundaries. So we will say that the boundary map applied to a formal sum is just the formal sum of the map applied to each simplex, for example

where ∂ is denotes the boundary map. So we just need to define ∂ on simplices.

To motivate the definition, we consider a 2-simplex <x,y,z> with the order x,y,z. Starting at x, we can think of the boundary as a loop that goes from x to y, then from y to z then from z back to x:

So we could represent the boundary as the formal sum <x,y>+<y,z>+<z,x>. Then written in our chosen order, the boundary is <x,y>+<y,z>-<x,z>. That is ∂(<x,y,z>)=<y,z>-<x,z>+<x,y>. In the first term, we remove the first vertex, in the second term we remove the second vertex and multiply by -1, and in the third term we remove the third vertex and multiply by -1 twice. So it would seem sensible to that the pattern here is the nth term in the boundary of a k-simplex is the simplex where the nth vertex is removed and we mutlipy by (-1)ⁿ⁻¹.

So the boundary of a 1-simplex <x,y> is <y>-<x>. But the boundary of a 0-simplex is always 0 since 0-simplices are just points and have no boundary!

We also have that the boundary of the boundary of a 2-simplex is 0. This makes intuitive sense since the boundary itself has no points at the edge of it but we can show this still works in our abstraction to formal sums:

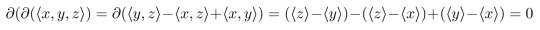
Now we have two special types of formal sums: those that have no boundary and those that are the boundary of something else. We call an n-chain that has no boundary an n-cycle and we call an n-chain that is the boundary of an (n+1)-chain an n-boundary. We can extend the first above argument to show that boundaries are always cycles, i.e. the boundary of a boundary is always 0. 1-cycles are what replace loops in our earlier test, that is we want to find 1-cycles that aren't 1-boundaries! An obvious yet important example of a boundary is 0, 0 is the boundary of 0 (we'll use this fact later). Two other important facts are the sum of n-cycles is also an n-cycle and the sum of n-boundaries is also an n-boundary. If c and c' are both cycles, then ∂(c+c')=∂c+∂c'=0+0=0 and if c=∂b anf c'=∂b', then c+c'=∂b+∂b'=∂(b+b').

Let's take a step back to summarise what we have so far. We have found a test for holes in a space but it didn't really allow for easy calculation of the number of holes in a space. So we restricted our view to simple spaces and have found a way of abstractly representing the building blocks of those spaces. This abstraction has allowed us to reframe our test for holes into a purely algebraic question!

But how can we be sure this test still works? Let's consider a circle. Using our first test, we can just take a loop around the circle. Then this loops isn't the boundary of anything since it bounds a disc of the same radius but this disc isn't part of the circle. So the circle has a hole. Now we triangulate the circle using three vertices and 3 edges, i.e. a triangle. If we label the vertices as <x>, <y> and <z> we already know an example of a cycle: <y,z>-<x,z>+<x,y>. Even though this calculation was done for a 2-simplex, it only involves the 1-simplices so it is valid in this situation too! But in this case, we don't have any 2-simplices in our space so this cycle can't be the boundary of anything! Conversely, suppose we get a positive result using our simplicial hole test, i.e. we've found a cycle that isn't the boundary of anything. Then we can construct a loop in the space using this cycle and this loop wouldn't be the boundary of anything so the first test would also be positive!

The final step that actually lets us count things is to define the homology groups! What we want to do is find cycles that aren't boundaries. Algebraically, we do this by considering cycles to be "the same" if their difference is a boundary. That is, we say two n-cycles c and c' are homologous if there is some (n+1)-chain b such that c-c'=∂b. We have that all n-boundaries are homologous to each other. Say both c and c' are n-boundaries and that b and b' are (n+1)-chains such that c=∂b and c'=∂b', then c-c'=∂b-∂b'=∂(b-b'). The since b and b' are (n+1)-chains, b-b' is an (n+1)-chain so c and c' are indeed homologous. In particular, 0 is a boundary so every boundary is homologous to 0. So now suppose that c is a cycle that is homologous to 0, then there exists an (n+1)-chain b such that c-0=∂b. So c=∂b and hence c is also an n-boundary. This means that a cycle is a boundary if and only if it is homologous to 0. So now if we want to find cycles which aren't boundaries, we look for cycles which aren't homologous to 0.

We define the homology class of a cycle c to be the set of all the cycles which are homologous to c and we denote it [c]. For example, the homology class of 0, [0], is the set of all boundaries! We can also define a notion of addition of homology classes: [c]+[c']=[c+c']. That is, the sum of two homology classes of two cycles is the homology class of their sum. We call the set of all homology classes of a cycles of a simplicial complex K, the (first) homology group of K and write H₁(K). If H₁(K) only has one element, i.e. H₁(K)={[0]} every cycle must be a boundary and K would have no holes. But if K has a hole, H₁(K) would have more than one element.

We are actually now quite close to being able to count the number of holes a space has! Let's come back to the example of a circle. Intuitively, a circle has 1 hole and we've already seen that we have one cycle which isn't a boundary: <y,z>-<x,z>+<x,y>. But by the way we defined the boundary, we also have that

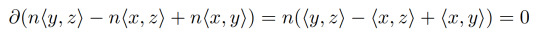
for any integer n. So for any non-zero integer n, we can find a cycle that is not a boundary. In particular, if m doesn't equal n, then n(<y,z>-<x,z>+<x,y>) is not homologous to m(<y,z>-<x,z>+<x,y>) since their difference is (n-m)(<y,z>-<x,z>+<x,y>) which is not a boundary unless n-m=0, which is not the case here since n doesn't equal m. Moreover, I claim that any cycle in a circle must be of this form. Remember, this cycle represents the loop going around the triangulation of the circle once. The only way we can get loops in the circle are obtained by going around the circle a whole number of times (where going in the opposite direction gives us a "negative" loop). Any other path you try to take will end up with not having the same start and end point and so would have a boundary! So there is a homology class of the circle for each integer. Moreover, adding these cycles represents going around a loop n+m times so adding the homology classes together is somehow the same as the regular addition we know for the integers! In formal terms, we say that H₁(circle) is isomorphic to the integers. Like how homeomorphism is the notion of "the same" for topologists, isomorphism is the notion of "the same" for algebrists! The important part of this is that all of the homology classes can be expressed as an integer multiple of [<y,z>-<x,z>+<x,y>] just like how an integer can be thought of as an integer multiple of the number 1. In this sense, we say that [<y,z>-<x,z>+<x,y>] generates H₁(circle), i.e. H₁(circle) has 1 generator. This cycle came about as a loop around the hole in the circle so it is sensible to guess that the number of generators corresponds to the number of holes!* This is how we will go about showing that a straw has 1 hole in the next part! That is, we shall figure out what the first homology group of a straw is and find out how many generators it has!

*technically, we actually count the free generators of H₁ since the torsion elements represent something else but it won't matter for what we're doing. Alternatively, we could have defined homology over a field to get vector spaces which naturally don't have any torsion but this doesn't feel quite as natural as doing homology with integral coefficients.

[andmaybegayer]

Last Monday of the Week 2024-11-11

Getting into situations

Listening: New job which means I have need for a quick and easy source of music that I can throw down on any device with internet while I figure out exactly where I draw the line on mixing personal music files with corporate hardware. Hence, soma.fm, a really good family of internet radio stations that I enjoy a lot.

There's several stations here but to call out ones I like in no particular order:

Beat Blender: Slower house music and electronica

Metal Detector: What it says on the tin, mixed metals

Sonic Universe: Weird jazz

Secret Agent: Normal jazz

SF 10-33: The San Francisco emergency radio broadcast channel mixed with ambient music

Vaporwaves: Look we all have to get stupid sometime

Watching: Movie Night was also a sort of belated Diwali Night because a friend of mine has been getting extremely into indian food, so we watched "Sita Sings the Blues", an 82 minute, Creative Commons, mostly one-woman animation project that is a retelling of the Ramayana and also a breakup jukebox jazz musical.

There's about 30 minutes of a decent movie in here and another 15-20 minutes of the breakup part that would be hard to cut since it's the reason it exists. It's an animation from 2008 and you can see that it's exactly what it needs to be to run on one person who knows Flash reasonably well. The "blues" part is because there's numerous musical segments that use pre-existing 1920's jazz numbers to set the tone which reportedly cost the author tens of thousands of dollars to license, and she's now a free culture advocate so this is how you get Cory Doctorows I guess.

Is it good? I mean there's some really good parts. The legend is delivered in the form of three shadow puppets half-remembering the story to put it together which is very endearing in a Bill Wurtz History Of Japan kind of way. The amount of effort on display for 2008 is enormous. The concept is impressive, in that you found all these songs, but you could have probably cut the songs and got this down to a tight 40.

Reading: Work! Documentation! Learning so much about [REDACTED]. Very weird not working in an open source company again.

Also started The Book of All Skies on the metro the other day, and have gotten to the end of the first act. Compelling! Love an Egan, one of very few authors who can put a topology lesson into a book without it sucking ass.

Making: Made Gulab Jamun for movie night. From spreading my diwali cooking over more than three days I'm learning that actually this shit is easy if you don't try to cram it all into three days. I should make this stuff more often.

Playing: Poking and fiddling with things a little. Still not in the headspace to pick up a full game again. Once I have a schedule I can get back into video games but when I don't have a schedule that includes video games.

Tools and Equipment: Keyd is the new-ish hotness for client-side remapping of keyboard keys. It's not quite a custom build, but it's close.

Allows you to get 99% of the way to whatever zany custom mapping you want under Linux with fairly universal coverage and minimal faff in a very compact and manageable package.

[laiqualaurelote]

F for the fanfic ask game 😊 You're great at getting character's voices down!

F: Share a snippet from one of your favourite dialogue scenes you’ve written and explain why you’re proud of it.

Thank you! this is from Beard's section in the Lasso's Eleven chapter of they will see us waving from such great heists:

“Did you know that in Athens, they call the vehicles of mass transportation metaphorai?” he says to Ted on the District Line.  “So we’re riding a metaphor now?”  “Yeah. The train is a metaphor.” “I like that,” says Ted. “I find it moving.” They rattle on towards Kew Gardens. “It’s funny how they call it the Tube,” says Ted. He pronounces it as an exaggerated “choob”.  “It’s because of the method of construction. The early lines were built using cut-and-cover, but after that they went deeper and started using tube tunnels.” “Tubes everywhere,” says Ted reflectively. “If you think about it, the human body is a tube.” “A torus. Topologically speaking.” “Pretty sure I’m a Libra.” “Torus, like a doughnut. We’re all doughnuts. Just long holes encased in flesh.” “Tubes on the Tube,” declares Ted. “Metaphorically and literally.” They get off at Richmond and walk to the green. “So what’s it to be?” Ted goes on. “Trick play?” “Kansas City Shuffle,” says Beard. “They look right, we go left.” “Old school. I like it.” Ted nods. “Think I might throw in a Lasso Special, spice things up a bit.” “You’re going to use the Lasso Special for this?” Beard eyeballs him. “You’ve been sitting on that one for years.” “I feel it’s time,” says Ted, stroking his moustache with relish, like the supervillain he totally isn’t. “Now or never, Andrew Lloyd Webber.” “Your call, chief.” They stop at the top of the ridge. “Gosh darn, but it is a pretty how town,” says Ted admiringly. “Kansas City bore me, Richmond and Kew undid me.” “Weialala, baby.” Beard peers into the distance. “They say you can see Windsor Castle from here.” “You know what Windsor Castle looks like?” Beard shrugs. “Think it’s kinda round on the top. You thought about crew?” “This is a big ‘un. We gotta have the basics - a Keanu, a Travolta, a Mick Taylor. I’m thinking a Charlie Bird, too. You want we should go for a Leo or a JLo?” “JLo. Keeps things fresh. Lasso Special needs a Tom Hardy.” “Add that to the list. Rebecca says she’s got a Denzel in mind. And we should get a Stath, to be on the safe side.” “Huh. Are we expecting trouble?” “We should,” says Ted. “Let’s hope trouble ain’t expecting us.” Beard counts on his fingers. “Plus us, that’s eleven.” Ted nudges him, jocular. “It’s like we’re a football team.”

This is probably the dialogue scene that went through the most number of rewrites in any of my fics - it is extremely difficult to nail the flavour of Ted and Beard's banter, and I went through several versions before I was satisfied. I wanted this to sound like the way Danny and Rusty communicate in Ocean's Eleven, but with Ted and Beard's particular brand of psychic entanglement.

This conversation contains three things I love: 1) Tube facts (I am very nerdy about the London Underground); 2) e e cummings and T. S. Eliot poem references (in a single line, too!); and 3) that trope in heist movies where they only refer to things by their codenames, which the audience has to work out themselves. This is the full code index (which I made up).

Keanu => The Matrix => hacker Travolta => Grease => greaseman Mick Taylor => Rolling Stones guitarist on Sticky Fingers => pickpocket Charlie Bird => saxophonist Charlie "Bird" Parker => blow => demolitions Leo => Leonardo DiCaprio in Catch Me If You Can => male grifter JLo => Jennifer Lopez in Hustlers => female grifter Tom Hardy => Eames in Inception => forger Denzel => Denzel Washington => Inside Man Stath => Jason Statham => hitter

Thank you for playing this fic ask game!

[positively-knotted]

Dissertationposting 2: Curvature & Hypersurfaces

(Note: I'm not gonna say anything about what I mean by "curvature", as if you haven't already seen it in some context I don't think you're gonna get much out of these posts :/. But for clarity, I'll only ever talk about scalar curvature and call it R. If you're used to Gaussian curvature written K, this is the same except R = 2K. Oh also all my manifolds are oriented.)

It may not be immediately obvious why we would want to consider hypersurfaces when trying to understand curvature - after all, R³ is flat, but contains surfaces with all kinds of curvature. So a motivating example may be in order. This is in fact the example that spurred all of the developments we'll talk about, and is of particular importance in theoretical cosmology! Maybe I'll say more about that later.

Consider a manifold homeomorphic to the n-torus Tⁿ - or more properly, Tⁿ with a choice of geometry (Riemannian metric). Intuitively, this shouldn't be able to have R > 0 everywhere, in the same way that T² can't. Proving this is surprisingly hard, but one sensible approach would be to try induction. After all, T³ is just T² × S¹, and S¹ is easy to understand. Thought of the other way around, we want to find nice hypersurfaces and do inductive descent until we reach dimension 2, then apply Gauss-Bonnet.

But if any old hypersurface doesn't say much, what about particularly nice ones? The obvious candidates are so-called stable minimal hypersurfaces. These are minimal points for area, in the sense that if you perturb them very slightly, their area must increase (e.g. the meridian of a standard torus in the motivating example). The big result about these is as follows:

Lemma 1.

If Σ is a stable minimal hypersurface in a manifold (M, g) and f is any function on Σ, then [1]

Here the left side is the gradient of f (in the normal calculus sense), and \II is the second fundamental form, a number that tells us something about how Σ sits inside M. You can think of it as a kind of error term, but the important bit is that it's squared, so non-negative. R is the scalar curvature of the ambient manifold M, and R_\Sigma is the induced scalar curvature of Σ.

You've probably never seen this before, even if you've done differential geometry. I don't know why this formula isn't better known, it's super useful, as with clever choices of f it gives big results. Just taking f=1 shows that for a stable minimal hypersurface, the intrinsic curvature has to be greater on average than the external curvature. This is a pretty big step forward!

Ok, so we have our choice of useful hypersurfaces. Now we just need to show that they always exist. And they do! In fact, they exist for each homology class:

Lemma 2.

Let (M, g) be a closed n-manifold, 3 ≤ n ≤ 7. Then for any class α ∈ H_{n−1}(M), we can find a closed stable minimal hypersurface Σ such that [Σ] = α in homology.

Let's unpack this a bit. We can think of hypersurfaces as living in a particular homology class in the usual geometric way. It's a standard result from differential topology [2] that we can in find a hypersurface living in any homology class, and that slightly perturbing it won't change that class. The interesting bit here is that we can always take a stable minimal representative, in sufficiently small dimensions. [3] Annoyingly, this means everything from here on out only applies in dimensions less than 8, even though there's no good topological reason why it isn't true more generally. (It definitely is true more generally, we just need a stronger version of this lemma and that makes it an analysis question.)

Next time, we'll use this to show that Tⁿ doesn't admit positive scalar curvature! Notes below the cut.

[1] Proof of Lemma 1. Start with the usual Gauss equation. Take the trace to pass to Ricci curvature, then again to pass to scalar curvature. It turns out that the irritating terms from varying dimensions cancel out! More detail in the screenshots below:

[2] Remember that there is a bijection between H¹(M) and homotopy classes of maps M -> S¹, pairing [f] with f^*(ω), where ω generates H¹(S¹). We can assume f is smooth, choose a regular value t, and set Σ = f^{-1}(t). Then [Σ] is Poincaré dual to f^*(ω).

[3] The actual argument here is pretty standard for the analysis I'll be omitting. In general, if we want to show that an object in space X with property P exists, we'll pass to a bigger space Y where standard results give us an object with that property; then somehow argue that P implies that it's actually of type X. Here, we pass from submanifolds to currents, and minimise area for currents in a given homology class. By measure theoretic magic, this minimisation forces the singular set of the current to have codimension at most 7, so in dimensions less than 8 it is in fact a submanifold.

[ask-numberjacks]

IT'S LORE TIIIIIIMEEEEE

SO

This is my theory on the Numberjacks' (and meanies', kind of?) creation and anatomy. To begin with, I'll talk about how I think they were created.

The Brain Gain Machine is quite obviously not fully machine. It can move, talk and a lot of weird green goop is involved??? Which I don't think would be there if it was completely machine. So I think it is a cyborg. And it originally looked something like this. I think it is parasite-esque, using the sofa as some kind of shell. My lore theory/AU(?) says that there were 2-3 of these, the others being destroyed and this one being damaged, so it was modified to be a cyborg. Since the Numberjacks and Meanies are somewhat alien, I think they all share a godlike creator that sent the Brain Gains to Earth to then later send signals to them (via the 'cables' on top of it) that 'spawned' the characters. The other Brain Gains would have been the ones that created the Meanies.

Numberjack birth I guess?

Since they are literally maths, the Numberjacks are just physical forms given to mathematical concepts/structures. Since they are created by the Brain Gain Machine, they do not need to reproduce (hence not having reproductive organs).

'But if the Numberjacks are maths given physical forms, what about the Meanies?' You might ask. Well, since they are more complex, with more specific abilities of their own, they are physical forms given to concepts, for example, topology (in Shape Japer's case).

Now on to the anatomy of the characters.

Their organs are somewhat similar to that of humans, but do not have all of the same ones. Since, as I've said before, they are just maths given a physical form, they do not grow or change in any way naturally. (The younger characters would be pretty small if that was the case.) However, since they are still living beings, they need to eat to survive. It'd also be pretty obvious if they did need to use the bathroom because Zero, One and possibly Two would be wearing nappies/diapers.

I think they'd also have an organ that I will call:

a Changeheart.

Which would be of similar size to that of their regular heart, except it gives them them a mild ability to change how things are mathematically described (and since the way things are described can't be changed, the thing being described has to change itself). The reason this would work is because I think the godlike being I mentioned earlier would be the Mathematical Universe Hypothesis given form, and the hypothesis is that our external reality is a mathematical structure. (You can tell I did a lot of research on this lol)

'Waste' products from their stomach are burned as fuel by this organ.

The changeheart gives out pulses (presumably bioelectric? Idk I'm not that good at science) containing the change that needs to be made to the surrounding area's structure. The Brain Gain Machine picks up on these pulses, concentrates them and sends them to a specific location to be used by another person with a changeheart.

The reason it has the same green goopy stuff as Brain Gain is because the Brain Gain itself has a changeheart, just a really big and more complex one.

Now on to human forms! Since I feel like it should be explained for various reasons.

Since they are 'aliens', they would not be born with a humanoid form. I think several other characters other than the Puzzler and the Numbertaker have humanoid forms since it has been implied that they have done things that only humans would be able to do (mostly shown in the audio stories). They may have one opportunity to visualize and shift into a human form that will be that form for as long as they live (which is forever). Since visualizing a human form means knowing what a human looks like, they would've only seen humans as they are usually, which also means their human forms would not have... you know. And anyway since they are all technically biologically agender they couldn't do that.

me right now

Oh gosh that was a lot. If you've made it this far, thank you so much for reading! I hope you found it interesting.

If you have any questions about this or want to know more about, for example, the Meanies' anatomies, feel free to ask in the ask box thingy!