#differential topology

[positively-knotted]

Some Basic Combinatorics Via Not-So-Basic Topology

Proposition. Let P(r; n,k) be the number of partitions of an integer r into n non-negative integers less than or equal to k. Then P(r; n,k) = P(r; k,n).

This is very easy to see with Young diagrams (count columns vs rows). It's also very difficult to see with topology, but that's more fun. This is probably going to be a bit long, but I think the pay-off is worth it.

The standard construction of (real) projective space Pⁿ is to call it the space of 1-dimensional subspaces of Rⁿ⁺¹. This generalises pretty naturally to the "Grassmann manifold" Gr(n; n+k) of n-dimensional subspaces of Rⁿ⁺ᵏ, so Pⁿ = Gr(1; n+1). Hopefully you believe that Gr(n; n+k) is still a compact nk-manifold. If you want, it's also the quotient O(n+k)/O(n) x O(k).

As well as being a manifold, this is naturally a CW complex. Let's think about how. For each point in Gr(n; n+k) (that is, n-dimensional subspace), it has a unique orthonormal basis where the final non-zero coordinate of each basis vector is positive (easy linalg exercise). Taking this basis, we let d_1,...,d_n be the the "dimension" of the basis vectors (i.e. the position of their final non-zero coordinate, so that (-1,2,0) is 2-"dimensional"). We can assume these are strictly increasing by permuting them. Thus, to each point in Gr(n; n+k), we are associating a unique list of n increasing integers between 1 and n+k.

Let e(d_1,...,d_n) be the subset of Gr(n; n+k) which give those integers. This is actually an open disc of dimension Σ(d_i-i)! Why? To choose the first basis vector, we can pick any unit vector in the upper half-space of dimension d_1. That is, we have a choice in the hemisphere=disc of dimension d_1-1. To choose the ith, we have a choice in a hemisphere=disc of dimension d_i-1, but we have to be orthogonal to the i-1 vectors we have already chosen, giving a choice in a disc of dimension d_i-i. A product of discs is a disc, and we're done!

Checking that this is actually a CW decomposition is kinda tricky, but also unenlightening, it just is true. So let's count how many cells of each dimension it has. An r-cell corresponds to a choice of partition r = Σ(d_i-i), where 1 ≤ d_1 < ... < d_n ≤ n+k. Equivalently, it is a choice of partition r = Σe-i, with 0 ≤ e_1 ≤ ... ≤ e_n ≤ k, by setting e_i = d_i-i. So the number of r-cells is exactly P(r; n,k)!

We're getting close! The final observation is this. Choosing a n-dimensional subspace is equivalent to choosing its orthogonal complement. That is, the map V → V^⊥ is a natural diffeomorphism between Gr(n; n+k) and Gr(k; n+k), and also a CW-isomorphism. (True because everything is naturally defined; slightly tedious to check.) In particular, it has to match up the number of r-cells, so P(r; n,k) = P(r; k,n)! No Young diagrams necessary.

I think this is kinda neat. It's also weird because these Grassmann manifolds completely classify vector bundles on compact manifolds and are how you define characteristic classes, so secretly under all of that differential topology there's really hard partition problems going on.

[superpte]

Quantum Ontology 

(Among The) Consequences: “Ontological” Existence of God Deconstructed By Quantum And Differential Topology… Ontology is the logic of… what is. No less. It’s an obscure word that philosophers love to brandish. But the concept has been at the core of the hardest problems in physics… for centuries… And progress has been made… Unbeknownst to most philosophers. My argument against ontology as the…

[thesomebodywho]

The biggest step of a mathematicians journey to maturity is no longer having to resist giggling at words like homogenous and homomorphic.

[miamaimania]

Mathematics in bloom ➤ A stratifold's beauty unfolds

[spectrallysequenced]

Personally I view this as math showing us that cohomology is a more natural PoV. I mean yes, singular cohomology is quite artificial bit cohomology just ends up being better so often.

In fact sometimes you can't even define homology in a reasonable manner, but you can define cohomology (sheaf cohomology as an example, not enough projectives).

Homology turns out to work in the case of topological spaces, but this is more of a special case than indicative of a larger picture.

Math people, reblog with your fav theorem and why.

I'll start, the Wedderburn-Artin theorem is a beautiful structure theorem on semisimple rings which says they decompose uniquely as a product of matrix rings over division rings. This is a beautiful result but it also underlies a lot of very cool theory like Brauer Theory, Galois Cohomology and the theory of Galois and Étale Algebras.

What's yours?

[isomorphismes]

Test functions and [tempered] distributions require the notion of topological vector space … distributions can be traced back to Green's functions in the 1830’s to solve ordinary differential equations … the 1936 work of Sergei Sobolev on hyperbolic PDE’s.

Laurent Schwartz introduced the term "distribution" by analogy with a distribution of electrical charge, possibly including not only point charges but also dipoles and so on.

tempered distribution

topological vector space

(^ if there is a dipole, there must be a notion of subtraction, hence the need for a vector, and to speak of this very conceptually, use a TVS)

[nablavii]

So today was the second course day into algebraic geometry. We've studied how projective geometry involves non-measurable stuff. I mean, once you step into real analysis or some algebra, you find things like metric, norm, and so on, but sometimes you gotta step back a little, where things lose measure and you only have a ruler and something to make circumferences. Then, you can ask: Are there any relations between geometrical symmetries and polynomial roots? Well... You've gotta find out.

ESFM IPN - Dr. César Lozano Huerta.

[lucythebrazen]

My girlfriend just asked me if tea is soup, this is my response

[positively-knotted]

Gauss-Bonnet is p sick, and my Masters Dissertation was on (two specific) higher-dimensional analogues, i.e. results linking the sign of scalar curvature to homotopy type.

Interestingly, nothing too similar to GB can be true in higher dimensions: every closed manifold in 3 or more dimensions admits a metric with negative scalar curvature, unlike S² and T². So we can only place restrictions on the existence of positive or zero scalar curvature.

<3

[lipshits-continuous]

Sorry for the de Rham cohomology posting but another thing I've been thinking about:

I also think it's really cool that we can use tools from algebraic topology to answer "when are closed forms exact?". Like even just the fact we have Mayer-Vietoris means that the problem for certain manifolds becomes a lot easier! You no longer have to worry as much about the differential forms themselves. And then obviously de Rham's theorem gives you an even more powerful tool for this!

[positively-knotted]

Dissertationposting 2: Curvature & Hypersurfaces

(Note: I'm not gonna say anything about what I mean by "curvature", as if you haven't already seen it in some context I don't think you're gonna get much out of these posts :/. But for clarity, I'll only ever talk about scalar curvature and call it R. If you're used to Gaussian curvature written K, this is the same except R = 2K. Oh also all my manifolds are oriented.)

It may not be immediately obvious why we would want to consider hypersurfaces when trying to understand curvature - after all, R³ is flat, but contains surfaces with all kinds of curvature. So a motivating example may be in order. This is in fact the example that spurred all of the developments we'll talk about, and is of particular importance in theoretical cosmology! Maybe I'll say more about that later.

Consider a manifold homeomorphic to the n-torus Tⁿ - or more properly, Tⁿ with a choice of geometry (Riemannian metric). Intuitively, this shouldn't be able to have R > 0 everywhere, in the same way that T² can't. Proving this is surprisingly hard, but one sensible approach would be to try induction. After all, T³ is just T² × S¹, and S¹ is easy to understand. Thought of the other way around, we want to find nice hypersurfaces and do inductive descent until we reach dimension 2, then apply Gauss-Bonnet.

But if any old hypersurface doesn't say much, what about particularly nice ones? The obvious candidates are so-called stable minimal hypersurfaces. These are minimal points for area, in the sense that if you perturb them very slightly, their area must increase (e.g. the meridian of a standard torus in the motivating example). The big result about these is as follows:

Lemma 1.

If Σ is a stable minimal hypersurface in a manifold (M, g) and f is any function on Σ, then [1]

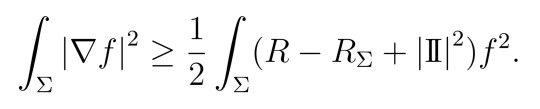
Here the left side is the gradient of f (in the normal calculus sense), and \II is the second fundamental form, a number that tells us something about how Σ sits inside M. You can think of it as a kind of error term, but the important bit is that it's squared, so non-negative. R is the scalar curvature of the ambient manifold M, and R_\Sigma is the induced scalar curvature of Σ.

You've probably never seen this before, even if you've done differential geometry. I don't know why this formula isn't better known, it's super useful, as with clever choices of f it gives big results. Just taking f=1 shows that for a stable minimal hypersurface, the intrinsic curvature has to be greater on average than the external curvature. This is a pretty big step forward!

Ok, so we have our choice of useful hypersurfaces. Now we just need to show that they always exist. And they do! In fact, they exist for each homology class:

Lemma 2.

Let (M, g) be a closed n-manifold, 3 ≤ n ≤ 7. Then for any class α ∈ H_{n−1}(M), we can find a closed stable minimal hypersurface Σ such that [Σ] = α in homology.

Let's unpack this a bit. We can think of hypersurfaces as living in a particular homology class in the usual geometric way. It's a standard result from differential topology [2] that we can in find a hypersurface living in any homology class, and that slightly perturbing it won't change that class. The interesting bit here is that we can always take a stable minimal representative, in sufficiently small dimensions. [3] Annoyingly, this means everything from here on out only applies in dimensions less than 8, even though there's no good topological reason why it isn't true more generally. (It definitely is true more generally, we just need a stronger version of this lemma and that makes it an analysis question.)

Next time, we'll use this to show that Tⁿ doesn't admit positive scalar curvature! Notes below the cut.

[1] Proof of Lemma 1. Start with the usual Gauss equation. Take the trace to pass to Ricci curvature, then again to pass to scalar curvature. It turns out that the irritating terms from varying dimensions cancel out! More detail in the screenshots below:

[2] Remember that there is a bijection between H¹(M) and homotopy classes of maps M -> S¹, pairing [f] with f^*(ω), where ω generates H¹(S¹). We can assume f is smooth, choose a regular value t, and set Σ = f^{-1}(t). Then [Σ] is Poincaré dual to f^*(ω).

[3] The actual argument here is pretty standard for the analysis I'll be omitting. In general, if we want to show that an object in space X with property P exists, we'll pass to a bigger space Y where standard results give us an object with that property; then somehow argue that P implies that it's actually of type X. Here, we pass from submanifolds to currents, and minimise area for currents in a given homology class. By measure theoretic magic, this minimisation forces the singular set of the current to have codimension at most 7, so in dimensions less than 8 it is in fact a submanifold.

[didsomeonesaysoup]

me after being 100% honest with my therapist

[mathematical-cheese]

3 exams down, 5 to go

[incorrect-moriarty-sherliam]

William sighs as he begins counting sheep. Instead of simply counting the fuzzy creatures, he starts to calculate permutations and combinations of numbers in his head, forming complex sequences.

William: "Five... Euler's number, pi. Six... Riemannian topology. Seven... Fourier series. Eight... differential equations. Nine... Pythagorean theorem..."

Sherlock: "Liam, aren't you supposed to be asleep?"

William, at the end, creates a new theorem... because he can XD

+++++++

@missshello contribution! Yeah!

[bubbloquacious]

What mathematical operators would you think make for the best fuck marry kill discussion

FMK: addition, multiplication, exponentiation

FMK: powers, roots, logarithms

FMK: group operation, inversion, unit element

FMK: polynomials, differential operators, continuous maps

FMK: greater than, less than, equal

FMK: one, two, three

FMK: numerator, denominator, quotient

FMK: rings, integral domains, fields

FMK: categories, functors, natural transformations

FMK: reflexivity, transitivity, antisymmetry

FMK: fundamental theorem of algebra, fundamental theorem of calculus, fundamental theorem of arithmetic

FMK: prime numbers, composite numbers, units

FMK: algebraic geometry, algebraic topology, algebraic number theory

FMK: compact Hausdorff spaces, abelian groups, algebraically complete fields

FMK: axiom of choice, well-ordering theorem, Zorn's lemma