emmatization

[emmatization]

Category Theorists love to say shit like "Automata Theory is all about Monoids actually" and the best part is that it always does manage to shed a cool new light on the underlying thing they're talking about

[emmatization]

Category Theorists love to say shit like "Automata Theory is all about Monoids actually" and the best part is that it always does manage to shed a cool new light on the underlying thing they're talking about

[emmatization]

Category Theorists love to say shit like "Automata Theory is all about Monoids actually" and the best part is that it always does manage to shed a cool new light on the underlying thing they're talking about

[emmatization]

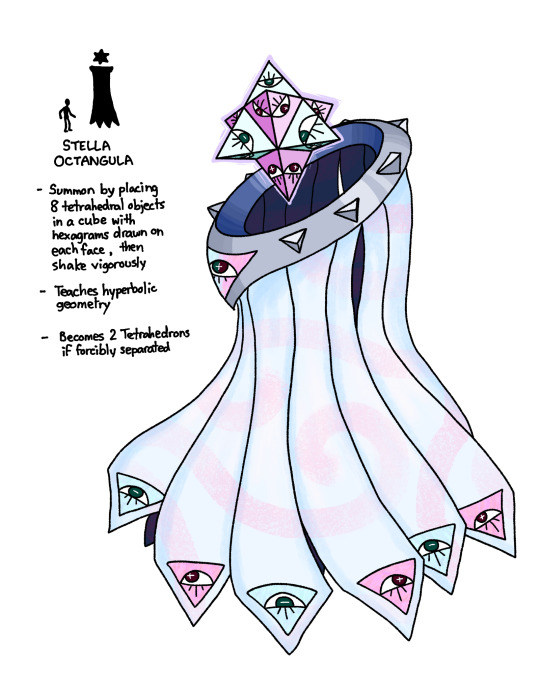
Polyhedron compounds are notoriously difficult to summon (the Stella Octangula is the simplest of these daemons). However, should the summoner succeed, they could answer unsolved mathematical problems. Assuming they don't go mad in the process of learning how...

[emmatization]

Shit man, this analyst war is fucked. I just saw a guy wipe his chalkboard and say "Calderón–Zygmund decomposition" or some similar shit, and every function around him split into cubes, had their large values explode, and then disappeared. A preprint wasn't even written, that's how common shit like this is. My ass is calculating epsilon-delta and second derivative. I think I just heard "power word: ergodicity" two research groups over. I gotta get the fuck outta here.

[emmatization]

now if you thought "group" is an unhelpful and nondescriptive name for a mathematical concept. just remember that the broader category of mathematical concepts that groups belong to is called, a "category". so it could always be worse

[emmatization]

I think math teacher don't focus enough on history. Like, yeah, Abel results on the convergence of series are great and all, but did you know Cauchy hated Abel and is indirectly responsible for his death ?

Galois was a math wizard and died in a duel. But did you know he also was kind of a leftist, got thrown out of École Normale Supérieure because of that, joked about killing Louis Philippe and probably died because of that ?

Gauss is cool, but did you know he was saved by Sophie Germain, discovered at the same time Sophie Germain was a woman, and wrote one of the coolest letter blaming "our customs and prejudices" for not allowing women in math ?

Urysohn's lemma is cool, but did you did you know he tragically died while swimming with Alexandrov ? Oh, also they were both gay and in love. And later Alexandrov had a relation with Kolmogorov

There's tons of other stories, even minor ones (like how Italian mathematicians argued against some notations in vector calculus because they were used by Germans). Focusing only on how "abstract" and "pure" math is, is pedantic. Mathematicians, on the other side, are way funnier and not just lost in their abstract and complicated world

[emmatization]

group presentation tomorrow (not a presentation with other people) (presentation about group theory) (about presentations of groups) (mathematics)

[emmatization]

physics is scary what the hell is the Riemann zeta function doing in the equation for the critical temperature of a Bose-Einstein condensate

[emmatization]

I do feel like the hardest part of category theory so far is keeping track of what exactly all of that notation is actually saying

like, if you make an itemized list of all of these letters, what objects they are referring to and what the types of those objects are, then this diagram (and by extension the proof of the yoneda lemma) actually does become totally sensible and not actually that hard to understand but like. that's a huge hurdle to clear at the start!

[emmatization]

Next semester I'm taking a seminar on programming language theory with a focus on functional programming and one of the available topics is a paper about an application of the yoneda lemma in that context.... and god I think I'd have to put in a ton of extra effort to properly understand a) all the category theory and b) all the type theory but it feels like thats both too cool and too fitting given my name for me to not pick that one

[emmatization]

does anyone have any recommendation for introductory physics textbooks (mechanics, electromagnetism etc. at an undergraduate level) that aren't scared of mathematical rigor? I was really enjoying reading the feynman lectures on mechanics but his introduction of vectors was absolutely horrendous and so now I really want to find another physics textbook that isn't scared of vector spaces and epsilon delta limits.

[emmatization]

does anyone have any recommendation for introductory physics textbooks (mechanics, electromagnetism etc. at an undergraduate level) that aren't scared of mathematical rigor? I was really enjoying reading the feynman lectures on mechanics but his introduction of vectors was absolutely horrendous and so now I really want to find another physics textbook that isn't scared of vector spaces and epsilon delta limits.

[emmatization]

does anyone have any recommendation for introductory physics textbooks (mechanics, electromagnetism etc. at an undergraduate level) that aren't scared of mathematical rigor? I was really enjoying reading the feynman lectures on mechanics but his introduction of vectors was absolutely horrendous and so now I really want to find another physics textbook that isn't scared of vector spaces and epsilon delta limits.

[emmatization]

does anyone have any recommendation for introductory physics textbooks (mechanics, electromagnetism etc. at an undergraduate level) that aren't scared of mathematical rigor? I was really enjoying reading the feynman lectures on mechanics but his introduction of vectors was absolutely horrendous and so now I really want to find another physics textbook that isn't scared of vector spaces and epsilon delta limits.

[emmatization]

Interesting math fact of the day #88:

88 is the largest number with no “n” up until 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.

[emmatization]

ordinals are usually described as being generated by 3 constructors, namely:

0 : 1 -> Ord

succ : Ord -> Ord

sup : P(Ord) -> Ord

(where P(Ord) is the class of small subsets of the class of ordinals).

arguably, the main property that makes ordinals interesting is that they're well-ordered; for any property satisfied by some ordinal there's a least such ordinal. in particular, this is almost exemplified in the supremum operation, which gives the least ordinal at least as large as every ordinal in a given set. I say "almost", because it leaves open the question - if the supremum operation is so central to ordinal theory, why do we need the other two constructors? we should expect the "universal well-order" to only be defined by one constructor, asserting somehow that it's a well-order.

the first hint that this is fixable is the equation sup(∅) = 0, which gets rid of one of the "redundant" constructors. the second hint is the fact that in nimber arithmetic, defined using the ordinals, the main operation turns out to be the minimum excludent (mex), which returns the least ordinal not in a given set; especially interesting is the equation mex(α) = α, in which the ordinal α is regarded as the set {β ∊ Ord | β < α}.

introducing what I view to be the one true foundational operation on ordinals - sup°succ! this takes in a set of ordinals, applies the successor operation to each term in the set, then takes the supremum. some important cases are:

sup°succ(∅) = 0

sup°succ({α}) = succ(α)

and for an infinite increasing sequence S = {α,β,γ,...},

sup°succ(S) = sup(S) [= lim(S)]

so this is a unified constructor that generates all the ordinals!

another way to view this operation is as returning the least ordinal strictly greater than all ordinals in a given set - which is, in a way, the discrete analogue of the continuous "supremum".

since this operation draws inspiration both from the supremum/limit ("minimally as large as any ordinal in the set") and from the minimum excludent ("not included in the set"), I suggest the name "supremum excludent", or in short "sex" :3