proof-by-intimidation

[proof-by-intimidation]

Coherent sheaf

perverse sheaf

[proof-by-intimidation]

If I made the rules, mathematicians would be obligated to wear wizard cloaks. Or robes or hats. Not like, legally or anything, just in a social obligation "it would be kinda weird if you didn't, because that's just what they do" kind of way

[proof-by-intimidation]

moving into a non-abelian accommodation such that you don't have to commute

[proof-by-intimidation]

category theory emergency? dial 00よ, now!

[proof-by-intimidation]

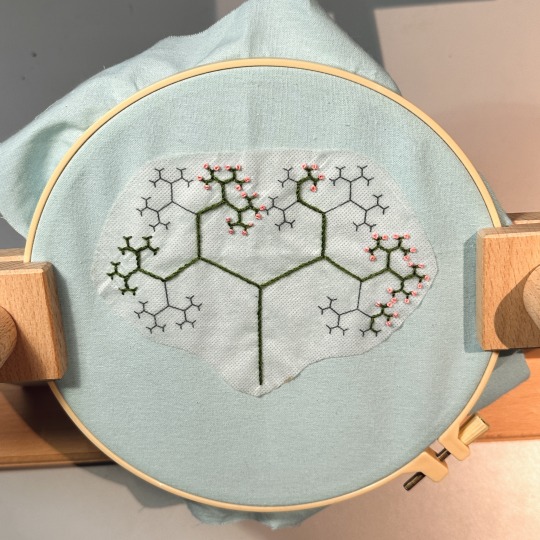
Work in progress of a binary tree.

[proof-by-intimidation]

you wish your bio was this cool.

[proof-by-intimidation]

in my regime all ads will be replaced by ads of mathematical objects

[proof-by-intimidation]

Letters from a stoic by Seneca

[proof-by-intimidation]

whenever a linear algebra professor catches you having too much fun with math they are legally obligated to make you do gram-schmidt as a way of humbling yourself

[proof-by-intimidation]

headache all day

drink water, eat food

hours pass

headache

watch category theory playlist by richard e borcherds

no more headache

[proof-by-intimidation]

Some mathematicians claim they can visualize R^4, or even higher-dimensional spaces. I think this is probably possible for the human mind to do, in principle; the human mind often proves surprisingly flexible. But I think it probably takes a lot of concerted practice, and because you are stretching your mind beyond its intended limits in a purely-internal, imaginative way with no external reference points to check against, I think it probably has some things in common with certain types of meditative practice.

It's also common to hear mathematicians say that if humans had visual intuition for dimensions higher than 3, higher-dimensional geometry may have advanced much farther, since visual intuition is so often crucial in thinking of proofs.

So, ok, I suspect that AI will obviate the utility of this before it could ever have the chance to get off the ground, but this all makes me imagine a world where techniques for learning to visualize higher dimensions are well-known and practiced, and have become a functional necessity for being a working geometer in higher-than-3-dimensions. And these techniques require a lot of persistent practice and training, which (by the nature of the thing) is hard to precisely communicate to students. So part of becoming a geometer involves training in what is basically a meditative practice, where, à la Zen, much of the process involves not directly teaching the student but giving them prompts and mental exercises that are meant to trigger internal, incommunicable revelation. But instead of enlightenment it's geometric intuition. And so if we're getting a math PhD in, say, differential equations or something, it's mostly like it is today. But if your PhD is in low-dimensional topology there's like a whole monastic apprenticeship style thing that just comes along with it. People sometimes drive themselves insane. People sometimes drive themselves insane.

[proof-by-intimidation]

I am wondering if anyone here can offer me a bit of insight into what the "big theorems" of algebraic geometry and/or algebraic topology obtained by infinity-categories are. The Beck's Monadicity Theorem's of the subject, so to speak. Just trying to get a feel of what the formalisms are building towards.

[proof-by-intimidation]

I've been thinking about A-infinity algebras and the homotopy transfer theorem a lot. There's this idea I've been working on and I now understand enough to be confident that my idea should work, but there are enough holes in my understanding that I can't quite write a proof. This is the part of math that is the most maddening. I want to just keep working until I've solved it but it'll probably still take dozens of hours until I have a solution. It's also the most physically exhausting part of the process. I can feel the gears in my head turning and it's so effortful

[proof-by-intimidation]

When you graduate from being interested in feet.

Is this anything?

[proof-by-intimidation]

As I resume my quest to become an algebraic geometer, I am awe struck by the sheer abundance of excellent resources available in terms of online lecture notes. I resumed my quest by purchasing Hartshorne, expecting to resume the struggle, but it turns out that is a very 2016-coded way of studying algebraic geometry.

What a wonderful world we are living in to have access to such resources so easily!

In particular I am really falling in love with the lecture notes of Gathmann.

[proof-by-intimidation]

My talk was uploaded on YouTube and one person commented (months later) that they found it useful. Ahhh, that was the whole point!! For a non-trivial number of people to get something out of it!

[proof-by-intimidation]