#how to simplify logarithms
Explore tagged Tumblr posts
Text
youtube
In this video, we delve into the art of solving logarithmic equations with different bases, demystifying the process for you step by step. Whether you're a student brushing up on logarithms or someone facing more complex problems, we've got you covered. Understanding how to work with different bases is crucial when faced with logarithmic equations. We break down the techniques, providing clear explanations using frequently used words to ensure that you grasp the concepts effortlessly. No more getting stuck on those seemingly perplexing logarithmic problems!
#Different bases for solving a log equation#logarithm questions basic#tricky logarithmic questions solve#logarithm formula#solving logarithms#logarithm base#logarithm applications#evaluate basic logarithm#formula of logarithms#solving logarithmic equations#logarithms explained#how to simplify logarithms#solving negative exponents#free math videos#logarithmic#algebra#mathematics#tutorial#Sami’s A Plus#sami’s a plus#math lessons#math for kids#learn math fast#Youtube
2 notes
·
View notes
Text
haaaghh. brain so tired
#marzi speaks#just got out of my math test. i had forgotten my calculator#i just had to do exponents. raw#thankfully i remembered how they work and found a way to simplify the amt of math i had to do. but AAAA my brain so tired#completely forgot how to do negative exponents tho. i think they’re logarithms? and i cannot do those at all#it’s ok. that professor is chill i’ll get partial credit it’ll be Fineeee
1 note
·
View note
Text
The Magic of Euler’s Identity
Mathematics has its moments of sheer beauty—when abstract concepts collide to form something elegantly simple, yet profoundly deep. Euler's Identity is the pinnacle of this beauty. Expressed as: eiπ+1=0e^{i\pi} + 1 = 0
It may seem deceptively simple, but it links five fundamental constants in mathematics:
e - Euler’s number, the base of natural logarithms (~2.718).
i - The imaginary unit, defined as −1\sqrt{-1}.
π - The famous constant, representing the ratio of a circle's circumference to its diameter (~3.1416).
1 - The multiplicative identity.
0 - The additive identity.
Why is Euler's Identity so Special?
At first glance, Euler's identity seems almost trivial—a relationship between numbers that don’t seem to belong together. Yet, it’s a striking result of complex analysis and trigonometry. The formula brings together exponentiation, complex numbers, geometry, and even calculus in a single equation. How is this possible?
Euler’s identity emerges from Euler’s formula, a fundamental equation in complex analysis: eix=cos(x)+isin(x)e^{ix} = \cos(x) + i \sin(x)
For any real number xx, this formula expresses the complex exponential eixe^{ix} as a combination of cosine and sine functions. When x=πx = \pi, we get: eiπ=cos(π)+isin(π)=−1+0i=−1e^{i\pi} = \cos(\pi) + i \sin(\pi) = -1 + 0i = -1
Thus, Euler's identity follows immediately: eiπ+1=0e^{i\pi} + 1 = 0
This result connects imaginary numbers, trigonometric functions, and exponentiation in an astonishingly compact form.
Why Do Mathematicians Love It?
Euler’s Identity is often called "the most beautiful theorem in mathematics." Why? Because it encapsulates the interplay between several areas of mathematics in one concise equation. It’s elegant, unexpected, and remarkably simple—an almost magical blend of different mathematical elements.
Mathematicians love it because it challenges our intuition. We tend to think of numbers like ee, π\pi, and ii as separate entities, each with its own mysterious properties. But Euler’s identity reveals that they are inextricably linked, suggesting that seemingly unrelated areas of math have hidden connections.
Some Mind-Blowing Examples and Connections
Trigonometry and Geometry: Euler’s formula gives rise to the unit circle in the complex plane. As eixe^{ix} traces a path around the unit circle, it maps directly onto the sine and cosine functions, giving a visual and geometric interpretation of trigonometric identities.
The Complex Plane: In the complex plane, eixe^{ix} represents a point on the unit circle with an angle xx from the positive real axis. This brings an entirely new way to think about rotations, using exponential functions.
Quantum Mechanics: Euler’s identity has practical applications in quantum mechanics. The wavefunctions in quantum physics often involve complex exponentials of the form eiθe^{i\theta}, linking Euler’s identity to the fundamental laws governing particles.
Differential Equations: The beauty of Euler’s formula shines in solving differential equations. In systems that oscillate (like springs or circuits), Euler’s formula simplifies the solution process and makes the math elegant and tractable.
#mathematics#math#mathematician#mathblr#mathposting#calculus#geometry#algebra#numbertheory#mathart#STEM#science#academia#Academic Life#math academia#math academics#math is beautiful#math graphs#math chaos#math elegance#education#technology#statistics#data analytics#math quotes#math is fun#math student#STEM student#math education#math community
10 notes
·
View notes
Text
Training Teachers to Teach Class 12 Maths — MathYug

In the ever-evolving landscape of education, having access to high-quality learning resources can make a world of difference. For Class 12 students, mastering mathematics is crucial, not only for academic success but also for future endeavors in various fields. At MathYug, we understand this importance and have dedicated ourselves to providing top-tier educational materials. Today, we’re excited to introduce our training program designed specifically for teachers who aspire to elevate their teaching skills and make a significant impact on their students’ learning journey.
Sample Videos: A Glimpse into Quality Education
To give you a taste of what MathYug has to offer, we are sharing a selection of sample videos from our Class 12 Maths tutorials. These videos exemplify the high-quality, in-depth teaching style that Ashish Kumar, affectionately known as Agam Sir, is known for.
Relations and Functions
youtube
2. One to One and Onto Functions
youtube
3. Inverse Trigonometric Functions
youtube
4. Continuity and Differentiability
youtube
5. Applications of Derivatives
youtube
6. Integrals
youtube
7. Inverse Trigonometric Functions
youtube
8. Basics of Logarithms, Log Table and Antilog Table
youtube
Why Choose MathYug for Teacher Training?
MathYug stands out as a premier platform for learning and teaching mathematics, especially for Class 12 students. Our resources are meticulously designed to cater to the diverse needs of both learners and educators, ensuring that each student can grasp complex mathematical concepts with ease. Here’s why MathYug is the best choice for your teaching journey:
Expert Guidance
All our content is created by Ashish Kumar (Agam Sir), a renowned educator with years of experience in teaching mathematics. His unique teaching style simplifies complex topics, making them easily understandable. By training with MathYug, teachers can learn how to effectively convey these methods to their students.
Comprehensive Coverage
Our tutorials cover the entire Class 12 Maths syllabus, aligned with the NCERT guidelines. This ensures that students are well-prepared for their board exams and other competitive exams. Teachers trained with MathYug will be equipped to offer their students a thorough and well-rounded mathematical education.
Interactive Learning
We believe in making learning engaging and interactive. Our video lessons are complemented by practical exercises, assignments, and downloadable PDFs to reinforce learning. Teachers will be trained to use these resources to create a dynamic and interactive classroom environment.
Elevate Your Teaching Experience with MathYug
At MathYug, we are committed to providing the best possible educational resources to help both students and teachers excel in mathematics. Our Class 12 Maths tutorials are designed to build confidence, enhance understanding, and foster a love for learning. By sharing these sample videos, we hope to give teachers a glimpse of the quality education that awaits them on our platform.
Join MathYug Today!
Experience the difference with MathYug and take your teaching skills to new heights. Subscribe to our Class 12 Maths membership and gain access to a comprehensive collection of video lessons, study materials, and expert guidance from Ashish Sir. Let’s embark on this journey of academic excellence together!
Visit MathYug now and start your journey towards mastering Class 12 Maths with ease and confidence.
#class 12 maths#teachers#educators#teacher training#mathyug#class 12 maths tutorials#class 12 maths videos#class 12 maths solutions#Youtube
3 notes
·
View notes
Note
🌻
(Oh man, the mortifying ordeal of actually having to pick something to talk about when I have so many ideas...)
Uh, OK, I'm talking about galactic algorithms, I've decided! Also, there are some links peppered throughout this post with some extra reading, if any of my simplifications are confusing or you want to learn more. Finally, all logarithms in this post are base-2.
So, just to start from the basics, an algorithm is simply a set of instructions to follow in order to perform a larger task. For example, if you wanted to sort an array of numbers, one potential way of doing this would be to run through the entire list in order to find the largest element, swap it with the last element, and then run though again searching for the second-largest element, and swapping that with the second-to-last element, and so on until you eventually search for and find the smallest element. This is a pretty simplified explanation of the selection sort algorithm, as an example.
A common metric for measuring how well an algorithm performs is to measure how the time it takes to run changes with respect to the size of the input. This is called runtime. Runtime is reported using asymptotic notation; basically, a program's runtime is reported as the "simplest" function which is asymptotically equivalent. This usually involves taking the highest-ordered term and dropping its coefficient, and then reporting that. Again, as a basic example, suppose we have an algorithm which, for an input of size n, performs 7n³ + 9n² operations. Its runtime would be reported as Θ(n³). (Don't worry too much about the theta, anyone who's never seen this before. It has a specific meaning, but it's not important here.)
One notable flaw with asymptotic notation is that two different functions which have the same asymptotic runtime can (and do) have two different actual runtimes. For an example of this, let's look at merge sort and quick sort. Merge sort sorts an array of numbers by splitting the array into two, recursively sorting each half, and then merging the two sub-halves together. Merge sort has a runtime of Θ(nlogn). Quick sort picks a random pivot and then partitions the array such that items to the left of the pivot are smaller than it, and items to the right are greater than or equal to it. It then recursively does this same set of operations on each of the two "halves" (the sub-arrays are seldom of equal size). Quick sort has an average runtime of O(nlogn). (It also has a quadratic worst-case runtime, but don't worry about that.) On average, the two are asymptotically equivalent, but in practice, quick sort tends to sort faster than merge sort because merge sort has a higher hidden coefficient.
Lastly (before finally talking about galactic algorithms), it's also possible to have an algorithm with an asymptotically larger runtime than a second algorithm which still has a quicker actual runtime that the asymptotically faster one. Again, this comes down to the hidden coefficients. In practice, this usually means that the asymptotically greater algorithms perform better on smaller input sizes, and vice versa.
Now, ready to see this at its most extreme?
A galactic algorithm is an algorithm with a better asymptotic runtime than the commonly used algorithm, but is in practice never used because it doesn't achieve a faster actual runtime until the input size is so galactic in scale that humans have no such use for them. Here are a few examples:
Matrix multiplication. A matrix multiplication algorithm simply multiplies two matrices together and returns the result. The naive algorithm, which just follows the standard matrix multiplication formula you'd encounter in a linear algebra class, has a runtime of O(n³). In the 1960s, German mathematician Volker Strassen did some algebra (that I don't entirely understand) and found an algorithm with a runtime of O(n^(log7)), or roughly O(n^2.7). Strassen's algorithm is now the standard matrix multiplication algorithm which is used nowadays. Since then, the best discovered runtime (access to paper requires university subscription) of matrix multiplication is now down to about O(n^2.3) (which is a larger improvement than it looks! -- note that the absolute lowest possible bound is O(n²), which is theorized in the current literature to be possible), but such algorithms have such large coefficients that they're not practical.
Integer multiplication. For processors without a built-in multiplication algorithm, integer multiplication has a quadratic runtime. The best runtime which has been achieved by an algorithm for integer multiplication is O(nlogn) (I think access to this article is free for anyone, regardless of academic affiliation or lack thereof?). However, as noted in the linked paper, this algorithm is slower than the classical multiplication algorithm for input sizes less than n^(1729^12). Yeah.
Despite their impracticality, galactic algorithms are still useful within theoretical computer science, and could potentially one day have some pretty massive implications. P=NP is perhaps the largest unsolved problem in computer science, and it's one of the seven millennium problems. For reasons I won't get into right now (because it's getting late and I'm getting tired), a polynomial-time algorithm to solve the satisfiability problem, even if its power is absurdly large, would still solve P=NP by proving that the sets P and NP are equivalent.
Alright, I think that's enough for now. It has probably taken me over an hour to write this post lol.
5 notes
·
View notes
Text
What human development entails?
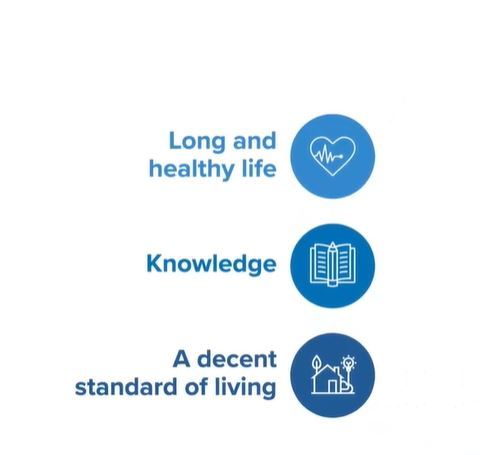
The Human Development Index (HDI) is the geometric mean of normalized indices for each of the three dimensions.
The health dimension is assessed by life expectancy at birth, the education dimension is measured by mean of years of schooling for adults aged 25 years and more and expected years of schooling for children of school entering age. The standard of living dimension is measured by gross national income per capita. The HDI uses the logarithm of income, to reflect the diminishing importance of income with increasing GNI. The scores for the three HDI dimension indices are then aggregated into a composite index using geometric mean. The HDI can be used to question national policy choices, asking how two countries with the same level of GNI per capita can end up with different human development outcomes. These contrasts can stimulate debate about government policy priorities. The HDI simplifies and captures only part of what human development entails. It does not reflect on inequalities, poverty, human security, empowerment, etc. The HDRO provides other composite indices as broader proxy on some of the key issues of human development, inequality, gender disparity and poverty. A fuller picture of a country's level of human development requires analysis of other indicators and information presented in the HDR statistical annex.

#HDI dimension#economic development#human development#health dimension#standard of living dimension#education dimension#GNI per capita
0 notes
Text
Today or night is 26 Sept 2024. My last night in Montclair. Every person I’ve met at the condo is probably over 80. Yeah. It’s like I moved to Florida. I went to the HOA meeting and the odd thing was that I had seen this entire event in a ‘dream’. And the rule for that to occur has been that those are unimportant moments. I think I have the math for that now. Let’s see.
BTW, I had a Jersey Mike’s sub. It was good. Best chain sub I’ve had since the early Subway, like the one run by the guy who started Subway or close to it. Those were good and this was like that. I ate half for dinner and half for lunch.
Oh right, the math. It’s the Bip construction off the grid, like watching the business signs on a divided highway. Learning from Las Vegas. The idea is they have passing interest but you remember them. Why can they be seen and not heavier moments? Because they’re lighter, meaning they attach to you in a relatively simple way. Like in this case, it was obvious the place is well managed so my worries disappeared then and that lightened the experience. That means the Bip is not so far off the path, off the axis, off the road, meaning the layers don’t count to the 1 which says oh here it is, you’ve found the spot.
That’s an almost cylindrical concept. It idealize to that, but also to spirals and everything else because I just saw how this links to the concept of Boundary. Wow. That was a lot to take in. This allows me to see the counting of logarithms, including the natural log. I’ve never been able to visualize that; it has remained words and labels and other ways of saying ideas but not intuitive like when I was in kindergarten.
Oh, the cat just pooped. Ugh.
————
A gloss on halting. The idea is that we can only abstractly create a process that runs ‘forever’ because all ‘forevers’ occur within 0Space and thus they are finite.
Uh oh, it wants to connect to the hydra game, which means cutting below the parent, meaning that if we treat the grandparent as -1, then 0 to 1 being the head cut off, then the process locates the new heads back at the grandparent, which then runs -1 to 0 to 1 in the ‘other’ direction but still forward in gsProcess. SBE2 in which the Between is what happens from grandparent over parent to child, and back. This makes the hydra finite; you will cut off all the child heads because all the new ones grow at the parent level. After you’ve run out of kids, you start on the parents and look back to great-grandparents. Until there’s no more hydra.
Halting requires a lookback to the creation of the program, to its start. We simplify that to grandparent over the Between of the parent to the child of the moment, to the current state of the created process. So when we compare hydras to SBE, that makes it easier to see the SBE form in halting. Remember, all 0Space process is finite by the nature of 0Space’s relationship to 1Space and how 0Space generates out of D-structure.
0 notes
Text
Harnessing The Power Of AI In Lead Generation

The evolution of lead generation has taken a turn, and almost all businesses are engaged in the process. The journey from conventional approaches to the most recent innovations is mind-bending. In this article, we will be looking at artificial intelligence (AI) and how it has been central to changing how companies get leads.
Understanding AI in lead generation
An Overview of Artificial Intelligence
Definition and Types of AI
AI, at its core, involves the creation of algorithms and systems able to do what would normally be considered tasks needing human intelligence. There are different types of AI, which include narrow AI built for specific tasks and general AI that has cognitive abilities similar to those possessed by humans.
2.Importance in Modern Business
Nowadays, AI is not just a buzzword but a must-have for all businesses. It is priceless, as it can process massive data volumes in no time and then act upon them. Such firms have a competitive advantage over the rest as they can simplify operations, which leads to the realisation of innovation drivers by such companies.
Role of AI in lead generation
Automation of Procedures
Lead generation in AI can simply be called automation, as it makes work easier. This is because AI systems take care of repetitive chores such as data searches and initial contacts so that human resources are left to handle more complicated aspects of the process.
Data Analysis and Insights
The power of AI lies in spotting patterns among large data volumes. For lead generation, this means a great understanding of customer behaviour, preferences, and trends. Such analytical jewels help companies modify their strategies with an objective approach towards targeting.
Key Components of AI in Lead Generation
Machine learning algorithms
Predictive Analytics
Artificial intelligence-powered lead generation heavily relies on machine learning algorithms that power predictive analytics. These logarithms evaluate past data to forecast the future, helping businesses anticipate consumer needs and adjust their actions accordingly.
Pattern Recognition
Pattern recognition is the strength of machine learning, in a nutshell. Personalised marketing strategies result from recognising patterns of consumer behaviour, thereby making companies resonate better with their prospective segment.
Natural Language Processing (NLP)
Communication Improvement
Natural Language Processing (NLP) allows machines to comprehend, construct, and produce human-like language. In lead generation, this enhances communication with potential customers, meaning better sales. Chatbots and automated responses become more instinctive so that the dialogues are meaningful.
Sentiment Analysis for Lead Qualification
Sentiment analysis helps in qualifying leads through NLP by analysing feelings expressed in communications. This way, businesses get to know what potential customers think about their products or services, enabling them to plan how to approach their audience.
Implementing AI-Driven Lead Generation
Choosing the Right AI Tools
CRM Integration
By integrating AI technologies with customer relationship management (CRM) systems, customer interactions are improved. AI-powered CRMs can make it easier for data management to offer a holistic view of customers’ interactions and preferences.
Marketing Automation Platforms
Marketing automation platforms powered by AI ensure the seamless implementation of targeted campaigns in businesses. Such platforms utilise AI to examine customer data, hence automating marketing efforts for optimal productivity.
Training AI Models for Specific Industries
Customisation for Maximum Efficiency
To realise high efficiency, artificial intelligence models should be customized to operate within specific sectors. This customisation enables the technology to match industry-specific peculiarities, resulting in optimised lead generation strategies.
Adapting to Changing Market Trends
The fact that markets are changing rapidly calls for AI models that are ever-evolving. Organisations must have systems that can respond to changing market trends, ensuring their continued effectiveness in generating leads.
Benefits of AI in Lead Generation
Increased efficiency and productivity
Simplifying workflows
The workflows are streamlined by the automation of routine tasks through AI, resulting in reduced manual effort and increased efficiency in overall operations. The time saved can be channelled to strategic planning and relationship management activities.
Reducing manual tasks
Mundane, time-consuming tasks are a thing of the past with AI. Lead generation processes are expedited, allowing teams to focus on high-value activities that contribute directly to business growth.
Enhanced Lead Qualification
Accurate Targeting
AI’s data analysis abilities guarantee precision in targeting. By determining the most important leads, businesses can allocate their resources better and enhance their overall conversion rate.
Increased conversion rates
The accuracy provided by AI in lead qualification means that businesses get more conversions. It makes the overall lead generation efforts of a company more effective if it interacts with prospects whose chances of purchasing are higher.
Overcoming Challenges in AI-Driven Lead Generation
Data privacy and security concerns
Complying with the regulations
Responsibility goes hand in hand with power. AI used for lead generation should strictly observe data protection laws. By ensuring compliance, customer trust is preserved, while businesses are also protected from legal consequences.
Building trust with customers
Open and clear communication regarding the utilisation of data fosters trust among customers. Businesses must convey how AI is employed in lead generation, emphasising the ethical and secure handling of sensitive information.
Integration Challenges
Overcoming technological barriers
The incorporation of AI into existing systems is not easy. What businesses require are solutions that can integrate well with their current infrastructure, overcome technological barriers, and ensure a safe journey there.
Employee Training and Adoption
Efficient AI installation demands extensive staff literacy in technology. The smooth adoption of AI through implemented training programmes guarantees the teams will exploit the full potential of AI.
Real-world examples of AI success in lead generation
Case Study: Company A’s AI-Driven Campaign
Purpose and Strategy
Company A’s excellence lies in strategic planning. Their lead generation campaign, which incorporated AI, focused on either personal touch or machine learning to create a sense of self as well as an understanding of marketing content suitable for customers.
Results and Key Takeaways
The results were just amazing: increased conversion rates, a streamlined workflow, and a better comprehension of customer behaviour. The key point is that AI is no longer simply a tool; it acts as the vehicle through which businesses experience transformational growth.
Innovations in AI for lead generation
Emerging Trends
AI in lead generation is a changing field where AI-powered chatbots, predictive analytics, and personalised experiences are getting better by the day, giving businesses new tools for a competitive edge.
Industry leaders and best practices
There have been some pioneering companies in terms of AI in lead generation that have set the standard for continuous learning or responding to market dynamics, such as leading companies, showing how boundless AI-driven strategies can be.
Future Trends in AI-Enhanced Lead Generation
AI-powered predictive lead scoring
Predicting customer behaviour
AI-powered predictive lead scoring is the next step in lead generation. In this way, businesses can interact with prospects even before they move on.
Improving sales targeting
This is due to better prediction, which has made it possible for organisations to have a more accurate sales targeting process. By doing so, the marketing and sales departments can optimise their sales funnels, thus becoming more efficient in closing deals, leading to increased conversion rates from leads identified using artificial intelligence.
Integration of AI with Emerging Technologies
AI and Blockchain in Lead Generation
By combining AI with blockchains in lead generation, there is greater transparency and security. This has resulted in decentralisation as well as a data-driven approach, which blockchain complements by way of its distributed ledger technology (DLT).
Integration of Augmented Reality (AR) and Virtual Reality (VR)
The future of lead generation will see it being done through immersive experiences. When AR and VR are combined with AI, they enable customisation, interaction, and engagement that are more personal in nature, thus providing a deeper understanding of products or services to prospective customers.
Conclusion
Conclusively, integrating AI into lead generation is an earth-moving power that launches businesses into a new day of effectiveness and efficiency. We are walking through an ever-evolving technological world, so adopting AI is not a matter of choice but a necessity for any business aspiring to be ahead in this tough market. As far as AI in lead generation goes, we are only at the beginning of the journey; there is no limit to this. For any lead generation services reaching out to us , Our innovative approach exemplifies the transformative potential of AI in revolutionising business strategies, ensuring a competitive edge in the dynamic landscape of today’s market.
Source URL - https://www.genleads.agency/lead-generation/harnessing-the-power-of-ai-in-lead-generation/
0 notes
Text
How to Use Calculator for Log: Master the Logarithm Functions

To use a calculator for log, simply press the "Log" button and enter the number. Logarithms help solve complex mathematical problems by finding the exponent for a given number. Logarithms are a fundamental mathematical concept with numerous applications in fields such as science, engineering, and finance. Using a calculator to compute logarithms can simplify complex calculations and help in problem-solving. By understanding how to use the log function on a calculator, individuals can efficiently determine the power to which a base must be raised to produce a specific number. This can aid in various scenarios, such as analyzing exponential growth or decay, calculating the time required for an investment to double, and solving equations involving exponential functions. Mastering the use of log on a calculator can enhance mathematical proficiency and streamline problem-solving processes in diverse academic and professional settings.
Using A Calculator
When it comes to solving logarithms, using a calculator can be a real time-saver. With the convenience of modern graphing calculators, you can easily calculate logarithms of any base, simplify complex equations, and perform calculations with small numbers. In this blog post, we will explore different ways to use a calculator for logarithms. Whether you are a student or a professional, this guide will help you make the most of your calculator's 'Log' button, enter logarithms on a graphing calculator, use other log bases, handle small numbers, and even divide natural logs with ease. Using The 'log' Button The 'Log' button on your calculator is specifically designed to calculate logarithms. To use it, simply enter the number you want to calculate the logarithm for and press the 'Log' button. The result displayed on your calculator is the exponent of the base number you entered. It's that simple! This feature is especially useful when you want to quickly find the logarithm of a number without manually performing complex calculations. Entering Logarithms On A Graphing Calculator If you're using a graphing calculator, entering logarithms is a little different. Most graphing calculators have a dedicated 'Log' button, usually located near the trigonometry functions. To calculate a logarithm on a graphing calculator, enter the base of the logarithm, followed by the value you want to find the logarithm of. For example, to calculate the logarithm base 10 of 100, you would enter "log(100,10)" into the calculator. The result will be displayed on the screen, giving you the logarithm of the specified number with the specified base. Using Other Log Bases Calculators usually default to base 10 logarithms. However, you may come across equations that require logarithms with different bases. Fortunately, most calculators allow you to enter logarithms with any base you desire. Simply use the log function followed by the base number in parentheses. For example, to calculate a logarithm base 2 of 8, enter "log(8,2)" into your calculator. The resulting value will be the logarithm of 8 with base 2. Using Logarithms With Small Numbers Working with small numbers can be tricky, but calculators make it much easier. To calculate the logarithm of a small number, simply enter the number as it appears in scientific notation. For example, if you want to find the logarithm of 0.001, you would enter "log(1 x 10^-3)" into your calculator. The calculator will then display the logarithm of the small number, giving you the solution you need. Dividing Natural Logs With A Calculator Dividing natural logs can be cumbersome, but with a calculator, it's a breeze. To divide natural logs, use the division operation ("/") and enter the two natural logs you want to divide. For example, to divide the natural log of 10 by the natural log of 2, you would enter "ln(10) / ln(2)" into your calculator. The result will be displayed on the screen, providing you with the answer to your division problem.
Tips And Tricks
When dealing with logarithms, there are various tips and tricks that can streamline the process and make calculations faster and more efficient. In this section, we will uncover some useful hacks that can help you quickly calculate logarithms without the need for a calculator. Quickly Calculate Logarithms Without A Calculator Calculating logarithms without a calculator can be simplified by utilizing a few strategic techniques. One method involves using the concept of inverses. Since logarithms are inverses of exponentials, you can utilize this relationship to simplify certain calculations. For example, if you need to find the logarithm of a number to a specific base, you can transform it into an exponential form and simplify the calculation. Another handy trick for quickly computing logarithms is to remember the common logarithm values. Having key logarithm values such as log 2, log 3, and log 5 memorized can aid in swiftly approximating logarithms of other numbers. Additionally, familiarizing yourself with the properties of logarithms, such as the product and quotient rules, can expedite the computation process and minimize the need for a calculator. https://www.youtube.com/watch?v=kqVpPSzkTYA
Calculating Logarithms On Different Calculator Brands
Calculating logarithms using different calculator brands can be a versatile skill. Below, we explore how logarithms can be calculated on various popular calculator brands. Using Logarithms On A Casio Calculator Calculating logarithms on a Casio calculator is straightforward. Follow these steps: - Press the "Log" button on your Casio calculator. - Enter the number you want to find the logarithm of. - Press the "=" button to display the result. Using Logarithms On An Iphone Calculator Utilizing logarithms on an iPhone calculator is convenient. Here's how you can do it: - Open the Calculator app on your iPhone. - Turn your iPhone to landscape mode to reveal the scientific calculator. - Tap the "Log" button followed by entering the number to calculate the logarithm. By following these simple steps, you can efficiently compute logarithms on your Casio calculator or iPhone calculator.

Frequently Asked Questions On How To Use Calculator For Log
How Do You Do Log On A Calculator? To calculate a logarithm on a calculator, press the "Log" button and enter the number you want to find the logarithm of. How Do You Do Log On A Normal Calculator? To find the logarithm on a normal calculator, press the "Log" button followed by the number. What Is The Easiest Way To Calculate Logs? The easiest way to calculate logs is using a calculator. Press the "Log" button, enter the number, and the result is the logarithm. How Do You Calculate Log10? To calculate log10, use a scientific calculator by pressing the "log" button and entering the number. The result displayed is the logarithm with base 10.
Conclusion
Using a calculator for logarithms can simplify complex calculations and save time. By following the steps outlined in this blog post, anyone can harness the power of logarithms in their mathematical endeavors with ease. So, go ahead, grab your calculator, and dive into the world of logarithms with confidence. Read the full article
0 notes
Text
Are You Harnessing the Power Of Natural Blogarithm? What Impact Does Natural Blogarithm Have on Website Success? How Can Natural Blogarithm Impact Your Website's Success? Not everyone understands what logarithm means when they see or hear the notation "ln," yet logarithm is ubiquitous - from decimal systems and computer representation of numbers, to supporting scientific principles like astronomy and biology. Logarithm is derived from Greek roots meaning proportion/ratio/word and "arithmos/number," giving its definition as an attempt at representing relationships between numbers. This article will explain its concept further. Mathematicians, astronomers and other scientists frequently need to take the logarithm with a base e of numbers in order to solve an equation or find their value. Henry Briggs created the common logarithm as an easier alternative; writing and calculating its formula are simplified due to less symbols required compared with its base e logarithm counterpart. To read the rest of this article, please click on the link below: https://websitebloggers.com/are-you-harnessing-the-power-of-natural-blogarithm/?feed_id=7611&_unique_id=661675073a415
0 notes
Text
Boost Your Website’s Conversion Rate with Hick’s Law
Every click, interaction, and minute spent on your website in this digital world can enhance your brand. In the fast-paced realm of online presence, understanding the art of user experience is critical. Enter website conversion rate with Hick’s Law, a guiding concept that has withstood the test of time in the ever-changing world of online design.
As we continue on this quest to increase the conversion rate of your website, it is critical to grasp the historical significance of Hick’s Law. This rule was proposed by psychologists William Edmund Hick and Ray Hyman in the 1950s. It states that the time it takes a person to decide is equal to the number of options available. When translated to the digital domain, it becomes a valuable tool for improving UI. It also directs visitors to desired behaviors.
Join us as we dig into the interesting development of Hick’s Law. We will investigate how its principles expedite user decision-making. Also, lift your website’s conversion rates to unparalleled heights. It’s time to combine past knowledge with present innovations to create a digital experience. It captivates and converts with precision and delicacy.

What is Hick’s law:
Hicks Law or the Hick-Hyman Law states that the more options available for the people, the longer time is taken to make a decision. You can say that as decision-making time increases, so does the quantity of options. As a result, if there are more options, the increase in time becomes less significant. So, it proposes to reduce the elements in the website. The fewer the options, the easier the usage. Users must reach out to their required section in an instant. Hence, it eases the decision-making process and removes the not-so-essential elements or barriers. In other words, it offers a responsive design to the website. The increased time on a website can enhance the conversion rates.
RT = a + b log2 (n)
Where:
RT = reaction time
a = the time that is not involved with decision-making
b = an empirically derived constant based on the time it takes to process each option cognitively
log2 = logarithm function
(n) = the number of equally probable alternatives
Also read about Fitts’ law in UX
Website conversion rate with Hick’s Law:
As already discussed, Hick’s Law is an important tool that helps people make decisions more easily. Here’s how to use Hick’s Law to your advantage in UX design to improve conversion rates:
Reduce Choices:
According to Hick’s Law, having too many options can cause indecision. Users with a limited amount of alternatives can choose more frequently. It is applicable, particularly on important sites like landing pages and checkout screens. Also, if you want users to choose components that can cause conversions and avoid distractions.
Clear and Concise Navigation:
Use Hick’s Law in your website navigation. Simply maintain menus that are orderly, concise, and easy to understand. Users should understand their options without being overwhelmed by a multitude of choices. Provide a user-friendly navigation menu with a logical structure and a clear path.
Simplify Forms:
Forms that are too long or too technical might be an obstacle to conversion. Reduce the amount of fields and steps necessary for completion using Hick’s Law. Use smart defaults, auto-fill options, and inline validation to make form-filling easier.
Read rest of the article here
0 notes
Text
Understanding Acoustics: How Curtains Can Improve Your Space

Introduction Welcome to Direct Fabrics, where we're dedicated to helping you understand the world of acoustics and how our products can make a difference in your living or working space. In this blog post, we will simplify the concept of acoustics, explain the importance of sound absorption and insulation, introduce you to our range of acoustic curtains, and guide you on choosing the right curtain for your specific needs.
Understanding the Issues
When it comes to acoustics, many people face various challenges in their living and working environments. These issues can include: - Noise entering your room or space. - Noise escaping from your space. - Poor acoustics during rehearsals or recordings. - Difficulty sleeping due to external noise, such as traffic, planes, or trains. - Echoey and large spaces that affect sound quality.
Who Are We, and How Can We Help?
Edward Simon, Director of Direct Fabrics, found himself drawn into the world of acoustics due to high demand for products like stage curtains and Hotel Co. We have been supplying curtains to care homes, schools, medical centers across the UK, and even global clients. Our commitment lies in providing clear information and certified products, ensuring you get the best value for your investment.
Understanding Acoustics
Sound absorption is a crucial concept in acoustics. It refers to the ability of materials to absorb sound, reducing echo and reverberation in a space. Even seemingly simple items like curtains can contribute to sound absorption. Adding soft furnishings, such as rugs, carpets, and curtains, can dampen sound and improve the acoustics in a room. Testing and Certification Our products undergo rigorous testing, including the EN ISO 354 acoustic absorption test. This test quantifies the sound absorption properties of materials, rating them from A to E, with A being the highest rating. Our face fabric achieves an impressive absorption rate of 0.95, which is equivalent to an A rating.
Sound Transmission and Acoustic Insulation
Another important aspect of acoustics is sound transmission and acoustic insulation. We test our products to evaluate how much sound they block and how effectively they insulate a space. For instance, our herringbone-lined curtain, combined with our blackout fleece, achieved an 11-decibel reduction in sound transmission. Innovative Testing We also conducted unique tests, such as mounting curtains over windows to measure their impact. This test resulted in a 4-decibel improvement in sound insulation, which, although not drastic, can make a noticeable difference in reducing noise from outside sources. Frequently Asked Questions We've compiled some common questions about our curtains: - Will the curtains reduce road noise? - Yes, our curtains can reduce road noise, yes, the curtain has been tested with double glazing to reduce external sound. See our review on the product page for success stories. - Does doubling the product improve performance? - Doubling the product does not necessarily double the performance. Sound reduction follows a logarithmic scale, so the improvements are less dramatic with additional layers. - Can the curtains stop sound from office doors? - While they can help, doors require specific soundproofing measures such as seals or heavier doors for better results. - Will the curtains stop sound from passing between rooms? - Our curtains add an extra layer of insulation, reducing sound transfer between rooms. However, results vary based on wall composition. - Do blackout curtains work well for acoustics? - Yes, our blackout curtains can help with acoustics due to their absorption properties and thickness. Choosing the Right Curtain To select the right curtain, consider your specific needs: - One-layer curtains are ideal for reducing echo and reverberation. - Two-layer curtains strike a balance between cost and performance. - Three-layer curtains, with two layers of lining, offer maximum sound absorption and insulation. Conclusion Direct Fabrics offers a range of certified curtains designed to improve acoustics in various spaces. While curtains may not work miracles, they can make a noticeable difference in reducing noise and improving sound quality. Contact our team for free samples, quotes, and personalized recommendations. We're here to help you find the perfect acoustic curtain for your needs. Thank you for reading! Read the full article
0 notes
Text
Simplifying Radicals with the Same Index and Exponent | The Westcoast Math Tutor
Simplifying Radicals with the Same Index and Exponent | The Westcoast Math Tutor https://www.youtube.com/watch?v=5rIswzOS_1U This video shows how to simplify radicals when the index and the exponent are the same. 🔔 Join The Westcoast Math Tutor to watch more content on High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ✅ Stay Connected To Me. 👉 Facebook: https://ift.tt/MxCju1p ✅ For Business Inquiries: [email protected] ============================= ✅ Recommended Playlists: 👉 Decimal to Fraction https://www.youtube.com/watch?v=3J8Dnl0wLQE&list=PLPSu23Z8U7JG3C22WEiDhDf2bBXZ2yQJK 👉 Improper Fraction to Mixed Number https://www.youtube.com/watch?v=VvL7fXAYtHg&list=PLPSu23Z8U7JG0ErjzsUGv6KfDThOE7SxO 👉 Linear Equation https://www.youtube.com/watch?v=UUeuIQ6bUxU&list=PLPSu23Z8U7JGhun3PPquRpkjrMdNFAggz&pp=iAQB ✅ Other Videos You Might Be Interested In Watching: 👉 Evaluating Logarithms https://www.youtube.com/watch?v=ve9BMVUC6fE 👉 Exponential to Logarithmic Form & Logarithmic to Exponential Form https://www.youtube.com/watch?v=KbEULbAjvtI 👉 Logarithms Easy ! 2 Explanations https://www.youtube.com/watch?v=77msni1vacc 👉Boundedness Theorem, 2 Examples https://www.youtube.com/watch?v=NWPFmBmu380 ================================ ✅ About The Westcoast Math Tutor: Hello Friends! I’m The Westcoast Math Tutor, and with this channel, I will provide tutorial videos to better your understanding of different high school math topics. Once in a while, I will also make other interesting math videos outside of high school math topics. If you have any questions, please ask me in the comments. This channel is what I’ve been doing for you. If you want to do something for me, hit the bell button, like, and share. Thanks for watching, and happy learning, everyone! ✅For Appointment and Business inquiries, please use the contact information below: 📩 Email: [email protected] 🔔Subscribe for more High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ================================= #logarithmroots #inverseproperty #logarithmbasics #logarithmtutorial #mathexplained #logarithmproblems Disclaimer: I do not accept any liability for any loss or damage incurred by you acting or not acting as a result of watching any of my publications. You acknowledge that you use the information I provide at your own risk. Do your research. Copyright Notice: This video and my YouTube channel contain dialogue, music, and images that are the property of The Westcoast Math Tutor. You are authorized to share the video link and channel and embed this video in your website or others as long as a link back to my Youtube Channel is provided. © The Westcoast Math Tutor via The Westcoast Math Tutor https://www.youtube.com/channel/UCqP_EgHF0TGr65xMEcFPcjA August 23, 2023 at 01:15PM
#logarithmroots#inverseproperty#logarithmbasics#logarithmtutorial#mathexplained#logarithmproblems#logarithm#mathhelp#easystepbystepmethod
0 notes
Text
Math Doodle #1: Logs, Intuition and Approximations
Shortly after sharing Math Doodle #0, I played around a bit more with the expansion of ln(1+x). In particular, I wanted to see if I could use it to find ln(3) or ln(5) [Spoiler: you can't, but you can]. That lead me to think more generally about logarithms and why my intuition for them is so poor. I consider myself math-savvy, and within the little math I know, I know it fairly well, so I set out to see if I can improve my intuition for calculating logarithms.
I spent considerable time thinking first about those transformations over which I am able to reason intuitively (linear equations, quadratics, squares). My first hunch was that, a prerequisite for this instinct might be convenience: these tend to be continuous monotonic transformations (well, not entirely - but squaring is almost a monotonic transformation, or at least, the change in rate of change is conveniently placed at x = 0).
Logarithms, despite being continuous and monotonic, offer very little in the way of similar intuition. I attempted to tighten the bounds - so if log_2 maps [128, 256) -> [7, 8), can we partition these and come up with maps of finer resolution, without doing a lot of involved calculations? A little bit. {Hint: log_2 maps [128, 128*(2^0.5)) -> [7, 7.5) approximately}, but not too useful.
All of this made me go back to the transformations I considered initially. It made me realize that I am able to claim intuition for those only under very specific conditions - I know how the squaring transformation behaves, but intuition about its behavior does not help me compute large squares, or invert them. So there is, in a way, a difference to note - intuition about the behavior of a transformation, and intuition about the cold hard calculation of a transformation.
Trivia: Interestingly, the history of logarithms shows that the initial motivation for them came from their ability to simplify other arithmetic calculations: multiplying numbers with many digits is quite tedious, and logarithms offered a way out. They did rely on logarithm tables for this, though.
Circling back to the opening of this post, I tried to see if I could use the Taylor expansion of ln(1 + x) derived in Math Doodle #0 to get some bigger logarithms. By direct substitution, that's not possible, and that's quite expected: the series diverges for all |x| > 1 (this condition can be derived from the convergence test for alternating series).
However, I found a neat trick that allows one to use this expansion for an arbitrary positive integer k. Of course, this gets tedious quickly for large values of k, but that it can be expressed so succinctly is still beautiful.
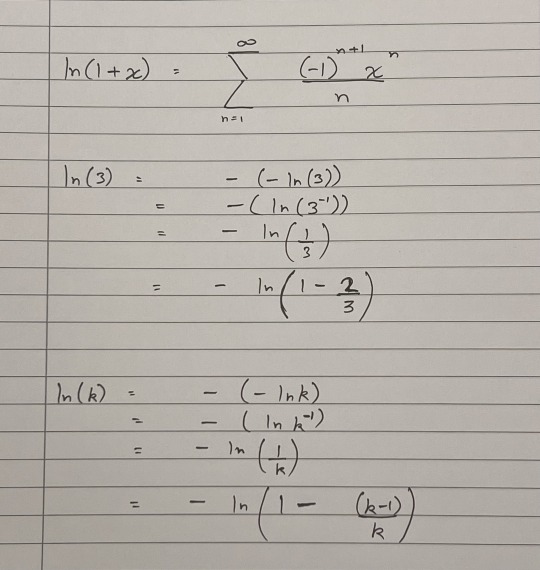
0 notes
Text
How to Solve Log: A Step-by-Step Guide with Maths.ai
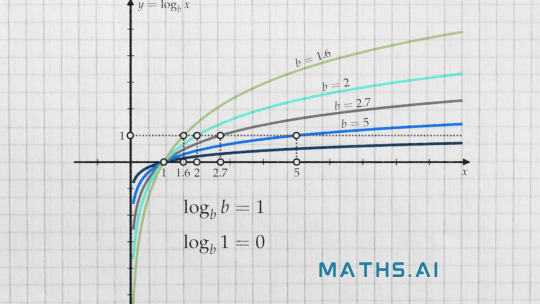
Welcome to Maths.ai, your reliable AI-based companion for solving challenging math problems! In this article, we'll dive into the world of logarithms, exploring their properties and presenting a comprehensive step-by-step guide to solve log equations. With the assistance of our Maths.ai, we'll walk you through the process and provide real-life examples to solidify your understanding.
Section 1: Understanding Logarithms
Before we jump into solving logarithmic equations, it's crucial to grasp the concept of logarithms. A logarithm is the inverse operation of exponentiation. In other words, it answers the question, "What exponent do I need to raise a particular base to, to obtain a given value?" The notation for a logarithm is as follows:
If \(b^x = y\), then \(\log_{b}(y) = x\).
Here, \(b\) is the base, \(x\) is the exponent, and \(y\) is the result of the exponentiation. Logarithms are particularly useful in solving problems involving exponential growth, decay, and complex calculations.
Section 2: Properties of Logarithms
Before we proceed with solving logarithmic equations, let's review some key properties of logarithms:
1. Product Rule: \(\log_b(xy) = \log_b(x) + \log_b(y)\)
2. Quotient Rule: \(\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)\)
3. Power Rule: \(\log_b(x^n) = n \cdot \log_b(x)\)
These properties allow us to manipulate logarithmic expressions and simplify complex equations into more manageable forms.
Section 3: Solving Basic Logarithmic Equations
Now, let's delve into solving basic logarithmic equations. Consider the equation:
\(\log_2(x) = 3\)
Step 1: Recognize the Base and Result
Identify the base of the logarithm, which is \(2\) in this case, and the result of the logarithmic expression, which is \(3\).
Step 2: Rewrite the Equation in Exponential Form
To solve for \(x\), rewrite the equation in exponential form:
\(2^3 = x\)
Step 3: Evaluate the Exponent
Compute the result of \(2^3\):
\(2^3 = 8\)
Step 4: Determine the Solution
The value of \(x\) that satisfies the equation \(\log_2(x) = 3\) is \(8\).
Section 4: Solving Logarithmic Equations with Variables
Now, let's tackle a more complex logarithmic equation involving variables:
\(\log_3(x+2) - \log_3(x) = 2\)
Step 1: Combine Logarithms
Apply the quotient rule to combine the two logarithms:
\(\log_3\left(\frac{x+2}{x}\right) = 2\)
Step 2: Express Equation in Exponential Form
Rewrite the equation in exponential form:
\(3^2 = \frac{x+2}{x}\)
Step 3: Solve for \(x\)
To solve for \(x\), isolate \(x\) on one side of the equation:
\(9x = x + 2\)
Step 4: Simplify and Solve
Combine like terms and isolate \(x\) on one side:
\(9x - x = 2\)
\(8x = 2\)
\(x = \frac{2}{8} = \frac{1}{4}\)
Step 5: Verify Solution
Check if the solution \(x = \frac{1}{4}\) is valid by ensuring that \(x\) is positive in the original equation:
\(\log_3\left(\frac{\frac{1}{4}+2}{\frac{1}{4}}\right) - \log_3\left(\frac{1}{4}\right) = \log_3\left(\frac{\frac{9}{4}}{\frac{1}{4}}\right) - \log_3\left(\frac{1}{4}\right) = \log_3(9) - \log_3(1) = 2 - 0 = 2\)
The solution \(x = \frac{1}{4}\) satisfies the original equation.
Section 5: Solving Logarithmic Equations with Advanced Techniques
In more advanced problems, logarithmic equations may require additional techniques for simplification. Let's consider an example:
\(\log_2(x^2 - 9) - \log_2(x+3) = 1\)
Step 1: Combine Logarithms
Apply the quotient rule to combine the two logarithms:
\(\log_2\left(\frac{x^2 - 9}{x+3}\right) = 1\)
Step 2: Express Equation in Exponential Form
Rewrite the equation in exponential form:
\(2^1 = \frac{x^2 - 9}{x+3}\)
Step 3: Solve for \(x\)
To solve for \(x\), isolate the expression on one side of the equation:
\(2(x+3) = x^2 - 9\)
Step 4: Expand and Simplify
Expand the left side of the equation:
\(2x + 6 = x^2 - 9\)
Step 5: Move All Terms to One Side
Move all terms to one side of the equation to obtain a quadratic equation:
\(x^2 - 2x - 15 = 0\)
Step 6: Factor and Solve
Factor the quadratic equation:
\((x-5)(x+3) = 0\)
Set each factor to zero and solve for \(x\):
\(x-5 = 0 \Rightarrow x = 5\)
\(x+3 = 0 \Rightarrow x = -3\)
Step 7: Verify Solutions
Check if the solutions \(x = 5\) and \(x = -3\) are valid by ensuring that the expressions inside the logarithms are positive:
For \(x = 5\):
\(\log_2(5^2 - 9) - \log_2(5+3) = \log_2(16) - \log_2(8) = 4 - 3 = 1\) For \(x = -3\):
\(\log_2((-3)^2 - 9) - \log_2((-3)+3) = \log_2(0) - \log_2(0)\)
Since the expression inside the first logarithm is non-positive, the solution \(x = -3\) is invalid.
Congratulations! You have now mastered the art of solving logarithmic equations, thanks to the step-by-step guidance of Maths.ai . Remember the fundamental properties of logarithms and apply them to simplify and solve log equations. With practice, you'll become adept at handling logarithms and excel in your mathematical journey. Keep exploring the fascinating world of mathematics with the support of Maths.ai, your online maths tutor for all your maths-related support.
1 note
·
View note
Text
How to solve for y
Solving for 'y' is a fundamental skill in mathematics that is often encountered in algebraic equations and functions. Whether you're a student learning the basics or an adult refreshing your math skills, understanding how to solve for 'y' opens the door to a deeper comprehension of equations and their solutions. In this article, we will provide you with a step-by-step guide on how to solve for 'y' in various scenarios, equipping you with the tools to tackle equations with confidence.
Understand the Equation Type: Before diving into solving for 'y', it's crucial to identify the type of equation you're working with. Equations can be linear, quadratic, exponential, logarithmic, or trigonometric, among others. Each equation type requires specific techniques and strategies for solving. Familiarize yourself with the characteristics of the equation at hand to determine the appropriate approach.
Isolate 'y' on One Side: The goal is to isolate the variable 'y' on one side of the equation. To achieve this, use algebraic operations such as addition, subtraction, multiplication, and division to move terms and constants from one side of the equation to the other. Perform the same operation on both sides to maintain equality. Continue simplifying the equation until 'y' is isolated.
Solve Linear Equations: In linear equations, 'y' typically appears as a coefficient multiplied by 'x' or other variables. To solve for 'y', isolate the term containing 'y' on one side of the equation by applying inverse operations. For example, if 'y' is multiplied by a coefficient, divide both sides of the equation by that coefficient. Simplify further until 'y' is isolated.
Solve Quadratic Equations: Quadratic equations involve 'y' raised to the power of 2. To solve for 'y', rearrange the equation into the standard quadratic form (ax^2 + bx + c = 0). Utilize factoring, completing the square, or the quadratic formula to find the values of 'y'. Be mindful of possible solutions, including real and complex numbers.
Solve Exponential and Logarithmic Equations: Exponential and logarithmic equations involve 'y' as the exponent or argument. To solve for 'y', use logarithmic properties to transform the equation into a manageable form. Apply inverse operations, such as exponentiation or taking the logarithm, to isolate 'y' and find its value.
Solve Trigonometric Equations: Trigonometric equations involve 'y' as part of a trigonometric function (sin, cos, tan, etc.). To solve for 'y', apply trigonometric identities and properties to simplify the equation. Utilize inverse trigonometric functions or trigonometric identities to isolate 'y' and determine its value. Pay attention to the specific domain restrictions and periodicity of trigonometric functions.
Check Your Solution: After obtaining a value for 'y', it's crucial to check your solution by substituting it back into the original equation. Ensure that the equation holds true when 'y' is replaced with the determined value. This step confirms the accuracy of your solution and verifies that you haven't made any calculation errors.
Solving for 'y' is an essential skill in mathematics that allows you to find solutions to various types of equations. By understanding the equation type, isolating 'y', and employing appropriate techniques for linear, quadratic, exponential, logarithmic, and trigonometric equations, you can confidently find the value of 'y'. Regular practice and familiarity with algebraic operations will strengthen your ability to solve equations and deepen your mathematical understanding. Embrace the challenge, apply the techniques, and enjoy the satisfaction of successfully solving for 'y' in any equation that comes your way.
0 notes