#binary notation

[allalfavincerho]

conta fino a 10

I counted to ten slowly, using binary notation. R. Heinlein, The Door into Summer

[keithbutgay]

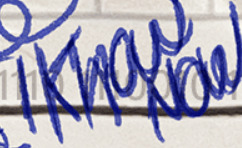
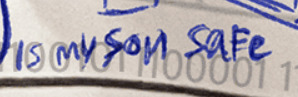
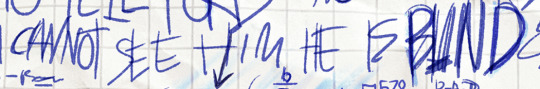
"i know now"

"is my son safe"

"i cannot see him, he is blind"

"i have to tell ford"

[math1089]

40 more Mathematical Wonders to Usher in a Joyful 2025

At the age of eleven, I began Euclid, with my brother as my tutor. This was one of the great events of my life, as dazzling as first love. I had not imagined there was anything so delicious in the world. From that moment until I was thirty-eight, mathematics was my chief interest and my chief source of happiness.Bertrand Russell Welcome to the blog Math1089 – Mathematics for All. As 2024 bids…

[nolinno-art]

I've developed mathematics for a non-human mind, for my comic "The book written by tiny paws"

Sapient distant descendants of rats, known as packers, living on Earth millions of years after the extinction of humans, began to develop mathematics using cognitive mechanisms never intended for such tasks. Due to an evolutionary quirk, multiplication came more naturally to them than addition, and their mathematics reflects this.

Packers write numbers as shapes, with each number having a corresponding number of corners.

And they write large numbers as nested shapes. The number inside is multiplied by the number outside.

Examples of some numbers:

Packers haven't invented 0 yet. They haven't even invented 1! In fact, they don’t need the concept of "one" much in their system. There's no need to say "I ate one fish" when they can simply say "I ate fish".

Packers can't yet write large prime numbers, like 101 or 10,501, because they would have to draw a huge shape to represent them! Even writing 17 or 19 would be quite difficult if they only used convex shapes.

So packers use non-convex shapes too!

Many years later, some packer noticed that large prime numbers look suspiciously symmetric.

So this packer improved the notation system and made it clearer.

Later, another packer simplified this system even more, deciding that there was no point in writing the same shapes twice.

This packer was the first in their culture to declare that "a dot isolated from a number" should also be considered a number. The packer called this dot "the wonderful number that's less than two".

Many years later, another packer made an important innovation: the "dot isolation" could be repeated multiple times as long as the result remained odd. When the result became even, it could undergo a "two isolation" (division by two). The final result will be a series of dots and twos.

This invention led to the creation of a binary system based on one and two, which had a significant impact on the technological advancement of packers.

The comic "the book written by tiny paws" talks about all of this in more detail. There will be mistakes, debates, the invention of rational, irrational, multivariate numbers, and some other stuff. Some stuff will be very much like human math, and some will be different. After all, math is still math, only the point of view has changed.

[lady-inkyrius]

123₁₆ has the advantage of being able to represent any arbitrary base, but having to use decimal to write it seems inelegant. There also exist systems to write this in ASCII plain text such as by using r to mark the radix like 123r16 or by bracketed indices like 123[16].

0x​123 and 123h/123ₕ have the advantage of not having to use decimal, but you can only really use bases which have a common one-letter shortening. This basically limits you to like binary, trinary, quaternary, seximal, octal, decimal, dozenal, and hexadecimal – b, t, q, s, o, d, z, and x/h respectively, perhaps with the addition of v for vigesimal – but these are admittedly the only bases anyone actually uses. Note that even then there isn't a consistent letter used to represent many of these: I've used s for seximal, but I've also seen h for seximal (“hexal”) and x for hexadecimal; as long as you define your notation you should be fine. Additionally the suffix d collides with systems used to represent double-precision floats in various languages.

HEX 123 feels like it's sort of in the middle of these two: you don't have to use decimal to write the base and you can write many more bases than the single-letter abbreviation, but it is a lot clunkier than either of the last two methods. Perhaps they could be combined like 123ₕₑₓ, though I've only rarely seen this. Note that not every base has an immediately intuitive three-letter abbreviation, though all the interesting ones do (apart from perhaps 60 and 64).

There are really two different contexts for writing these that require two different approaches: plain text with no markup like source code, and fully marked up text like output from LaTeX or another typesetting program. I don't really care how you weigh these and I'm not about to make two separate polls for them.

Note that for the last two bulletpoints, Unicode subscript letters are not a great idea in actual use: they have poor font support, and Unicode doesn't even cover the entire alphabet (b, c, d, f, g, and q are missing, as well as w, y, and z until Unicode 17). For contexts without markup, the three-letter abbreviation can use its standard prefix form, and the one-letter abbreviation has many different forms, (C-style: 0α123, x86-style: 123α, bracketed indices: 123[α], etc.)

Another style I've seen, mostly as a joke, is just using the name of the base written out as a subscript like 123ₛᵢₓₜₑₑₙ; this is pretty funny honestly.

[nerdygaymormon]

I liked your post with all the scriptures showing that we are to love trans people. What are your thoughts about the changes made to the church handbook?

The LDS Church used to ban gay students from attending BYU. The church used to put a permanent notation on gay member's records and forbid them from having callings that work with children or youth. The church used to promote conversion therapy even when every major medical and mental health organization denounced such practices. The church forbade the children of gay couples from getting baptized.

Eventually the church reversed all these positions.

I used to speak up behind closed doors for queer youth to get to participate, it's been many years since my local leaders tried to do something like forbid a lesbian from attending girls camp or want her to be isolated at night in a cabin separated from the rest of the young women.

It is sad to me to see these same mistakes being implemented against trans/nb/genderfluid/gender nonconforming/intersex members.

Gay people were not predators, we were not the danger they imagined us to be. The same is true for those whose gender doesn't conform to the imagined binary.

How does preventing an 8-year-old child from getting baptized fit with Jesus' admonition to "suffer the little children and forbid them not to come unto me"?

How does limiting someone from gender-specific classes and callings fit with the apostle Paul's teaching that in Christ we are one, that "there is neither male nor female"?

Why is forbidding a trans youth from spending the night at FSY acceptable? It will be so stigmatizing.

We're really going to police the restrooms? Even me, an openly gay man, I am allowed to use the facilities with men even though I might be attracted to some of them.

This ban on "social transitioning" (meaning name/pronouns/grooming/clothing) continues the false notion that appearance equals worthiness and is in direct contradiction to God telling the prophet Samuel that "the Lord looketh on the heart." Social norms are not eternal norms and shouldn't determine whether an individual can receive gospel ordinances.

The top LDS leaders prefer the term "same sex attraction" instead of gay, lesbian and bisexual, and I think a similar thing is now happening as the Handbook language has shifted from "transgender individuals" to "individuals who identify as transgender" and "individuals who transition away from their biological sex."

None of these policies are required by doctrine, evidence for this is these restrictions didn't exist 5 years ago or even last week.

It's depressing the church doesn't remember the lessons from its treatment of gay people as it replicates similar policies.

It was already hard to be a gender diverse member of the LDS Church, and it just got more difficult. Everyone should have access to a spiritual home and church community if they want it.

While I can't control what the LDS Church does, I want you to know I embrace and support you. I wish I could sit on the pew with all of you and I wish I had a table large enough to break bread with all of you.

[librarycards]

do you have any recommendations for readings or memoirs or anything about non-binary identity?

yes! so, I feel obligated to share a few that I've done ––

Co/notations, an annotated essay chapbook.

Social Skills: A transdyke autie-biography in Sinister Wisdom

In Praise of -Less in AZE Journal

Others' Memoirs/Poetics:

Stacey Waite, Love Poem to Androgyny

Vivek Shraya, She of the Mountains

Akwaeke Emezi, Dear Senthuran

Eli Clare, Exile and Pride

Ivan E. Coyote, Tomboy Survival Guide

Leah Lakshmi Piepzna-Samarasinha, Dirty River

T. Fleischmann, Time is the Thing A Body Moves Through

Sabrina Imbler, Dyke [geology]

Joan Nestle, ed., Genderqueer: Voices From Beyond the Sexual Binary [warning: this is pretty old]

Fiction [beyond Stone Butch Blues]:

Megan Milks, Margaret and the Mystery of the Missing Body

Sassafras Lowry, Roving Pack

John Elizabeth Stintzi, Vanishing Monuments

-

These are obviously not all of the gender-noncompliant/nonbinary/genderqueer/etc books I've read, nor all of the ones I recommend, but they do apply directly to your specification that they be about identity as such. Hope you find something you like!

[hbmmaster]

I've been using and thinking about this for a while, but what do you think of the programmatic notation '0s' for seximal?

I mean this as it relates to '0x' for hex, '0b' for binary and '0' for octal.

('0h' for Heximal also works, but it WILL get confused with hexidecimal)

You may be disappointed to learn that there currently exist no programming languages with seximal numbers.

it's a nice idea but I'd rather a programming language use a more robust system that can accommodate arbitrary bases than just add in more single-letter codes for my favorites you know

[enterprise-bee]

do you think vulcans have arguments over which mathematical logic system they should use. like, okay, most computing and aristotle's logic is boolean logic/algebra, in which there are two possible values for any statement: TRUE/FALSE. a few computing languages (SQL being the most notable) use three-value logic: TRUE/FALSE/NEITHER (with the 'neither' sometimes being 'unknown' or 'null'). or do you think they use a many-valued logic system of some kind, with other logical states. what do they think of the law of the excluded middle? do they have their own symbolic logic notation? do they have a different word for logic (the mathematical and philosophical discussion) and logic (doing things that make sense, as is the colloquial use of the word in english). do you think their philosophers get into fights when they come across planets that use different mathematical logic systems? because there is nothing stating every society uses the same base assumptions about math, or even the same type of electronic circuits/computing systems that we do that so heavily rely on binary logic,

[mathematical-cheese]

🌻 :3

I will tell you& about a cool topology fact that uses one of my favourite theorems!

First, a primer of finitely presented groups:

Given a finite set with n elements S={a₁,...,aₙ}, we define a word to be a finite concatenation of elements in S. For example, a₁a₇aₙ is a word. We define the empty word e to be the word containing no elements of S. We also define the formal inverse of the element aᵢ in S, written aᵢ⁻¹, to be the word such that aᵢaᵢ⁻¹=e=aᵢ⁻¹aᵢ, for all 1≤i≤n.

We define the set ⟨S⟩ to be the collection of all words generated by elements of S and their formal inverses. If we consider concatenation to be a binary operation on ⟨S⟩, then we have made a group. This is the free group generated by S, and is called the free group generated by n elements.

Some notation: if a word contains multiple of the same element consecutively, then we use exponents as short hand. For example, the word babbcb⁻¹ is shortened to bab²cb⁻¹.

Note: concatenation is not commutative. So ab and ba are different words!

We now define a relation on the set ⟨S⟩ to be a particular equality that we want to be true. For example, if we wanted to make the elements a and b commute, we include the relation ab=ba. This is equivalent to aba⁻¹b⁻¹=e. In fact, any relation can be written as some word equal to the empty word. In this way, we can view a relation as a word in ⟨S⟩. So we collect any relations on ⟨S⟩ in the set R.

Finally, we define the group ⟨S|R⟩ to be the group of words generated by S subject to the relations in R. This is called a group presentation. An example is ⟨z,z²⟩, which is isomorphic to the integers modulo 2 with addition ℤ/2.

If both S and R are finite, we say that ⟨S|R⟩ is a finite group presentation. If a group G is isomorphic to a finite group presentation we say G is a finitely presented group. It is worth noting that group presentation is by no means unique so as long as there is one finite group presentation of G, we are good.

In general, determining whether two group presentations is really really hard. There is no general algorithm for doing so.

Lots of very familiar groups of finitely presented. Every finite group is finitely presented. The addative group of integers is finitely presented (this is actually just the free group generated by one element).

Now for the cool topology fact:

Given a finitely presented group G, there exists a topological space X such that the fundamental group of X is isomorphic to G, i.e. π₁(X)≅G. This result is proved using van Kampen's Theorem which tells you what happens to the fundamental group when you glue two spaces together.

The proof involves first constructing a space whose fundamental group is the free group of n elements, which is done inductively by gluing n loops together at a single shared basepoint. Each loop represents one of the generators. Then words are represented by (homotopy classes of) loops in the space. Then we use van Kampen's Theorem to add a relation to the fundamental group by gluing a disc to the space identifying the boundary of the disc to the loop in the space that represents the word for the relation we want. We do this until we have added all of the relations we want to get G.

We can do a somewhat similar process to show that any finitely presented group is the fundamental group of some 4-manifold (a space that locally looks like 4-dimensional Euclidean space, the same way a sphere locally looks like a plane). This means that determining whether two 4-manifolds are homeomorphic or not using their fundamental groups is really hard in general because distinguishing finitely generated groups is hard in general.

P.s. I also want to tell you that you're really wonderful :3 <2

[variablejabberwocky]

oh shit, base-20 is just base-2 but Big Size!

so like base number positional notation each spot from right to left is another order of magnitude in value

so in base-10 your rightmost spot is the "1's place" because it goes from 0-9 with 1 being the first numbery-number (instead of a placeholder zero), the next one to the left is the "10's place", and the next one from there is the "100's place"

so each of these could also be notated like this:

10^0 is 0-9

10^1 is 10-99

10^2 is 100-999

10^3 is 1,000-9,999

10^4 is 10,000-99,999

so if you do the same with base-20 you get:

20^0 is 0-19

20^1 is 20-399

20^2 is 400-7,999

20^3 is 8,000-159,999

20^4 is 160,000-3,199,999

which if you compare to the same sort of thing in base-2:

2^0 is 0-1

2^1 is 2-3

2^2 is 4-7

2^3 is 8-15

2^4 is 16-31

like there is a PATTERN here

base-20 is basically just binary but each "^" up from "^0" adds another zero to the starting position for that slot

...oh shit does this mean we could use the kaktovik numbers for base-16 too? or would we have to modify them? could we do the same cool math tricks?

I HAVE SO MANY QUESTIONS

[tower-of-hana]

Trying to explain why the hull-hall merger happens

So I have this weird merger where I round [ʌ] to [ɔ] before [l]. This would be depicted in binary notation like this [-cons] > [+ round] /_[+lat], which makes no sense because where the fuck is the rounding coming from. So I looked it up and it turns out that [ɫ] sometimes becomes labialized and this happened in English. But in English the /w/ was inserted before the [ɫ] and I've noticed that I tend to replace [ʌ] with [ɔʷ] so maybe what's happening is [ʌɫ] > [ʌʷɫ] > [ɔ(ʷ)l] which would make more sense because /w/ can actually cause rounding.

[raspberryjamnnn]

A couple months ago I came up with a pen-and-paper shortcut for converting 3 digit decimal numbers to binary.

The reason I say 3 digits specifically is because for 4 digits and up you have to use the full algorithm, but a simplification can be made for lengths 1 through 3. And on the other end, 1 and 2 digits are simple enough that it can just be easier to do it more in your head.

Anyways, what is this method?

Well first, if I were to ask you what 5,394,092 × 6 is, you would no doubt have a difficult time answering. But, if I were to ask you what 1,101,001 × 6 was you'd probably have a much easier time answering.

Lets look as positional notation, which is the typical way we write numbers. The number 123 represents the "constant-valued polynomial" (1×10² + 2×10¹ + 3×10⁰)

If I were to multiply 123 by 4, I could just multiply the polynomial by 4 and distribute it across the additions

4×123 = (4×10² + 8×10¹ + 12×10⁰)

Doing that, the polynomial suggests I should have a 12 in the 1s place, which shouldn't technically be allowed.

But here's the thing, evaluating the polynomial still gives you a value of 492, the correct answer. So my thought is, let's leverage those past two facts for this example:

1<10> in binary is 1<2>

10<10> in binary is 1010<2>

100<10> in binary is 1100100<2>

▪︎ 295<10>

= 2*100<10> + 9*10<10> + 5*1<10>

= 2*1100100<2> + 9*1010<2> + 5*1<2>

= 2200200<2> + 9090<2> + 5<2>

= 2209295<2>

Now how do we convert 2209295<2> to normal binary? Well, we scan from least significant bit up, carrying that slot over 2, leaving the remainder:

2209295

2209291 + 20 = 22092(11)1

2209211 + 500 = 2209711

2209111 + 3000 = 220(12)111

2200111 + 60000 = 2260111

2200111 + 300000 = 2500111

2100111 + 2000000 = 4100111

0100111 + 20000000 = 20100111

00100111 + 100000000 = 100100111

(okay I will say the textual format of a tumblr post doesnt lend itself well to how youd actually do it on paper, which when youre done would look like these three lines):

＿＿２２０９２９５

１２２３６３５２＿

１００１００１１１

Anyways, the magic here is that the starting wonky-base-2 number of 2209295 is analogous for all 3-digit base 10 numbers, my mnemonic is 1102123<2> (one-one oh two, one two three) equalling 123<10>

The reason 1000 doesnt fit in is because it collides in a way 1, 10, and 100 dont

１１１１１０１０００<2> = 1000<10>

＿＿＿２２０３２３４<2> = 234<10>

＿＿＿ＸＸ＿Ｘ＿＿＿, where the Ｘs represent collisions between the bits of 1000 and the bits of 234.

If I were to make a mnemonic for 4-digit numbers, it would have to be 111(1+2)(1+2)0(1+3)234, really not as snaply as 1102123

yeah

[catgirl-lucy]

Cantor space and Baire space

Part two of catgirl learning descriptive set theory.

Given two spaces X and Y, X × Y is the product space of X and Y.

Definition. Let X and Y be topological spaces. X × Y is a topology with {(x,y) | x ∈ X ∧ y ∈ Y} as points and {U × V | U ⊂ X is open ∧ V ⊂ Y is open} as basis.

If X and Y are both discrete spaces, X × Y is always discrete. If X and Y are both Polish spaces, X × Y is also always Polish. You can also take infinite products of spaces.

Definition. Let (X_i | i ∈ κ) be a family of spaces. Π[i ∈ κ] X_i is a topology with {f: κ → ⋃[i ∈ κ] X_i | ∀i ∈ κ. f(i) ∈ X_i} as points and with {Π[i ∈ κ] U_i | {i ∈ κ | U_i ≠ X_i} is finite ∧ ∀i ∈ κ. U_i ⊂ X_i is open}.

Taking infinite products doesn't always preserve the properties of spaces. The product Π[i ∈ κ] X of κ copies of the same space X is written X^κ. 2 = {0,1} and ω, the set of natural numbers, are both endowed with the discrete topology. In this blog post, we'll focus on two topological spaces:

Definition. The Cantor space, denoted 𝒞, is the space 2^ω.

Definition. The Baire space, denoted 𝒩, is the space ω^ω.

Let n = {0,…,n-1}. I call a function s: n → X an X-list, for which I use the notation s = (s_0,…,s_{n-1}), and a function α: ω → X an X-sequence, for which I use the notation α = (α_0,α_1,…). The set of X-lists is denoted X^<ω and the set of X-sequences is denoted X^ω. Points in the Cantor and Baire space are thus 2-sequences and ω-sequences respectively. Instead of taking the basic open sets as defined in the product topology, we can also take the basis {{α ∈ 2^ω | s ⊂ α} | s ∈ 2^<ω} and {{α ∈ ω^ω | s ⊂ α} | s ∈ ω^<ω} for the Cantor and Baire space respectively.

Closed sets are complements of open sets. They have a nice interpretation in the Cantor and Baire space in terms of trees:

Definition. A tree on X is a set T ⊂ X^<ω of X-lists such that, for any s ∈ T and any list t ⊂ s, we have t ∈ T. [T] = {α ∈ X^ω | ∀n. α|n ∈ T} is the set of branches of T (α|n is the length n initial segment of α).

The lists in the tree T are the nodes of T. Closed sets are exactly those sets of the form [T] for some tree T. For a closed set C, there can be multiple trees T for which C = [T], but there is always only one tree T for which C = [T] and ∀s ∈ T ∃α ∈ [T]. s ⊂ α, i.e. all nodes in T extend to an infinite branch. From now on, I'll assume every node extends to an infinite branch with every tree we work with. If we take T = 2^<ω (T = ω^<ω) to be the full tree, then [T] = 2^ω ([T] = ω^ω) is the Cantor (Baire) space itself, thus we can view the Cantor (Baire) space as an infinite tree, where the points are the branches. In the Cantor space, this is a binary tree, while in the Baire space, every node has infinitely many children.

The basic open sets U_s = {α | s ⊂ α} in the Cantor and Baire space are clopen: the tree T = {t | s ⊂ t ∨ t ⊂ s}, which goes up to s and branches out everywhere from there, has [T] = U_s. Thus, unlike the real line, the Cantor space and Baire space have a rich structure of clopen sets. They're completely disconnected: for any two distinct points, there is a clopen set separating them. Intuitively, clopen sets can be thought of as disconnected parts of a space.

I mentioned in my last blog post that the Cantor and Baire space are Polish spaces. I encourage the reader to prove themselves that they are Polish spaces before reading my proof.

Proposition. The Cantor space and the Baire space are Polish.

Proof. Recall that a Polish space is a non-empty perfect, separable, completely metrizable space. Proving they're non-empty and perfect is trivial. To show they're separable: the set of sequences that are eventually 0 (i.e. start with a finite list of things and end in infinitely many 0s) is countable and dense. The complete metric d(α,β) = 2^(-min{n | α(n) ≠ β(n)}) works for both spaces. ∎

Though the Cantor space 𝒞 and the Baire space 𝒩 look a lot like each other, they're not the same space. The Cantor space is compact while the Baire space is not.

Definition. Let (X,τ) be a topological space. An open cover is a set Σ ⊂ τ of open sets such that ⋃Σ = X. A subcover of Σ is an open cover T such that T ⊂ Σ. (X,τ) is compact iff every open cover has a finite subcover.

For metric spaces, the following is equivalent:

Definition. A space X is sequentially compact iff every sequence (xₙ) of points xₙ in X has a converging subsequence (x_iₙ), where (iₙ) is an increasing sequence of natural numbers/indices.

In the Baire space, ((0,0,0,…),(1,0,0,…),(2,0,0,…),…) is an example of a sequence that has no converging subsequence. In the Cantor space, however, every sequence has a converging subsequence. Proving this is left as an exercise to the reader.

Both the Cantor space and the Baire space have embeddings into the real line. An embedding, here, is a continuous injection. The image of the embedding of the Cantor space in the real line is the Cantor set, which results from starting with the closed interval [0,1] and recursively taking out middle thirds, resulting in [0,1/3] ∪ [2/3,1], [0,1/9] ∪ [2/9,1/3] ∪ [2/3,7/9] ∪ [9/8,1], etc, and then taking the intersection. The image of the Baire space in ℝ is 𝕀, the set of irrational numbers. Filling in the details is left to the reader. We thus have that 𝒩 and 𝕀 are homeomorphic (the same topologically), hence Baire reals (points in the Baire space) are sometimes called irrationals.

The Cartesian plane ℝ² is not homeomorphic to the real line, while having basically the same structure as far as descriptive set theory is concerned (they're Borel equivalent). It's easier to work with the Baire space as it's homeomorphic to its own square: 𝒩 is homeomorphic to 𝒩 × ω (i.e. ω copies of itself), 𝒩 × 𝒩 and 𝒩^ω. I won't prove this rigorously (as i don't wanna), but here is an informal argument: 𝒩 × ω = ω^ω × ω = ω^(ω+1) and since ω+1 and ω are equinumerous, ω^(ω+1) and ω^ω are homeomorphic. 𝒩 × 𝒩 = ω^ω × ω^ω = ω^(ω+ω), and since ω and ω+ω are equinumerous, ω^(ω+ω) and ω^ω are homeomorphic. 𝒩^ω = (ω^ω)^ω = ω^(ω × ω), and as ω × ω and ω are equinumerous, ω^(ω × ω) and ω^ω are homeomorphic. The Cantor space also has some of these properties: 𝒞 ≅ 𝒞 × 𝒞 ≅ 𝒞^ω, however 𝒞 is not homeomorphic to 𝒞 × ω as the latter is not compact.

Though it's easy to work with the Baire space, as there is no discrepancy of dimension (the Baire space is 0-dimensional), I didn't yet explain whether it is valid. Do things proven about the Baire space also apply to other Polish spaces? In most cases, yes! Though things are often not explicitly proven about Polish spaces other than the Baire space, most theorems still apply (as long as they're about the higher complexity classes). The Baire space, besides being simple to work with, has a surjection onto every other Polish spaces, making it in some sense also a "universal" Polish space.

Proposition. Let X be a Polish space. There exists a continuous surjection π: 𝒩 ↠ X.

I won't give a full proof here, but basically, you use the fact that X is separable to make finer and finer open covers of X with sets enumerated by ω-lists, mapping the irrationals in 𝒩 to the unique point in the intersection of open sets indexed by initial segments of the irrational, giving you a function that is continuous and surjective. If you want to build an injection from 𝒩 into X instead, instead of making covers, you can make disjoint families of open sets in X in a similar way using the fact that X is perfect*, thus proving that all Polish spaces have cardinality 𝔠.

*Not everyone considers being perfect as a condition for being Polish (I'm not sure if anyone does), making the countable space ω a Polish space.

I'll probably explain pointclasses next.

[daisychainsandbowties]

three body problem ❤-💛-💙 -> LB Lilith-Ava-Bea, always in orbit of each other

i can’t get over it sometimes that those are the colours of their lightsabers but anyway time for a shameless excerpt from my favourite thing i’ve ever written 😌😌 written, in part, because i knew that luminous beings would be dark, plagued by scatterings of light and little else, but i wanted to make it plain as daylight on this tiny planet that there is always peace in the end

orbital mechanics

///

the ceiling in their bedroom has a domed viewport that shows the stars, and beatrice watches a bright spot in the impossible distance and remembers what they told her about star nurseries, and what lilith called the three-body problem.

lilith, staring out of the viewport, the abyss of space reflected in her dark eyes.

stars have violent birthplaces. a cloud of dust collapses so completely that it forms a hydrostatic core. a point that draws heat towards itself, growing denser and denser, helplessly eating up everything around it. and then, eventually, it forms a star.

sometimes several stars. they form together.

with her red marker ava drew three circles, colouring them in with a loud squeaking sound that made lilith close her eyes momentarily and sigh.

where three stars become gravitationally bound – caught, shall we say, in one another’s pull – we call them a trapezia. like this one.

the Mantis sat on the edge of the system, where it was safe.

young, by the standard of stars, and incredibly unstable. prone to ejecting parts of itself at high velocities. a trapezia is an example of a three-body problem.

ava laughed.

this problem attempts to predict the motion of three bodies, taking their initial conditions to solve for their subsequent motion.

at this point, ava’s red marker began drawing with proper notation. nothing beatrice could read. just letters to the power of numbers. radical signs and brackets and factoring. some subtraction.

the problem with this problem is that the orbits of three massive bodies quickly become complicated. they seldom repeat their trajectories – after all they are pulling at each other at different times in different places, moving along strange orbits. they compete for the stability of their want without forming a proper hierarchy, as many other systems must. they just careen, wildly, through their space.

it is possible for these stars to collide. it is possible for these stars to be ejected from their system. binary orbits are far simpler, far safer.

there is an inevitability to the three-body problem. lilith said this strangely, and beatrice reached out to take her hand. a violence and a beauty and a tragedy to them. three bodies do not easily exist in this way. or, perhaps it is easy for them. perhaps it is wonderful, and free in its unpredictability, but it is probably doomed.

what could survive against all the laws of physics?