#bijective

[arcsin27]

if youre bisexual youre also insexual and sursexual

[nontrivialproof]

I have three siblings and so a time-honored group activity is sorting ourselves into any other group of four. And since Thanksgiving I have been intermittently thinking about when we were doing this for The Beatles and my older brother said with zero hesitation, "Well, Raina is definitely Paul." What did he mean by that. It's not a compliment.

[nicholasandriani]

Mastering Isometric & Isomorphic Game Design: A Quickstart Guide to Unlocking 3D Potential in 2D Worlds

We say that: “oh I love that Baldur Gate, let’s crack out an isometric.” Or, “oh, digging this Final Fantasy Tactics stuff, let’s do that sideways angle thing.” But what does that mean? Let’s break it down mathematical. T:(X,∥⋅∥X)→(Y,∥⋅∥Y) is a isometric isomorphism if it is a linear isomorphism, and it is an isometry, that is ∥T(x)∥Y=∥x∥X∀x∈X; T:(X,∥⋅∥X)→(Y,∥⋅∥Y) is a topological…

[unnonexistence]

well, it finally happened, i finally found the math version of "the average person probably only knows the formulas for olivine and one or two feldspars" in my writing

[cleverusername01]

pride month is getting to be a little much this year. I mean love is love and everything but what the FUCK is “bijective”

[trilobyteme]

countability

[mellifiedman]

Ough I've had the worst cold for like 4 days now. Also had an exam yesterday and I thiiiink I hit exactly the right balance of off-label narcolepsy medicine and edibles to make me lucid and capable of problem-solving for the full two hours, but I guess we'll see about that

[ulysses-but-somehow-more-transer]

shirt that says bigender bisexual bijective

[mathhombre]

Are there more big dots or small dots?

Pluie, 1995

Yayoi Kusama

[despondent-beauty]

Tfw you believe you've somehow created an ordered list of every single real number even though such a thing contradicts its own existence and you back this up by raging about how everyone who disagrees is just spewing what they were taught at school because you can't deal with the fact that you've spent 15 years of your life failing to prove something in a field you don't understand.

God, I love bringing you topical content.

[leibnizstan]

Gender equality? Broke. Gender bijective homomorphism? Woke

[fazedlight]

Awakening (Kara character study, small part supercorp softness)

“But why can’t I be matched to Tali, mom? She’s my best friend!”

Alura turned to Kara, her jaw tensed with frustration with the stubborn child. “Kara, you know better than this. Stable matching can only be achieved if there is a true bijection between disjoint sets-”

“We don’t even have a true bijection because the population is constantly changing, we don’t sort according to all possible preferences, we don’t even have-” “It is not in our nature, Kara,” Alura said, with a dangerous tone in her voice. “We are not Daxamites.”

“But-” 

“The answer is no.”

---

Kara is thirteen Earth years the first time she’s called “dyke.” She doesn’t know what it means. She had only been to school for a couple of weeks. Before that, the only substantial English she had spoken was the couple months with Eliza, Jeremiah, Alex, and Kal. 

Clark, not Kal. Saying “Kal” would put her baby cousin- her older cousin- her cousin in danger.

Alex’s face flushes, and her eyes almost burn with anger, as she shoves Jake Howell against a locker. Kara could do it easily herself, but showing her newfound strength to humans would put her in danger too, somehow. Kara doesn’t think asshole is a nice word, given how Alex growled it. But she suspects dyke isn’t a nice word either.

That night after dinner, Eliza sighs, and hugs Kara gently - and Kara resolves to never get called dyke again.

---

“She’s gorgeous, she’s smart, she smells nice. Hell, I want to date her.” Kara flushed with discomfort, as the words came unbidden from her lips. But Alex didn’t remark on the odd statement, and Kara shoved the thought away.

Just weeks later, awkwardness would turn to tension as Lucy growled. “You and Hank, why do you all lie?”

“When you are an alien,” Kara choked, “You’re willing to sacrifice anything, everything, betray your fundamental instincts - just to fit in.” Something tugged in Kara’s soul at that moment. That she had always tried to fit in, long before she became an alien. But there simply hadn’t been time to linger.

It was only weeks later, when Lucy was saying her goodbyes before leaving National City to rejoin the military, that Kara felt the uncomfortable spike again. “I do know what it’s like to hide,” Lucy confessed.

Kara tilted her head, questions like why? and what do you mean? floating through her mind. But she thought it would be kinder not to ask. “I hope someday, you can be all that you are.”

Lucy gave a small smile. “Me too.”

---

She hadn’t expected meeting Lena to feel like lightning in her veins. The younger Luthor was quick-witted, and beautiful, and playful. Kara felt herself flush with the gentle teasing during their first coffee, and found herself marveling at never quite having a friendship like this before. 

---

“So… so she’s gay?” Kara asked, the word heavy in her throat. “And are you saying, you’re gay too?”

Alex sighed and paced in front of Kara, her frustration just as apparent as her confusion. How can you not know if you’re gay?, Kara wondered, at the same time feeling strangely allergic to the conversation. Wouldn’t it be obvious? ��What’s changed?” Kara asked.

---

Yeah, he was… immature. Irresponsible. But they connected - orphans of a lost planet, who spoke the same tongue, who had the same bewilderment in their first moments on an alien planet with newfound powers. And if being in his bed brought her pleasure, it was only proof of their connection, that a good relationship could come of it.

Sometimes there were those flashes - Mon-El had been confused by Alex’s coming out, not understanding the concept. The more the merrier would ring in Kara’s head, and she’d chase away the image of Lena’s face.

---

“I couldn’t have done it, Kara.”

Kara’s chest heaved as she gazed down at Lena, hearing Kal’s words flash through her mind. Lena clung to Kara’s arm as Kara hovered above the reservoir, and some corner of Kara’s mind knew that she should go land, that the danger was over. That Lena was safe. That the city was safe.

But she could only stare down at Lena, whose heart hammered in her chest, whose panting breaths from her climb had not yet slowed. I almost lost her, Kara thought, forlorn. I couldn’t lose her…

It was that moment that her world came crashing down, that realization made her feel like she was drowning. That romantic love wasn’t merely a combination of friendship and lust. That shared experience didn’t mean a shared connection. There was something that ran deeper.

She was in love with Lena, and she could no longer deny it.

---

It was a drunken movie night, after Lena’s breakup with James, when Kara heard I love you fall from Lena's lips.

“It was always you,” Lena confessed, her words slightly slurred from the alcohol as Kara finished pulling the covers over her. “I just wanted to be close to you.”

Kara stood back, feeling her heart pound as she watched Lena slip into slumber. I wish I had told you, Kara thought, her mind flashing to a moment long ago in a forest. I wish I had told you, before…

Kara spent a fitful night trying to sleep on her couch, and Lena’s eyes flashed with shame the next morning as she woke. But they left for Noonan’s, leaving the conversation behind.

---

It felt impossibly brief, that window of time after Kara had revealed her secret, where everything felt almost right with the world. Maybe someday, she and Lena could finish that conversation.

But she found herself in a kryptonite shell.

The universe ended soon after, and even magic couldn’t fix how they had broken. Until the day Kara finally found her hands in Lena’s, vowing together to take down her brother, and Kara felt again that hopeful wonder of what a future with Lena could hold.

And then she found herself in the Phantom Zone again, the words ringing in her head, I wish I had told you.

---

Sleep had eluded Kara in the weeks back from the Phantom Zone. So she was already wide awake at 2am, when she heard Lena’s heart begin to hammer. 

Kara tensed, rushing to her window and ears tuning in as she prepared to fight off an assassination attempt or catch Lena as she fell.

But as she shot into the sky, she nearly tumbled when she realized that Lena wasn’t in distress. The shaky breaths and small laughs caused Kara’s chest to tighten in anguish. She’s fine, Kara thought, feeling tears prick the edges of her vision. She’s fine. 

---

“Are you okay?” Lena said, when she finally found Kara in the Tower, sitting on a step. “Alex said she couldn’t find you - you were in the Fortress?”

Kara glanced up from the steps. “I just, um. I was reading in the Fortress, I fell asleep there.” It had the benefit of being true. The Fortress was far enough to drown the sound of Lena’s heart out.

Lena shuffled next to Kara, taking a seat. “I don’t remember seeing any beds there.”

“I float in my sleep,” Kara shrugged, staring at her hands as she let silence fall.

Lena shifted, uncomfortable with the quiet. “Are you okay?”

Yeah, Kara almost said, but something stopped her this time. Perhaps it was the poor sleep. Perhaps it was the litany of I wish I had told you that would replay in her mind.

How many more times am I going to do this?, Kara thought. How many more times am I going to carry that regret? “I love you,” Kara said finally, sensing Lena tense up next to her. “I know… I know that door is closed. But I love you. I should’ve told you so long ago.”

“You… you heard me last night,” Lena wondered softly. “So you went to the Fortress?”

Kara grimaced. “I stopped listening as soon as I realized,” Kara said, fighting a panic. Will she be angry? “I never meant to- to invade your privacy. I’ll be more careful.”

“The door isn’t closed,” Lena said. “If you don’t want it to be.”

Those words made Kara brave enough - or maybe just confused enough - to finally tilt her head up to meet Lena’s gaze. “But- last night-”

“I’ve been trying to get over you. Not very successfully,” Lena added, with a wry grin.

“Really?” Kara smiled.

“Really.” 

---

The matching laws had been long dismantled by the time a smiling Alura officiated their marital rites. Kryptonians didn’t have concepts like best man or matron of honor, but that didn’t stop the two women from inviting Alex and Kelly to stand at each of their sides as they said their vows.

Kara never imagined that it’d be a woman’s wrist she’d place her wedding bracelet on. Though she supposed she never imagined marrying on an asteroid of her father’s creation, or marrying for romantic love, or marrying someone her people would call Hero of Argo for the creation of a black rock.

She never imagined finally telling Lena her secret. She never imagined Lena’s forgiveness. She never imagined the feel of Lena’s lips pressed against her own, hands tugging at her robes, as she whispered zhao against Lena’s lips.

And she never imagined being the one to make Lena’s heart race.

[boycritter]

is this function bisexual i mean bijective

[locally-normal]

Today in higher algebra class, prof introduced adjunctions, stated the condition that the bijection between hom sets is natural, and then said

"In practice, I've never checked this condition."

[lipshits-continuous]

A Short Intro to Category Theory

A common theme in mathematics is to study certain objects and the maps between that preserve the specific structure of said objects. For example, linear algebra is the study of vector spaces and linear maps. Often we have that the identity maps are structure preserving and the composition of maps is also structure preserving. In the case of vector spaces, the identity map is a linear map and the composition of linear maps is again a linear map. Category theory generalises and axiomatises this common way of studying mathematical objects.

I'll introduce the notion of a category as well as the notion of a functor, which is another very important and ubiquitous notion in category theory. And I will finish with a very powerful result involving functors and isomorphisms!

Definition 1:

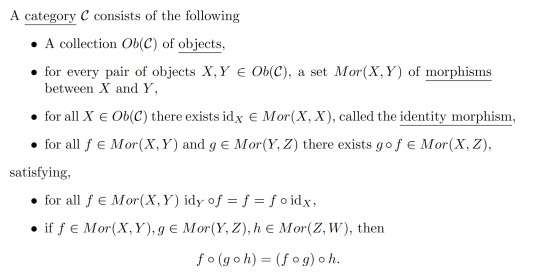
We call the last property the associative property.

Here are some examples:

Examples 2:

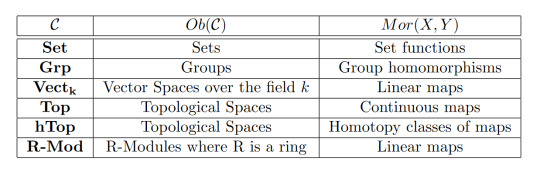
Note that whilst all of these examples are built from sets and set functions, we can have other kinds of objects and morphisms. However the most common categories are those built from Set.

Functors:

In the spirit of category theory being the study of objects and their morphisms, we want to define some kind of map between categories. It turns out that these are very powerful and show up everywhere in pure maths. Naturally, we want a functor to map objects to objects and morphisms to morphisms in a way that respects identity morphisms and our associative property.

Definition 3:

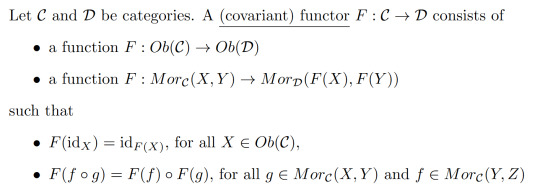
Example 4:

For those familiar with a some topology, the fundamental group is another exmaple of a covariant functor from the category of based spaces and based maps to Grp.

We also have another kind of functor:

Defintion 5:

It may seem a bit odd to introduce at first since all we've done is swap the directions of the morphisms, but it turns out that contravariant functors show up a lot!

This example requires a little bit of knowledge of linear algebra.

Example 6:

In fact, this is somewhat related to example 5! We can produce a contravariant functor Mor(-,X) is a similar way. For V and W vector spaces over k, we have that Mor(V,W) is a vector space over k. In particular, V*=Mor(V,k). So really this -* functor is just Mor(-,k)!

Isomorphisms

Here we generalise the familiar notion of isomorphisms of any algebraic structure!

Definition 7:

For a category of algebraic objects like Vectₖ, isomorphism are exactly the same as isomorphisms defined the typical way. In Top the isomorphisms are homeomorphisms. In Set the isomorphisms are bijective maps.

Remark:

So if f is invertible, we call it's right (or left) inverse, g, the inverse of f.

Isomorphisms give us a way to say when two objects of a category are "the same". More formally, being isomorphic defines an equivalence relation.

Lemma 8:

A natural question one might as is how do functors interact with isomorphisms? The answer is the very important result I hinted at in the intro!

Theorem 9:

Remark: In general, the converse is not true. That is F(X) isomorphic to F(Y) does not imply X is isomorphic to Y. An example of this is the fundamental groups of both S² and ℝ² are isomorphic to the trivial group but these spaces are not homeomorphic.

Taking the negation of Theorem 9 gives us a very powerful result:

Corollary 10:

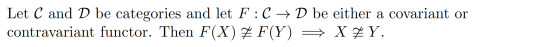
This means that if we can find a functor such that F(X) and F(Y) aren't isomorphic, we know that X and Y are not isomorphic. This is of particular importance in algebraic topology where we construct functors from Top or hTop to a category of a given algebraic structure. This gives us some very powerful topological invariants for telling when two spaces aren't homeomorphic or homotopy equivalent. (In fact, this is where category theory originated from!)