#Class 0

[fftype-0-mybeloved]

Plotting to do all of them bit by bit ✌️🍷

[milkbreadtoast]

quick SHJ phone doodle... from memory because i was too scared to pull out ref(???)😇

My first time drawing him...!!! gotta get the first one out of the way so i can draw better ones later🥹💦 Now that I've broken the ice I hope I can draw him a lot more...!!

[https-hunter]

Pete confronts Carol | “The Silent Partner”

[minimuii]

~ Portrait of a lady ~

[icewindandboringhorror]

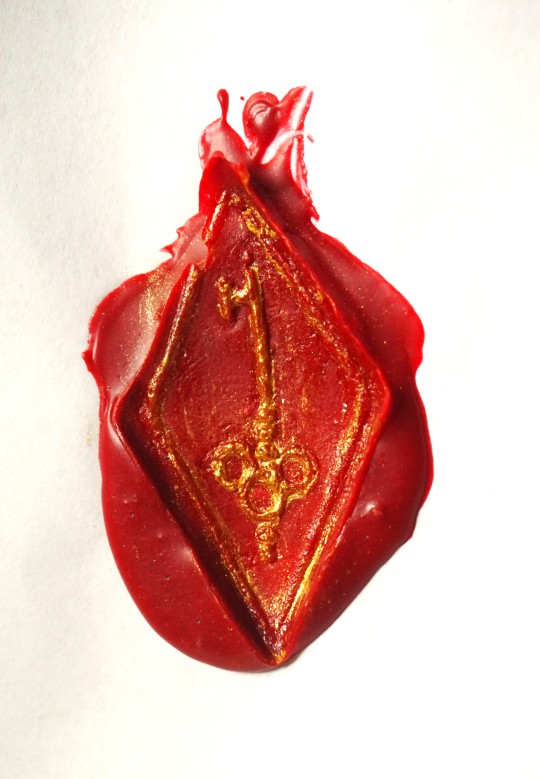
I made a few new wax seal stamps out of clay (like the ones I did for my worldbuilding stuff forever ago), this time just of random symbols that I thought might look good done in the style of painting over the raised part of the wax or etc. :0c Some of them aren't carved deep enough to really show up that well, but overall they worked okay for being clay lol

[godisasimp]

Shiver me timbers are those Spooky Herrschers. And their weird cat?

[soaps-mohawk]

Price is absolutely the type to hide training within activities like hiding a dog's medicine in a piece of cheese.

Oh? Fun date night? Well, it's an escape room. Let's work on your problem solving abilities.

Oh? You want to play video games? He finds games to buy that work on your reaction time and perception.

Wanna stay in and play a board game? We're playing chess. Let's work on your strategy.

I stand by this headcanon 100% 😆

Oh absolutely. He's gotta make sure you're fully prepared for anything, that you're always aware and capable of making snap decisions when necessary.

Gotta keep that brain sharp.

[eerna]

see Asuna Yuuki in another writer's hands could have been one of the coolest pop culture heroines ever. her character concept in Aincrad is truly the closest mainstream gamer media ever got to balancing female gamer sterotypes with an interesting concept. she is neither a gamer girl who is basically one of the guys, nor a traditional support character. she never touched a mainstream video game in her life before and ended up in SAO on accident, but she is a quick learner and manages to climb to the top of the charts within a year. let me remind you, she is tied with Kirito for the second most powerful player in the game - she is his equal in absolutely everything, but from a different angle, and they share basically no overlap. it could have been such a cool duality, where our two protagonists each represent one facet of digital existence. Kirito would be the seasoned veteran, he has completely retreated into video games and has nothing else going for him in his life, so this situation where his empowerment suddenly becomes real instead of make-believe is a heady drug. Asuna has no idea how video games work and doesn't understand the culture surrounding them at all, but this is a whole new realism-oriented approach to gaming, which means her lack of understanding could actually be a boon, which in turn allows her to live out her overachiever fantasies brought over from the real world (because there's nothing the Golden Child loves more than mastering something in a very short, very unhealthy timeframe). and then they meet each other, two sides of the same coin who would have never ever met in real life, and it reframes how they see themselves and their goals and dreams. we could have had an epic romantic gaming opera. we could have had it all. if only mainstream gaming media understood itself

[gundamfight]

[getvalentined]

Differentiating the "Black Robes"

For folks who didn't catch it on their own playthrough or (or watch-through) of FF7 Rebirth, here's a quick breakdown of the apparent nature of the people in black robes seen throughout both this game, and previously in Remake.

This differs from OG canon, where everyone in a black robe was a Sephiroth Copy, but in the FF7R timeline they appear to be broken into three "types."

SPOILERS BELOW — READ AT YOUR OWN RISK

NO NUMBER TATTOO means this is a G-type SOLDIER suffering from degradation. These people are terminally ill. Degradation sets in within five years of enhancement [see Note 1 below], and accelerates very quickly without aggressive treatment.

Known G-type SOLDIERs: Roche, Azul, Rosso, and Shelke Rui. Population: over 100.

A ONE- OR TWO-DIGIT NUMBER TATTOO indicates S-type SOLDIERs in the throes of Reunion. These people are not terminally ill, based on dev comments confirming that S-type SOLDIERs don't degrade, but they have a cellular leash that is being constantly yanked on by Sephiroth/Jenova. Without Reunion taking place, most of them would presumably live long, fairly healthy lives. [See Note 2 below.]

Known S-type SOLDIERs: Zack Fair, Kunsel, Luxiere, and Broden. Population: presumed fewer than 100.

A TATTOO STARTING WITH "SC" confirms these people are successful Sephiroth Copies. Failures do not receive a tattoo. They may or may not be terminally ill, contingent upon which type of SOLDIER they were prior to the procedure to make them into a Copy, and the leash on their own cellular makeup is much stricter, much more direct, and gives them a clearer concept of where to go and what to do.

Known Sephiroth Copies: Roche (successful), Zack Fair (declared failure), and Cloud Strife (declared failure). Population: 4 subjects in total, plus 2 known failures.

Tattoos don't seem to be applied at the time of enhancement, since none of the SOLDIERs in Crisis Core have them, but it's possible that early inductees like Broden were marked when they survived the treatments; this seems likely, as Broden's tattoo is in a slightly different typeface than the tattoos of others in his "type."

I didn't include Sephiroth, Genesis or Angeal under known members of their given types, as they were never normal humans and were not enhanced using one method or the other as teens or young adults. Those who are Jenova babies from birth don't count. I also didn't include two members of DeepGround due to the fact that they canonically cannot actually be G-type SOLDIERs based on the lore of how the two of them were made and how they function in general; they may be G-type on paper, but they are not G-type for the purposes of this analysis.

Lastly, I'll admit that this breakdown may appear to be slightly inconsistent during gameplay, but this seems to be due only to the reuse of models between black robed individuals, presumably to take stress off the dev team. I'm fine with this, obviously, no crunch is good crunch. As far as I can tell it's pretty consistent in full cutscenes, though, so I'm sticking with it until the third game proves me wrong.

—

NOTE 1: The timeframe for degradation is based on Roche suffering from the condition prior to his becoming a Sephiroth Copy, which is visible in the fact that he has a handful of incongruously pale streaks through his hair prior to the procedure; an attempt to cure this is presumably the reason he volunteered to work with Hojo in the first place.

According to the Remake Ultimania, Roche joined SOLDIER after the Nibelheim Incident, so he's only been in the program for five years at the most; this timeframe also allows us to recognize S-type SOLDIERs, as they've been in the program for significantly longer with no known ill effects (e.g.: Kunsel has been in the program since at least 2000, but is mentioned by name and indicated to be at headquarters in Remake, showing that he's still on active duty in 0007; this wouldn't be the case if he were suffering from degradation, so he can't be a G-type.)

NOTE 2: The capacity of S-type SOLDIERs to live fairly normal lives with minimal major health issues is proven by the existence of Broden, who identifies himself as a SOLDIER but was certainly part of Project 0; he and Mildred left home as teenagers and wound up with Shinra, but Mildred doesn't know the name of the project into which he was conscripted, only that it was "top secret."

Combined with the apparent age of both characters in-game, this indicates that Broden took part in the project before SOLDIER was even SOLDIER, putting him as one of its earliest successful operatives, probably enhanced sometime between 1983 and 1985 based on the timeline provided in the First SOLDIER Battle Royale opening cutscene—hence why his number is the lowest shown on a person in a black robe in the entire game. This puts him in his forties at the youngest during the Crisis, and he functions just fine (albeit with some other issues we can assume were caused by the enhancement procedure being imperfect at the time of his enlistment) until Reunion starts to call him toward the end of 0007.

[miles-is-so-gay]

presenting the far cry ds spin off: john seed, ace attorney

[danis-artss]

Why draw danny on csp if u can draw him during politics class ? Not that i rlly wrote anything anyway lmfao

[bubbloquacious]

Okay so to get the additive group of integers we just take the free (abelian) group on one generator. Perfectly natural. But given this group, how do we get the multiplication operation that makes it into the ring of integers, without just defining it to be what we already know the answer should be? Actually, we can leverage the fact that the underlying group is free on one generator.

So if you have two abelian groups A,B, then the set of group homorphisms A -> B can be equipped with the structure of an abelian group. If the values of homorphisms f and g at a group element a are f(a) and g(a), then the value of f + g at a is f(a) + g(a). Note that for this sum function to be a homomorphism in general, you do need B to be abelian. This abelian group structure is natural in the sense that Hom(A ⊗ B,C) is isomorphic in a natural way to Hom(A,Hom(B,C)) for all abelian groups A,B,C, where ⊗ denotes the tensor product of abelian groups. In jargon, this says that these constructions make the category of abelian groups into a monoidal closed category.

In particular, the set End(A) = Hom(A,A) of endomorphisms of A is itself an abelian group. What's more, we get an entirely new operation on End(A) for free: function composition! For f,g: A -> A, define f ∘ g to map a onto f(g(a)). Because the elements of End(A) are group homorphisms, we can derive a few identities that relate its addition to composition. If f,g,h are endomorphisms, then for all a in A we have [f ∘ (g + h)](a) = f(g(a) + h(a)) = f(g(a)) + f(h(a)) = [(f ∘ g) + (f ∘ h)](a), so f ∘ (g + h) = (f ∘ g) + (f ∘ h). In other words, composition distributes over addition on the left. We can similarly show that it distributes on the right. Because composition is associative and the identity function A -> A is always a homomorphism, we find that we have equipped End(A) with the structure of a unital ring.

Here's the punchline: because ℤ is the free group on one generator, a group homomorphism out of ℤ is completely determined by where it maps the generator 1, and every choice of image of 1 gives you a homomorphism. This means that we can identify the elements of ℤ with those of End(ℤ) bijectively; a non-negative number n corresponds to the endomorphism [n]: ℤ -> ℤ that maps k onto k added to itself n times, and a negative number n gives the endomorphism [n] that maps k onto -k added together -n times. Going from endomorphisms to integers is even simpler: evaluate the endomorphism at 1. Note that because (f + g)(1) = f(1) + g(1), this bijection is actually an isomorphism of abelian groups

This means that we can transfer the multiplication (i.e. composition) on End(ℤ) to ℤ. What's this ring structure on ℤ? Well if you have the endomorphism that maps 1 onto 2, and you then compose it with the one that maps 1 onto 3, then the resulting endomorphism maps 1 onto 2 added together 3 times, which among other names is known as 6. The multiplication is exactly the standard multiplication on ℤ!

A lot of things had to line up for this to work. For instance, the pointwise sum of endomorphisms needs to be itself an endomorphism. This is why we can't play the same game again; the free commutative ring on one generator is the integer polynomial ring ℤ[X], and indeed the set of ring endomorphisms ℤ[X] -> ℤ[X] correspond naturally to elements of ℤ[X], but because the pointwise product of ring endomorphisms does not generally respect addition, the pointwise operations do not equip End(ℤ[X]) with a ring structure (and in fact, no ring structure on Hom(R,S) can make the category of commutative rings monoidal closed for the tensor product of rings (this is because the monoidal unit is initial)). We can relax the rules slightly, though.

Who says we need the multiplication (or addition, for that matter) on End(ℤ[X])? We still have the bijection ℤ[X] ↔ End(ℤ[X]), so we can just give ℤ[X] the composition operation by transfering along the correspondence anyway. If p and q are polynomials in ℤ[X], then p ∘ q is the polynomial you get by substituting q for every instance of X in p. By construction, this satisfies (p + q) ∘ r = (p ∘ r) + (q ∘ r) and (p × q) ∘ r = (p ∘ r) × (q ∘ r), but we no longer have left-distributivity. Furthermore, composition is associative and the monomial X serves as its unit element. The resulting structure is an example of a composition ring!

The composition rings, like the commutative unital rings, and the abelian groups, form an equational class of algebraic structures, so they too have free objects. For sanity's sake, let's restrict ourselves to composition rings whose multiplication is commutative and unital, and whose composition is unital as well. Let C be the free composition ring with these restrictions on one generator. The elements of this ring will look like polynomials with integers coefficients, but with expressions in terms of X and a new indeterminate g (thought of as an 'unexpandable' polynomial), with various possible arrangements of multiplication, summation, and composition. It's a weird complicated object!

But again, the set of composition ring endomorphisms C -> C (that is, ring endomorphisms which respect composition) will have a bijective correspondence with elements of C, and we can transfer the composition operation to C. This gets us a fourth operation on C, which is associative with unit element g, and which distributes on the right over addition, multiplication, and composition.

This continues: every time you have a new equational class of algebraic structures with two extra operations (one binary operation for the new composition and one constant, i.e. a nullary operation, for the new unit element), and a new distributivity identity for every previous operation, as well as a unit identity and an associativity identity. We thus have an increasing countably infinite tower of algebraic structures.

Actually, taking the union of all of these equational classes still gives you an equational class, with countably infinitely many operations. This too has a free object on one generator, which has an endomorphism algebra, which is an object of a larger equational class of algebras, and so on. In this way, starting from any equational class, we construct a transfinite tower of algebraic structures indexed by the ordinal numbers with a truly senseless amount of associative unital operations, each of which distributes on the right over every previous operation.

[poly-space-nerds]

hmmm thinking about Todoroki and Midoriya being childhood friends where they promised to marry each other so that todoroki could protect midoriya from bullies and he protects todoroki from his dad but one day todoroki just vanished and he doesn’t hear from him again until they end up in UA.

cue todoroki not wanting to get close because he’s still consumed by anger at his father and thinks Izuku won’t want to be his friend anymore since he’s changed so much and ignores him. Midoriya is hurt yet can’t stop thinking about him and the scar on his eye. i.e. they don’t interact in season 1. then sports festival happens and todoroki tells him everything. Midoriya is obvious like ‘i’m always gonna be your friend’ and ‘it’s your power isn’t it?’ while Todoroki is ‘i’m sorry’ and ‘thank you’.

The day after the sports festival has ended and everyone is back in class, Todoroki walks into the classroom, eyes set on Midoriya, gets on one knee and proposes. much to literally everyone else’s confusion.

[oddthesungod]

went to check in on the bells hells lads stats cuz I wanted to see what Orym's Strength score was (its 10 btw in case you didn't remember like me asjhda) and i had a laugh at the fact that both Chetney and Ash are at 18 Strength. Man... I gotta draw Chet more beefy!

[ruiwe]

Song Taewon and Changelingg~ two of the best characters to ever freakin exist make them talking a thing please 🙏 amen