#Cardinality

[bluekino]

have anyone ever think about the cardinality of the infinity train? like, is the infinity train infinite as in the integers or is it infinite as in the real numbers?

[oneefin]

finished huntinality 3! whew what a great time

our super small super casual team "huh?" consists of me, @nivrad00, and @lunacyecho. we had fun!

i'll do a writeup of at least one puzzle from it sometime - there were many great moments in there for me. for now here's a screenshot of our spreadsheet's landing page (contains hunt spoilers)

[adjoint-law]

Honestly I felt so vindicated knowing this. Thanks, gacha game~

[talkingnumbers]

Counting, Counting

Mathober Day 8: Counting

We talk a lot with preservice teachers about the importance of counting. And with each new kind of number! Low counting numbers, double digit, higher place value, fractions, decimals, negatives, and, bending the definition a bit, imaginary and matrices. We need to connect number with quantity before learners have cardinality.

To some extent, we did that today with radians!

[algebra-as-praxis]

First post!! I wanted to show you how deep a rabbit hole you can dig with a very simple concept like, "What does 'four' mean?"

I have a number line.

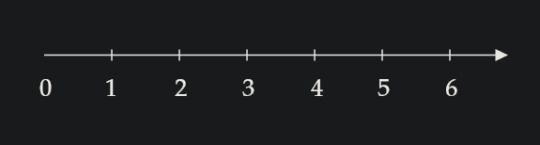
So, I'd like you to imagine that you've sat down across from me on your first day in class, and I put some kind of math worksheet with this number line on it that gives you a very simple-sounding task: "Circle four."

If you are like nearly every one of the older students I've had, you'll circle the number 4 on the line. And I'd say something like, "That is a perfectly reasonable response to this request. There is nothing wrong with what you've done. But aren't you suspicious about how simple this question sounds? Did you see that there was a twist coming?"

On a number line, the place where we've written 4 is not actually the value 4. It is more like the position 4; we would call this the ordinal number (a number used to track the positional order of things; another example of an ordinal number is the word "fourth," which tells you that there are three other things before that one).

So, if you just circled the number 4, you definitely circled the position, but the thing you circled isn't worth 4. If you were going to circle the thing that has the value (or cardinality, since we're counting individual objects) of 4, it would look something more like this:

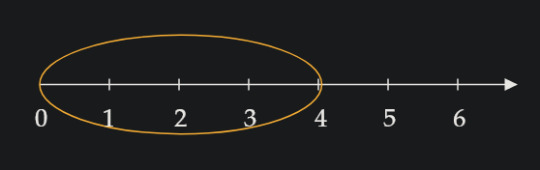
This is because in order to have the value of 4, you need everything that came before it! Imagine counting out candy while your kid sister steals and eats the candies you counted already. When you get to your final number, that number is not how many candies you have, but rather how many you counted cuz your sister's got 'em all! For the value of your candies to stay the same, you need all of them to be there!

"Four" could also look, less straightforwardly, like this:

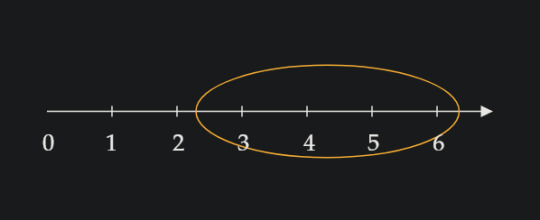
The distance from the start of the circle to the end is four; and since we're circling the line, the length of the line that is circled is four. If we imagine the circle starts (from the left) at the position of 2.3, it would have to end at the position (from the right) 6.3. If we find the difference of the numbers at these positions, we would be doing the equation 6.3 - 2.3 = 4.

A quick summary:

The position of a number is shown with an ordinal number.

The actual physical quantity of the individual items is shown with a cardinal number, which we more typically call the value.

We can find a value inside the ordinals by finding the distance between any two ordinals, via subtraction.

Okay... But notice we've used two words here that seem to imply the same thing: difference and distance. Let's clear this up real quick:

Difference is the result of subtraction. Generally, if we want to find the difference between two things, we subtract the first thing from the second thing:

second - first = difference

But that's not a rule, so much as a norm. In reality, if you wanted to find the difference of two numbers, the person asking had best be very clear which way they want you to do it, because if you reverse this you will get the negative of the result above!

For example, if you were asked to find the difference between 6 and 15, you would do 15 - 6 = 9. But if it's not clear and you instead did 6 - 15, you get -9.

If, however, someone wanted to know how far apart these two numbers are, they would not be asking the difference but rather the distance between these numbers. The result would therefore be the absolute value of either one of these subtractions:

|15 - 6| = |9| = 9, |6 - 15| = |-9| = 9 Same result!

This is in actuality the real use of absolute values. Absolute value is typically shown as "the distance from zero," which is kind of true? But it's really for finding distances of any kind -- in fact, it's later used to mean exactly that when you get into complex algebra (that is, algebra with imaginary numbers) and linear algebra (matrices and vectors).

But that's for later.

[g0fckur531f]

[beaft]

can anyone tell me why i enter the grocery store a normal person and emerge as some sort of vile ravening monster

[redactedrem]

Headcanon where after so many arguments between the batkids and Bruce over his paranoia and complete disregard for his kids privacy, the entire family had compromised with (in the healthiest way possible) downloading life360 on their phones and that's how they all keep track of each other.

Now Bruce knew that this is mostly for his benefit and is supposed to be a healthy alternative for his unhealthy paranoia and helicopter parenting, but what he wasn't expecting was for his kids to start keeping track of him.

He's putting gas in his car and Dick calls him because apparently Dick has been watching him drive around on the app? And Bruce is currently at a gas station thats right around the corner from a Taco Bell and now Dick wants him to get food for everyone since he's already there.

He's driving home from a meeting and Steph calls him because her and Duke were shopping in the area and wants to know if he can pick them up, when he asks how she knew he was on the same street, he gets a "Oh I just like to stalk everyone on the app for funsies." as an answer.

Jason calls him and he can barely get out a hello before Jason cuts him off, "Bruce why the fuck is your phone battery on 5%, charge your damn phone" which completely stuns him because why does he know that. He clears his throat before answering. "Jason, what?"

"Everyone can see each others phone batteries on '360, now charge your phone." Is all he gets before Jason hangs up on him.

[canisalbus]

✦ Freshly ordained ✦

[kaphkas]

Turn my haters to consumers / I make vets feel like they juniors 📿⛪️🕯️

[sassydefendorflower]

Not me scrolling through the Conclave tag only to see no one talk about the deliberate positioning and framing of the women in this movie.

Pulling up this movie I completely expected to only encounter Sister Agnes as the one woman we see in the trailer, the conclave a space that has been kept from the female members of the church. Now, color me surprised when I started the movie and most of the establishing shots we got were focused on all the women working in the Vatican.

And it is such a deliberate choice, it does the film a disservice not to talk about it.

Because while Cardinal Lawrence is having his fifteenth breakdown during sequestering and Bellini finds the ambitious asshole within himself, Ray does all the leg work, and Bel---- we see the women work.

We see the kitchens, we see them cook, we see them stand aside. Most of the time when the Cardinals are conspiring it is the women who interrupt because they are busy working, walking, running errands.

And there is power in that.

I think it is very deliberate how often (and with such lingering gaze) the camera shows us the lives of the other half - partially to connect to the wider themes of the movie, on how Bellini asks for women to get more power but never thanks them, and how Benitez stumps them all by thanking the women preparing their meals when asked to say the prayer (considering his own probably tumultuous relationship to gender within the church).

But it also stands in direct opposition to a long tradition in story telling: servants don't exist. How often the heroes of a regency romance are "alone" because the two hand maidens and three maids don't really count.

Conclave doesn't do that.

It doesn't let us look away.

Between all the petty drama, the politics, and the real life consequences of the conclave, we never stop looking at the people doing all the work.

Yes, we follow the ups and downs of Lawrence and Co, but in doing so the movie reminds us again and again of the women working the kitchen.

And that was just such a powerful artistic choice in a movie about a famously misogynistic church... I loved it. And I had to talk about it.

[thoughtkick]

Be very, very careful what you put into your head, because you’ll never, ever get it out.

homas Cardinal Wolsey

[charyou-tree]

If that hurts your brain, get this: There are different infinities, and some are bigger than others.

There are an infinite amount of Natural Numbers (counting numbers), but if you had an infinite amount of time you could list them all one by one.

You know, 1, 2, 3, 4, 5, 6, ...

Where the ... implies an endlessly continuing sequence. It would take forever to get through them all, but if you actually had forever you could do it.

But, while there are also an infinite amount of Real Numbers, there are vastly more of them than there are natural numbers. You couldn't even begin to list them all, even with unlimited time.

Like, ok, maybe you start at 0. That's sensible enough.

What's the next Real Number?

Its not 1, there's plenty of real numbers between 0 and 1, like 1/2 and 0.95 and 1/pi. You might say its 0.00001 or something, but you can always find numbers between 0.00001 and 0. You could start to think that maybe its something like 0.0000...1 with some arbitrary number of zeroes after the decimal place, but no matter how small of a real number you pick, you can always find infinitely more Real Numbers between it and 0.

Not only can you never finish listing all the Real Numbers, but there are so many of them there's not even any reasonable way to start listing them.

For a more formal sense of why this must be true, look into Cantor's Diagonal Argument:

Fundamentally, the amount of Natural Numbers is the smallest type of infinity, which is referred to as Countably Infinite, while the amount of Real Numbers is a larger size of infinity referred to as Uncountably Infinite. (many mathematicians define even larger types of infinite sets called Large Cardinals, although it is an open--and perhaps undecidable--question of whether there are any sizes of infinite sets in between Countably and Uncountably Infinite, see: Continuum Hypothesis)

Poetry Comics Month, Day 30: Infinity

[rodrickheffeley]

this photo is so cunt

[g0fckur531f]