#meshgrid

[prashantgujjar]

What would be the equation of the following surface?

 I have the raw data of X, Y, Z, where X and Y are inputs and Z is the output. Plotting the surface gives the red curve in the below picture:

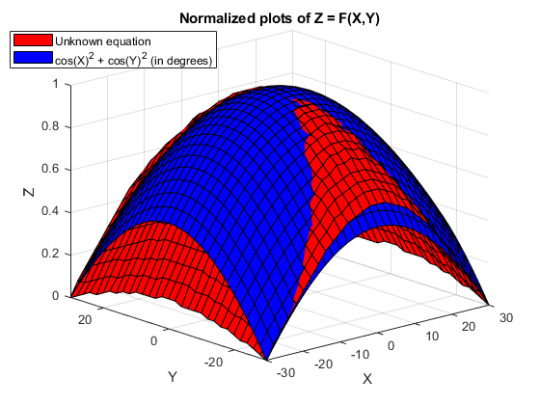
The surface seems to be a simple function involving trigonometric functions. For example, plotting the equation cos(X)^2 + cos(Y)^2 gives the blue surface and it looks similar to the red graph (but the RMS error is very large).

I have tried introducing variables (a1*cos(X)^2 + a2*cos(Y)^2), where a1 and a2 vary from 0 to 1) but the RMS error is still large.

I also tried the surface fitting functions (MATLAB's fit function) but it's models are limited (unlike the curve fitting models which include Fourier series, sin series, etc).

How can I find the equation which gives the red surface?

Edit for clarity: I am able to use the lsqcurvefit (or any other curve fitting toolbox functions) to find which coefficients to use, but I am not sure what the equation should be. cos(X)^2 + cos(Y)^2, for example, is not the right equation but it does have a similar shape.

If this seems improbabilistic, how can I vary cos(X)^2 + cos(Y)^2 to align the end curves of the surface (where there seems to be highest misalignment)?

NOTE:-

Matlabsolutions.com provide latest MatLab Homework Help,MatLab Assignment Help , Finance Assignment Help for students, engineers and researchers in Multiple Branches like ECE, EEE, CSE, Mechanical, Civil with 100% output.Matlab Code for B.E, B.Tech,M.E,M.Tech, Ph.D. Scholars with 100% privacy guaranteed. Get MATLAB projects with source code for your learning and research.

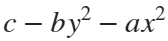
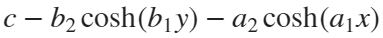
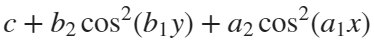
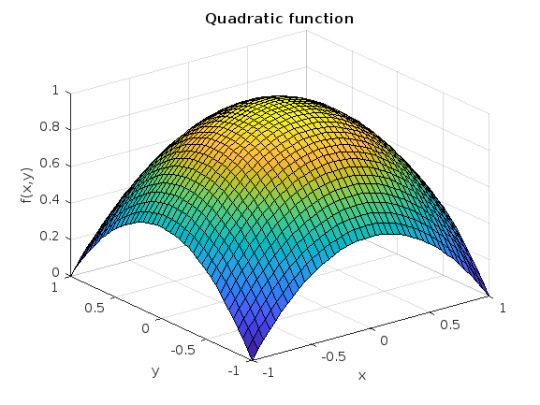
Update 3: Added some surface plots.[X, Y] = meshgrid(-1:0.05:1); %% Polynomial function c = 1; b = 1/2; a = b; Z = c - b*Y.^2 - a*X.^2; % can try higher-order polynomial functions surf(X, Y, Z), grid on title('Quadratic function'), xlabel x, ylabel y, zlabel f(x,y)

SEE COMPLETE ANSWER CLICK THE LINK

[vespasiane]

"The meshgrid function supports two indexing modes: ‘xy’ for Cartesian indexing and ‘ij’ for matrix indexing." Explain.

"We can see that X has the same shape as x and Y has the same shape as y." I don't think so.

[daredge]

la gloom (mesh grid) bw photo by george regout @thegrovela #la #lagloom #gloom #gloomy #gloomyla #lalife #losangeles #lasun #cloudedsun #mesh #meshgrid #grid #dark #edgy #greyla #grayla #bw #bwphoto #bwphotography #bnw #bnwphoto #bnwphotography #blackandwhite #blackandwhitephoto #blackandwhitephotography #abstract #abstractphoto #abstractphotography #artkills #artkillsgallery #georgeregout (at The Grove)

[attorneynahas]

Gnu octave 3d plot

#Gnu octave 3d plot how to

#Gnu octave 3d plot code

Rows is limited to the order of the piecewise polynomials, order. Vector of the x-locations of the constraints.Ĭoefficients (matrix). The optional property, constaints, is a structure specifying linearĬonstraints on the fit. The splines are constructed of polynomials with degree order. The fitted spline is returned as a piecewise polynomial, pp, and Values close to unity may cause instability or rank With the knowledge gained, the second part of the project will be to implement a Property Inspector. Semiconductor material often described by diamond crystal lattice (or the related zincblende lattice). 3D distribution can then be plotted using Matlab/Octave. In this project we use ELK to simulate the spatial distribution of electronic charge density in diamond. The initial phase of the project will be learning how the implementation was done. 3D plot of the charge density of diamond using ELK, Octave an VESTA. Increasing values of beta reduce the influence of Octave has a preliminary implementation of a Variable Editor: a spreadsheet-like tool for quickly editing and visualizing variables. Viewed 193 times -1 I was trying to draw four points in 3D using GNU Octave. The value ofīeta is restricted to the range, 0

#Gnu octave 3d plot code

Three iterations of weighted least squares are performed. A waterfall plot is similar to a meshz plot except only mesh lines for the rows of z (x-values) are shown. Code function animcamera(fname) draw a sombrero and turn it around n 50 x y linspace (-8, 8, n) xx, yy meshgrid (x, y) r sqrt. If robust fitting is to be applied to reduce the influence of outlyingĭata points. The optional property robust is a logical value which specifies Length of the period is max ( breaks) - min ( breaks). Whether a periodic boundary condition is applied to the spline. Everytime I try to run the following program it keeps saying invalid use of script in index notation. To plot multiple one- or two-argument groups, separate each group with an empty format string, as plot3 ( x1, c1, '', c2, '', ) Multiple property-value pairs may be specified which will affect the line objects drawn by plot3. The optional property periodic is a logical value which specifies It used to be able to plot 3D graphs but not anymore. P is a positive integer defining the number of intervals along N-D array, then x(j) is matched to y(:,…,:,j). X is a vector, and y is a vector or N-D array. I don't see such an option when I plot 3D surfaces in Octave using GNUplot. In Matlab I can generate a 3D surface plot/mesh plot and rotate it to whatever reference frame I choose. But I have a question regarding plot rotation. Plot(time,velocity,’:bo’,’LineWidth’,7.: pp = splinefit ( x, y, breaks) : pp = splinefit ( x, y, p) : pp = splinefit (…, "periodic", periodic) : pp = splinefit (…, "robust", robust) : pp = splinefit (…, "beta", beta) : pp = splinefit (…, "order", order) : pp = splinefit (…, "constraints", constraints)įit a piecewise cubic spline with breaks (knots) breaks to the I am relatively new to Octave but have relied on Matlab knowledge to get around. Velocity=sqrt(gravity*mass/c)* tanh(sqrt(gravity*c/mass).*time) Gnu Octave is a matlab work-a-like that does array manipulations and provides a programmable mathematical workbench. It is based in matGeom and extends it with several other functionalities, e.g. Last I check, it incorporates gnuplot for its graphing functions. Gnuplot does line graphs and some 2D plotting of regular array data. The geometry package is multipackage providing functions to manipulate geometrical entities in 2D and 3D. The basic command is plot(x,y), where x and y are the co-ordinate. Octave has powerful facilities for plotting graphs via a second open-source program GNU-PLOT.

#Gnu octave 3d plot how to

Long In this tutorial you will learn how to plot data in Octave. The octave script with comments shown below to plot the time vs velocity graph. Octave Tutorial 5: How to plot data in Octave with extracts from Introduction to Octave, by P.J.G. Let’s learn the steps involved to specify markers in the Octave/Matlab plot command with attributes like edge color, face color, and marker size, etc.

[codehunter]

What is the purpose of meshgrid in Python / NumPy?

Can someone explain to me what is the purpose of meshgrid function in Numpy? I know it creates some kind of grid of coordinates for plotting, but I can't really see the direct benefit of it.

I am studying "Python Machine Learning" from Sebastian Raschka, and he is using it for plotting the decision borders. See input 11 here.

I have also tried this code from official documentation, but, again, the output doesn't really make sense to me.

x = np.arange(-5, 5, 1)y = np.arange(-5, 5, 1)xx, yy = np.meshgrid(x, y, sparse=True)z = np.sin(xx**2 + yy**2) / (xx**2 + yy**2)h = plt.contourf(x,y,z)

Please, if possible, also show me a lot of real-world examples.

https://codehunter.cc/a/python/what-is-the-purpose-of-meshgrid-in-python-numpy

[timo-cruiz]

Lakeland SEO company | SEO services Lakeland city | best SEO services Lakeland | Digital Piloto

Digital Piloto is a leading #Gainesville SEO company. We are the best #SEO service provider in Gainesville and specialize in Organic Leads Generation, Google Ads Management, and 360-degree SEO solutions for all industries. With 100 years of combined experience, Digital Piloto has successfully completed over 100 projects. Our team is certified by Microsoft and Google which guarantees that you will get ROI-driven #Marketing strategies from us!

Subscribe Now: https://bit.ly/DigitalPiloto-YouTube Stay Updated! 🔔

Get in touch with us: 📧  info@digitalpiloto.com 🌍https://www.digitalpiloto.com/seo-company-gainesville/

Follow us to stay updated: ► Facebook: https://www.facebook.com/digitalpiloto/ ► Twitter: https://twitter.com/digitalpiloto ► Instagram: https://www.instagram.com/digitalpiloto/ ► LinkedIn: https://www.linkedin.com/company/digitalpiloto/

LICENSE CERTIFICATE: Envato Elements Item ================================================= This license certificate documents a license to use the item listed below on a non-exclusive, commercial, worldwide and revocable basis, for one Single Use for this Registered Project.

Author Username: meshgrid Licensee: A Maiti Registered Project Name: Digital Piloto

[hyperbolicgifs]

HERE IS A MATLAB TEMPLATE WHICH ANYONE CAN USE TO MAKE ANY GIF IMAGINABLE ALL YOU NEED IS A TILING AND A TRANSFORMATION

function gif_machine

height = 540; width = 540; frames = 120; framerate = 60;

[Z im] = initialize_gif(height,width,frames);

X = real(Z); Y = imag(Z);

for idx = 1:frames

 t = idx/frames;

 F = 1./Z; %transformation  A = mod(floor(real(F*2+t))+floor(imag(F*2+t)),2); %tiling

 im(:,:,1,idx) = A;  im(:,:,2,idx) = A;  im(:,:,3,idx) = A;  idx end make_gif('filename.gif',im,framerate); end

function [Z,im] = initialize_gif(width,height,number_of_frames)

y = -1:2/(height-1):1; x = -width/height:2*(width/height)/(width-1):width/height; [X,Y] = meshgrid(x,y); Z = complex(X,Y); im = zeros(height,width,3,number_of_frames); end

function make_gif(filename,image,framerate)

for idx = 1:size(image,4)   [A,map] = rgb2ind(image(:,:,:,idx),256);   if idx == 1       imwrite(A,map,filename,'gif','LoopCount',Inf,'DelayTime',1/framerate);   else       imwrite(A,map,filename,'gif','WriteMode','append','DelayTime',1/framerate);   end end end

[vespasiane]

Show me examples of using mgrid and ogrid.

What are the similarities and differences of opinion meshgrid, mgrid and ogrid in numpy?

[daredge]

la gloom (mesh grid) bw photo by george regout @thegrovela #la #lagloom #losangeles #lalife #lawinter #lainsta #mesh #meshgrid #grid #gloom #gloomy #gloomyla #sun #lasun #bw #bwphoto #bwphotography #bnw #bnwphoto #bnwphotography #blackandwhite #blackandwhitephoto #blackandwhitephotography #abstractphoto #abstractphotography #artkills #artkillsgallery #georgeregout (at The Grove)

[themepluginpro]

Download Twisted Red Paint Splash V4 4K motion graphics on videohive

Description Twisted Red Paint Splash V4 4K :

Download Twisted Red Paint Splash V4 4K. The venture releases on Friday 26th February 2021 By The author meshgrid on videohive. It’s Tagged with 3d,summary,acrylic,artwork,artist,creative,art work,background,bleed,blood,broadcast,cinematic,shade,shade combine,coloured,vibrant,industrial,creativity,darkish pink,drops,explode,stream,fluid,fluid animation,footage,ink,ink collision,ink splash,liquid,trendy,paint,paint animation,paint collision,paint drop,paint splash,realflow,pink,pink shade,pink paint,pink paint combine,simulation,sketch,smooth pink,particular impact,splash,Splash Ink,splat,splatter,vfx,water. Project Title: Twisted Red Paint Splash V4 4K Category: motion-graphics/components/water Price: $25 Creator: meshgrid Publish Date: Friday 26th February 2021 02:34:03 PM More Info / Download

Twisted Red Paint Splash V4 4K alpha prepared to make use of for motion graphic, vfx, movie, promoting or animation. Works properly with all modifying applications.

Alpha and background variations included

Total clip length 18 seconds

Individual clip length 9 seconds

Ultra HD 3840×2160px

29.97 fps

If you've gotten any questions contact me by way of my profile web page. More Info / Download #Twisted #Red #Paint #Splash

[nirmaljoshi]

Fractals in matlab/octave

Codes in matlab/octave for generating some popular fractals:

Mandelbrot

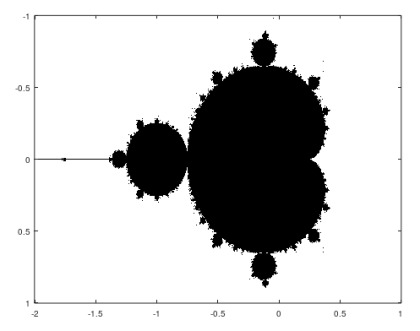
function mandelbrotmain() clear variables; clc;

maxit=200; x=[-2,1]; y=[-1 1];

xpix=601; ypix=401;

x=linspace(x(1),x(2),xpix); y=linspace(y(1),y(2),ypix); [xG, yG]=meshgrid(x,y);

c=mb(maxit,xG,yG);

figure imagesc(x,y,c); colormap([1 1 1;0 0 0]); axis on; grind on;

endfunction

function count=mb(maxItr,xG,yG) c=xG+1i*yG; count=…

[prashantgujjar]

How can I use Matlab to evaluate ∫10∫10∫101(xyz)xyz dx dy dz?

I was struggling with my MATLAB Assignment help and then a good friend told me about MatlabSolutions.com website and they gave me the best Assignment help ever. I hope to always count on the quality and efficiency of your services.

Numerical approach: sample Two methods have been suggested here for the numerical approach, regular sampling and random sampling. In many cases, however, semi-random sampling has superior convergence.

​

​ The problem of regular grid sampling, is that you sample at fixed spatial frequencies, risking under/oversampling of important frequencies.The problem of random sampling, is that you could easily under/oversample important regions by chance.

A better approach is semi-random sampling, in which the sampled points are globally more uniformly distributed. In this example, I chose to sample near each point in the regular grid, however, the relative distance to this gridpoint was varied. In each dimension I randomly selected the deviation from the a uniform distribution on the interval [-1/2*d, 1/2*d] in which d is the distance between the regular gridpoints.

In the figure below it is seen how semi-random sampling (blue line) converges faster than random sampling (red line) or regular sampling (green line).

​

​ Semi random sampling (blue line) converges faster than random sampling (red line) or regular sampling (green line). The horizontal axis (N) represents the number of gridpoints in each dimension, leading to N³ sampled points. (Also N³ samples for random sampling).

​

​ Same figure, but now for ten simulations. %% MATLAB CODE: Nseries = 50:50:400; results = zeros(3, length(Nseries)); for m = 1:length(Nseries) N = Nseries(m); % Random sampling xyz = rand(1,N³).*rand(1,N³).*rand(1,N³); results(1, m) = mean(1./xyz.^xyz); % Regular sampling gridPoints_1D = linspace(1/(2*N),1–1/(2*N),N); [x,y,z] = meshgrid(gridPoints_1D); % on exact grid nodes: xyz = x(:).*y(:).*z(:); results(2, m) = mean(1./xyz.^xyz); % near grid nodes, random deviation: x = x + (rand(size(x))-0.5)/N; y = y + (rand(size(x))-0.5)/N; z = z + (rand(size(x))-0.5)/N; xyz = x(:).*y(:).*z(:); results(3, m) = mean(1./xyz.^xyz); end figure; semilogx(Nseries, results(1,:), ‘r’); hold on; semilogx(Nseries, results(2,:), ‘g’); semilogx(Nseries, results(3,:), ‘b’);

[baddtraxxportfolio]

I got asked a few times how one does transform meshgrids, or anything in CSP and PShop. Its actually quite simple and is a perfect way to form clothes or limbs arounds. I do not have GIMP but it should be similar there.

[mathematicianadda]

PhysiCell Tools : python-loader

The newest tool for PhysiCell provides an easy way to load your PhysiCell output data into python for analysis. This builds upon previous work on loading data into MATLAB. A post on that tool can be found at:

http://www.mathcancer.org/blog/working-with-physicell-snapshots-in-matlab/.

PhysiCell stores output data as a MultiCell Digital Snapshot (MultiCellDS) that consists of several files for each time step and is probably stored in your ./output directory. pyMCDS is a python object that is initialized with the .xml file

What you’ll need

python-loader, available on GitHub at

https://github.com/PhysiCell-Tools/python-loader/tree/development

Python 3.x, recommended distribution available at

https://www.anaconda.com/distribution/

A number of Python packages, included in anaconda or available through pip

NumPy

pandas

scipy

Some PhysiCell data, probably in your ./output directory

Anatomy of a MultiCell Digital Snapshot

Each time PhysiCell’s internal time tracker passes a time step where data is to be saved, it generates a number of files of various types. Each of these files will have a number at the end that indicates where it belongs in the sequence of outputs. All of the files from the first round of output will end in 00000000.* and the second round will be 00000001.* and so on. Let’s say we’re interested in a set of output from partway through the run, the 88th set of output files. The files we care about most from this set consists of:

output00000087.xml: This file is the main organizer of the data. It contains an overview of the data stored in the MultiCellDS as well as some actual data including:

Metadata about the time and runtime for the current time step

Coordinates for the computational domain

Parameters for diffusing substrates in the microenvironment

Column labels for the cell data

File names for the files that contain microenvironment and cell data at this time step

output00000087_microenvironment0.mat: This is a MATLAB matrix file that contains all of the data about the microenvironment at this time step

output00000087_cells_physicell.mat: This is a MATLAB matrix file that contains all of the tracked information about the individual cells in the model. It tells us things like the cells’ position, volume, secretion, cell cycle status, and user-defined cell parameters.

Setup

Using pyMCDS

From the appropriate file in your PhysiCell directory, wherever pyMCDS.py lives, you can use the data loader in your own scripts or in an interactive session. To start you have to import the pyMCDS class

from pyMCDS import pyMCDS

Loading the data

Data is loaded into python from the MultiCellDS by initializing the pyMCDS object. The initialization function for pyMCDS takes one required and one optional argument.

__init__(xml_file, [output_path = '.']) ''' xml_file : string String containing the name of the output xml file output_path : String containing the path (relative or absolute) to the directory where PhysiCell output files are stored '''

We are interested in reading output00000087.xml that lives in ~/path/to/PhysiCell/output (don’t worry Windows paths work too). We would initialize our pyMCDS object using those names and the actual data would be stored in a member dictionary called data.

mcds = pyMCDS('output00000087.xml', '~/path/to/PhysiCell/output') # Now our data lives in: mcds.data

We’ve tried to keep everything organized inside of this dictionary but let’s take a look at what we actually have in here. Of course in real output, there will probably not be a chemical named my_chemical, this is simply there to illustrate how multiple chemicals are handled.

  The data member dictionary is a dictionary of dictionaries whose child dictionaries can be accessed through normal python dictionary syntax.

mcds.data['metadata'] mcds.data['continuum_variables']['my_chemical']

Each of these subdictionaries contains data, we will take a look at exactly what that data is and how it can be accessed in the following sections.

Metadata

The metadata dictionary contains information about the time of the simulation as well as units for both times and space. Here and in later sections blue boxes indicate scalars and green boxes indicate strings. We can access each of these things using normal dictionary syntax. We’ve also got access to a helper function get_time() for the common operation of retrieving the simulation time.

>>> mcds.data['metadata']['time_units'] 'min' >>> mcds.get_time() 5220.0

Mesh

The mesh dictionary has a lot more going on than the metadata dictionary. It contains three numpy arrays, indicated by orange boxes, as well as another dictionary. The three arrays contain \(x\), \(y\) and \(z\) coordinates for the centers of the voxels that constiture the computational domain in a meshgrid format. This means that each of those arrays is tensors of rank three. Together they identify the coordinates of each possible point in the space.

In contrast, the arrays in the voxel dictionary are stored linearly. If we know that we care about voxel number 42, we want to use the stuff in the voxels dictionary. If we want to make a contour plot, we want to use the x_coordinates, y_coordinates, and z_coordinates arrays.

# We can extract one of the meshgrid arrays as a numpy array >>> y_coords = mcds.data['mesh']['y_coordinates'] >>> y_coords.shape (75, 75, 75) >>> y_coords[0, 0, :4] array([-740., -740., -740., -740.]) # We can also extract the array of voxel centers >>> centers = mcds.data['mesh']['voxels']['centers'] >>> centers.shape (3, 421875) >>> centers[:, :4] array([[-740., -720., -700., -680.], [-740., -740., -740., -740.], [-740., -740., -740., -740.]]) # We have a handy function to quickly extract the components of the full meshgrid >>> xx, yy, zz = mcds.get_mesh() >>> yy.shape (75, 75, 75) >>> yy[0, 0, :4] array([-740., -740., -740., -740.]) # We can also use this to return the meshgrid describing an x, y plane >>> xx, yy = mcds.get_2D_mesh() >>> yy.shape (75, 75)

  Continuum variables

The continuum_variables dictionary is the most complicated of the four. It contains subdictionaries that we access using the names of each of the chemicals in the microenvironment. In our toy example above, these are oxygen and my_chemical. If our model tracked diffusing oxygen, VEGF, and glucose, then the continuum_variables dictionary would contain a subdirectory for each of them.

For a particular chemical species in the microenvironment we have two more dictionaries called decay_rate and diffusion_coefficient, and a numpy array called data. The diffusion and decay dictionaries each complete the value stored as a scalar and the unit stored as a string. The numpy array contains the concentrations of the chemical in each voxel at this time and is the same shape as the meshgrids of the computational domain stored in the .data[‘mesh’] arrays.

# we need to know the names of the substrates to work with # this data. We have a function to help us find them. >>> mcds.get_substrate_names() ['oxygen', 'my_chemical'] # The diffusable chemical dictionaries are messy # if we need to do a lot with them it might be easier # to put them into their own instance >>> oxy_dict = mcds.data['continuum_variables']['oxygen'] >>> oxy_dict['decay_rate'] {'value': 0.1, 'units': '1/min'} # What we care about most is probably the numpy # array of concentrations >>> oxy_conc = oxy_dict['data'] >>> oxy_conc.shape (75, 75, 75) # Alternatively, we can get the same array with a function >>> oxy_conc2 = mcds.get_concentrations('oxygen') >>> oxy_conc2.shape (75, 75, 75) # We can also get the concentrations on a plane using the # same function and supplying a z value to "slice through" # note that right now the z_value must be an exact match # for a plane of voxel centers, in the future we may add # interpolation. >>> oxy_plane = mcds.get_concentrations('oxygen', z_value=100.0) >>> oxy_plane.shape (75, 75) # we can also find the concentration in a single voxel using the # position of a point within that voxel. This will give us an # array of all concentrations at that point. >>> mcds.get_concentrations_at(x=0., y=550., z=0.) array([17.94514446, 0.99113448])

  Discrete Cells

The discrete cells dictionary is relatively straightforward. It contains a number of numpy arrays that contain information regarding individual cells.  These are all 1-dimensional arrays and each corresponds to one of the variables specified in the output*.xml file. With the default settings, these are:

ID: unique integer that will identify the cell throughout its lifetime in the simulation

position(_x, _y, _z): floating point positions for the cell in \(x\), \(y\), and \(z\) directions

total_volume: total volume of the cell

cell_type: integer label for the cell as used in PhysiCell

cycle_model: integer label for the cell cycle model as used in PhysiCell

current_phase: integer specification for which phase of the cycle model the cell is currently in

elapsed_time_in_phase: time that cell has been in current phase of cell cycle model

nuclear_volume: volume of cell nucleus

cytoplasmic_volume: volume of cell cytoplasm

fluid_fraction: proportion of the volume due to fliud

calcified_fraction: proportion of volume consisting of calcified material

orientation(_x, _y, _z): direction in which cell is pointing

polarity:

migration_speed: current speed of cell

motility_vector(_x, _y, _z): current direction of movement of cell

migration_bias: coefficient for stochastic movement (higher is “more deterministic”)

motility_bias_direction(_x, _y, _z): direction of movement bias

persistence_time: time in-between direction changes for cell

motility_reserved:

# Extracting single variables is just like before >>> cell_ids = mcds.data['discrete_cells']['ID'] >>> cell_ids.shape (18595,) >>> cell_ids[:4] array([0., 1., 2., 3.]) # If we're clever we can extract 2D arrays >>> cell_vec = np.zeros((cell_ids.shape[0], 3)) >>> vec_list = ['position_x', 'position_y', 'position_z'] >>> for i, lab in enumerate(vec_list): ... cell_vec[:, i] = mcds.data['discrete_cells'][lab] ... array([[ -69.72657128, -39.02046405, -233.63178904], [ -69.84507464, -22.71693265, -233.59277388], [ -69.84891462, -6.04070516, -233.61816711], [ -69.845265 , 10.80035554, -233.61667313]]) # We can get the list of all of the variables stored in this dictionary >>> mcds.get_cell_variables() ['ID', 'position_x', 'position_y', 'position_z', 'total_volume', 'cell_type', 'cycle_model', 'current_phase', 'elapsed_time_in_phase', 'nuclear_volume', 'cytoplasmic_volume', 'fluid_fraction', 'calcified_fraction', 'orientation_x', 'orientation_y', 'orientation_z', 'polarity', 'migration_speed', 'motility_vector_x', 'motility_vector_y', 'motility_vector_z', 'migration_bias', 'motility_bias_direction_x', 'motility_bias_direction_y', 'motility_bias_direction_z', 'persistence_time', 'motility_reserved', 'oncoprotein', 'elastic_coefficient', 'kill_rate', 'attachment_lifetime', 'attachment_rate'] # We can also get all of the cell data as a pandas DataFrame >>> cell_df = mcds.get_cell_df() >>> cell_df.head() ID position_x position_y position_z total_volume cell_type cycle_model ... 0.0 - 69.726571 - 39.020464 - 233.631789 2494.0 0.0 5.0 ... 1.0 - 69.845075 - 22.716933 - 233.592774 2494.0 0.0 5.0 ... 2.0 - 69.848915 - 6.040705 - 233.618167 2494.0 0.0 5.0 ... 3.0 - 69.845265 10.800356 - 233.616673 2494.0 0.0 5.0 ... 4.0 - 69.828161 27.324530 - 233.631579 2494.0 0.0 5.0 ... # if we want to we can also get just the subset of cells that # are in a specific voxel >>> vox_df = mcds.get_cell_df_at(x=0.0, y=550.0, z=0.0) >>> vox_df.iloc[:, :5] ID position_x position_y position_z total_volume 26718 228761.0 6.623617 536.709341 -1.282934 2454.814507 52736 270274.0 -7.990034 538.184921 9.648955 1523.386488

Examples

These examples will not be made using our toy dataset described above but will instead be made using a single timepoint dataset that can be found at:

https://sourceforge.net/projects/physicell/files/Tutorials/MultiCellDS/3D_PhysiCell_matlab_sample.zip/download

Substrate contour plot

One of the big advantages of working with PhysiCell data in python is that we have access to its plotting tools. For the sake of example let’s plot the partial pressure of oxygen throughout the computational domain along the \(z = 0\) plane. Once we’ve loaded our data by initializing a pyMCDS object, we can work entirely within python to produce the plot.

from pyMCDS import pyMCDS import numpy as np import matplotlib.pyplot as plt # load data mcds = pyMCDS('output00003696.xml', '../output') # Set our z plane and get our substrate values along it z_val = 0.00 plane_oxy = mcds.get_concentrations('oxygen', z_slice=z_val) # Get the 2D mesh for contour plotting xx, yy = mcds.get_mesh() # We want to be able to control the number of contour levels so we # need to do a little set up num_levels = 21 min_conc = plane_oxy.min() max_conc = plane_oxy.max() my_levels = np.linspace(min_conc, max_conc, num_levels) # set up the figure area and add data layers fig, ax = plt.subplot() cs = ax.contourf(xx, yy, plane_oxy, levels=my_levels) ax.contour(xx, yy, plane_oxy, color='black', levels = my_levels, linewidths=0.5) # Now we need to add our color bar cbar1 = fig.colorbar(cs, shrink=0.75) cbar1.set_label('mmHg') # Let's put the time in to make these look nice ax.set_aspect('equal') ax.set_xlabel('x (micron)') ax.set_ylabel('y (micron)') ax.set_title('oxygen (mmHg) at t = {:.1f} {:s}, z = {:.2f} {:s}'.format( mcds.get_time(), mcds.data['metadata']['time_units'], z_val, mcds.data['metadata']['spatial_units']) plt.show()

Adding a cells layer

We can also use pandas to do fairly complex selections of cells to add to our plots. Below we use pandas and the previous plot to add a cells layer.

from pyMCDS import pyMCDS import numpy as np import matplotlib.pyplot as plt # load data mcds = pyMCDS('output00003696.xml', '../output') # Set our z plane and get our substrate values along it z_val = 0.00 plane_oxy = mcds.get_concentrations('oxygen', z_slice=z_val) # Get the 2D mesh for contour plotting xx, yy = mcds.get_mesh() # We want to be able to control the number of contour levels so we # need to do a little set up num_levels = 21 min_conc = plane_oxy.min() max_conc = plane_oxy.max() my_levels = np.linspace(min_conc, max_conc, num_levels) # get our cells data and figure out which cells are in the plane cell_df = mcds.get_cell_df() ds = mcds.get_mesh_spacing() inside_plane = (cell_df['position_z'] < z_val + ds) \ & (cell_df['position_z'] > z_val - ds) plane_cells = cell_df[inside_plane] # We're going to plot two types of cells and we want it to look nice colors = ['black', 'grey'] sizes = [20, 8] labels = ['Alive', 'Dead'] # set up the figure area and add data layers fig, ax = plt.subplot() cs = ax.contourf(xx, yy, plane_oxy, levels=my_levels) # plot the cells (its hacky I know, I'll fix it!) for i in range(len(colors)): if i == 0: plot_cells = plane_cells[plane_cells['cycle_model'] < 6] if i == 1: plot_cells = plane_cells[plane_cells['cycle_model'] > 6] ax.scatter(plot_cells['position_x'].values, plot_cells['position_y'].values, facecolor='none', edgecolors=colors[i], alpha=0.6, s=sizes[i], label=labels[i]) # Now we need to add our color bar cbar1 = fig.colorbar(cs, shrink=0.75) cbar1.set_label('mmHg') # Let's put the time in to make these look nice ax.set_aspect('equal') ax.set_xlabel('x (micron)') ax.set_ylabel('y (micron)') ax.set_title('oxygen (mmHg) at t = {:.1f} {:s}, z = {:.2f} {:s}'.format( mcds.get_time(), mcds.data['metadata']['time_units'], z_val, mcds.data['metadata']['spatial_units']) ax.legend(loc='upper right') plt.show()

Future Direction

The first extension of this project will be timeseries functionality. This will provide similar data loading functionality but for a time series of MultiCell Digital Snapshots instead of simply one point in time.

from MathCancer Blog https://ift.tt/2IjFSpw from Blogger https://ift.tt/31LvTRI

[cancersfakianakis1]

Secondary Neutron Dose from a Dynamic Collimation System During Intracranial Pencil Beam Scanning Proton Therapy: A Monte Carlo Investigation

Publication date: Available online 14 August 2018

Source: International Journal of Radiation Oncology*Biology*Physics

Author(s): Blake R. Smith, Daniel E. Hyer, Patrick M. Hill, Wesley S. Culberson

Abstract

Patients receiving pencil beam scanning (PBS) proton therapy with the addition of a Dynamic Collimation System (DCS) are potentially subject to additional neutron dose from interactions between the incident proton beam and the trimmer blades. This study investigates the secondary neutron dose rates for both single field uniform dose and intensity modulated proton therapy treatments. Secondary neutron dose distributions were calculated for both a dynamically collimated and uncollimated, dual-field chordoma treatment plan and compared to previously published neutron dose rates from other contemporary scanning treatment modalities. Monte Carlo N-Particle transport code was used to track all primary and secondary particles generated from nuclear reactions within the DCS during treatment through a model of the patient geometry acquired from the CT planning dataset. Secondary neutron ambient dose equivalent distributions were calculated throughout the patient using a meshgrid with a tally resolution equivalent to that of the treatment planning CT. The median healthy brain neutron ambient dose equivalent for a dynamically collimated intracranial chordoma treatment plan using a DCS was found to be 0.97 mSv/Gy, 1.37 mSv/Gy, and 1.24 mSv/Gy for the right lateral single field uniform dose (SFUD) field, apex SFUD field, and composite intensity modulated proton therapy distribution from two fields, respectively. This was at least 55 % lower than what has been reported for uniform scanning modalities with brass apertures but is still an increase in the excess relative risk of secondary cancer incidence compared to an uncollimated PBS treatment using only a graphite range shifter. Regardless, the secondary neutron dose expected from the DCS for these PBS proton therapy treatments appears to be on the order of, or below, what is expected for alternative collimated proton therapy techniques.

https://ift.tt/2KVPRQi