#linear equations in one variable class 8 formulas

[mathswithnarendrasir]

Class-8 Mathematics NCERT Solution Execrise 2.4 Question 3,4,5

[speedywonderlandtrash]

Class 9 math final preaparion for annual examination

Class 9 math final preaparion for annual examination

  Class 9 Math Final Exam Crash Course,Last-Minute Class 9 Math Exam Tips and Tricks,Quick Revision Guide for Class 9 Math Exam,Class 9 Math Syllabus Summary for Finals,Top 10 Tips for Scoring High in Class 9 Math, Final Hour Class 9 Math Exam Preparation,Class 9 Math Most Important Topics for Exam,Essential Class 9 Math Formulas for Finals,Class 9 Math Problem Solving Techniques for Exams,Class 9 Math Exam Day Preparation Checklist,Class 9 Math Final Preparation Tips,Last Minute Math Revision for Class 9,Class 9 Math Quick Revision Guide,Class 9 Math Exam Success Tips,Effective Study Plan for Class 9 Math Final,Math Exam Boosters for Class 9,Class 9 Math Formula Cheat Sheet,Quick Math Review for Class 9 Finals,Class 9 Math Last-Minute Practice, Class 9 Math Preparation Strategies   Mathematics Time: 3 hours                    Full Marks: 100 Section A: Objective (25 Marks) Multiple Choice Questions: Write the correct answer in your answer sheet                                                                                             1 × 15 = 15 1. Fibonacci was ---- (a) Mathematician (b) Statistician (c) Physicist (d) Chemist 2. What is the sum of n natural numbers? (a) (b) (c) (d) 3. If the general term of a sequence is , what is the second term? (a) (b) (c) (d) 4. The base of an exponent and the base of log are ----- i The same ii Equal iii Different Which of the following is correct? (a) i and ii (b) ii and iii (c) i and iii (d) i ii and iii 5. Under what condition is always positive for all values of n? (a) b > 0 (b) b (c) b = 0 (d) b ≠ 1 6. = Which of the following? (a) (b) (c) (d) 7. Which of the following points is located on the x-axis? (a) (2, 0) (b) (-3, 5) (c) (0, 3) (d) (-2, -2) 8. How many primary methods are there for solving linear equations with two variables? (a) 2 (b) 3 (c) 4 (d) 5 Based on the following information, answer questions 9 and 10:

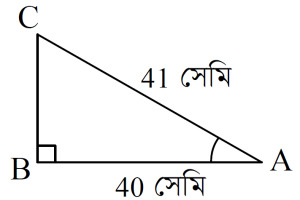
9. What is the length of BC? (a) 9 cm (b) 29 cm (c) 39 cm (d) 49 cm Class nine math for annual exam part 1 10. What is the value of sin ∠BAC? (a) (b) (c) (d) 11. If a right-angled triangle is formed with sides of 17 cm, 8 cm, and 15 cm, what will be the length of the hypotenuse? (a) 8 (b) 13 (c) 17 (d) 23 12. Which of the following distances do the hands of a wall clock traverse? (a) Linear distance (b) Perpendicular distance (c) Angular distance (d) Parallel distance 13. Dividing a complete rotation by 360 results in what kind of angular distance? (a) 1' (minute) (b) 10° (degree) (c) 1'' (second) (d) 1c (radian) 14. Mushfiq's runs in 10 matches are: 56, 30, 26, 37, 78, 65, 28, 48, 54, 16. What is the median of his runs? (a) 72.5 (b) 42.5 (c) 70 (d) 77.5 15. Last year's minimum temperature was 11°C, and the temperature range was 33°C. What was the maximum temperature last year? (a) 42°C (b) 32°C (c) 35°C (d) 44°C Answer in one word: 1 × 10 = 10 16. If the n-th term, = 1, what type of sequence is it? 17. What is the tenth term of the sequence 0, 1, 1, 2, 3, 5, ......? 18. Write the formula for . 19. In , what is the condition for a = b? 20. In a graph, what does each line of a linear equation represent? 21. In a right-angled triangle, the base and height are named with respect to what? 22. Which type of angle has an undefined measure? 23. In the standard position, what is the value of tan ( theta ) relative to the point (15, 0)? 24. What is the term for the difference between the central value and other data points? 25. How is the range of measurement represented? Section B: Short and Descriptive (75 Marks) 1. Answer the following questions:                                     2 × 13 = 26 (a) In an arithmetic sequence, if the fifth term is 16 and the ninth term is 28, find the first term and common difference. (b) For a sequence with the sum of the first n terms as n(n + 1), what is the sum of the first 10 terms? (c) Find the general term of the sequence , ... (d) If , find the value of ( x ). (e) Show that an earthquake measuring 8 on the Richter scale is 1000 times stronger than one measuring 5. (f) Verify the solvability of the equations x + y = p + q and . (g) Determine the nature of the roots of the equation and solve it. (g) is a right-angled triangle with , cm, cm, and . Find the value of . (h) What is the value of ? (i) Express in radians. (j) Express the point in terms of . (k) Find the range of the data set . (l) If the arithmetic mean of the data series is , find the mean deviation. 2. Observe the following sequences: (i) 1 − 3 + 9 − 27 + ..... and (ii) 54 + 18 + 6 + ... + (a) Find the sum of the first 7 terms of sequence (i). 3 (b) Find the sum of sequence (ii). 4 3. Anika and Mim are two sisters. Their parents decide to give them pocket money for 10 days using two different methods. On the first day, both Anika and Mim receive 2 taka each. Anika receives double the previous day’s amount each day, while Mim receives 2 taka more than the previous day. (a) Determine who receives more pocket money on the fifth day, Anika or Mim. 3 (b) Verify whether Anika receives 18 times more total pocket money than Mim over the first 10 days. 4 4. and (a) If , find the value of . 3 (b) If , what is the value of ? 4 5. The intensity of sound emitted from a motorcycle is W per square meter. An autorickshaw emits 60 decibels of sound, and a rickshaw emits 50 decibels of sound. (a) How many decibels of sound are emitted from the motorcycle? 2 (b) What is the intensity of sound emitted per square meter from the autorickshaw? 2 (c) Compare the sound intensity between the autorickshaw and the rickshaw. 3 6. Kona bought 5 guava saplings and 4 lemon saplings for 410 taka at a tree fair. Raju bought 4 guava saplings and 5 lemon saplings at the same rate for 400 taka. The price of each lemon sapling is 10 taka less than each guava sapling. (a) Form a system of equations based on the given information. 1 (b) Solve the system of equations obtained in (a) using the cross-multiplication method. 3 (c) Solve the system of equations obtained in (a) using the elimination method. 3 7. A fruit seller bought mangoes at 20 taka each and bananas at 10 taka each, spending a total of 1000 taka. He sold each mango and banana at a profit of 2 taka, making a total profit of 120 taka. (a) Form two equations based on the information provided. 3 (b) How many mangoes and bananas did the fruit seller buy? 4 8. A student was standing at point P in front of a tower. The angle of elevation to the top of the tower from point P is 30°. Moving 50 meters closer to the tower to point Q, the angle of elevation becomes 45°. (a) Represent the information with a diagram. 3 (b) Find the height of the tower. 4 9. Noyon went on a trip with his family from Dhaka to Cox’s Bazar in their own car. The radius of their car’s wheels is 0.6 meters, and the radius of the Earth is 6440 km. (a) If Dhaka and Cox’s Bazar subtend an angle of 20° at the Earth’s center, find the distance between them. 3 (b) How many rotations will the car's wheels make to cover the total distance from Dhaka to Cox’s Bazar? 4 10. Shakib’s runs in eight matches are as follows: 72, 55, 100, 67, 82, 40, 76, 80 (a) Calculate Shakib’s average runs. 2 (b) Show that Shakib’s median runs are higher than his average runs. 2 (c) Find the mean deviation from the median. 11. The run data of two batsmen over 6 matches is as follows: Tamim's runs 45 75 100 25 65 55 Soumya's runs 102 20 85 35 10 35   (a) Calculate the range of runs for both batsmen. 2 (b) Find the mean, median, and mode of Tamim's runs. 2 (c) Calculate the mean deviation from the mean, median, and mode for Tamim's runs. 3   Read the full article

[cbsesamplepapersblog]

CBSE Class 10 Syllabus has been designed to help students gain a deeper understanding of the subject matter.

[ss1986us]

ncert solutions for class 8 maths

NCERT Solutions for class 8 Maths

in case if you are looking for accurate, comprehensive and free ncert solutions for class 8 maths then you are at very right place. These ncert solutions for class 8 maths are available in the PDF format, which can be easily shared and accessed among friends. The diligent efforts of faculties at Entrancei have made sure the best of all solutions are available for students.

In order to make the learning process very easy, the students need to just go throw the study material. These ncert solutions for class 8 maths are the best tool for a quick revision of your concepts. The complete syllabus has been broke down into various parts in the manner of chapters. Students need to just sign up at Entracei. The categorization of chapters is made below

Ø  Chapter 1: Rational Number

This chapter of ncert solutions for class 8 maths helps the students with giving them a deep understanding of number system and rational numbers.

Ø  Chapter2: Linear Equations in One Variable

This chapter of ncert solutions for class 8 maths helps the students in getting acquainted with the method of solving contextual problems based upon linear equations

Ø  Chapter 3: Understanding Quadrilaterals

This chapter of ncert solutions for class 8 maths helps the students with knowledge of angles and their sum. This chapter helps the students with convex, concave and parallelograms.

Ø  Chapter 4: Practical Geometry

This chapter of ncert solutions for class 8 maths helps the students with enhancing their knowledge regarding rhombus, parallelograms, squares, and rectangles.

Ø  Chapter 5: Data Handling

This chapter enhances students’ knowledge with the method of representing data in the form of bar graphs and charts.

Ø  Chapter 6: Square and Square roots

This chapter of ncert solutions for class 8 maths teaches the students in solving critical square roots through factor method and division method

Ø  Chapter 7: Cube and Cube roots

This method presents a stepwise representation of methods to determine cube roots.

Ø  Chapter 8: Comparing Quantities

This chapter of ncert solutions for class 8 maths helps the students with unit quantities like percentage, ratio, sales tax, and compound interests.

Ø  Chapter 9: Algebraic expressions and Identities

This chapter of ncert solutions for class 8 maths helps the students in solving algebraic expression with addition, subtraction, division, and multiplication.

Ø  Chapter 10: Visualising solid shapes

This chapter of ncert solutions for class 8 maths helps the students regarding 3D objects and their plotting on map.

Ø  Chapter 11: Mensuration

This chapter of ncert solutions for class 8 maths helps the students in determining areas of polygon and trapezium.

Ø  Chapter 12: Exponents and powers

This chapter of ncert solutions for class 8 maths helps the students regarding the integers in the number system.

Ø  Chapter 13: Direct and Inverse Proportions

This chapter of ncert solutions for class 8 maths helps the students regarding the variation which is direct and in-direct quantities in NCERT book.

Ø  Chapter 14: Factorization

This chapter helps the students in enhancing their concepts associated with algebraic identities and factorization.

Ø  Chapter 15: Introduction to Graphs

This chapter of ncert solutions for class 8 maths helps the students reading numbers, perimeters, and length of square graphs.

Ø  Chapter 16: Playing with numbers

This chapter of ncert solutions for class 8 maths is more of like a fun game where students need to plot 2 digits and 3 digit number from the puzzles.

 Why ncert solutions for class 8 maths at Entancei

Ø  Since maths has been crucial in building strong foundation, we make sure you get the best of all.

Ø  The ncert solutions for class 8 maths are up-to-date and as per the latest NCERT regulations

Ø  The expert provided ncert solutions for class 8 maths is sufficient to score great marks in Examination

Ø  While solving the NCERT class 8 maths the most important think you required is maths formula. Check out all maths formula in one page

[iamsharma]

Get all formulas related to linear education in one variable for class 8 with notes and practice exercise questions and solved answers with updates on 2022-2023.

[entrancei0012]

class 9 maths

The class 9 maths study material is available in PDF format which can be easily downloaded from our site. One can also access a very specific and examination focused strategy for class 9 maths by just simple signup at Entrancei. The sole idea has been to create a most accurate and detailed solution for class 9 maths that is free of cost. The experienced teachers at Entrancei have very extensively revealed the complete class 9 maths content. They have completely made sure all that is provided is important with respect to examinations. The class 9 maths solutions can be easily utilized for scoring good marks as one can reliably practice form them.

All the class 9 maths notes prepared as per the guidelines of CBSE Syllabus and guidelines. One can also go through test services for class 9 maths as it will help in gauging out the overall progress. The choosing union the class 9 maths optimum solutions helps in acing the students with the atmosphere of examination.

As general pattern, the class 9 maths should be taken very seriously as it helps in building strong concepts for further boards in 10th. The completecategorization of the syllabus of class 9 maths has been done in chapters, which helps students to easily go through it.

Ø  Chapter 1: Number systems

This chapter throws light upon number lines and how effectively they can be used. The class 9 maths solutions provided helps the students regarding laws of integral and rational powers of real numbers.

Ø  Chapter 2: Polynomials

The class 9 maths solutions to this unit give a vivid explanation about polynomials and their detailed terminologies. One will be acknowledged with various types of polynomials such as linear, Constant, quadratic and cubic polynomials.

Ø  Chapter 3: Coordinate Geometry

This chapters in class 9 maths help the students in understanding the concepts of Cartesian place and coordinates.

Ø  Chapter 4: Linear Equations in two Variables

This chapter in class 9 maths helps the students in understanding the equations presented in two variables. Plotting the equations on graph has been explained in a very detailed format in class 9 maths solutions provided.

Ø  Chapter 5: Introduction to Euclid’s Geometry

This chapter of class 9 maths throws minor lights upon how Indian history is associated with Geometry followed in the world. One will be explained regarding the geometry through axiom, Postulates, and Theorems of class 9 maths in detailed format.

Ø  Chapter 6: Lines and Angles

The chapter as lines and angles is generally asked as theorems and postulates in class 9 mathsexaminations. The level of difficulty is very minor compared to other units.

Ø  Chapter 7: Triangles

In this chapter of class 9 maths, you will study regarding the congruence of triangles and their associating theorems. This chapter of class 9 maths has various properties such as inequalities and properties in triangles.

Ø  Chapter 8: Quadrilaterals

This chapter of class 9 maths comprises of only one theorem as proof. Questions asked in this chapter are relatively very easy.

Ø  Chapter 9: Areas of Parallelograms and Triangles

One will be brought to the note of areas in geometrical shapes. The examples of the median can be used in various examples of this in class 9 maths of chapter.

Ø  Chapter 10: Circles

This chapter of class 9 maths gives brief insights about subtended angle chord, equal chords, Arc of the circle, cyclic quadrilaterals. This detailed solution of theorems based on triangles, Quadrilaterals, and circles are based in this chapter.

Ø  Chapter 11: Constructions

This chapter throws light upon bisecting and creating line segments to angles and lines. The student’sclass 9 maths would be learning the creation of triangles with different properties and different base angles.

Ø  Chapter 12: Heron’s formula

This chapter of class 9 maths comprises of only three exercises. This chapter givesan extension to the application of heron’s formula in polygons and quadrilaterals and triangles.

Ø  Chapter 13: Surfaces Areas and Volumes

The students need not be introduced with this topic as they well studied the mensuration in their earlier classes. One would be acknowledged with volumes of cubes, cylinders, spheres, cones, and the hemisphere’s in their class 9 maths syllabus.

Ø  Chapter 14: Statistics

The statistics chapter of class 9 maths is like a simple method of collection of data in different aspects. In total, this chapter of class 9 maths helps one to find the measure of central tendency, mean, median and mode of any raw data provided.

Ø  Chapter 15: Probability

With only about 1 exercise in class 9 maths, this chapter is very easy. This is based on observation and frequency of day to day examples.

 Why choose Entrancei

 There might be times when students are stuck with exercises, so there comes the team of Entrancei with an innovative solution to class 9 maths students. The students can any time give a call in order to get their doubts resolved associated with class 9 maths.

[biomedgrid]

Biomed Grid | Comparative Osteology: A Cross-Species Study of First Rib Parameters and Their Relation to Body Mass with Emphasis on the Woolly Mammoth

Introduction

Scaling addresses the structural and functional consequences of changes in size or scale among otherwise similar organisms. In terms of biology, one finds non-isometric scaling, often referred to as allometric which has its roots in the Greek term alloios meaning different. Indeed an amazing number of morphological and physiological variables can be scaled, relative to body size, according to the general allometric equation; y = a × Xb [1]. To the best of the authors knowledge, Galileo Galilei in his volume Dialogues Concerning Two New Sciences (1637) was the first to postulate that the skeleton and bones of very large animals must be scaled out of proportion to their linear dimensions in order to support the weight of the animal, and that the weight increases with the third power of linear dimensions. Logically, then if one assumes the legs of large animals simply serve as supportive “load bearing” columns, then it would be safe to assume that the greater the diameter of the said column, the greater the load it should be capable of bearing. However, one reaches a natural limit, as quite clearly the mass of an animal’s skeleton cannot increase out of proportion with body mass, at least not to the extent that the whole leg is comprised bone.

In a very recent study [2] it was shown that body height of an extinct species, namely the Woolly Mammoth (Mammuthus primigenius), could be derived from fossil remains, collected from the Flemish valley, according to the following formula; skeletal height = 4.35 * greater length of tibia (cm) + 12.7 cm [3]. Shoulder height was then estimated by adding a further 15 cm to the skeletal height to account for subcutaneous tissue and skin thickness [5]. Finally, the body mass of Woolly Mammoths was estimated using regression equations based on African elephants derived by Laws et al. [4], who computed from Ugandan elephant bulls that body mass (kg) 5.07×10−4 * SH2.803 where SH is shoulder height in centimeters. However, the findings of Christiansen [5] reveal a considerable degree of variation in terms of predicted body mass depending on which bone parameters and formulas are adopted as being the most suitable. For instance, tibia parameters recorded for the Hebior Mammoth (Mammuthus primigenius) which has a recorded shoulder height of 318 cm, estimated from its skeletal fossil remains, produced a body mass estimate that ranged from 4728 to 6852 kg [5].

Indeed, suggestions that Woolly Mammoths could have weighed as much as 8000 to 10000 kg or more, based on predictions from single limb bones have been made for the Brussels Museum and the Field Museum of Natural History in Chicago [5]. Interestingly, the heavier body masses are often associated with equations [5] that are applied to the humerus and femur bones rather than calculations that take their starting point from tibia measurements. Finally, there is an estimate of the body mass of Woolly Mammoth remains based on measurements of shoulder height [6], without making it at all clear as to what equations or constants have been adopted. Since oxygen consumption by body tissues must logically be related to body weight and since both the total number of alveoli in the lung as well as the total exchange surface are likely to be related to oxygen consumption, it is predictable that alveolar surface area should be related to body weight, which is indeed the case [7]. Furthermore, continuing this line of reasoning, the lung volume of a mammal constitutes approximately 5% of the body volume, irrespective of body size.

If a plot of lung volume (VL) in liters (dm3) is made against body mass (Mb) in kilograms a regression line with a slope of 1.06 is found, which represents a slight deviation from strict proportionality since larger animals tend to have proportionately larger lung volumes than smaller animals (thus 0.046 1.06 L b V = xM ) [8]. Furthermore, a test as to whether mass-specific pulmonary diffusion capacity for 02 ( o2 DL ) is proportional to mass-specific oxygen consumption o2 V , in such species as the horse and cow of body mass ~ 500 kg has already been investigated [9,10]. Indeed when one makes such a comparison it appears that, within a given size class (e.g. small, medium, large), o2 DL is closely matched to o2 V . Continuing with this comparative approach, it has also been consistently found that, over the size range of mammals ( 2 g < Mb < 1000 kg ), O2std V scales with 0.75 b M [8]. Indeed in support of which, Cook et al. [11] found that in terms of respiratory parameters, functional residual capacity was closely related over a range of body sizes to the height of a subject, raised to the power of 2.86.

In the light of the recent use of limb bones to predict body mass [12], and other studies with often wide ranging values, and sometimes apparently excessive estimates, this study has sought;

i. to establish whether parameters associated with the first rib, which helps define the shape of an animals rib-cage, can be closely related to body mass, and

ii. to investigate whether such a correlation might not be a better predictor of body mass than predictions of skeletal height based on limb bone (tibia) parameters.

Material and Methods

Measurements of first rib parameters (greater length – GL representing the outer curvature of the rib, lesser length – LL representing the inner curvature of the rib, medial circumference - MC) were taken from the skeletons of a number of species housed in the Dept. of Animal and Veterinary Basic Sciences, or made available to the author through the kind assistance of Copenhagen Zoo, Scandinavian Animal Park Djursland, and Oxford University Museum. Thereafter, skeletal (shoulder) height and body mass were either measured or recorded from notes kept about the specimens. In total, nine species were measured, including a lion, a cow, a goat, a giraffe, a horse, a female human, a rhinoceros and an Asian elephant. Measurements were taken by hand with care being made to avoid excessive handling of museum specimens, yet at the same time ensuring that accurate recordings were taken. The greater and lesser lengths of the ribs were used to arrive at a medial bone length, and it was at this derived mid-point along the length of the bone that the measurement of medial circumference was taken. Any remaining fossilized cartilage was not included in the greater and lesser length measurements. A similar procedure was then followed for the measurements of tibial length and its medial circumference, where these measurements were possible.

The measurement of skeletal height was taken from the spine at the region between the shoulder blades, for most of the mammals measured, however, in the case of the female human skeleton, the height was taken as being the distance between the base of the heel and the crown of the skull. The collected 1st rib measurements, when plotted, were found to best fit a polynomial (first order; see below) equation where rib parameters GL, LL and MC (cm) were related to the intercept plus the slope times the body weight (kg).

Equation 0: Polynomial first order (linear )Y = Intercept + Slope* X

Data were plotted using Prism 4 for Macintosh (version 4.0b, 2004), and the same software was used to analyze the curve of the plot as well as determine any significance with regard to the fitted equation.

Bone Mineral Density & Bone Mineral Content

A total of 4 Mammoth bones and the identical bones from an adult Indian Elephant were measured for their bone mass density - BMD (g/cm2) and bone mineral content -BMC (g) using a DEXA scanner with both the Total body scan program for the larger bones (tibia, rib, lumbar vertebra), and the Small animal program for the phalanges (GE Luna Prodigy, Madison WI, USA, encore 2005 software, version 9,15,010).

Statistical tests

Values are presented as means ± SEM. Differences between means were tested for statistical significance with the use of a oneway ANOVA and an additional test for Gaussian Normal Distribution (GraphPad Instat 3 for Mac; Version 3.0b, 2003; Graph- Pad Inc., La Jolla, CA). Data were found to be normally distributed and to have equal variance. Differences showing a P value >0.05 were considered non-significant.

ResultsCorrelation of rib parameters with body mass

The measurements of Greater Length (GL) for the first rib of the species examined were found to be best fitted by the following equation;

Equation 1: GL (cm) = 8.53+ 0.02236*Body Mass (kg )

The measurements of Lesser Length (LL) for the first rib of the species examined were found to be best fitted the following equation;

Equation 2: LL (cm) = 7.48 + 0.01265*Body Mass (kg )

Finally, the measurements of Medial Circumference (MC) for the first rib of the species examined was found to be best fitted the following equation (See Figure 1);

Figure 1:First rib - medial circumference parameter (Log2) measurements versus body mass (Log2): a cross-species correlation. The best fit equation derived from the recorded data is given, as is the best fit curve – small red dots joined by a faint dotted line. See the results section for equations. The 95% confidence interval for the slope was found to be between 0.00335 and 0.00483 (mean = 0.00409 ± 0.00034). The fit of the curve was found to be significant P<0.0001 with 14 df.

Equation 3: MC (cm) = 3.00 + 0.00409*Body Mass (kg )

A goodness of fit test revealed an R2 of 0.83, 0.69 and 0.94 (all with 14 degrees of freedom), for equations 1, 2 & 3, respectively (Figure 1).

First rib and tibia measurements for Woolly Mammoth fossilized specimens

Of the two fossilized first ribs and tibia specimens accessible to the author, only one of the tibia bones was from a fully grown adult, the other bones were from juvenile Woolly Mammoths, judging by the lack of cartilage at the bone ends. The first ribs were found to have the following parameters; GL = 46.0 cm, LL = 45.5 cm, MC = 11.3 cm, and GL = 50.5 cm, LL = 48.5 cm, MC = 14.0 cm. Measurements for the two fossilized Woolly Mammoth tibia bones were as follows; GL = 54.5 cm, MC = 26.5 cm and GL = 68.5 cm, MC = 35.0 cm. Thus, using Equation 3 and the MC measurements for the first ribs of the two Woolly Mammoths, it was possible to arrive at an estimate of average body mass for the two extinct animals. For the smaller of the two fossilized Woolly Mammoth first ribs an estimated body mass of 2029 kg was calculated (MC = 11.3 cm). Similar measurements for the second of the two fossilized Woolly Mammoth first ribs gave an estimated body mass of 2689 kg (MC = 14.0 cm).

Tibia parameters as an estimate of body mass

In order to assess the often used tibia-length-based equation for skeletal height (Equation 4), and body mass (Equation 5), subsequently derived from skeletal height, this study chose to examine a number of large species, of known body mass, among them the Asian elephant Coco, which had lived for many years at Copenhagen Zoo (born 22-01-1986 and died 21-09-2003).

Equation 4: Skeletal Height = 4.35*Tibia Length(cm) +12.7cm

Equation 5: Body Mass (kg ) = 5.07x10−4 *Skeletal Height2.803

Table 1: A cross-species comparison of tibia-length-based predictions of skeletal height and body mass cf actual body mass. For details regarding equations 4 and 5 see results section.

Note: () = percentage of actual body mass, [] = measured skeletal height.

The Asian elephant Coco had a tibia length of 59.0 cm with a medial circumference of 24.5 cm (diameter = 7.8 cm) and represented a mature adult male with a body mass of 3646 kg. Thus using the equation of Germonpré et al. (Equation 4) [2] a skeletal height of 269 cm, cf. an actual value of 259 cm, was predicted, and using this value in the equation of Laws et al. (Equation 5) [4] it was possible to arrive at a predicted body mass of 3277 kg, which was some 369 kg lighter than the actual animal. Thus, the methodology of estimating skeletal height from tibia length, followed by the use of the derived skeletal height value to predict body mass proved to be 89% accurate in this instance. It should be noted that in a recent study, the ratio of tibia length to predicted skeletal shoulder height was found to be 23.2% for Mammuthus primigenius, and in this study we arrived at a value of 21.7%, which is in close agreement [13] (Table 1).

Using equations 4 & 5, which appear to be 89% accurate for modern day Proboscidae of the Elephas (Eurasian elephant) genus, one might be able to derive some estimate of body mass when taking into account a fossilized Mammoth tibia with a length of 68.5 cm and a medial circumference of 35.0 cm (diameter = 11.1 cm). Indeed, equation 4 predicts a skeletal height of 310 cm, and equation 5 subsequently returns a predicted body mass of 4878 kg for the Woolly Mammoth (Mammuthus primigenius) whilst alive.

Alternatively, the following equation;

Equation 6: L * d2 = Mb

has been used to estimate body mass (Mb), taking into account not only bone length (L in cm) but also its weight bearing properties as represented by its diameter (d in cm). Using equation 6 one derives a body mass for a 59.0 cm long and 7.8 cm diameter tibia from Coco the Asian elephant at Copenhagen Zoo of 3589 kg, which in this instance proves to be 98% accurate. Likewise, the use of equation 6 derives a body mass for a 59.0 cm long and 6.7 cm diameter tibia from the Giraffe of 2648 kg, which represents 296% of the actual body mass (892 kg). However, when one turns to the Rhino, and applies equation 6 for a 38.0 cm long and 7.1 cm diameter tibia, a body mass of 1915 kg is predicted, which compares favourably (103%) with the actual body mass (1859 kg) for this animal.

Figure 2:Tibia – Woolly Mammoth fossil. This tibia is from an adult male and was found, caught in fishing nets, in the North Sea just off the Dutch coast. The length and medial circumference sites are identified by the white arrows, whilst the red dotted lines represent the region of fossilized cartilage which were not included in the overall length measurement. The scale bar represents 50 cm. Bone Mineral Density images are courtesy of Prof. Klaus Ølgaard & colleagues, Rigshospitalet, Dept of Nephrology and Endocrinaology, Blegdamsvej 9, Copenhagen DK 2100 Ø, and were made using a Norland DEXA scanner. Authors private collection.

Finally, returning to the fossilized Woolly Mammoth tibia with a length of 68.5 cm and a medial circumference of 35.0 cm (diameter = 11.1 cm), and using the alternative equation (Equation 6) of which seems to be a fairly accurate predictor of body mass in the Asian elephant Coco, a body mass for the Woolly Mammoth of 8500 kg is then derived (Figure 2).

In order to further validate these equations, the authors took measurements from the first ribs and tibia of an almost complete Woolly Mammoth skeleton at the Scandinavian Animal Park outside Kolind, Denmark. This specimen, known affectionately as “Manse” appears to be of a juvenile, with a skeletal height of 260 cm. Using equation 4 and a measured tibia length of 50.0 cm, a skeletal height of 230 cm was derived for “Manse”, representing 88.4 % of the actual measured skeletal height. Continued use of the estimated 230 cm skeletal height in equation 5 yielded a body mass of 2118 kg, whilst use of the actual 260 cm skeletal height gave a value of 2979 kg. However, use of the first rib measurements from “Manse” (MC = 16.0 cm) and equation 3, predicted a body mass of 3178 kg. The combined use of tibia length and diameter (50.0 and 8.4 cm, respectively) in equation 6 estimated a body mass for “Manse” of 3528 kg.

In contrast, measurements taken from a wild adult male African elephant to be found at Oxford University Museum of Natural History, gave a tibia length of 66.0 cm and a diameter of 9.7 cm, a first rib medial circumference of 16.5 cm and a skeletal height of 287 cm. Using equation 4 a skeletal height of 299 cm was derived for the Oxford African elephant representing 104.0 % of the actual measured skeletal height. Continued use of the estimated 299 cm skeletal height in equation 5 yielded a body mass of 4408 kg. However, use of the first rib measurements (MC = 16.5 cm) and equation 3, predicted a body mass of 3300 kg. Finally, the combined use of tibia length and diameter (66.0 and 9.7 cm, respectively) in equation 6 estimated a body mass for the Oxford African elephant of 6209 kg.

Bone Mineral Density

The BMD and BMC values for the selected Mammoth and Elephant bones measured in this study are to be found in Table 2. Whilst these have been measured as accurately as possible, the fact remains that the BMC, in particular for the first rib, may be an underestimate of the true value due to leaching of minerals to the North Sea. Moreover, this explanation would fit with the findings of a higher BMC in the vertebrae and phalanges of the Woolly Mammoth cf values obtained for the Asian Elephant (Table 2).

Table 2:A comparison of the BMD and BMC measurements of selected Woolly Mammoth and Asian Elephant bones. For details see the material & methods section.

Values marked with a * represent measurements taken from bones collected from the North Sea.

Discussion

The results of this study clearly show a good correlation between the medial circumference (cm) of the first rib of the mammals measured and that of their body mass. This novel scaling equation provides an additional tool for those working with comparative aspects of biology and physiology, for those involved in the assessment of museum specimens and fossil remains, as well as those working in the field of forensic science all of which, from time-to-time, assess incomplete skeletons in terms of predicting an individual´s height whilst alive. Moreover, to the authors knowledge, this is the first time that an equation based on respiratory-linked parameters has been used to assess the body mass of Woolly Mammoths.

Scaling issues

The issue of scalability in animals is a very fascinating topic, and one that is grounded in a wish to compare animal size at the level of common denominators. There are a great many papers that address this topic and nearly as many equations. Indeed in addition to those equations mentioned so far, one should also mention the work done in the 1970´s by McMahon, who showed that for any supporting bone, the diameter (d) scaled with the 3/8th power of the body mass (Mb), and the length (l) scaled with 1/4th the body mass [14]. However, it is important that one should also consider scaling in terms of elasticity, that is to say the properties a bone has to withstand bending forces. It is the property of elasticity that enables a bone to maintain its shape without distortion arising from an imposed and often very sudden stress or load. Failure to maintain such an elastic property results of course in buckling and fracturing. Thus the critical variables that need to be considered are not only the length and diameter of a given bone (column), but also the elastic modulus of the material used. This being said, it is known though that bones of different animals have the same material composition, crystalline calcium apatite embedded in a matrix of collagen, and that surprisingly, measurements of failure stress in bones of mammals ranging from 50 g to 700 kg body weight (a 14,000-fold range) have very similar values; 233 ± 53 MN/m2 – small versus 200 ± 28 MN/m2 – large animals [15]. The BMD measurements show the lowest values 1.9 g/cm2 for the rib, and the highest values 8.2 g/cm2 for the vertebra, with the tibia ranging 6.2 to 7.1 g/cm2.

The body mass of elephants has been shown to be much less than the estimated weights of adult Wooly Mammoths [16], which may be possible to see from not only their skeletal dimensions, but perhaps also their bone structure, in particular their BMD. This study has shown that a BMD comparison of the first rib are very similar for both elephants and Woolly Mammoths (1.45 versus 1.54 g/cm2), however, this is not true of the other bones looked at. The tibia, lumbar vertebra and the phalanges of the Woolly Mammoth were all found to have a higher BMD than those of the elephant. The BMC values are far from conclusive. The Mammoth rib has a much lower value than the elephant, perhaps due to leaching of minerals to sea water, as this sample was found in the North Sea. In contrast the tibias have a very similar BMC, despite the Mammoth samples also being sourced from the North Sea, although they may have been less exposed than the rib, perhaps covered with silt. Then there are the BMC values for the lumbar vertebra and the phalanges, both of which are higher in the Mammoth compared with the elephant, perhaps lending weight to the greater body mass of Mammoths cf Elephants?

Perhaps of greater relevance in terms of this study, is the finding that body mass can be scaled to the medial circumference of the first rib of a number of animals. This is perhaps not so surprising since lung tissue represents allometrically 1.13 0.01 b M − of body mass [17]. Thus when one plots the log of lung volume for small and large animals alike against the log of body weight, one finds that a straight-line correlation is achieved, with a regression line slope of 1.02. Put another way, mammalian lung volume (Vl in ml) relates to body mass (Mb in kg) in the following way; 53.5 1.06 0.02 l b V = M ± [18] (Figure 3).

Figure 3: First rib – Upper Panel: a comparison of an isolated Woolly Mammoth first rib alongside a complete and single Mammoth skeleton to be found on display at the Scandinavian Animal Park (Djursland, Nødager, Kolind, Denmark) – inset panel shows the two first ribs alongside one another. Note how similar they are in size and length. Lower Panel: a comparison of an isolated Woolly Mammoth first rib alongside the complete skeleton of the Asian Elephant Coco to be found on display in Copenhagen Zoo (Denmark) – inset panel shows the Elephant and Mammoth ribs alongside one another.

Appropriate body mass equations

The issue still remains, however, as to which equation should one choose when attempting to predict body mass? Whilst this study has introduced a new equation based on the medial circumference of the first rib and shown that this can serve as a good predictor of body mass in a number of species, an attempt has also been made to validate existing body mass predictors. To this end an assessment of tibia length as an estimator of skeletal height has been investigated, and the accuracy of this two-tier system, employing an equation to estimate skeletal height, followed by a second equation using the estimated skeletal height to finally predict body mass, has been made. This study has found that this two-tier equation system works very well for elephants, but then this system was derived using elephant data, so this is perhaps not so surprising. When equations 4 and 5 are applied to giraffe and rhinoceros tibia data, the accuracy of the body mass prediction is less than ideal; gross over estimation for the giraffe compared with 50% underestimation for the rhinoceros. Clearly, then this two-tier system appears to be more or less species specific, which begs the question as to whether it is suitable for assessing the body mass of Woolly Mammoths?

In defence of the two-tier system, one has to acknowledge that equation 4 proved an accurate predictor of the skeletal height of the African and Asian elephants on display at Oxford University Museum of Natural History, which is interesting as the African elephant was captured from the wild. It is also worth noting that equation 4 serves as a very accurate predictor of skeletal height for “Manse” the adolescent Woolly Mammoth skeleton on display at the Scandinavian Animal Park, Djursland. The combined use of not only bone length but that of bone diameter in equation 6, does seem to improve the accuracy of body mass prediction. In the case of “Coco” the Asian elephant skeleton on display at Copenhagen Zoo, equation 6 improved body mass prediction from 89% to 98%. This equation also proved a very accurate predictor of body mass in the rhinoceros, taking the 55% body mass prediction of equations 4 & 5 to a103% accuracy. Of particular interest, however, is the fact that equation 6, whilst an improvement on the prediction made by equations 4 & 5, still grossly overestimated the body mass of the giraffe (296%). Perhaps then equation 6 is only accurate as a predictor of body mass in so long as the animal in question is rather robust, compact and solid in structure?

Finally, validation of the aforementioned equations in terms of fossilized remains, and in particular the skeletal height and body mass predictions for Woolly mammoths, continues to provide mixed results. In the case of “Manse” the Woolly Mammoth skeleton on display at the Scandinavian Animal Park, Djursland, equation 4 was able to predict skeletal height with a degree of accuracy equivalent to 88%, and equation 5 predicted a live body mass of 2979 kg. When equation 3 was used to predict body mass based on first rib medial circumference, a body mass of 3178 kg was arrived at. However, use of equation 6, which has proved the most accurate assessor of body mass in both the elephant and rhinoceros, derived a predicted live body mass of 3528 kg for this adolescent Woolly Mammoth. This final value is interesting as it equates to the final adult body mass of a male Asian elephant, and perhaps implies that Woolly Mammoths were appreciably heavier than modern day elephants. Indeed, this thought is supported by the body mass prediction arrived at when equation 6 is used on the fossilized tibia measurements of what must have been a large adult Woolly Mammoth; some 8500 kg, which is considerably heavier than the body mass predicted for the large adult African elephant on display at Oxford University Museum of Natural history; 6209 kg. Sadly the accuracy of later prediction cannot be confirmed as no records remain of the body mass of this particular specimen. However, the value of 8500 kg is in very close agreement with the recent estimates of Woolly Mammoth body mass derived at using volumetric methods (8241 kg) [13]. What can be concluded, however, is that body mass prediction varies greatly with the type of equation selected and appears also to be speciesspecific in the case of some often used equations. In this study, the most accurate predictor of body mass was found to be equation 6, which combined both length and diameter parameters of the bone.

Concluding Issues

This study, which is the first to explore the relation between first rib parameters and body mass has important implications for furthering our understanding of basic biology, physiology and scaling, as well as potential applications in terms of estimating the body mass of extinct species as well as in the field of forensic science.

Acknowledgments

The authors are indebted to Birgitte Holle, Lennart Engberg Carlsen, Vibeke Bøgelund Hansen, Jan Henrik Woller and Dr Jan Odderskov Martin, Faculty of Health & Medical Sciences, Copenhagen University, for their kind help and assistance with the specimens, and very grateful to the staff of Copenhagen Zoo for allowing access to the rhinoceros and elephant skeletons in their possession, as well as the owner, Dr Frank Vigh Larsen, of the Scandinavian Animal Park, Djursland for granting access to ”Manse” their Woolly Mammoth skeleton. The authors also wish to thank Kole Carter and North Sea Fossils for supplying the Woolly Mammoth first rib and tibia fossils, respectively. Finally, thanks are due to Dr Malgosia Nowak-Kemp, Vertebrate Collection Manager, Oxford University Museum of Natural History for facilitating measurements of the Asian and African Elephants in the collection.

Read More About this Article:

For more about: Journals on Biomedical Science :Biomed Grid

[davetutsacademy-blog]

2019 FURTHER MATHEMATICS EXAM PREP

This is the Exam Prep for your Further Mathematics Examination. We will work through one of the past questions from WAEC as we prepare you for academic excellence in your exam.

Going all the Way with you

We will work through the detailed solution to the Theory Paper of WAEC WASSCE GCE 2018 Exam in a bid to prepare you ahead of your Exams.

As an advocate for academic excellence, what I will like you to do is to first attempt the question on your own. Don't be afraid of making mistakes. You learn by trying, by failing, and then by success. Only check the solution presented here after you have made a judicious attempt on each question.Remember that there is no "singular right way" to go about solving the questions. Just check for consistency in the rules and formulae and guidelines as you work along.

The video link to the solutions are included and if you feel you need further explanations, simply check out the video to enhance your study. But make sure you attempt the question first. For this reason, the blog is broken such that you have to “READ MORE” to see the solution to the question attempted.

Who we are

At Davetuts Academy, we explores the STEM subjects with the aim of preparing students for academic excellence in their O' Level, A'Levels, JAMB UTME, POST-UTME, GED, GCSE and IGCSE exams. We feature comprehensive solution to examination past questions as we explore the basics of the STEM subjects and utilize appropriate soft tools with tips and tricks to prepare students for academic excellence.

Have a look at our welcome video below:

If by any means you find this exam prep useful, then go ahead and share and subscribe to our YouTube channel, Davetuts Academy as we aim at building academic excellence together!

So here we go with the Exam Prep for Further Mathematics. All the best with the questions!

A Question on Surd

So first, question 1 from WAEC WASSCE 2018 Further Mathematics Exam:

This is a question on surd operations and you just need to follow the correct steps in evaluating multiplication of surds and then finding the conjugate as appropriate.

The solution is shown below and you can watch the accompanying video for better understanding on how to solve such questions.

Watch the video solution by clicking here.

Evaluating the Upper Limit of a Definite Integral

Question 2 below is a question on definite integral. Go ahead and lay your hands on it.

All you have to do to solve this question is to integrate with respect to x, substitute for the upper and lower limit, and subtract the lower limit function from the upper limit function which is an equation in variable t. The catch is that you have to pick the appropriate value for t from the resulting quadratic equation.

The solution is shown below and you can watch the accompanying video for better understanding on how to solve such questions.

Watch the video solution here.

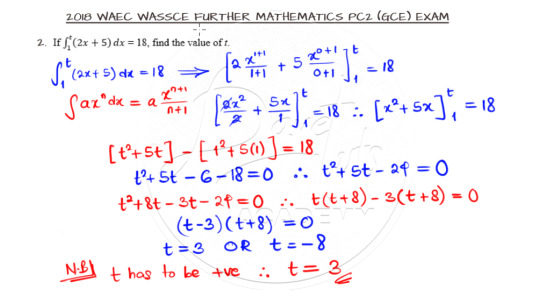
Algebra of Matrices

The next question is on Algebra of matrices. Attempt it first before moving on.

You have to understand the multiplication of matrices to evaluate the square of B and correctly define the identity Matrix I. Once that is done, the matrix N can be evaluated easily.

Click here to watch the video solution to Question 3.

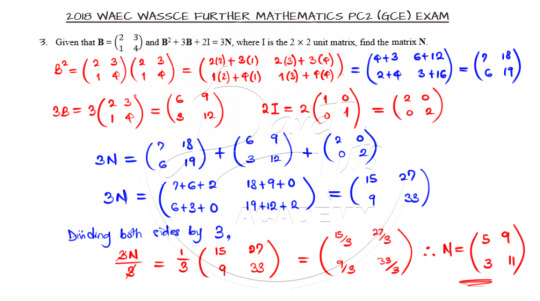
Transform the Equation of a Circle

Question 4 is based on the equation of a circle. Go ahead and try solving on your own first before checking out the solution presented.

Key stuff to simplify the solution include the general equation of a circle and the standard equation of the circle. Furthermore, the process of using completing the square to transform the general equation to the standard equation is quite important to the solution as shown below:

And here is the video for your further study.

Unordered Selection of Fruits

An unordered selection of fruit is to be carried out in question 5 from combination and you can work it out first.

The confusion to avoid here is the matter of ripe and unripe oranges. Once you can sort that out, the combination formula comes in handy to solve the question.

Click here to watch the accompanying video solution.

Estimate Mode using the Graph

Question 6 is asking us to estimate the modal age of a number of workers using graphical method. So bring out the graph paper and let’s get to work.

Obviously, you need to know the type of graph that can be used to get the mode of a set of data. And histogram is the go-to diagram to help us out. But first, you have to generate your table of values featuring the class boundary. And then you note the highest bar and cross from the adjoining bars to get the point of intersection which can be traced to get the mode.

If you still have some glitches, click here for the video solution.

Finding an Angle of a Triangle using Vector Method

Vectors is here!!! I so much love vectors. And this question is asking us to use vector method to solve for one of the angles of a triangle. So try it out.

First, locate the vertices of the triangle and then you will observe that the point Q is the point at which the angle is to be evaluated. So, taking vectors PQ and RQ, you can find the dot product from which the angle of inclination of the two vectors can be evaluated to yield the answer. 

Watch the video solution by clicking on this line. 

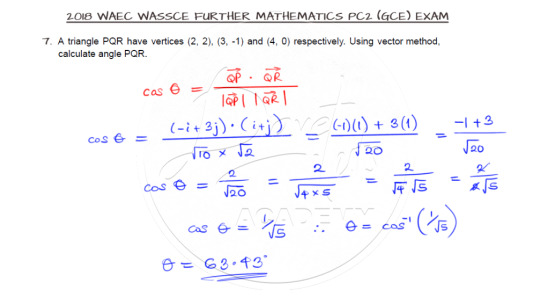
A travelling Motorist in Linear Motion

Next is question 8 based on a travelling motorist. Try it out, please.

So we need the Linear equations of motion to handle this question. But you have to interpret the question correctly before you can get it right. And there are at least two ways to go about answering this question. One way to solve it is given below.

Click here to watch the video. 

Equation of the Side of a Triangle

Question 9 asks us to evaluate the equation of a line, but not just any line. It is the side of a triangle whose vertices were given. So go ahead and try solving the question.

You need to know that joining the midpoints of two sides of a triangle will yield a line parallel to the third side and since two parallel lines have the same slope, the question can be solved by using the coordinate of the midpoint of the line AB as requested.

Further clarity are presented here in the video solution

Simultaneous Equation + Quadratic Factors

Question 10a is combining a problem on simultaneous equation and factorization of a quadratic polynomial. Try it out and make sure you are on track by making use of your calculator.

To solve this question, you will have to solve a set of simultaneous equations in 3 variables. This will enable you to solve for the values of p, q and r. The resulting quadratic equation can be factored out to get the factors of the given function.

The video solution is presented here. 

Expressing Rational Function in Partial fractions

Partial fraction is the next question in 10b and the question is as shown below:

The point to note is the splitting of the rational function into its partial fraction components. Once the LCM is sorted out, we can equate the numerators to get the values of the introduced unknowns as shown.

The video solution can be gotten here.

Differentiation from First Principles

Question 11a is on differentiation and we have a simple function to differentiate. But wait a minute. We are to use first principles! So go ahead and attempt this on your own.

I hope you really try this question out. Knowing the technique of differentiation from first principles is vital here. Once the formula is applied, e need to work at eliminating any stand-alone h in the denominator so that we will not have an undefined function while working. For questions like this, the more you practice, the better you become.

Watch the video solution from Davetuts Academy by clicking here.

Integration by substitution

Question 11b is based on integration but you need a little trick to solve it. All the best as you attempt this question.

Okay, the little trick is to use substitution. As you can see, trying to integrate straight will constitute the Herculean task of integrating the root of (1-x). So introducing another variable as a function of x and substituting appropriately is the way to go on this type of questions.

And the video is here for better understanding.

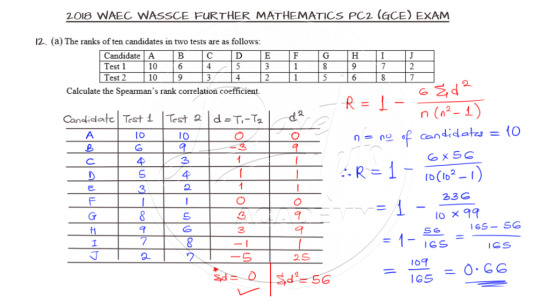
Finding the Spearman’s Rank Correlation Coefficient

Question 12a is on  Spearman’s Rank Correlation Coefficient and as expected, go ahead and lay your hands on this question.

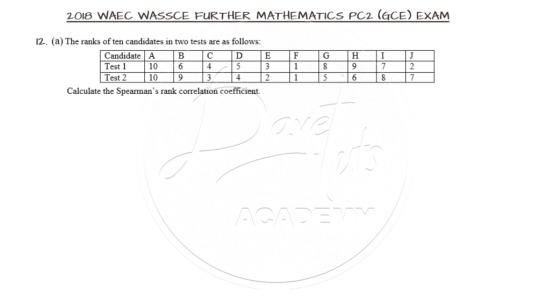
The Spearman's Rank Correlation Coefficient is used to summarize the strength and direction (negative or positive) of a relationship between two variables. For this question, we need to get the square of the difference in the two tests and use that in the formula for the Coefficient as shown below. As a guide, confirm that the sum of the differences equate to zero, otherwise, something is wrong with your calculation.

The video for the solution can be accessed here.

Evaluating Conditional Selection

A conditional selection is to be carried out in Question 12b and you can go ahead to attempt the question.

The first case is quite straightforward, but on the second instance, we need to apply our ingenuity to solve for that “harder” case as shown below.

Here is the video solution for the question.

Working with Binomial Probability 

Binomial Probability is featured in Question 13 for us to solve as shown.

Binomial probability refers to the probability of exactly x successes on n repeated trials in an experiment which has two possible outcomes. So here our possible outcomes from the selection is picking either a defective bolt or a non-defective bolt. The solution is as shown below:

Check the video tutorial for detailed explanation of the solution to the question.

Resolution of Concurrent Co-planar Forces

Question 14 is on the resolution of co-planar forces.

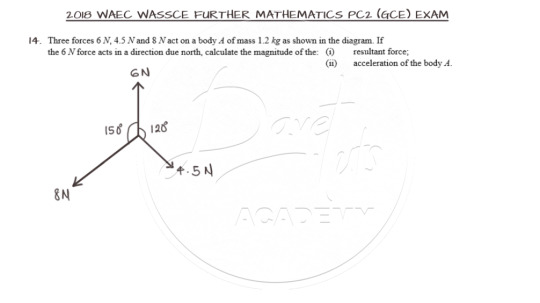
The solution warrants that the inclined forces be resolved to the horizontal and vertical components. This can be done in a variety of ways. You may prefer using the angles 150 and 120 degrees as given or the angles minus 90 degrees or as used in the solution, 180 minus the given angles. 

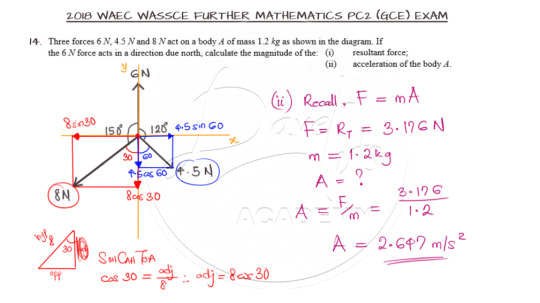
You can watch the video solution as shown below:

Final Velocity of a Stone under Free Fall

Question 14b features a free falling stone whose final velocity is to be determined.

The equation of motion comes in handy in solving the question as shown below

And here is the link to the video solution too.

Algebra of Vectors

Question 15a features the algebra of vectors. Go through and attempt the question on your own.

The solution involves opening the brackets and equating the components of the resulting vector equation to get the scalars as requested.

The video solution can be gotten here.

Parallelogram Law of Vectors

Finally, our last question features the parallelogram law of vectors.

The cosine rule comes in handy in solving this question and all you need to note is the requested angle as opposed to the angle used in the cosine rule. 

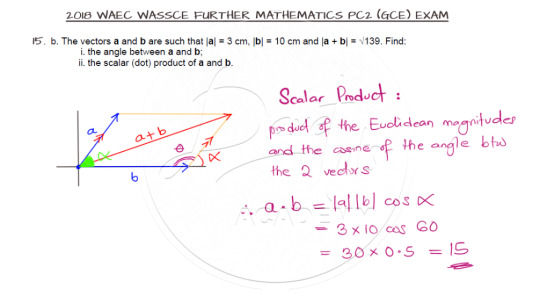
And here is the video solution:

So that is all about that.

Hopefully, you laid your hands on the questions first before checking with the solution featured here.

Kindly share this and let’s build academic excellence in students together.

Don’t forget to follow #davetutsacademy and visit our YouTube channel for more stuff like this by clicking here: Davetuts Academy.

[entrancei010]

Become A Maths Master With NCERT Solutions

Does your child want to excel in his or her exam? Strengthening the school foundation has become the primary motive of yours? If yes, then the best solution lies with NCERT (National Council of Educational and Research) as your little champ can easily grasp the idea behind the array of questions. The solutions of NCERT give in depth, chapter-wise solutions to the queries of the subject. It also helps students to compare the subject answers with sample answers. Deep learning with polishing the basics of subject materials brings clarity of concept in student minds.

Students find maths, a typical subject during their academy life and to be very honest maximum students says “Maths is quite scary”. To get out from the crux of the marks scoring problem, NCERT solutions for class 8 maths is the best option. The textbook has been designed for the students to give a solid foundation of the subject thoroughly. The most important and difficult subject students find in their 8 exams is maths and scoring highest marks become their main concern. NCERT solutions for class 8 maths cover all chapters step by step detail theory with objective and subjective solved questions.

You can also download NCERT solutions for class 8 maths from the website in just a few clicks. The solutions for maths problems are prepared by professionals which includes the problems from the newest edition of NCERT books and according to CBSE pattern. The brilliant NCERT solutions for class 8 maths give a quick understanding of the subject and assist in solving tough problems too.  

Few more tips to excel in your maths exam:

·        Make a habit of never missing your maths coaching or classes

·        Read the topics before going for the classes

·        Use highlighter to mark the important formula

·        Studying maths every day not only makes you master for your field but also keeps your concept clear

·        First of all, solve all the questions of NCERT and then jump into NCERT solutions for class 8 maths

 Apart from this, NCERT solutions for class 8 maths cover the following chapters:

8 Maths Chapter wise Solutions

Chapter 1 - Rational Numbers

Chapter 2 - Linear Equations in One Variable

Chapter 3 - Understanding Quadrilaterals

Chapter 4 - Practical Geometry

Chapter 5 - Data Handling

Chapter 6 - Squares and Square Roots

Chapter 7 - Cubes and Cube Roots

Chapter 8 - Comparing Quantities

Chapter 9 - Algebraic Expressions and Identities

Chapter 10 - Visualising Solid Shapes

Chapter 11 - Mensuration

Chapter 12 - Exponents and Powers

Chapter 13 - Direct and Inverse Proportions

Chapter 14 - Factorisation

Chapter 15 - Introduction to Graphs

Chapter 16 - Playing with Numbers

 Math can be a little bit hard for your children, but in case they focus in class and practice the NCERT sums, success is 100 percent. You just keep in mind of not getting so much of rush in solving the question, simply take your time in solving them. Your child must avoid cramming, ask him/her not to stress out, and make sure to ask for rest and eat well before the test. This will keep them energizes and the power to solve the problems increases.

[mathswithnarendrasir]

Class-8 Mathematics NCERT Soluction Ex-2.5 chapter-2 #Mathswithnarendrasir #Narendrasir

[entranceicbse-blog]

CBSE Sample Papers class 8 Maths

About Entrancei CBSE Sample Papers class 8 Maths

In case if you are in search of the best collection of accurate, comprehensive and free PDF with can be read anywhere and anytime, then Entrancei is the place. The expert team of Entrancei have chalked out the most prominent topics of the chapter in CBSE Sample Papers class 8 Maths and placed very precisely. The solution prepared for CBSE Sample Papers class 8 Maths has been reviewed very effectively.

While going through the maths subject Maths formula can help you a lot so do read and revise entire maths formula from entrancei.

Right Approach to use CBSE Sample Papers class 8 Maths

The CBSE Sample Papers class 8 Maths solution provided here will help you to enhance your command over questions in the textbook. One can have their access to the CBSE Sample Papers class 8 Maths questions in a simple process of just signup. The solution to CBSE Sample Papers class 8 Maths is available in a PDF format which could be accessed on mobile and Laptop as well.

The best thing about CBSE Sample Papers class 8 Maths notes is that they have been curated with a very detailed approach. The exercise presented would help you ace over the CBSE Sample Papers class 8 Maths examination. The most prominent thing about CBSE Sample Papers class 8 Maths solution that they are totally free of any cost. They can be a very effective medium of learning the old concepts. These PDF’s can be an effective medium of clearing doubts, which can lead to you losing marks in final examination. All you need to do is just sign up for your free course.

The categorization to the complete CBSE Sample Papers class 8 Maths has been on the basis of fragmenting out the tough and making it simpler. One can go through the detailed categorization made in terms of a chapter.

Chapters covered in CBSE Sample Papers class 8 Maths

Chapter 1: Rational Numbers

This chapter throws light upon properties of real numbers, integers, rational numbers which are crucial with respect to class 8 maths syllabus.

Chapter 2: Linear Equation in one Variable

This chapter of class 8 maths helps in guiding the students in understanding the intrinsic details of solving the linear expression dealing with variable expressions. It is crucial for one to understand the concepts of varied equations in class 8 maths.

Chapter 3: Understanding Quadrilaterals

The students are highlighted regarding the various polygon shapes in class 8 maths before they proceed to the higher levels of mathematics. The theorems and postulates responsible for tetragon and quadrilateral are presented in this chapter.

Chapter 4: Practical Geometry

This chapter of class 8 maths brings a very specific fun engagement among the students as they need to create some very common quadrilaterals and triangles with varied angles.

Chapter 5: Data Handling

This chapter guides the student regarding the methods to check and analyze any data or a case study. The students in class 8 maths would likely be introduced regarding the pie graphs, bar graphs, pictograph, and histogram.

Chapter 6: Squares and Square roots

It helps the class 8 maths students regarding the ways to find sq. roots to various decimal values. It is often utilized in higher categories.  

Chapter 7: Cubes and Cube Roots

The procedure to determine the cube roots to various higher values have been explained to class 8 maths students.

Chapter 8: Comparing quantities

This class 8 maths chapter helps in comparing quantitates such as percentage, marked values, discounts, and market values. It throws light upon interest and its types.

Chapter 9: Algebraic Expressions and Identities

This chapter of class 8 maths bring the students close to the expressions and identities utilized in pure mathematics.

Chapter 10: Visualising Solid Shapes

The students are taught in this class 8 maths subject regarding the methods to study varied solid objects such as cylinders, spheres, and hemispheres. One needs to work upon Faces, Vertices, and Edges of different solid geometrical shapes.

Chapter 11: Mensuration

In this chapter of class 8 maths, students will be taught regarding determining the surface areas and perimeters of closed surfaces and open geometrical objects.

Chapter 12: Exponents and Powers

The Exponents and Powers as the name signifies describes regarding the varied number description. It helps the students understanding the documentation decimal numbers I scientific forms. After learning this chapter of class 8 maths one can easily compare large and small numbers in terms of powers.

Chapter 13: Direct and Inverse Proportions

This chapter helps the students regarding the increase and decrease of inverse proportions. The general questions in this chapter of class 8 maths will be quite interesting and based upon daily life.

Chapter14:  Factorization

This chapter of class 8 maths throws light upon factorization of natural numbers, algebraic variables, and algebraic numbers.

Chapter 15: Introduction to Graphs

In these students of class 8 maths will be introduced with the plotting and data collection through the graph.

Chapter 16: Playing with Numbers

This chapter of class 8 maths is more of a fun chapter where students will be dealing with various puzzles and games.

Why choose Entrancei for CBSE Sample Papers class 8 Maths

Since students in CBSE Sample Papers class 8 Maths are just in their schools. They need to be well focused and have clear concepts regarding various analogies of CBSE Sample Papers class 8 Maths. The educators and experts at Entrancei have prepared very extensive study material keeping in mind the requirement of examinations. Solve all questions given in Important Questions for class 8 Maths prepared by Entrancei experts.

SOURCE:- https://entranceincert.blogspot.com/2020/09/cbse-sample-papers-class-8-maths.html

[entranceiin]

MATH REVIEW NOTES FOR CLASS 10

Mathematics is one of the most important subjects in student life. It is not a topic to read or just listen to, it needs to be revised to remember all of the concepts, and a review grade is very important for grade 10 because grades are just a word, but they are make up each point for that. Studies that become very useful during the exam period. Incoming teachers with academic experience created Grade 10 review notes explaining key concepts, theorems and formulas. Class 10 has a very important class in our careers and mathematics is one of the main subjects that will play an important role in our future. The excellent mastery of Grade 10 mathematics helps students advance their careers to a great extent.

CLASS 10 MATH REVIEW CHAPTER

1. Real numbers

2. Polynomials

3. Pair of linear equations with two variables.

4. Quadratic equations

5. arithmetic progression

6. Coordinated geometry

7. Triangles

8. Trigonometry

9. Applications of trigonometry.

Tenth circles

11. Constructions

12. Area linked to circles.

13. Measure

14. Statistics

15. Probability

WHY IS ENTRY IMPORTANT FOR CLASS 10 REVIEW NOTES?

The appearance of class 10 creates pressure among the students. The Entrancei Academy team develops class 10 mathematical solutions. Our Entrancei university teachers have prepared a NCERT solution of class 10 math which answers all the questions in the NCERT manual in accordance with the CBSE guidelines for board reviews. Solving step by step The pupils have problems, then they come to our department for questions and then our teachers come directly to solve their difficulties. In addition to all of these preparations, expert teachers have prepared math resources, including NCERT solutions, RD Sharma class 10 math solutions and weekly exams, etc. which is very useful for the exam.

 HOW IS THE CLASS 10 MATH TEST EFFECTIVE?

Solving math questions regularly can improve your addition skills on a daily basis. Always remember that math is not about reading and listening. You must solve math questions daily to improve your ability to solve questions. Many students are often stuck in difficult numbers, so our academic teachers will help you with these difficulties. Students can follow the Grade 10 NCERT revision notes for math solutions created by our teachers. The complete NCERT solutions for class 10 was made available free of charge.

Source Url: https://bit.ly/3eJH8Rc

[ss1986us]

ncert solutions for class 9 maths

Brace up like scholars

https://www.entrancei.com/topics-topics-class-9-mathematics

 The class 9 maths study material is available in PDF format which can be easily downloaded from our site. One can also access a very specific and examination focused strategy for class 9 maths by just simple signup at Entrancei. The sole idea has been to create a most accurate and detailed solution for class 9 maths that is free of cost. The experienced teachers at Entrancei have very extensively revealed the complete class 9 maths content. They have completely made sure all that is provided is important with respect to examinations. The class 9 maths solutions can be easily utilized for scoring good marks as one can reliably practice form them.

While going through the maths subject Maths formula can help you a lot so do read and revise entire maths formula from entrancei.

All the class 9 maths notes prepared as per the guidelines of CBSE Syllabus and guidelines. One can also go through test services for class 9 maths as it will help in gauging out the overall progress. The choosing union the class 9 maths optimum solutions helps in acing the students with the atmosphere of examination.

As general pattern, the class 9 maths should be taken very seriously as it helps in building strong concepts for further boards in 10th. The complete categorization of the syllabus of class 9 maths has been done in chapters, which helps students to easily go through it.

Ø  Chapter 1: Number systems

This chapter throws light upon number lines and how effectively they can be used. The class 9 maths solutions provided helps the students regarding laws of integral and rational powers of real numbers.

Ø  Chapter 2: Polynomials

The class 9 maths solutions to this unit give a vivid explanation about polynomials and their detailed terminologies. One will be acknowledged with various types of polynomials such as linear, Constant, quadratic and cubic polynomials.

Ø  Chapter 3: Coordinate Geometry

This chapters in class 9 maths help the students in understanding the concepts of Cartesian place and coordinates.

Ø  Chapter 4: Linear Equations in two Variables

This chapter in class 9 maths helps the students in understanding the equations presented in two variables. Plotting the equations on graph has been explained in a very detailed format in class 9 maths solutions provided.

Ø  Chapter 5: Introduction to Euclid’s Geometry

This chapter of class 9 maths throws minor lights upon how Indian history is associated with Geometry followed in the world. One will be explained regarding the geometry through axiom, Postulates, and Theorems of class 9 maths in detailed format.

Ø  Chapter 6: Lines and Angles

The chapter as lines and angles is generally asked as theorems and postulates in class 9 maths examinations. The level of difficulty is very minor compared to other units.

Ø  Chapter 7: Triangles

In this chapter of class 9 maths, you will study regarding the congruence of triangles and their associating theorems. This chapter of class 9 maths has various properties such as inequalities and properties in triangles.

Ø  Chapter 8: Quadrilaterals

This chapter of class 9 maths comprises of only one theorem as proof. Questions asked in this chapter are relatively very easy.

Ø  Chapter 9: Areas of Parallelograms and Triangles

One will be brought to the note of areas in geometrical shapes. The examples of the median can be used in various examples of this in class 9 maths of chapter.

Ø  Chapter 10: Circles

This chapter of class 9 maths gives brief insights about subtended angle chord, equal chords, Arc of the circle, cyclic quadrilaterals. This detailed solution of theorems based on triangles, Quadrilaterals, and circles are based in this chapter.

Ø  Chapter 11: Constructions

This chapter throws light upon bisecting and creating line segments to angles and lines. The student’s class 9 maths would be learning the creation of triangles with different properties and different base angles.

Ø  Chapter 12: Heron’s formula

This chapter of class 9 maths comprises of only three exercises. This chapter gives an extension to the application of heron’s formula in polygons and quadrilaterals and triangles.

Ø  Chapter 13: Surfaces Areas and Volumes

The students need not be introduced with this topic as they well studied the mensuration in their earlier classes. One would be acknowledged with volumes of cubes, cylinders, spheres, cones, and the hemisphere’s in their class 9 maths syllabus.

Ø  Chapter 14: Statistics

The statistics chapter of class 9 maths is like a simple method of collection of data in different aspects. In total, this chapter of class 9 maths helps one to find the measure of central tendency, mean, median and mode of any raw data provided.

Ø  Chapter 15: Probability

With only about 1 exercise in class 9 maths, this chapter is very easy. This is based on observation and frequency of day to day examples.

 Why choose Entrancei

 There might be times when students are stuck with exercises, so there comes the team of Entrancei with an innovative solution to class 9 maths students. The students can any time give a call in order to get their doubts resolved associated with class 9 maths.

[aakash3568]

How to Score Good Marks in Class 7 with the Help of RS Aggarwal Solutions

This page is prepared by renowned faculty of maths who are part of Entrancei academic team. From this page, you can download any exercise or questions from RS Aggarwal class 7 maths book.

If you want to score good marks in class 7 maths you required good practice of numerical with the concept clarity. RS Aggarwal Class 7 solutions maths book is full of questions and the theory is explained very nicely with solved examples.

Read the theory of RS Aggarwal textbook and start solving the exercise. Follow NCERT textbook for theory or your school class notes and then start solving RS Aggarwal class 7 solutions maths book while solving questions from exercise if you face any problem you can take help from RS Aggarwal solutions class 7 maths book prepared by expert faculty members of Entrancei.

Chapter-1 Integers

Chapter-2 Fractions

Chapter-3 Decimals

Chapter-4 Rational Numbers

Chapter-5 Exponents

Chapter-6 Algebraic Expressions

Chapter-7 Linear Equations in One Variable

Chapter-8 Ratio and Proportion

Chapter-9 Unitary method

Chapter-10 Percentage

Chapter-11 Profit and Loss

Chapter-12 Simple Interest

Chapter-13 Lines and Angles

Chapter-14 Properties of Parallel Lines

Chapter-15 Properties of Triangles

Chapter-16 Congruence Chapter-17 Constructions

Chapter-18 Reflection and Rotational Symmetry

Chapter-19 Three-Dimensional Shapes

Chapter-20 Mensuration

Chapter-22 Bar Graphs

Chapter-21 Collection and Organisation of Data

Also Read: How to Study RS Aggarwal Class 8 Solutions Effectively?

How to score good marks in class 7 with the help of RS Aggarwal solutions

Class 7 maths start with the revision of maths what you have read in class 6. You will learn a few new concepts like integers application of integers and few new concepts of geometry as of now the syllabus is not vast nor it is difficult. This is a very crucial class for your upcoming maths chapter and upcoming maths as a subject.

From class 7, students develop an interest in maths. So be serious and plan accordingly. While solving class 7 maths RS Aggarwal maths book will give you an additional edge over the NCERT textbook. RS Aggarwal maths book consists of questions and the best part is the level of difficulty. 

In RS Aggarwal class 7 solutions maths book increasing slowly to give a higher level of understanding to the topic and boost your confidence. One must try each and every question given in RS Aggarwal Book by yourself and if there is any question which you unable to solve try 4 to 5 times before referring to RS Aggarwal solutions class 7. 

Academic team of Entrancei prepared RS Aggarwal solutions class 7 for your reference. Our team prepared solution of all question in the textbook of RS Aggarwal maths which will help you to have a better understanding of chapter and questions. Always remember that maths is a subject of practice and RS Aggarwal class 7 maths book consist of almost 200 questions in each chapter which is sufficient to have confidence in that chapter. 

After that, you can give chapter wise online test of the chapter from Entrancei to have more clarity on the chapter. We have uploaded thousands of questions for class 7 maths and science do check it out. Never try to memorise RS Aggarwal solutions class 7 it will decrease your thinking ability. 

While reading the theory from RS Aggarwal class 7 maths book or NCERT always try to write down the most important formula in your notebook this habit will pay you in final revision as well as help you to retain the formula for a long time. These formulas you are going to use in almost all the higher class. So guys all the very best for your preparation.

Academic team of Entrancei prepared different type of resource for class 7 Maths which includes detail theory, notes, revision notes, question bank for class 7 maths, NCERT solutions for class 7 maths, RS Agarwal solutions for class 7 maths & Maths formula.

Do your revision with Entrancei resource and practice. Solve questions from all chapter of class 7 maths from Entrancei resources all resource are available freely to students don’t forget to share our resource with your friends.

The following flow chat is added to explain the best strategies to enhance your potential in class 7 maths syllabus and boost your confidence with an increased level of interest in class 7 maths. 

Source URL: https://www.entrancei.com/rs-aggarwal-class-7-solutions

[ashishkumarletslearn]

Free education is the right of every student. Ashish Kumar – Let’s Learn is providing deep and detailed explanations of full syllabus, all important questions, all important examples and all NCERT solutions for Class 11 Maths through videos on YouTube Channel as well as Blogs and PDFs on website.

Students can learn through videos and blogs and can ask their doubts on Website’s Discussion panel or on YouTube’s Comments Page. Students will also be provided notes, assignments, books and various other educational resources in electronic forms like PDFs, Docs, mp4 etc., which will help them to prepare for CBSE Class 12 Board Exams but more importantly for their upcoming life’s adventures.

You can easily access all chapters with NCERT Solutions for class 11 maths on this page:  https://www.ashishkumarletslearn.com/cbse/class-11/maths/

Following are summaries of chapter wise syllabus recommended by CBSE for Class 11 mathematics students with their YouTube as well as Website links.

Unit-I: Sets and Functions

1. Sets: 

Sets and their representations. Empty set. Finite and Infinite sets. Equal sets. Subsets. Subsets of a set of real numbers especially intervals (with notations). Power set. Universal set. Venn diagrams. Union and Intersection of sets. Difference of sets. Complement of a set. Properties of Complement.

2. Relations & Functions:

Ordered pairs. Cartesian product of sets. Number of elements in the Cartesian product of two finite sets. Cartesian product of the set of reals with itself (upto R x R x R). Definition of relation, pictorial diagrams, domain, co-domain and range of a relation. Function as a special type of relation. Pictorial representation of a function, domain, co-domain and range of a function. Real valued functions, domain and range of these functions, constant, identity, polynomial, rational, modulus, signum, exponential, logarithmic and greatest integer functions, with their graphs. Sum, difference, product and quotients of functions.

3. Trigonometric Functions:

Positive and negative angles. Measuring angles in radians and in degrees and conversion from one measure to another. Definition of trigonometric functions with the help of unit circle. Truth of the identity sin2x+cos2x=1, for all x. Signs of trigonometric functions. Domain and range of trigonometric functions and their graphs. Expressing sin (x±y) and cos (x±y) in terms of sinx, siny, cosx & cosy and their simple applications. Deducing identities. Identities related to sin2x, cos2x, tan2x, sin3x, cos3x and tan3x. General solution of trigonometric equations of the type siny = sina, cosy = cosa and tany = tana.

Unit-II: Algebra

4. Principle of Mathematical Induction:

Process of the proof by induction, motivating the application of the method by looking at natural numbers as the least inductive subset of real numbers. The principle of mathematical induction and simple applications.

5. Complex Numbers and Quadratic Equations:

Need for complex numbers, especially √ , to be motivated by inability to solve some of the quadratic equations. Algebraic properties of complex numbers. Argand plane and polar representation of complex numbers. Statement of Fundamental Theorem of Algebra, solution of quadratic equations (with real coefficients) in the complex number system. Square root of a complex number.

6. Linear Inequalities:

Linear inequalities. Algebraic solutions of linear inequalities in one variable and their representation on the number line. Graphical solution of linear inequalities in two variables. Graphical method of finding a solution of system of linear inequalities in two variables.

7. Permutations and Combinations:

Fundamental principle of counting. Factorial n. (n!) Permutations and combinations, derivation of formulae for and and their connections, simple applications.

8. Binomial Theorem:

History, statement and proof of the binomial theorem for positive integral indices. Pascal’s triangle, General and middle term in binomial expansion, simple applications.

9. Sequence and Series:

Sequence and Series. Arithmetic Progression (A. P.). Arithmetic Mean (A.M.) Geometric Progression (G.P.), general term of a G.P., sum of n terms of a G.P., infinite G.P. and its sum, geometric mean (G.M.), relation between A.M. and G.M. Formulae for the following special sums.

Unit-III: Coordinate Geometry

10. Straight Lines:

Brief recall of two dimensional geometry from earlier classes. Shifting of origin. Slope of a line and angle between two lines. Various forms of equations of a line: parallel to axis, point -slope form, slope intercept form, two-point form, intercept form and normal form. General equation of a line. Equation of family of lines passing through the point of intersection of two lines. Distance of a point from a line.

Unit-IV: Calculus

13. Limits and Derivatives:

Derivative introduced as rate of change both as that of distance function and geometrically. Intuitive idea of limit. Limits of polynomials and rational functions trigonometric, exponential and logarithmic functions. Definition of derivative relate it to scope of tangent of the curve, derivative of sum, difference, product and quotient of functions. Derivatives of polynomial and trigonometric functions.

[learnviaelearn-blog]

Welcome to Learn-Via-Elearn Classes | An Educational Channel |SUBSCRIBE | LIKE | COMMENT | DISLIKE

Contact details: Email:- learnviaelearn@gmail.com Whatsapp:- +91 96190 94404 Twitter:  https://twitter.com/learn_viaelearn Facebook Page:https://bit.ly/2xh5UU7 Instagram: https://instagram.com/learnviaelearn Google Plus: https://plus.google.com/u/0/+learnvia... Dear Students, In this video I'm explaining Concise Mathematics Class 10 Chapter 1 - Value Added Tax There are many more videos on this including all other 25 chapters so keep watching and do subscribe Feel free to Contact me on below details in case of any queries. Name: Shailendra Email; learnviaelearn@gmail.com Concise Mathematics Class 10 ICSE Solutions have been solved by expert teachers from across the nation to help students ace the class 10 board exams conducted by the ICSE (Indian Council of Secondary Education) board. The ICSE Class 10 Maths Solutions solve problems related to various topics which are prescribed in most ICSE Maths textbooks. Problems are solved step-by-step in a cohesive manner in order to allow students to grasp concepts easily and get solutions at the tip of their fingers. The solutions included in this video revolve around chapters like Value Added Tax, Banking, Shares and Dividend, Linear Inequations, Ratio and Proportion, Matrices, and others.  Studying the solutions prescribed in the ICSE Mathematics Class 10 Solutions PDF will enable students to prepare and tackle their Class 10 board examinations easily. One can download the Concise Mathematics Class 10 ICSE Solutions video as well. Chapter 1 - Value Added Tax Chapter 2 - Banking (Recurring Deposit Account) Chapter 3 - Shares and Dividend Chapter 4 - Linear Inequations (In one variable) Chapter 5 - Quadratic Equations Chapter 6 - Solving (simple) Problems (Based on Quadratic Equations) Chapter 7 - Ratio and Proportion (Including Properties and Uses) Chapter 8 - Remainder and Factor Theorems Chapter 9 - Matrices Chapter 12 - Reflection Chapter 13 - Section and Mid-Point Formula Chapter 14 - Equation of a Line Chapter 15 - Similarity (With Applications to Maps and Models) Chapter 16 - Loci (Locus and Its Constructions) Chapter 17 - Circles Chapter 18 - Tangents and Intersecting Chords Chapter 19 - Constructions (Circles) Chapter 20 - Cylinder, Cone and Sphere Chapter 21 - Trigonometrical Identities Chapter 23 - Graphical Representation Regards Shailendra learnviaelearn987 #learnviaelearn