#inversion
Explore tagged Tumblr posts
Text


oh my god
#tdp spoilers#tdp s7#ezran#tdp ezran#tdp parallels#tdp#the dragon prince#continuethesaga#giveusthesaga#be still my parallel loving heart#inversion
1K notes
·
View notes
Text

29 April, 2024
#roped girl#ropeplay#ropeart#tattoed#tattooed girls#shibari#rope suspension#suspended#inversion#rope baby#rope bottom#ropebondage#bd/sm rope
2K notes
·
View notes
Text




Autumn of art.
#photography#my photography#art#my art#flower#flowers#floral#nature#beauty#photographers on tumblr#original photographers#beautiful photos#photooftheday#japan#aestheitcs#2024#flower photography#flower aesthetic#写真#花#コスモス#秋桜#cosmos#秋#autumn#fall#autumn aesthetic#autumn vibes#reflection#inversion
175 notes
·
View notes
Text

273 notes
·
View notes
Text
Sam x Lovely headcanons
STRICTLY PLATONIC/CLOSE AS SIBLINGS
⚕️Ever since Sam healed them after Adam’s attack, he saw how distraught Vincent was and vowed then and there he would protect Lovely no matter what.
🍿Vincent and Lovely and Sam and Darlin’ have movie nights as unstated double dates.
📞If Vincent tells Lovely updates on Quinn, they call Sam to let him vent out things he doesn’t want to put on Darlin’s shoulders.
🍼Sam calls Lovely to babysit Vincent after asking him to babysit Fredrick and Bright Eyes.
🫂They hug every time they meet up.
🩸Sam held Lovely’s hand while Vincent turned them.
💬In the beginning of their relationship, Lovely would text Sam to ask Vincent’s favorite things so they could surprise him.
😠Lovely was pretty upset with Sam when he ambushed them with Porter, but after they got to hit him, they were better.
🧛🧛🧛During the Summit, when Porter started antagonizing Vincent into a fight, Lovely said Sam’s name quietly, knowing he would hear them, and he rushed over to break it up.
👩⚖️At the “trial” after Alexander’s murder, Sam stayed close to Lovely ready to jump in if he needed to. Especially when Christopher was explaining how it could have been one of the Solaires who did it and things were getting tense.
I really wish we could see if they have any sort of relationship.
#asmr roleplay#redacted asmr#redacted listener#headcanon#redacted audio#redactedverse#redacted sam#redacted lovely#redacted vincent#redacted darlin#redacted summit#inversion#redacted inversion#redacted frederick
127 notes
·
View notes
Text

Going up upside down... That's it, just a gif of me going up haha 😂 It was my first time being fully inverted in the winch and OMG it was AMAZING. (Look at my face -- is my radiant joy showing??) I am so unspeakably happy that I've discovered a way to dance again. It's not a little bit ironic that I had to kind of invent it, and that as incredible and frankly dangerous as it is, I can dance in literally no other way. Fuck chronic illness, and fuck gravity. Today, we dance in the air.
#tragic romance#defying gravity#death defying#fuck gravity#rope suspension#shibari suspension#air suspension#inversion#aerial arts#aerial acrobatics#aerial dance#aerial#bd/sm rope#roped girl#ropeart#roped up#shibari#queer swer#queer artist#kink tumblr#kinkblr#kink content#disabled artist#did recovery#did representation#ptsd recovery#complex ptsd#ptsd#art therapy#dance therapy
112 notes
·
View notes
Text
Mundus Inversus (or something about feet)
In 203, Ed gives himself up to the dark blue waters of purgatory. His feet are bare, a symbol often associated with death and mourning in art and literature, and his soles are facing upwards. Ed’s literally turning up his toes; dying.

The scene cuts immediately to Stede’s slippered feet, continuing, but altering the motif. The slippers are blue, similar to Ed’s surroundings; but as well as being clothed, indicating a living state, Stede’s feet are contrary to Ed’s - soles down, signifying life. Importantly, Stede’s feet are also in contact with water.

What strikes me is the clarity of the reflection of Stede’s feet, a soles up, but clothed, living version of Ed’s. And if we think about this reflection, it might stretch all the way down, meaning there is an upside down ‘living’ Stede in a sort of Mundus Inversus or mirror world.
Stede’s feet are also getting wet, and if we believe in the truths of folklore, certain ‘monsters’ transform in such conditions.

Our inverted Stede emerges out of the darkness into Ed’s purgatory, transformed. Tail replacing feet, pointing upwards, mimicking Ed’s death plunge. Stede enters this mirror world and meets Ed where he is.
There is also a kind of evolutionary inversion to Stede’s appearance, a fetal shape in a womb-like state. And of course, This Woman’s Work is playing, indicating a chance for rebirth.

As they mirror one another, neither Stede nor Ed are inverted any longer; they are soles (tail) down, ready to ascend out of this upside-down mirror world into a state of renewal.

And as they ascend, we glimpse them in the post-credit scene, returned each by their own agency, heads above water, back to the land of the living.
They have moved from soles mirroring to souls mirroring. Choosing life, together.
(some ideas inspired by @follows-the-bees)
31 notes
·
View notes
Text

Wanda in the cabin with the Darkhold lol
#wanda maximoff#scarlet witch#marvel#shibari#suspension#rope bottom#poetry#girlswholikegirls#wlw#inversion#wandavision#halloween#witchblr
25 notes
·
View notes
Text
"Rayla loves me. she believes in me. this version of myself.” “it’s not about you, is it?" absolute insane fucking line no notes oh my god
#the whole like#“i don't care what you think of me i don't care if you hate me i'm doing what's best for you no matter what happens to me”#thing is so MMMMMFSDhfsdfgHJSGFHSDGFG#AND THAT BEING THE SAME THING RAYLA DID BY LEAVING???? MOTHER OF CHRIST#rayllum#callum#tdp callum#tdp s7#tdp#the dragon prince#continuethesaga#giveusthesaga#tdp spoilers#inversion
87 notes
·
View notes
Text
Don’t Imagine David and Asher going to sleep next to their mates
Don’t Imagine Angel and Babe smiling down at them as they sleep
Don’t imagine Angel and Babe staying up almost all night scrolling through the internet, trying to find out if humans can learn magic.
Their search for information failing, and ultimately falling into researching non-magical ways to ensure they can help their mates, to make sure they never feel as useless as they did behind that other side of the wall.
Don’t Imagine them adding medical equipment into their carts, reading articles about how to stop bleeding from a wound, how to treat scars, how to help.
Cause while they are un empowered, they’re not going to let their mates almost slip out of their hands and not even attempt to do anything about it again
#redacted asmr#redacted audio#shaw pack#redacted asher#redacted david#redacted angel#redacted babe#inversion#redacted inversion
293 notes
·
View notes
Text




Gaze at the beautiful morning sun from the cosmos picture frame.
#photography#my photography#art#my art#flower#flowers#floral#nature#beauty#photographers on tumblr#original photographers#beautiful photos#photooftheday#japan#aestheitcs#2024#flower photography#flower aesthetic#写真#花#コスモス#秋桜#cosmos#morning sun#sun#sunrise#symmetry#inversion
131 notes
·
View notes
Text
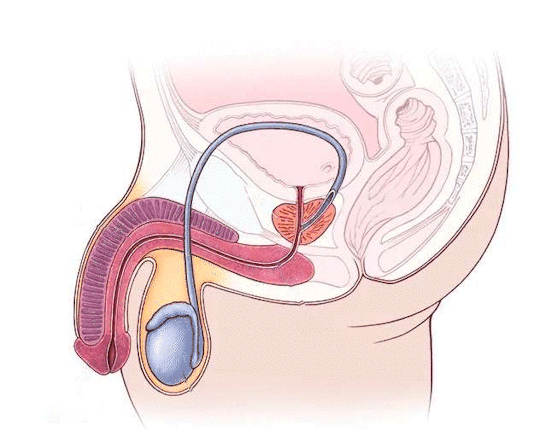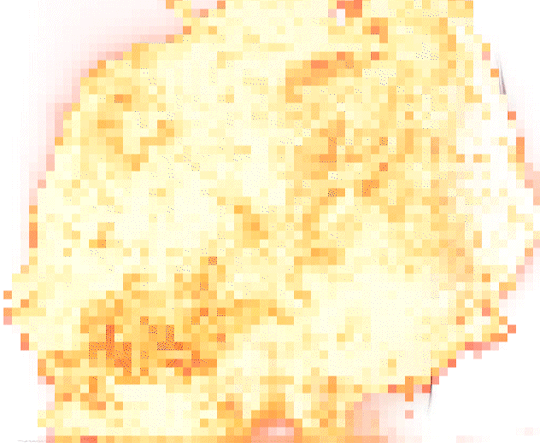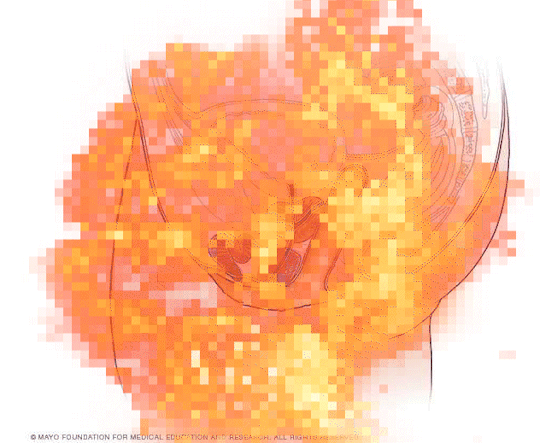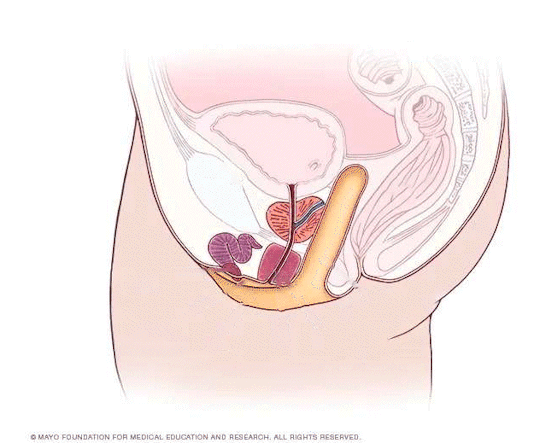
Penile Inversion Blast!!!!!!
#penile#inversion#blast#bottom surgery#transgender#transgirl#queer#demigirl#transfem#queer community#trans woman#shitpost
69 notes
·
View notes
Text
BRAVO EMILIO Como siempre. Qué grande!!!!!! Más como tu necesita este país,a ver si despertamos en este pais. 👏👏👏👏👏👏 @EmilioDelgadoOr Video publicado por SisuMisu @SisuMisu3 HAY ALGUIEN AL VOLANTE?
#Sisu#industriamadrileña#fabricasmadrileñas#trumpismo#Villaverde#peugeot#algomasutil#novioAyuso#parejaAyuso#brics#comunidaddemadrid#aranceles#iveco#citroen#inversion#ayusodimision#AyusoAPrision7291#ayusoabuso#ayusoveteya#ayusononoscalla#madrid#carabanchel
12 notes
·
View notes
Text

Me re-listening to Milo's audio where sweetheart helps him shift
(I've listened to it so many times and I still cry)
#redacted milo#redacted asmr#redacted audio#redactedverse#inversion#my poor werewolf man#I love milo
27 notes
·
View notes
Text

Doth the Dark one rises! Ahhhhhhh….,
10 notes
·
View notes