#i just like the current ones better

[saegull]

Kaoru Hana wa Rin to Saku PV

[hyacinthsdiamonds]

I'm sorry but James Vowles criticising how Red Bull has treated their drivers in the past, only to go and then treat Logan far worse while pulling the exact same shit Red Bull did, ie the exact behaviour he criticised and called them out for, is so freaking infuriating like the sheer hypocrisy -

[s0fter-sin]

soap's whole deal being sniper and demolitions gets me going bc on the surface they sound so different but when you get into it, you realise it's bc soap's smart

sniping is all math; calculating distances and wind interference and bullet drop. something i think people overlook is he was listed as a sniper first so it can be implied that he's better at it than demolitions. he does more sniping in both campaigns than demolitions work; in capture or kill, ghost specifically calls on him to take down the aq snipers

and demolitions is math with a hit of chemistry; knowing what mixes with what, knowing how much to use, recognising environmental factors and adjusting accordingly. it's not just about the boom; so much work goes into contained/ planned explosions. especially when having enough power for a breacher charge and not bringing down the whole building is the difference between mission success and failure

the chemical bombs he makes in alone can't just be any old cleaners, they have to have the correct reaction to each other; he just knew off the top of his head what would mix with what to create what reaction. he would also potentially have to recognise them by sight/smell bc they would’ve been written in spanish

soap would also have to know architecture; recognising structural integrity and weak points so he knows exactly where to plant a charge to bring it down and how it'll come down

he has an incredible soldier's mind people just forget that bc he's sociable which itself is a skill

we know he tends to buck against orders he doesn't agree with like when he pushes back against ghost in capture or kill and shepherd when he tells them to release hassan

he gets closer to people and sees if he can trust them and that's when he follows them without question. really think about how he talks to alejandro and rudy; he asks about their home and alejandro's family and rudy's relationship with him. those aren't questions you ask a stranger after a few hours of knowing them. that's not even touching on his relationship with ghost

he also deliberately brings people of higher ranks down to his level; talking informally with ghost and giving him a shoulder punch, addressing alejandro (a colonel!!) by his first name and rudy by his nickname despite literally just meeting them. he personalises all of them and it’s in direct opposition to the reason most characters do that; it’s not due to insubordination or lack of respect, the more he respects and trusts someone, the more casual he is with them

he digs into people; he wants to know what makes them tick and that determines if he can one, trust them and two, follow their orders. once he decides that, he's the ultimate soldier; he bleeds loyalty which makes him vicious when that loyalty is taken for granted

he isn't naive or bubbly or insecure; he's an incredibly smart and aware soldier. he's aggressive and bloodthirsty and loyal and intuitive and i love him so much

[hinata-boke]

the greatest decoy

[physicallyimprobable]

what's the 3-dimensional number thing?

Well I'm glad you asked! For those confused, this is referring to my claim that "my favorite multiplication equation is 3 × 5 = 15 because it's the reason you can't make a three-dimensional number system" from back in this post. Now, this is gonna be a bit of a journey, so buckle up.

Part One: Numbers in Space

First of all, what do I mean by a three-dimensional number system? We say that the complex numbers are two-dimensional, and that the quaternions are four-dimensional, but what do we mean by these things? There's a few potential answers to this question, but for our purposes we'll take the following narrative:

Complex numbers can be written in the form (a+bi), where a and b are real numbers. For the variable-averse, this just means we have things like (3+6i) and (5-2i) and (-8+3i). Some amount of "units" (that is, ones), and some amount of i's.

Most people are happy to stop here and say "well, there's two numbers that you're using, so that's two dimensions, ho hum". I think that's underselling it, though, since there's something nontrivial and super cool happening here. See, each complex number has an "absolute value", which is its distance from zero. If you imagine "3+6i" to mean "three meters East and six meters North", then the distance to that point will be 6.708 meters. We say the absolute value of (3+6i), which is written like |3+6i|, is equal to 6.708. Similarly, interpreting "5-2i" to mean "five meters East and two meters South" we get that |5-2i| = 5.385.

The neat thing about this is that absolute values multiply really nicely. For example, the two numbers above multiply to give (3+6i) × (5-2i) = (27+24i) which has a length of 36.124. What's impressive is that this length is the product of our original lengths: 36.124 = 6.708 × 5.385. (Okay technically this is not true due to rounding but for the full values it is true.)

This is what we're going to say is necessary to for a number system to accurately represent a space. You need the numbers to have lengths corresponding to actual lengths in space, and you need those lengths to be "multiplicative", which just means it does the thing we just saw. (That is, when you multiply two numbers, their lengths are multiplied as well.)

There's still of course the question of what "actual lengths in space" means, but we can just use the usual Euclidean method of measurement. So, |3+6i| = √(3²+6²) and |5-2i| = √(5²+2²). This extends directly to the quaternions, which are written as (a+bi+cj+dk) for real numbers a, b, c, d. (Don't worry about what j and k mean if you don't know; it turns out not to really matter here.) The length of the quaternion 4+3i-7j+4k can be calculated like |4+3i-7j+4k| = √(4²+3²+7²+4²) = 9.486 and similarly for other points in "four-dimensional space". These are the kinds of number systems we're looking for.

[To be explicit, for those who know the words: What we are looking for is a vector algebra over the real numbers with a prescribed basis under which the Euclidean norm is multiplicative and the integer lattice forms a subring.]

Part Two: Sums of Squares

Now for something completely different. Have you ever thought about which numbers are the sum of two perfect squares? Thirteen works, for example, since 13 = 3² + 2². So does thirty-two, since 32 = 4² + 4². The squares themselves also work, since zero exists: 49 = 7² + 0². But there are some numbers, like three and six, which can't be written as a sum of two squares no matter how hard you try. (It's pretty easy to check this yourself; there aren't too many possibilities.)

Are there any patterns to which numbers are a sum of two squares and which are not? Yeah, loads. We're going to look at a particularly interesting one: Let's say a number is "S2" if it's a sum of two squares. (This thing where you just kinda invent new terminology for your situation is common in math. "S2" should be thought of as an adjective, like "orange" or "alphabetical".) Then here's the neat thing: If two numbers are S2 then their product is S2 as well.

Let's see a few small examples. We have 2 = 1² + 1², so we say that 2 is S2. Similarly 4 = 2² + 0² is S2. Then 2 × 4, that is to say, 8, should be S2 as well. Indeed, 8 = 2² + 2².

Another, slightly less trivial example. We've seen that 13 and 32 are both S2. Then their product, 416, should also be S2. Lo and behold, 416 = 20² + 4², so indeed it is S2.

How do we know this will always work? The simplest way, as long as you've already internalized the bit from Part 1 about absolute values, is to think about the norms of complex numbers. A norm is, quite simply, the square of the corresponding distance. (Okay yes it can also mean different things in other contexts, but for our purposes that's what a norm is.) The norm is written with double bars, so ‖3+6i‖ = 45 and ‖5-2i‖ = 29 and ‖4+3i-7j+4k‖ = 90.

One thing to notice is that if your starting numbers are whole numbers then the norm will also be a whole number. In fact, because of how we've defined lengths, the norm is just the sum of the squares of the real-number bits. So, any S2 number can be turned into a norm of a complex number: 13 can be written as ‖3+2i‖, 32 can be written as ‖4+4i‖, and 49 can be written as ‖7+0i‖.

The other thing to notice is that, since the absolute value is multiplicative, the norm is also multiplicative. That is to say, for example, ‖(3+6i) × (5-2i)‖ = ‖3+6i‖ × ‖5-2i‖. It's pretty simple to prove that this will work with any numbers you choose.

But lo, gaze upon what happens when we combine these two facts together! Consider the two S2 values 13 and 32 from before. Because of the first fact, we can write the product 13 × 32 in terms of norms: 13 × 32 = ‖3+2i‖ × ‖4+4i‖. So far so good. Then, using the second fact, we can pull the product into the norms: ‖3+2i‖ × ‖4+4i‖ = ‖(3+2i) × (4+4i)‖. Huzzah! Now, if we write out the multiplication as (3+2i) × (4+4i) = (4+20i), we can get a more natural looking norm equation: ‖3+2i‖ × ‖4+4i‖ = ‖4+20i‖ and finally, all we need to do is evaluate the norms to get our product! (3² + 2²) × (4² + 4²) = (4² + 20²)

The cool thing is that this works no matter what your starting numbers are. 218 = 13² + 7² and 292 = 16² + 6², so we can follow the chain to get 218 × 292 = ‖13+7i‖ × ‖16+6i‖ = ‖(13+7i) × (16+6i)‖ = ‖166+190i‖ = 166² + 190² and indeed you can check that both extremes are equal to 63,656. No matter which two S2 numbers you start with, if you know the squares that make them up, you can use this process to find squares that add to their product. That is to say, the product of two S2 numbers is S2.

Part Four: Why do we skip three?

Now we have all the ingredients we need for our cute little proof soup! First, let's hop to the quaternions and their norm. As you should hopefully remember, quaternions have four terms (some number of units, some number of i's, some number of j's, and some number of k's), so a quaternion norm will be a sum of four squares. For example, ‖4+3i-7j+4k‖ = 90 means 90 = 4² + 3² + 7² + 4².

Since we referred to sums of two squares as S2, let's say the sums of four squares are S4. 90 is S4 because it can be written as we did above. Similarly, 7 is S4 because 7 = 2² + 1² + 1² + 1², and 22 is S4 because 22 = 4² + 2² + 1² + 1². We are of course still allowed to use zeros; 6 = 2² + 1² + 1² + 0² is S4, as is our friend 13 = 3² + 2² + 0² + 0².

The same fact from the S2 numbers still applies here: since 7 is S4 and 6 is S4, we know that 42 (the product of 7 and 6) is S4. Indeed, after a bit of fiddling I've found that 42 = 6² + 4² + 1² + 1². I don't need to do that fiddling, however, if I happen to be able to calculate quaternions! All I need to do is follow the chain, just like before: 7 × 6 = ‖2+i+j+k‖ × ‖2+i+j‖ = ‖(2+i+j+k) × (2+i+j)‖ = ‖2+3i+5j+2k‖ = 2² + 3² + 5² + 2². This is a different solution than the one I found earlier, but that's fine! As long as there's even one solution, 42 will be S4. Using the same logic, it should be clear that the product of any two S4 numbers is an S4 number.

Now, what goes wrong with three dimensions? Well, as you might have guessed, it has to do with S3 numbers, that is, numbers which can be written as a sum of three squares. If we had any three-dimensional number system, we'd be able to use the strategy we're now familiar with to prove that any product of S3 numbers is an S3 number. This would be fine, except, well…

3 × 5 = 15.

Why is this bad? See, 3 = 1² + 1² + 1² and 5 = 2² + 1² + 0², so both 3 and 5 are S3. However, you can check without too much trouble that 15 is not S3; no matter how hard you try, you can't write 15 as a sum of three squares.

And, well, that's it. The bucket has been kicked, the nails are in the coffin. You cannot make a three-dimensional number system with the kind of nice norm that the complex numbers and quaternions have. Even if someone comes to you excitedly, claiming to have figured it out, you can just toss them through these steps: • First, ask what the basis is. Complex numbers use 1 and i; quaternions use 1, i, j, and k. Let's say they answer with p, q, and r. • Second, ask them to multiply (p+q+r) by (2p+q). • Finally, well. If their system works, the resulting number should give you three numbers whose squares add to 15. Since that can't happen, you've shown that the norm is not actually multiplicative; their system doesn't capture the geometry of three dimensions.

[ratwithhands]

Read Right to Left (Manga Format)

I have returned to watching demon slayer after a year and it came up while I was having a serious late night talk with my big sister. I was talking about the relationship between Michikatsu/Kokushibo and Yoriichi and it turns out we both see each other in Yoriichi's shoes and ourselves in Michikatsu's place. Definitely surprising, but really relieving to know that we both worry too much and we are not so far apart in skill as we believe.

This is technically the first piece of fanart I've ever made for the characters in Demon Slayer, I have made OCs before but I never drew an actual character from the story. For context this is mostly just a fun "what if" scenario with them meeting in the afterlife. I like to think Yoriichi's love would reawaken Michikatsu's humanity.

[gamebunny-advance]

"Sharp Teeth" (Sketch)

I liked the idea of this doodle, but it's just not coming together the way I'd like. Maybe I'll come back to it as a concept, but whatever I'm doing right now just isn't working for me >_<;

[stealingpotatoes]

What's your opinion on Barriss and her story in Tales of the empire?

I liked it!! it was still a bit messy and needed more time or focus to work better, but it was LEAGUES better than morgan's episodes. my 2 pet peeves were "why was 4th sister 4th when she was clearly there before trilla (2nd) and reva (3rd)" (@just-prime pointed out they seem to have run out of inquisitor names LOL) and barriss' designs (partly cause head covering where???) or at least her inquisitor and episode 6 designs. both were so mid but i did a little sketchbook redesign of her inquisitor fit i watched it to heal myself

[beaulesbian]

I was once again thinking about this goofy Luffy moment after his Lucci punch™ and i had to see it frame by frame.

first the force of it throws them both away, and while Lucci is seen on screen tumbling for a long moment, Luffy is just away in a blink of an eye.

and then his funny scene - his legs are like jelly that he tries to get under control,

he stumbles, falls, rolls into a mix of all his limbs and eyes,

and then only the cloud behind him cushions his fall

- which would be interesting if he can subconsciously control that while he tries to regain the control over his movements - that the environment around him still adapts to his awakened Devil Fruit abilities and morphs to help him. Where others would probably fall through that cloud, for Luffy that cloud backs him up like a trampoline.

It's just fascinating!

[personishfive]

in which goro demonstrates the influence of capitalism in a cognitive world

unused panel

[hylianane]

I have a feeling that Sanji and Zoro’s death pact will be properly resolved in Elbaf, as it certainly doesn’t feel like we’re done with it. And while Elbaf is gearing up to be very Usopp-centric (and I can not overstate how hyped I am to see him take the spotlight again, finally), let’s not forget that this all ties back to Little Garden, the arc that properly introduced Zoro and Sanji’s rivalry by paralleling them with two rival giants who fought each other every day for over a century, but who also lost themselves in their grief when one thought the other death. The parallel isn’t even subtle, Little Garden’s biggest landmarks are the remnants of Dorry and Brogy’s dinosaur hunting competition. You know. The very same competition Zoro and Sanji posed to each other at the start of the arc?

But here’s the thing. I’m a little worried about how it’s going to be resolved. Because. Despite how readily Zoro agreed to kill Sanji if need be, he must have known that the crew would never forgive him. Zoro is Luffy’s specialest guy but Luffy would not accept any excuse as to why Sanji had to die. Nor anyone else in the crew. But. Does Sanji realize that?

Does he know that killing him would literally be the hardest thing Zoro would ever do, because it would mean literally betraying his Captain and crew? Luffy said he can’t become Pirate King without Sanji, and Zoro and Luffy swore they’d commit fucking ritualistic suicide if they got in the way of each other’s dreams, so does Sanji know where that would leave the swordsman in this case? With no Captain, no crew, and yet another dead rival and best friend (who, mind you, began to live in fear of his own biology betraying him right before dying. but the parallels between Kuina and Sanji and how they relate to Zoro could be a long ass post for another day).

I think he doesn’t know. But he can’t find out how Zoro would mourn him unless the pact actually follows through. But still, I don’t think Oda would kill Sanji, cause that’s no way to resolve this issue. So here’s my speculation about how I think it could potentially play out, following that initial line of thinking of the death pact’s resolution being set in Elbaf, specifically because of Sanji and Zoro’s parallels to Dorry and Brogy.

Like Brogy, Zoro would have to believe that he killed Sanji. That he won their final duel. He’d have to believe that Sanji has fallen and, also like Brogy, have to face that grief and hurt all alone. But in the end, like Dorry, Sanji would survive, having never actually been hurt. Because their edges have dulled after fighting for so long, no longer as capable of landing killing blows as they thought. “Not even the blades of Elbaf could endure two giants fighting for 100 years”? Something of the sort. And maybe this line of speculation is simplistic or optimistic, but the chances of it playing out like this aren’t zero, so just in case, I would want to be able to say that I called it.

[niinnyu]

Here's why I think the Gojo bait is not great writing and why you should maybe think so too (Spoilers till jjk 260).

We've spent the last few chapter consistently establishing a few things about our protagonist (Yuuji) and our antagonist(Sukuna).

1. Yuuji's father's soul is a reincarnation of Sukuna's twin: This instantly creates a connection between Sukuna and Yuuji.

As if you needed one outside of Sukuna's constant mockery of his former vessel's lack of "competance", and that most of yuuji's biggest losses can be attributed to Sukuna, building his wrath brick by brick. But surely adds to it all.

2. Yuuji feels incredibly lonely right now: Anyone he's created any sort of meaningful (?) Bond with outside of just 'hey you're an ally I can fight alongside with' is currently either dead or greatly incapacitated.

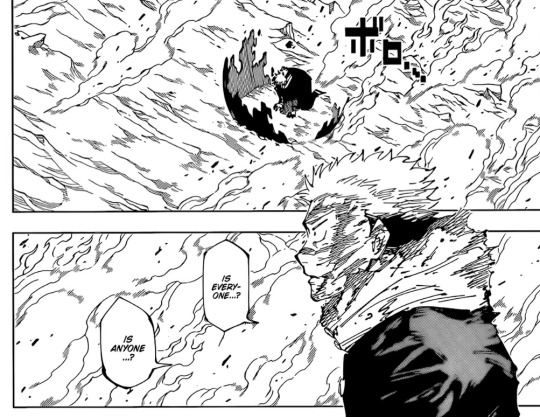
3. Also ofc the absolute damage that Yuuji has started incurring on sukuna. Damage that the slew of sorcerors before him couldn't. Forget about everyone teaching him abou love, Yuuji will show him Burning Rage.

This while also having hinted at Yuuji being possibly strong enough to do so on his own. He can go head to head with the King Of Curses with or without the help of his fellow sorcerors once he is able to harness this power.

Anything that was Gojo vs Sukuna feels absolutely irrelevant with the build up that Gege themself has been creating through the past few chapters.

Gojo's form right at the end of the chapter undercuts the pacing completely. Readers are more interested in those last 2 panels of Gojo which are completely removed from and rather jarring to the buildup between Yuuji and Sukuna. Fan interest in Gojo isn't their fault because that's what the chapter makes you focus on.

The only way I see this continue the buildup is if this is somehow Yuuji's doing or done with his knowledge, in which case it'd have been better to end the chapter by showing that Yuuji is aware of it and has an ace up his sleeve, bringing it back to the 2 relevent characters, and for people to stew in what Yuuji could be up to for a week.

But no matter what Gojo's visage there means, Yuuji in this moment has been so greatly undermined, not by his lack of strength, not by Sukuna outright demeaning him, but by the writing itself. By Gege.

And oh, how Yuuji deserves better.

[maladaptivedaydreamsx]

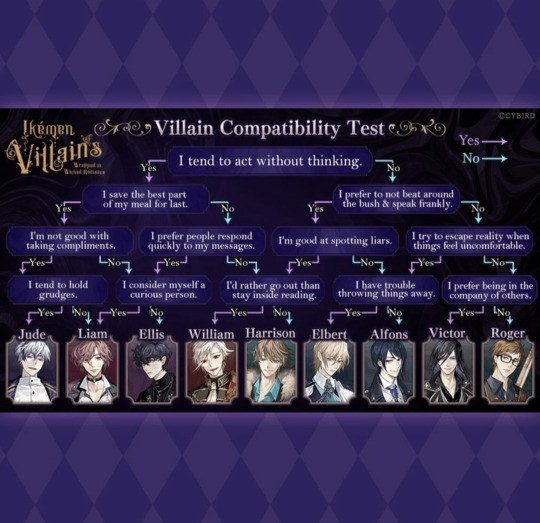
not me immediately getting jude from this

who did you guys get? 👀

[daffi-990]

WIP Wednesday 📝

Tagged by @tizniz

It’s nice having something to share ☺️. Here’s something that’s not angsty from my secret buddie wip

Eddie smiles at him, all warm and bright like the sunrise slipping in between the curtains. His fingers caresses Buck’s cheek as they travel up to card through his hair, his thumb gently stroking over Buck’s birthmark before pulling Buck towards him for another kiss.

Their lips move languidly against one another’s, the soft sounds of their kisses and content exhales filling the room.

“I love you,” Eddie says, burying his face into the crook of Buck’s neck.

He’s heard Eddie say those three words countless times over the past year and a half, yet he still feels them ignite a warm sensation that spreads throughout his body like he did that first time.

Like there’s a star in his chest bursting with colour and light, its shimmering particles embedding themselves into Buck’s bloodstream until he’s glowing with Eddie’s love.

No pressure tagging: @diazsdimples @spotsandsocks @hippolotamus @hoodie-buck @the-likesofus @wikiangela @wildlife4life @watchyourbuck @wellcollapse @alliaskisthepossibilityoflove @sibylsleaves @steadfastsaturnsrings @rainbow-nerdss @exhuastedpigeon @elvensorceress @eddiebabygirldiaz @queerdiazs @spagheddiediaz @devirnis @dangerpronebuddie @diazheartsbuckley @thewolvesof1998 @theotherbuckley @monsterrae1 @missmagooglie @captain-hen @bekkachaos @neverevan @jeeyuns @jesuisici33 @giddyupbuck @honestlydarkprincess @homerforsure @kitteneddiediaz @lover-of-mine @lonelychicago @disasterbuck @inell @smilingbuckley @bucksbignaturals @ladydorian05 and as always, anyone who has something they’d like to share -> consider this your offical tag 🏷️

[royaltea000]

Finally redrew that gangstalia Gil whore pinup! ･:*+.\(( °ω° ))/.:+🔞

[bleue-flora]