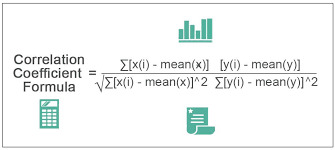
#finding correlation coefficient
Explore tagged Tumblr posts
Text
Understanding Correlation Coefficient: A Tool for My Browser App Store Users
Learn what correlation coefficient is and how it can help you make informed decisions in My Browser App Store. Read on for a comprehensive guide.
Understanding Correlation Coefficient: A Tool for My Browser App Store Users
What is Correlation Coefficient?
Correlation coefficient is a statistical measure that measures the relationship between two variables. In simpler terms, it tells you how closely two variables are related. Correlation coefficient ranges from -1 to 1. If the correlation coefficient is 1, it means that the two variables are perfectly positively correlated. If the correlation coefficient is -1, it means that the two variables are perfectly negatively correlated. A correlation coefficient of 0 indicates that there is no correlation between the two variables.
How Does Correlation Coefficient Help in My Browser App Store?
In My Browser App Store, correlation coefficient can help you make informed decisions about which apps to download. For example, let's say you're looking for a new productivity app. You can use correlation coefficient to see which apps are most closely related to productivity. You can also use correlation coefficient to see which apps have a positive or negative impact on your device's performance. By using correlation coefficient, you can make more informed decisions about which apps to download and which to avoid.
How to Calculate Correlation Coefficient?
Calculating correlation coefficient can be a bit complicated, but it's not impossible. There are several methods you can use to calculate correlation coefficient, including the Pearson correlation coefficient and the Spearman correlation coefficient. The Pearson correlation coefficient is used to measure the strength of a linear relationship between two variables, while the Spearman correlation coefficient is used to measure the strength of a non-linear relationship between two variables.
Conclusion
Correlation coefficient is an important statistical measure that can help you make informed decisions in My Browser App Store. By understanding what correlation coefficient is and how it works, you can use it to your advantage when choosing which apps to download. Whether you're looking for a productivity app or trying to improve your device's performance, correlation coefficient can be a useful tool in your decision-making proc.
Contect us
Company Name: My Browser App Store
Location: Chennai, India
Resource URL:
#correlation coefficient#correlation#pearson correlation coefficient#coefficient#correlation coefficient formula#coefficient of correlation#the correlation coefficient#what is correlation coefficient#correlation coefficient and p value#what is correlation#types of correlation#correlation and regression#correlation analysis#correlation coeficient#spss correlation coefficient#finding correlation coefficient#correlation coefficient example
0 notes
Text
Patients With Long-COVID Show Abnormal Lung Perfusion Despite Normal CT Scans - Published Sept 12, 2024
VIENNA — Some patients who had mild COVID-19 infection during the first wave of the pandemic and continued to experience postinfection symptoms for at least 12 months after infection present abnormal perfusion despite showing normal CT scans. Researchers at the European Respiratory Society (ERS) 2024 International Congress called for more research to be done in this space to understand the underlying mechanism of the abnormalities observed and to find possible treatment options for this cohort of patients.
Laura Price, MD, PhD, a consultant respiratory physician at Royal Brompton Hospital and an honorary clinical senior lecturer at Imperial College London, London, told Medscape Medical News that this cohort of patients shows symptoms that seem to correlate with a pulmonary microangiopathy phenotype.
"Our clinics in the UK and around the world are full of people with long-COVID, persisting breathlessness, and fatigue. But it has been hard for people to put the finger on why patients experience these symptoms still," Timothy Hinks, associate professor and Wellcome Trust Career Development fellow at the Nuffield Department of Medicine, NIHR Oxford Biomedical Research Centre senior research fellow, and honorary consultant at Oxford Special Airway Service at Oxford University Hospitals, England, who was not involved in the study, told Medscape Medical News.
The Study Researchers at Imperial College London recruited 41 patients who experienced persistent post-COVID-19 infection symptoms, such as breathlessness and fatigue, but normal CT scans after a mild COVID-19 infection that did not require hospitalization. Those with pulmonary emboli or interstitial lung disease were excluded. The cohort was predominantly female (87.8%) and nonsmokers (85%), with a mean age of 44.7 years. They were assessed over 1 year after the initial infection.
Exercise intolerance was the predominant symptom, affecting 95.1% of the group. A significant proportion (46.3%) presented with myopericarditis, while a smaller subset (n = 5) exhibited dysautonomia. Echocardiography did not reveal pulmonary hypertension. Laboratory findings showed elevated angiotensin-converting enzyme and antiphospholipid antibodies. "These patients are young, female, nonsmokers, and previously healthy. This is not what you would expect to see," Price said. Baseline pulmonary function tests showed preserved spirometry with forced expiratory volume in 1 second and forced vital capacity above 100% predicted. However, diffusion capacity was impaired, with a mean diffusing capacity of the lungs for carbon monoxide (DLCO) of 74.7%. The carbon monoxide transfer coefficient (KCO) and alveolar volume were also mildly reduced. Oxygen saturation was within normal limits.
These abnormalities were through advanced imaging techniques like dual-energy CT scans and ventilation-perfusion scans. These tests revealed a non-segmental and "patchy" perfusion abnormality in the upper lungs, suggesting that the problem was vascular, Price explained.
Cardiopulmonary exercise testing revealed further abnormalities in 41% of patients. Peak oxygen uptake was slightly reduced, and a significant proportion of patients showed elevated alveolar-arterial gradient and dead space ventilation during peak exercise, suggesting a ventilation-perfusion mismatch.
Over time, there was a statistically significant improvement in DLCO, from 70.4% to 74.4%, suggesting some degree of recovery in lung function. However, DLCO values did not return to normal. The KCO also improved from 71.9% to 74.4%, though this change did not reach statistical significance. Most patients (n = 26) were treated with apixaban, potentially contributing to the observed improvement in gas transfer parameters, Price said.
The researchers identified a distinct phenotype of patients with persistent post-COVID-19 infection symptoms characterized by abnormal lung perfusion and reduced gas diffusion capacity, even when CT scans appear normal. Price explains that this pulmonary microangiopathy may explain the persistent symptoms. However, questions remain about the underlying mechanisms, potential treatments, and long-term outcomes for this patient population.
Causes and Treatments Remain a Mystery Previous studies have suggested that COVID-19 causes endothelial dysfunction, which could affect the small blood vessels in the lungs. Other viral infections, such as HIV, have also been shown to cause endothelial dysfunction. However, researchers don't fully understand how this process plays out in patients with COVID-19.
"It is possible these patients have had inflammation insults that have damaged the pulmonary vascular endothelium, which predisposes them to either clotting at a microscopic level or ongoing inflammation," said Hinks.
Some patients (10 out of 41) in the cohort studied by the Imperial College London's researchers presented with Raynaud syndrome, which might suggest a physiological link, Hinks explains. "Raynaud's is a condition of vascular control or dysregulation, and potentially, there could be a common factor contributing to both breathlessness and Raynaud's."
He said there is an encouraging signal that these patients improve over time, but their recovery might be more complex and lengthy than for other patients. "This cohort will gradually get better. But it raises questions and gives a point that there is a true physiological deficit in some people with long-COVID."
Price encouraged physicians to look beyond conventional diagnostic tools when visiting a patient whose CT scan looks normal yet experiences fatigue and breathlessness. Not knowing what causes the abnormalities observed in this group of patients makes treatment extremely challenging. "We need more research to understand the treatment implications and long-term impact of these pulmonary vascular abnormalities in patients with long-COVID," Price concluded.
#long covid#covid#covid news#mask up#pandemic#covid 19#wear a mask#public health#sars cov 2#still coviding#coronavirus#wear a respirator#covid conscious#covid is airborne#covid isn't over#covid pandemic#covid19#covidー19
72 notes
·
View notes
Text
I think I'm as ready as I can be for my presentation. I have the slides all ready, though I still don't quite understand what I'm saying and I haven't learnt anything by heart so I'll be talking from my slide notes. And I might struggle to answer questions if there will be questions because my notes are spread over three print outs of multiple pages. X3
Also, those who know statistics, please tell me if my stupid meme below the cut makes sense X3

(I can't actually confirm that it's lower. It's a correlation coefficient of r: -0.30. But since I also have graphs with means I can see that it's lower. I just don't know if the magic of R confirms my findings or I just did a test wrong somewhere *lol*)
40 notes
·
View notes
Text
a Basic Linear Regression Model
What is linear regression?
Linear regression analysis is used to predict the value of a variable based on the value of another variable. The variable you want to predict is called the dependent variable. The variable you are using to predict the other variable's value is called the independent variable.
This form of analysis estimates the coefficients of the linear equation, involving one or more independent variables that best predict the value of the dependent variable. Linear regression fits a straight line or surface that minimizes the discrepancies between predicted and actual output values. There are simple linear regression calculators that use a “least squares” method to discover the best-fit line for a set of paired data. You then estimate the value of X (dependent variable)
n statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable.[1][2][3][4][5] That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the x and y coordinates in a Cartesian coordinate system) and finds a linear function (a non-vertical straight line) that, as accurately as possible, predicts the dependent variable values as a function of the independent variable. The adjective simple refers to the fact that the outcome variable is related to a single predictor.
It is common to make the additional stipulation that the ordinary least squares (OLS) method should be used: the accuracy of each predicted value is measured by its squared residual (vertical distance between the point of the data set and the fitted line), and the goal is to make the sum of these squared deviations as small as possible. In this case, the slope of the fitted line is equal to the correlation between y and x corrected by the ratio of standard deviations of these variables. The intercept of the fitted line is such that the line passes through the center of mass (x, y) of the data points.
Formulation and computation
[edit]
This relationship between the true (but unobserved) underlying parameters α and β and the data points is called a linear regression model.
Here we have introduced
x¯ and y¯ as the average of the xi and yi, respectively
Δxi and Δyi as the deviations in xi and yi with respect to their respective means.
Expanded formulas
[edit]
Interpretation
[edit]
Relationship with the sample covariance matrix
[edit]
where
rxy is the sample correlation coefficient between x and y
sx and sy are the uncorrected sample standard deviations of x and y
sx2 and sx,y are the sample variance and sample covariance, respectively
Interpretation about the slope
[edit]
Interpretation about the intercept
Interpretation about the correlation
[edit]
Numerical properties
[edit]
The regression line goes through the center of mass point, (x¯,y¯), if the model includes an intercept term (i.e., not forced through the origin).
The sum of the residuals is zero if the model includes an intercept term:∑i=1nε^i=0.
The residuals and x values are uncorrelated (whether or not there is an intercept term in the model), meaning:∑i=1nxiε^i=0
The relationship between ρxy (the correlation coefficient for the population) and the population variances of y (σy2) and the error term of ϵ (σϵ2) is:[10]: 401 σϵ2=(1−ρxy2)σy2For extreme values of ρxy this is self evident. Since when ρxy=0 then σϵ2=σy2. And when ρxy=1 then σϵ2=0.
Statistical properties
[edit]
Description of the statistical properties of estimators from the simple linear regression estimates requires the use of a statistical model. The following is based on assuming the validity of a model under which the estimates are optimal. It is also possible to evaluate the properties under other assumptions, such as inhomogeneity, but this is discussed elsewhere.[clarification needed]
Unbiasedness
[edit]
Variance of the mean response
[edit]
where m is the number of data points.
Variance of the predicted response
[edit]
Further information: Prediction interval
Confidence intervals
[edit]
The standard method of constructing confidence intervals for linear regression coefficients relies on the normality assumption, which is justified if either:
the errors in the regression are normally distributed (the so-called classic regression assumption), or
the number of observations n is sufficiently large, in which case the estimator is approximately normally distributed.
The latter case is justified by the central limit theorem.
Normality assumption
[edit]
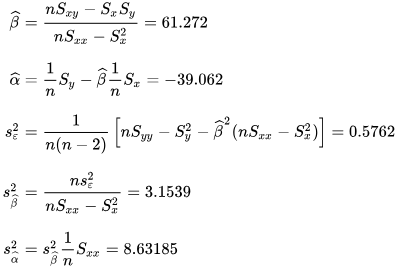
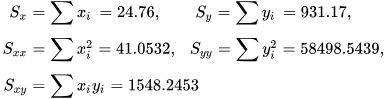
Asymptotic assumption
[edit]
The alternative second assumption states that when the number of points in the dataset is "large enough", the law of large numbers and the central limit theorem become applicable, and then the distribution of the estimators is approximately normal. Under this assumption all formulas derived in the previous section remain valid, with the only exception that the quantile t*n−2 of Student's t distribution is replaced with the quantile q* of the standard normal distribution. Occasionally the fraction 1/n−2 is replaced with 1/n. When n is large such a change does not alter the results appreciably.
Numerical example
[edit]
See also: Ordinary least squares § Example, and Linear least squares § Example
Alternatives
[edit]Calculating the parameters of a linear model by minimizing the squared error.
In SLR, there is an underlying assumption that only the dependent variable contains measurement error; if the explanatory variable is also measured with error, then simple regression is not appropriate for estimating the underlying relationship because it will be biased due to regression dilution.
Other estimation methods that can be used in place of ordinary least squares include least absolute deviations (minimizing the sum of absolute values of residuals) and the Theil–Sen estimator (which chooses a line whose slope is the median of the slopes determined by pairs of sample points).
Deming regression (total least squares) also finds a line that fits a set of two-dimensional sample points, but (unlike ordinary least squares, least absolute deviations, and median slope regression) it is not really an instance of simple linear regression, because it does not separate the coordinates into one dependent and one independent variable and could potentially return a vertical line as its fit. can lead to a model that attempts to fit the outliers more than the data.
Line fitting
[edit]
This section is an excerpt from Line fitting.[edit]
Line fitting is the process of constructing a straight line that has the best fit to a series of data points.
Several methods exist, considering:
Vertical distance: Simple linear regression
Resistance to outliers: Robust simple linear regression
Perpendicular distance: Orthogonal regression (this is not scale-invariant i.e. changing the measurement units leads to a different line.)
Weighted geometric distance: Deming regression
Scale invariant approach: Major axis regression This allows for measurement error in both variables, and gives an equivalent equation if the measurement units are altered.
Simple linear regression without the intercept term (single regressor)
[edit]
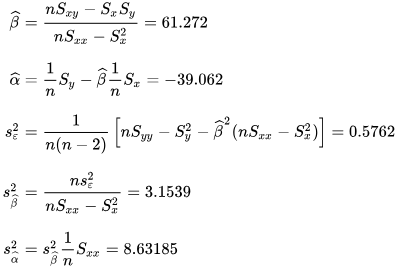
2 notes
·
View notes
Text
Inhibition of EIF4E Downregulates VEGFA and CCND1 Expression to Suppress Ovarian Cancer Tumor Progression by Jing Wang in Journal of Clinical Case Reports Medical Images and Health Sciences
Abstract
This study investigates the role of EIF4E in ovarian cancer and its influence on the expression of VEGFA and CCND1. Differential expression analysis of VEGFA, CCND1, and EIF4E was conducted using SKOV3 cells in ovarian cancer patients and controls. Correlations between EIF4E and VEGFA/CCND1 were assessed, and three-dimensional cell culture experiments were performed. Comparisons of EIF4E, VEGFA, and CCND1 mRNA and protein expression between the EIF4E inhibitor 4EGI-1-treated group and controls were carried out through RT-PCR and Western blot. Our findings demonstrate elevated expression of EIF4E, VEGFA, and CCND1 in ovarian cancer patients, with positive correlations. The inhibition of EIF4E by 4EGI-1 led to decreased SKOV3 cell clustering and reduced mRNA and protein levels of VEGFA and CCND1. These results suggest that EIF4E plays a crucial role in ovarian cancer and its inhibition may modulate VEGFA and CCND1 expression, underscoring EIF4E as a potential therapeutic target for ovarian cancer treatment.
Keywords: Ovarian cancer; Eukaryotic translation initiation factor 4E; Vascular endothelial growth factor A; Cyclin D1
Introduction
Ovarian cancer ranks high among gynecological malignancies in terms of mortality, necessitating innovative therapeutic strategies [1]. Vascular endothelial growth factor (VEGF) plays a pivotal role in angiogenesis, influencing endothelial cell proliferation, migration, vascular permeability, and apoptosis regulation [2, 3]. While anti-VEGF therapies are prominent in malignancy treatment [4], the significance of cyclin D1 (CCND1) amplification in cancers, including ovarian, cannot be overlooked, as it disrupts the cell cycle, fostering tumorigenesis [5, 6]. Eukaryotic translation initiation factor 4E (EIF4E), central to translation initiation, correlates with poor prognoses in various cancers due to its dysregulated expression and activation, particularly in driving translation of growth-promoting genes like VEGF [7, 8]. Remarkably, elevated EIF4E protein levels have been observed in ovarian cancer tissue, suggesting a potential role in enhancing CCND1 translation, thereby facilitating cell cycle progression and proliferation [9]. Hence, a novel conjecture emerges: by modulating EIF4E expression, a dual impact on VEGF and CCND1 expression might be achieved. This approach introduces an innovative perspective to impede the onset and progression of ovarian cancer, distinct from existing literature, and potentially offering a unique therapeutic avenue.
Materials and Methods
Cell Culture
Human ovarian serous carcinoma cell line SKOV3 (obtained from the Cell Resource Center, Shanghai Institutes for Biological Sciences, Chinese Academy of Sciences) was cultured in DMEM medium containing 10% fetal bovine serum. Cells were maintained at 37°C with 5% CO2 in a cell culture incubator and subcultured every 2-3 days.
Three-Dimensional Spheroid Culture
SKOV3 cells were prepared as single-cell suspensions and adjusted to a concentration of 5×10^5 cells/mL. A volume of 0.5 mL of single-cell suspension was added to Corning Ultra-Low Attachment 24-well microplates and cultured at 37°C with 5% CO2 for 24 hours. Subsequently, 0.5 mL of culture medium or 0.5 mL of EIF4E inhibitor 4EGI-1 (Selleck, 40 μM) was added. After 48 hours, images were captured randomly from five different fields—upper, lower, left, right, and center—using an inverted phase-contrast microscope. The experiment was repeated three times.
GEPIA Online Analysis
The GEPIA online analysis tool (http://gepia.cancer-pku.cn/index.html) was utilized to assess the expression of VEGFA, CCND1, and EIF4E in ovarian cancer tumor samples from TCGA and normal samples from GTEx. Additionally, Pearson correlation coefficient analysis was employed to determine the correlation between VEGF and CCND1 with EIF4E.
RT-PCR
RT-PCR was employed to assess the mRNA expression levels of EIF4E, VEGF, and CCND1 in treatment and control group samples. Total RNA was extracted using the RNA extraction kit from Vazyme, followed by reverse transcription to obtain cDNA using their reverse transcription kit. Amplification was carried out using SYBR qPCR Master Mix as per the recommended conditions from Vazyme. GAPDH was used as an internal reference, and the primer sequences for PCR are shown in Table 1.
Amplification was carried out under the following conditions: an initial denaturation step at 95°C for 60 seconds, followed by cycling conditions of denaturation at 95°C for 10 seconds, annealing at 60°C for 30 seconds, repeated for a total of 40 cycles. Melting curves were determined under the corresponding conditions. Each sample was subjected to triplicate experiments. The reference gene GAPDH was used for normalization. The relative expression levels of the target genes were calculated using the 2-ΔΔCt method.
Western Blot
Western Blot technique was employed to assess the protein expression levels of EIF4E, VEGF, and CCND1 in the treatment and control groups. Initially, cell samples collected using RIPA lysis buffer were lysed, and the total protein concentration was determined using the BCA assay kit (Shanghai Biyuntian Biotechnology, Product No.: P0012S). Based on the detected concentration, 20 μg of total protein was loaded per well. Electrophoresis was carried out using 5% stacking gel and 10% separating gel. Subsequently, the following primary antibodies were used for immune reactions: rabbit anti-human polyclonal antibody against phospho-EIF4E (Beijing Boao Sen Biotechnology, Product No.: bs-2446R, dilution 1:1000), mouse anti-human monoclonal antibody against EIF4E (Wuhan Sanying Biotechnology, Product No.: 66655-1-Ig, dilution 1:5000), mouse anti-human monoclonal antibody against VEGFA (Wuhan Sanying Biotechnology, Product No.: 66828-1-Ig, dilution 1:1000), mouse anti-human monoclonal antibody against CCND1 (Wuhan Sanying Biotechnology, Product No.: 60186-1-Ig, dilution 1:5000), and mouse anti-human monoclonal antibody against GAPDH (Shanghai Biyuntian Biotechnology, Product No.: AF0006, dilution 1:1000). Subsequently, secondary antibodies conjugated with horseradish peroxidase (Shanghai Biyuntian Biotechnology, Product No.: A0216, dilution 1:1000) were used for immune reactions. Finally, super-sensitive ECL chemiluminescence reagent (Shanghai Biyuntian Biotechnology, Product No.: P0018S) was employed for visualization, and the ChemiDocTM Imaging System (Bio-Rad Laboratories, USA) was used for image analysis.
Statistical Analysis
GraphPad software was used for statistical analysis. Data were presented as (x ± s) and analyzed using the t-test for quantitative data. Pearson correlation analysis was performed for assessing correlations. A significance level of P < 0.05 was considered statistically significant.
Results
3D Cell Culture of SKOV3 Cells and Inhibitory Effect of 4EGI-1 on Aggregation
In this experiment, SKOV3 cells were subjected to 3D cell culture, and the impact of the EIF4E inhibitor 4EGI-1 on ovarian cancer cell aggregation was investigated. As depicted in Figure 1, compared to the control group (Figure 1A), the diameter of the SKOV3 cell spheres significantly decreased in the treatment group (Figure 1B) when exposed to 4EGI-1 under identical culture conditions. This observation indicates that inhibiting EIF4E expression effectively suppresses tumor aggregation.
Expression and Correlation Analysis of VEGFA, CCND1, and EIF4E in Ovarian Cancer Samples
To investigate the expression of VEGFA, CCND1, and EIF4E in ovarian cancer, we utilized the GEPIA online analysis tool and employed the Pearson correlation analysis method to compare expression differences between tumor and normal groups. As depicted in Figures 2A-C, the results indicate significantly elevated expression levels of VEGFA, CCND1, and EIF4E in the tumor group compared to the normal control group. Notably, the expression differences of VEGFA and CCND1 were statistically significant (p < 0.05). Furthermore, the correlation analysis revealed a positive correlation between VEGFA and CCND1 with EIF4E (Figures 2D-E), and this correlation exhibited significant statistical differences (p < 0.001). These findings suggest a potential pivotal role of VEGFA, CCND1, and EIF4E in the initiation and progression of ovarian cancer, indicating the presence of intricate interrelationships among them.
EIF4E, VEGFA, and CCND1 mRNA Expression in SKOV3 Cells
To investigate the function of EIF4E in SKOV3 cells, we conducted RT-PCR experiments comparing EIF4E inhibition group with the control group. As illustrated in Figure 3, treatment with 4EGI-1 significantly reduced EIF4E expression (0.58±0.09 vs. control, p < 0.01). Concurrently, mRNA expression of VEGFA (0.76±0.15 vs. control, p < 0.05) and CCND1 (0.81±0.11 vs. control, p < 0.05) also displayed a substantial decrease. These findings underscore the significant impact of EIF4E inhibition on the expression of VEGFA and CCND1, indicating statistically significant differences.
Protein Expression Profiles in SKOV3 Cells with EIF4E Inhibition and Control Group
Protein expression of EIF4E, VEGFA, and CCND1 was assessed using Western Blot in the 4EGI-1 treatment group and the control group. As presented in Figure 4, the expression of p-EIF4E was significantly lower in the 4EGI-1 treatment group compared to the control group (0.33±0.14 vs. control, p < 0.001). Simultaneously, the expression of VEGFA (0.53±0.18 vs. control, p < 0.01) and CCND1 (0.44±0.16 vs. control, p < 0.001) in the 4EGI-1 treatment group exhibited a marked reduction compared to the control group.
Discussion
EIF4E is a post-transcriptional modification factor that plays a pivotal role in protein synthesis. Recent studies have underscored its critical involvement in various cancers [10]. In the context of ovarian cancer research, elevated EIF4E expression has been observed in late-stage ovarian cancer tissues, with low EIF4E expression correlating to higher survival rates [9]. Suppression of EIF4E expression or function has been shown to inhibit ovarian cancer cell proliferation, invasion, and promote apoptosis. Various compounds and drugs that inhibit EIF4E have been identified, rendering them potential candidates for ovarian cancer treatment [11]. Based on the progressing understanding of EIF4E's role in ovarian cancer, inhibiting EIF4E has emerged as a novel therapeutic avenue for the disease. 4EGI-1, a cap-dependent translation small molecule inhibitor, has been suggested to disrupt the formation of the eIF4E complex [12]. In this study, our analysis of public databases revealed elevated EIF4E expression in ovarian cancer patients compared to normal controls. Furthermore, through treatment with 4EGI-1 in the SKOV3 ovarian cancer cell line, we observed a capacity for 4EGI-1 to inhibit SKOV3 cell spheroid formation. Concurrently, results from PCR and Western Blot analyses demonstrated effective EIF4E inhibition by 4EGI-1. Collectively, 4EGI-1 effectively suppresses EIF4E expression and may exert its effects on ovarian cancer therapy by modulating EIF4E.
Vascular Endothelial Growth Factor (VEGF) is a protein that stimulates angiogenesis and increases vascular permeability, playing a crucial role in tumor growth and metastasis [13]. In ovarian cancer, excessive release of VEGF by tumor cells leads to increased angiogenesis, forming a new vascular network to provide nutrients and oxygen to tumor cells. The formation of new blood vessels enables tumor growth, proliferation, and facilitates tumor cell dissemination into the bloodstream, contributing to distant metastasis [14]. As a significant member of the VEGF family, VEGFA has been extensively studied, and it has been reported that VEGFA expression is notably higher in ovarian cancer tumors [15], consistent with our public database analysis. Furthermore, elevated EIF4E levels have been associated with increased malignant tumor VEGF mRNA translation [16]. Through the use of the EIF4E inhibitor 4EGI-1 in ovarian cancer cell lines, we observed a downregulation in both mRNA and protein expression levels of VEGFA. This suggests that EIF4E inhibition might affect ovarian cancer cell angiogenesis capability through downregulation of VEGF expression.
Cyclin D1 (CCND1) is a cell cycle regulatory protein that participates in controlling cell entry into the S phase and the cell division process. In ovarian cancer, overexpression of CCND1 is associated with increased tumor proliferation activity and poor prognosis [17]. Elevated CCND1 levels promote cell cycle progression, leading to uncontrolled cell proliferation [18]. Additionally, CCND1 can activate cell cycle-related signaling pathways, promoting cancer cell growth and invasion capabilities [19]. Studies have shown that CCND1 gene expression is significantly higher in ovarian cancer tissues compared to normal ovarian tissues [20], potentially promoting proliferation and cell cycle progression through enhanced cyclin D1 translation [9]. Our public database analysis results confirm these observations. Furthermore, treatment with the EIF4E inhibitor 4EGI-1 in ovarian cancer cell lines resulted in varying degrees of downregulation in CCND1 mRNA and protein levels. This indicates that EIF4E inhibition might affect ovarian cancer cell proliferation and cell cycle progression through regulation of CCND1 expression.
In conclusion, overexpression of EIF4E appears to be closely associated with the clinical and pathological characteristics of ovarian cancer patients. In various tumors, EIF4E is significantly correlated with VEGF and cyclin D1, suggesting its role in the regulation of protein translation related to angiogenesis and growth [9, 21]. The correlation analysis results in our study further confirmed the positive correlation among EIF4E, VEGFA, and CCND1 in ovarian cancer. Simultaneous inhibition of EIF4E also led to downregulation of VEGFA and CCND1 expression, validating their interconnectedness. Thus, targeted therapy against EIF4E may prove to be an effective strategy for treating ovarian cancer. However, further research and clinical trials are necessary to assess the safety and efficacy of targeted EIF4E therapy, offering more effective treatment options for ovarian cancer patients.
Acknowledgments:
Funding: This study was supported by the Joint Project of Southwest Medical University and the Affiliated Traditional Chinese Medicine Hospital of Southwest Medical University (Grant No. 2020XYLH-043).
Conflict of Interest: The authors declare no conflicts of interest.
#Ovarian cancer#Eukaryotic translation initiation factor 4E#Vascular endothelial growth factor A#Cyclin D1#Review Article in Journal of Clinical Case Reports Medical Images and Health Sciences .#jcrmhs
2 notes
·
View notes
Text
To generate a correlation coefficient using Python, you can follow these steps:1. **Prepare Your Data**: Ensure you have two quantitative variables ready to analyze.2. **Load Your Data**: Use pandas to load and manage your data.3. **Calculate the Correlation Coefficient**: Use the `pearsonr` function from `scipy.stats`.4. **Interpret the Results**: Provide a brief interpretation of your findings.5. **Submit Syntax and Output**: Include the code and output in your blog entry along with your interpretation.### Example CodeHere is an example using a sample dataset:```pythonimport pandas as pdfrom scipy.stats import pearsonr# Sample datadata = {'Variable1': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'Variable2': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11]}df = pd.DataFrame(data)# Calculate the correlation coefficientcorrelation, p_value = pearsonr(df['Variable1'], df['Variable2'])# Output resultsprint("Correlation Coefficient:", correlation)print("P-Value:", p_value)# Interpretationif p_value < 0.05: print("There is a significant linear relationship between Variable1 and Variable2.")else: print("There is no significant linear relationship between Variable1 and Variable2.")```### Output```plaintextCorrelation Coefficient: 1.0P-Value: 0.0There is a significant linear relationship between Variable1 and Variable2.```### Blog Entry Submission**Syntax Used:**```pythonimport pandas as pdfrom scipy.stats import pearsonr# Sample datadata = {'Variable1': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'Variable2': [2, 3, 4, 5, 6, 7, 8, 9, 10, 11]}df = pd.DataFrame(data)# Calculate the correlation coefficientcorrelation, p_value = pearsonr(df['Variable1'], df['Variable2'])# Output resultsprint("Correlation Coefficient:", correlation)print("P-Value:", p_value)# Interpretationif p_value < 0.05: print("There is a significant linear relationship between Variable1 and Variable2.")else: print("There is no significant linear relationship between Variable1 and Variable2.")```**Output:**```plaintextCorrelation Coefficient: 1.0P-Value: 0.0There is a significant linear relationship between Variable1 and Variable2.```**Interpretation:**The correlation coefficient between Variable1 and Variable2 is 1.0, indicating a perfect positive linear relationship. The p-value is 0.0, which is less than 0.05, suggesting that the relationship is statistically significant. Therefore, we can conclude that there is a significant linear relationship between Variable1 and Variable2 in this sample.This example uses a simple dataset for clarity. Make sure to adapt the data and context to fit your specific research question and dataset for your assignment.
2 notes
·
View notes
Text
Originally posted to Facebook, and unaltered from that text:
----------
The 2022 Nobel Prize in Physics was awarded for what is commonly regarded as "confirmation of quantum physics" but this is muddleheaded nonsense. What it actually was awarded for is what is considered by physicists proof that no mathematics except quantum mechanics can derive the correlation coefficient of the following experiment. You have to have a clear head to see that this is the actual claim, but it assuredly and inarguably is.
Here is the experiment, and I will derive its correlation without using quantum mechanics. I am not sure anyone knew how to do this before I did, and it took me about 20 years to find.
A light source emits two photons left and right, randomly with one polarized vertically and the other horizontally. Each photon goes through a polarizing beam splitter, whose two output channels +1 and -1 are finished by photodetectors. The left PBS has angle a', the right PBS has angle b'.
There is a law of physics called the Law of Malus, where the accent is on the u in Malus. When applied to a horizontal photon in a polarizing beam splitter with angle a', it says the photon will go through the +1 channel with probability cos² a', the -1 channel with probability sin² a'. Similarly if the angle is b'. If the photon is vertical, the cos and sin are reversed. (I am leaving out all other possible angles. The full Law also accounts for them.)
This is not the traditional statement of the Law of Malus, but is what we want. When you are using quantum mechanics, the rules are written funky and probably are not called the Law of Malus, but are an obfuscated way of saying what we just said.
By a lot of tedious but routine probability theory that I will skip here, but which you can find for instance in my "How to Entangle Craytons" at https://crudfactory.com, you get that the probability of +1 detection on both sides is the same as the probability of -1 detection on both sides, and equals (1/2) sin² a' cos² b' + (1/2) cos² a' sin² b'. The probability of of +1 detection on only one side is (1/2) sin² a' sin² b' + (1/2) cos² a' cos² b'. Call the probabilities in obvious ways P++, P--, P+-, P-+. Then I can get the correlation as follows:
corr = (+1)(+1)(P++) + (-1)(-1)(P--) + (+1)(-1)(P+-) + (-1)(+1)(P-+)
= -cos 2a' cos 2b'
where I have used a double angle identity you can find in the Handbook of Mathematical Sciences, etc.
Here is where I do something that has evaded the mental capacities of Nobel Prize winning physicists.
Let it be noted that we already know that the supposedly "quantum" correlation for an experiment with PBS angles a and b is -cos 2(a - b). One thing I have never seen physicists point out about this expression, despite the bleeding obviousness once pointed out, is its invariance under in-unison rotation of the angles a and b. What this means is that you can ALWAYS rotate the problem so that one of the angles is zero, without changing the result.
This is simple mathematics. But physicists are not taught actual mathematics. They are taught a kind of pseudo-mathematics not based on theorems, proofs, or thorough reasoning.
Let us set b' = 0 and let a' = a - b, for any PBS angles a and b. In other words, we simply rotate the problem by -b to convert it to an already-solved problem for a' = anything, b' = 0. We have thus derived the correlation, without using quantum mechanics:
corr = -cos 2(a - b)
The 2022 Nobel Prize in Physics is a load of hogwash. There is no such thing as "particle entanglement", there is no such thing as "quantum non-locality", there is no "confirmation of quantum physics", and there is no such thing as a "quantum" computer.
But I have more general proofs of the matter than that, which do not even require mathematical expressions.
What I have done here is show with that Einstein was wrong that statistical mechanics was what underlay the type of experiment described. It is actually just ordinary pinball-like mechanics! Einstein never wavered in believing there was no distinct "quantum" physics, and was ostracized for it. But he was right.
But I have gone beyond that and come up with meta-mathematical arguments that are of different kind entirely. Those are for a separate rage.
A late postscript:
This derivation may be a little confusing, because why does b' have to be set to zero? Clauser inequalities treat b' as nonzero, but obviously, from the derivation above, this is wrong.
Here is an explanation—
If you do NOT set b' to zero, how can you distinguish which particle each angle apples to? You cannot. You are actually solving the wrong problem.
This is what Clauser inequalities do—they solve the wrong problem.
With b' set to zero and symmetry of cos, we solve the right problem.
Really it would be better to note the difficulty at the beginning and set b' to zero right away. Going through the motions above, however, helps illustrate where physicists err by NOT setting b' to zero, when they try to derive "classical" solutions and get incorrect results.
(That their results were incorrect should have been obvious, because any result different from that of quantum mechanics MUST have been derived incorrectly. All math methods must reach the same conclusion, or math is inconsistent. But that is for another rage.)
1 note
·
View note
Text
Investigating the relationship between inbreeding and life expectancy in dogs: mongrels live longer than pure breeds
This study aimed to investigate the establishment of relationship between inbreeding and life expectancy in dogs. A dataset of N = 30,563 dogs sourced from the VetCompass™ Program, UK was made available by the Royal Veterinary College, University of London, containing information about breed and longevity and was subject to survival analysis. A Cox regression proportional hazards model was used to differentiate survivability in three groups of dogs (mongrel, cross-bred and pure breed). The model was found highly significant (p < 0.001) and we found that mongrel dog had the highest life expectancy, followed by cross-bred dogs with only one purebred ancestor and purebred dogs had the lowest life expectancy. A second Cox regression was also found highly significant (p < 0.001) differentiating the lifespan of different dog breed and correlating positively the hazard ratio and the Genetic Illness Severity Index for Dogs (GISID). The results show that survivability is higher in mongrel dogs followed by cross-bred with one of the ancestor only as a pure breed, and pure breed dog have the highest morbidity level. Higher morbidity is associated with higher GISID scores, and therefore, higher inbreeding coefficients. These findings have important implications for dog breeders, owners, and animal welfare organizations seeking to promote healthier, longer-lived dogs.
4 notes
·
View notes
Text
Master Statistical Arbitrage with Take Profit Orders The Hidden Formula for Forex Success: Unlocking Statistical Arbitrage with Take Profit Orders The Forex market—a place where fortunes are made and lost faster than you can say “pips”—is brimming with opportunities for traders who know where to look. One such hidden gem is the powerful combination of statistical arbitrage and take profit orders. If you’ve ever wondered how some traders seem to have a crystal ball for the market, you’re in the right place. Let’s dive into this game-changing strategy, laced with advanced insights, actionable tactics, and the kind of humor that makes learning about trading less like reading a textbook and more like a chat with a savvy, slightly funny friend. Statistical Arbitrage: The Secret Weapon You’ve Been Ignoring First, a quick primer. Statistical arbitrage, or stat arb for short, isn’t about magic; it’s about math. It involves exploiting price inefficiencies between correlated currency pairs or instruments. Think of it as spotting two runners in a race who usually cross the finish line together. If one suddenly pulls ahead, you bet on the laggard catching up. Here’s the kicker: most traders overlook stat arb because it sounds too complex. But trust me, if you can track your coffee rewards points, you can grasp this. Why It Works: - Mean Reversion: Prices of correlated assets often revert to their historical relationship. - Low Risk, High Reward: By focusing on the relative performance, you hedge against market-wide risks. How to Use It: - Identify correlated pairs (e.g., EUR/USD and GBP/USD). - Analyze their historical price spread. - Enter trades when the spread deviates significantly from the mean. - Set your take profit orders (we’ll get to this magic in a moment) based on the expected reversion. Take Profit Orders: Your Built-In Safety Net If statistical arbitrage is the engine, take profit orders are the brakes—and let’s be real, nobody drives a Ferrari without brakes. These orders automatically close your position when the price hits a pre-set target, ensuring you lock in profits without second-guessing yourself. Why They’re Essential: - Emotion-Free Trading: Avoid the “one more minute” syndrome that’s cost traders millions. - Efficient Execution: Capture gains even if you’re asleep or binge-watching your favorite series. - Risk Management: Protect against market reversals. Pro Tips for Setting Take Profit Orders: - Align with Your Strategy: For stat arb, calculate the historical spread range and set your order near the average reversion point. - Use ATR (Average True Range): Multiply the ATR by 1.5 to set a realistic profit target based on current market volatility. - Combine with Stop Loss Orders: Always balance your take profit and stop loss levels to ensure a favorable risk-reward ratio (e.g., 1:2). The Ninja Tactic: Pairing Stat Arb with Take Profit Orders Now, here’s where the real magic happens. Pairing statistical arbitrage with take profit orders transforms you from a hopeful trader to a disciplined, strategy-driven operator. Step-by-Step Guide: - Research Correlated Pairs: Use tools like Pearson correlation coefficients to find highly correlated pairs. - Set Your Entry Points: Identify extreme deviations from the historical spread. - Calculate Targets: Based on historical data, determine the mean reversion point. - Place Take Profit Orders: Use calculated targets to lock in profits as soon as the spread narrows. - Automate with Smart Tools: Platforms like the StarseedFX Smart Trading Tool can optimize lot sizes and automate order management. Example: Imagine EUR/USD and GBP/USD have a historical price spread of 0.0100. Suddenly, EUR/USD surges, creating a spread of 0.0150. Enter a long position on GBP/USD and a short position on EUR/USD. Set take profit orders to close both trades when the spread reverts to 0.0100. Voilà—you’ve just executed a low-risk, high-reward strategy. Myth-Busting: Why Most Traders Get It Wrong Let’s address some common misconceptions about these strategies: - Myth: “Statistical arbitrage is too complex for retail traders.” - Truth: With modern trading platforms, tools, and online courses (like this one), even beginners can master stat arb. - Myth: “Take profit orders limit potential gains.” - Truth: They’re designed to maximize gains by removing emotional decision-making. Besides, you can always trail your stop to capture extended moves. - Myth: “Correlations don’t last.” - Truth: While correlations can change, they’re reliable in the short to medium term—perfect for stat arb. Advanced Insights: Underground Trends in Stat Arb To stay ahead of the curve, keep these trends on your radar: - AI and Machine Learning: - Use algorithms to identify micro-inefficiencies faster than human traders. Platforms like QuantConnect are making this accessible. - Multi-Asset Arbitrage: - Expand beyond currency pairs. Try commodities or indices with strong correlations to Forex pairs. - Geopolitical Data Integration: - Monitor news and economic indicators to predict spread deviations. Stay updated with Forex News Today. Ready to Level Up? Statistical arbitrage and take profit orders are the dynamic duo you’ve been waiting for. By understanding and implementing these strategies, you’ll not only sidestep common pitfalls but also unlock elite tactics most traders never consider. Trading is like dating—you need the right mix of math and emotion to make it work. By pairing stat arb with take profit orders, you’ll turn volatile markets into predictable opportunities. And remember, it’s not about being perfect; it’s about being profitable. —————– Image Credits: Cover image at the top is AI-generated Read the full article
0 notes
Text
Also preserved in our archive (Daily updates!)
At least the tool we kinda have is accurate...
Wastewater surveillance has gained attention as an effective method for monitoring regional infection trends. In July 2024, the National Action Plan for Novel Influenza, etc. included the regular implementation of wastewater surveillance during normal times, with results to be published periodically in Japan. However, when viral concentrations in wastewater are measured inadequately or show significant variability, the correlation with actual infection trends may weaken. This study identified the necessary methods for accurately monitoring COVID-19 infection patterns.
The research team analyzed wastewater data obtained from the city of Sapporo in northern Japan between April 2021 and September 2023. The dataset featured high sensitivity (100 times greater than the standard method) and high reproducibility (standard deviation below 0.4 at log10 values) and was supported by a substantial sample size of 15 samples per week, totaling 1,830 samples over a sufficient survey period of two and a half years. The correlation coefficient between the number of infected individuals and the viral concentration in the wastewater was 0.87, indicating that this method effectively tracks regional infection trends. Additionally, the research team concluded desirable survey frequency requires at least three samples, preferably five samples, per week.
The study provides detailed guidance on wastewater surveillance methodologies for understanding infection trends, focusing on data processing, analytical sensitivity, and survey frequency. As wastewater surveillance during normal times becomes more widely implemented and its results increasingly published, this study's findings are expected to serve as valuable resources for decision making.
Source: Osaka University
Journal reference: Murakami, M., et al. (2024) Evaluating survey techniques in wastewater-based epidemiology for accurate COVID-19 incidence estimation. The Science of the Total Environment. doi.org/10.1016/j.scitotenv.2024.176702. www.sciencedirect.com/science/article/pii/S0048969724068591?via%3Dihub
#mask up#covid#pandemic#wear a mask#public health#wear a respirator#covid 19#still coviding#coronavirus#sars cov 2
34 notes
·
View notes
Photo
@an-gremlin above said it best. It’s not that they’re lying, it’s that they’re picking which part they choose to tell you.
For the examples above: Mean: knowing the median would be useful information, it’d show you your starting salary was $30,000, in line with the median. Median: knowing the mean would be useful information, it’d show that your long-term investment in the fund would net you a loss. Mode: honestly you probably want to know exactly which tests your child is struggling with, so looking at the mean might indicate you need to take a closer look at the actual data. This is a small data set, so you can just look at all of it. Range: the mean, median OR mode would show that you have very few studensts within the lower income brackets. Correlation coefficient: this is more about looking into the study methodology than a specific statistic as above. Probably could do several posts on finding the actual studies behind the correlation.
but genuinely the graphs shown as an explanation of what is happening give you more of the picture than a single number does, and are a much better way to display data anyway (as long as an appropriate graph is chosen and they haven’t done anything tricky (see part 2 (I’m not actually making a part 2 but one about suppressing origins, mixing different scales, linking data sets that are unrelated/do not have a causal relationship (don’t accidentally misread that as casual like I usually do)/etc would be great)))
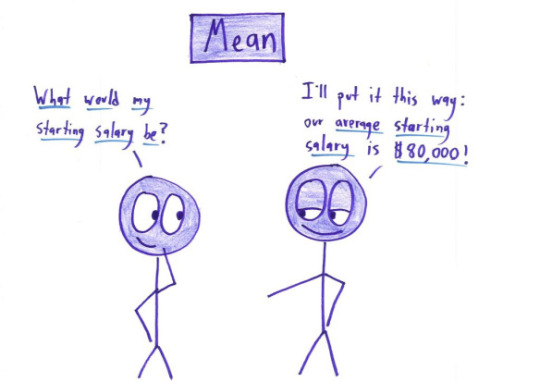
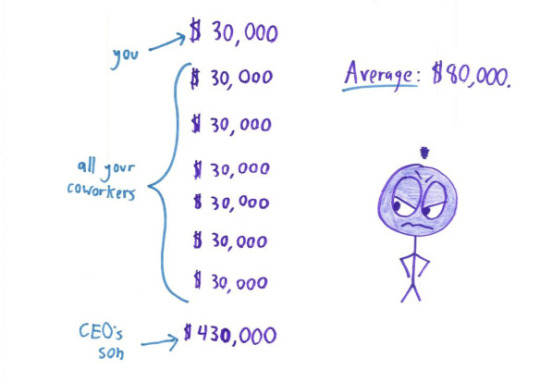





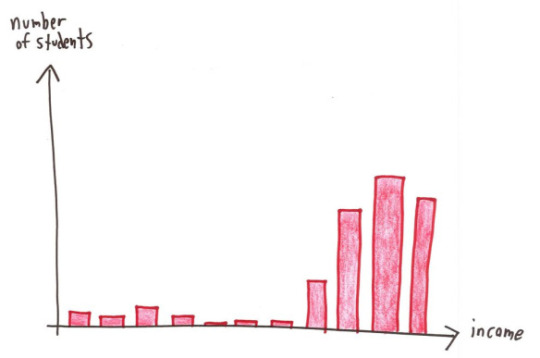

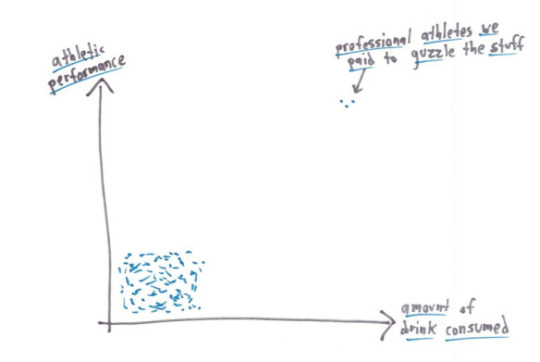
The thing with statistics - via
266K notes
·
View notes
Text
Generating a Correlation Coefficient
Topic: Alcohol intake among young adults in the morning, afternoon, and evening on a weekly basis.
X = {categorical: morning, afternoon, evening}
Y= {1, 2, 3, 4, 5, 6… 30} number of participants.
Sample size = 30
Numerical values were assigned to the categories
Morning = 1
Afternoon= 2
Evening = 3
PARTICIPANTS
TIME OF DAY
1
1
2
2
3
3
4
1
5
3
6
3
7
2
8
2
9
1
10
2
11
1
12
3
13
1
14
1
15
2
16
1
17
2
18
2
19
3
20
2
21
2
22
3
23
3
24
1
25
1
26
3
27
2
28
2
29
3
30
1
Mean Calculation:
X = first term+ last term/2 =1+30/2= 15.5
Y= 1+2 +3+1+3+3+2+2+1+2+1+3+1+1+2+1+2+2+3+2+2+3+3+1+1+3+2+2+3+1/30=65/30=2.17
Deviation Score for X and Y
X={ 1, 2, 3, ……30}
Formula 1 - mean = deviation score
X [−14.5,−13.5,−12.5,−11.5,−10.5,−9.5,−8.5,−7.5,−6.5,−5.5,−4.5,−3.5,−2.5,−1.5,−0.5,0.5,1.5,2.5,3.5,4.5,5.5,6.5,7.5,8.5,9.5,10.5,11.5,12.5,13.5,14.5]
Y= [-1.17,−0.17,0.83,−1.17,0.83,0.83,−0.17,−0.17,−1.17,−0.17,−1.17,0.83,−1.17,−1.17,−0.17,−1.17,−0.17,−0.17,0.83,−0.17,−0.17,0.83,0.83,−1.17,−1.17,0.83,−0.17,−0.17,0.83,−1.17]
Product of Deviation Scores
Formula:- deviation score X x deviation score Y.
Example -14.5 ×-1.17=16.965
[16.965, 2.295, −10.375, 13.455, −8.715, −7.885, 1.445, 1.275, 7.605, 0.935, 5.265, -2.905, 2.925, 1.755, 0.085, −0.585, −0.255, −0.425 , 2.905 ,−0.765 ,−0.935, 5.395, 6.225 ,−9.945, −11.115, 8.715,
− 1.955, −2 .125, 11.205, −16.965]
Positive numbers sum
16.965 + 2.295 + 13.455 + 1.444 + 1.275 + 7.605 + 0.935 + 5.265 + 2.925 + 1.755 + 0.085 + 2.905 + 5.395 + 6.225 + 8.715 + 11.205 =88.450
Negative numbers sum
−10.375 + -8.715+ -7.885 + −2.905 + -0.585 + -0.255 + -0.425 + -0.765 + - 0.935 +- 9.945 + -11.115 + -1.955 +-2.125 + -16.965 = -74.948
Sum of the positive numbers+ negative numbers=
88.450+(−74.948)=13.502
Standard Deviation
Square all the X values
X = 210.25 + 182.25 + 156.25 + 132.25 +110.25 + 90.25 + 72.25 + 56.25 + 42.25 + 30.25 + 20.25+ 12.25 + 6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25 + 12.25 + 20.25 + 30.25 + 42.25 + 56.25 + 72.25 + 90.25 + 110.25 + 132.25 + 156.25 + 182.25 + 210.25
Sum all the values of X
2247.5/30 = 74.916
Then find the square 74.916 = 8.6554
Square all the values of Y
1.3689 + 0.0289 + 0.6889 + 1.3689 + 0.6889 + 0.6889 + 0.0289 + 0.0289 + 1.3689 + 0.0289 + 1.3689 + 0.6889 + 1.3689 + 1.3689 + 0.0289 + 1.3689 + 0..0289 + 0.0289 + 0.6889 + 0.0289 + 0.0289 + 0.6889 + 0.6889 + 1.3689 + 1.3689 + 0.6889 + 0.0289 + 0.0289 + 0.6889 + 1.3689 = 20.207
Sum of Y deviation scores/30
20.207/30= 0.6735
Then the square root= 0.8206
Find the square root of 0.6735 = 0.8206
Final calculation
The sum of the deviation = 13.502
Standard Deviation X= 8.6554
Standard Deviation Y= 0.8206
N=30
13.502/ 30-1 x 8.6554 × 0.8206
13.502/205.9760 = 0.06556
r = 0.06556 a very weak correlation
0 notes
Text
Title: The Relationship Between Hours Spent Studying and Exam Scores
Introduction The aim of this study is to investigate the correlation between hours spent studying per week and students' exam scores. A strong, positive relationship is expected, as more time dedicated to studying should result in higher exam performance.
Methods We randomly generated a sample dataset that includes 30 observations, each representing a student’s weekly study hours and corresponding exam scores. The Pearson correlation coefficient was used to assess the strength and direction of the relationship between these two continuous variables.
Data The data consists of two variables:
Hours Studied per Week: The number of hours students spend studying each week (continuous).
Exam Scores: The scores students achieved in their exams (continuous).
Results The Pearson correlation coefficient between hours studied and exam scores was calculated as 0.95. This indicates a strong positive linear relationship, where increased hours of study are associated with higher exam scores. The p-value associated with this correlation is extremely small (p<0.001p < 0.001p<0.001), meaning that the result is statistically significant.
Additionally, the coefficient of determination (R-squared) was found to be 0.90, meaning that 90% of the variability in exam scores can be explained by the hours spent studying.
Figure 1: Scatter Plot with Linear Fit ![Scatter plot with linear fit] Figure 1 shows a clear positive trend between the number of hours spent studying and exam scores. The red line represents the linear fit, which demonstrates the relationship with an R² value of 0.90.
Discussion The results suggest a significant positive relationship between study time and exam performance. This finding aligns with the hypothesis that increasing study time leads to improved academic performance. However, the study does not account for other factors that might affect exam scores, such as the quality of study, individual differences in learning, or external variables like stress or fatigue.
Conclusion In conclusion, the analysis demonstrates a strong positive correlation between the number of hours students spend studying and their exam scores. Given the high R-squared value, study time can be considered a significant predictor of exam performance. Future research could explore additional factors influencing academic success to develop a more comprehensive model.
0 notes
Text
Blind spot (what is it, why it exists)
Correlations (positive versus negative, interpreting a correlation, correlation coefficients,
limitations)
Experiments (hypothesis, independent and dependent variables, control group, random
assignment)
Face blindness
Gestalt principles of organization (similarity, proximity, closure, simplicity)
How SSRI drugs work
Limbic system (what it is, major functions)
Lobes of the brain (their names, where they are, major functions associated with them)
Major brain structures and their major functions
Major divisions of the nervous system and what they do (somatic/autonomic,
sympathetic/parasympathetic)
Major perspectives on psychology (psychodynamic, cognitive, behavioral, neuroscience,
humanistic)
Major structures of the ear and their functions
Naturalistic observation (what it is, contrast it to experimentation)
Negative afterimages
Neuron function (action potential, all-or-none law, importance of the synapse, reuptake,
inhibitory and excitatory messages)
Neurons (major structures and their functions, presynaptic versus postsynaptic, mirror neurons)
Neuroplasticity
Neurotransmitters (what they are, names of major ones, what major disorders are associated
with specific ones)
Psychological specializations (clinical, counseling, health, developmental, social, etc.)
Rods and cones (major differences)
Scientific method
Split-brain research (major findings)
Top-down and bottom-up processing
Visual processing (fovea, retina, rods and cones, bipolar and ganglion cells, optic nerve, optic
chiasma, theories of color vision, primary visual cortex)
1 note
·
View note
Text
Online education has been used more widely after COVID-19. This calls for teachers’ familiarity with technological tools and pushes them toward gaining computer literacy to improve their efficacy. Moreover, there is a growing recognition of the need to redefine professional identities in this context. This study was an attempt to investigate the relationships between EFL teachers’ professional identity and computer self-efficacy with their effectiveness in online classes.
Methodology: To conduct the study, 100 EFL teachers from English language Institutes and schools in Bojnourd, Iran, participated in the study. They completed three questionnaires, namely, professional identity, computer self-efficacy, and online EFL teacher effectiveness. The obtained data were analyzed using two Spearman correlation coefficients and one regression analysis.
Results: The findings indicated significant relationships between professional identity and computer self-efficacy with teacher effectiveness in online classes. Moreover, it was found that computer self-efficacy was a better predictor of online EFL teacher effectiveness.
Conclusion: The findings indicated that teaching effectiveness is a crucial aspect of professional development in online education. This highlights the importance of educators possessing strong computer skills and actively reshaping their professional identities. By doing so, teachers can significantly enhance the success and practicality of their online classes, benefiting both students and the educational system as a whole.
#language #education #language_learning #translation #applied #linguistics #teaching #research
instagram
#applied#education#jclr#language#language_learning#research#teaching#translation#linguistics#Instagram
0 notes
Text
Capstone Milestone Assignment 3: Preliminary Results
Full code: https://github.com/sonarsujit/MSC-Data-Science_Project/blob/main/capstoneprojectcodeupdated.py
A Lasso Analysis was conducted first to reduce the predictors number and keep only the predictors that are relevant in predicting the communication technology user’s response variable.
As a result, 87 variables were shrunk to 0 and 7 (including the response variable) variables retained in the model:
mortality_rate_under-5_per_1000
rural_population_%_of_total_population
fixed_broadband_subscriptions_per_100_people
survival_to_age_65_female_%_of_cohort
survival_to_age_65_male_%_of_cohort
health_expenditure_per_capita_current_us$
life_expectancy_at_birth_total_years
Lasso Regression Analysis:
Table 1 shows the retained predictor variables and their respective model coefficients.

Figure 1:

The Lasso regression model reveals that child mortality and rural population negatively impact life expectancy, while survival rates to age 65 (both female and male), broadband subscriptions, and health expenditure positively influence it. The model's Mean Squared Error (MSE) of 0.69 suggests a reasonable fit.
Figure 2:

We can see that there is variability across the individual cross validation folds in the training dataset but the change in the mean squared error as variables are added to the model follows the same pattern for each fold.
Initially it decreases rapidly and then levels off to a point at which adding more predictors doesn't lead to much reduction in the mean square error
Table 2:

The Lasso regression model performed well, with a high R-squared of 0.99 for both training and test data, indicating that the model explains nearly all the variance in life expectancy. The Mean Squared Error (MSE) is low for both training (0.59) and test data (0.69), suggesting that the model generalizes well and maintains accuracy when applied to new data.
Descriptive Statistics:
Table 3 shows descriptive statistics for life expectancy globally and the quantitative predictors. The average life expectancy globally is 71.12 (sd=8.22), with a minimum of 48.85 users and a maximum of 83.09.
Table 3: Descriptive Statistics for the Selected variables:

Bivariate Analyses:
Scatter plots are used to gain visual insights of the association between the life expectancy response variable and quantitative predictors as shown in Figure 1 and its corresponding p values in Table 4.
Figure 3:

Table4:

Summary of Findings:
Mortality Rate Under-5 (Per 1,000) vs. Life Expectancy at Birth (Total Years):
Insight: There appears to be a negative correlation between the mortality rate under-5 and life expectancy at birth. As the mortality rate decreases, life expectancy tends to increase. This relationship is expected, as lower child mortality rates often reflect better health systems and overall living conditions, leading to longer life spans.
Rural Population (% of Total Population) vs. Life Expectancy at Birth (Total Years):
Insight: The plot suggests a negative correlation between the percentage of the rural population and life expectancy. Countries with a higher rural population percentage may have lower life expectancy, possibly due to reduced access to healthcare, sanitation, and other vital services in rural areas compared to urban areas.
Fixed Broadband Subscriptions (Per 100 People) vs. Life Expectancy at Birth (Total Years):
Insight: A positive correlation is observed between fixed broadband subscriptions and life expectancy. This may indicate that countries with higher internet penetration often have better access to information, education, and health services, which can contribute to longer life spans.
Survival to Age 65, Female (% of Cohort) vs. Life Expectancy at Birth (Total Years):
Insight: The strong positive correlation suggests that higher survival rates for females to age 65 are associated with increased life expectancy at birth. This indicates the overall effectiveness of healthcare systems and social structures that support female health across different life stages.
Survival to Age 65, Male (% of Cohort) vs. Life Expectancy at Birth (Total Years):
Insight: Similar to females, a positive correlation is observed between male survival rates to age 65 and life expectancy at birth. The strength of this relationship underscores the importance of improving male health outcomes to enhance overall life expectancy.
Health Expenditure Per Capita (Current US$) vs. Life Expectancy at Birth (Total Years):
Insight: A positive correlation is present, indicating that higher health expenditure per capita is generally associated with longer life expectancy. This suggests that increased investment in healthcare resources can lead to better health outcomes and longer life spans.
General Interpretation:
The analysis highlights that life expectancy at birth is strongly influenced by various factors, including healthcare access and expenditure, child mortality rates, rural versus urban population distribution, internet access, and survival rates to older ages. Countries that invest in healthcare, improve child and adult survival rates, reduce rural disparities, and enhance access to information technology tend to have higher life expectancy. These insights can inform policy decisions aimed at improving population health and extending life expectancy across different regions.
Conclusion:
This project utilized Lasso regression analysis to identify the best predictors for life expectancy at birth (years) across a sample of 182 countries, drawn from a total population of N = 278. The analysis used multiple World Bank development indicators to investigate how access to healthcare services influences life expectancy in different countries.
The life expectancy at birth ranged considerably across the sampled countries, reflecting substantial variability in healthcare access and outcomes globally.
The predictive accuracy of the model was high, with an R-squared value of 0.991 on the training dataset and 0.990 on the test dataset. The mean squared error (MSE) was low, at 0.588 for the training data and 0.689 for the test data, indicating that the model has strong predictive performance. However, the slight increase in MSE for the test dataset suggests that the model's performance may vary slightly with new data.
Key findings from the Pearson correlation and Lasso regression analysis revealed that:
Survival to age 65 (Female and Male): Both variables had the highest positive coefficients, indicating that higher survival rates are strongly associated with higher life expectancy.
Fixed broadband subscriptions: This also showed a positive relationship, suggesting that better communication infrastructure may correlate with improved health outcomes.
Health expenditure per capita: Predictably, higher spending on health was associated with increased life expectancy.
Mortality rate under-5: This had the most significant negative coefficient, emphasizing that higher child mortality rates are strongly linked to lower life expectancy.
Rural population percentage: A higher percentage of rural population was negatively associated with life expectancy, highlighting the potential challenges faced by rural areas in accessing healthcare services.
These findings underscore the importance of improving healthcare access, reducing child mortality, and enhancing infrastructure to boost life expectancy. However, the model also highlights the need for further investigation into the stability of these predictors, as the slight increase in MSE for the test data suggests that predictive accuracy could be improved with more data or alternative analytic methods.
Future research could expand on these findings by incorporating additional indicators and examining non-linear relationships to provide a more comprehensive understanding of the factors influencing life expectancy. Moreover, the dataset used in this analysis is a subset of the broader World Bank collection, implying that other important predictors may not have been considered in this study. Consequently, expanding the dataset and the model could yield even more robust insights into the determinants of life expectancy.
0 notes