#cardinality of the continuum
Explore tagged Tumblr posts
Text
If that hurts your brain, get this: There are different infinities, and some are bigger than others.
There are an infinite amount of Natural Numbers (counting numbers), but if you had an infinite amount of time you could list them all one by one.
You know, 1, 2, 3, 4, 5, 6, ...
Where the ... implies an endlessly continuing sequence. It would take forever to get through them all, but if you actually had forever you could do it.
But, while there are also an infinite amount of Real Numbers, there are vastly more of them than there are natural numbers. You couldn't even begin to list them all, even with unlimited time.
Like, ok, maybe you start at 0. That's sensible enough.
What's the next Real Number?
Its not 1, there's plenty of real numbers between 0 and 1, like 1/2 and 0.95 and 1/pi. You might say its 0.00001 or something, but you can always find numbers between 0.00001 and 0. You could start to think that maybe its something like 0.0000...1 with some arbitrary number of zeroes after the decimal place, but no matter how small of a real number you pick, you can always find infinitely more Real Numbers between it and 0.
Not only can you never finish listing all the Real Numbers, but there are so many of them there's not even any reasonable way to start listing them.
For a more formal sense of why this must be true, look into Cantor's Diagonal Argument:
Fundamentally, the amount of Natural Numbers is the smallest type of infinity, which is referred to as Countably Infinite, while the amount of Real Numbers is a larger size of infinity referred to as Uncountably Infinite. (many mathematicians define even larger types of infinite sets called Large Cardinals, although it is an open--and perhaps undecidable--question of whether there are any sizes of infinite sets in between Countably and Uncountably Infinite, see: Continuum Hypothesis)

Poetry Comics Month, Day 30: Infinity
567 notes
·
View notes
Text
Forcing & Independence of the Continuum Hypothesis
My favourite result in maths is probably the independence of the continuum hypothesis. In this post, I aim to explain forcing and why the continuum hypothesis cannot be proven in ZFC. The continuum hypothesis (CH) is the statement that there is no cardinal number between ℵ₀ and 2^ℵ₀. When forcing, you start with a model V of ZFC and extend it to a model V[G] by adding some object G, in such a way that V[G] satisfies the axioms of ZFC but also the existence of G, with the intention of showing that G can exist without contradicting the axioms of ZFC. For example, when starting with a model V of ZFC + CH and G contains information for how to build ℵ₂ distinct reals, V[G] would satisfy the existence of ℵ₂ many reals and thus not satisfy CH.
I assume everyone who reads this knows the theory ZFC and has basic understanding of ordinal and cardinal numbers.
A theory T is a set of axioms in first order logic. A proof in T is a sequence φ₁ .. φₙ of formulas such that each formula is an axiom of T or follows logically from previous formulae in the sequence, this proof is said to prove the formula φₙ. For a formula φ, we write T ⊦ φ to mean that there is a proof φ₁ .. φₙ (φ = φₙ) of φ in T. T is inconsistent if it proves the always false statement ⊥, T is consistent if it does not prove this statement. We write Con(T) for “T is consistent”. T ⊬ φ is equivalent to Con(T + ¬φ), so to show that ZFC cannot prove or disprove CH, we want to show Con(ZFC + ¬CH) and Con(ZFC + CH), assuming that ZFC is consistent.
To show that Con(ZFC) implies Con(ZFC + ¬CH), we start with a model V of ZFC and add ω₂ many reals (subsets of ω) to it. However, we don't have anywhere to get those ω₂ reals from ¯\(˙˘˙)/¯ We can't get them simply out of V as that'd mean V already has at least ω₂ many reals. What we do is assume the existence of a larger universe V⁺ that V lives in. Usually, when forcing, the existence of the larger universe V⁺ is implicit, but I state its existence explicitly to avoid confusion.
We can try to define a theory ZFC⁺ extending ZFC by adding a constant symbol V (the universe of ZFC⁺ is called V⁺ rather than V) and the axiom “V is a model of ZFC”, however, even without assuming nice properties of V like it being a well-founded model, the consistency of ZFC⁺ is stronger than that of ZFC, but ideally, we want to show that Con(ZFC + ¬CH) follows from Con(ZFC), not Con(ZFC⁺).
Luckily, ZFC already sort-of proves the existence of models of ZFC. To be more precise, for every finite fragment t of ZFC, ZFC proves that there is a model of t. However, ZFC does not prove the statement ‘for all finite fragments t of ZFC, there is a model of t’! ∀n T ⊦ φ(n) and T ⊦ ∀n φ(n) are two different statements, it's important to know the distinction!
Let t be a finite fragment of ZFC, aiming to show that ZFC ⊦ ∃M M ⊧ t (⊧ is the symbol for ‘satisfies’ or ‘is a model of’). We'll build the model M by starting with the empty set M_0 = ∅ and adding more and more elements to it until it satisfies ZFC. Since t is a finite fragment of ZFC, we have that V ⊧ t. If t were to be infinite, V ⊧ t would be an infinite conjunction of the formulas in t, and infinite formulas don't exist in first order logic, hence we assume t to be finite. To build the next model M_1, for every formula of the form ∃x φ(x) that t proves, we have that V ⊧ ∃x φ(x), and thus there is some x such that φ(x). We add some x that satisfies φ(x) to M_1 for every such formula ∃x φ(x). We do the same for M_2, but instead of adding x for each ∃x φ(x), we add some x for every y in M_1 and every formula of the form ∃x φ(x,y) that t proves. We do the same with M_3: we add some x satisfying φ(x,y) for every y ∈ M_2 and every formula of the form ∃x φ(x,y) that t proves. We continue this infinitely, and we then define M = ⋃{M_n | n ∈ ℕ} as the union of all M_n. By induction on the complexity of formulas, we can show that M ⊧ φ for every φ such that t ⊦ φ, proving this is left as an exercise to the reader.
Since there are only countably many formulas, every M_n must be countable, and so their union, M, is countable as well. We also have that M is a standard model: it has sets x and uses the real membership relation as its own membership relation. Besides showing that for every finite fragment t of ZFC, ZFC proves that there exists a model of t, we have shown that we can assume this model to be standard and countable.
The construction of the model M we have performed is called a Skolem hull. Usually, when taking Skolem hulls, we take all formulas φ that the original model (in this case, V) satisfies instead of only those that are proven by some theory t, but we couldn't do that as there are an infinite amount of models that V satisfies and a proof in ZFC may only use a finite number of axioms. Skolem hulls are my second favourite thing from model theory and it could be useful to have it in your toolbox.
Although M is a standard model of the theory t, it isn't transitive. A transitive set is a set X such that, for every x ∈ X, we have x ⊂ X. It's usually easier to work with transitive models. We can turn M into a transitive model by the use of a Mostowski collapse. You can read the Wikipedia article on it if you want to know what that is, this is a post about forcing, not Mostowski collapses and Skolem hulls.
Instead of adding the axiom ‘V is a model of ZFC’ to ZFC⁺, we can add, for each individual axiom φ of ZFC, the axiom ‘V ⊧ φ’. And, as we have shown above, we can also add the axiom ‘V is countable and transitive’. Since proofs in ZFC⁺ may only use a finite amount of axioms, they may only use a finite amount of axioms of the form ‘V ⊧ φ’, so ZFC⁺ thinks that V satisfies finite fragments of ZFC without realizing it satisfies the whole of ZFC: it might think there is a very long formula φ that V doesn't satisfy while, in reality, such a formula would be infinitely long and doesn't actually exist.
One theorem from logic that we'll use is the compactness theorem. This theorem states that, for a theory T of first order logic, if T is inconsistent then a finite fragment of T is inconsistent. Contrapositively, if every finite fragment of T is consistent, then T must be consistent as well. A proof of this theorem is quite easy.
Another important lemma we'll use is that if a theory T proves a finite theory S is consistent, then S must be consistent. If S were to be inconsitent, then there must be some proof φ₁ .. φₙ of ⊥ in S, and T would prove that φ₁ .. φₙ is a proof of ⊥ as checking if a proof is correct is as simple as just running an algorithm. Thus, for a finite fragment S of ZFC+¬CH, if ZFC⁺ proves S is consistent, then S must be consistent. And if ZFC⁺ proves S is consistent for every finite fragment S of ZFC+¬CH, then ZFC+¬CH must be consistent by compactness.
Since V is countable in V⁺, the ω₂ of V, written ω₂^V, is a countable ordinal in V⁺ while the ω₂ of V⁺, written ω₂^V⁺, doesn't exist in V. I'll work in the universe V unless otherwise specified, so ω₂ refers to ω₂^V rather than ω₂^V⁺, and countable means countable in V rather than countable in V⁺. For some object x and a model M, x^M refers to the interpretation of x in M.
So now that we have the little universe V and the big universe V⁺, we want to add ω₂ reals to V. Since V is countable in V⁺, there are a lot of things outside of V in V⁺. For example, P(ω) ∩ V is countable in V⁺, while the P(ω) of V⁺ is uncountable in V⁺, meaning that P(ω) \ V must be uncountable, so V is missing a lot of reals that can be added into V. However, if we simply take a set X ⊂ P(ω)^V⁺ such that V thinks X has cardinality ω₂, and then add it to V by just adjoining it like so: V ∪ {X}, this new model is no longer a model of ZFC. It has a universe V, but also just another object X adjoint to it, and things like X ∪ ℕ, X × X, etc, don't exist, while they should for V ∪ {X} to be a model of ZFC.
Thus, instead of adding a single new element X, forcing aims to add an object G in such a way that the axioms of ZFC are still satisfied. It does this through the use of names. A name is an object in V that describes an object in the extended universe V[G], but without a way to interpret the name in V, those objects that exist in V[G] don't yet exist in V. The object G gives a way to interpret the names in V, and interpreting every name in V through G gives the new model V[G]. Explaining what that means exactly requires the definition of a forcing poset, which I'll now explain.
A partial ordered set (poset) is a structure (P,≤) with a set P and a binary relation ≤ on P, such that:
≤ is reflexive: x ≤ x for all x ∈ P.
≤ is transitive: if x ≤ y and y ≤ z then x ≤ z for all x,y,z ∈ P.
≤ is antisymmetric: if x ≤ y and y ≤ x then x = y for all x,y ∈ P.
Two elements x,y ∈ P are compatible if there is some z such that z ≤ x and z ≤ y. x and y are incompatible if no such z exists. A forcing poset is a poset P with the additional axioms:
There is a greatest element 1 ∈ P.
For every x ∈ P, there are y,z ∈ P such that y ≤ x, z ≤ x and y and z are incompatible.
The last axiom is called the splitting condition. Members of a forcing poset P are called forcing conditions. x ≤ y is read as ‘x is stronger than y’ or ‘x extends y’. Forcing conditions can be thought of as statements that can be true or false, these statements say something about the object being added, where the greatest element 1 is a statement that is always true. The forcing poset that we'll focus on in this blog post is called Cohen forcing. Forcing conditions are finite partial functions from ω₂ × ω to {0,1}. That is, functions from a finite subset of ω₂ × ω to the set {0,1}. For forcing conditions p and q, p ≤ q iff p is a function extension of q, i.e. dom(p) ⊃ dom(q) and p(α,n) = q(α,n) for all (α,n) ∈ dom(q). A forcing condition p: ω₂ × ω ⇀ {0,1} says something about the object g: ω₂ × ω → {0,1} that is being added, namely, that g(x) = p(x) for all x ∈ dom(p). For every α < ω₂, {n | g(α,n) = 1} will be a new real in the new model V[G], meaning that there will be ω₂ many new reals and CH will break.
For a forcing poset P, a P-name is a set of tuples (σ,p) where σ ∈ V^P is a P-name and p ∈ P is a forcing condition, this set may be empty. Alternatively, the class of P-names, V^P, can be defined by induction:
V^P_0 = ∅.
V^P_α+1 = P(V^P_α × P) for an ordinal α.
V^P_α = ⋃{β<α} V^P_β for limit ordinal α.
Then, V^P = ⋃{α ∈ Ord} V^P_α is the class of P-names. A P-name {(σ,p)} means ‘this set contains σ iff p is true’. Thus, for a set x, we can define a P-name &x for x as follows &x = {(&y,1) | y ∈ x} as 1 is always true. We can also define the set of all true forcing conditions as &G = {(&p,p) | p ∈ P}, which contains p iff p is true.
A way to decide which forcing conditions are true and which are false is done using a filter. A filter F on P is a subset F ⊂ P such that:
1 ∈ F.
If x ∈ F and x ≤ y, then y ∈ F.
For all x,y ∈ F, there is some z ∈ F such that z ≤ x and z ≤ y.
A filter decides what forcing conditions are true and which are false: members of the filter are true forcing conditions, while things that aren't in the filter are false. The first axiom of a filter, 1 ∈ F, states that the statement 1 is true, the second axiom states that x is true and x implies y, then y is true, and the third statement states that no members of the filter contradict each other (i.e. none are incompatible).
However, not any filter will do. If the filter F is already in the model V, then we don't add anything new to V. It might also be possible to break axioms of ZFC such as comprehension with certain filters. Because of this, we use a special filter called a generic filter.
A forcing poset P has a topology. An open set in P is a set O ⊂ P that is downwards closed, i.e. for every x ∈ O and every y ∈ P such that y ≤ x, we have y ∈ O. A set D is dense if it meets all non-empty open sets. In P, that means that D is dense iff ∀x ∈ P ∃y ∈ D y ≤ x. For a family D of dense subsets of P, a filter G ⊂ P is D-generic iff G meets all dense D ∈ D. One important theorem used to construct generic sets is the Rasiowa-Sikorski lemma. This lemma states that, if P is a forcing poset, p ∈ P is a forcing condition, and D is a countable family of dense subsets of P, then there is a D-generic filter G on P that contains p. A proof of this lemma is left as an exercise to the reader. Since V is countable in V⁺, we can apply the Rasiowa-Sikorski lemma to it: we can define a V-generic filter as a filter that is D-generic filter for D = {D ∈ V | D is a dense subset of P}, and since D is countable in V⁺, such a generic filter G exists in V⁺. I'll often call a V-generic filter simply a generic filter.
Given a forcing poset P ∈ V, a generic filter G ⊂ P on P and a P-name σ ∈ V^P, the interpretation of σ by G is defined as σ^G := {τ^G | ∃p ∈ G (τ,p) ∈ σ}. One can verify that, for x ∈ V, we have &x^G = x and &G^G = G for &G = {(&p,p) | p ∈ P}. V[G] is defined as V[G] = {σ^G | σ ∈ V^P}. Now, all we have to do is verify that V[G] is indeed a model of ZFC and, when P is Cohen forcing, that V[G] satisfies ¬CH.
Im eepy. I'll do that another day -.- Good night.
Hi. I hope you slept well. I'll now continue with explaining forcing.
For a forcing condition p ∈ P, P-names τ₁ .. τₙ and a formula φ, p forces φ(τ₁ .. τₙ), denoted p ⊩ φ(τ₁ .. τₙ), if for all generic G ⊂ P with p ∈ G, we have V[G] ⊧ φ(τ₁^G .. τₙ^G). The following three lemmas are important in forcing:
Definability For every formula φ, there is a formula ψ such that for all forcing conditions p and all P-names τ₁ .. τₙ, p ⊩ φ(τ₁ .. τₙ) iff V ⊧ ψ(p,τ₁ .. τₙ). I.e. ‘p forces φ(τ₁ .. τₙ)’ is definable in V.
Coherence If p ⊩ φ(τ₁ .. τₙ) and q ≤ p, then q ⊩ φ(τ₁ .. τₙ).
Truth If V[G] ⊧ φ(τ₁^G .. τₙ^G) then there is some forcing condition p such that p ⊩ φ(τ₁ .. τₙ). That is, a statement is true iff it is forced.
I encourage you to try proving these lemmas yourself. Coherence is quite easy, but the other two might be more difficult to prove. I'll give a proof for definability and truth.
First, we'll define ⊩* by induction on the complexity of formulas. We'll start with atomic formulas. When does p force σ ∈ τ? One naive guess might be if ∃q ≥ p (σ,q) ∈ τ, however, this doesn't quite work. There might be a P-name ρ such that σ ≠ ρ, yet p ⊩ σ = ρ and ∃q ≥ p (ρ,q) ∈ τ but ∄q ≥ p (σ,q) ∈ τ. Thus, we define p ⊩* σ ∈ τ as ∃(ρ,q) ∈ τ p ⊩* σ = ρ.
So now we need to define p ⊩* σ = τ. By the axiom of extensionality, two sets are equal if they contain the same elements. Thus, we can define p ⊩* σ = τ as ∀ρ ∈ V^P p ⊩* "ρ ∈ σ" ⇔ p ⊩* "ρ ∈ τ". This might seem self-referential, as we define equality in terms of membership, which is itself defined in terms of equality, but we can define it inductively as the rank of the names always decrease. The rank of σ is the smallest ordinal α such that σ is in V^P_{α+1}. The quantor '∀ρ ∈ V^P' currently ranges of all P-names (thus, also those with higher rank than σ or τ), but we can fix that by defining ⊩* ≠ instead of ⊩* =, and then we can define p ⊩* σ = τ as p ⊩* ¬σ ≠ τ.
p ⊩* σ ≠ τ iff (∃(ρ,q) ∈ τ q ≥ p ∧ p ⊩* ¬ρ ∈ σ) ∨ (∃(ρ,q) ∈ σ q ≥ p ∧ p ⊩* ¬ρ ∈ τ).
So now we can define ⊩* ¬, ⊩* ∨ and ⊩* ∃ as follows:
p ⊩* ¬φ(τ₁ .. τₙ) iff ∀q ≤ p ¬q ⊩* φ(τ₁ .. τₙ).
p ⊩* "φ(τ₁ .. τₙ) ∨ ψ(τ₁ .. τₙ)" iff p ⊩* "φ(τ₁ .. τₙ)" ∨ p ⊩* "ψ(τ₁ .. τₙ)".
p ⊩* ∃x φ(x, τ₁ .. τₙ) iff ∃σ ∈ V^P p ⊩* φ(σ, τ₁ .. τₙ).
This internal definition of forcing is almost complete. However, what if a formula φ is forced by p, not because φ is immediately apparent, but because the only forcing conditions that extend p immediately force φ? To give a more concrete example, suppose σ = ∅, τ = {(σ,p), (σ,q)} are P-names, and p = {((0,0),0)} and q = {((0,0),1)} are (incompatible) forcing conditions in Cohen forcing. Then, we don't have 1 ⊩* σ ∈ τ, however, σ ∈ τ is still forced by 1 as any generic filter that contains 1 also contains p or q. Thus, the final step of the definition of forcing is p ⊩ φ(τ₁ .. τₙ) iff {q | q ⊩* φ(τ₁ .. τₙ)} is dense below p, equivalently, p ⊩ φ(τ₁ .. τₙ) iff p ⊩* ¬¬φ(τ₁ .. τₙ).
The last part of the proof of definability is checking that our internal definition of forcing is correct. This is left as an exercise to the reader.
Now I'll give a proof of truth. Although in no point in the proof of definability genericity is relevant, it is very important for truth. Truth states that for a formula φ and P-names τ₁ .. τₙ, if V[G] ⊧ φ(τ₁ .. τₙ), then there is some p ∈ G so that p ⊩ φ(τ₁ .. τₙ). That is, a formula is true if and only if it is forced.
For a statement φ and P-names τ₁ .. τₙ, we can define the set D_φ = {p | p ⊩ φ(τ₁ .. τₙ) ∨ p ⊩ ¬φ(τ₁ .. τₙ)}. Thus, D_φ is the set of forcing conditions that decide φ. We can verify that D_φ is a dense set: we have 1 ⊩ φ ∨ ¬φ as φ ∨ ¬φ is always true, this is equivalent to 1 ⊩* ¬¬(φ ∨ ¬φ) when using the internal definition, i.e. {p | p ⊩* φ ∨ ¬φ} = {p | p ⊩* φ ∨ p ⊩* ¬φ} is dense, and since D_φ is a superset of this set, it must be dense as well. Since D_φ is dense and G is generic, G ∩ D_φ must be non-empty, so some p ∈ G must force φ or force ¬φ. Thus, every formula that is true in V[G] is forced by some forcing condition in G.
We can use definability, coherence and truth to prove that V[G] ⊧ ZFC. I'll leave this as an exercise to reader, cuz... why not ¯\(˙˘˙)/¯ Extensionality and foundation hold in V[G] as V[G] is a transitive model of ZFC, union and infinity aren't too difficult to prove, separation and powerset might be a bit more tricky, the argument for why V[G] satisfies replacement is similar to that of separation, and choice might be a little bit more difficult than the others. I'll give a proof for why V[G] satisfies the axiom lemma of pairing so you have some inspiration for your proof.
Given sets x and y in V[G], we want to show that {x,y} is a set. x and y have P-names, let's call them σ and τ. We can now define a P-name ρ := {(σ,1), (τ,1)}. We can see that ρ^G = {σ^G, τ^G} = {x,y} ∈ V[G], and thus V[G] satisfies the lemma of pairing.
So now that we know V[G] is a model of ZFC (at least, for every finite fragment t of ZFC, ZFC⁺ proves that V[G] is a model of t), we now need to show that V[G] ⊧ ¬CH when using Cohen forcing. We want to add more than ω₁ reals, e.g. ω₂ reals, to the model V. We thus want G to encode information for a set of ω₂ distinct reals. Since a real is an infinite sequence of 0s and 1s, we thus want a ω₂ × ω table of 0s and 1s so that none of the rows are equal. In Cohen forcing, the forcing conditions encode partial information about this ω₂ × ω table. The forcing conditions are finite partial functions from ω₂ × ω to {0,1}, i.e. functions with finitely many pairs (α,n) for ordinals α < ω₂ and natural numbers n as domain, that maps each (α,n) in its domain to either 0 or 1. For forcing conditions p and q, we have p ≤ q iff p is a function extension of q, i.e. dom(q) ⊂ dom(p) and p(α,n) = q(α,n) for all (α,n) ∈ dom(q). A generic filter G on P would thus consist of finite partial functions p: ω₂ × ω ⇀ {0,1} that together form a function g: ω₂ × ω → {0,1} defined as g = ⋃G. For each ordinal α, r_α = {n | g(α,n) = 1} ⊂ ω is a real in the model V[G]. We can use the genericity of G to show that all reals r_α are distinct: suppose we have r_α = r_β for some α ≠ β. Then, there must be some p ∈ G such that p ⊩ r_α = r_β. However, no such p can exist: p may only contain finite information about r_α and r_β, but r_α = r_β means that g(α,n) and g(β,n) are equal on all, and thus infinitely many, n. We can define a dense set D_{α,β} = {p ∈ P | ∃n p(α,n) ≠ q(β,n)}, it's easy to check that this set is dense for α ≠ β, and thus G ∩ D_{α,β} is non-empty. This means that all reals r_α are indeed distinct reals. We thus have added ω₂ distinct reals to V.
But we're still missing something. Can you spot it? No..? Oh, okay. Don't worry. I'll tell you. We have added ω₂^V reals, but we need ω₂^V[G] reals, and nothing so far tells us that ω₂^V and ω₂^V[G] should be equal!
Luckily, they are equal. Here is proof:
Cohen forcing satisfies the countable chain condition. A (strong) antichain A ⊂ P is a set of forcing conditions that are pairwise incompatible, i.e. ∀p,q ∈ A p ≠ q → p ⊥ q. Usually, the word antichain is used to refer to sets of pairwise incomparable elements, but incomparability is kinda useless when forcing as opposed to incompatibility (two objects x and y in a poset are incomparable iff x ≰ y and y ≰ x). The κ-chain condition (κ-c.c) states that, given any antichain A ⊂ P, the cardinality of A is <κ. The countable chain condition (c.c.c) is the ω₁-chain condition, i.e. all antichains are countable.
If P satisfies the c.c.c, then for every function f ∈ V[G] from some D ∈ V to V, there is a function F ∈ V[G] from D to V such that, for every x ∈ D, F(x) is countable and f(x) ∈ F(x). I.e. functions in V[G] can be approximated by "countable covering functions" in V (‘countable covering function’ is not a term, I just made that up :p).
The above lemma can be used to show that, when P has the countable chain condition, if κ is an uncountable regular cardinal in V, then κ must also be uncountable regular in V[G]. In otherwords, for any uncountable regular cardinal κ, P does not collapse κ (P collapses κ if κ is no longer a regular cardinal in the forcing extension V[G]). Proving these three things ((i) Cohen forcing has the c.c.c, (ii) if P has the c.c.c then for every function f: D → V in V[G] for D ∈ V has a "countable covering function" and (iii) if P has the c.c.c then it collapses no regular cardinals) are left as an exercise to the reader.
And that completes the proof of Con(ZFC) → Con(ZFC + ¬CH). Good night everyone! mi wile lape -.- If you have trouble understanding something in this blog post, or you have some other questions, you can tell me! Holidays are starting for me now so I currently have a lot of free time.
I was planning to make an introduction to set theory, but that post isn't going that well. I don't know what my next maths post will be about.
Bye!~
22 notes
·
View notes
Text
81 notes
·
View notes
Text
Exploring the Infinity Paradox: What Does Infinity Really Mean?
Infinity is a concept that challenges our intuitions. It isn’t just a number; it’s an idea that can stretch across mathematical fields, appearing both simple and mind-boggling.
1. Zeno’s Paradox: Halfway There… Forever
Zeno’s paradoxes, particularly the famous Achilles and the Tortoise, deal with infinity in the context of motion and time. In the paradox, Achilles runs ten times faster than the tortoise, but the tortoise gets a head start. Zeno argues that Achilles can never overtake the tortoise because, by the time he reaches the point where the tortoise was, the tortoise will have moved further ahead.
While the reasoning seems absurd, it introduces the idea of infinite divisions of time or space. In reality, calculus helps us solve this paradox—by summing the infinite series of steps, we conclude that Achilles will indeed surpass the tortoise in a finite amount of time.
2. Cantor’s Set Theory: The Sizes of Infinity
The concept of infinity is explored profoundly in Cantor's set theory, which shows that not all infinities are equal. Cantor introduced the idea of countable and uncountable infinities. A countable infinity is an infinity where you can list all elements, like the set of natural numbers {1,2,3,4,… }\{1, 2, 3, 4, \dots\}. This type of infinity is represented by the cardinal number ℵ0\aleph_0 (aleph-null).
However, uncountable infinity is much more interesting. Consider the set of real numbers between 0 and 1. No matter how much you try, you can’t list them all in a sequence because for any number you list, there’s always another real number that isn’t on the list. This is a larger infinity—the continuum. Cantor showed that the real numbers form an uncountable set, and the cardinality of this infinity is represented by 2ℵ02^{\aleph_0}, often referred to as the cardinality of the continuum.
3. Hilbert’s Hotel: A Hotel with an Infinite Number of Rooms
Hilbert's Hotel is a famous thought experiment that demonstrates the paradoxes of infinity in a concrete way. Imagine a hotel with infinitely many rooms, all occupied. The hotel manager is faced with a new guest arriving, yet there is no available room. But because the hotel has infinitely many rooms, the manager asks each guest to move from room nn to room n+1n+1. This frees up room 1 for the new guest. The paradox shows that even with all rooms occupied, infinity can accommodate more guests.
The real kicker? If an infinite number of new guests arrive, the manager can still accommodate them by shifting guests in a similar pattern. Infinity has no "end," and this seemingly impossible scenario exposes the counterintuitive nature of infinite sets.
4. The Paradox of Infinite Sets: The Size of the Continuum
Cantor’s discovery wasn’t just theoretical; it had deep implications for how we think about the continuum of real numbers. The real number line is uncountably infinite—there are more real numbers between 0 and 1 than there are natural numbers, even though both sets are infinite. This raises the issue of infinite sets with different cardinalities. While ℵ0\aleph_0 is the size of the set of natural numbers, the set of real numbers between 0 and 1 has a larger size, denoted 2ℵ02^{\aleph_0}. This revelation left mathematicians questioning the true nature of infinity, as it seems there’s no upper bound on the size of sets.
5. The Infinite Hotel of Cantor: A Deeper Dive
Cantor’s paradoxes are further developed by thinking of sets of different "sizes" of infinity. Consider Hilbert's Hotel again, but now with infinitely many floors, and each floor is also infinite, forming a 2D array. This two-dimensional infinity shows that even within the same "size" of infinity, there are many different levels of infinity. As Gödel and Cohen later proved, infinity is not fully understood: questions like the Continuum Hypothesis—whether there is a set whose size is strictly between the size of the natural numbers and the real numbers—remain unresolved.
6. The Unknowable Future: Limits of Infinity
Infinity isn’t just something that mathematicians wrestle with—it’s tied to the very limits of knowledge and computation. Turing’s halting problem and the limits of computability further illustrate the practical consequences of infinity. No matter how powerful a computer becomes, it will never be able to calculate all the possible outcomes of an infinitely large problem.
Infinity is also central to modern physics—from the infinite expanse of space to the singularity at the center of black holes. As much as we strive for understanding, the paradoxes of infinity challenge even our fundamental laws of the universe.
#mathematics#math#mathematician#mathblr#mathposting#calculus#geometry#algebra#numbertheory#mathart#STEM#science#academia#Academic Life#math academia#math academics#math is beautiful#math graphs#math chaos#math elegance#education#technology#statistics#data analytics#math quotes#math is fun#math student#STEM student#math education#math community
11 notes
·
View notes
Note
To add to all of the above, there is another way to construct countable many different cardinality, and it's with power sets! For any given set A, the power set which I will denote P(A) is the set of all subsets of A. For example, P({1,2})={{},{1},{2},{1,2}}. With our friend cantor's diagonalization argument, it can be shown the cardinality of P(A) is strictly greater than that of A, even if A was infinite. That means that we can construct infinitely many cardinalities simply by taking power sets of power sets. If we denote the cardinality of A to be |A|, then |A|<|P(A)|<|P(P(A))|<|P(P(P(A)))|<... and so we have countable many infinite infinities.
You can even complicate things! What if you take the union of all of A,P(A),P(P(A))... ? You get a set that's even larger than all the previous ones! let's denote it A_2. What then of P(A_2)? and P(P(A_2))? We can take the infinite union of all of those and get an even larger set, which we will call A_3. We can then recursively define A_4, A_5 etc. And if we take the infinite union of all the A_n? We get a new larger set! If we denote it B, and then repeat this process taking the infinite union of B, P(B), P(P(B))... we get B_2 and similarly B_3 and so on. We can in fact repeat this process infinitely many times, getting C, then D, and continuing even after we run out of letters! And THEN we can take the union of this infinite process, and denote that Alpha, and take P(Alpha) and P(P(Alpha)) and so on and so forth, and the more you look at this, the more similar it starts to seem to cardinals.
Tell me everything about infinity.
Oh, a very loaded question! All right. Let's start with the sizes of infinity!
Roughly speaking, there are two sizes of infinity; or, in proper terminology, "cardinalities." (There is some debate, as I recall, over whether there are more sizes of infinity. But we know there are two.) The first cardinality is the same size as the integers, which are the positive and negative whole numbers; essentially tick marks going in a line forever. 1, 2, 3, and so on; and in the opposite direction, -1, -2, -3, and so on.
The second cardinality is the same size as the real numbers, which are all the numbers that most people use on a daily basis; think, instead of tick marks, a line, and every place on that line is a number. No matter how close two places on that line are, there's always another number in between them. So you have 2.5 and 2.6, but between them you have 2.55 and 2.5932, and infinitely many more.
The concept of infinity, of course, gets a bit weird once you move into more than one dimension; it's easy enough to point in the same direction as a line and say, "that goes to infinity," but once you have multiple dimensions, is it meaningful to talk about a negative or positive infinity? Oh, and adding and subtracting get weird once you start adding infinitely many things together. Addition loses commutativity (e.g. 5+3 = 3+5), which still blows my mind, even though I've seen the proof for it. It's the kind of thing that keeps me up at night.
Generally mathematicians get around the multiple-dimensions problem by using the modulus of a number, which is the distance from the number to zero, measured using our dear old friend the Pythagorean Theorem: so, if your point is at 4 in one dimension and at 3 in another, you use the Pythagorean theorem to get 5, and then you consider that point to be 5 away from zero. (This would be easier to explain if I had a chalkboard!) Then, infinity is sort of a circle that surrounds the whole plane; or, if you think of your 2d plane like a flat circle, if you folded it up into a ball, infinity would be all the points at the very top of the ball, and zero would be the point at the bottom. (Obviously this gets weirder if we have three dimensions, but you get the idea.) Okay, so that's a quick introduction to infinity from a mathematical perspective. I think there were also some physics questions re: the expanding universe and spacetime? I'm happy to write a bit about that, too, but I think it belongs in a separate post! So if you have questions about that, please let me know and I'll try to share what I do know! Disclaimer: while I DO know more math than the average person, I have essentially a bachelor's-degree level of knowledge in math. I think everything I've typed out is correct, but I may very well have missed some details! Dear readers, please feel free to correct me if you have greater knowledge than I.
Edit: also, I should have mentioned that the pythagorean theorem only works in a euclidean space. But I feel like going into non-Euclidean stuff is a bit past the scope of (this) tumblr post.
#BTW prev I think you had a typo and meant to say the continuum hypothesis is that Aleph 1 is the cardinality of the reals#as aleph null is the cardinality of the naturals
50 notes
·
View notes
Text
Understanding the Four Elements and Directions
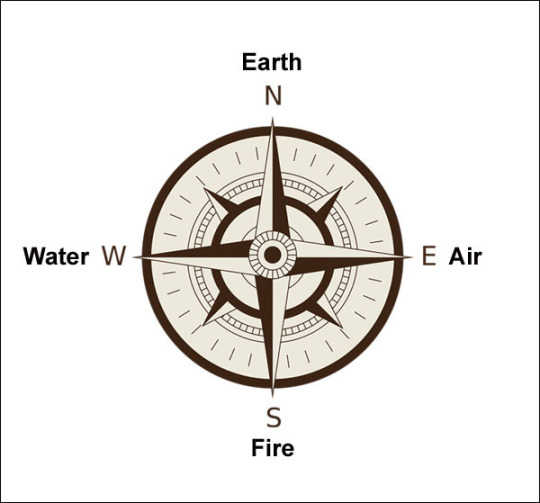
The cardinal directions, North, East, South, and West, represent more than navigational tools. Each direction has a deep meaning that is tied to one of the four elements of life: Earth, Air, Fire, and Water. The interplay between the elements and the cardinal directions is a concept that has fascinated humanity for centuries. Each direction is associated with an element of the natural world, and represents some part of our human nature as well. Understanding how we relate to the four elements and directions can teach us a lot about ourselves, help us to grow and can support us through life's many changes.
The four elements, as shown in the accompanying diagram, are charted around a cosmic compass or wheel of life. The cosmic wheel is a mandala, a symbolic blueprint or map of reality. It represents a multidimensional, interwoven web of relationships that are in constant communion with each other. The sacred wheel exists simultaneously in a horizontal and vertical axis, as well as in the unfolding continuum of time--past, present, and future. The cosmic wheel serves as a portal to consciously enter the cyclic, time-space unfolding of the universe through a practice of reverent, harmonious relationship. It is based on the belief that the universe is alive, sentient, and constantly communicating its wisdom to who ever makes an effort to listen.
The cosmic wheel represents the archetypal journey each of us takes in life. This journey has four stages, each associated with a cardinal direction. To move around the wheel and develop a relationship with each direction is to step onto a path of learning and fulfillment. Each direction and its associated element has qualities and attributes that help us spiral toward completion on the wheel of life. All creatures walk the circumference of the cosmic wheel, experiencing the four stages of human life: birth, youth, adulthood, and death. After completing a cycle of learning on the sacred wheel, each of us returns to the source at the center or heart of the circle.
Attributes of the Elements and Cardinal Directions
Air/East
Air is the element of the East, connected to the soul and the breath of life. Air signifies intellect, communication, and freedom. It is the element of thought, representing the mind and the power of ideas. Air's qualities include lightness, movement, and expansiveness. It is associated with clarity, insight, and the ability to connect with others through language and expression. In many traditions, Air is seen as the breath of life, essential for mental and spiritual well-being. Though the qualities attributed to each of the four cardinal directions tend to vary from culture to culture, the energy of the East is typically associated with spring, morning, birth, beginnings, illumination, knowledge, learning and intellectual curiosity. The East represents new life being brought into the world. It is the direction of the sunrise, heralding the start of a new day and the promise of opportunities. In many cultures, the East is seen as a place of renewal and vision, where one can gain insight and inspiration. It encourages openness, curiosity, and the pursuit of knowledge.
Fire/South
Fire is purifying, masculine yang energy associated with the South, and connected to strong will and energy. Fire represents energy, transformation, and passion. It is the element of action and drive, associated with the sun and the spark of life. Fire's qualities include warmth, intensity, and the ability to consume and regenerate. It is often seen as a catalyst for change, symbolizing both destruction and rebirth, and is connected to creativity and the willpower to achieve goals. The cardinal direction South is related to summer, midday, logic, youth, trust, and expansion. The South represents youth and adolescence--a time of growth, learning and development of the self. From the South rises the vital energy of renewal, regeneration, and growth. From the South we learn to plant seeds of good cause. We learn that our thoughts and actions create our reality. It is a place of action and movement, encouraging individuals to pursue their goals with enthusiasm and determination.
Water/West
Used for healing, cleansing, and purification, Water is a feminine yin energy associated with the West. Water is essential to life; it flows through all plants, people, and wildlife. Water embodies fluidity, emotions, and intuition. It is the element of change and adaptability, capable of taking various forms and influencing all it touches. Water is linked to the subconscious mind, dreams, and the ebb and flow of feelings. Its qualities include flexibility, continuity, depth, and the ability to cleanse and purify, making it a vital component of spiritual and physical renewal. The cardinal direction West is associated with fall, twilight, the moon, and the emotional self. In the West, we are drawn into the experience of our emotions. It is a direction that calls us to self-reflection and self-understanding. The West represents adulthood and meeting the fulfillment of life as we find our meaning and place. It is the direction of the setting sun, signifying the end of a cycle and the transition into reflection and rest. It is a space for understanding and integrating experiences, fostering emotional growth and wisdom.
Earth/North
Connected to the North, Earth is considered the ultimate feminine element, often associated with the Goddess. Earth is widely associated with stability, grounding, and the material world. It represents the physical aspects of existence, including the body and the tangible environment. In various traditions, Earth is considered the foundation upon which all life is built. Its qualities include form, solidity, endurance, and fertility, making it a symbol of sustenance and growth. The cardinal direction North is typically associated with winter, night, introspection, death and completion of the life cycle. This is the place of wisdom and of imparting the knowledge gained from a lifetime of living in the physical world to the younger generations. It is a time of reflection, rest and increased understanding of the aspects of the spiritual world. In the North we assimilate our life experiences before we exit the realm of physical experience and join into vast levels of experience in the spirit worlds of light, or we choose to return and walk again the sacred wheel of life.
The Building Blocks of Nature
The four elements are the building blocks of nature and interact with humans in the creative process. The elements are living energies, which change and move as we think, and then take the form of our thoughts. Thought is the tool of the mind that shapes physical reality. Every thought, idea, or image in the mind has form and substance. Everything that we perceive began with a thought, for it is the blending of thought forms with the elemental rhythms that shape physical reality. It is the consciousness of humanity that holds the present physical form of all that we perceive. It is the mind that determines the destiny of forms. We are mind. Our Earth is mind. We live in a universe of mind. From photons to galaxies, life is conscious intelligent energy that can form itself into any pattern or function.
The key to understanding the creative process is to realize that the universe is made of vibrational energy: that it is a single, flowing, rhythmic being. According to quantum physics, everything in the universe, from the smallest subatomic particle to the largest star, has an inherent vibrational pattern. The entire universe is created through vibration and can be influenced through vibration. T'an Ch'iao, a Taoist adept of the tenth century, expressed this potential when he wrote, "When energy moves, sound is emitted; when sound comes forth, energy vibrates. When energy vibrates, influences are activated and things change. Therefore it is possible thereby to command wind and clouds, produce frost and hail, cause phoenixes to sing, get bears to dance, make friends with spiritual luminescences."(1)
The compass or circular arrangement of the elements illustrates the sequence of development in the process of manifestation. Born of the silent emptiness of the center, vibration cycles around the periphery of the circle. Moving from East (Air) to South (Fire) to West (Water) to North (Earth), vibration bonds the elements, and then reverses its rotation toward emptiness to begin the cycle anew. The unmanifest essence of vibration precipitates this bonding sequence in order to manifest a desired form. The energy of vibration is alive and, because it is alive, it seeks ways in which to express or manifest itself. As Ute-Tiwa shaman Joseph Rael concludes in his book, Being and Vibration, "Apparently materialization occurs because vibration is seeking to purify the center (heart) of its newly formulated form."(2)
Conclusion
In the Native American traditions, the wheel or sacred hoop of life defines all that is the Great Mystery, the source of all creation. The Great Mystery reveals itself as the powers of the four directions and these four powers provide the organizing principle for everything that exists in the world. There are four elements, four winds, four seasons, four phases of the moon, four stages to humanity's spiritual evolution, and so on. We are here on Earth to experience and realize the mystery. The vision of that mystery is ever present within each of us. When we mindfully connect with the elements and cardinal directions, we begin to realize the sacred vision. We orient ourselves in the living web of life, yielding greater awareness and perspective. We develop a meaningful understanding of the natural world and our place within it.
Thomas Cleary, Vitality, Energy, Spirit: A Taoist Sourcebook (Shambhala, 1991).
Joseph Rael and Mary Marlow, Being and Vibration (Tulsa: Council Oak Books, 1993), p 185.
18 notes
·
View notes
Text
Theories of Personality
Theories of personality aim to explain how and why individuals differ in their patterns of behavior, thinking, and emotions. There are several major theories that attempt to describe and categorize personality traits and development.
1. Psychoanalytic Theory (Sigmund Freud)
Core Idea: Freud’s theory of personality revolves around the interaction of the id (basic instincts), ego (rational thought), and superego (moral standards). He believed that personality develops through early childhood experiences and unconscious conflicts.
Structure of Personality: Freud proposed that the unconscious mind plays a key role in shaping behavior and personality, with unresolved internal conflicts influencing behavior.
Defense Mechanisms: Freud also suggested that individuals use defense mechanisms, such as repression or denial, to cope with anxiety and protect their self-image.
Stages of Development: The theory includes psychosexual stages (oral, anal, phallic, latency, and genital stages), with conflicts at each stage influencing adult personality.
2. Humanistic Theory (Carl Rogers, Abraham Maslow)
Core Idea: Humanistic theories emphasize personal growth, free will, and self-actualization. These theories view humans as inherently good, striving to reach their full potential.
Self-Actualization: Maslow's Hierarchy of Needs posits that individuals move through a series of needs, from basic physiological needs to self-actualization, where they fulfill their potential and experience personal growth.
Carl Rogers’ Person-Centered Theory: Rogers introduced the concept of the self-concept, which is how people perceive themselves. He believed that for individuals to achieve their full potential, they need an environment that provides genuineness, acceptance, and empathy.
Unconditional Positive Regard: Rogers argued that receiving unconditional love and acceptance is key to developing a healthy personality and self-esteem.
3. Trait Theory (Gordon Allport, Raymond Cattell, Hans Eysenck)
Core Idea: Trait theories suggest that personality is made up of broad, enduring traits or characteristics that determine behavior.
Gordon Allport: He identified three types of traits: cardinal traits (dominant traits that define an individual), central traits (general traits that form the basic foundation of personality), and secondary traits (more specific traits that appear in certain situations).
Raymond Cattell: Cattell used factor analysis to identify 16 personality factors, suggesting that a combination of these factors defines a person’s unique personality.
Hans Eysenck: Eysenck's model focused on three dimensions of personality: extraversion-introversion, neuroticism-stability, and psychoticism (related to aggressiveness and antisocial tendencies).
4. The Big Five (Five-Factor Model)
Core Idea: The Big Five personality traits are the most widely accepted framework for understanding personality. These traits are thought to exist along a continuum, and people fall at different points within these five dimensions:
Openness to Experience: Creative, curious, open to new ideas vs. traditional, routine-oriented.
Conscientiousness: Organized, responsible, goal-oriented vs. careless, impulsive.
Extraversion: Sociable, outgoing vs. introverted, reserved.
Agreeableness: Cooperative, compassionate vs. antagonistic, competitive.
Neuroticism: Emotionally unstable, anxious vs. emotionally stable, calm.
This model is considered to capture the basic structure of personality across different cultures and contexts.
5. Social-Cognitive Theory (Albert Bandura)
Core Idea: Personality is shaped by the interaction between personal factors (cognitive abilities, beliefs, emotions), behavior, and environment. This is known as reciprocal determinism.
Self-Efficacy: Bandura introduced the concept of self-efficacy, which is the belief in one's ability to succeed in specific situations. High self-efficacy leads to more persistence and confidence in challenging tasks, while low self-efficacy can lead to avoidance of difficult situations.
Observational Learning: Bandura also emphasized the role of modeling and observational learning in personality development, arguing that people learn behaviors and emotional responses by observing others.
6. Behaviorist Theory (B.F. Skinner)
Core Idea: Behaviorists argue that personality is the result of learned behaviors, shaped by rewards and punishments in an individual's environment.
Operant Conditioning: Skinner focused on operant conditioning, where behavior is influenced by reinforcement (positive or negative) or punishment. Over time, individuals develop consistent behavioral patterns based on their experiences with rewards and consequences.
Environmental Determinism: Behaviorists view personality as a product of the external environment rather than internal traits or unconscious forces.
7. Biological and Evolutionary Theories (Hans Eysenck, David Buss)
Core Idea: Biological theories emphasize that personality traits have genetic underpinnings and that human behavior is influenced by evolutionary processes.
Eysenck’s Biological Basis of Personality: Eysenck proposed that personality traits like extraversion and neuroticism are linked to biological differences in brain arousal and functioning.
Evolutionary Psychology: David Buss and other evolutionary psychologists argue that personality traits evolved to solve problems related to survival and reproduction. For instance, traits like aggression or cooperation may have developed as adaptive strategies in human evolutionary history.
8. Cognitive-Behavioral Theory
Core Idea: This theory integrates elements from both cognitive and behavioral psychology. It suggests that cognitive processes (thought patterns, beliefs) play a crucial role in determining behavior and, therefore, personality.
Aaron Beck’s Cognitive Theory: Beck emphasized how automatic thoughts and cognitive distortions (like overgeneralization or catastrophic thinking) shape personality and emotional responses.
Cognitive Restructuring: In cognitive-behavioral therapy (CBT), individuals learn to identify and change negative thought patterns, which in turn influences their behavior and personality over time.
9. Narrative Identity Theory
Core Idea: Narrative identity theory suggests that individuals construct a life story or narrative to make sense of their experiences and define their identity. This narrative evolves over time, reflecting personal growth, values, and social influences.
Dan McAdams: McAdams proposed that personal identity is shaped by the stories we tell about ourselves. People seek coherence and meaning in their life stories, which reflect their personality traits, goals, and values.
This approach emphasizes that personality is not just a set of static traits but an evolving narrative shaped by personal choices and experiences.
10. Existential and Phenomenological Theories
Core Idea: These theories focus on individual experience, freedom, and the search for meaning. Existential psychologists like Rollo May and Viktor Frankl argue that personality is shaped by how individuals confront fundamental existential questions, such as the meaning of life, freedom, and death.
Frankl's Logotherapy: Viktor Frankl emphasized the importance of finding meaning in life, even in suffering, as the central drive in human behavior. He believed that the quest for meaning shapes personality and behavior.
Authenticity and Choice: Existential psychology stresses that individuals are responsible for their own choices, and living authentically means confronting existential realities and making choices in alignment with one’s values.
Theories of personality offer different perspectives on the factors that shape human behavior and individual differences. From Freud’s focus on unconscious drives to the modern trait theories like the Big Five, these approaches explore the intricate dynamics of behavior, thought, and emotion that constitute personality.
#philosophy#epistemology#knowledge#learning#education#chatgpt#psychology#Personality Theory#Psychoanalysis#Humanistic Psychology#Trait Theory#Big Five#Social-Cognitive Theory#Behaviorism#Cognitive Theory#Evolutionary Psychology#Narrative Identity
11 notes
·
View notes
Text








“The author types the words ‘the author types the words’. Stand, and feel the energy that crowds the room, a current siphoned back through time from all those future readings, all those other people and the varying degrees of their absorption, their awareness half-submerged within the text and half-detached from moment, from continuum, and therefore reachable.
Lacking any territory that is not subjective, we can only live upon the map. All that remains in question is whose map we choose, whether we live within the world’s insistent texts or else replace them with a stronger language of our own.
The task is not unthinkable. There are those weak points on the borderline of fact and fabrication, crossings where the veil between what is and what is not rends easily.
Go to the crossroads, and draw up the necessary lines. Make evocations and recite barbaric names; the Gorgo and the Mormo. Call the dogs, the spirit animals, and light imaginary fires.
Walk through the walls into the landscape of the words, become one more first-person character within the narrative’s bitter procession. Make the real a story and the story real, the portrait struggling to devour the sitter.
Obviously, this is a course of action not without its dangers, this attempted wedding of the language and the life; this ju-ju shit. Always the risk of a surprise twist ending ….
When Odin asked for wisdom from the head of Mimir, he paid with an eye: this knowledge carries with it a curtailment of perception, or at least a narrowing. The depth-vision is forfeit.
The time has come to end and seal this working; to complete the story-path with absolute immersion of the teller, a commitment and a sacrifice.
The rite is simple, of its kind, intended only as a point of focus, a conceptual platform on which to stand amid the swirl and shift of this delusory terrain: imaginary serpents are placed at the compass points to guard against the mental snares those cardinal directions symbolize, while at the same time an appeal is made to equally symbolic virtues.
Idea is the only currency in this domain, and all ideas are real ideas. A heavy language is engendered and employed to fix these images as marker buoys within the mind.
This incantation and the novel both progress towards the pregnant, hanging silence of their culmination. This is how we do things here, and always have done.
Wine and passionflower and other substances of earth. Shapes painted with contorted fingers on to empty space. Deranged, of course, but then derangement is the point.
Speak the desire in terms both lucid and transparent. Write it down lest it should be forgotten when the spasm hits.
…
These are the times we dread and hunger for. The mutter of our furnace past grows louder at our backs, with cadence more distinct. Almost intelligible now, its syllables reveal themselves. Our world ignites.
The song wells up, from a consuming light.”
Text from the final chapter of “Voice of the Fire’ by Alan Moore (1996).
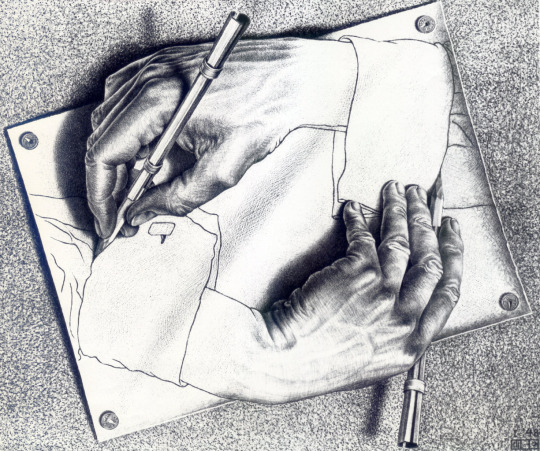
Images (in order) are:
”Drawing Hands“ by M. C. Escher (1948).
"A Map of Days” by Grayson Perry. (2013)
“Hecate” by Jane Estelle Trombley.
“The Hanged Man” by Lakandiwa (2013).
Page from “The Horrorist” by Jamie Delano and David Lloyd (1995).
Collage image of Austin Osman Spare by Kenneth Grant.
Photo of Brion Gysin and William S. Burroughs with the Dream Machine.
“I Am That I Am” permutations by Gysin & Burroughs (“The Third Mind”).
“Holy Fire” (Left panel) by Alex Grey (1987).
For more on art, magic & ritual, please visit “Noise vs. Signal”.
9 notes
·
View notes
Note
Thoughts on the transfinite? The higher infinite?
cardinals/ordinals above the continuum are like. theyre clearly fake as hell. im sure theyre valid as algebraic objects but theyre not "infinities" theyre just like. things. certain classes of (countably) infinite graphs. or something.
13 notes
·
View notes
Text
youtube
What? No. The different sizes of infinity have nothing to do with the expansion of the universe. I don't know much about GR but I know enough to know that it says the universe is a smooth manifold, and every smooth manifold has the same infinity of points (cardinality of the continuum). This person appears to be talking out of her ass on this point. I don't think it matters but like, come on.
14 notes
·
View notes
Text
Rereading my own posts about JJK and the tags I left in those posts is making me want to chew wood. I knew virtually nothing but yeah yeah. The parallels between Gojo and Sukuna not only exist, but they are key. Yeah, Gojo indeed knows, trusts and relies on the people around his age he interacts with in that flippant, intimate and vulnerable way (Ijichi, Shoko, Nanami, Utahime); they were his classmates and childhood friends. Yes, Megumi and Gojo do go way back, I wasn't hallucinating it; in the last chapters, this will weight on the scenes in which Megumi laughs and smiles faintly. Yes, Gojo does sincerely care about things and the kids, and tries his best to do good and be good, even if he's also annoying and rude. Yes, indeed it is all very lonely. Yes, indeed there's ontological alienation. Yes, indeed love is like a curse, it is even stated that way. Yes, indeed last words doom, and keep people going; that too is a blessing and a curse, like love is. Yes, there's significance in Gojo using "boku". Yes, "when granted everything, you can't do anything... but just die peacefully" does apply to Gojo's life miserably. Yes, indeed there is a mix of longing for a normal life and being drunk on power, the feeling that one is hindering the future generations and a desire to make it better for them. Yes, indeed it is a mix of selfish and selfless motives. Yes, Gojo musing about Nobara's power being intriguing is indeed shady. Yes, Gojo's death will be done in a way that imply continuity kinda similarly to Cantor's hypothesis on the cardinality of the Continuum. And so on and on. Unfair how well constructed this manga is. Unfair how much wasted potential there is in it too. I can't stop thinking about it. I can't stop being frustrated about it all. It's so good. It's so unsatisfactory. The last chapter made me smile because oh it made so much sense, of course; it also broke my heart, because of course. I wish I had never gotten into it. It's given me a lot of joy, despite everything. I've drowned in remembrance. I've had a lot of fun. And in short, I love it, quite honestly. I can't even wish I didn't. I resent it, but I can't even wish I didn't. I love it, it's both a blessing and a curse; but that's how it always goes when it comes to love.
#I can't believe how spot on I was at times and I say this not in the 'heh! I was right!'#but in the 'damn that was planned *and conveyed* from the start'#From time to time people like my posts from last August (how they find them is beyond me)#and it hits me every time just how well constructed some things are enough to foresee what was going to be of them#Still frustrated over many things but for a change I am feeling too lazy to ramble in tags even though I intended to do so initially#I should keep watching the anime#It's been well over a month since I last watched one episode. At this rate I'm going to have to start over#and I don't trust it won't keep me again weeks? a month? to get over the first time Gojo expands his domain#I should also read the manga from beginning to end instead of playing hopscotch because of fear of commitment lol#I do love this after all. I guess the harm's already done#And if faintly I still hope reading the entire thing in order from beginning to end will save Geto's writing for me#because what a waste otherwise#I talk too much#I should probably delete this later#Sorry I wish tumblr didn't put this in the general tag after so many tags#but I do want to find this post in the future and compare my past and present thoughts if I do not end up deleting it in a couple days#Jujutsu Kaisen
3 notes
·
View notes
Note
hi! how you doing! I'd like your help w a little something.
So I'm having real analysis in my coming sem and I'd approached my math prof about it. So I'd asked him like how do I prep myself to properly and fully understand real analysis that we'll see? like to understand it in the abstract sense and have a good intuition abt it. he suggested to try and understand the definition of real numbers and get back to him
soo uhh. I'm looking for resources to study field theory? lectures, textbooks. Any suggestions?
Thank you!
Well tbh, fields on their own are pretty tame, and as far as algebraic field theory goes, R is one of the tamest. Which is to say, a "field" just implies that you have + - × ÷ 0 1, and as long as you understand these basic arithmetic properties (as well as basic functions like sqrt, exp, log) you should be golden. Finite fields and rationals have all these crazy complicated algebraic things like field extensions and Galois theory, but R is barely interesting in that aspect.
R really shines in topology, though. For a deep understanding of the definition of R, you might want to look at some introductory point-set topology books. Key words to look out for are metric space (including the notion of open and closed sets), norm (i.e. absolute value), Hausdorff space (sometimes called T2), cardinality (of the continuum specifically), completeness.
The sources I learned these from are in my own language, so I doubt they would be of much use to you. You could internet search any of these terms though, or search for introductory point set topology books. Good luck!
#pretty much assuming you dont mean calculus here#most important thing imo is completeness#that is#every cauchy sequence converges#like thats the fundamental difference between R and Q#you can have rational Cauchy sequences that approach sqrt(2)#but they wont converge in Q since sqrt(2) is not in Q#R doesnt have these kinds of shenanigans#the cardinality thing is fun also#like to really get a grasp of uncountable infinity
4 notes
·
View notes
Text
cruising through a tag and i see someone's drabble post that fundamentally mischaracterises the cardinality of the continuum
gonna call that willpower training
#please don't write about different infinities without understanding what makes infinities different
5 notes
·
View notes
Text
Tbh I am skeptical now whenever someone says some 'infinite amount' of anything (good) but then specifies it as being specifically some transfinite cardinal number amount of things (bad).
In order to be able to do this you need to give your metaphor space more specification! It's entirely reasonable to imagine a hotel of ℵ₀ rooms because our common conception of how space works locally is sensibly modeled by Euclidean space, which is second countable/separable/𝜎-finite or whatever. But to conceive of a boat containing continuum-many guests you would need to specify how the rooms on this ship are arranged! The thought experiment is not specified enough by simply giving the cardinality. For one, you would need at least a continuum-indexable set of directions (though not necessarily such a set of dimensions everywhere) to store your passengers in, assuming that your space is connected and locally Euclidean-ish (an infinite-dimensional Hilbert space for example, which again will depend on your choice of how lengths and angles interact).
#math#i love these kinds of thought experiments though#giving tangible interpretations of mathematical concepts in weird worlds
8 notes
·
View notes
Note
Regarding the Continuum Hypothesis: there are things called “cardinal characteristics of the continuum”. One example is “the smallest cardinality of a set of non-meager reals”. By Baire category theorem, this is strictly larger than countable. Clearly it is at most continuum.
When you say CH is true, you are claiming there exists a bijection between this well defined cardinal and the continuum. Show me such a bijection.
(The point of this ask is “existence claims need justification” does not favor CH over non-CH)
That's right! I already said as much here (x) :)
3 notes
·
View notes
Text

ST. PAUL, MN — Local man Dean Richardson caused a rift to open in the space-time continuum this morning when he foolishly used a credit card to purchase a Dave Ramsey book.
"I'm ready to finally get my financial life in order," said Mr. Richardson as he approached the checkout desk with The Total Money Makeover. "I'm just going to put this on my Masterca--Aaaa!!!!!"
Bystanders reported that Mr. Richardson's actions caused an instant tear in the very fabric of reality. "Mr. Richardson broke the cardinal rule of financial peace in order to gain financial peace," said onlooker Thomas Gaines. "It was like he took an elevator heading down in order to go up. He should have known better - Dave is literally cutting a credit card in half on the cover. The man got what he deserved."
According to his wife, Mr. Richardson had been trying for months to take a course on Dave Ramsey's financial strategies. "Dean had signed up for Financial Peace University at a church across town. His car broke down though, so he went and bought a brand-new car and put zero money down," explained Mrs. Richardson. "The class got cancelled, but he saw Dave was doing an event in Chicago. So, he took an early distribution from his retirement account to pay for the registration. Sadly, Dean got sick and couldn't make it. So, he finally just went to the bookstore with the credit card we've maxed out, and I haven't seen him since."
At publishing time, Mr. Richardson had reportedly made it back through the rift in space-time and, having glimpsed the future, immediately applied to be a UPS driver.
2 notes
·
View notes