#The Theology of Arithmetic

[noosphe-re]

The monad is like a seed in containing in itself the unformed and also unarticulated principle of every number; the dyad is a small advance towards number, but is not number outright because it is like a source; but the triad causes the potential of the monad to advance into actuality and extension. 'This' belongs to the monad, 'either' to the dyad, and 'each' and 'every' to the triad.

Iamblichus, The Theology of Arithmetic, translated by Robin Waterfield

[xyymath]

Why the Number Zero Changed Everything

Zero: a concept so foundational to modern mathematics, science, and technology that we often forget it wasn’t always there. Its presence in our world today seems obvious, but its journey from controversial abstraction to indispensable tool has shaped entire civilizations.

1. The Birth of Zero: A Revolutionary Idea

The concept of zero didn't exist in many ancient cultures. For example, the Greeks, despite their advancements in geometry and number theory, rejected the idea of a placeholder for nothingness. The Babylonians had a placeholder symbol (a space or two slashes) for zero, but they didn't treat it as a number. It wasn't until Indian mathematicians in the 5th century, like Brahmagupta, that zero was truly conceptualized and treated as a number with its own properties.

Zero was initially used as a place-holder in the decimal system, but soon evolved into a full-fledged number with mathematical properties, marking a huge leap in human cognition.

2. The Birth of Algebra

Imagine trying to solve equations like x + 5 = 0 without zero. With zero, algebra becomes solvable, opening up entire fields of study. Before zero’s arrival, solving equations involving unknowns was rudimentary, relying on geometric methods. The Indian mathematician Brahmagupta (again) was one of the first to establish rules for zero in algebraic operations, such as:

x + 0 = x (additive identity)

x × 0 = 0 (multiplicative property)

These properties allowed algebra to evolve into a system of abstract thought rather than just arithmetic, transforming the ways we understand equations, functions, and polynomials.

3. Calculus and Zero: A Relationship Built on Limits

Without zero, the foundation of calculus—limits, derivatives, and integrals—wouldn’t exist. The limit concept is intrinsically tied to approaching zero as a boundary. In differentiation, the derivative of a function f(x) is defined as:

f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}

This limit process hinges on the ability to manipulate and conceptualize zero in infinitesimal quantities. Similarly, integrals, which form the backbone of area under curves and summation of continuous data, rely on summing infinitely small quantities—essentially working with zero.

Without the concept of zero, we wouldn’t have the means to rigorously define rates of change or accumulation, effectively stalling physics, engineering, and economics.

4. Zero and the Concept of Nothingness: The Philosophical Impact

Zero is more than just a number; it’s an idea that forces us to confront nothingness. Its acceptance was met with philosophical resistance in ancient times. How could "nothing" be real? How could nothing be useful in equations? But once mathematicians recognized zero as a number in its own right, it transformed entire philosophical discussions. It even challenged ideas in theology (e.g., the nature of creation and void).

In set theory, zero is the size of the empty set—the set that contains no elements. But without zero, there would be no way to express or manipulate sets of nothing. Thus, zero's philosophical acceptance paved the way for advanced theories in logic and mathematical foundations.

5. The Computing Revolution: Zero as a Binary Foundation

Fast forward to today. Every piece of digital technology—from computers to smartphones—relies on binary systems: sequences of 1s and 0s. These two digits are the fundamental building blocks of computer operations. The idea of Boolean algebra, where values are either true (1) or false (0), is deeply rooted in zero’s ability to represent "nothing" or "off."

The computational world relies on logical gates, where zero is interpreted as false, allowing us to build anything from a basic calculator to the complex AI systems that drive modern technology. Zero, in this context, is as important as one—and it's been essential in shaping the digital age.

6. Zero and Its Role in Modern Fields

In modern fields like physics and economics, zero plays a crucial role in explaining natural phenomena and building theories. For instance:

In physics, zero-point energy (the lowest possible energy state) describes phenomena in quantum mechanics and cosmology.

In economics, zero is the reference point for economic equilibrium, and the concept of "breaking even" relies on zero profit/loss.

Zero allows us to make sense of the world, whether we’re measuring the empty vacuum of space or examining the marginal cost of producing one more unit in economics.

7. The Mathematical Utility of Zero

Zero is essential in defining negative numbers. Without zero as the boundary between positive and negative values, our number system would collapse. The number line itself relies on zero as the anchor point, dividing positive and negative values. Vector spaces, a fundamental structure in linear algebra, depend on the concept of a zero vector as the additive identity.

The coordinate system and graphs we use to model data in statistics, geometry, and trigonometry would not function as we know them today. Without zero, there could be no Cartesian plane, and concepts like distance, midpoint, and slope would be incoherent.

[kiki-de-la-petite-flaque]

If an opinion contrary to your own makes you angry, that is a sign that you are subconsciously aware of having no good reason for thinking as you do. If someone maintains that two and two are five, or that Iceland is on the equator, you should feel pity rather than anger, unless you know so little of arithmetic or geography that his opinion shakes your own contrary conviction.

The most savage controversies are those about matters as to which there is no good evidence either way. Persecution is used in theology, not in arithmetic, because in arithmetic there is knowledge, but in theology there is only opinion. So whenever you find yourself getting angry about a difference of opinion, be on your guard; you will probably find, on examination, that your belief is going beyond what the evidence warrants!

Bertrand Russell, Unpopular Essays (An Outline of Intellectual Rubbish)

[scotianostra]

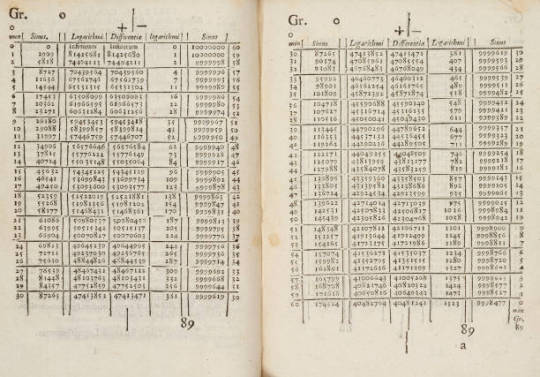
On April 4th 1617 John Napier, the mathematician, died.

It’s said that Napier is the nearest Scotland has produced to a 'Renaissance Man', at least as far as mathematics and the sciences are concerned. To the philosopher David Hume he was "the person to whom the title of a great man is more justly due than any other whom his country ever produced". The historian Christopher Smout has listed his achievements as including "a new type of screw-drainage for coal mines", "the use of salt as an agricultural fertiliser", "military burning glasses" and "self-propelled armoured chariots like tanks".

His enduring fame rests on his 'discovery' of logarithms in 1614 which propelled him into the front rank of European scientists alongside his contemporaries Kepler and Tycho Brahe.

Not much is known about his early life except for the fact that he was the son of a Scottish landowner and official and received a privileged upbringing. As a member of the nobility, he was tutored privately at home for a few years before being sent to St Salvator’s College, St Andrews. It was here that he first became deeply interested in theology though he did not acquire in-depth knowledge in mathematics until later.

For reasons unknown, he left the college before earning his degree and it is believed that he moved to some other educational institute for his higher studies. Eventually he began managing his estates and pursued mathematics as a hobby. Among his several contributions to the field, his invention of logarithms is regarded as his greatest.

In 1614 he wrote Mirifici Logarithmorum Canonis Descriptio which contained 90 pages of tables of natural logarithms and also contained theorems in spherical trigonometry known as Napier’s Rules of Circular Parts.

Now I can appreciate why these things are necessary in science etc I have to say, I hate maths, don’t mistake that with arithmetic, as I am quite adept at counting, the times table and division etc, trigonometry, algebra, logarithms can quite simple GTF.

Our archives at The National Library of Scotland has the original copies of Napiers memoirs, I will give you an example of his work;

L w~^ i/i*<<y*» & -^

’(^»^i<:

,/^V D<

‘£

Vo6^k -i—, ’.t/<C

1

iU’\,^M,«rT ^Wmfcw ^^.*v- zr fi* y$£/&

OtvOT"

nd- 6«X*Hv

fast

t^^^mP^^n&

JsX f-K-V- y*$P

\>>r~4/-Av-~oA tvc)

^<5~“

I mean come on, what kind of sorcery is this?

Which leads me to the final party of this post, John Napier was seen as a devoted and deeply religious family man, but in fact several members of John Napier’s family – respected and wealthy participants of Edinburgh society - were commonly known to be wizards or sorcerers. Their necromantic power was feared by nobles as well as peasants from far and wide.

This was at a time when James VI was actively attending and persecuting many poor people, mainly women, putting them to death after days and weeks of torture, had Napiers family not been landed gentry, they would have been the ideal candidates for these actions, money eh, changes everything.

Was John Napier involved in this? Well there is no proof of it, he was however a free thinker and thought outside the box, a very clever man, two examples of this here, initially caused the witchcraft tag to be be placed on him……

Rumours spread that he was a warlock after he enlisted the help of the cockeral to discover which if his servants had been stealing from him. Each servant was ordered to go into a darkened room and stroke the cockeral - the bird would crow, said Napier, when the guilty servant touched it.

The bird remained silent but Napier stunned the household by immediately identifying the culprit. Surely this was sorcery. But all he had done was put soot on the cockerel’s feathers - the innocent servants all had black on their hands, while the guilty one’s were clean because he was afraid to touch the bird.

At Merchiston, when pigeons belonging to a neighbouring landowner had been eating Napier’s grain, he threatened to restrain them. 'Do so, if you can catch them,�� scoffed his neighbour. Next morning, Napier’s servants could be seen stuffing hundreds of semi-conscious pigeons into sacks. Onlookers were convinced Napier had bewitched them - in fact he had simply scattered succulent peas soaked in wine to get the birds drunk and incapable.

But before his death Napier had left full details of how his logarithms had been calculated, and had left one final invention as a boon to the merchant classes. Napier’s Rods, or Napier’s Bones as they were called from the material they were made of, were in effect a powerful "pocket calculator”, as seen in the second pic.

Napier was twice married; first, in 1571, to Elizabeth, daughter of Sir James Stirling of Keir, by whom he had a son and a daughter; secondly, to Agnes, daughter of James Chisholm of Cromlix, by whom he had ten children. His eldest son, Archibald, who succeeded him, was raised to the rank of a baron by Charles I., in 1627, under the title of lord Napier, which is still borne by his descendants. A very elaborate life of him was published in 1835.

[luxe-pauvre]

If an opinion contrary to your own makes you angry, that is a sign that you are subconsciously aware of having no good reason for thinking as you do. If some one maintains that two and two are five, or that Iceland is on the equator, you feel pity rather than anger, unless you know so little of arithmetic or geography that his opinion shakes your own contrary conviction. The most savage controversies are those about matters as to which there is no good evidence either way. Persecution is used in theology, not in arithmetic, because in arithmetic there is knowledge, but in theology there is only opinion. So whenever you find yourself getting angry about a difference of opinion, be on your guard; you will probably find, on examination, that your belief is going beyond what the evidence warrants.

Bertrand Russell, The Basic Writings of Bertrand Russell

[hexagr]

Originally, there were seven traditional liberal arts taught in the Middle Ages and throughout the Renaissance, which were later codified in Rome: grammar, logic, rhetoric, arithmetic, geometry, music, and astronomy. A French painter, Coëtivy Master (Henri de Vulcop?), who was active between 1450 - 1485 and whom historians today still know very little about, painted this piece, Philosophy Presenting the Seven Liberal Arts to Boethius. Boethius was a Roman senator and philosopher from the Middle Ages who wrote about math, music, linguistics, theology, and logic.

[thepastisalreadywritten]

SAINT OF THE DAY (January 9)

Adrian, also spelled Hadrian (born before 637), was a North African scholar in Anglo-Saxon England and the abbot of Saint Peter's and Saint Paul's in Canterbury.

He was a noted teacher and commentator of the Bible. He also played a pivotal role in the early history of the English Church.

The famous abbot was likely born in Libya Cyrenaica, North Africa.

Adrian decided to become a monk early in life and eventually became Abbot of Nerida, not far from Naples.

Adrian became a valuable advisor to the pontiff and, three years later, was offered the position of Archbishop of Canterbury. 

He declined the papal appointment but was persuaded to accompany Theodore to England as a trusted counselor.

After spending time in France, he arrived in Britain and immediately succeeded Benedict Biscop as Abbot of St. Augustine's Abbey in Canterbury.

He established a flourishing monastic school, where many future bishops and abbots were educated in Latin, Greek, scripture, theology, Roman law, and arithmetic.

In addition to the knowledge he passed on through literature and teaching, Adrian also had a considerable impact on the Anglo-Saxon liturgy.

With Theodore, he spread the use of music in church services, which had hitherto been confined to Kent.

It is also due to Adrian that the feasts of several central Italian saints were introduced to the calendar of the Anglo-Saxon Church.

Hadrian died on 9 January 710 and was buried at his Canterbury monastery.

His remains – or relics – were rediscovered in 1091. His body was discovered in an incorrupt state.

Numerous miracles were attributed to him.

His feast day is celebrated on January 9, keeping alive the memory of the man who played such an important role in turning the Anglo-Saxon Church into an intellectual powerhouse of the early medieval world. 

[izvletchenie]

“The brain provides the source for man, the heart for animals, […].”

Attributed to Iamblichus, The Theology of Arithmetic

[knightofdeer]

Assuming that standard fantasy is based on Medieval Europe, there shouldn't be a separate magic university altogether.

In European Universities students first were learning subjects of trivium and quadrivium (Latin, logics, rhetorics, geometry, arithmetics, harmonics, and astronomy), and for plenty that was enough but those who wanted more could pursue some advanced subjects (what exactly was available was different, but it's usually theology and some others like medicine, law, natural philosophy).

So depending on how magical is your setting occult sciences are placed either in advanced subjects or somewhere in liberal arts.

(Also occult texts were popular in Medieval universities and students specifically were target audience of those Solomonic demons who teach sciences and languages)

And like obviously there are different ways to handle wizard education even in psedo-Medieval Europe, but whatever

[teenageascetic]

“Wisdom falls into three divisions.

The first division is the science of nature, called in Arabic, "Al-Ilm al-tibi". This branch of knowledge deals with the essential and incidental properties of material bodies.

The second division consists of the practical sciences, called in Arabic, "Al-Ilm al-riazi. These comprise arithmetic, engineering, astronomy, and music.

The third division, called in Arabic, "Al-Ilm al-ilahi. is the science of theology, which deals with the knowledge of G-d, knowledge of His torah, and other spiritual things, such as the soul, the intellect, and spiritual beings.

All these divisions of wisdom, and their respective branches, are gates which the Creator has opened for men through which they may attain a comprehension of religion and of the world. Only that some sciences are more needed for religious matters while others are more needed for secular interests.

The sciences whose use is closest to worldly matters is the science of nature, which is the lowest science and the practical science, which is second. These two sciences instruct on all the secrets of the physical world, its uses and benefits, its industries and trades and is conducive to physical and material well-being.

The science which is most needed for religion is the highest science - Theology.

We are under duty to study it in order to understand and obtain a knowledge of our religion. But to study it in order to attain worldly benefits is forbidden. Our teachers said (Nedarim 62a): "[expounding the verse: to love the L-rd your G-d, to hearken to His voice, and to cleave to Him' [This means that one should not say, I will read Scripture that I may be called a scholar. I will study mishna, that 1 may be called Rabbi, I will study [Talmud, to be an Elder, and sit in the assembly of elders; but learn out of love, and honor will come in the end". And "Do [good] deeds for the sake of their Maker, and speak of them words of torah for their own sake. Make not of them a crown wherewith to magnify yourself, nor a spade to dig with" (ibid). And "Fortunate is the man that fears the L-ord, that delights greatly in His commandments' (Ps. 112:1),

R. Eleazar expounds thus: In His commandments' but not in the reward of His commandments. This is just what we have learnt. He used to say, Be not like servants who serve the master on the condition of receiving a reward; but be like servants who serve the master without the condition of receiving a reward." (Avodah Zara 19a).”

-Rabbeinu Behaye, Chovot HaLevavo.

[mask131]

Occult Paris (2-A)

In the spring of 1948, three sisters – Leah, Margaret and Kate Fox, living in a rural town near Rochester in the state of New-York – claimed to have communicated with the dead, thanks to a turning table. People became obsessed with this trio of mediums and their poltergeists, and this was the start of the “spiritism craze”. This passion for communicating with the spirits soon reached Europe – and nor France, nor its capital Paris escaped it. In the upper classes of the capital, or in the “avant-garde milieu”, everybody tried to invoke the souls of the deceased inside tables for a little chat. Turning tables became one of the main entertainments of the time – or rather, a “spiritual sport”. It was the “greatest phenomenon” of the century, for many. But for the Church of France, it was something quite different… To quote the Chevalier Gougenot des Mousseaux, in his “La magie au dix-neuvième siècle” (Magic in the 19th century), “Magic, magnetism, somnambulism, spiritism, hypnotism – they are all but Satanism!”. The situation was taken very seriously by the religious authorities, to the point that the abbot Mautain, vicar of the archdiocese of Paris and doctor in theology, published a text tiled “Avertissement aux Chrétiens sur les tables tournantes”, “Warning for Christians about turning tables”. In it he described his experience seeing one day a basket twist itself “like a snake” and flee by crawling in front of a Gospel. The abbot Chevrojon, vicar of Saint-Roch, rather confessed having to battle against a “possessed stool”. For all the men of God of the time, spiritism was the work of the devil. As for the scientists of the Académie des sciences, it was all just charlatanism. For these rational and rigorist scholars, these tables could only turn through magician tricks, or by the subconscious muscular impulsions of the participants. For them, it was all just collective hallucinations, or autosuggestions.

But despite all the condemnations, despite all the warnings, despite all the debunking, people never stopped being obsessed with spiritism. In 1856, the emperor Napoléon III himself received officially in the Tuileries the Scottish medium Daniel Dunglas Home. During the séance they organized, a tale, several chairs and several furniture pieces started to float, while a host of famous spirits were invoked: Hortense de Beauharnais, Napoléon Ier, Marie-Antoinette, Jean-Jacques Rousseau and Blaise Pascal! But Home wanted to impress his imperial hosts too much, and this was his downfall: he was proven a fake when the Imperial Court went with him to Biarritz. There, “ghost hands” caressed the face of the empress Eugénie – but it was revealed to be the foot of the medium, wearing a glove! As it turns out, Home wasn’t a medium but a talented illusionists and hypnotists. Home was asked to leave France immediately – but despite this disgrace at the highest level of the government, secret societies and occult organizations of all sorts kept flowering and multiplying throughout France: spiritualists, theosophists, martinists, Rosicrucians, kabbalists, gnostics, neo-pagans, luciferians, Satanists… But three men in particular became extremely famous.

1) Allan Kardec

Born in Lyon in 1804, Hippolyte Léon Rivail settled at a very young age in Paris, where he opened a school (35, rue de Sèvres) where he taught based on the modern methods of the Swiss pedagogue Jean-Henry Pestalozzi, himself a fervent follower of Rousseau’s theories. Unfortunately, Rivail’s schools barely hold for a few years before closing – Rivail switched to the writing of manuals of grammar, arithmetic, chemistry and biology. It is when he was writing a chapter about the magnetism of animals that a friend of his told him about his personal “table experience”. Rivail had reached his fifties when he first took part in a séance of turning tables. He soon regularly visited these mediumnic séances – one rue de la Grange-Batelière, another rue Tiquetonne, a third rue de Rochechouart… One medium claimed that Rivail was actually the reincarnation of an old Breton druid by the name of Allan Kardec – and so the former teacher took this pseudonym as his new name. In 1857, the “new” Allan Kardec published the first and the most famous of his books, “Le Livre des Esprits”, The Book of Spirits, that he claims to have written under the command of… spirits! On the first day of April 1858, he creates in his home (8, rue des Martyrs) la Société spirite de Paris (The Spiritualist Society of Paris), and a newspaper by the name of “La Revue spirite” (The Spiritualist Review). Since his apartment becomes too small to welcome his many friends and disciples, Allan Kardec starts hosting reunions at the Palais-Royal, first in the galerie de Valois, than in the galerie Montpensier, and finally at the rue Sainte-Anne. Kardec created a true religion, whose influenced reached all of Europe – and even Brazil! He wrote many, many books: Qu’est-ce que le spiritisme? (What is spiritism?), Instruction pratique sur les manifestations spirites (Pratical instructions about spiritualist manifestations), Le Livre des médiums (The Book of mediums), L’Evangile selon le spiritism (The Spiritism Gospel), Le Ciel et l’Enfer ou La Justice Divine (Heaven and Hell, or the Divin Justice), and finally, La Genèse, les Miracles et les Prédictions selon le spiritisme (The Genesis, the Miracles and the Predictions according to spiritualism). In 1869, Allan Kardec did not die – but rather was “disembodied”, and his empty body buried in the Père-Lachaise cemetery. His grave, in the shape of a dolmen, is still one of the most famous tombstones of the entire cemetery.

2) Éliphas Lévi

Eliphas Lévi was the man who invented in the French language the word “occultisme”, “occultism”. Born Alphonse-Louis Constant in 1810, in the Odéon neighborhood, son of a shoemaker, he soon enters the seminary of Saint-Sulpice and he could have become a priest… if only he could “keep it in his pants”, if you excuse the expression. Young Constant was sent to a young girl’s house to catechize her, only for him to seduce and flirt with her – which officially put an end to his possible priestly career. His mother, who was a very pious woman, was so despaired and heartbroken by this she killed herself. Gifted for drawing, the young Constant started to live and work in artists studios, while enjoying a very lustful and un-chaste life. He notably was the lover of Flora Tristan, a socialist and feminist activist who would later become famous for being the grandmother of Paul Gauguin. Constant then became part of the staff of the collège oratorien de Juilly – and it was during this time that he wrote his first book, La Bible de la liberté (The Bible of freedom).

As soon as it was published, the book was pulled out of libraries, forbidden from being published, and both the author and edtor were summoned in the assize court of Paris for “attack against the public and religious property and moral”. Constant was locked up in the Sainte-Pélagie prison for eleven months, and when he got out he married Marie-Noémie Cadiot, an eighteen year old woman (he was over thirty!). He wrote a pamphlet called “La Voix de la famine” (The Voice of famine), and he was once again condemned to one year of prison. He however only did half of his time in prison – which allowed him to participate in the revolution of February 1848. He was now a wanted man – in fact, a revolutionary who happened to look like him was shot dead rue Saint-Martin! A few years later, in the 120 boulevard du Montparnasse, he wrote the book that truly started his legend: Dogme et rituel de la haute magie (Dogma and ritual of the high magic). To publish this book he took the pseudonym of Éliphas Lévi, which was the Hebraic translation of Alphonse-Louis. In this book, the author created the portrait of a fantastical creature that was then copy-pasted and spread through the press: Baphomet, the so-called idol worshiped by the Templar Knights. Lévi described the creature as having the head of a goat, the breast of a woman, hooves, wings, and a pentagram on the forehead – sitting cross-legged while flames burn over its head. After this first success, Lévi kept producing best-sellers: Histoire de la magie (History of magic), La Clef des grands mystères (The Key of great mysteries), La Science des esprits (The Science of spirits), Le Grand Arcane (The Great Arcana)… Admired by the occultists of his time, he regularly gave tarot readings or chiromancy readings, and he started practicing alchemical experiments. He became friend with Alexandre Dumas, wrote several songs, became a guest in several literary salons, and he even was presented to Victor Hugo throughout the daughter of Théophile Gautier, Judith Gautier. He died in 1875 and was buried in the cemetery of Ivry.

3) Papus

Born in Spain of a French father and Spanish mother, Gérard Encausse was just a child when his parents settled in Montmartre. He had a pretty normal childhood at the Rollin school (today’s Jacques-Decour highschool), where he had already created an esoteric journal and a secret society with other teenagers. Becoming a medicine student, he actually spends most of his time studying divinatory arts, the tarot, the Kabbalah, and the arts of chiromancy, numerology and hypnosis. He takes the pseudonym of “Papus”, the name of a genius doctor of Antiquity. Papus was a “bon vivant”, as we say in France, a man who enjoyed all the pleasures of life and hanged out with the bohème of Montmartre – he notably spent a lot of time in Le Chat noir cabaret. Papus was for a time part of the Theosophical Society created in the United-States by Helena Petrovna Blavatsky, but he soon decided to stay independent and create his own organization. Or rather, re-crate, as he resurrected l’Ordre martiniste (The Martinist Order), inspired by the mage of the 18th century, Martinès de Pasqually. The first Martinist loge was in the 24, rue Pigalle. Papus had a clear sense of hierarchy and of mise en scène: as the leader of the Order, he goes by the title “The Unknown Philosopher”, while his right hands take titles such as “The Unknown Brother”, “The Initiated Brother”, “The Associated Brother”. During their ceremonies, the members of the Order wear a red dress, a black silk mask and Egyptian cloth-strips similar to the one wrapping up mummies, while holding a sword. In its peak, the Order had twenty thousand members spread across Europe, Russia and the United-States.

Papus worked however outside of his personal organization: he also worked to rebuild the ancient brotherhood of the Kabbalistic Rose Cross. In 1889, he participates to the first International Spiritualist Congress, that takes place in Paris, rue Cadet, while also founding the GIEE – the Groupe indépendant d’études ésotériques (The Independent Group of Esoteric Studies), which is opened by a conference at the 44, rue Turbigo, and which gathers all of the spiritualists of Paris. All the disciples participating to this opening conference notably obtain a diploma. The next yar, Papus creates with the poet Lucien Chamuel “la librairie du Merveilleux”, the book-shop of the Marvelous, 29 rue de Trévise. In the back-room, Papus and his friend work on creating their journal “L’Initiation”, that Rome itself blacklisted, their monthly publication L’Union occulte (The Occult Union), as well as their weekly “Le Voile d’Isis” (The Veil of Isis), and various almanacs. It was also in the backroom of the bookshop that you could find the seat of La Faculté libre des sciences hermétiques (The Free Faculty of Hermetic Sciences).

In 1902, Papus and Lucien Chamuel sell the book-shop of the Marvelous to open a new bookshop, this one called “librairie d’Hermétisme” (Bookshop of Hermetism), at the 3 and 5 rue de Savoie – plus an annex rue Séguier. By now, the personal office of the occult master looked like an Egyptian temple: he notably wrote there many of the 160 various texts that were attributed to him. In 1905, the tsar Nicolas II invites him to Saint-Petersburg for a spiritism séance: it was said that during this meeting, the French wizard managed to invoke the ghost of Alexandre III (which, according to the rumors, made Rasputin very jealous). In June of 1908, Papus gathers at Paris the Spiritualist Congress, gathering thirty thousand members from all of Europe – it took place in the salle des Sociétés savants, in the 8th of rue Danton. During the Great War, Papus was named chief-physician paramedic, but he did not survive the war, dying of tuberculosis before the end of the conflict. Some whispered that he might have been cursed by an envious Rasputin…

 Some additional notes, to understand the Papus article:

# Helena Petrovna Blavatsky, born in Russia, founded in New-York in 1875 the Theosophical Society, which soon spread world-wide. Her teachings were a syncretism of Buddhism, Hinduism, Christianism and esoteric thinking. In Paris, the theosophy received its first disciples in 1883. A journal, Le Lotus Bleu (The Blue Lotus) was founded. The seat of the French Theosophical Society was at the 4, square Rapp, in the seventh arrondissement.

# Jacques Martinès de Pasqually, a Portuguese Jew that converted himself to Catholicism, travelled in France in 1750 and founded there the society of the Order of the Mason Knights elected Cohen (Cohen, in Hebrew, meaning “priests”). Louis Claude de Saint-Martin, nicknamed “The Unknown Philosopher”, was his secretary. The Martinist Order, or Martinism, offered to its adepts to become “beings of God” by mixing spirituality and magic.

# The Rose Cross is a secret and mystic brotherhood created by Christian Rosenkreutz in Germany in the 17th century. Very soon, it became a phenomenon in Paris. The Rosicrucian Order preaches justice and truth.

[noosphe-re]

[alphaman99]

Bertrand Russell

“If an opinion contrary to your own makes you angry, that is a sign that you are subconsciously aware of having no good reason for thinking as you do. If some one maintains that two and two are five, or that Iceland is on the equator, you should feel pity rather than anger, unless you know so little of arithmetic or geography that his opinion shakes your own contrary conviction.

The most savage controversies are those about matters as to which there is no good evidence either way. Persecution is used in theology, not in arithmetic, because in arithmetic there is knowledge, but in theology there is only opinion. So whenever you find yourself getting angry about a difference of opinion, be on your guard; you will probably find, on examination, that your belief is going beyond what the evidence warrants.“

— Bertrand Russell, An Outline of Intellectual Rubbish (1943)

[whatisyoulike]

St. Thomas Aquinas

St. Thomas Aquinas (1225-1274) was an Italian Dominican friar, philosopher, and theologian who made significant contributions to the fields of philosophy, theology, and natural law theory. He is regarded as one of the most influential Christian thinkers in history.

Early Life and Education: Thomas Aquinas was born into a noble family in Roccasecca, Italy, in 1225. At the age of five, he was sent to the Benedictine monastery of Monte Cassino to receive his education. Later, he enrolled at the University of Naples, where he studied the liberal arts, including grammar, logic, rhetoric, arithmetic, geometry, music, and astronomy. Despite initial opposition from his family, who wanted him to pursue a career in the Church, Thomas joined the Dominican Order in 1244.

Philosophy and Theology: Thomas Aquinas studied under Albertus Magnus, a prominent philosopher and theologian of his time. He combined the ideas of Aristotle with Christian theology, seeking to reconcile faith and reason. Aquinas believed that both faith and reason were valid paths to knowledge, and they complemented each other rather than contradicting one another.

One of Aquinas's most significant works is the "Summa Theologica," a comprehensive synthesis of Christian theology. It consists of several volumes and addresses a wide range of theological and philosophical topics, including the existence and nature of God, ethics, human nature, and the sacraments. The "Summa Theologica" remains one of the most influential works of Christian theology.

Natural Law Theory: Aquinas is also known for his development of the theory of natural law. According to Aquinas, natural law is an inherent moral order that is accessible to human reason. It is based on the belief that God's eternal law, which governs the universe, is imprinted on the nature of all things. By using reason, humans can discern this natural law and understand how to live morally and fulfill their purpose.

Aquinas's natural law theory suggests that there are certain fundamental principles of morality that are universally applicable to all human beings. These principles include preserving life, procreation, seeking knowledge and truth, living in society, and worshiping God. Aquinas argued that by following natural law, individuals can achieve their ultimate happiness and fulfillment.

Legacy: St. Thomas Aquinas had a profound and lasting impact on Western philosophy and theology. His works continue to be studied and debated by scholars, and his ideas have influenced countless thinkers throughout history. Aquinas's synthesis of Aristotelian philosophy and Christian theology helped shape the intellectual landscape of the Middle Ages and beyond.

Aquinas was declared a saint in 1323 and was given the title "Doctor of the Church" by Pope Pius V in 1567. He is honored as the patron saint of Catholic universities, colleges, and schools. St. Thomas Aquinas's intellectual contributions and his commitment to integrating faith and reason have left a lasting mark on the Christian intellectual tradition.

[casualflowerglitter]

"Persecution is used in theology, not in arithmetic, because in arithmetic there is knowledge, but in theology there is only opinion."

― Bertrand Russell, Unpopular Essays (1950), Ch. VII: An Outline of Intellectual Rubbish, p. 104

"What appears to justify persecution is dogmatic belief. Kindliness and tolerance only prevail in proportion as dogmatic belief decays."

― Bertrand Russell, What Is an Agnostic? (1953)

[thepastisalreadywritten]

SAINT OF THE DAY (January 9)

The famous Abbot of St. Augustine's in Canterbury was likely born between 630 and 637 in Libya Cyrenaica, North Africa.

Adrian decided to become a monk early in life and eventually became abbot of Nerida, not far from Naples.

Adrian became a valuable advisor to the pontiff, and three years later, was offered the position of Archbishop of Canterbury. 

He declined the papal appointment but was persuaded to accompany Theodore to England as a trusted counselor.

After spending time in France, he arrived in Britain and immediately succeeded Benedict Biscop as Abbot of St. Augustine's Abbey in Canterbury.

He established a flourishing monastic school, where many future bishops and abbots were educated in Latin, Greek, scripture, theology, Roman law, and arithmetic.

Adrian died on 9 January 709 at Canterbury, Kent. Several hundred years after his death, Adrian’s body was discovered in an incorrupt state.

He came to be regarded as a saint and his relics were re-deposited in the new monastery on 9 January 1091, which is now his feast day.