#Pythagoras squares

[demonicseries]

me fighting the urge to tell every alt person wearing a pentagram that it originated from an Ancient Greek math cult led by the guy who’s credited with “discovering” a^2 + b^2 = c^2, and proceed to give a short lecture on the golden ratio and the Fibonacci sequence

[whats-in-a-sentence]

An artificial distinction of women from men formed part of Pythagoras' dualistic view of the world. The ancient Greek mathematician and philosopher defined a set of ten opposites, which include 'male : female':

Limited : Unlimited

Odd : Even

Unity : Plurality

Right : Left

Male : Female

At Rest : In Motion

Straight : Curved

Light : Darkness

Good : Evil

Square : Oblong

"Normal Women: 900 Years of Making History" - Philippa Gregory

[peeterjoot]

A silly geometry problem: length of side of square in circular quadrant

[Click here for a PDF version of this post] Problem from: My solution (before numerical reduction), using basic trig and complex numbers, is illustrated in fig. 1. fig. 1. With complex numbers. We have \begin{equation}\label{eqn:squareInCircle:20} \begin{aligned} s &= x \cos\theta \\ y &= x \sin\theta \\ p &= y + x e^{i\theta} \\ q &= i s + x e^{i\theta} \\ \Abs{q} &= y + 5 \\ \Abs{p – q} &=…

[k-star-holic]

Cha Joo-young, Pythagoras (Oh really)

Source: k-star-holic.blogspot.com

[yourplayersaidwhat]

Player, observing 5ft by 5ft squares that are also 5ft diagonally (DM said we don't need math):

"Pythagoras is rolling in his grave rn"

[merpmonde]

Sangaku Saturday #4

In the previous info post, we went over the debate on the religious aspect of sangaku, and the fact that the absence of prayers on these tablets was more puzzling to some than the mathematics. As such, the tablets are not ema prayer tablets, but donations, which usually don't feature prayers on them. Case in point, some consecrated sake and French wine seen at Meiji-jingû in 2016.

Beyond wishing for good fortune and health, such donations serve two very worldly purposes: to contribute to the life and prestige of the shrine or temple (having a famous contributor makes the shrine famous by association), and to advertise the donor in return, as their name is on display. See this large torii at Fushimi Inari Taisha paid for by TV Asahi (テレビ朝日).

With that in mind, Meijizen's cynical comment from 1673 that sangaku aim "to celebrate the mathematical genius of their authors" may not far from the truth. The authors of sangaku are looking to gain notoriety through the publicity that the shrine or temple provides. But was the bemused Meijizen the target audience?

More on that in a couple of weeks. Below the cut is the solution to last week's problem.

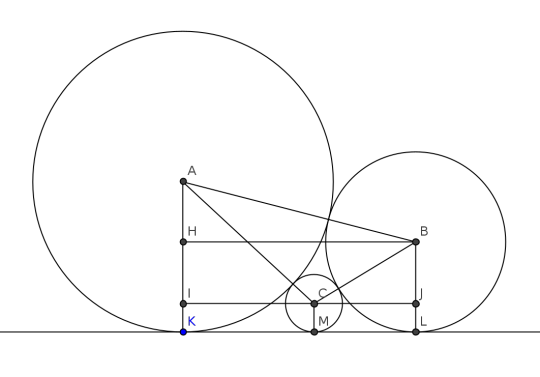
The solution to the first problem (below the cut in this post) is the key. Name K, L and M the intersections of the three circles with the horizontal line. Then, by using that previous result,

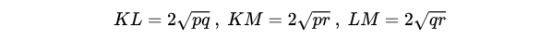
Indeed, as in that problem, we can construct three right triangles, ABH, ACI and BCJ and apply Pythagoras's theorem in each.

Now, it suffices to note that KL = KM + LM, so

or, dividing by 2*squareroot(pqr), we get the desired result:

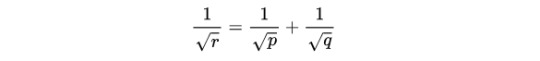
Inverting and squaring this yields the formula for r:

This gives us the means to construct this figure on paper using a compass and a marked ruler. Having chosen two radii p and q and constructed the two large circles (remember that AB=p+q) and a line tangent to both, placing M and C is done after calculating the lengths IK=CM=r and IC=KM=2*sqrt(pr).

[thedoctorisgroovy]

Schooled - Chapter 3

Chapter 1 Chapter 2

» Pairing: Spencer Reid x BAU!Reader

» Word count: 1640

» Warnings/Tags: bad relationship with family, unsupportive family, feelings of failure, Spencer being cute and protective.

» A/N: Final chapter of backstory I promise! Thank you for the support on the first two chapters, now that I have an outline I think this will be around 8-10 chapters to complete. I really enjoyed writing the team this way, they really are a family and it's adorable.

Taglist: @esposadomd, @gghostwriter

Until you sat down on the jet, you didn’t realise that your brain hadn’t stopped from the moment you left the briefing room. Settling into a seat next to Spencer and opposite Emily, you let out a big sigh and leaned your head on Spencers’ shoulder. He shuffled in his seat next to you to put his arm around you and pull you closer for maximum comfort. From across the aisle Emily gave you a gentle smile. You half expected Spencer to press you for “that chat” now that you were sat down but he also respected your feelings and knew you’d explain when you were ready to.

The air in the jet was different this time. You’d travelled on this plane hundreds of times and everyone was usually just in focus mode. Heads buried in case files, studying every aspect before landing to make sure you were all fully prepared. This time however, the rest of team were laughing and joking. Reminiscing on their own personal high school memories, eliciting groans when certain hairstyle choices were brought up or dating horror stories or the fact that Prentiss used to be a goth. You closed you eyes and listened absent-mindedly to the banter happening a few feet away from you. It felt strange to be relaxed at a time like this. You were heading to a disappearance/kidnap/potential homicide and yet it was like you were all heading on vacation. You wondered if this new energy was a slight farce planned by everyone to keep your anxiety at bay, but currently you didn’t care. It was nice to hear laughter for once in this line of work. You would've bet that with your eyes closed, you could tell that even Hotch was smiling.

“So Hotch, how come Reid got picked to be the teacher?” Morgan asked, a slight pang of jealousy in his tone.

“Because he’s a genius.” JJ retorted. You felt Spencer tense at the moniker. You didn’t have to open your eyes to know he was rolling his right now. He’d once confided in you that being called a genius made him uncomfortable. When he first joined the BAU, he revelled in it. He loved being the youngest, the smartest and being trusted to do the job he does based on his intellect. He felt it gave him a sense of importance and authority. Agent Gideon, his previous boss used to introduce him as “Doctor” on purpose to make sure others respected him despite his age. But after 5 years, he didn’t want the identifier anymore. After the things he’d seen, the things he’d been through and the cases he’d solved for the bureau, he felt he’d earned his place based on merit and hard work. He wasn’t desperate to fit in and be respected any more, he just did and was. You decided to open your eyes and watch how this was going to play out.

“And? You don’t need to be a genius to teach high school.” Morgan rebuffed defensively.

“Okay tough guy, explain Pythagoras to me right now then.” Prentiss scoffed at him. Morgan adjusted himself in his seat, sitting up slightly, taking the situation very seriously. He looked around nervously at all the eyes on his, awaiting his explanation.

“Yeah alright, it’s that E=Mc squared thing right?” Morgan mumbled slight, his bravado trying to compensate for what he didn’t know. The jet was full of people trying to stifle their laughs, not wanting to be to mean to Morgan, he had tried after all. JJ hit his shoulder playfully, the mistake and embarrassment dawning on his face before clearing his throat to try and save face.

“Okay so maybe I don’t know Math, but I’d still take any of you in an arm wrestle.” - Morgan booed, holding his hands up in mock surrender. Spencer had bolted upright in his seat, bouncing his knee waiting his for turn to speak. Any chance to explain something made him so excited. You looked up at him and saw the sparkle in his eyes that you absolutely adored.

“Pythagoras is the theory that when dealing with a right angled triangle, the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. "A squared + B squared = C squared" is the equation you were trying to think of. We shouldn’t really call it a theory anymore in my opinion because it’s been proved many times. An interesting fact about Euclidean geometry is that it uses a Cartesian coordinate system…” God you loved this man.

“Okay kid, we get it, you’re the right one for the job.” You scowled slightly at Morgan for cutting Spencer off, you loved his facts and trivia, it was one of the few times you knew he was relaxed and right now that’s all you wanted for him. Spencer sat back in his chair, and you repositioned yourself on his shoulder giving his arm a small squeeze to show you cared about what he was saying.

“Reid is the most experienced, he’s taught at the university before and knows a lot of information about a lot of subjects, simple as that.” - Hotch asserted.

“Can’t believe you’re jealous that they both have to go back to highschool” Emily teased. Morgan just blew her off with a wave of his hand, clearly done with the conversation. You tapped Spencer’s arm lightly and he hummed in response. You turned your body into his slightly and looked at up his kind eyes. Emily realised this was about to be a private conversation by the way you’d made your own little bubble and tried to look anywhere but at you two, much to your gratitude. You knew you’d still likely be heard - it was a small jet after all - but you still appreciated the gesture. Taking a big breath, you locked your fingers with Spencers’ and thought carefully about your words.

“I’m sorry I worried you back at Quantico, I was just in shock about my home being in danger. I realised it’s more than that though.” Your eyes dropped from his face, looking down into your lap, watching the way your fingers fidgeted nervously with his, an anxious habit you’d picked up a while ago.

“Spencer I feel like a failure.” You said in the smallest voice possible, admitting it felt like the most vulnerable secret in the world.

“My family and I, we don’t exactly have the best relationship. In my town, people don’t really do much after highschool. When I told my parents that I wanted to leave and join the FBI they acted like I was crazy, they thought that I thought that I was better than everyone else. They think I’m pretentious, all high and mighty. They’ve never once told me they’re proud of what I do, and even though I’m coming back now to try and save lives, it feels like it doesn’t matter.” Tears start welling your eyes, you don’t want to cry - not here, not now - but the dam is close to breaking. Spencer lifts one of his hand to your chin, tilting your head back up to meet his eyes. Those eyes. So full of kindness, compassion and understanding. He presses a small kiss to your forehead before speaking,

“Listen to me, you are not a failure. I know they’re your family but they’re idiots. I’m sorry but they are. Actually, I’m not sorry, because anyone who can’t see how smart and incredible you are deserves to be insulted. You’re not returning because you did anything wrong, or because you couldn’t cope. You’re returning with the best criminal analyst team within the FBI, that’s so small and exclusive you have to be brilliant to work for. You don’t need to prove anything to anyone and if your parents say anything when we meet them, I have no problem defending you.” And with that, he pulled you into him, his long limbs enveloping every part of your body. You laugh/cried softly against his chest. You knew he meant that last part - you’d seen him be sassy and assertive with cops and other FBI members, he certainly wasn’t going to be afraid of your parents. It was Hotch who broke the moment between you two.

“I’m sorry to eavesdrop, but I’m afraid you won’t be able to see your family. We can’t risk anyone recognising you or giving away your identity. We know there’s already risk of that since it’s only been a few years since you’ve been around but seeing your family would give away the connection straight away. As soon as we land, you and Reid will be going separate ways.” You felt Reid’s grip tighten on you, pre-emptively holding onto you.

“Agents’ Prentiss, Morgan, JJ and myself will be heading straight to the station to meet with the local PD. If this unsub sees us arriving it might cause him to get nervous and slip up, meaning we can catch him sooner. We’ll be able to stay in contact with you both through calls and emails but we can’t be seen physically together, I’m sorry. Garcia will send you your accommodation details when we land.” And with that, the jet become reminiscent of how it always is before a case, quiet and contemplative.

Hearing that you’d be able to stay in touch provided minimal comfort to the pounding heart in your chest. The remaining time on the flight was spent nestled into Spencers’ side, trying to calm your thoughts. You were used to going into the field alone sometimes but never like this. “At least you’d see him at school everyday” you thought chuckling internally.

All that was left to do was to await the call from Penelope at touchdown.

Chapter 4

[tensorboi]

Why is the Pythagorean theorem true, really? (and a digression on p-adic vector spaces)

ok so if you've ever taken a math class in high school, you've probably seen the Pythagorean theorem at least a few times. It's a pretty useful formula, pretty much essential for calculating lengths of any kind. You may have even seen a proof of it, something to do with moving around triangles or something idk. If that's as far as you've gotten then you are probably unbothered by it.

Then, if you take a math class in university, you'll probably see the notion of an abstract vector space: it's a place where you can move things and scale them. We essentially use these spaces as models for the physical space we live in. A pretty important thing you can't do yet, though, is rotate things or say how long they are! We need to put more structure on our vector spaces to do that, called a norm.

Here's the problem, though: there are a *lot* of different choices of norm you can put on your vector space! You could use one which makes Pythagoras' theorem true; but you could also use one which makes a³ + b³ = c³ instead, or a whole host of other things! So all of a sudden, the legitimacy of the most well-known theorem is called into question: is it really true, or did we just choose for it to be true?

And if you were expecting me to say "then you learn the answer in grad school" or something, I am so sorry: almost nobody brings it up! So personally, I felt like I was going insane until very recently.

(Technical details: the few that do bring it up might say that the Pythagorean norm is induced from another thing called an inner product, so it's special in that way. But also, that doesn't really get us anywhere: you can get a norm where a⁴ + b⁴ = c⁴ if you are allowed to take products of 4 vectors instead!)

How is this resolved, then? It turns out the different norms are not created equal, and the Pythagorean norm has a very special property the others lack: it looks the same in every direction, and lengths don't change when you rotate them. (A mathematician would say that it is isotropic.) Now, all of a sudden, things start to make sense! We *could* choose any norm we like to model our own universe, but why are we going to choose one which has preferred directions? In the real world, there isn't anything special about up or down or left or right. So the Pythagorean norm isn't some cosmic law of the universe, nor is it some random decision we made at the beginning of time; it's just the most natural choice.

But! That's not even the best part! If you've gone even further in your mathematical education, you'll know about something called p-adic numbers. All of our vector spaces so far have been over the field of real numbers, but the p-adic numbers can make vector fields just as well. So... are the Pythagorean norms also isotropic in p-adic spaces? Perhaps surprisingly, the answer is no! It turns out that the isotropic norms in p-adic linear algebra are the ∞-norms, where you take the maximum coordinate (rather than summing squares)! So the Pythagorean theorem looks very different in p-adic spaces; instead of a² + b² = c², it looks more like a^∞ + b^∞ = c^∞.

If you're burning to know more details on this, like I am right now as I'm learning it, this link and pregunton's linked questions go into more details about this correspondence: https://math.stackexchange.com/questions/4935985/nature-of-the-euclidean-norm

The interesting thing is that these questions don't have well-known answers, so there is probably even more detail that we have yet to explore!

tl;dr: the pythagorean theorem is kind of a fact of the universe, but not really, but it kinda makes sense for it to be true anyway. also we change the squares to powers of infinity in p-adic numbers and nobody really knows why

[xyliaxart]

Math class in Hell

the Joke™ is that Pythagoras was like really into ratios. and on the board is a proof that the square root of 2 is irrational, aka cant be written as a ratio.

Also yes this implies that pythagoras is In Hell and that my imp has beef with him

[aromanticduck]

Hippasus: The length of the diagonal of a square can’t be expressed as a whole number proportion.

Pythagoras: *pushing him off the boat*

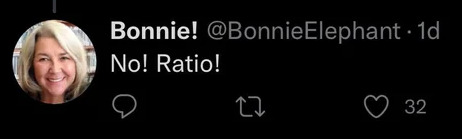
[Image description: a tweet from Bonnie! which says:

‘No! Ratio!’

End description]

[janmisali]

Number Tournament: THREE vs THE SQUARE ROOT OF TWO

[link to all polls]

3 (three)

seed: 2 (72 nominations)

previous opponent: Rayo's number

class: prime number

definition: the only threeven prime

the square root of two

seed: 34 (15 nominations)

previous opponent: twenty-one

class: irrational number

definition: the number that proved Pythagoras wrong

[luimagines]

Adding to more human-Hylian differences, their minds.

What if human brains are more mathematical, logical, etc, while Hylian brains are better at pattern recognition? Think of the dungeons. A human might need a guide, but the Links could all solve the puzzles, even at 8 years old. But then, you ask a Hylian to do Pythagoras' theorem, and it's more difficult, because their brains aren't built like that, while human adolescents are perfectly fine with a squared + b squared = c squared. Humans are way better at abstract concepts, while Hylians need the puzzle to be in front of them. Hylians are also more elaborate in their puzzle solving. You ask an average human, and they will hit the puzzle until it works, while a Hylian will analyse the pattern and quickly find the solution. Sheikah are like a branch of Hylian that evolved the more human-like mind, but not quite, because they still used magic as a crutch. Hylians also seem to value aesthetics a lot, even over practicality, because look at those dungeons where people apparently lived. All those pretty structures and yet you can't feasibly imagine it being convenient to live there. And the Divine Beasts, along with the Guardians. Are those terminals in practical locations? They look cool, sure, but then you wonder just why in the world they have such glaring weaknesses. They added unsecured entrances all over the place, it's no wonder the Blights could invade, and the Guardians have the eyes **right there**. And then, when their magical power source backfired, instead of electing to fix it, they turned them all to scrap and buried them underground. Also, as a history nerd, Lookout Landing is honestly terrible for defense, if you've seen Bread Pirate's video, you'll know, along with most places in Hyrule. And then, you compare all these settlements to Ordon, human run. Bridge can be blocked prevent enemies from crossing if I recall, and they have a sustainable food source inside the village if they get trapped, along with trained fighters, and it's surrounded by mountains. It actually seems like one of the better places in terms of defense. Humans are practical, while Hylians are still living in Hyrule, the place with an active volcano, a resurging evil, and a monster infestation. Meanwhile, Hytopia, another human populated land, is doing so well that they can turn all their focus to fashion with no consequences for their safety. It is no wonder Hyrule keeps getting taken over and attacked.

Dang, you out a lot of thought into this. ^.^*

I completely agree with what your saying.

But maybe instead of inherent pattern recognition, maybe Hylians are just better at processing/working with abstract concepts. If their society is more magic based anyway, it would be pretty difficult to be more abstract than literal magic.

I think you're right about Humans being more mathematical in that sense. They would have to be better at crunching numbers and all the logistics that follow because they don't have the luxury of throwing things at the wall and seeing if it sticks or not.

That being said- yeah, I can totally see Hyrule just keeping up with this cycle of post apocalyptical destruction, (curse aside, of course) while literally everyone else is just moving on with their lives and staying happily in their own lane.

[mathhombre]

Triangular and Square Numbers

Mel Bochner, via Peter Freeman Inc

Theory of Syntax #2

Meditation on the Theorem of Pythagoras

(Always the damn 3 4 5. There's an infinite family of triples out there, people!)

Five Scupltures

(Good joke.)

Cardinal vs Ordinal

Five by Four

5 ≠ 5

Three, Five, Four

Measurement Plants

[oliviabutsmart]

Physics Friday #14: Sound (Part 2/2)

Preamble: Let's get straight into it

Education Level: Primary School (Y5/6)

Topic: Sonic Physics (Mechanics)

The previous part 1 of my sound post is here.

Pitch and Frequency

Pitch and frequency are related to eachother, the only difference being that frequency is a physical interpretation of sound and pitch is our own mental interpretation of it.

But what exactly is frequency?

Go back to last time's example of a tick sound occurring at regular intervals ... because this sound is repeating, we can describe it's behaviour by measuring mathematical properites:

How much time passes in-between each tick (Period)

How many ticks occur every second (Frequency)

These two ideas are related to eachother, in fact Frequency is 1/Period. If you have a tick every half-second, then you can say the tick occurs twice every second.

We measure sound in Hertz, which is effectively a measure of ticks per second.

Most sounds, however, don't work this way, with repeated ticks. They act as proper waves. With zones of high pressure (peaks), and low pressure (troughs). This is where we have to introduce another variable into our equation:

The physical difference separating each peak (Wavelength)

Since these waves travel forward in the air, a detector (like our ears) will pick up the peaks and troughs as they reach our ear. We can measure frequency or period by recording the speed at which our peaks reach our ear.

But we also can relate frequency to wavelength. After all, the further apart the waves are separated, the more time it'll take for a peak to reach us after the previous one.

We quantify this relationship using c = fλ. Where c is the speed of the wave, f is the frequency, and λ is the wavelength.

Notice that we can also say cT = λ, where T is the period. This demonstrates that the physical wavelength is proportional to the amount of time between each peak.

So where does pitch come in?

As mentioned in part 1, if we continue to decrease the time between each tick, or increase the frequency, at some point we'll begin to hear a sound.

This is our brain playing a trick on us. It's like frames-per-second but for our ears. Below some fps threshold, we can see the individual pictures of a video, but above the threshold, it looks like a continuous film. Notice that fps is also another form of frequency.

When we reach this level, our brain can't distinguish between each tick and sees it as one sound. We begin to hear our first sound.

At this point, frequency becomes tied to pitch. The more rapid the ticking becomes, the higher of a pitch we hear. This is a choice that our brain makes - it's purely psychological.

Mixing different pitches

Combining different pitches allows us to create a foundation for music. In western music, our source of harmonics comes from Pythagoras, who kinda fucked it up by not using irrational numbers.

An octave is defined as a higher sound that has twice the frequency of the lower sound i.e. a ratio of 2:1. One octave above middle C (at about 262 Hz) gives us C5 (at about 524 Hz).

We can create further subdivisions like a perfect fifth, where frequencies form a 3:2 ratio. Or a perfect fourth, which has a ratio of 4:3.

Volume, Intensity, and the Inverse Square Law

Volume is directly related to the amplitude of a sound wave. Effectively, how strongly is the air being compressed at each peak?

Again, volume is just another psychological interpretation of a physical phenomena. Similar to how our eyes see brightness.

Amplitude isn't just interpreted as volume, it is also the power that the sound waves carry. Smaller amplitudes correspond to less energy contained within the moving particles.

We measure intensity logarithmically, because that's what our ears here. Effectively a wave sounds twice as loud only if the wave is 100 times as amplified. It's a similar effect to pitch, where we multiply frequencies instead of adding them.

That's where the decibel scale comes in. 1 dB = a 10x increase in the sound's power output. The decibel scale is used generally for a lot of measurements of wave/power intensity. However it just so happens that our ears behave in very similar ways.

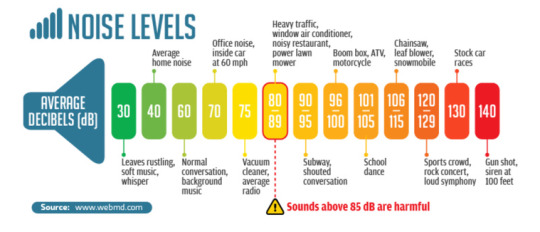
Image credit: soundear.com

Notice that louder sounds are more likely to damage our ear. That's because when loud sounds reach our ear, it causes the inner components to vibrate. This vibration amplitude generally is proportional to the amplitude of the waves.

Too loud of a sound means that our eardrums are vibrating with too great of a physical movement. This can create tears in tissue that damage our ears' sensitivity to sound.

Sound looses power over distance

If you stand far away enough from a sound source, it sounds fainter, eventually becoming unhearable.

This is because of the inverse square law. As sound spreads out over distance, it has to emanate in the form of a sphere, going outward in every direction, in order to maintain consistency of direction.

The same amount of power gets spread thinner and thinner over the bubble that it creates. The surface area of a sphere increases to the square of it's radius.

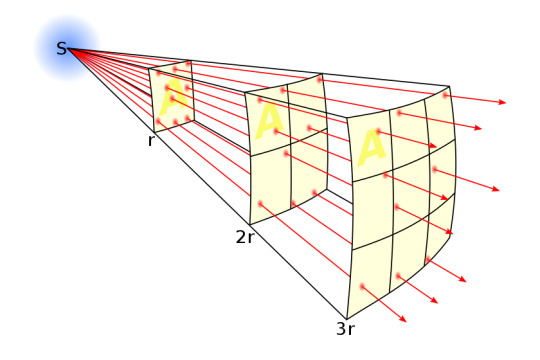
Image Credit: Wikipedia

Thus we get a decrease in volume over time.

What the Actual Fuck is Timbre, and how do you pronounce it? (also Texture too)

Unfortunately I still don't know how to pronounce it.

Timbre is defined as the quality and the colour of the sound we hear. It also includes the texture of the sound. It's sort of the catch-all for every other phenomena of sound.

Timbre is a bit more complex of a phenomena. In that, it combines basically everything else we know about how we hear sound. So I'll go one by one and explain each component of what makes Timbre Timbre.

Interference

Wave interference is an important property that needs to be understood before we actually talk about timbre. Sound waves often can overlap eachother in physical space, normally caused by multiple sound sources being produced at different locations.

These sound sources often will create new shapes in their waveform, via interference.

Constructive interference is when the high-pressure zones of two sound waves combine to produce an even-higher-pressure zone of wave. Effectively pressure gradient add onto eachother.

Destructive interference is when a high-pressure zone overlaps with a low-pressure zone, causing the pressure to average out to baseline, or something close to the baseline.

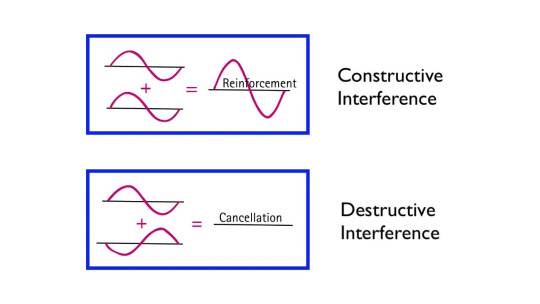
Image Credit: Arbor Scientific (Youtube)

We can look at multiple waves acting continuously over a medium to see how their amplitudes will add up together using interference. This is the origin of more unique wave patterns.

The shape of a wave

Sound waves can come in different varieties. While the most basic shape is the sine wave. We can add different intensities, frequencies and phases of sine waves to produce more complex patterns.

I won't go into how this combination works because that's better left for a Fourier series topic. Just know that pretty much any sound can be broken down into a series of sine waves.

These patterns have a different texture, as they combine multiple different monotone sounds. Take a listen to a sawtooth wave vs a sine wave:

Warning: the sawtooth wave will sound a lot louder than the sine wave.

This gives us a different sound texture.

Resonance

When you play a musical instrument at a particular frequency, the instrument is often resonating.

Say you produce sound within an enclosed box. Producing it at one end. Eventually the sound will reach the end of the box and bounce back from reflection (as we'll see later).

The sound will bounce back and forth, combining itself with the previous waves to produce more and more complex waveforms.

But there is a particular frequency, at which, the waves will perfectly interfere with eachother to produce what's known as a standing wave.

A standing wave will oscillate, but it will appear as if it's not moving forward. Of course, power is still moving throughout the wave, as we'll still be able to hear something.

This standing wave can only occur at a particular frequency, one in which the wave perfectly interferes with it's reflection within the box.

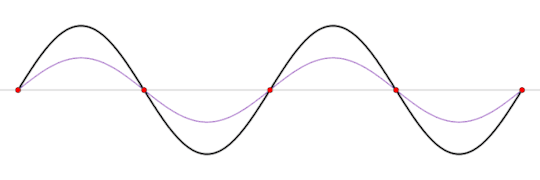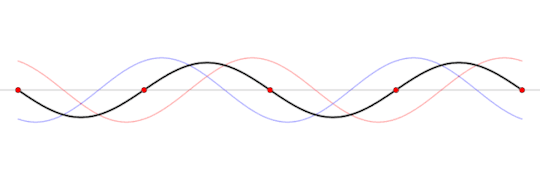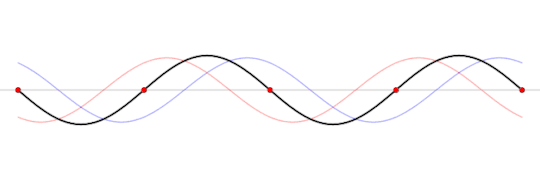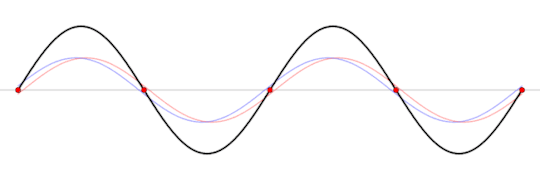
A standing wave (black) that is produced by two sine waves (blue and red) moving in opposite directions Image source: Wikipedia

This frequency is called the resonant frequency of the box. This frequency depends on several factors like the speed of the wave, the material inside the box, the shape of the box, and the length of the box.

The resonant frequency can be activated by our voices, as our voices or just blowing air is already a combination of different sound frequencies. The non-resonant frequencies will eventually loose all of their power as they destructively interfere, leaving only the resonant frequency, which gets amplified by what we put in

For example, you can fill a glass bottle halfway with some water, blow in it, and it will produce a particular sound. Fill it with more water, and the pitch increases - i.e. by adding the water we increase the resonant frequency.

All instruments have one or more resonant frequencies based on their material and shape (I say multiple because some instruments can me modelled as multiple boxes. Like a violin will have the inside of the wood, the wood itself, the strings, etc.).

Instruments also allow us to alter the resonant frequency by playing it differently (like putting a finger over your recorder's hole (phrasing)).

These differences in how we obtain resonance can also affect the quality of the sound.

Overtones

Resonance is not just generated with a single resonant frequency, we can create resonance with higher multiples of the the same fundamental frequency.

This is because in our box model, multiplying the fundamental frequency will allow us to create a standing wave, just with a shorter wavelength:

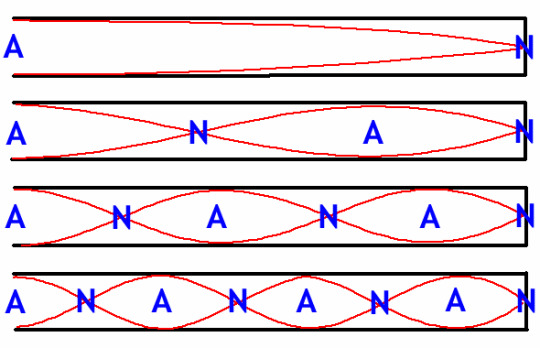
The A's stand for antinodes, which vibrate in the standing wave with the maximum amplitude. The N's stand for nodes, which do not move at all.

Image Credit: Macquarie University

Direct multiples of the fundamental frequency are called harmonics. Instruments can also produce other frequencies not directly harmonic depending on the structure of the 'box' they utilise.

These additional frequencies, ones which come often in fractional multiples of the fundamental are called partials. Both partials and harmonics represent the overtones of an instrument.

Overtones are what give sound additional character, as they allow instruments to not just resonate at the note they play, but at other combined frequencies. In some instruments, the overtones dominate over the fundamental - creating instruments that can play at much higher pitches.

Envelopes and Beats

Say we add two sine waves together (red and blue), each with slightly different frequencies, what we get is this:

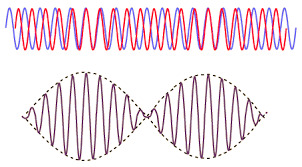
Image Credit: HyperPhysics Concepts

We can see that the brown wave has a singular oscillation frequency, but also it's amplitude continuously scales with reference to this hidden envelope frequency, called the beat frequency (dotted line).

This difference between the actual wave's real frequency and the wave's overall frequency envelope. Is another source of timbre.

Notes, and the way we play them will often generate unique and different envelopes depending on how they are played. For example a staccato quarter-note will have a different envelope to a softly played quarter-note.

Other properties of Sound

Reflection

Different mediums mean different speeds of sounds e.g. molecules in wood (solid) are harder to move than molecules in air (gas).

These different speeds create several effects. Including the reflection of waves. Often waves require a bit of power in order to physically overcome the resistances to vibration of a particular medium.

Often this leads to sound waves bouncing back off harder-to-traverse surfaces.

Say that a sound wave travels through the air and reaches a wooden wall. The atoms vibrating in the air will hit against the wooden wall, transferring only some of their energy to the resistant wood.

The wood atoms on the border of the wall will bounce back, as expected. But this time they will transfer energy back into the air at a much greater magnitude due to newton's third law.

Thus while some of the sound wave ends up going deeper into the wood, the wood will push back and cause the air to vibrate in the opposite direction, creating a reflected wave.

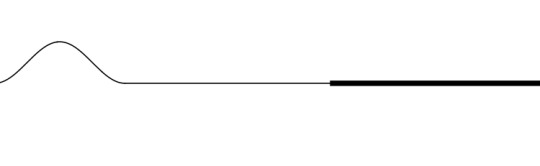
Image credit: Penn State

We characterise the amount of power being reflected versus transmitted versus absorbed using portions:

A + R + T = 1

A = Power absorbed into the material (e.g. warms up the material)

R = Power reflected back

T = Power transmitted into the new medium

This is both an explainer as to why rooms are both very good, and very bad at keeping sound inside them. It really depends on the rigidity and shape of the material they are bordered by.

Refraction

Just like light, sound waves can also refract. Refraction is actually a lot simpler to understand once you already realise that waves will both reflect and transmit across medium changes.

Refraction is just combining the results of incomplete reflection (i.e. transmission) with some angle.

I won't go into refraction in too much detail, as it's worth a different topic. But effectively we experience snell's law but modified for sound.

Diffraction

Sound waves, like all waves propagate spherically (or circularly in 2D).

When travelling around corners, sound can often appear louder than if you were further away, looking at the source more directly.

This is because spherical waves will often 'curve' around corners. This is better described by light diffraction. Which is something for another time.

Conclusion

In conclusion, that's how sound works, mostly. This is a topic that is a little less closer to my expertise. Mainly because it delves into more musically-inclined phenomena that I am less familiar with. But I'm sure I did a good job.

Unfortunately, it seems like the plague of the long post is not yet over. Perhaps I need to get into a lot more specific topics to make things better for me and you (the reader).

Anyways, my exams are done. I am done. I do not have to do school anymore. Until I remember to have to get ready for my honours year (a.k.a. a mini-masters degree tacked on after your bachelor's degree).

Until next time, feel free to gib feedback. It's always appreciated. Follow if you wanna see this stuff weekly.

Cya next week where I will probably try another astronomy topic, or something like that.

[threestripeslider]

oc lore through shenanigans bc who tf cares that Sophie will tell you the pythagoras theorem is about squares, she can infodump you about plants that will kill a man in under three minutes

[novelties-and-notions]

FLOSTRE: This Pythagoras was an interesting character. Everything is numbers – that's quite a smart idea. And he had his theorem – Pythagoras's Theorem, you know the one. Where would we be without it? Let's hear it for the square on the hypotenuse.

[The more suggestible contingent among the audience bursts into applause and cheering on cue.]

MUFFLED VOICE OFF-STAGE: Never mind the hypotenuse. Where are the dancing girls?

FLOSTRE: As I was saying before I was interrupted, Pythagoras has his theorem. But as well as that, he had some… comment dire? Outré ideas. He founded a sort of monastery at a place called Croton, where his followers had to obey lots of rules. Above all, they had to avoid eating beans. This was very important to Pythagoras.

MUFFLED VOICE OFF-STAGE: Why not tell them about his golden thigh?

FLOSTRE: We are not concerned with wild stories, just the facts. His followers were forbidden to eat beans. But the main thing for Pythagoras was metempsychosis.

MUFFLED VOICE OFF-STAGE: Sounds as if he should see a psychiatrist.

FLOSTRE: En effet, but metempsychosis really means the transmigration of souls. The idea that the soul is immortal and, after death, is transferred to another body. Which brings me to Stanley Green. [A solitary whoop from the back of the auditorium. Flostre acknowledges the cheer with a grin.] Somebody knows Stanley, I see.

[The band plays a few bars of Do The Stanley. Nobody recognises it except an elderly audience member, who is instantly transported to the beer-soaked dance floor of Churchill College disco in 1974, to the consternation of his wife who suddenly finds herself next to an empty seat.]

Stanley Green was – as you say in English – a nutcase. Although that's perhaps not the mot juste, because Stanley didn't approve of nuts. Nor of any protein: meat, fish, eggs, cheese, peas – and beans. He used to stand in Oxford Circus holding up a placard exhorting the passers-by to avoid all these foods. He said that they promoted lust, and that was something Pythagoras didn't like either. At least, not for his followers. So we know what happened to Pythagoras's soul.

MUFFLED VOICE OFF-STAGE: But we don't know what happened to his golden thigh, do we?

FLOSTRE [In a more sombre tone.]: Poor Stanley's been dead for some years now, so Pythagoras's soul has been transferred to yet another body. So if you come across somebody preaching against eating beans, transmettez-lui mes amitiés. Give him my regards.