#Akaike Information Criterion (AIC)

[raffaellopalandri]

Statistical Tools

Daily writing promptWhat was the last thing you searched for online? Why were you looking for it?View all responses Checking which has been my most recent search on Google, I found that I asked for papers, published in the last 5 years, that used a Montecarlo method to check the reliability of a mathematical method to calculate a team’s efficacy. Photo by Andrea Piacquadio on Pexels.com I was…

[sak-shi]

The ABCs of Regression Analysis

Regression analysis is a statistical technique used to understand the relationship between a dependent variable and one or more independent variables. Here’s a simple breakdown of its key components—the ABCs of Regression Analysis:

A: Assumptions

Regression analysis is based on several assumptions, which need to be met for accurate results:

Linearity: The relationship between the independent and dependent variables is linear.

Independence: The residuals (errors) are independent of each other.

Homoscedasticity: The variance of the residuals is constant across all levels of the independent variables.

Normality: The residuals should be approximately normally distributed.

No Multicollinearity: The independent variables should not be highly correlated with each other.

B: Basic Types of Regression

There are several types of regression, with the most common being:

Simple Linear Regression: Models the relationship between a single independent variable and a dependent variable using a straight line.

Equation: y=β0+β1x+ϵy = \beta_0 + \beta_1 x + \epsilon

yy = dependent variable

xx = independent variable

β0\beta_0 = y-intercept

β1\beta_1 = slope of the line

ϵ\epsilon = error term

Multiple Linear Regression: Extends simple linear regression to include multiple independent variables.

Equation: y=β0+β1x1+β2x2+⋯+βnxn+ϵy = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_n x_n + \epsilon

Logistic Regression: Used for binary outcomes (0/1, yes/no) where the dependent variable is categorical.

C: Coefficients and Interpretation

In regression models, the coefficients (β\beta) are the key parameters that show the relationship between the independent and dependent variables:

Intercept (β0\beta_0): The expected value of yy when all independent variables are zero.

Slope (β1,β2,…\beta_1, \beta_2, \dots): The change in the dependent variable for a one-unit change in the corresponding independent variable.

D: Diagnostics and Model Evaluation

Once a regression model is fitted, it’s important to evaluate its performance:

R-squared (R2R^2): Represents the proportion of variance in the dependent variable explained by the independent variables. Values closer to 1 indicate a better fit.

Adjusted R-squared: Similar to R2R^2, but adjusted for the number of predictors in the model. Useful when comparing models with different numbers of predictors.

p-value: Tests the null hypothesis that a coefficient is equal to zero (i.e., no effect). A small p-value (typically < 0.05) suggests that the predictor is statistically significant.

Residual Plots: Visualize the difference between observed and predicted values. They help in diagnosing issues with linearity, homoscedasticity, and outliers.

E: Estimation Methods

Ordinary Least Squares (OLS): The most common method used for estimating the coefficients in linear regression by minimizing the sum of squared residuals.

Maximum Likelihood Estimation (MLE): Used in some regression models (e.g., logistic regression) where the goal is to maximize the likelihood of observing the data given the parameters.

F: Features and Feature Selection

In multiple regression, selecting the right features is crucial:

Stepwise regression: A method of adding or removing predictors based on statistical criteria like AIC (Akaike Information Criterion) or BIC (Bayesian Information Criterion).

Regularization (Ridge, Lasso): Techniques used to prevent overfitting by adding penalty terms to the regression model.

G: Goodness of Fit

The goodness of fit measures how well the regression model matches the data:

F-statistic: A test to determine if at least one predictor variable has a significant relationship with the dependent variable.

Mean Squared Error (MSE): Measures the average squared difference between the observed actual outcomes and those predicted by the model.

H: Hypothesis Testing

In regression analysis, hypothesis testing helps to determine if the relationships between variables are statistically significant:

Null Hypothesis: Typically, the null hypothesis for a coefficient is that it equals zero (i.e., no effect).

Alternative Hypothesis: The alternative is that the coefficient is not zero (i.e., the predictor has an effect on the dependent variable).

I: Interpretation

Interpreting regression results involves understanding how changes in the independent variables influence the dependent variable. For example, in a simple linear regression:

If β1=5\beta_1 = 5, then for every one-unit increase in xx, the predicted yy increases by 5 units.

J: Justification for Regression

Regression is often used in predictive modeling, risk assessment, and understanding relationships between variables. It helps in making informed decisions based on statistical evidence.

Conclusion:

Regression analysis is a powerful tool in statistics and machine learning, helping to predict outcomes, identify relationships, and test hypotheses. By understanding the basic principles and assumptions, one can effectively apply regression to various real-world problems.

Click More: https://www.youtube.com/watch?v=5_HErZ3A_Hg

[abhinav3045]

Test a Logistic Regression Model

Full Research on Logistic Regression Model

1. Introduction

The logistic regression model is a statistical model used to predict probabilities associated with a categorical response variable. This model estimates the relationship between the categorical response variable (e.g., success or failure) and a set of explanatory variables (e.g., age, income, education level). The model calculates odds ratios (ORs) that help understand how these variables influence the probability of a particular outcome.

2. Basic Hypothesis

The basic hypothesis in logistic regression is the existence of a relationship between the categorical response variable and certain explanatory variables. This model works well when the response variable is binary, meaning it consists of only two categories (e.g., success/failure, diseased/healthy).

3. The Basic Equation of Logistic Regression Model

The basic equation for logistic regression is:log⁡(p1−p)=β0+β1X1+β2X2+⋯+βnXn\log \left( \frac{p}{1-p} \right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_nlog(1−pp​)=β0​+β1​X1​+β2​X2​+⋯+βn​Xn​

Where:

ppp is the probability that we want to predict (e.g., the probability of success).

p1−p\frac{p}{1-p}1−pp​ is the odds ratio.

X1,X2,…,XnX_1, X_2, \dots, X_nX1​,X2​,…,Xn​ are the explanatory (independent) variables.

β0,β1,…,βn\beta_0, \beta_1, \dots, \beta_nβ0​,β1​,…,βn​ are the coefficients to be estimated by the model.

4. Data and Preparation

In applying logistic regression to data, we first need to ensure that the response variable is categorical. If the response variable is quantitative, it must be divided into two categories, making logistic regression suitable for this type of data.

For example, if the response variable is annual income, it can be divided into two categories: high income and low income. Next, explanatory variables such as age, gender, education level, and other factors that may influence the outcome are determined.

5. Interpreting Results

After applying the logistic regression model, the model provides odds ratios (ORs) for each explanatory variable. These ratios indicate how each explanatory variable influences the probability of the target outcome.

Odds ratio (OR) is a measure of the change in odds associated with a one-unit increase in the explanatory variable. For example:

If OR = 2, it means that the odds double when the explanatory variable increases by one unit.

If OR = 0.5, it means that the odds are halved when the explanatory variable increases by one unit.

p-value: This is a statistical value used to test hypotheses about the coefficients in the model. If the p-value is less than 0.05, it indicates a statistically significant relationship between the explanatory variable and the response variable.

95% Confidence Interval (95% CI): This interval is used to determine the precision of the odds ratio estimates. If the confidence interval includes 1, it suggests there may be no significant effect of the explanatory variable in the sample.

6. Analyzing the Results

In analyzing the results, we focus on interpreting the odds ratios for the explanatory variables and check if they support the original hypothesis:

For example, if we hypothesize that age influences the probability of developing a certain disease, we examine the odds ratio associated with age. If the odds ratio is OR = 1.5 with a p-value less than 0.05, this indicates that older people are more likely to develop the disease compared to younger people.

Confidence intervals should also be checked, as any odds ratio with an interval that includes "1" suggests no significant effect.

7. Hypothesis Testing and Model Evaluation

Hypothesis Testing: We test the hypothesis regarding the relationship between explanatory variables and the response variable using the p-value for each coefficient.

AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) values are used to assess the overall quality of the model. Lower values suggest a better-fitting model.

8. Confounding

It is also important to determine if there are any confounding variables that affect the relationship between the explanatory variable and the response variable. Confounding variables are those that are associated with both the explanatory and response variables, which can lead to inaccurate interpretations of the relationship.

To identify confounders, explanatory variables are added to the model one by one. If the odds ratios change significantly when a particular variable is added, it may indicate that the variable is a confounder.

9. Practical Example:

Let’s analyze the effect of age and education level on the likelihood of belonging to a certain category (e.g., individuals diagnosed with diabetes). We apply the logistic regression model and analyze the results as follows:

Age: OR = 0.85, 95% CI = 0.75-0.96, p = 0.012 (older age reduces likelihood).

Education Level: OR = 1.45, 95% CI = 1.20-1.75, p = 0.0003 (higher education increases likelihood).

10. Conclusions and Recommendations

In this model, we conclude that age and education level significantly affect the likelihood of developing diabetes. The main interpretation is that older individuals are less likely to develop diabetes, while those with higher education levels are more likely to be diagnosed with the disease.

It is also important to consider the potential impact of confounding variables such as income or lifestyle, which may affect the results.

11. Summary

The logistic regression model is a powerful tool for analyzing categorical data and understanding the relationship between explanatory variables and the response variable. By using it, we can predict the probabilities associated with certain categories and understand the impact of various variables on the target outcome.

[ensafomer]

Test a Logistic Regression Model

Full Research on Logistic Regression Model

1. Introduction

The logistic regression model is a statistical model used to predict probabilities associated with a categorical response variable. This model estimates the relationship between the categorical response variable (e.g., success or failure) and a set of explanatory variables (e.g., age, income, education level). The model calculates odds ratios (ORs) that help understand how these variables influence the probability of a particular outcome.

2. Basic Hypothesis

The basic hypothesis in logistic regression is the existence of a relationship between the categorical response variable and certain explanatory variables. This model works well when the response variable is binary, meaning it consists of only two categories (e.g., success/failure, diseased/healthy).

3. The Basic Equation of Logistic Regression Model

The basic equation for logistic regression is:log⁡(p1−p)=β0+β1X1+β2X2+⋯+βnXn\log \left( \frac{p}{1-p} \right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_n X_nlog(1−pp​)=β0​+β1​X1​+β2​X2​+⋯+βn​Xn​

Where:

ppp is the probability that we want to predict (e.g., the probability of success).

p1−p\frac{p}{1-p}1−pp​ is the odds ratio.

X1,X2,…,XnX_1, X_2, \dots, X_nX1​,X2​,…,Xn​ are the explanatory (independent) variables.

β0,β1,…,βn\beta_0, \beta_1, \dots, \beta_nβ0​,β1​,…,βn​ are the coefficients to be estimated by the model.

4. Data and Preparation

In applying logistic regression to data, we first need to ensure that the response variable is categorical. If the response variable is quantitative, it must be divided into two categories, making logistic regression suitable for this type of data.

For example, if the response variable is annual income, it can be divided into two categories: high income and low income. Next, explanatory variables such as age, gender, education level, and other factors that may influence the outcome are determined.

5. Interpreting Results

After applying the logistic regression model, the model provides odds ratios (ORs) for each explanatory variable. These ratios indicate how each explanatory variable influences the probability of the target outcome.

Odds ratio (OR) is a measure of the change in odds associated with a one-unit increase in the explanatory variable. For example:

If OR = 2, it means that the odds double when the explanatory variable increases by one unit.

If OR = 0.5, it means that the odds are halved when the explanatory variable increases by one unit.

p-value: This is a statistical value used to test hypotheses about the coefficients in the model. If the p-value is less than 0.05, it indicates a statistically significant relationship between the explanatory variable and the response variable.

95% Confidence Interval (95% CI): This interval is used to determine the precision of the odds ratio estimates. If the confidence interval includes 1, it suggests there may be no significant effect of the explanatory variable in the sample.

6. Analyzing the Results

In analyzing the results, we focus on interpreting the odds ratios for the explanatory variables and check if they support the original hypothesis:

For example, if we hypothesize that age influences the probability of developing a certain disease, we examine the odds ratio associated with age. If the odds ratio is OR = 1.5 with a p-value less than 0.05, this indicates that older people are more likely to develop the disease compared to younger people.

Confidence intervals should also be checked, as any odds ratio with an interval that includes "1" suggests no significant effect.

7. Hypothesis Testing and Model Evaluation

Hypothesis Testing: We test the hypothesis regarding the relationship between explanatory variables and the response variable using the p-value for each coefficient.

AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) values are used to assess the overall quality of the model. Lower values suggest a better-fitting model.

8. Confounding

It is also important to determine if there are any confounding variables that affect the relationship between the explanatory variable and the response variable. Confounding variables are those that are associated with both the explanatory and response variables, which can lead to inaccurate interpretations of the relationship.

To identify confounders, explanatory variables are added to the model one by one. If the odds ratios change significantly when a particular variable is added, it may indicate that the variable is a confounder.

9. Practical Example:

Let’s analyze the effect of age and education level on the likelihood of belonging to a certain category (e.g., individuals diagnosed with diabetes). We apply the logistic regression model and analyze the results as follows:

Age: OR = 0.85, 95% CI = 0.75-0.96, p = 0.012 (older age reduces likelihood).

Education Level: OR = 1.45, 95% CI = 1.20-1.75, p = 0.0003 (higher education increases likelihood).

10. Conclusions and Recommendations

In this model, we conclude that age and education level significantly affect the likelihood of developing diabetes. The main interpretation is that older individuals are less likely to develop diabetes, while those with higher education levels are more likely to be diagnosed with the disease.

It is also important to consider the potential impact of confounding variables such as income or lifestyle, which may affect the results.

11. Summary

The logistic regression model is a powerful tool for analyzing categorical data and understanding the relationship between explanatory variables and the response variable. By using it, we can predict the probabilities associated with certain categories and understand the impact of various variables on the target outcome.

[itfeature-com]

Akaike Information Criteria Simple Guide

The Akaike Information Criteria/Criterion (AIC) is a method used in statistics and machine learning to compare the relative quality of different models for a given dataset. The AIC method helps in selecting the best model out of a bunch by penalizing models that are overly complex. Akaike Information Criterion provides a means for comparing among models i.e. a tool for model selection. A…

[adaleecrypto]

Panel VAR in Stata and PVAR-DY-FFT

Preparation

xtset pros mm (province, month)

Endogenous variables:

global Y loan_midyoy y1 stock_pro

Provincial medium-term loans year-on-year (%)

Provincial 1-year interest rate (%) (NSS model estimate, not included in this article) (%)

provincial stock return

Exogenous variables:

global X lnewcasenet m2yoy reserve_diff

Logarithm of number of confirmed cases

M2 year-on-year

reserve ratio difference

Descriptive statistics:

global V loan_midyoy y1 y10 lnewcasenet m2yoy reserve_diff sum2docx $V using "D.docx", replace stats(N mean sd min p25 median p75 max ) title("Descriptive statistics")

VarName Obs Mean SD Min P25 Median P75 Max

loan_midyoy 2232 13.461 7.463 -79.300 9.400 13.400 16.800 107.400

y1 2232 2.842 0.447 1.564 2.496 2.835 3.124 4.462

stock_pro 2232 0.109 6.753 -24.485 -3.986 -0.122 3.541 73.985

lnewcasenet 2232 1.793 2.603 0.000 0.000 0.000 3.434 13.226

m2yoy 2232 0.095 0.012 0.080 0.085 0.091 0.105 0.124

reserve_diff 2232 -0.083 0.232 -1.000 0.000 0.000 0.000 0.000

Check for unit root：

foreach x of global V { xtunitroot ips `x',trend }

Lag order

pvarsoc $Y , pinstl(1/5)

pvaro(instl(4/8)): Specifies to use the fourth through eighth lags of each variable as instrumental variables. In this case, in order to deal with endogeneity issues, relatively distant lags are chosen as instrumental variables. This means that when estimating the model, the current value of each variable is not directly affected by its own recent lagged value (first to third lag), thus reducing the possibility of endogeneity.

pinstl(1/5): Indicates using lags from the highest lag to the fifth lag as instrumental variables. Specifically, for the PVAR(1) model, the first to fifth lags are used as instrumental variables; for the PVAR(2) model, the second to sixth lags are used as instrumental variables, and so on. The purpose of this approach is to provide each model variable with a set of instrumental variables that are related to, but relatively independent of, its own lag structure, thereby helping to address endogeneity issues.

CD test (Cross-sectional Dependence Test): This is a test to detect whether there is cross-sectional dependence (ie, correlation between different individuals) in panel data. Values close to 1 generally indicate the presence of strong cross-sectional dependence. If there is cross-sectional dependence in the data, cluster-robust standard errors can be used to correct for this.

J-statistic: The J-statistic that detects model over-identification of constraints and is usually related to the effectiveness of instrumental variables.

J pvalue: The p value of the J statistic, used to determine whether the instrumental variable is valid. A low p-value (usually less than 0.05) means that at least one of the instrumental variables is probably not applicable.

MBIC, MAIC, MQIC: These are different information criterion values, used for model selection. Lower values generally indicate a better model.

MBIC: Bayesian Information Criterion.

MAIC: Akaike Information Criterion.

MQIC: Quantile information criterion.

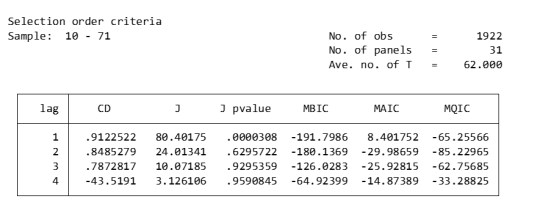
Interpretation: The p-values of the J-test are 0.00 and 0.63 for Lag 1 and Lag 2 respectively. The p-value for the first lag is very low, indicating possible instrumental variable inefficiency. The p-value for the second lag is higher, indicating that instrumental variables may be effective. In this example, Lag 2 seems to be the optimal choice because its MBIC, AIC, and MQIC values are relatively low. However, it should be noted that the CD test shows that there is cross-sectional dependence, which may affect the accuracy of model estimation.

Model estimation：

pvar $Y, lags(2) instlags(1/4) fod exog($X) gmmopts(winitial(identity) wmatrix(robust) twostep vce(cluster pros))

pvar: This is the Stata command that calls the PVAR model.

$Y: These are the endogenous variables included in the model.

$X: These are exogenous variables included in the model.

lags(2): Specifies to include 2-period lags for each variable in the PVAR model.

number of lag periods for the variable

instlags(1/4): This is the number of lags for the specified instrumental variable. Here, it tells Stata to use the first to fourth lags as instrumental variables. This is to address possible endogeneity issues, i.e. possible interactions between variables in the model.

Lag order selection criteria:

Information criterion: Statistical criteria such as AIC and BIC can be used to judge the choice of lag period.

Diagnostic tests: Use diagnostic tests of the model (e.g. Q(b), Hansen J overidentification test) to assess the appropriateness of different lag settings.

fod/fd: medium fixed effects.

fod: The Helmert transformation is a forward mean difference method that compares each observation to the mean of its future observations. This method makes more efficient use of available information than simple difference-in-difference methods when dealing with fixed effects, especially when the time dimension of panel data is short.

A requirement of the Helmert transformation on the data is that the panel must be balanced (i.e., for each panel unit, there are observations at all time points).

fd: Use first differences to remove panel-specific fixed effects. In this method, each observation is subtracted from its observation in the previous period, thus eliminating the influence of time-invariant fixed effects. First difference is a common method for dealing with fixed effects in panel data, especially when there is a trend or horizontal shift in the data over time.

Usage Scenarios and Choices: If your panel data is balanced and you want to utilize time series information more efficiently, you may be inclined to use the Helmert transformation. First differences may be more appropriate if the data contain unbalanced panels or if there is greater concern with removing possible time trends and horizontal shifts.

exog($X): This option is used to specify exogenous variables in the model. Exogenous variables are assumed to be variables that are not affected by other variables in the model.

gmmopts(winitial(identity) wmatrix(robust) twostep vce(cluster pros))

winitial(identity): Set the initial weight matrix to the identity matrix.

wmatrix(robust): Use a robust weight matrix.

twostep: Use the two-step GMM estimation method.

vce(cluster pros): Specifies the standard error of clustering robustness, and uses `pros` as the clustering variable.

GMM criterion function

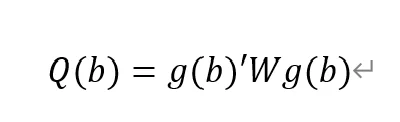
Final GMM Criterion Q(b) = 0.0162: The GMM criterion function (Q(b)) is a mathematical expression that measures how consistent your model parameter estimates (b) are with these moment conditions. Simply put, it measures the gap between model parameters and theoretical or empirical expectations.

is a vector of moment conditions. These moment conditions are a series of assumptions or constraints set based on the model. They usually come in the form of expected values (expectations) that represent the conditions that the model parameter b should satisfy.

W is a weight matrix used to assign different weights to different moment conditions.

b is a vector of model parameters. The goal of GMM estimation is to find the optimal b to minimize Q(b).

No. of obs = 2077: This means there are a total of 2077 observations in the data set.

No. of panels = 31: This means that the data set contains 31 panel units.

Ave. no. of T = 67.000: Each panel unit has an average of 67 time point observations.

Coefficient interpretation (not marginal effects)

L1.loan_midyoy: 0.8034088: When the one-period lag of loan_midyoy increases by one unit, the current period's loan_midyoy is expected to increase by approximately 0.803 units. This coefficient is statistically significant (p-value 0.000), indicating that the one-period lag has a significant positive impact on the current value.

L2.loan_midyoy: 0.1022556: When the two-period lag of loan_midyoy increases by one unit, the current period's loan_midyoy is expected to increase by approximately 0.102 units. This coefficient is not statistically significant (p-value of 0.3), indicating that the effect of the two-period lag on the current value may not be significant.

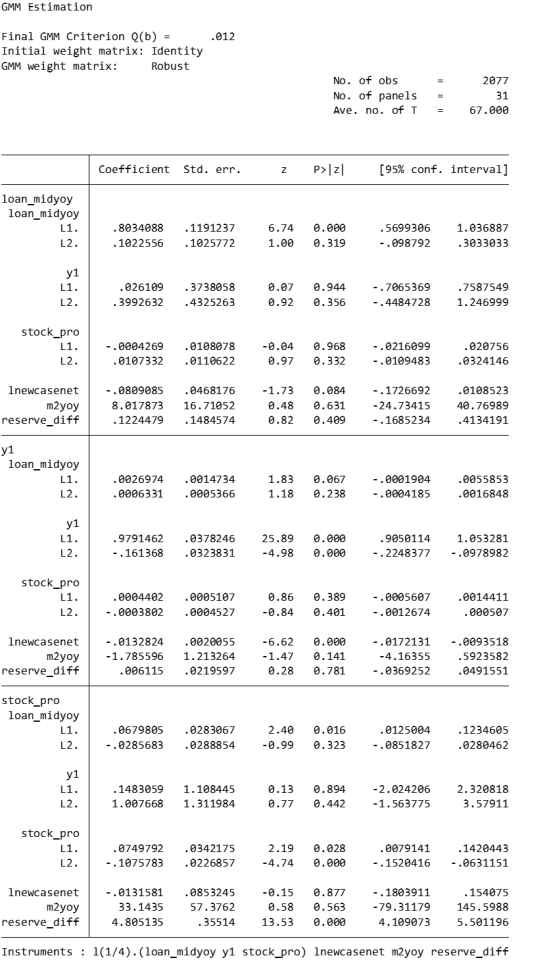
overidentification test

pvar $Y, lags(2) instlags(1/4) fod exog($X) gmmopts(winitial(identity) wmatrix(robust) twostep vce(cluster pros)) overid (written in one line)

Statistics: Hansen's J chi2(18) = 24.87 means that the chi-square statistic value of the Hansen J test is 24.87 and the degrees of freedom are 18.

P-value: (p = 0.137) means that the p-value of this test is 0.129. Since the p-value is higher than commonly used significance levels (such as 0.05 or 0.01), this indicates that there is insufficient evidence to reject the null hypothesis. In the Hansen J test, the null hypothesis is that all instrumental variables are exogenous, that is, they are uncorrelated with the error term. Instrumental variables may be appropriate.

Stability check:

pvarstable

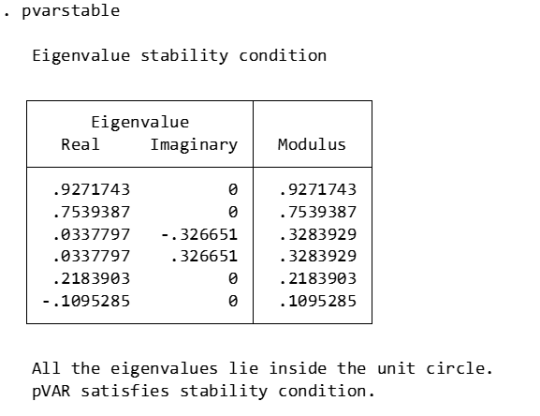
Eigenvalues: Listed eigenvalues ​​include their real and imaginary parts. For example, 0.9271743 is a real eigenvalue. 0.0337797±0.326651i is a pair of conjugate complex eigenvalues.

Modulus: The module of an eigenvalue is its distance from the origin on the complex plane. It is calculated as the square root of the sum of the squares of the real and imaginary parts.

Stability condition: The stability condition of the PVAR model requires that the modules of all eigenvalues ​​must be less than or equal to 1 (that is, all eigenvalues ​​are located within the unit circle).

Granger causality:

pvargranger

Ho (null hypothesis): The excluded variable is not a Granger cause (i.e. does not have a predictive effect on the variables in the equation).

Ha (alternative hypothesis): The excluded variable is a Granger cause (i.e. has a predictive effect on the variables in the equation).

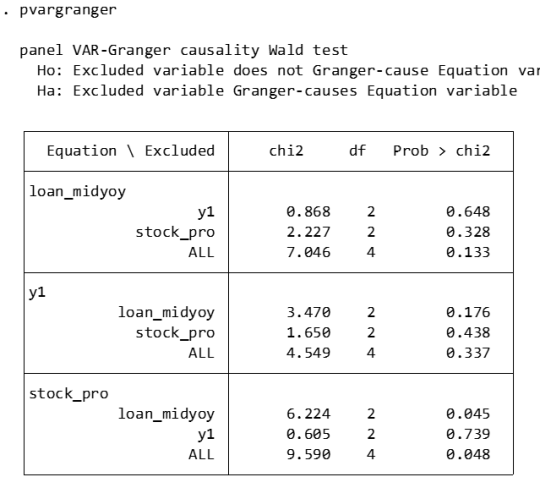
For the stock_pro equation:

loan_midyoy: chi2 = 6.224 (degrees of freedom df = 2), p-value = 0.045. There is sufficient evidence to reject the null hypothesis, indicating that loan_midyoy is the Granger cause of stock_pro.

y1: chi2 = 0.605 (degrees of freedom df = 2), p-value = 0.739. There is insufficient evidence to reject the null hypothesis indicating that y1 is not the Granger cause of stock_pro.

Margins:

The PVAR model involves the dynamic interaction of multiple endogenous variables, which means that the current value of a variable is not only affected by its own past values, but also by the past values ​​of other variables. In this case, the margins command may not be suitable for calculating or interpreting the marginal effects of variables in the model, because these effects are not fixed but change dynamically with time and the state of the model. The following approaches may be considered:

Impulse response analysis

Impulse response analysis: In the PVAR model, the more common analysis method is to perform impulse response analysis (Impulse Response Analysis), which can help understand how the impact of one variable affects other variables in the system over time.

pvarirf,oirf mc(200) tab

Orthogonalized Impulse Response Function (OIRF): In some economic or financial models, orthogonalized processing may be more realistic, especially when analyzing policy shocks or other clearly distinguished externalities. During impact. If the shocks in the model are assumed to be independent of each other, then OIRF should be used. Orthogonalization ensures that each shock is orthogonal (statistically independent) through a mathematical process (such as Cholisky decomposition). This means that the effect of each shock is calculated controlling for the other shocks.

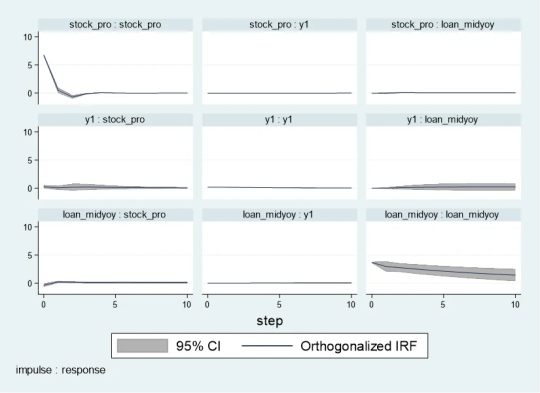
When stock_pro is subject to a positive shock of one standard deviation, loan_midyoy is expected to decrease slightly in the first period, with a specific response value of -0.0028833, indicating that loan_midyoy is expected to decrease by approximately 0.0029 units.

This effect gradually changes over time. For example, in the second period, the shock response of loan_midyoy to stock_pro is 0.0700289, which means that loan_midyoy is expected to increase by about 0.0700 units.

pvarirf, mc(200) tab

For some complex dynamic systems, non-orthogonalized IRF may be better able to capture the actual interactions between variables within the system. Non-orthogonalized impulse response function: If you do not make the assumption that the shocks are independent of each other, or if you believe that there is some inherent interdependence between the variables in the model, you may choose a non-orthogonalized IRF.

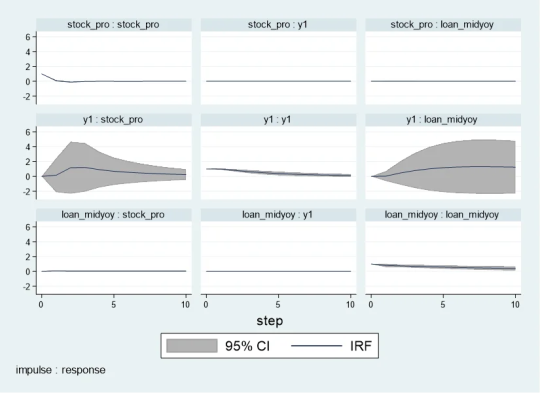
When stock_pro is impacted: In period 1, loan_midyoy has a slightly negative response to the impact on stock_pro, with a response value of -0.0004269.

This effect gradually changes over time. For example, in period 2, the response value is 0.0103697, indicating that loan_midyoy is expected to increase slightly.

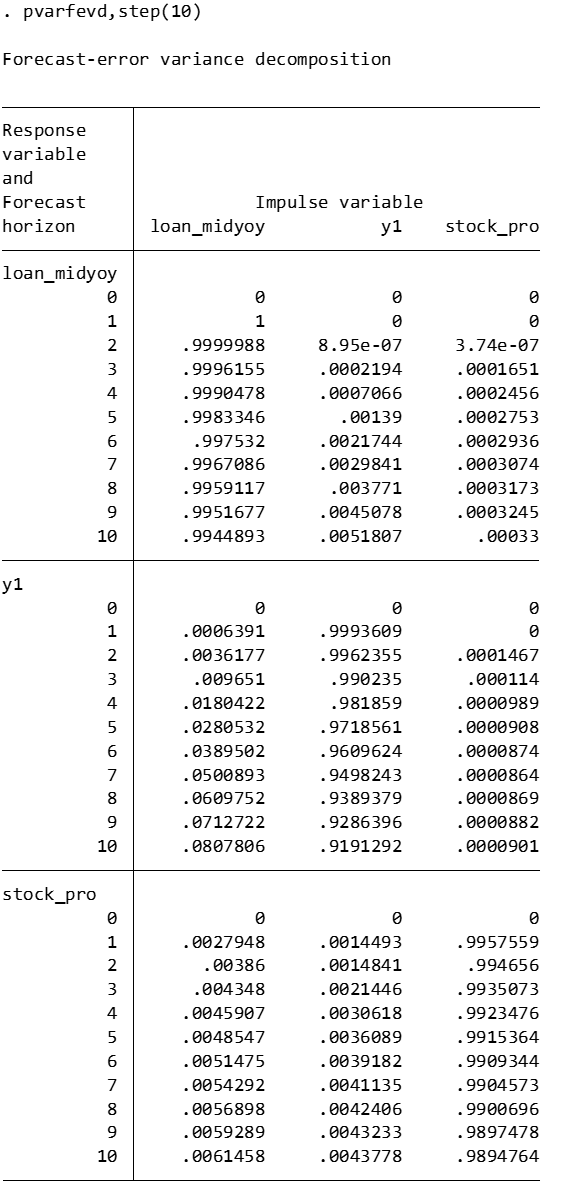
Forecast error variance decomposition

Forecast Error Variance Decomposition is also a useful tool for analyzing the dynamic relationship between variables in the PVAR model.

Time point 0: The contribution of all variables is 0, because at the initial moment when the impact occurs, no variables have an impact on loan_midyoy.

Time point 1: The forecast error variance of loan_midyoy is completely explained by its own shock (100%), while the contribution of y1 and stock_pro is 0.

Subsequent time points: For example, at time point 10, about 99.45% of the forecast error variance of loan_midyoy is explained by the shock to loan_midyoy itself, about 0.52% is explained by the shock to y1, and about 0.03% is explained by the shock to stock_pro.

Diebold-Yilmaz (DY) variance decomposition

Diebold-Yilmaz (DY) variance decomposition is an econometric method used to quantify volatility spillovers between variables in time series data. This approach is based on the vector autoregressive (VAR) model, which is used particularly in the field of financial economics to analyze and understand the interaction between market variables. The following are the key concepts of DY variance decomposition:

basic concepts

VAR model: The VAR model is a statistical model used to describe the dynamic relationship between multiple time series variables. The VAR model assumes that the current value of each variable depends not only on its own historical value, but also on the historical values of other variables.

Forecast error variance decomposition (FEVD): In the VAR model, FEVD analysis is used to determine what proportion of the forecast error of a variable can be attributed to the impact of other variables.

Volatility spillover index: The volatility spillover index proposed by Diebold and Yilmaz is based on FEVD, which quantifies the contribution of the fluctuation of each variable in a system to the fluctuation of other variables.

"From" and "to" spillover: DY variance decomposition distinguishes between "from" and "to" spillover effects. "From" spillover refers to the influence of a certain variable on the fluctuation of other variables in the system; while "flow to" spillover refers to the influence of other variables in the system on the fluctuation of that specific variable.

Application

Financial market analysis: DY variance decomposition is particularly important in financial market analysis. For example, it can be used to analyze the fluctuation correlation between stock markets in different countries, or the extent of risk spillovers during financial crises.

Policy evaluation: In macroeconomic policy analysis, DY analysis can help policymakers understand the impact of policy decisions (such as interest rate changes) on various areas of the economy.

Precautions

Explanation: DY analysis provides a way to quantify volatility spillover, but it cannot be directly interpreted as cause and effect. The spillover index reflects correlation, not causation, of fluctuations.

Model setting: The effectiveness of DY analysis depends on the correct setting of the VAR model, including the selection of variables, the determination of the lag order, etc.

mat list e(Sigma)

mat list e(b)

Since I have previously made a DY model suitable for variable coefficients, I only need to fill in the time-varying coefficients in the first period. Because when there is only one period, the results of the constant coefficient and the variable coefficient are the same.

Since stata does not have the original code of dy, R has the spillover package, which can be modified without errors. Therefore, the spillover package of R language is recommended. It is taken from the code in bk2018 article.

Therefore, you need to manually fill in the stata coefficients into the interface part I made in R language, and then continue with the BK code.

```{r} library(tvpfft) library(tvpgevd) library(tvvardy) library(ggplot2) library(gridExtra) a = rbind(c(0,.80340884 , .02610899, -.00042695, .10225563, .39926325, .01073319 ), c(0, .00269745, .97914619, .00044023, .00063315, -.16136799, -.00038024), c(0, .06798046, .1483059 , .07497919, -.02856828, 1.0076676, -.10757831)) ``` ```{r} Sigma = rbind(c( 13.495069, .01625753, -1.3143064), c( .01625753, .03064462, .04350408 ), c( -1.3143064, .04350408, 45.800811)) df=data.frame(t(c(1,1,1))) colnames(df)=c("loan_midyoy","y1","stock_pro") fit = list() fit$Beta.postmean=array(dim =c(3,7,1)) fit$H.postmean=array(dim =c(3,3,1)) fit$Beta.postmean[,,1]=a fit$H.postmean[,,1]=Sigma fit$M=3tvp.gevd(fit, 37, df) ```

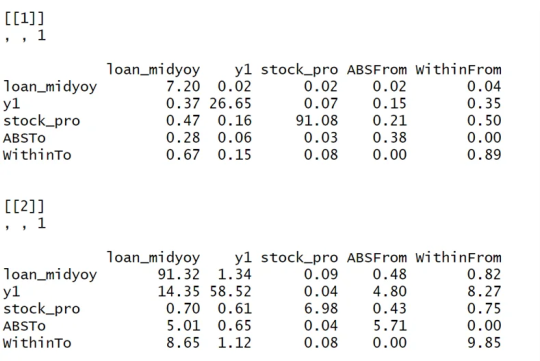
Diagonal line (loan_midyoy vs. loan_midyoy, y1 vs. y1, stock_pro vs. stock_pro): shows that the main source of fluctuations in each variable is its own fluctuation. For example, 98.52% of loan_midyoy's fluctuations are caused by itself.

Off-diagonal lines (such as the y1 and stock_pro rows of the loan_midyoy column): represent the contribution of other variables to the loan_midyoy fluctuations. In this example, y1 and stock_pro contribute very little to the fluctuation of loan_midyoy, 1.37% and 0.11% respectively.

The "From" row: shows the overall contribution of each variable to the fluctuations of all other variables. For example, the total contribution of loan_midyoy to the fluctuation of all other variables in the system is 0.49%.

"To" column: reflects the overall contribution of all other variables in the system to the fluctuation of a single variable. For example, the total contribution of other variables in the system to the fluctuation of loan_midyoy is 5.30%.

Analysis and interpretation:

Self-contribution: The fluctuations of loan_midyoy, y1, and stock_pro are mainly caused by their own shocks, which can be seen from the high percentages on their diagonals.

Mutual influence: y1 and stock_pro contribute less to each other's fluctuations, but y1 has a relatively large contribution to the fluctuations of loan_midyoy (14.72%).

System Fluctuation Impact: The “From” and “To” columns provide an overall measure of spillover effects. For example, stock_pro has a small contribution to the fluctuation of the system (0.65% comes from the impact of stock_pro), but the system has a greater impact on the fluctuation of stock_pro (6.08% of the fluctuation comes from the system).```{r} tvp.gevd.fft(fit, df, c(pi+0.00001,pi/12,0),37) ```

The same goes for Fourier transform. It is divided into those within 1 year and 1-3 years, and the sum is the previous picture.

DY I used the R language's spillover package to modify the interface.

Part of the code logic:

function (ir1, h, Sigma, df) { ir10 <- list() n <- length(Sigma[, 1]) for (oo in 1:n) { ir10[[oo]] <- matrix(ncol = n, nrow = h) for (pp in 1:n) { rep <- oo + (pp - 1) * (n) ir10[[oo]][, pp] <- ir1[, rep] } } ir1 <- lapply(1:(h), function(j) sapply(ir10, function(i) i[j, ])) denom <- diag(Reduce("+", lapply(ir1, function(i) i %*% Sigma %*% t(i)))) enum <- Reduce("+", lapply(ir1, function(i) (i %*% Sigma)^2)) tab <- sapply(1:nrow(enum), function(j) enum[j, ]/(denom[j] * diag(Sigma))) tab0 <- t(apply(tab, 2, function(i) i/sum(i))) assets <- colnames(df) n <- length(tab0[, 1]) stand <- matrix(0, ncol = (n + 1), nrow = (n + 1)) stand[1:n, 1:n] <- tab0 * 100 stand2 <- stand - diag(diag(stand)) stand[1:(n + 1), (n + 1)] <- rowSums(stand2)/n stand[(n + 1), 1:(n + 1)] <- colSums(stand2)/n stand[(n + 1), (n + 1)] <- sum(stand[, (n + 1)]) colnames(stand) <- c(colnames(df), "From") rownames(stand) <- c(colnames(df), "To") stand = round(stand, 2) return(stand) }

[sekolahstata]

Pengantar Ekonometrika Time series

Pengantar Ekonometrika Time series

Ekonometrika adalah ilmu yang mempelajari hubungan antara variabel ekonomi dengan menggunakan metode statistik. Salah satu jenis data yang sering digunakan dalam ekonometrika adalah data deret waktu atau time series, yaitu data yang mengukur nilai suatu variabel pada interval waktu tertentu, misalnya bulanan, triwulanan, atau tahunan.

Apa itu Ekonometrika Time series?

Definisi dan Konsep Dasar Ekonometrika time series adalah cabang ekonometrika yang berfokus pada analisis data deret waktu dengan menggunakan model matematika yang menggambarkan perilaku dinamis dari variabel-variabel tersebut1. Konsep dasar dari ekonometrika time series adalah bahwa nilai suatu variabel pada periode tertentu dipengaruhi oleh nilai variabel itu sendiri atau variabel lain pada periode sebelumnya. Oleh karena itu, untuk menganalisis hubungan antara variabel-variabel deret waktu, kita perlu memperhatikan aspek temporal atau urutan waktu dari data. Tujuan dan Manfaat Tujuan utama dari ekonometrika time series adalah untuk mengestimasi parameter yang mengukur kekuatan dan arah hubungan antara variabel-variabel deret waktu2. Dengan mengetahui parameter tersebut, kita dapat melakukan berbagai hal, seperti: - Menguji hipotesis tentang hubungan kausalitas antara variabel-variabel deret waktu - Mengevaluasi dampak kebijakan ekonomi terhadap variabel-variabel deret waktu - Membuat peramalan tentang nilai variabel-variabel deret waktu di masa depan - Mendeteksi adanya perubahan struktural atau anomali dalam perilaku variabel-variabel deret waktu Manfaat dari ekonometrika time series adalah bahwa kita dapat memanfaatkan informasi historis dari data untuk meningkatkan akurasi analisis kita. Selain itu, kita juga dapat mengakomodasi adanya karakteristik khusus dari data deret waktu, seperti: - Adanya tren atau pola berkala dalam data - Adanya ketergantungan antara observasi sekarang dengan observasi masa lalu - Adanya heteroskedastisitas atau variasi dalam ukuran kesalahan - Adanya non-stasioneritas atau perubahan dalam rata-rata atau varians dari data

Metode Analisis Ekonometrika Time series

Ada banyak metode analisis yang dapat digunakan dalam ekonometrika time series, Model Autoregresif dan Moving Average (ARMA) Model ARMA adalah model deret waktu yang merupakan campuran antara model autoregresif (AR) dan moving average (MA). Model AR mengasumsikan bahwa data sekarang dipengaruhi oleh data sebelumnya, sedangkan model MA mengasumsikan bahwa data sekarang dipengaruhi oleh nilai residual data sebelumnya123. Definisi Model ARMA Model ARMA(p,q) dapat didefinisikan sebagai: X_t = c + phi_1 X_{t-1} + phi_2 X_{t-2} + ... + phi_p X_{t-p} + Z_t + theta_1 Z_{t-1} + theta_2 Z_{t-2} + ... + theta_q Z_{t-q} dimana: - X_t adalah variabel deret waktu pada waktu t - c adalah konstanta - phi_i adalah koefisien autoregresif untuk lag i - theta_j adalah koefisien moving average untuk lag j - Z_t adalah white noise dengan rata-rata nol dan varians konstan sigma^2 Identifikasi Model ARMA Untuk mengidentifikasi model ARMA yang sesuai dengan data deret waktu, kita dapat menggunakan beberapa metode seperti: - Plot fungsi korelogram sederhana (ACF) dan parsial (PACF) dari data deret waktu untuk melihat pola korelasi antara observasi pada lag yang berbeda - Menggunakan kriteria informasi seperti Akaike Information Criterion (AIC) atau Bayesian Information Criterion (BIC) untuk memilih model dengan jumlah parameter yang optimal - Menggunakan uji Ljung-Box untuk menguji apakah ada korelasi serial yang signifikan di antara residu model Estimasi Model ARMA Untuk mengestimasi parameter model ARMA, kita dapat menggunakan beberapa metode seperti: - Metode kuadrat terkecil biasa (OLS) untuk kasus sederhana seperti model AR(1) - Metode maksimum likelihood (ML) untuk kasus umum dengan menggunakan algoritma iteratif seperti Newton-Raphson atau Broyden-Fletcher-Goldfarb-Shanno (BFGS) - Metode Bayesian dengan menggunakan prior distribusi tertentu untuk parameter dan melakukan simulasi Markov Chain Monte Carlo (MCMC) Diagnostik Model ARMA Untuk mendiagnostik model ARMA yang telah diestimasi, kita dapat melakukan beberapa hal seperti: - Memeriksa apakah residu model berdistribusi normal dengan menggunakan plot histogram, plot normal probability atau uji normalitas seperti uji Jarque-Bera atau uji Shapiro-Wilk - Memeriksa apakah residu model homoskedastik atau tidak dengan menggunakan plot scatterplot residu terhadap nilai prediksi atau uji heteroskedastisitas seperti uji White atau uji Breusch-Pagan - Memeriksa apakah residu model tidak berkorelasi serial dengan menggunakan plot ACF dan PACF residu atau uji korelasi serial seperti uji Durbin-Watson atau uji Ljung-Box. Aplikasi Ekonometrika Time series dalam Bidang Ekonomi Ekonometrika time series adalah cabang ilmu ekonometrika yang mempelajari metode analisis data deret waktu (time series), yaitu data yang tergantung pada waktu. Data deret waktu sering ditemukan dalam bidang ekonomi, seperti data inflasi, pertumbuhan ekonomi, nilai tukar, bunga, saham, dan lain-lain12. Beberapa aplikasi ekonometrika time series dalam bidang ekonomi adalah: - Menguji hubungan kausalitas antara variabel-variabel ekonomi dengan menggunakan uji Granger atau uji Toda-Yamamoto - Menguji hubungan kointegrasi antara variabel-variabel ekonomi dengan menggunakan uji Engle-Granger atau uji Johansen - Membuat model prediksi variabel-variabel ekonomi dengan menggunakan model ARIMA, VAR, VECM, GARCH, dan lain-lain - Menganalisis dampak kebijakan makroekonomi dengan menggunakan model impulse response function (IRF) atau variance decomposition (VD) - Menganalisis transmisi kejutan global ke perekonomian domestik dengan menggunakan model GVAR atau PVAR3 Baca juga: - PLS SEM adalah Sebuah Metode Alternatif Dari OLS, Mikroekonometrika, Time series dan Quasi - Ekonometrika Time Series - https://jurnal.asyafina.com

Referensi

- https://opac.perpusnas.go.id/DetailOpac.aspx?id=1183960 - https://www.researchgate.net/publication/358895236_Ekonometrika - https://www.researchgate.net/publication/275715130_Ekonometrika_Deret_Waktu_Teori_dan_Aplikasi - https://ris.uksw.edu/download/makalah/kode/M01351 - https://stats.libretexts.org/Bookshelves/Advanced_Statistics/Time_Series_Analysis_(Aue)/3_ARMA_Processes/3.1_Introduction_to_Autoregressive_Moving_Average_(ARMA)_Processes - https://stats.libretexts.org/Bookshelves/Advanced_Statistics/Time_Series_Analysis_(Aue)/3_ARMA_Processes/3.1_Introduction_to_Autoregressive_Moving_Average_(ARMA)_Processes - https://www.academia.edu/22417320/MODEL_AUTOREGRESSIVE_INTEGRATED_MOVING_AVERAGE_ARIMA - https://jagostat.com/analisis-time-series/model-arma - https://scholar.ui.ac.id/en/publications/analisis-ekonometrika-time-series-edisi-2 - https://opac.perpusnas.go.id/DetailOpac.aspx?id=1183960 - https://www.ipb.ac.id/event/index/2015/07/training-ekonometrika-untuk-time-series-dan-data-panel/594c4d37f659e892d9ae35f1182047ce - https://www.researchgate.net/publication/275715130_Ekonometrika_Deret_Waktu_Teori_dan_Aplikasi Read the full article

[santuario77]

Capstone Project Week 2: Methods

I. DESCRIPTION OF THE SAMPLE

The study uses the National Graduates Survey (NGS), a survey designed to determine whether graduates of postsecondary (PSE) programs had obtained employment since graduation, whether there is a match between the graduates' programs of study and the employment obtained, the graduates' job and career satisfaction, the rates of employment, the type of employment obtained related to career expectations and qualification requirements, and the influence of PSE education on occupational achievement.  

The survey includes graduates of university programs that lead to bachelor's, master's or doctoral degrees, or that lead to specialized certificates or diplomas; graduates of post-secondary programs

(that require a secondary school completion or its equivalent for admission) in Colleges of Applied Arts and Technology (CAAT), CEGEP, community colleges, technical schools or similar institutions; and graduates of skilled trades (pre-employment programs of three months or more in duration) from post-secondary institutions.  It does not include graduates from private post-secondary institutions (for ex. computer training and commercial secretarial schools), graduates who completed "continuing education" courses at universities and colleges (unless they led to a degree or diploma), or graduates in apprenticeship programs.

The NGS is a cross-sectional sample survey with a stratified simple random sample design. Two variables were used for stratification: i) province or territory of the institution; and ii) level of study (college, bachelor's, master's, doctorate). The sample selection of graduates within strata was done without replacement using a systematic method.

The target population of the 2018 NGS consisted of all graduates from a recognized public postsecondary institution who graduated from their program in 2015, and who were living in the country at the time of the survey. The total sample size sent to collection was 59,795.

Sample selection criteria for the effects of this study was based on variables whose contribution  may help to explain the probability of working in a STEM occupation. The size of the selected sample was 19,564.

II. MEASURES

The likelihood of young graduates to be employed in a STEM occupation, the response variable, was measured by combining the contribution of twelve predictors including: age at time of graduation, gender, citizenship status, level of study, main factor in choice of program, aggregated CIP, participation in a co-op program, level of education required for the job held, full-time/part-time status of job, industry of occupation, employment income, father education level, and region of residence.

The response and explanatory variables used in this study were all categorical. The response variable was transformed into a binary variable with two outcomes: whether graduates were working in a STEM occupation or not. The explanatory variables related to field of study (CIP), employment income, citizenship status, father education level, were aggregated for simplification. Also, frequencies were taken of all the variables included in the model.

III. ANALYSIS

In this research study, the response variable was categorical, with two levels, therefore a binary logistic regression analysis was performed to identify the subset of variables that best predicted the response variable. Given that all explanatory variables used were also categorical, frequency tables  for the predictors and the response variable were examined.

Predictive accuracy of the model was assessed through various tools, such as the Model Convergence Status, which describes whether the maximum likelihood algorithm has converged or not; the Model Fit statistics, where the Akaike Information Criterion (AIC) estimates and the Schwartz Criterion (SC), were examined for the model with and without predictors. Also, three Chi-square tests were analyzed: the Likelihood ratio, the Score test, and the Wald Chi-square test, which measure that at least one of the predictors’ regression coefficient is not equal to zero in the model.

The analysis of  Maximum likelihood provided statistics on coefficients, standard errors, Wald Chi-square estimates, and p-values of the different predictors and intercept. Furthermore, an analysis of the Odds ratio estimates was performed, to identify the impact of the point estimates of each predictor on the probability of the response variable to occur. Finally, to determine the association of predicted probabilities and observed responses, the Concordant statistics (c) was assessed.

[lupine-publishers-ctbb]

Lupine Publishers-Biometrics and Biostatistics Journal

Model Selection in Regression: Application to Tumours in Childhood by Annah Managa

We give a chronological review of the major model selection methods that have been proposed from circa 1960. These model selection procedures include Residual mean square error (MSE), coefficient of multiple determination (R2), adjusted coefficient of multiple determination (Adj R2), Estimate of Error Variance (S2), Stepwise methods, Mallow’s Cp, Akaike information criterion (AIC), Schwarz criterion (BIC). Some of these methods are applied to a problem of developing a model for predicting tumors in childhood using log-linear models. The theoretical review will discuss the problem of model selection in a general setting. The application will be applied to log-linear models in particular. 

https://lupinepublishers.com/biostatistics-biometrics-journal/fulltext/model-selection-in-regression-application-to-tumours-in-childhood.ID.000101.php

For more Lupine Publishers Open Access Journals Please visit our website https://www.lupinepublishers.com/

For more Biostatistics & Biometrics Articles Please Click Here: https://lupinepublishers.com/biostatistics-biometrics-journal/

[lupine-publishers-lojpcr]

Lupine Publishers | Alignment of SARS-Cov-2 Spike Protein Compared with Ebola, and Herpes Simplex Viruses in Human Murine and Bats

Lupine Publishers | LOJ Pharmacology & Clinical Research

Abstract

Our analytical approach consisted in sequence alignment analysis of spike protein in different viruses, followed by construction of phylogenetic tree. Additionally, we investigated some commotional parameters on the protein sequence determining chemical composition as well as estimated PI .Our observation revealed significant difference in S protein between the 3 tested viruses in different species These differences may have significant implications on pathogenesis and entry to host cell.

Introduction

Viruses are inert outside the host cell which are unable to generate energy. As obligate intracellular parasites, during replication, they are fully reliant on the complex biochemical machinery of eukaryotic or prokaryotic cells. The central purpose of a virus is to transport its genome into the host cell to allow its expression by the host cell [1]. Binding of a single surface glycoprotein of virus to its host receptor promotes pH-dependent conformational variations once within the endosome acidic environment, thereby transporting the viral bilayer in closeness with the host cell membrane to promote fusion [2]. The structural physiognomies of virus coats (capsids) are extremely appropriate to virus propagation. The coat must enclose and protect the nucleic acid, flexible against interference be talented of broaching the outer wall of a target cell and provide a confident pathway for attending nucleic acid into the target cell. Hollow spikes on the capsid fulfill the latter two roles, from which it has been deduced that they must have unusually high strength and stiffness in axial compression [3]. The spike protein (S protein) is a type I transmembrane protein, a sequence of amino acids ranging from 1,160 for avian infectious bronchitis virus (IBV) and up to 1,400 amino acids for feline coronavirus [4]. Spike proteins assemble to create the distinctive “corona” or crown-like look in trimers on the surface of the virion. The ectodomain of all CoV spike proteins portions the same organization in two domains: a receptor-binding N-terminal domain called S1 and a fusionresponsible C-terminal S2 domain The variable spike proteins (S proteins) reflect CoV diversity, which have developed into forms that vary in their receptor interactions and their reaction to different environmental triggers of virus-cell membrane fusion [5]. A notable peculiarity between the spike proteins of diverse coronaviruses is whether it is cleaved or not during assembly and exocytosis of virions [6]. The entry Herpesvirus and membrane fusion to the host cell equire three virion glycoproteins, gB and a gH/gL heterodimer, that function as the “core fusion machinery” [7]. The viral envelope of Ebola virus contains spikes consisting of the glycoprotein (GP) trimer. These viral spike glycoprotein docks viral particles to the cell surface, endosomal entry, and membrane fusion [8]. Acute respiratory syndrome coronavirus (SARS-CoV) is a zoonotic pathogens that traversed the species barriers to infect humans. These coronaviruses hold a surface-located spike (S) protein that recruits infection by mediating receptor-recognition and membrane fusion [9]. Bioinformatics plays an important role in all aspects of protein analysis, including sequence analysis, and evolution analysis. In sequence analysis, several bioinformatics techniques can be used to provide the sequence comparisons. In evolution analysis, we use the technique like phylogenetic trees to find homologous proteins and identified the most related taxa. With bioinformatics techniques and databases, function, structure, and evolutionary history of proteins can be easily identified [10]. Several bioinformatics methods can be used in sequence analysis to provide sequence comparisons.

Materials and Methods

Sequences, alignment, and construction of phylogenetic tree

Amino acids sequences for the spike protein of Covid-19, Ebola, and herpes simplex viruses from bats, murine as well as Homo sapiens were taken from the National Center for Biotechnology Information database. The accession numbers of the corresponding database entries and species names are listed in Table 1 and Figure 1. Sequences were aligned with by CLUSTALW [11]. Selection of conserved blocks was performed using GBlocks (version 0.91 to eliminate divergent regions and poorly aligned positions using standard settings according to Castresana [12]. The Akaike information criterion (AIC) were performed, using a maximum-likelihood (ML) starting tree to estimates the quality of each model, relative to each of the other models (Table 2). The most suitable model was WAG+G+F [13]. Then phylogenetic tree was constructed with neighbor-joining and maximum likelihood algorithms using MEGA version 5 [14]. The stability of the topology of the phylogenetic tree was assessed using the bootstrap method with 100 repetitions [15].

  Computation of the theoretical pI (isoelectric point) of protein sequences

Estimation of the isoelectric point (pI) based on the amino acid sequence was determined using isoelectric Point Calculator (IPC), a web service and a standalone program for the accurate estimation of protein and peptide pI using different sets of dissociation constant (pKa) values [16]. Models with the lowest BIC scores (Bayesian Information Criterion) are considered to describe the substitution pattern the best. For each model, AICc value (Akaike Information Criterion, corrected), Maximum Likelihood value (lnL), and the number of parameters (including branch lengths) are also presented [1]. Non-uniformity of evolutionary rates among sites may be modeled by using a discrete Gamma distribution (+G) with 5 rate categories and by assuming that a certain fraction of sites is evolutionarily invariable (+I). Abbreviations: TR: General Time Reversible; JTT: Jones-Taylor-Thornton; rtREV: General Reverse Transcriptase; cpREV: General Reversible Chloroplast; mtREV24: General Reversible Mitochondrial.

Results

In order to unravel the phylogenetic relationship of Spike protein between the different taxa, a phylogenetic consensus tree was constructed using the Bayesian Inference (BI) and Maximum Likelihood (ML) methods (Figure 1). The present results revealed that the identity between different taxa was nonsignificant, However alignment of human Coronavirus (Covid-19) and Bat Coronavirus revealed identity equal to 57.98% followed by Murine Coronavirus which displayed 27.61% when compared by human Coronavirus. The chemical composition of the tested protein is illustrated in Table 3. Figures 2 & 3 show the correlation plots between the theoretical isoelectric points for spike protein of different corona virus in different species. The current results displayed that estimated pI of spike protein sequence in three investigated viruses in different species ranges from 5.59 to 8.08. With highest value for spike protein in herpesvirus of bat. The Estimated charge over pH range of the investigated were listed in Table 4. The current results revealed that the behavior of s protein in different species exhibited different estimated charge at different pH ranges. Some S protein reveled low negative charge as pH increases such as Ebola Virus of bat while S protein of Corona virus in murine showed high negative charge as pH elevated.

 Discussion

One aspect that may provide some insight into the interactions of the S protein is the electrostatic potential it generates. the affinity constant for the receptor-binding domain (RBD) of viron protein potentially contributing to its transmission efficiency [17]. The S protein remains predominantly in the closed conformation to mask its receptor-binding domains (RBDs), thereby impeding their binding. To bind with ACE2, the S protein transforms into its open conformation, revealing its binding interface [18]. The present study relies on a comparative investigation, regarding the identity of spike protein of 3 viruses (Covid-19, Ebola, and herpes simplex) to identify the most related taxa. Our investigation revealed high similarities of Spike protein of coronaviruses in human and bats [19]. The computed amino acid composition of spike protein. Several residues showed a significant difference between the compositions in spike proteins in the three investigated virus in different species. This result reveals the importance of specific residues in these classes of proteins. The polar uncharged residues, especially Serine, Asparagine, and Glycine, have higher occurrence in spike protein of murine, which are important for the folding, stability, and function of such class of proteins [20]. Our analysis revealed that the Coronavirus spike protein of murine may be more efficient in discovering suitable vaccine for Coronavirus. The S protein amino acids variations among different coronaviruses such as (SARS, herpes and ebola). The SARS-CoV-2 virus shares 57.98% of its genome with the other bat coronaviruses. The sequence identity in the S protein bat coronavirus appears to be the closest relative of SARS-CoV-2. Our results in accordance with Rothan [21]. The isoelectric point (pI) is the pH value at which a molecule’s net charge is zero [22]. Information about the isoelectric point is important because the solubility and electrical repulsion are lowest at the pI. Hence, the tendency to aggregation and precipitation is highest. In the case of viruses, the value thus provides information about the viral surface charge in a specific environment [23]. In polar media, such as water, viruses possess a pH-dependent surface charge [23]. This electrostatic charge governs the movement of the soft particle in an electrical field and thus manages its colloidal behavior, which plays a major role in the processes of virus entry. The pH value at which the net surface charge changes its sign is called the isoelectric point and is a characteristic parameter of the virion in equilibrium with its atmosphere in water chemistry [24]. For some viruses the attachment influences that encourage binding to accommodating cells are extremely definite, but the arrangement of actions that activates viral entry is only now establishment to be understood. The charge of attachment protein may play an important role in attachment and entry of virus [25]. The current results revealed that the pH affect the net charge of S protein of different taxa with different behavior. All the investigated taxa exhibit increases in negative charge as the pH increased except for the Ebola virus form Bats which showed unstable behavior regarding the S protein charge.

Conclusion

In our study, we have investigated the variation of pHdependent changes in charges of a protein. The current results revealed that the pH affect the net charge of S protein of different taxa with different behavior.

 https://lupinepublishers.com/pharmacology-clinical-research-journal/pdf/LOJPCR.MS.ID.000140.pdf

https://lupinepublishers.com/pharmacology-clinical-research-journal/fulltext/alignment-of-sars-cov-2-spike-protein-compared-with-ebola-and-herpes-simplex-viruses-in-human-murine-and-bats.ID.000140.php

For more Lupine Publishers Open Access Journals Please visit our website: https://lupinepublishersgroup.com/ For more Pharmacology & Clinical Research Please Click Here: https://lupinepublishers.com/pharmacology-clinical-research-journal/ To Know more Open Access Publishers Click on Lupine Publishers

Follow on Linkedin : https://www.linkedin.com/company/lupinepublishers Follow on Twitter   :  https://twitter.com/lupine_online

[allenkellish-blog]

Tips For Modern Survival

Moreover, for the intercept and tilt  Pandemic Survival Review random execution, bi = (bi0, bi1)T, a bivariate ordinary classification with naught disgraceful and unknown unstructured disagreement-covariance matrix D is supposed, where and d12 = Cov(bi0, bi1) = ρb0b1σb0σb1. The Akaike Information Criterion (AIC) was employment as a panoptic goodness-of-meet measure and its luminosity help as the base for rankly the fitted models. The nethermost AIC value write to exponentially weighted records, which step to the hence slam of medical services interest in the last year of person (accounting for the everywhere weight) on the departure chance rate.

The people in the stories I read scramble backcountry cliffs; they outlast plane crashes; they languish thousands of performance to the dregs without a parachute. And they often burst dice. One key to their survival? A splint, which can relieve reduce smart, prevent further loss to ligaments, pluck and blood vessels, and concede them to move to a unendangered place while they postpone for sustain. This video from Backpacker editor Rachel Zurer will give you the basics for creating a splinter from materials you have on act. Take these first coöperate steps immediately when you have a wrench ankle.

Other small kits are wearable and built into workaday bear survival bracelets or belts. Most often these are paracord bracelets with instrument textile inside. Several weapon such as firestarter, contend, toot and compass are on the exterior of the gear and smaller tools are woven internal the bijoutry or belt and only accessible by taking the bracelet aside.

To Get More Details  Click Here --->>>   Benifits Of Pandemic Survival

[lupinepublishers]

Model Selection in Regression: Application to Tumours in Childhood in #CTBB in #Lupine Publishers

We give a chronological review of the major model selection methods that have been proposed from circa 1960. These model selection procedures include Residual mean square error (MSE), coefficient of multiple determination (R2 ), adjusted coefficient of multiple determination (Adj R2 ), Estimate of Error Variance (S2 ), Stepwise methods, Mallow’s Cp , Akaike information criterion (AIC), Schwarz criterion (BIC). Some of these methods are applied to a problem of developing a model for predicting tumors in childhood using log-linear models. The theoretical review will discuss the problem of model selection in a general setting. The application will be applied to log-linear models in particular.

https://lupinepublishers.com/biostatistics-biometrics-journal/fulltext/model-selection-in-regression-application-to-tumours-in-childhood.ID.000101.php

[evoldir]

Course: UK.AnalysingBehaviouralData.19-23March2018

PS statistics are running a course aimed specifically at analysing behavioural data and is therefor highly relevant to those studying the evolution of behaviour (both human and animal) "Behavioural data analysis using maximum likelihood in R (BDML01)" http://bit.ly/2GwQAqm This course is being devilled by Dr Will Hoppitt and will run from 19th - 23rd March 2018 in Glasgow Course Overview: This 5-day course will involve a combination of lectures and practical sessions. Students will learn to build and fit custom models for analysing behavioural data using maximum likelihood techniques in R. This flexible approach allows a researcher to a) use a statistical model that directly represents their hypothesis, in cases where standard models are not appropriate and b) better understand how standard statistical models (e.g. GLMs) are fitted, many of which are fitted by maximum likelihood. Students will learn how to deal with binary, count and continuous data, including time-to-event data which is commonly encountered in behavioural analysis. 1) After successfully completing this course students should be able to: 2) fit a multi-parameter maximum likelihood model in R 3) derive likelihood functions for binary, count and continuous data 4) deal with time-to-event data 5) build custom models to test specific behavioural hypotheses 6) conduct hypothesis tests and construct confidence intervals 7) use Akaikes information criterion (AIC) and model averaging 8) understand how maximum likelihood relates to Bayesian techniques Full details and time table can be found at http://bit.ly/2GwQAqm We offer accommodation packages as well to make travel cheaper, easier and stress free. Please email any questions to oliverhooker@PSstatistics.com Also check out our sister sites, http://bit.ly/2BpXxpa (ecology courses) and wwwPRinformatics.com (data science courses) Other up-coming PS stats courses Oliver Hooker PhD. PS statistics Introduction to Bayesian hierarchical modelling using R (IBHM02) http://bit.ly/2GuEm1n Behavioural data analysis using maximum likelihood in R (BDML01) http://bit.ly/2GwQAqm Introduction to statistical modelling for psychologists in R (IPSY01) http://bit.ly/2rRnm1X Social Network Analysis for Behavioural Scientists using R (SNAR01) http://bit.ly/2Gv8A4c PSstatistics.com facebook.com/PSstatistics/ twitter.com/PSstatistics 6 Hope Park Crescent Edinburgh EH8 9NA +44 (0) 7966500340 via Gmail

[maxihealth]

How to justify your survival curve extrapolation methodology

Clinical trials are typically of (relatively) short duration, but innovative treatments may impact patient survival over multiple years. Health economists and outcomes researchers often are faced with the challenge of extrapolating clinical trial survival curves to estimate long-term survival gains for the typical patient. These estimates may be done parameterically (e.g., exponential, Weibull, Gompertz, log-logistic, gamma, piecewise), using expert elicitation, or other methods. But a key question is how do researchers justify this choice?

A paper by Lattimer (2013) provides options for justifying extrapolation choice. The first option is visual inspection. This approach just visually checking whether the model fits the data well. While this is a useful first step, it clearly is not a statistically-based approach. Statistical tests can help formalize model fit. Akaike information criterion (AIC) and Bayesian information criterion (BIC) are commonly used statistical tests that measure model fit, traded off against model complexity [see this video comparing AIC and BIC]. Log-cumulative hazard plots are useful for determining which parametric models are compatible with the observed hazard ratios as well as validating whether the proportional hazards assumption is valid. To determine the suitability of accelerated failure time models–such as lognormal or log-logistic models–quantile-quantile plots can be used (see Bradburn et al. 2003). External data can also be used to extrapolate survival curves. For instance, real-world data on survival can be used to extrapolate the control arm and then various hazard assumptions can be applied to the control arm extrapolated curve. Registry data–such as SEER data for US cancer survival estimates–is often used. Clinical validity is also an important input. One can ask for clinical experts to weigh in on the best models either informally through interviews or more formally via a Delphi Panel or SHeffield ELicitation Framework (SHELF).

Lattimer recommends using the more standard approaches (e.g., exponential, Gompertz, Weibull, log-logitic, lognormal) first and then only moving to more complex models (e.g., generalized gamma, piecewise, cure models) if the model four approaches described above justify the need for the more complex modelling. Also, researchers should formally document how the combination of visual inspection, statistical tests, external data and clinical input were used to inform the preferred extrapolation specification used in any health economic evaluation.

Sources:

Latimer NR. Survival analysis for economic evaluations alongside clinical trials—extrapolation with patient-level data: inconsistencies, limitations, and a practical guide. Medical Decision Making. 2013 Aug;33(6):743-54.

Bradburn MJ, Clark TG, Love SB, Altman DG. Survival analysis part III: multivariate data analysis—choosing a model and assessing its adequacy and fit. Br J Cancer. 2003;89(4):605–11. 38. Liverpool Reviews and Implementation Group. Pemet

SHELF: the Sheffield Elicitation Framework (version 3.0). School of Mathematics and Statistics, University of Sheffield, UK [http://tonyohagan.co.uk/shelf]. Accessed 1 Apr 2017.

How to justify your survival curve extrapolation methodology posted first on https://carilloncitydental.blogspot.com

[healthtimetaylor]

These results suggest that air pollution increased the risk of cardiovascular deaths in Hefei.

PMID:  Environ Sci Pollut Res Int. 2019 Dec 4. Epub 2019 Dec 4. PMID: 31802340 Abstract Title:  Study on the association between ambient air pollution and daily cardiovascular death in Hefei, China. Abstract:  Cardiovascular disease has always been the most serious public health problem in China. Although many studies have found that the risk of death caused by cardiovascular disease is related to air pollutants, the existing results are still inconsistent. The aim of this study was to investigate the effects of air pollutants on the risk of daily cardiovascular deaths in Hefei, China. Daily data on cardiovascular deaths, daily air pollutants, and meteorological factors from 2007 to 2016 were collected in this study. A time-series study design using a distributed lag nonlinear model was employed to evaluate the association between air pollutants and cardiovascular deaths. First, a single air pollutant model was established based on the minimum value of Akaike information criterion (AIC), and the single day lag effects and multi-day lag effects were discussed separately. Then, two-pollutant models were fitted. Subgroup analyses were conducted by gender (male and female), age (

read more

[fbreschi]

Introduction to AIC — Akaike Information Criterion

http://bit.ly/34Y7wRn