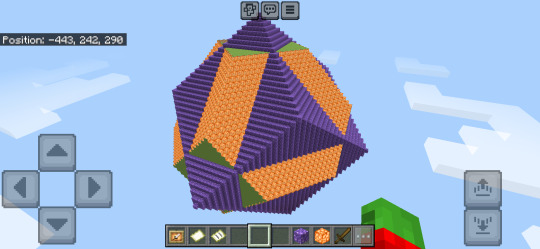
#truncated dodecahedron

[knotty-et-al]

Truncated dodecahedron

By cutting off the vertices of the dodecahedron you get the truncated dodecahedron.

This results in the 12 pentagonal faces of the dodecahedron turning into 12 dekagonal (10-gonal) and 20 triangular faces.

(As the dodecahedron has 20 vertices, truncation results in 20 triangular faces.)

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 2

Propaganda

Cube:

Also called the Regular Hexahedron

Platonic Solid

Regular

Dual of the Regular Octahedron

It has 6 square faces, 12 edges, and 8 vertices.

Image Credit: Tumblr

Rhombicuboctahedron:

Also called the Small Rhombicuboctahedron

Archimedean Solid

Semiregular

Dual of the Deltoidal Icositetrahedron

It has 18 square faces, 8 regular triangular faces, 48 edges, and 24 vertices.

Image Credit: @anonymous-leemur

Cube and Rhombicuboctahedron Together

Oh, cmon! The cube is great! It tiles space, its one of the platonic solids that has analouges in all dimensionalities, its vertices are can be mapped to the strings of three binary digits in a structurepreserving way, and its literally the most iconic shape of all time!

What is the rhombicuboctahedron? it has cubical symmetries, its by far the least interesting archimedean solid, it has a bullshit rotated version that noone can decide is archimedean or not, and its much worse than the cube in every way. The fact its winning is damning the entire electorate of this poll as pretentious neophytes who have seriosly considered polyhedra as beautiful and interesting construct in their on right, and are just voting for the shiniest thing they havent seen before.

Truncated Dodecahedron:

Archimedean Solid

Semiregular

Dual of the Triakis Icosahedron

It has 12 regular decagonal faces, 20 regular triangular faces, 90 edges, and 60 vertices.

Image Credit: Cyp

[the-silly-words-on-your-screen]

hello there old friend

TRUNCATED DECACHORON

SPREAD THIS ALL OVER TUMBLR FOR NO REASON

[sozeugs]

[dailypolyhedra]

Polyhedron of the Day #194: Truncated great dodecahedron

The truncated great dodecahedron is a uniform star polyhedron. It has 24 faces (12 pentagrams and 12 decagons), 90 edges, and 60 vertices. It is also known as the great truncated dodecahedron. Its Bowers-style acronym is tigid. Its Schläfli symbol is t{5,5/2}. As the name implies, it is constructed by truncating the great dodecahedron. Its vertex figure is an isosceles triangle. Its dual is the small stellapentakis dodecahedron.

Maeder, R. E. (1997). "Truncated great dodecahedron (37)." MathConsult AG. https://www.mathconsult.ch/static/unipoly/37.html.

[pancakeke]

[phaseshapes]

Iridescence Star, my other Truncated Great Stellated Dodecahedron. Or you could think of it as "parking lot oil rainbow star". This was a nice shape to make, but don't expect to see any more of them. It's been thoroughly replaced by cooler shapes that I'd rather make! Coming soon!

[xyymath]

Fun with Geometry: Shapes You Didn’t Know You Needed

Geometry is far more than the basic shapes we learn in high school; it’s a world brimming with bizarre and captivating figures that push the boundaries of our imagination.

1. The Hypercube (Tesseract)

The hypercube, or tesseract, is the 4-dimensional analog of the cube. While we live in a 3-dimensional world, the concept of a fourth dimension has fascinated mathematicians and artists alike. A hypercube consists of 16 vertices, 32 edges, and 24 square faces, each one being a 3D cube in a higher-dimensional space.

In the real world, hypercubes don’t physically exist, but they serve as key tools in higher-dimensional geometry and theoretical physics. Think of them as a "spatial metaphor" for the kinds of higher-dimensional spaces used in string theory or machine learning. Mathematicians use them to explore the complex relationships between different dimensions. The tesseract also shows up in pop culture, notably in the movie Interstellar, where it represents the connection between time and space.

2. The Pentagon (Not Just in Architecture)

The regular pentagon (five sides of equal length and five equal angles) has a fascinating relationship with the golden ratio. If you draw diagonals within a regular pentagon, they intersect in such a way that the ratio of the longer segment to the shorter segment is the golden ratio (ϕ ≈ 1.618). This means that pentagons are not just aesthetically pleasing in architecture, they have deep connections to mathematical beauty.

In nature, sunflowers and pine cones exhibit pentagonal symmetry. The arrangement of seeds in the flower follows a Fibonacci spiral, and the spirals are governed by golden angle, which closely ties to the pentagon’s unique proportions.

3. The Dodecahedron

A dodecahedron is a regular polyhedron made up of 12 pentagonal faces, 30 edges, and 20 vertices. It is one of Platonic solids, which means each face is identical, and the same number of faces meet at each vertex. This geometric shape is not just abstract; it appears in various 3D modeling applications and is used in architecture, like in the London 2012 Olympic torch design.

What’s particularly fascinating is its appearance in pop culture. The dodecahedron serves as a crucial symbol in the book and movie adaptation of The Hitchhiker's Guide to the Galaxy (the "Meaning of Life" puzzle) and is part of a well-loved mathematical riddle known as the "dodecahedron paradox."

4. The Möbius Strip

The Möbius strip is a non-orientable surface with only one side and one edge, and it is a staple of topological geometry. The twist in a Möbius strip turns the concept of inside and outside on its head. Take a strip of paper, give it a half twist, and then join the ends. The result is a surface where you can trace your finger along its edge endlessly, without ever lifting it or reaching a boundary.

Mathematically, the Möbius strip is a symbol of non-orientability and plays a crucial role in knot theory and the study of 3-manifolds. The Möbius strip also sneaks its way into art and architecture, often used as a visual symbol of infinity or paradox in both visual and sculptural art forms.

5. The Klein Bottle

Another topological marvel is the Klein bottle, a non-orientable surface with no boundary. Unlike the Möbius strip, which has only one side, the Klein bottle essentially has a single continuous surface where both sides are connected in a higher-dimensional space. If you attempted to build one in 3D, it would have to intersect itself. However, it can be imagined in 4-dimensional space.

The Klein bottle's properties make it a critical concept in topology, with applications in advanced physics and geometry, particularly when studying the shape of the universe and space-time curvature.

6. The Truncated Icosahedron (Football Shape)

Have you ever wondered about the shape of a soccer ball? It’s a truncated icosahedron. This polyhedron has 12 black pentagonal faces and 20 white hexagonal faces, a geometric structure that makes it easy to create spherical objects with flat faces. The truncated icosahedron is a close-packed shape and appears in carbon molecule structures such as buckyballs (or fullerenes) used in nanotechnology.

7. The Archimedean Solids

The Archimedean solids are a set of 13 convex polyhedra, where each face is a regular polygon and the same number of faces meet at each vertex. These shapes, such as the icosahedron (20 faces) and octahedron (8 faces), pop up in all kinds of real-world applications, like in architecture and crystallography. In fact, many molecular structures (like the shape of viruses) reflect these highly symmetrical solids.

Next time you look at a soccer ball, admire a piece of modern art, or even browse through a movie with some mind-bending geometry, remember: the world is built on shapes you never knew you needed, and math is at the heart of them all.

[real-british-empire]

STOP POSTING TRUNCATED DODECAHEDRON

No, it’s revenge :3

[art-of-mathematics]

Drawing a snub dodecahedron (in isometric perspective) is quite lot of work, because I have to start with a dodecahedron (easy), then make an isocidodecahedron out of it (quite a lot of work) , and then make a truncated icosidodecahedron out of it (very much work) and then, after all these steps I can make the snub dodecahedron from this.

It is a similar procedure I used for drawing the snub cube:

Started with cube, then cuboctahedron, then truncated cuboctahedron, then snub cube.

[knotty-et-al]

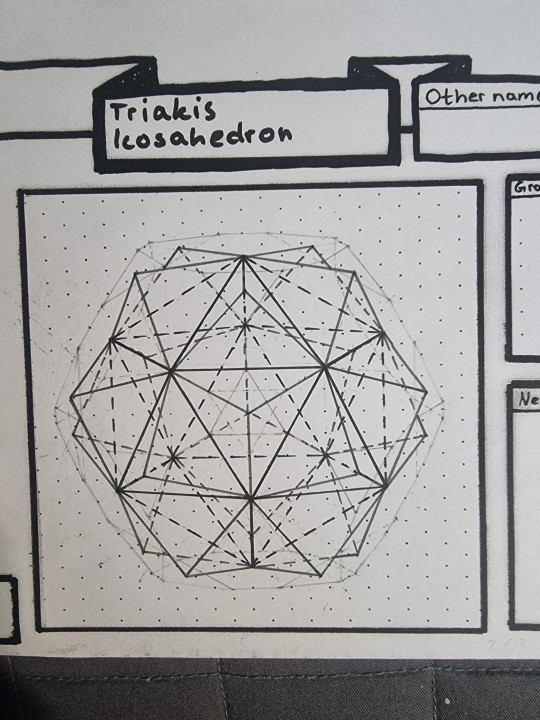
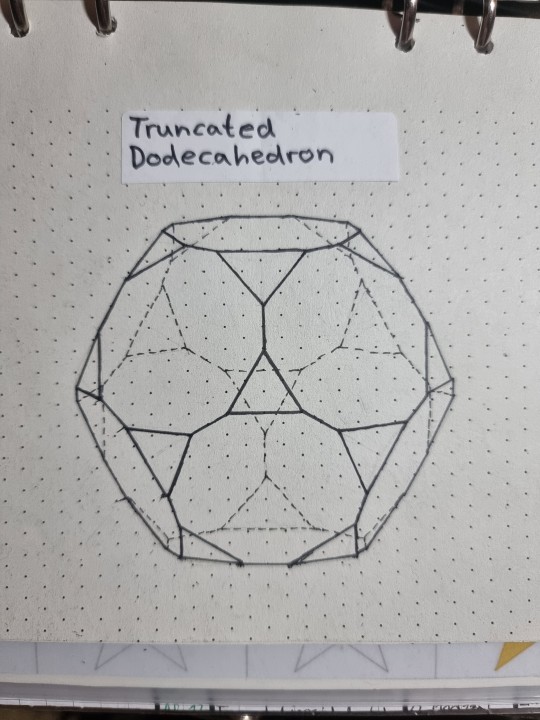
New polyhedron drawing just dropped:

Triakis Icosahedron [dual of the Truncated Dodecahedron]

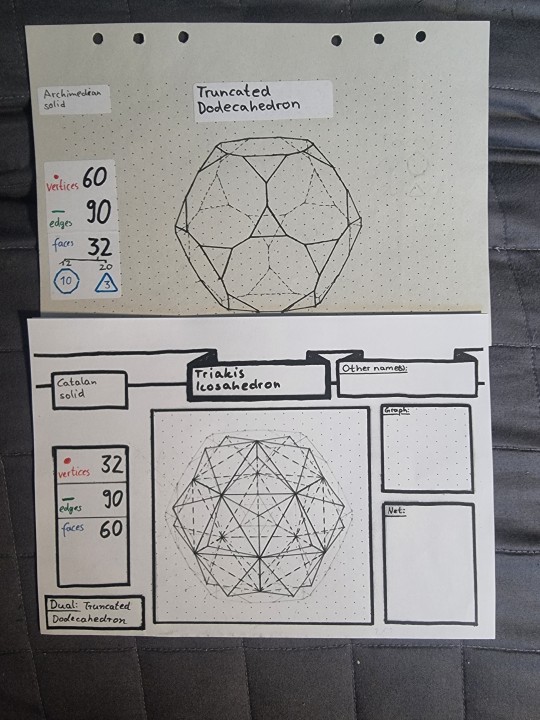
In order to draw that triakis icosahedron I drew a truncated dodecahedron (picture of truncated dodecahedron attached above)

[best-shapes]

Regular-ish Convex Polyhedra Bracket — Round 1

Propaganda

Truncated Dodecahedron:

Archimedean Solid

Semiregular

Dual of the Triakis Icosahedron

It has 12 regular decagonal faces, 20 regular triangular faces, 90 edges, and 60 vertices.

Image Credit: Cyp

Snub Dodecahedron:

Also called the Snub Icosidodecahedron

Archimedean Solid

Semiregular

Dual of the Pentagonal Hexecontahedron

It has 12 regular pentagonal faces, 80 regular triangular faces, 150 edges, and 60 vertices.

Chiral so it has two forms that are mirror images of each other.

With 92 faces it has the most of the Archimedean Solids.

Image Credit: Cyp

[robotblues]

A Space-Filling Pair of Polyhedra: The Cuboctahedron and the Octahedron There are only a few polyhedra which can fill space without leaving gaps, without “help” from a second polyhedron. This filling of space is the three-dimensional version of tessellating a plane. Among those that can do this are the cube, the truncated octahedron, and the rhombic dodecahedron. If multiple polyhedra are allowed in a space-filling pattern, this opens new possibilities. Here is one: the filling of space by cuboctahedra and octahedra. There are others, and they are likely to appear as future blog-posts here. Software credit: I made this virtual model using Stella 4d, polyhedral-manipulation software you can buy, or try as a free trial download, at http://www.software3d.com/Stella.php.

[dailypolyhedra]

Polyhedron of the Day #152: Small ditrigonal dodecicosidodecahedron

The small ditrigonal dodecicosidodecahedron is a uniform star polyhedron. It has 44 faces, 120 edges, and 60 vertices. It is also known as the small dodekified icosidodecahedron. Its Bowers-style acronym is sidditdid. It shares its vertex arrangement with the great stellated truncated dodecahedron. Its vertex figure is a crossed quadrilateral. Its dual is the small ditrigonal dodecacronic hexecontahedron.

Maeder, R. E. (1997). Small ditrigonal dodecicosidodecahedron (43). [Image]. MathConsult AG. https://www.mathconsult.ch/static/unipoly/43.html.

[k00294490]

Tuesday 21st November

I realised today that the shape I was thinking of wasn't made out of octagons at all. I was looking at a truncated octahedron but that wasn't quite it either.

After speaking with Mike Fox who showed me the platonic solids shapes, I chose a dodecahedron. It's made out of pentagons.

I struggled to draw it so I found a template to fold it and help me visualise it.

[phaseshapes]

The Uranium Urchin

When an icosahedron is covered in 36º pyramids, it's called a Great Stellated Dodecahedron. These pyramids have been truncated, making this a "Truncated Great Stellated Dodecahedron". The paint is "iridescent graphite" with sand gel. And neon green, as you can see in the blacklight video above. I printed this shape in 2022 and finished it in 2023.