#triangleposting
Explore tagged Tumblr posts
Text

the factory has been abandoned for decades. there's nothing here for you anymore. there hasn't been for years.
381 notes
·
View notes
Text

My contribution to triangleposting
58 notes
·
View notes
Text
Triangle Tuesday 7: the joy of coordinates, railroads, and you didn't see that coming
"There is no royal road to geometry," Euclid supposedly said to Ptolomey, and this is true. There is, however, a commuter rail line called analytic methods, and that's what I want to talk about today.
Everything I have discussed in this series so far falls under the heading of synthetic geometry -- that is, geometry done only using axioms such as Euclid's, without recourse to numerical formulas or coordinate systems. This is in contrast to analytic geometry, which most people are familiar with from the cartesian coordinate system of the plane.
Today, we're doing a different coordinate system, but the cartesian system provides a familiar jumping-off point. In the cartesian plane, we specify a point relative to two reference axes. The coordinates represent the perpendicular distances from the axes, and these distances are positive or negative depending on which side of the axes the point lies.
We are going to do something like that, but rather than orthogonal axes, we will take the sidelines of a triangle as our reference. This will give us three coordinates for only two dimensions, which seems redundant, but hold on and it will make sense in a bit.
First we'll look at the basics of this system, then I'll go through and find the coordinates for each of the triangle centers we've looked at so far, and we'll end with a bit of a surprise.
Coordinates for triangles
Why do I call this a commuter rail line? Because unlike a royal road, anyone can use it, and it can be a faster way to get to certain places. On the other hand, it doesn't always go exactly where you want, and we have to build some infrastructure before it becomes useful.
Let's work our way there by first adding some notation to our triangle. It's conventional in triangle geometry to use the uppercase letters A, B, and C for both the vertices and the size of the angles at the vertices, and lowercase letters a, b, and c for both the sides opposite the corresponding vertices and also the length of those segments.

This may seem liable to confusion in theory, but in practice context makes clear which sense is intended. If B or b appear in a drawing, they refer to points and lines. If they appear in a numerical expression, they refer to angle sizes or lengths.
Now let's look at a point P. We will label its feet on sides a, b, and c as Pa, Pb, and Pc, and the segments joining P to the feet as p1, p2, and p3. I don't know of any standard term for these segments. I'm just going to go with the obvious and call them legs.

And because we are all comfortable now with using the same symbol for a line segment and the length of that segment, I will also use p1, p2, and p3 as the signed distances from P to the sidelines of the reference triangle. The distance will be positive when P is on the same side of the sideline as the triangle, negative when P is on the other side, and zero when P is on a side line.

Here's P lying outside the reference triangle, with a negative p1 (in red) because it lies on the opposite side of line a from the triangle, a zero p2 because it is on line b, and a positive p3 (in blue) because it is on the same side of line c as the triangle.
Okay, so far so good. This is not too different from cartesian coordinates, except our axes aren't perpendicular and we have a seemingly unnecessary third coordinate. Two signed distances ought to uniquely identify a point, right?
Here's the difference that makes the third coordinate necessary: we are going to ignore absolute distances and only consider ratios between the coordinates. If we have a point with legs measuring p1, p2, and p3, we will consider any three numbers k*p1, k*p2, k*p3 to be the same coordinates (as long as k is not zero). We'll write this triple ratio as p1 : p2 : p3 in order to distinguish these coordinates from triples of cartesian coordinates in R^3.
This coordinate system is called homogeneous trilinear coordinates. (The homogeneous part comes from abandoning absolute distances and considering only ratios. If we kept to absolute distances, we would have exact trilinear coordinates. Hereafter I will just refer to the homogeneous version as trilinear coordinates, or trilinears.)
Why is this useful? Various reasons. One of them is that with one exception, any three real numbers specify a point. No point can lie on the outer side of all three side lines, so with exact coordinates, three negative numbers don't correspond to any point. But with homogeneous coordinates, we can multiply any coordinate triple by any nonzero real number k and it still represents the same point. Letting k = -1, we have x : y : z = -x : -y : -z. No problem with negatives.
But the main advantage of trilinears is that we can give a nice representation to important points of the triangle, and that lets us easily use analytic methods on them. The vertex A, for instance, has zero distance from sidelines b and c, so its trilinears are 1 : 0 : 0 (or equivalently any other nonzero real number for the first coordinate, but using 1 is simplest). Similarly vertex B is 0 : 1 : 0 and vertex C is 0 : 0: 1 . No point can lie on all three lines of the triangle at once, so 0 : 0 : 0 is the single coordinate that does not correspond to any point.
The incenter
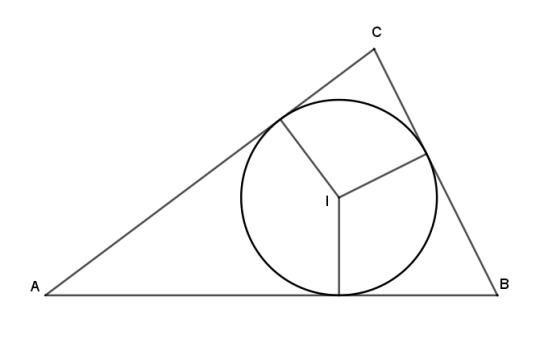
Let's see how this works using the incenter as an example. The incenter is inside the triangle and equally distant from the three sides. With the three legs being equal, its trilinear coordinates are as simple as they can be:
The trilinears of the incenter are I = 1 : 1 : 1.
That's a very nice and neat expression, but not actually very informative. We already knew this about the legs of the incenters, because they are all radii of a common circle. Furthermore it's easier to understand "the incenter is the point that is equidistant from the sides" than "the incenter is the point with trilinear coordinates 1 : 1 : 1." So far our coordinate system hasn't shown us anything new or made anything clearer. Well, we're still building our commuter rail line. It will pay off after we complete more ground work.
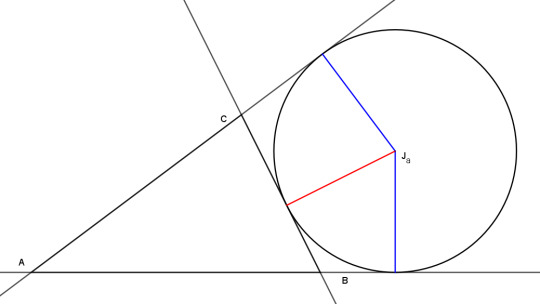
But while we are at this stop, we might as well take note of the excenters. Here is excenter Ja, equidistant from the sidelines of the triangle, but on the negative side of line a and on the positive sides of lines b and c. So its trilinears are -1 : 1 : 1, and similarly for the other two excenters.
The centroid
The centoid is defined as the intersection of the medians, and the medians are defined as the lines that join the vertices and midpoints of the opposite sides. So let's start by finding the coordinates of the midpoints. The midpoint of side a, Ma, has first coordinate 0, so we just need to figure out the ratio of distances to the other two sides. To do that, we'll first take a look at the altitudes of the triangle.
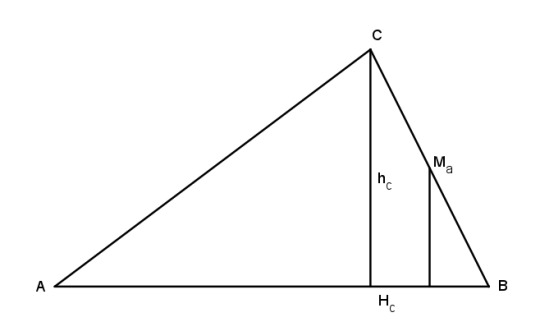
Let hc be the altitude from C to c, and let △ be the area of triangle ABC. Then by the standard formula for area of a triangle,
△ = 1/2 * c * hc
hc = 2 △ / c.
Now look at the midpoint of side a. By similar triangles, the length of its leg to side c is half the length of hc, or △/c. By the same logic, the leg extending to side b has length △/b. That gives us the ratio we were looking for, so the trilinears are 0 : △/b : △/c. Since this is a ratio, se we can divide through by △ to get 0 : 1/b : 1/c, which is nice and clean.
Repeating this for the other two sides, we get trilinears for the midpoints of the sides as:
Ma = 0 : 1/b : 1/c
Mb = 1/a : 0 : 1/c
Mc = 1/a : 1/b : 0
Now, in general, when we have two points, we can find an equation for the line that runs through them, and given two lines, we can find their point of intersection. The first method uses the fact that three points P, Q, and R with trilinears p1, p2, p3, etc. are colinear when this determinant is zero:

And by letting one of the points be variable x : y : z, we get this determinant

which gives us the general form of an equation for a line:
d x + e y + f z = 0.
Don't know what a determinant is? Don't worry! We don't need to use this method. I'm just mentioning it out of a sense of duty to completeness. In this case we're working with a median, which is a cevian, which makes things very convenient. Recall that a cevian is a line that runs through one of the vertices.

We worked out that for the point Ma, the legs to the b and c sides are in the ratio 1/b : 1/c. By similar triangles, any point P on this cevian will have legs to those sides in the same ratio. In other words, a point on the c-median must have triinears of the form u : 1/b : 1/c for some u.
The centroid G is one such point. It's also on the b-median, so it must also have trilinears of the form 1/a : v : 1/c. It's also on the c-median, so it must also have trilinears of the form 1/a : 1/b: w. So instead of working with the equations for the medians, we can get the trilinears directly from points known to lie on the medians. Therefore,
The trilinears of the centroid are G = 1/a : 1/b : 1/c.
For more completeness, here are equations for the medians:
y/b - z/c = 0
x/a - z/c = 0
x/a - y/b = 0
To find the intersection of two lines m and n with coefficients m1, m2, m3, etc., take this determinant:

The trilinears are then equal to the minor determinants:

If you are familiar with linear algebra and enjoy finding determinants, go ahead and calculate it using the coefficients above and you will get 1/a : 1/b : 1/c. Otherwise, don't worry about it.
The symmedian point

Let's now look at the symmedian point, which is the isogonal conjugate of the centroid. Recall that when P and Q are isogonal conjugates, the cevians of P are the reflections of the cevians of Q across the angle bisectors, and vice versa. In other words, at each vertex the cevians of P and Q make the same angle (in red) with the angle bisector (dashed line). Equivalently, they make the same angle (in blue) with the sides adjacent to the vertex. And that sets us up for our next shortcut:
Theorem: If a point P has trilinear coordinates p1 : p2 : p3, then its isogonal conjugate has coordinates 1/p1 : 1/p2 : 1/p3.

Proof: as the two green triangles are similar and the two blue triangles are similar, we have CP/PPa = CQ/QQb and CP/PPb = CQ/QQa. Then
PPa/QQb = CP/CQ = PPb/QQa
PPa/PPb = QQb/QQa.
Then given a ratio d : e : f, the ratio 1/d : 1/e : 1/f gives the desired reciprocal ratio between any corresponding pair.
With that result, and knowing that the centroid is 1/a : 1/b : 1/c, finding the coordinates of the symmedian point is simple:
The trilinears of the symmedian point are K = a : b : c.
Before moving on, we should take note of two things about our theorem on isogonal conjugates. First, the formula is undefined for any point with a zero coordinate, so points on the sidelines of the triangle don't have isogonal conjugates. Also, the incenter is its own isogonal conjugate, as are the three excenters, and they are the only points with this property.
The orthocenter
To find the coordinates of the orthocenter, let's go back and look at that altitude again.

Let h be the altitude from C to Hc. Draw leg hc1 from Hc to side a. Then the triangles to the right of h are similar and the two angles marked in red are equal. The length of segment hc1 is therefore h * cos B. In the same way, the blue angles are equal and hc2 = h * cos A. Thus the trilinears of Hc are cos B : cos A : 0.
This is an inconvenient form, though, because the first coordinate is in terms of B and the second in terms of A, which is the reverse of what we want. So we'll divide through by the factor cos A * cos B:
cos B / (cos A * cos B) : cos A / (cos A * cos B) : 0
= 1/ cos A : 1/cos B : 0
= sec A : sec B : 0.
That's the c-altitude. By symmetry, the a- and b- altitudes are:
0 : sec B : sec C
sec A : 0 : sec C
And conveniently, altitudes are also cevians, so we can use the same shortcut here that we used for the cetroid, and get the trilinears directly from these points.
The trilinears of the orthocenter are H = sec A : sec B : sec C.
If you want to play around with the determinant formula, you can go ahead and find the equations for the altitudes. I found it a little more convenient to use the forms cos B : cos A : 0, etc..
The circumcenter
Cevians are nice to work with, but not useful for the circumcenter, which isn't defined by cevians. It's defined by perpendiculars, and while there is a formula for perpendicular lines in trilinear coordinates, it's awful and I'd rather not use it. Sometimes the commuter rail line doesn't run where you want and it's easier to go a different way.
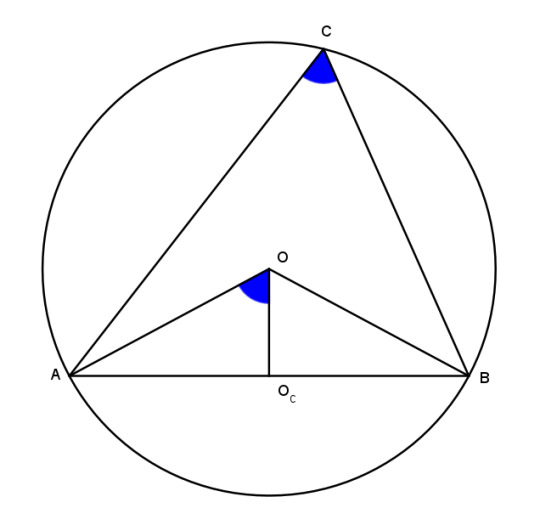
So we'll fall back on synthetic methods. The circumcenter O is the intersection of perpendicular bisectors of the sides, and is the center of the circumcircle. In particular, note that the segments OA, OB, and OC are radii of the circumcircle and equal.
Now consider angle ACB. It subtends the segment AB and has measure C. By our old friend the inscribed angle theorem, angle AOB = 2C. Segment OOc, one of the legs of O, bisects AB perpendicularly, so angle AOOc is half of AOB, equal to C.
Now by the definition of cosine,
cos AOOc = OOc/AO = cos C
OOc = AO cos C.
Similarly we can establish lengths of the other legs:
OOa = BO cos A
OOb = CO cos B.
Therefore the trilinears of O are BO cos A : CO cos B : AO cos C. But AO, BO, and CO are all radii of the circumcircle and equal, so
The trilinears of the circumcenter are O = cos A : cos B : cos C.
But look back at the orthocenter! The secant is the reciprocal of the cosine. And what did we just learn about reciprocal coodinates? Doesn't that mean -- yes, yes it does!
The circumcenter and the orthocenter are isogonal conjugates.
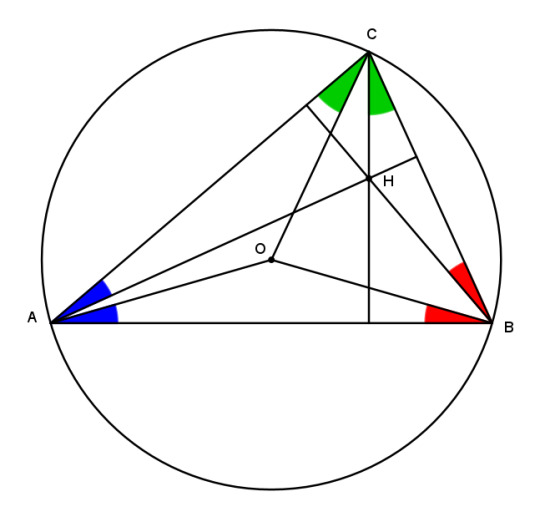
They've been conjugating away right under your nose this whole time and you never even noticed!
And this, finally, brings us a result that is much easier to establish with trilinears than with synthetic methods. There probably is a clever synthetic proof that O and H are isogonal conjugates, or even many proofs, but I would have to stare at a bunch of lines for a long time before I could come up with one. Using trilinear coordinates, we can establish this relationship at a glance. And that sort of quick trip that anyone can take is the reason we use the commuter railroad of analytic methods.
If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.
An index of all posts in this series is available here.
26 notes
·
View notes
Text

who the fuck watermarks a goddamn triangle
32 notes
·
View notes
Text
Obsessed with the guy at the triangle factory. The simplicity of the format. The sheer flexibility. The little hard-hat that's just two lines. Idk something about it just tickles my brain the eay that one drawing you make when you're five is just. Your favourite. It looks like the hundreds you made before, and the hundreds you will make after, but something about it is just different in a way only you can see through the magical lense of childhood.
2 notes
·
View notes
Text
I think glasses guy and hard hat guy should kiss
5 notes
·
View notes
Text
i guess we doin magnezone now

1 note
·
View note
Text

Another good set of triangleposts, courtesy of SteinMakesGames
12K notes
·
View notes
Text
Triangleposting this, triangleposting that, when do I get to be in a toxic love triangle with two bossy goths who decide to dominate me together as a compromise for both wanting to dom the other
2 notes
·
View notes
Photo

Triangle Art, Triangle Poster, Green Wall Art https://www.etsy.com/listing/589364811/triangle-art-triangle-poster-green-wall #TriangleArt #TrianglePoster #Green #HomeDecor #Geometrical #art #artmium
1 note
·
View note
Text
Triangle Tuesday 2: The circumcenter, pedal triangles, degeneracy, and what even is a triangle anyway?
The circumcenter is almost as simple an idea as the centroid, which we looked at before. To define it, you start the same way. Take triangle ABC, find the midpoints of the sides Ma, Mb, and Mc. Then instead of drawing lines to the midpoints from the vertices, draw perpendicular lines through the midpoints. These lines all coincide at a point O, which is the center of a circle that you can draw through the vertices. The circle is called the circumcircle, and that's why the point is called the circumcenter.
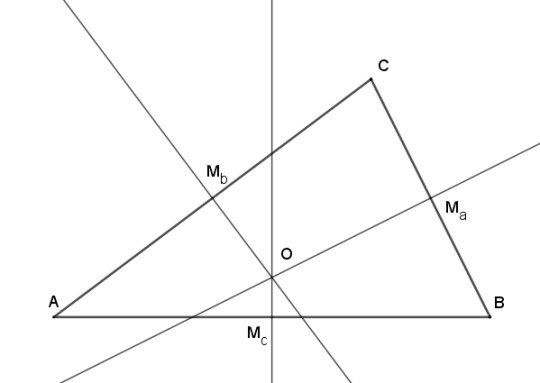
I say almost as simple, but in a sense the circumcenter is simpler than the centroid, because you could easily discover it by accident in the process of simply finding the midpoints. Drawing that perpendicular line, the perpendicular bisector, is the standard way of finding the midpoint of a line segment. It's covered all the way back in Book 1, Proposition 10 of Euclid's Elements, and it's simply this:
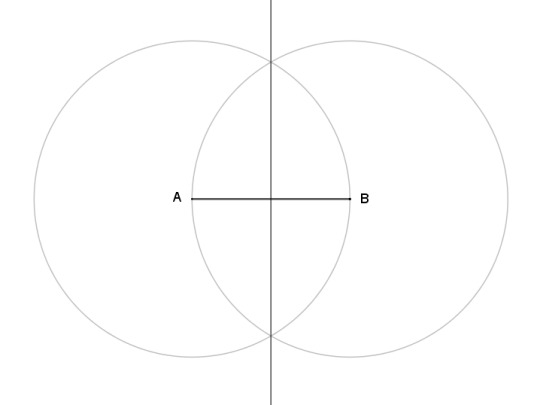
So if you find the midpoint of all three sides of a triangle with this method, you've already identified the circumcenter. But that doesn't prove that the perpendicular bisectors always coincide, nor that their point of crossing is the center of the circumcircle. For that, let's return to Euclid (Elements, book 4, proposition 5). Euclid's proof is very straightforward, and leads nicely into something interesting, so we'll follow that, but I will state the theorem differently.
Theorem: the perpendicular bisectors of a triangle coincide and their point of intersection is the center of a circle that meets all three vertices.
Let ABC be a triangle with midpoints of the sides Ma opposite A, similarly for Mb and Mc. Draw perpendiculars to sides AC and BC from their midpoints to meet at point O. Connect three segments from O to A, B, and C.
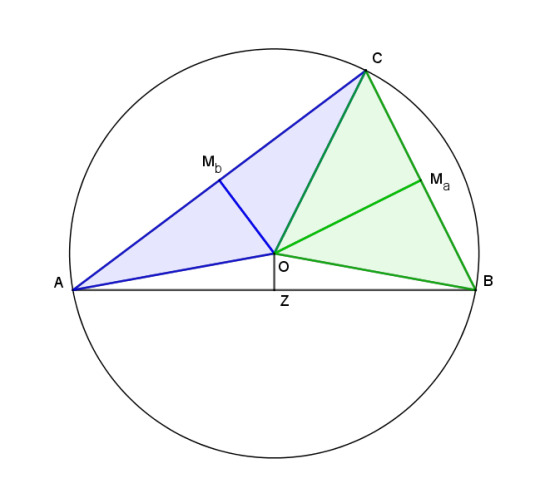
Consider the two blue triangles. Their sies AMb and CMb are equal, since Mb is the midpoint of AC. They also have OMb in common. Their angles at Mb are right angles, and therefore equal. So they have two sides and one angle the same, making them congruent, and therefore OA = OC.
The same argument applied to the green triangles shows that OB and OC are equal. By transitivity, OA = OB and O is equidistant from the three vertices. The radii of a circle are all equal, so a circle centered at O passing through A also passes through B and C.
Finally, draw a line from O perpendicular to AB. This creates two white triangles with sides OA and OB equal, side OZ in common, and equal right angles at Z. The two triangles are then congruent and the two sides AZ and BZ are equal. So Z is the midpoint Mc, showing that the perpendicular bisectors all meet.
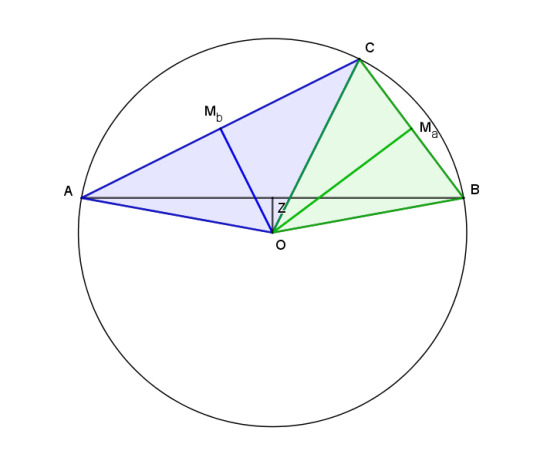
And the same argument works when ABC is obtuse. The circumcenter lands outside the triangle, and in this coloring the white triangles are no longer white, but all the relationships between the segments are the same.
(What Euclid didn't prove is that the perpendicular bisectors of AC and BC do in fact meet somewhere, that is, that they aren't parallel. It's not difficult, but I'm not going to prove that either, at least not yet, for reasons.)
Let's develop another idea. We located the circumcenter by drawing the perpendicular bisectors, but now consider doing this construction in reverse. That is, pick a point, and then draw perpendiculars to the three sides. The intersection of the perpendicular and the side is called the foot of that point with respect to that side. If you do that with with the circumcenter, the feet are of course the midpoints, but you can find the feet for any point.
And if we connect those three feet, we get a triangle. In this case, the medial triangle, which we have seen before. For a point in general, the triangle formed by its feet is called the pedal triangle of that point. ("Pedal" meaning "related to feet," and yes, that is why a lever operated with your foot is also called a pedal.)

So let's draw the pedal triangle for an arbitrary point, move it around, and see what happens. The point is going to sometimes be outside the triangle, but that's all right. With extended sides (dashed lines) we will still be able to draw a perpendicular to find a foot, no matter where the point is.

So there's something interesting -- the three feet become colinear and the pedal triangle flattens out into a straight line when the point is on the circumcircle. Does that always happen?
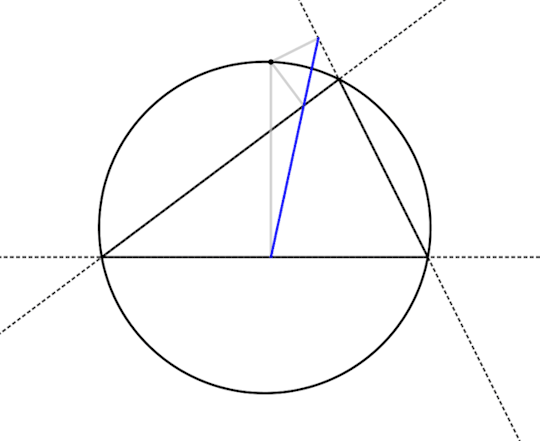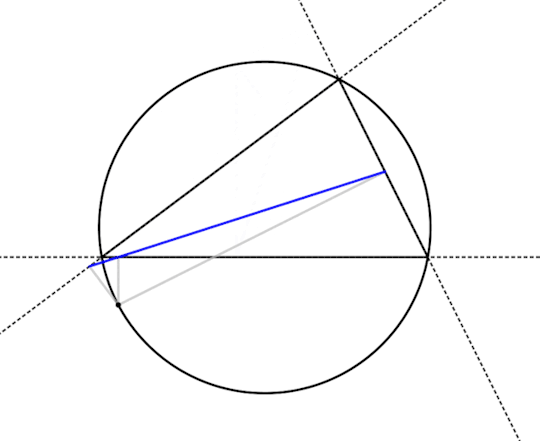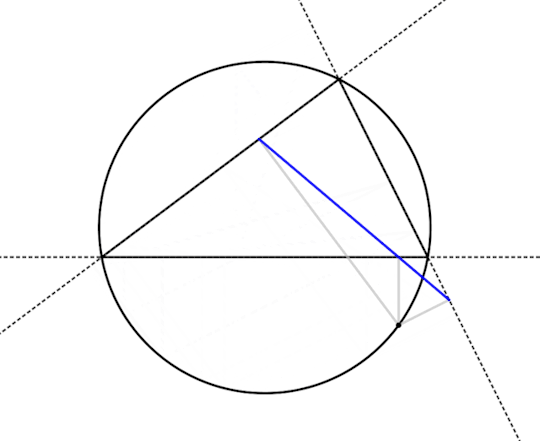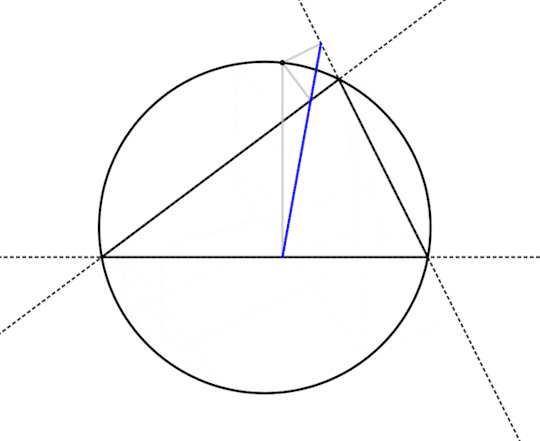
Looks like it does! So let's prove that. Below is a drawing of the flattened-out pedal triangle of a point on the circumcircle, all labeled up. I've also added a couple dashed lines to make following the proof easier. What we would like to show is that ∠JKP + ∠PKL = 180°.
We're going to extract some information from this drawing based on two facts: a) in a cyclic quadrilateral (meaning it has all vertices on the same circle), opposite angles sum to 180° and b) if two right triangles have the same hypotenuse, the triangles have the same circumcircle. I'm not going to prove either of those here because this post is long enough already, but both of these results follow straightforwardly from the inscribed angle theorem.

Theorem: For a point P on the circumcircle of a triangle ABC, the feet J, K, and L with respect to ABC are colinear.
Okay. PCBA is a cyclic quadrilateral, so
1) ∠BAP + ∠PCB = 180°.
And ∠BAP is the same as ∠LAP, so
2) ∠LAP + ∠PCB = 180°.
The two triangles AKP and ALP are right triangles with the same hypotenuse (the dashed segment AP), so all four points are on the same circle and ALKP is a cyclic quadrilateral. Therefore,
3) ∠LAP + ∠PKL = 180°,
4) ∠PKL = ∠PCB.
Quadrilateral PKCJ is also cyclic (again because of right triangles sharing the same hypotenuse), so
5) ∠JKP = ∠JCP
by the inscribed angle theorem. ∠PCB is supplemental to ∠JCP, so
6) ∠JKP = 180° - ∠PCB
and then combining 4) and 6),
7) ∠JKP + ∠PKL = ∠PCB + (180° - ∠PCB) = 180°,
which means that the pedal triangle of a point on the circumference of a circle is flattened to a line segment. Can we consider such a figure to be a triangle?
Now we can return to Euclid's omission in the existence proof of the circumcircle. Proving that the perpendicular bisectors aren't parallel is equivalent to proving that no two sides of a triangle are parallel, or that the three vertices of a triangle aren't colinear. Euclid didn't do that, but it's pretty simple, so he could have. And then he would simply have said that such an arrangement of line segments isn't a triangle. Modern geometers working with projective geometry can answer differently, and might say that this is a degenerate triangle, but we haven't gotten into that yet.
Let's do one more thing. We can extend the flattened line segment into a line, called the Simson line, after Robert Simson, who never wrote anything about it. It was actually discovered by William Wallace, but not named for him, because that's how things work in math.
The set of all Simson lines from all points on the circumcircle form an envelope in the shape of a deltoid, the Steiner deltoid, named for Jakob Steiner, who for all I can tell was its actual discoverer.

The deltoid is tangent to the sides of the triangle at three points where the Simson line coincides with the sides. I'll have more to say about this lovely deltoid later, but for now, please just enjoy this gif. It took me several hours to figure out how to make it, so if people reading this could spend a collective several hours staring at it, that would be great.
If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.
An index of all posts in this series is available here.
31 notes
·
View notes
Photo

Repost @trianglepostals @ainaplaplanas explicant el procés de creació d'una guia turística a l'equip d'Els Entusiastes d' @ib3 Gràcies al•lots! #trianglepostals #ib3 #elsentusiastes #accio #guia #menorca #turismo"
0 notes
Text


Yet more triangleposting
9K notes
·
View notes
