#seno cosseno e tangente

[tioneu]

Trigonometria (Questão 06) Seno, cosseno e tangente

[classificaesdesportrecife]

Quais são as melhores estratégias para ganhar em apostas de sinuca em jogos online?

🎰🎲✨ Receba 2.000 reais e 200 rodadas grátis, além de um bônus instantâneo para jogar jogos de cassino com apenas um clique! ✨🎲🎰

Quais são as melhores estratégias para ganhar em apostas de sinuca em jogos online?

Técnica de tacada

A técnica de tacada é um elemento fundamental em diversos esportes, especialmente no bilhar e no golfe. Essa habilidade envolve não apenas força física, mas também precisão e controle do movimento. No bilhar, por exemplo, uma boa técnica de tacada é essencial para acertar as bolas nos ângulos desejados e controlar a velocidade da jogada.

No golfe, a técnica de tacada é ainda mais complexa, envolvendo uma série de movimentos precisos que começam desde a postura do jogador até o momento do impacto com a bola. Um bom golfista domina não apenas a força da tacada, mas também a rotação do corpo, o posicionamento das mãos e o ângulo do taco.

Independentemente do esporte, a técnica de tacada requer prática constante e atenção aos detalhes. Pequenos ajustes na postura, na posição das mãos ou no movimento do corpo podem fazer uma grande diferença no resultado final. Além disso, é importante entender as características da superfície de jogo, como a inclinação do campo no golfe ou a textura da mesa no bilhar, para adaptar a técnica de tacada de acordo com as condições.

Para aprimorar a técnica de tacada, é recomendável buscar a orientação de instrutores qualificados e praticar regularmente. A repetição dos movimentos ajuda a desenvolver a coordenação motora necessária para executar tacadas precisas e consistentes. Além disso, assistir a vídeos de jogadores profissionais pode fornecer insights valiosos sobre técnicas avançadas e estratégias de jogo.

Em resumo, a técnica de tacada é uma habilidade fundamental em diversos esportes, exigindo não apenas força física, mas também precisão, controle e constante aprimoramento. Com dedicação e prática, é possível desenvolver uma tacada poderosa e precisa, capaz de fazer a diferença em qualquer competição.

Análise de ângulos

Claro, aqui está o artigo sobre "Análise de ângulos":

A análise de ângulos é um ramo da matemática que se dedica ao estudo das medidas e relações entre os ângulos. Os ângulos são formados pela intersecção de duas retas ou de uma reta com uma superfície plana, e sua medida é expressa em graus (°).

Uma das aplicações mais comuns da análise de ângulos está na geometria, onde os ângulos são utilizados para descrever formas, calcular áreas e determinar propriedades de figuras geométricas. Por exemplo, ao analisar um triângulo, os ângulos internos podem fornecer informações sobre a natureza do triângulo (equilátero, isósceles, escaleno) e até mesmo ajudar a calcular suas medidas.

Além disso, a análise de ângulos é fundamental em áreas como a trigonometria, onde os ângulos são estudados em relação às proporções dos lados de triângulos retângulos. Nesse contexto, as funções trigonométricas como seno, cosseno e tangente são definidas com base nos ângulos de um triângulo e são amplamente utilizadas em diversas áreas, incluindo engenharia, física, e ciências aplicadas em geral.

Na física, por exemplo, a análise de ângulos é essencial para compreender o movimento de corpos em sistemas de referência diferentes, como na cinemática e na dinâmica. Também é crucial em áreas como a astronomia, onde os ângulos são usados para descrever a posição e o movimento dos corpos celestes no espaço.

Em resumo, a análise de ângulos desempenha um papel fundamental em várias áreas do conhecimento, proporcionando ferramentas essenciais para compreender e descrever fenômenos naturais e construídos pelo ser humano. Seu estudo é fundamental para o avanço da ciência e da tecnologia.

Estratégias de defesa

Estratégias de defesa são planos e ações desenvolvidos para proteger indivíduos, organizações ou países contra ameaças externas. No contexto militar, essas estratégias são essenciais para garantir a segurança nacional e a soberania de um país. No entanto, as estratégias de defesa também podem ser aplicadas em outras áreas, como segurança cibernética, saúde pública e até mesmo em situações pessoais.

Uma das estratégias de defesa mais comuns é a dissuasão, que envolve demonstrar capacidade e disposição para resistir a uma ameaça, a fim de desencorajar potenciais agressores. Isso pode incluir a manutenção de forças militares bem treinadas e equipadas, além de alianças estratégicas com outros países.

Além da dissuasão, a diversificação das fontes de segurança é outra estratégia importante. Isso envolve não depender exclusivamente de uma única fonte de defesa, mas sim investir em uma variedade de recursos e táticas para enfrentar diferentes tipos de ameaças.

A cooperação internacional também desempenha um papel fundamental nas estratégias de defesa modernas. Por meio de tratados e acordos bilaterais ou multilaterais, os países podem trabalhar juntos para enfrentar desafios comuns, como o terrorismo, a proliferação de armas de destruição em massa e ameaças cibernéticas.

Além disso, investir em inteligência e vigilância é essencial para identificar e neutralizar ameaças antes que elas se materializem. Isso pode incluir monitoramento de fronteiras, interceptação de comunicações e análise de dados para identificar padrões de atividade suspeita.

Em suma, as estratégias de defesa são fundamentais para garantir a segurança e proteção de uma nação ou entidade contra ameaças internas e externas. Ao adotar uma abordagem abrangente e adaptativa, é possível enfrentar os desafios de segurança do século XXI com eficácia e resiliência.

Estudo de velocidade da mesa

O estudo de velocidade da mesa é uma análise fundamental para qualquer jogador de tênis de mesa que deseje aprimorar suas habilidades e desempenho. A velocidade da mesa, que se refere à rapidez com que a bola de tênis de mesa viaja sobre a superfície da mesa, desempenha um papel crucial no jogo, influenciando diretamente a dinâmica dos ralis e a estratégia utilizada pelos jogadores.

Para conduzir um estudo de velocidade da mesa, é essencial utilizar equipamentos adequados, como cronômetros e dispositivos de medição de velocidade. Os pesquisadores geralmente realizam uma série de testes, variando fatores como a força do golpe, o tipo de empunhadura e o ângulo de contato da raquete com a bola. Esses testes fornecem dados valiosos sobre como diferentes variáveis afetam a velocidade da bola e permitem que os jogadores compreendam melhor os mecanismos por trás do jogo.

Além disso, o estudo de velocidade da mesa também pode revelar insights sobre a técnica de cada jogador. Por exemplo, um jogador com uma empunhadura mais firme pode ser capaz de gerar mais velocidade na bola em comparação com alguém com uma empunhadura mais solta. Compreender essas nuances técnicas pode ajudar os jogadores a aprimorar suas habilidades e desenvolver estratégias mais eficazes para enfrentar diferentes estilos de jogo.

Em última análise, o estudo de velocidade da mesa não apenas contribui para o avanço do conhecimento no esporte do tênis de mesa, mas também oferece benefícios tangíveis para os praticantes, ajudando-os a alcançar um desempenho superior e a desfrutar ainda mais do jogo.

Aperfeiçoamento do controle de bola

O controle de bola é uma habilidade fundamental no futebol, que pode determinar o sucesso ou fracasso de um jogador em campo. Aperfeiçoar essa habilidade é essencial para qualquer atleta que deseje se destacar e alcançar o sucesso no esporte.

Existem diversas técnicas e exercícios que podem ajudar os jogadores a melhorar seu controle de bola. Um dos aspectos mais importantes a serem trabalhados é o domínio da bola com os pés. Isso inclui não apenas a capacidade de receber passes precisos, mas também a habilidade de controlar a bola em movimento e em diferentes situações de jogo.

Além do domínio com os pés, é igualmente importante desenvolver habilidades de controle de bola com outras partes do corpo, como o peito, as coxas e até mesmo os ombros. Isso permite que os jogadores sejam mais versáteis e capazes de lidar com passes e lançamentos de diferentes alturas e velocidades.

Para aperfeiçoar o controle de bola, os jogadores também devem dedicar tempo ao treinamento específico, realizando exercícios que visam melhorar sua coordenação, agilidade e percepção espacial. Isso pode incluir drills de condução de bola em velocidade, exercícios de domínio em espaços reduzidos e jogos simulados que replicam situações de jogo real.

Além disso, a prática constante e a repetição são fundamentais para o aprimoramento do controle de bola. Os jogadores devem dedicar tempo regular ao treinamento individual, bem como participar de sessões de treinamento em equipe, onde possam aplicar e aperfeiçoar suas habilidades em um ambiente de jogo.

Em resumo, o aperfeiçoamento do controle de bola requer dedicação, prática e foco. Com o tempo e o esforço adequados, os jogadores podem melhorar significativamente sua habilidade nesse aspecto crucial do jogo, o que pode fazer a diferença entre a vitória e a derrota em campo.

[marciorjusto]

"... Matemática nos permite perceber, conhecer e até imaginar a realidade ao nosso redor. Como? Através da comparação com coisas já conhecidas (que chamamos de "medir"), do agrupamento de coisas (porque os conceitos de "quantidade" e todas as operações envolvem Grupos, ou seja, coisas que possuem uma Relação entre si) e da dedução a partir de "receitas de bolo" (se identificamos a essência de um processo, podemos "guardá-lo" em uma fórmula e assim conseguimos aplicar quaisquer valores sobre ela e simular os resultados desse processo) ..."

" ... Matemática vem da Lógica, que vem da Filosofia.

Filosofia: "O que é essa coisa? Como percebo-a? Como descrevê-la?"

Lógica: "Essa coisa apresenta-se ou comporta-se de forma racionalmente coerente?"

Matemática: "Quando essa coisa junta-se a outras coisas com características semelhantes, é possível identificar outras características e comportamentos racionalmente coerentes?" ..."

"... O conhecimento/currículo matemático apresentado no ensino atual é estudado desde o que é estável e previsível até chegar no n��vel universitário, onde estuda-se o que é instável e imprevisível ..."

"... Razão, Proporção, Porcentagem, Juros, Equações, Monômios e Polinômios, Produtos Notáveis, Bháskara, Trigonometria e Cálculo apóiam-se no conceito de Proporcionalidade para obter medidas de forma indireta (ou seja, formam as "receitas de bolo" ou "contas de X" para obtermos resultados para duas, duzentas ou duas mil coisas, por exemplo. Essa proporcionalidade é que forma os padrões evolutivos intrínsecos aos processos dos conceitos acima. E esse padrão geralmente é registrado (e condensado) como uma fórmula, na linguagem matemática ..."

" ... Em algumas situações, a proporcionalidade não necessariamente está associada ao comportamento de um fenômeno, mas à forma (literalmente) com que as medições de um fenômeno relacionam-se umas com as outras, como ocorre na Geometria e em Matrizes e Determinantes ..."

" ... Qual a principal utilidade da Matemática? Gerenciar melhor os recursos que garantem nossa sobrevivência (comida, água, construção, transportes, saúde, dinheiro para as trocas econômicas, etc ... A Lógica nos diz: "Tenho ou não tenho comida para viver. A Matemática diz: Quanto tenho de comida, por quanto tempo, etc..."

"... Trigonometria também serve para estudar oscilações e fenômenos cíclicos, utilizando as medidas-padrão de um triângulo retângulo conhecidas como seno, cosseno, tangente, etc ..."

#PalestradeMatematicaMRJnoFatima

[ptbr-hypmic]

OWN STAGE

O Próprio Palco (Own Stage) é a terceira faixa do álbum Ah, Osaka Dreamin’ Night, realizada por Rosho Tsutsujimori.

É…

Nós dois somos como o Sol e a Lua

Caminhando na direção oposta

Muitas luas atrás, sempre que assisto TV

Por vezes, eu relembrava desses tempos

Eu queimei essas memórias

E disse “adeus”

Não irei voltar para esses lados, não irei olhar para trás

Esses tempos acabaram, eu me diverti um pouco

Mas eu vou ficar bem

O gênio dessa pessoa era tão radiante que eu não pude evitar

Eu pensei que parecia estar brilhando dentro de mim

Até ao ponto que tudo o que eu consegui ver foi escuridão

Eu não entendo

Eu sempre quis ser como o Sol

Eu deveria perseguir o meu sonho

Mas continuo perseguindo até hoje

Eu não posso transmitir bem

Até mesmo agora, tudo bem

De qualquer forma, a Lua continua linda, não é?

Não importa quantas vezes eu tenha que cair

Mesmo se existirem contratempos ou se meus cadarços se perderem

Eu irei chegar ao meu destino

Você consegue entender o significado das feridas em seus joelhos?

Nós precisamos de sabedoria

Nós precisamos de sabedoria

Sempre que eu me recordo daquele tempo

Mesmo agora, a minha mente apaga

É

Assistindo TV o tempo todo

Esse foi o dia em que eu desisti do meu sonho

Eu não quero fugir desta amarga vida

Bom, um bom remédio é sempre amargo na boca

O palco onde eu me situo se tornou limitado

É diferente do palco desta pessoa

Existe apenas um quadro preto na minha frente

É por isso que é bom que você leve o memorando

Escute e sinta a harmonia de hoje também

Aqui é onde eu pertenço

Ei, já está desistindo?

É o suficiente, então persiga seus sonhos, idiota

Há tangente no seno e no cosseno

Quantas vezes a minha vida vai ter que mudar?

Me diga, Einstein

Eu escolhi o caminho certo?

Me diga, Einstein

O que eu ganhei com meu fracasso?

Me acorde, Sol radiante

Chuveiro, então eu me pergunto o que vou desafiar hoje

Vou ficar no lado direito dos sinais da igualdade

Não importa quantas vezes eu tiver que cair

Mesmo se existirem contratempos ou se meus cadarços se perderem

Eu irei chegar ao meu destino

Você consegue entender o significado das feridas em seus joelhos?

Nós precisamos de sabedoria

Nós precisamos de sabedoria

Créditos: Tive ajuda da minha amiga, Inês, com a tradução. Agradeço muito pela ajuda. 

[grupogen]

Calculadora Científica Benko / Kenko 240 Funções Display 2 Linhas

Calculadora Científica Benko / Kenko 240 Funções Display 2 Linhas

Descomplique os cálculos com a Calculadora Científica Benko/Kenko! Segue funções: Display de 2 linhas 10 + 2 dígitos 9 Memórias de variáveis Super visualização das formulas algébricas Permutação e combinação Calculo Fracionário Calculo Seno, Cosseno, Tangente e Arco de cada um Calculo Estatístico: Desvio Padrão e anal. regressivo Conversão de sexagesimal para decimal Funções hiperbólicas e…

[vestibulandx]

Espero que estas dicas e macetes sejam úteis. 

Física

Calorimetria 1. Fórmula: Q = M.C.T Uso: Fórmula para medir variação de calor de um corpo Macete: Qui MaCeTe?

2. Fórmula: Q = M.L Uso: Fórmula para medir variação de calor de um corpo Macetes: Qui MoLeza! Quem Matou Lineu? Quem Matou Lampião?

3.  Macete: Croquete. (Capacidade térmica)

Pressão 1. Fórmula: P.v = n.R.t Uso: Fórmula para medir a pressão de gases e líquidos Macetes: Por Você nunca Rezei tanto Para vereador não Roubar tanto

Empuxo 1. Fórmula: E= d.V.g Uso: Para calcular a força hidrostática exercida por um corpo Macete: Empuxo é deVagar.

Velocidade 1. Fórmula: V = Vo + A.T Uso: Fórmula para medir a velocidade final, inicial, tempo de deslocamento ou aceleração de um corpo Macete: Vi Você à Toa Vovô Alfaiate Vi Você Atirar Vovô ateu

2. Macete: Vi você mais 2 amigos num triângulo sentimental. (Equação de Torricelli)

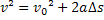
Movimentos

Para Movimento Retilíneo Uniforme (MRU): Fórmula: S= So + V.t Uso: Fórmula para medir o tempo, espaço e velocidade no MRU Macetes: Sorvete Sempre sonhei em ver-te.

Para Movimento Retilíneo Uniformemente Variado (MRUV): S = So + Vo.t + 1/2 a.t² Uso: Fórmula para medir o tempo, espaço e velocidade no MRUV Macetes: Sorvetão Sozinho no Sofá, Vendo Tevê à Toa Sentado Sozinho Vendo Tevê até Meia-Noite

Campo Elétrico E = F/Q Uso: para determinar a intensidade do campo elétrico Macetes: É Fraqueza! Fique Elegante, Querida!

Q = ti Uso: para calcular a intensidade da corrente elétrica Macete: Quero te iludir

Força F = m.a Uso: para medir força, massa ou aceleração de um corpo Macetes: Fama A força é má

Velocidade de ondas 1. V = λ.f (λ= letra grega lâmbida) Uso: para calcular a frequência de ondas Macete: Você lambe a faca Vistosas lambidas com frequência

2.  Macete: Fofoca a vizinha vem ouvir, fofoca a vizinha vem fazer! (efeito Doppler)

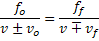
Óptica

Macete: Uma flor = uma pétala mais uma petalinha. (Equação de Gauss)

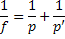
Matemática

Análise combinatória

O conteúdo de Análise Combinatória é muito cobrado em vestibulares, devido ao fato de conter três tipos de fórmulas que devem ser utilizadas de acordo com o enunciado. Confira quais são as três fórmulas, em qual caso usar cada uma e uma frase para auxiliar na memorização das mesmas:

Fórmula: A n,p = n! / (n-p)! Uso da fórmula: A fórmula do Arranjo Simples é utilizada quando você precisa arrumar os elementos em uma determinada ordem, e essa ordem é importante. Macete:   Ainda não posso = não! /( não posso)!

Fórmula: C n,p = n! / p! . (n-p)! Uso da fórmula: A fórmula da Combinação é usada quando você precisa ordenar os elementos, mas a ordem não é importante.  Macete: Comigo não pode = não! / pode! . (não pode)!

Geometria Analítica

Para se encontrar a equação da reta que passa por um determinado ponto P(xo, yo) usa-se a equação y – yo = m (x – xo). Essa equação pode ser memorizada pela frase YoYô, Mixoxô.

Pi

O Pi é um número irracional que contém centenas de números após a vírgula. Apesar disso, é muito utilizado em fórmulas que contém círculos e esferas. Porém, o valor do Pi não é fornecido nas provas e no ENEM. Para se memorizar o número Pi com 10 casas após a vírgula utiliza-se a frase: sim, é útil e fácil memorizar um número. Grato aos sábios! Cada palavra corresponde a um número:

sim = 3

é = 1

útil = 4

e = 1

fácil = 5

memorizar = 9

um = 2

número = 6

grato = 5

aos = 3

sábios = 6

Assim o Pi tem o valor de 3,1415926536!

Fórmulas Trigonométricas

As fórmulas trigonométricas envolvem os elementos do triângulo retângulo – cateto oposto, cateto adjacente e hipotenusa. Para os vestibulares e o ENEM é importante saber as três fórmulas mais importantes da trigonometria:

Seno = co / hip, usa-se a palavra corri;

Cosseno = Ca / hip, usa-se a palavra caí;

Tangente = co / ca; usa-se a palavra coca.

Também é importante saber a posição dos seno e do cosseno, para isso utiliza-se o macete:

quem ta de pé ta sem sono: seno no eixo y, que é vertical

quem ta deitado ta com sono: cosseno no eixo x, que é horizontal

Fórmulas de PA

fórmula do termo geral:

 an = a1 + (n-1) . r: Ainda não arranjei um namorado rico! 

fórmula da soma da PA:

Sn = (a1 + an) . n / 2: Sem namorado? arranja um namorado novo e divide para nós duas!

Áreas de figuras planas

Algumas músicas podem ser utilizadas para memorizar alguns assuntos da matemática. A música abaixo auxilia na memorização das áreas de figuras planas:

Lá vem o triângulo, que eu conheço bem Polígono fechado que três lados tem Calculo sua área que é pra ver depois Base (vezes) altura, divido por dois

Todo triângulo. três alturas tem Se não for dada a altura Determino também Altura é quando sai De um vértice um segmento Vai até o lado oposto, Ao seu prolongamento

A altura sempre forma angulo reto Com o lado oposto ao vértice ou seu prolongamento Acuntângulo, retângulo E também obtusângulo É a classificação baseada no ângulo

O tal do quadrado eu entendo bem E que quatro lados iguais ele tem Calculo sua área, que é um barato Se eu multiplico lado por lado

Falo de trapézio, sua área também Bases paralelas eu sei que ele tem Eu somo as bases, multiplico depois Pela sua altura e divido por dois

O círculo é roda, não fica parado E o raio que parte do centro ele tem Calculo sua área e fico ligado Que é pi vezes a raio elevado ao quadrado

[jeffmami-blog]

Aula 19 - Olho

Nesta tarefa, foi solicitado fazer com que um olho olhe na direção do mouse.

Para fazer isso, iremos precisar: Da distância entre o olho e o mouse e a tangente do mouse para saber a direção do entre o mouse e o olho, já q ele fica no centro.

Com a ajuda das coordenadas polares, podemos utilizar o valor da tangente e usar o seno(altura) e o cosseno(largura) para as coordenadas da elipse.

Outra técnica utilizada para que funcione é: caso a distância entre o mouse e o a Iris for maior que 150, a distância volta a ser 150, assim, a iris continua dentro do olho.

O código da aplicação pode ser encontrado aqui:

https://github.com/JeffersonJales/jeffmamiufc/blob/master/Aula_19_Olho/olho/olho.pde

[marianamurimami-blog]

Atividade 19 – Olho

A atividade consiste em criar um olho (círculo preto pequeno no interior de círculo branco grande) que se encontra sempre voltada para o cursor do mouse.

Inicialmente foram criadas as duas elipses, centralizadas na tela, uma com a cor branca e a outra com a cor preta, para representar o olho.

Em seguida, criamos variáveis. Na primeira variável atribuímos os valores do raio, usando a função dist, onde inserimos como parâmetro o tamanho da elipse(x e y) e as coordenadas do mouse através do mouseX e mouseY, e na segunda, atribuímos os valores para calculo da tangente da elipse maior levando em consideração o seu tamanho e a posição do mouse em X e Y, gerando assim, seus valores radianos.

Prosseguindo, usamos as coordenadas polares criadas em sala (p2cX e p2cY) para calcularmos o seno e cosseno, que serão nossos pontos horizontais e verticais, respectivamente.

Finalizando, foi criada uma condição onde, se o raio for maior que o tamanho da esfera branca, ele irá permanecer dentro dela, porém continuando a acompanhar o mouse seguindo sua movimentação, porém, sem sair do “globo ocular”.

Resultado:

Link para download do código:

https://drive.google.com/file/d/1QEC-Xo6b5baKRsZW1Wzpf5SRWuvdEKKj/view?usp=sharing

[penssematematica-blog]

Trigonometria

E aí galera, tudo bem?

Hoje vou mostrar pra vocês um dos diversos questionários que respondi pra garantir minha notinha e passar direto na matéria! Esse aqui é sobre Trigonometria, então se liguem:

1.      O que é trigonometria?

É um ramo da matemática que estuda triângulos retângulos. As relações entre lados, ângulos e algumas extensões dessas relações.

 2.      Em que contexto histórico ela surge?

O início do desenvolvimento da Trigonometria surgiu devido aos problemas gerados na Astronomia, Agrimensura e Navegações (por volta do séc IV, V a.C.) com os egípcios e babilônicos.  Não se sabe ao certo se o conceito “ângulo” surgiu com os gregos, mas eles fizeram estudos sistemáticos sobre suas relações numa circunferência e comprimentos de suas cordas.

 3.      Diferencie a trigonometria no triângulo retângulo da trigonometria na circunferência trigonométrica

A trigonometria no triângulo retângulo é dada entre as relações dos lados (conhecidos como cateto oposto, cateto adjacente e hipotenusa) e ângulos desse triângulo. As relações principais são: seno, cosseno e tangente. Já o círculo trigonométrico está representado no plano cartesiano com um raio medindo uma unidade, sendo utilizado para auxiliar nas relações trigonométricas.

 4.      Em que situações podemos relacionar os conceitos de funções periódicas com outras áreas do conhecimento?

As funções periódicas podem ser relacionadas com a astronomia, análise de mercado, economia, desenvolvimento de jogos, entre outros.

 5.      Como a trigonometria é usada para abordar outros conceitos da matemática?

A trigonometria é usada como uma ferramenta para explicar as geometrias ou até mesmo outros conceitos matemáticos. Muitas vezes é utilizada para a demonstração de fórmulas, a partir das relações nos triângulos.

 6.      Quais são os conhecimentos prévios para que um estudante aprenda trigonometria?

São necessários conhecimentos de razão, interpretação de problemas e por se tratar de uma área da geometria, espera-se que o aluno tenha conhecimentos básicos de tal matéria.

 7.      O ensino da trigonometria pode ser abordado de forma diferente das propostas do livro didático?

Sim, a trigonometria pode ser tratada em oficinas para construir um ciclo trigonométrico com um material concreto, por exemplo. Também pode ser abordada com jogos para uma melhor fixação do conceito e até mesmo fazer uma.

[mamiplsmd-blog]

Aula 19 - Funções Trigonométricas Inversas

A atividade consiste em: “Criar um olho (círculo preto pequeno no interior de círculo branco grande) que se encontra sempre voltado para o cursor do mouse.”

Para fazer essa aplicação é necessário usar algo parecido com a atividade feita anteriormente que consistia numa bola aparecendo um retângulo no meio da tela de acordo com onde estivermos na tela, mas agora usando funções trigonométricas. Primeiramente, temos que ter duas variáveis para as posições, elas serão distancia do mouse até o centro da tela que ficara um circulo onde estará o olho. Após isso será criado um angulo a partir dessas variáveis, esse angulo será o valor em graus do retorno da função atan2() que irá retornar a tangente resultante e com isso calcular o angulo(esse angulo indo de 0 à 360). Após isso é necessário fazer elipses que acompanharam o mouse , elas terão que ir em posições do centro da tela até os limites. Assim, elas serem de um limite multiplicado pelo cosseno na posição x e a posição y pelo seno do angulo, já que esse limite funciona como a hipotenusa.

Para esse olho não sair do circulo do meio deve-se limitar o tamanho dessa distancia (limite) e testando eles o limite máximo que ficou foi de 75, em que não sai do circulo do meio. Para as cores dos olhos usei uma aplicação feita em sala que usa cores HSB para de acordo com o angulo formado é emitido uma cor.

Aplicação Final.

[thaisluciomami]

Atividade 18 - Olho.

A atividade pede para criar um olho que siga a posição do mouse na tela.

Primeiro vamos desenhar as esferas necessárias para criar o olho.

Agora é necessário descobrir a tangente do ângulo das posições mouseX e mouseY da tela e depois calcular a cotangente que vai gerar os valores em radianos. E para estar centralizado é preciso somar o valor da metade do tamanho da janela que estamos usando como tela.

Depois usando as coordenadas polares desenvolvidas em sala (p2cX e p2cY) para calcular o Seno e o Cosseno. Seno será a coordenada horizontal e Cosseno será a coordenada vertical da elipse.

Mas ainda vai ficar fora, é preciso somar metade do tamanho da janela tanto na posição horizontal quanto na posição vertical. Por fim, vamos criar uma condição para caso o raio seja maior que o tamanho da esfera maior ele permanecer nele, fazendo assim a espera menor nunca sair de dentro da outra e mesmo assim continuar acompanhando o movimento do mouse

Este é o resultado:

Código:

https://drive.google.com/drive/folders/1jY5glqQ8wbWXnoiQfHiL1Zw3rzktgvj_?usp=sharing

[musicoviniciusrodrigues]

Seno, cosseno, tangente

Seno, cosseno e tangente são elementos que compõem  o conhecimento geométrico. Saber para que serve, como utilizar e calcular é fundamental para que se obtenha um conhecimento abrangente em trigonometria. O texto a seguir aborda esse assunto, espero que ele contribua para a sua aprendizagem.

O que é seno, cosseno e tangente?

Seno, cosseno e tangente são razões trigonométricas obtidas por meio das relações existentes entre os lados de um triângulo retângulo. Lembre-se que esse tipo de triângulo possui:

Um ângulo medindo 90°.

Dois catetos e uma hipotenusa.

Observando a figura é possível notar que a hipotenusa sempre está oposta ao ângulo de 90°, e que os segmentos de reta que formam o ângulo de 90° são os catetos.

Fórmulas do seno, do cosseno e da tangente

As fórmulas gerais do seno, cosseno e tangente estão descritas a seguir:

SENO

Descrição: Seno é a razão trigonométrica estabelecida em um triângulo retângulo entre o cateto oposto e a hipotenusa.

COSSENO

Descrição: Cosseno é a razão trigonometria estabelecida em um triângulo retângulo entre o cateto adjacente e a hipotenusa.

TANGENTE

Descrição: Tangente é a razão trigonométrica estabelecida em um triângulo retângulo entre o cateto adjacente e a hipotenusa.

Obs. α pode assumir qualquer valor em graus do ciclo trigonométrico e também pode assumir valores em π rad, ou seja, pi radianos.

Como identificar um cateto oposto e um adjacente?

Para responder a essa pergunta devemos voltar os nossos olhos para os ângulos agudos internos do triângulo retângulo.

Veja que cada ângulo foi nomeado com uma letra grega. O cateto oposto e o adjacente para cada ângulo são segmentos de reta diferentes, mas a hipotenusa sempre será o mesmo segmento de reta.

Para você compreender como identificar o cateto oposto e o adjacente, observe os segmentos de retas que são utilizados em cada razão trigonométrica.

Ângulo α

Ângulo β

Seno, cosseno e tangente dos ângulos notáveis

Os ângulos considerados notáveis são: 30°, 45° e 60°. Isso porque esses ângulos aparecem com maior frequência no cálculo trigonométrico .

Confira na tabela a seguir os valores numéricos que esses ângulos notáveis assumem ao calcularmos o seno, o cosseno e a tangente.

Com a frequente utilização dessa tabela você irá memorizar os valores. Caso você tenha dificuldade na memorização, poderá aprender a canção a seguir ou no tópico seguinte descubra como encontrar os valores dos ângulos notáveis por meio de cálculos matemáticos.

Canção ângulos notáveis

Obtendo os valores dos ângulos notáveis por meio de cálculos matemáticos

Para demonstrar como obter os valores do seno, cosseno e tangente para os ângulos notáveis, esboce inicialmente um triângulo equilátero. Lembre-se que: o triângulo equilátero possui todos os lados com a mesma medida e todos os ângulos medem 60°.

Em seguida iremos determinar a altura desse triângulo, para isso trace a bissetriz do ângulo (A). Essa bissetriz irá de encontro ao seguimento de reta (CB). A bissetriz será a mediana, e a mediana determinará o ponto médio do seguimento de reta (CB).

Temos então que:

Obs. O triângulo equilátero possui todas as propriedades e características específicas que permitem que a altura, bissetriz e mediana sejam o mesmo seguimento. É importante ressaltar que existem muitos outros casos na geometria em que isso não ocorre.

Iremos agora determinar a altura desse triângulo aplicando o Teorema de Pitágoras no triângulo ACD, acompanhe:

Para obtermos os valores referentes aos ângulos notáveis, considere somente um dos lados do triângulo representado anteriormente.

Aplicaremos agora as fórmulas do seno, cosseno e tangente já apresentadas anteriormente.

Após descobrirmos os valores numéricos do seno, cosseno e tangente para os ângulos notáveis 30° e 60°, falta descobrirmos para 45°. Para obter os valores referentes ao seno, cosseno e tangente desse ângulo precisaremos desenhar um quadrado e traçar a sua diagonal, veja:

Um quadrado possui todos os quatro ângulos internos medindo 90°. Ao traçarmos a diagonal(d) do quadrado, dividimos o ângulo de 90° pela metade, ou seja, os novos ângulos passam a ter 45°.

Iremos aplicar o Teorema de Pitágoras para descobrir o valor da diagonal do triângulo ABC em termos de (a).

Com o valor da diagonal/ hipotenusa e os catetos em termo de (a), conseguimos calcular o seno, cosseno e tangente de 45°, acompanhe:

Caso você não consiga memorizar os valores correspondentes aos ângulos notáveis, agora ao menos já sabe calculá-los.

Como saber quando usar seno cosseno e tangente

A imagem ilustra a utilização do triângulo em uma das pontes mais famosas do mundo, a Golden Gate, nos Estados Unidos (Foto: depositphotos)

Utilizaremos seno, cosseno e tangente quando precisarmos encontrar a medida referente a qualquer um dos lados do triângulo retângulo ou quando precisamos saber a medida dos ângulos agudos internos.

A estrutura dos triângulos é amplamente usada na construção de objetos e estruturas, podendo ser facilmente encontrada na construção civil. Isso porque o triângulo é considerado uma figura geométrica rígida, ou seja, que não se deforma facilmente. Com isso, toda a construção que possui triângulos em sua estrutura é uma construção mais estável.

Lembre-se que por meio dos conceitos geométricos é possível obter-se triângulos retângulos em qualquer outro triângulo.

Saber utilizar o seno, cosseno e tangente, pode lhe ajudar caso um dia você precise construir ou modelar algo e opte pelo modelo geométrico do triângulo. Você saberá como encontrar a medida dos ângulos e dos lados desse triângulo.

Espero que esse texto tenha contribuído para que você compreenda melhor o tema. Bons estudos!

Referências

» LEZZI, Gelson; MURAKAMI, Carlos (2004). Fundamentos de Matemática elementar 3, trigonometria. Editora atual.

O post Seno, cosseno, tangente apareceu primeiro em Estudo Prático.

Seno, cosseno, tangente publicado primeiro em https://www.estudopratico.com.br

[editalenem]

Como aprender operações com frações

As frações são temas recorrentes no Enem, pois fazem parte da matemática – uma das disciplinas cobradas no exame.

Se você não lembra mais como aprender operações com frações, confira um resumo do assunto neste artigo!

Índice

* História das frações

* Como aprender operações com frações

* Como utilizar as frações em nosso dia-a-dia

* Matemática, frações e o Enem

* Exemplo de questões do Enem sobre frações

* Macetes para você se dar bem na matemática no Enem

História das frações

Diz-se que no Antigo Egito no ano 3.000 antes de Cristo, as terras das margens do Rio Nilo foram distribuídas pelo faraó Sesóstris a alguns agricultores.

Essas terras eram privilegiadas porque anualmente no mês de julho, as águas do próprio Rio Nilo alagavam a região e fertilizavam os campos.

Depois que as águas baixavam, era necessário remarcar as propriedades de cada agricultor pelos agrimensores ou também chamados de estiradores de corda.

As cordas eram hasteadas em todo o terreno, mas nem sempre cabiam inteiras neles. Os egípcios então descobriram o número fracionário (que era igual a 1), representado por um sinal oval em cima do denominador.

Esses símbolos foram ser vistos muitas vezes nas representações de medida dos egípcios. Tempos depois os hindus criaram o Sistema de numeração decimal, representando as frações pela razão e dois números naturais.

As frações passaram a ser usadas na resolução de diversos problemas matemáticos no mundo todo, em diferentes culturas e países.

Como aprender operações com frações

É possível aplicar as quatro operações matemáticas nas frações: a subtração, a divisão, a soma e a multiplicação.

Como fazer adição e subtração de frações?

Adição

Para somar as frações, é necessário identificar primeiramente se os denominadores são iguais ou diferentes.

Se forem iguais, basta repeti-los na operação, somando os numeradores.

Mas se forem diferentes, você precisará encontrar o mesmo denominador comum, através do MMC (mínimo múltiplo comum).

Confira os exemplos: 3/8 + 4/8 = 7/8

2/3 + 4/5 = 3.4 + 2.5/15 = 22/15

Subtração

Na subtração entre frações, é o mesmo princípio. Se os denominadores forem comuns, basta subtrair os numeradores.

Se forem distintos, deve-se também encontrar o mínimo múltiplo comum.

Multiplicação

Como aprender operações com frações na multiplicação? Basta multiplicar os numeradores e denominadores entre si, revelando o resultado da fração.

3/4 X 2/5 = 6/20

4/5 X 3/6 = 12/30

Divisão

Para dividir as frações, basta multiplicar a primeira fração com o inverso da segunda, invertendo o numerador e o denominador da segunda fração.

3/5 : 4/6 = 3/5 x 6/4 = 18/20

Como utilizar as frações em nosso dia-a-dia

Quando você for pensar em dividir um alimento em partes iguais, contar dinheiro ou simplesmente fazer uma prova ou vestibular, você vai se lembrar de como aprender operações com frações!

Se aplicarmos a matemática em nosso cotidiano, nossa relação com essa matéria tão polêmica e complexa mudará drasticamente.

Nenhuma disciplina deve ser aprendida isoladamente, como se fosse algo distante de nossa rotina. Isso vale não só na matemática, como também na Física, Química, Biologia, Português e etc.

Matemática, frações e o Enem

Prepare-se para estudar os assuntos que mais caem no Enem em matemática além das frações:

– Problemas de primeiro e segundo grau

– Grandezas proporcionais e médias algébricas

– Funções de segundo grau e inequações matemáticas

– Porcentagem e a matemática financeira

– Noções de Estatística básica

– Problemas de probabilidade

– Área de figuras: planas, polígonos, geometria

– Análise combinatória de números

– Circunferência

– Aritmética

– Cilindros

– Gráficos e cônicas relacionados ao Enem

– Funções trigonométricas seno, cosseno e tangente

– Geometria espacial

– Logaritmos

– Paralelepípedos

– Potências e conjuntos numéricos

– Retas

– Triângulos e polígonos regulares

– Troncos

– Sequências numéricas

Esses são os assuntos que mais caem nas provas de matemática no Enem, mas o candidato precisará também mandar bem na interpretação de texto em todas as disciplinas do exame.

Exemplo de questões do Enem sobre frações

Citaremos aqui alguns exemplos de questões do Enem sobre frações.

Exemplo 1 – Em determinado país, os trabalhadores recebem dois salários mínimos no mês de dezembro: o salário inteiro e o 13º. Se um funcionário trabalhou os 12 meses do ano, os salários recebidos serão iguais.

Se alguém trabalhou apenas uma fração no ano, o 13º salário irá corresponder a essa fração do salário normal. Se o salário normal de um funcionário é 516 reais e ele trabalhou 7 meses no ano, quanto ela vai receber de 13º salário?

Resolução: se um determinado funcionário não trabalhou o ano inteiro que é 12 meses, ele trabalhou apenas 7. A fração que corresponde a esse exemplo é 7/12 avos.

Na situação foi informado que o funcionário recebe partes iguais de salário e décimo terceiro, este em específico receberá 7/12 do seu salário normal.

Se o valor do salário é 516 reais, para descobrir o valor do 13º, devemos calcular:

– 7/12 : 516 = 516 : 12 = 43 x 7 = 301.

Podemos entender então que o valor do 13º salário recebido pelo funcionário será de 301 reais, correspondentes aos 7 meses do ano.

Exemplo 2- João Carlos é operário e seu salário é de apenas 520 reais por mês. Ele gasta ¼ com aluguel e 2/5 com a alimentação da família.

Nesse mês ele teve uma despesa extra de 3/8 destinados aos remédios. Devemos saber então se sobrou algum dinheiro do salário de João.

Precisamos descobrir se o salário de João é o suficiente para pagar as despesas dele de aluguel, alimentação e remédios.

1/4 de 520 = 520 : 4 x 1 = 130.

2/5 de 520 = 520 : 5 x 2 = 208.

3/8 de 520 = 520 : 8 x 3 = 195.

Agora basta somar todas essas despesas: 130 + 208 + 195 = 533 – 520 = 13 reais.

Portanto, não sobrou nada do salário de João, pelo contrário, faltou 13 reais para o pagamento de suas despesas.

Exemplo 3- Enem 2011 – O pantanal é um dos mais valiosos patrimônios naturais do Brasil.

É a maior área úmida continental do planeta – com aproximadamente 210 mil km quadrados, sendo 140 mil km quadrados em território brasileiro, cobrindo parte dos estados de Mato Grosso e Mato Grosso do Sul.

As chuvas fortes são comuns nesta região. O equilíbrio desse ecossistema depende, basicamente, do fluxo de entrada e saída de enchentes.

As cheias chegam a cobrir até 2/3 da área pantaneira. Durante o período chuvoso, a área alagada pelas enchentes pode chegar a um valor aproximado de:

91,3 mil km quadrados

93,3 mil km quadrados

140 mil km quadrados

152,1 mil km quadrados

233,3 mil km quadrados

Resposta certa: letra c. Resolução:

210 mil km quadrados de área total

2/3 é o valor que as cheias cobrem a área

210.000 . 2/3 = 420.000/3 = 140 mil km quadrados.

Exemplo 4 – Enem 2016 – No tanque de um certo carro de passeio cabem até 50 litros de combustível, e o rendimento médio deste carro na estrada é de 15 km/L de combustível.

Ao sair para uma viagem de 600 km o motorista observou que o marcador de combustível estava exatamente sobre uma das marcas da escala divisória do marcador, ente ½ e 1/1 no carro.

Como o motorista conhece o percurso, sabe que existem, até a chegada do seu destino, cinco postos de abastecimento de combustível, localizados a 150 km 187 km, 450 km, 500 km e 570 km do ponto de partida.

Qual a máxima dist��ncia, em quilômetros, que poderá percorrer até ser necessário reabastecer o veículo, de modo a não ficar sem combustível na estrada?

570

500

450

187

150

Resposta certa: letra b. Resolução:

Cerca de ¾ do tanque estão cheios. Precisamos saber quantos litros correspondem a essa fração. Já que o tanque cabe 50 litros, então vamos encontrar ¾ de 50:

O rendimento do carro é de 15 km com 1 litro, então basta fazer a regra de três.

15 km ———– 1 litro

X —————— 37,5 km

X=15 . 37,5

X= 562,5 km

Entende-se então que o carro poderá percorrer 562,5 km com o combustível presente no tanque. A distância máxima que deverá ir será de 500 km até o próximo posto.

Exemplo 5- Enem 2017 – Em uma cantina, o sucesso de vendas no verão são sucos preparados à base de polpa de frutas.

Um dos mais vendidos é o de morango com acerola, que é preparado com 2/3 de polpa de morango e 1/3 de polpa de acerola.

Para o comerciante, as polpas são vendidas em embalagens de igual volume. Atualmente, a embalagem da polpa de morango custa R$ 18 e a de acerola R$ 14,70. Porém, está prevista uma alta no preço da embalagem da polpa de acerola no mês seguinte, que será de R$ 15,30.

Para não aumentar o preço do suco, o comerciante negociou com o fornecedor uma redução no preço da embalagem da polpa de morango. A redução em real, no preço da embalagem da polpa de morango deverá ser de:

1,20

0,90

0,60

0,40

0,30

Resposta certa: letra e. Resolução:

Com dois terços do volume da embalagem, tem-se 23 x 18 = 12 reais. Adicionamos um terço do volume da embalagem da polpa da acerola, 1/3 x 14,70 = 4,90.

12 + 4,90 = 16,90.

Aumentando-se o preço da polpa da acerola a 0,60 centavos, o custo passa a ser de:

1/3 x 15,30 = 5,10

O preço gasto com o morango será: 16,90 – 5,10 = 11,80, representando 2/3 x = 11,80 sendo x = 17,70. A diminuição foi de 0,30 centavos.

Macetes para você se dar bem na matemática no Enem

Nunca se sabe ao certo o que vai cair nas provas de matemática do Enem, não é mesmo?

Além de buscar como aprender operações com frações, os estudantes precisam se empenhar um pouco mais em outras questões do exame.

Confira alguns macetes que podem te salvar na prova de matemática do Enem!

Sinais

– Na multiplicação de sinais iguais, o resultado é positivo.

– Na adição, some os sinais iguais e mantenha-os.

– Com sinais diferentes, subtraia e mantenha o sinal do maior número.

– Multiplicar potências de 10: pense sempre na vírgula, onde o número de casas a serem deslocadas para a direita é igual ao expoente da potência 10.

– Multiplicação pela propriedade distributiva: decomponha os números em múltiplos de 10, multiplique os fatores obtidos pelo outro número disposto, depois some os resultados.

– Fórmula dos juros simples: J = C.i.t

J= juros

C= capital

T= tempo

Para memorizar facilmente a fórmula, pense na palavra Jota City.

– Leia bastante, faça exercícios complementares

– Tire as suas dúvidas com professores, orientadores, amigos e colegas.

– Escreva resumos de tudo o que aprender para reler e estudar depois.

– Monte um cronograma de estudos diários, semanais e mensais.

– Leia o edital do Enem.

– Não chegue atrasado no dia da prova, programe o seu percurso.

As notas adquiridas no Enem, podem ser usadas como portas de entrada em universidades públicas e privadas do país.

Milhares de estudantes já conseguiram bolsas de estudo parciais e totais pelo ProUni – Programa Universidade para Todos, Financiamento Estudantil – FIES, e no Sistema de Seleção Unificada – SISU.

O post Como aprender operações com frações apareceu primeiro em Edital do Enem 2020.

from WordPress https://ift.tt/2TVLnkZ via IFTTT

[olimpiorodrigues]

Como como calcular seno, cosseno e tangente

[rayane1001]

Em calculo um, estuda-se limites. Limites é um conceito bem abstrato em matemática, apesar de ser bem simples imaginar a existência de limites. Limites é basicamente um assunto onde se aprender a fazer cálculos envolvendo infinitos e números do grupo dos reais. Os números reais são uma abstração interessante, pois o que os números reais expressam é o conceito de que, entre zero e um, existem infinitos números. Essa abstração é resolvida com o conceito de limites laterais, onde que usa-se uma simbologia capaz de saber se o limite é atingido pela esquerda (negativo) ou pela direita (positivo). Simples imaginar isso, porém complexo fazer cálculo com isso.

A partir dai que entra a sacada do cálculo de limites envolve o fato de que não é possível fazer cálculos com infinitos ou com polinômios, funções racionais ou irracionais, que tenha como solução o zero como denominador ou numerador, ou o zero em ambos os casos. Para solucionar esse conflito de indeterminação, é necessário a aplicação de conceitos matemáticos que eliminem a indeterminação e chegue a um resultado concreto, por mais que o resultado seja o próprio infinito, negativo ou positivo, e que não se saiba o que ele realmente seja.

Basicamente, é preciso observar a função limite e primeiro substituir a tendência do limite no valor da variável. Se o resultado desse cálculo for zero, no denominador e numerador, é preciso eliminar a indeterminação nos dois lugares da função. Caso a indeterminação se dê somente no denominador ou somente no numerador, então a indeterminação deve ser eliminada somente nesse lugar específico. Feito essa análise a partir das possibilidades de resultado, então inicia verdadeiramente o cálculo de limites. 

Caso o limite seja composto somente de numerador, ou seja, que o denominador seja 1, então a estratégia a usar é a fatoração, de acordo a maior potência da variável. Essa fatoração pode ser de acordo com o modelo de potência ao quadrado, ao cubo ou à quarta. Esse modelo de fatoração, para os três modelos, é decorado, pois não é necessário calcular como se chega ao padrão.

Outra possibilidade de limites é quando envolve raíz, no denominador. Pois, nessa situação, a opção é racionalizar. Essa racionalização se dá multiplicando pelo oposto dos elementos contidos dentro da raíz, tanto no numerador quanto no denominador. Feito isso, elimina-se a raiz e, geralmente, elimina-se também a indeterminação. Caso a indeterminação se mantenha, ainda se faz necessário fatorar ou manter algum elemento em evidência a fim de eliminar essa indeterminação.

Há também o cálculo de limites envolvendo funções trigonométricas, como seno, tangente e cosseno. Para se cálculo essa tipologia de limites é necessário transformar a função dada colocando em evidência a função fundamental. Feito isso, caso a função fundamental seja do tipo seno, então ela possui valor de 1, caso o limite tenda a 0, pois seno de 0 é 1. Caso seja a função fundamental do tipo cosseno, então ela possui o valor de 0, pois o cosseno de 0 é 0.

Cálculo limites

[2018]