#linear graphs

[the-chemistry-side-of]

Graphing Linear Functions

Last time I went over the general concept of graphing; here I will go over the graph of a line. The general equation of a line is y=mx+b, where m is the slope of the line and b is the y-intercept of the line. The slope is how much the y variable changes for a corresponding change in x. For example, if the slope is 2, then the y variable increases by two units for every one unit increase in the x…

[chikoyama]

3, 4, 5, 13, 16

Romance & Relationship Headcanons

3. has your muse been mainly attracted to men, women, non-binary people, another identity not specified, or an even split (between two, many, or all of the options specified)?

Uhm... just to preface: I don't really think Chiyori distinguishes between gender like that. She doesn't care if a person identifies as man or woman, or whatever. As long as she feels safe around them, and they’re genuienly nice and fun to be around, and are able to take decently care of themselves, she's not going to be picky.

Though, to answer the question using normative gender terms: So far, Chiyori has mostly been attracted to people identifying as men, but she's also had fleeting crushes on women in the past. To be honest though, some women could make it to the list very soon!

But basically, gender is not an important factor for Chiyori to be attracted to someone. In fact, in her world it's not a factor at all, because a human is a human, you know? What matters to her is whether or not that person is nice. Most likely Chiyori would just reciprocate whatever efforts are made towards her.

4. does your muse find any specific features particularly attractive?

In terms of physical attributes, probably hands and forearms, because those would be the main body parts someone would use to display their affections towards her. She'd likely observe the manner of which that person uses their hands. Are they gentle, are they rough? Are their movements attentive, playful, unpredictable? A mix? Depending?

For personal traits, Chiyori is attracted to people able to display mastery of gentle assertiveness. While capable of handling herself most of the time, Chiyori definitely do experience moments of doubt, so she’d need someone able to both ground and believe in her. Someone to give her a gentle nudge forward when they notice that she's about to get lost in her own head.

5. what is your muse's ideal first date?

Mhmm… for Chiyori, it’s more about the execution, I think. As long as it's an activity that doesn’t hinder the opportunity to start interesting conversations, or prevent her from randomly share what's on her mind, then it should be good.

For example bungee jumping, or swimming with sharks would be too wild, lol, and going to the cinema is just awkward, because they wouldn't be able to talk during the movies.

Though, depending on her mood, and the other person, a first date at a café/restaurant can be just as enjoyable as a date at an amusement park, or an aquarium. Basically, something relatively chill and low-profile.

13. what traits does your muse value in a romantic partner?

Open-mindedness, attentiveness and playfulness. Maybe someone willing to challenge her and indulge her in her curiosities.

16. what is/are your muse's love language(s)?

Chiyori values quality time. Everything else shares a solid second place spot.

[art-of-mathematics]

Perhaps some people might have a lot of fun with detangling this cryptic "brain knot clot" of odd metaphor soup....

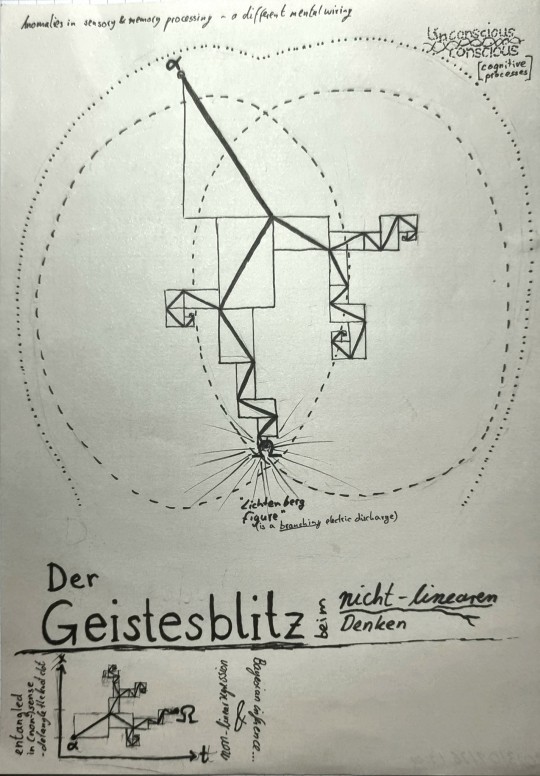
"Geistesblitz" is German and describes an Eureka-Moment. I like this German word, because it contains the word "Blitz" - which translates to "lightning bolt" or "flash". This reminds me of the Lichtenberg figures.

Lichtenberg figures are branching electric discharges with fractal properties:

On this website is a great video/gif showcasing Iichtenberg figures burned into a wood table:

[please, everyone reading this, do not attempt to reproduce Lichtenberg figures; the amount of voltage needed kills]

----

For the topic of non-linear/divergent thinking I found this German website helpful and well-summarized. (Unfortunately it is only available in German.)

---

The alpha and omega in my drawing represent "point A" - the starting point of thought, and "point B" - the final thought. The branching plot between these points describes the "detours" into partially related topics to "point A/staring thought" - the core feature of divergent thinking. Often this kind of thinking appears merely incoherent.

In short, this branching plot just illustrates a non-linear train of thought, which disperses into many other detours of thought - that feed back - or loop back to the previous or main train of thought.

This is literally the behavior of a chaotic system.

[a9saga]

i don’t remember leaving this answer on quora over a year ago

[tenderflint]

currently listening to sleeping with sirens and playing coolmathgames. how well are YOU coping

[industrialorganiser]

Y'all need more dimensions

[math-journal2]

<— Unit 4: Part 2 — Unit 5 —>

Inequality Graphing Steps

Graphing Inequality

Page 11 —>

[wingedcatgirl]

30 Day Tales of Symphonia Challenge

7. Favorite Couple

I admit I don't have strong feelings about pairings in this setting. Honestly, I don't have strong feelings about pairings in any setting (I've seen fics that executed their pairing badly, but I've never seen a pairing that I thought couldn't make sense)

Most fandoms could do with more F/F though, I think. And/or polyamory.

[math-journal]

[faggot-friday]

all maths past a year 5 level should die forever and ever actually

[b4b31]

All 25 algorithms: HOW TO NAVIGATE

SEARCHING:

Linear Search: Imagine you have a bunch of love letters, and you want to find a specific letter from someone special. You start by looking at the first letter and check if it's the one you're looking for. If it's not, you move on to the next letter and keep going until you find it or reach the end of the letters.

Binary Search: Your collection of love letters are arranged in alphabetical order. Binary search is like playing a guessing game where you try to find a secret love letter. You start by guessing the letter in the middle. If your guess is too late in the alphabet, you know the secret letter must be in the earlier part of the collection. If your guess is too early, you know the secret letter must be in the later part. You keep dividing the collection in half and guessing until you find the secret love letter.

Depth First Search: In your stack of love letters from different people you are going through each letter and exploring deeply before moving on to the next letter. If you find a reply or another love letter within a letter, you read and explore that before continuing with the rest of the stack.

Breadth First Search: In a box full of love letters from different people you are going through all the letters from the same sender before moving on to letters from other senders. You explore all the letters from one person, then move to the next person and explore their letters, and so on.

SORTING:

Insertion Sort: You want to arrange a messy pile of love letters in order of the senders name. With insertion sort, you start with an empty hand and pick one letter at a time from the messy pile. Each time you pick a letter, you put it in the correct position in your hand among the letters you've already sorted.

Heap Sort: You want to sort a big pile of love letters, based on the date they were written. Heap sort is like organizing the letters by putting the most recent one at the top. You keep picking the most recent letter and putting it in a separate pile until all the letters are sorted.

Selection Sort: You want to arrange a stack of love letters from different people in order of the length of the letter. With selection sort, you start by finding the shortest letter and put it aside. Then, you find the next shortest letter and put it next to the first one. You keep doing this until all the letters are arranged by length.

Merge Sort: You want to sort a big collection of love letters from different people, based on the emotions expressed. With merge sort, you divide the collection into smaller groups, sort each group individually based on emotions, and then merge them back together in the correct order. You keep dividing, sorting, and merging until all the letters are sorted.

Quick Sort: You want to sort love letters, based on the intensity of love expressed. With quick sort, you pick one letter as a "special letter" called the base. Then, you divide the line into two groups: letters with less intense expressions of love and letters with more intense expressions. You repeat this process for each group until all the letters are sorted.

Counting Sort: You want to sort a collection of love letters from different people, based on the number of words. Counting sort is like counting how many letters have a specific number of words and then putting them in order.

GRAPHS:

Kruskal’s Algorithm: Imagine you have a map with different locations connected by lines, and you want to build the shortest possible network of lines between all the locations. This algorithm helps you select and connect the lines in a way that forms the minimum spanning tree, which means the total length of the lines is minimized.

Dijkstra’s Algorithm: Think of a map with different locations and lines connecting them, and you want to find the shortest path from one location to another. This helps you find the path with the minimum total distance. You start at one location and keep moving to neighboring locations, always choosing the path with the shortest distance until you reach the destination.

Bellman-Ford Algorithm: Imagine a treasure map with different paths and each path having a certain cost. This algorithm helps you find the shortest path to the treasure by considering the costs of the paths. You keep comparing and updating the total cost of reaching each location until you find the shortest path.

Floyd-Warshall Algorithm: Picture a map with different routes connecting the locations, and you want to find the shortest path between all pairs of locations. This algorithm helps you calculate the shortest path between any two locations in the most efficient way. It considers all possible paths and updates the distances until it finds the shortest paths between all pairs of locations.

Topological Sort Algorithm: Imagine you have a list of tasks, and some tasks depend on others. This sort helps you order the tasks in such a way that no task depends on another task that comes later in the order. It ensures a proper sequence for completing the tasks without any dependency issues.

Flood Fill Algorithm: Picture a coloring book with different shapes. This algorithm helps you fill a shape with a specific color. You start by selecting a shape and filling it with the desired color. Then, you move to neighboring shapes and fill them if they are the same color as the starting shape. You continue this process until you’ve filled all the connected shapes with the chosen color.

Lee Algorithm: Imagine you have a maze, and you want to find the shortest path from the starting point to the end point. This algorithm helps you explore the maze step by step to find the shortest path. You start at the beginning and keep moving to neighboring cells, marking them with the number of steps taken until you reach the destination.

ARRAYS:

Kadane’s Algorithm: Imagine you have an array representing the number of posts baked each day. This algorithm helps you find the longest consecutive period of baking the most posts. You start with the first day and keep adding the posts counts, but if the sum becomes negative, you start over with the next day, searching for the longest streak of baking the most posts.

Floyd’s Cycle Detection Algorithm: Picture an array of post reviews, where each element represents a unique review. This algorithm helps you find if there is a repeating pattern of reviews in the array. You have two pointers—one moving slowly and another moving faster. If the pointers meet, it means there is a repeating pattern of reviews in the array.

Knuth-Morris-Pratt Algorithm: Imagine you have an array representing a series of post ingredients, and you want to find occurrences of a specific ingredient pattern within the array. This algorithm helps you efficiently find instances of the ingredient pattern within the array. It uses a smart way of skipping unnecessary ingredient comparisons based on previously matched patterns, helping you identify the relevant occurrences efficiently.

Quick Select Algorithm: Picture an array of posts sizes, and you want to find the post size that ranks at a specific position when the array is sorted. Quick select algorithm helps you find the post size at the desired position efficiently by partitioning the array based on pivot elements (post sizes), narrowing down the search space iteratively until the desired position is found.

Boyer-Moore Majority Vote Algorithm: Imagine you have an array of post flavors, where each element represents a flavor preference. This algorithm helps you find the most popular post flavor within the array—the flavor that appears more frequently than any other. It iterates through the array, canceling out pairs of different flavors, and the majority flavor eventually remains as the most popular one.

BASICS:

Huffman Coding Compression Algorithm: Imagine you have a collection of love letters, and you want to send them to your sweetheart with reduced file size to save storage or transmission space. This algorithm helps you compress the letters by assigning shorter codes to the most frequently used letters or words, and longer codes to the less frequent ones. This way, you can represent the love letters using fewer bits, making them more efficient to store or send.

Euclid's Algorithm: Picture a scenario where you have a huge archive of posts that you want to distribute equally among your blogs. This algorithm helps you find the largest possible number of posts you can distribute, ensuring each blog gets an equal number without any posts left over. You keep dividing the posts into smaller groups until you can no longer divide them evenly, ensuring a fair distribution.

[maccadeau]

i may have been wrong about the suicide devil (re: falling devil) but at least i was right about asa being a kms enjoyer

[varunrajkalse]

6 Algorithms Every Developer Should Know

6 Algorithms Every Developer Should Know As a developer, it is essential to understand algorithms to create efficient and scalable software applications. Algorithms are sets of instructions that perform a specific task, such as sorting data or searching for information. By learning about these six essential algorithms, you can improve your coding skills and create better applications. By…

[pteren]

ever seen this gizmo below a tumblr post? (you'll need to be using a browser)

the reblog tree tab is one of the first things i noticed when i joined tumblr. it shows a graph of all a post's reblogs, branching out from the root post. i was disappointed to learn that it's almost useless for any potentially interesting shenanigans, due to some major limitations (it's hard to click on individual posts, there's no way to prune the tree or filter out results you aren't interested in, you can't search for posts you ARE interested in, trees with lots of notes get laggy real fast if you try to render the whole thing, the display is way too small).*

this is really sad because there is so much potential in a tool like this. imagine if you could click on a node and only see responses to that post in the reblogs below. imagine if you could filter out empty reblogs (or ones with only tags) and see a whole network of pure and obscure tumblr discourse spread out before you like flourishing mycelium. imagine if you could count how many juicy notes hang from a specific branch.

i know there isn't much hope, but if @staff ever has one of those "bursts of motivation" i keep hearing about, i would LOVE to see this feature expanded upon.

*it is probably intended as some kind of demographic tool, where you can see which of your mutuals helped your post gain the most traction by counting how many people reblogged it from them. this is about the only thing the reblog tree is good for.

[this post is non-linear]

who says every piece of writing has to be a boring old line?? cool kids communicate via constantly branching trees of thought. allow me to demonstrate.

[a9saga]

Programming is boring.

[todays-xkcd]

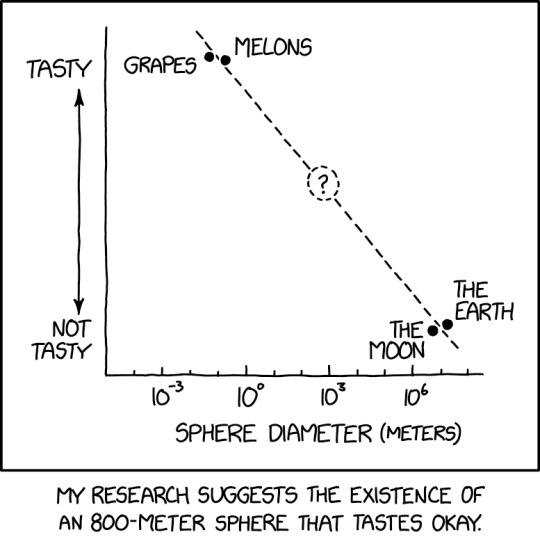
Baseballs do present a challenge to this theory, but I'm convinced we just haven't found the right seasoning.

Sphere Tastiness [Explained]

Transcript

[Graph with Y axis using and arrow indicating tastiness from "Not Tasty" to "Tasty" and X axis labeled "Sphere Diameter (meters)" with a logarithmic scale running from 10-4 to 108 (with 10-3, 100, 103 and 106 labeled).] [The graph contains two points points for "Grapes" and "Melons" at the "Tasty" end of the Y axis, between 10^-2 and 10^-1 meters, and two points for "The Earth" and "The Moon" at the "Not Tasty" end, both around 10^7 meters. A straight dashed line shows a linear interpolation between the points. There's a circle with a question mark about halfway between them.]

[Caption below the panel:] My research suggests the existence of an 800-meter sphere that tastes okay.