#integity

[professorgtnt]

The supreme quality for leadership is unquestionably integrity. Without it, no real success is possible.

[oneinteger-daily]

day 11 ! the first of many 1-numeral-only days

[realreadysetrose]

I’m afraid I can’t do that, Dirk

[nonotoff]

May not feel sexual/romantic attraction but that doesn’t mean we don’t exist

[weepingicegiant]

quick doodles

[zorionbbq]

guy who says heh-heh!

[eulerseverything]

I love math I wish numbers were real

[knightmareaceblue]

Cyberweek 2024 Day Five: Crossover

Pfft, I've been on an AvA kick recently, so I guess it's not too surprising that I chose this. On one hand, this crossover works well in theory. The stick figures are all fast, kinetic learners and really good at demonstrating their earned skills and knowledge.

On the other hand, the sheer tonal dissonance is hilarious.

[sufficientlylargen]

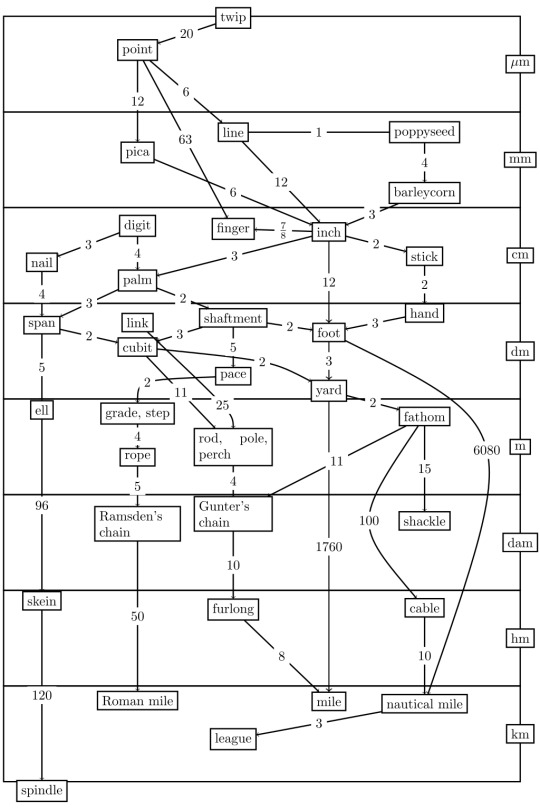
I've found my new favorite units chart (from wikimedia commons).

[fixing-bad-posts]

gawain updates?

the king hath made a knight of me

[icy-saturday]

Happy New Year from my beloved companions :) 🔢🪺🛰️💕

[jimmerzz0905]

lalalalala

whatever… go my algebralien oc except they’re not really an algebralien because they’re a robot who was originally built to “reincarnate” a dead variable who couldn’t be revived but ended up becoming their own person and has a bunch of people around them who care for and love them but develops really bad identity issues (and is also vaguely autistic-coded)

more about them can be read here!

[oneinteger-daily]

day TWO!

no, i did not survive tpot 15 either . thanks for asking

[8ftfurby]

Evil critters

[ozdical]

wip :]

[positivelyprime]

Eisenstein primes (and integers)

You've heard of integer primes, but have you heard of different kind of primes? One of the most beautiful pictures in mathematics I've recently seen is this:

This is a picture displaying the Eisenstein primes and the rest of the post will be me explaining where this comes from.

Firstly, to understand what Eisenstein primes are, we need to know what Eisenstein integers are! An Eisenstein integer is a complex number of the form z = a + b w where a,b are integers and w = e^(2/3 pi i). Normally a small letter omega is used instead of w. Notice that w is a third root of unity, i.e. w³ = 1.

Appending this complex w to the regular integers has some consequences. In particular, we can now view the eligible numbers on the complex plane to get this picture:

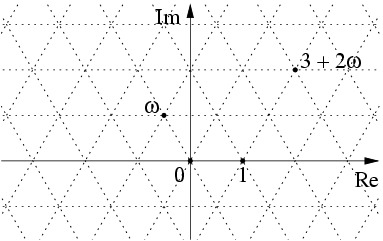
The Eisenstein integers correspond exactly to places where two dotted lines cross. As such, where normally one can view integers as laying on a 1-d line, we can now view Eisenstein integers as laying on a 2-d lattice!

Now one may start to wonder if, just like in the integers, one can have Eisenstein integers which are not divisible by other Eisenstein integers. In more mathematics: We call a number p an Eisenstein prime if p cannot be written as a*b where a,b are Eisenstein numbers which are not +-1, +-w, +-w² (the units in this system).

It turns out that some regular primes are still primes in the Eisenstein integers. For example, 2 can still not be decomposed. However, 3 can! We may write 3 = -(1+2w)(1+2w) which means that 3 is not an Eisenstein prime. One may investigate this further (using abstract algebra) to arrive at the picture at the top of this post. The 6-fold rotational symmetry is due to the Eisenstein integers having 6 units.

Of course a natural question is why take a third root of unity and not an nth root? This is a very interesting question and leads to the study of (integer rings of) cyclotomic fields! This concludes fun math fact tuesday