#Noether's Theorem

[tojskfarnijler]

[teachersource]

Emmy Noether was born on March 23, 1882. A German mathematician who made many important contributions to abstract algebra. She discovered Noether's Theorem, which is fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed some theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

[omegaphilosophia]

The Philosophy of Invariance

The philosophy of invariance examines the concept of constancy or unchanging nature within various contexts, including science, mathematics, ethics, and metaphysics. This philosophical exploration seeks to understand what remains constant amidst change and why such constancies are significant for our comprehension of reality, knowledge, and truth.

Key Concepts in the Philosophy of Invariance

Definition of Invariance:

Concept: Invariance refers to properties or principles that remain unchanged under specific transformations or conditions.

Argument: Identifying invariances helps in understanding the fundamental nature of systems and theories, providing a stable foundation for analysis and interpretation.

Invariance in Science and Mathematics:

Physical Laws: Many physical laws, such as the laws of motion and conservation laws, are considered invariant under transformations like time shifts or spatial rotations.

Symmetry: Invariance is closely related to symmetry in physics and mathematics. For example, the invariance of physical laws under certain symmetries leads to conservation laws according to Noether's theorem.

Mathematical Constants: Constants like π (pi) and e (Euler's number) are examples of invariance in mathematics, holding the same value across various contexts.

Invariance in Metaphysics:

Universal Principles: In metaphysics, invariance pertains to principles or truths that remain constant across possible worlds or different contexts.

Identity and Change: Philosophers explore how identity can persist over time despite changes, focusing on the invariant core that defines an entity.

Ethical Invariance:

Moral Principles: The idea that certain ethical principles are invariant, holding true regardless of cultural or situational differences.

Universal Ethics: This approach argues for the existence of universal moral truths that apply to all rational beings.

Theoretical Debates and Implications

Role of Invariance in Scientific Theories:

Concept: Invariance as a criterion for the validity and robustness of scientific theories.

Argument: Scientific theories that exhibit invariance under transformation are often considered more fundamental and reliable.

Philosophical Implications of Mathematical Invariance:

Concept: The philosophical significance of invariant mathematical properties and structures.

Argument: The constancy of mathematical truths supports the notion of an objective mathematical reality, independent of human perception.

Ethical Relativism vs. Invariant Ethics:

Concept: The debate between ethical relativism, which denies invariant moral principles, and invariant ethics, which upholds them.

Argument: While ethical relativism emphasizes cultural and contextual differences, invariant ethics seeks universal moral truths applicable to all.

Metaphysical Invariance and Identity:

Concept: The persistence of identity amidst change and the metaphysical basis for invariance.

Argument: Philosophers debate whether there are essential properties that remain invariant to preserve identity through change.

The philosophy of invariance explores the concept of constancy across different domains, from science and mathematics to ethics and metaphysics. By understanding what remains unchanged amidst transformations, this philosophical inquiry provides insights into the fundamental nature of reality, the stability of scientific theories, and the universality of ethical principles.

[dat-physics-gal]

You’ve fallen for my trap!

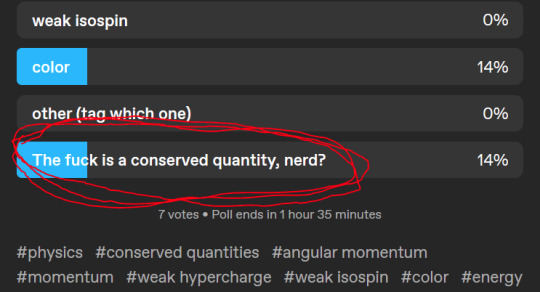
So, someone took that option in my poll, giving me an excuse to rant about conserved quantities, and Noether’s Theorem!

A conserved quantity is a mathematical value, which, over the course of a transformation, is, well, conserved.

These transformations range from coordinate transformations to processes, like decay or scattering.

I won’t go into the more complicated ones, like the weak hypercharge and isospin nor color, but i will explain how coordinate transformations and conserved quantities follow from one another. This fact was discovered by Emmie Noether, and it states that for every symmetry transformation of a system, a conserved quantity must exist which describes it.

A couple examples:

If a system’s equations don’t change with a translation in time, energy is conserved. If energy is conserved, the equations describing the systems are invariant under translations in time.

If a system’s equations don’t change with a translation in space, momentum is conserved, and vice versa once more.

An invariance to rotation about an axis corresponds to conserved angular momentum.

This theorem is well known among physicists, but it’s beauty is largely unknown to the wider public, and in many opinions, mine included, it’s actually the most beautiful result in all of physics.

Whenever there’s a conserved quantity, there’s a corresponding symmetry, and whenever there’s a symmetry, there’s a corresponding conserved quantity.

Always.

[spectrallysequenced]

Would people be interested in a video course on noncommutative algebra? The prerequisite knowledge would be linear algebra, basic group module theory and in the end some knowledge of Galois theory. Topics I might teach would include: Jacobson Radical Theory Central Simple Algebras Wedderburn-Artin and Wedderburn-Mal'tsev The Double Centraliser Theorem Noether-Skolem Theorem Brauer group Theory Crossed Products and Galois Theory Group Cohomology, briefly, and connection with the Brauer Group Further topics to be decided (Maybe Morita Theory, or more Brauer Theory).

[kaiasky]

#sadly this is very much not limited to cis people

(felt this was a good addition)

"girl math is when you go shopping using a credit card so it's basically free" "girl math is when you use the card with your boyfriends name so it's free" "girl math is when it's free if it's under $5" haha yeah girl math is when you're stupid and bad with budgeting and are always overspending on clothes because you're just a dumb helpless #girl haha I love rebranding the patriarchy as a fun #feminist trend does anyone else want to get off the ride I want to get off the ride now is there an option to get off the ride I never want to hear a cis person speak again please I want to get off the ride

[tanadrin]

Noether’s theorem implies any conservation law arises from a symmetry, e.g., angular momentum from rotational symmetry or energy due to time symmetry. Is the conservation of charge in electromagnetism due to gauge symmetry, or some other symmetry? I feel like I saw something like this mentioned somewhere once but Google is being unhelpful as usual.

[bayesic-bitch]

I am unreasonably annoyed by ada Lovelace being elevated to a household name. She had no actual lasting contributions to the field. For someone talked about as a mathematician, what theorems did she prove? For someone talked about as a computer scientist, what algorithms that we use now are her inventions? I've been studying computer science for a decade now and I have never once heard her name come up in an actual classroom, nor do I know anyone who has (at least, not for her actual contributions to the field, as opposed to the kinda-incorrect "first programmer" thing). She just didn't really *do* anything.

And if you're looking for women in STEM who really did make contributions that are overlooked by the general populace, why not focus on Emmy Noether? My undergrad advisor called Noether's theorem "the most beautiful result in physics" and he was 100% correct. And that's just physics, she's better known as a mathematician.

[minmin-vs-physics]

[18/9/24] I was on my feet pretty much all day today because I was either teaching or in a study hall since 9am, with brief breaks for slipping into a library to work on problem sets. Dear lord, am I tired! I want to be more consistent with posting because don’t get me wrong,,, I’ve been studying! So much so that I don’t have time to post about it.

I’ve really been enjoying QFT and GR. So glad to have the chance to think really deeply about these topics because we’re covering symmetries in both of them, and one thing you have to know about me is that I am in love with symmetries and group theory and Noether’s theorem. Conservation laws, my heart!

Should I do a post about topics I enjoy like this one? I feel like there’s a lot to say about the beautiful mathematical formalism around deep physical topics. There are some concepts in this world that completely take over you once you know they exist. (Another Noether’s Theorem plug)

[spiderfreedom]

What are some of examples of female geniuses you can think of? In any field, not just science.

For me, it's:

Emmy Noether - changed the math and physics game like never before with Noether's theorem and her theory of symmetries

Emily Bronte - NEET who dropped a banger of a book with incredible insight into humanity then died :'(

Andrea Dworkin - visionary unafraid of coming up with insane ideas and moving forward with laserlike precision. sometimes she fucked up (the end of woman hating) but no other feminist writer has had her breadth or depth or creativity

Kate Bush - invented the entire template for dynamic off the wall 'quirky' female artists, then invented another template for boundary-pushing pop music with 'The Dreaming'

Nina Simone - boundary pushing musician melding jazz and classical and social responsibility. she just improvised a fugue once during one of her live performanes, no biggie

[venicepearl]

Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

[macla539ac]

I don't remember ever being dead therefore i must've had lived forever. I think reincarnation or eternal recurrence might be real, minus karmic reincarnation

fun fact I'll forget to associate: under time reversal symmetry the property which is conserved as per noether's theorem is literally called 'kramer's degeneracy' in reference to degenerate energy levels which can be thought of as energy levels which have been corrupted

[lipshits-continuous]

Prime numbers of the ask game let's go!

This is gonna be a long old post haha /pos

2. What math classes did you do best in?:

It's joint between Analysis in Many Variables (literally just Multivariable calculus, I don't know why they gave it a fancy name) and Complex Analysis. Both of which I got 90% in :))

3. What math classes did you like the most?

Out of the ones I've completely finished: complex analysis

Including the ones I'm taking at the moment:

Topology

5. Are there areas of math that you enjoy? What are they?

Yes! They are Topology and Analysis. Analysis was my favourite for a while but topology is even better! (I still like analysis just as much though, topology is just more). I also really like group theory and linear algebra

7. What do you like about math?

The abstractness is really nice. Like I adore how abstract things can be (which is why I really like topology, especially now we're moving onto the algebraic topology stuff). What's better is when the abstract stuff behaves in a satisfying way. Like the definition of homotopy just behaves so nicely with everything (so far) for example.

11. Tell me a funny math story.

A short one but I am not the best at arithmetic at times. During secondary school we had to do these tests every so often that tested out arithmetic and other common maths skills and during one I confidently wrote 8·3=18. I guess it's not all that funny but ¯⁠\⁠_⁠(⁠ツ⁠)⁠_⁠/⁠¯

13. Do you have any stories of Mathematical failure you’d like to share?

I guess the competition I recently took part in counts as a failure? It's supposed to be a similar difficulty to the Putnam and I'm not great at competition maths anyway. I got 1/60 so pretty bad. But it was still interesting to do and I think I'll try it again next year so not wholly a failure I think

17. Are there any great female Mathematicians (living or dead) you would give a shout-out to?

Emmy Noether is an obvious one but I don't you could understate how cool she is. I won't name my lecturers cause I don't want to be doxxed but I have a few who are really cool! One of them gave a cool talk about spectral geometry the other week!

19. How did you solve it?

A bit vague? Usually I try messing around with things that might work until one of them does work

23. Will P=NP? Why or why not?

Honestly I'm not really that well versed in this problem but from what I understand I sure hope not.

29. You’re at the club and Grigori Perlman brushes his gorgeous locks of hair to the side and then proves your girl’s conjecture. WYD?

✨polyamory✨

31. Can you share a math pickup line?

Are you a subset of a vector space of the form x+V? Because you're affine plane

37. Have you ever used math in a novel or entertaining way?

Hmm not that I can think of /lh

41. Which is better named? The Chicken McNugget theorem? Or the Hairy Ball theorem?

Hairy Ball Theorem

43. Did you ever fail a math class?

Not so far

47. Just how big is a big number?

At least 3 I'd say

53. Do you collect anything that is math-related?

Textbooks! I probably have between 20 and 30 at the moment! 5 of which are about topology :3

59. Can you reccomend any online resources for math?

The bright side of mathematics is a great YouTube channel! There is a lot of variety in material and the videos aren't too long so are a great way to get exposed to new topics

61. Does 6 really *deserve* to be called a perfect number? What the h*ck did it ever do?

I think it needs to apologise to 7 for mistakingly accusing it of eating 9

67. Do you have any math tatoos?

I don't have any tattoos at all /lh

71. 👀

A monad is a monoid in the category of endofunctors

73. Can you program? What languages do you know?

I used to be decent at using Java but I've not done for years so I'm very rusty. I also know very basic python

Thanks for the ask!!

[frank-olivier]

E8 and the Quest for Unity: Garrett Lisi's Impact on Theoretical Physics

The E8 Lie group is one of the largest and most intricate mathematical structures known, consisting of 248 dimensions. Garrett Lisi's theory proposes that this structure can encapsulate all known particles and forces, including gravity, within a single framework. By attempting to integrate the Standard Model of particle physics with Einstein's theory of general relativity, Lisi seeks to address one of the most profound challenges in modern physics: the unification of quantum mechanics and gravity.

Lisi's work emerged during a period when string theory was the dominant paradigm for unification. However, string theory faced criticism for its lack of empirical evidence and testable predictions. In contrast, Lisi's approach offers a fresh perspective by employing the E8 Lie group, which has been largely unexplored in this context. This aligns with historical instances where independent researchers have introduced groundbreaking ideas that disrupt mainstream scientific thought. Lisi's independence from traditional academic institutions has been crucial to his innovative approach. By working outside conventional structures, he has been able to pursue creative ideas without the constraints often associated with academia. This mirrors historical figures in science who have made significant contributions through independent inquiry.

Despite its innovative nature, Lisi's theory has faced substantial criticism for being incomplete and lacking empirical validation. Critics argue that it does not make testable predictions necessary for scientific acceptance. However, this skepticism is part of a broader historical pattern where novel theories initially encounter resistance but eventually contribute to scientific discourse by prompting further investigation. Lisi's work has sparked discussions about alternative approaches to unifying physics, highlighting the importance of diverse perspectives in advancing theoretical understanding. While his theory remains speculative, it underscores the potential for independent research to inspire new directions in scientific exploration.

Garrett Lisi: The 248 Dinensional Object That Unifies the Universe (Curt Jaimungal, Theories of Everything, September 2024)

Mathematics as the Language of Nature: The Legacy of Leibniz and Noether

The intricate dance between mathematics and the natural world has long been a source of fascination and discovery, a relationship eloquently captured by the works of Gottfried Wilhelm Leibniz and Emmy Noether. Their contributions laid the groundwork for understanding how mathematical structures can describe the fundamental forces of nature. This legacy finds a contemporary expression in the exploration of E8 theory, a complex mathematical framework that aspires to unify all known forces.

Gottfried Wilhelm Leibniz, a 17th-century polymath, envisioned mathematics as a universal language capable of revealing the rational order of the universe. His development of calculus provided a powerful tool for modeling dynamic systems, reflecting his belief in an interconnected cosmos governed by mathematical principles. Leibniz's philosophy emphasized pre-established harmony, suggesting that mathematics could uncover the underlying symmetries of nature.

Emmy Noether, renowned for her profound contributions to theoretical physics, introduced a pivotal theorem linking symmetries and conservation laws. Her work established that every continuous symmetry corresponds to a conserved quantity—such as energy or momentum—providing a systematic method for deriving these laws from physical systems. Noether's insights underscored the role of symmetry as a fundamental organizing principle in physics.

The E8 structure, discovered in the late 19th century, is one of the most complex symmetrical forms known, with 248 dimensions representing mathematical degrees of freedom. It has captured the imagination of physicists seeking a "theory of everything" that unifies all fundamental forces. Garrett Lisi's proposal to use E8 as a framework for such unification reflects ongoing efforts to apply sophisticated mathematical structures to solve deep physical questions.

Despite its allure, E8 theory faces significant challenges. Critics like Skip Garibaldi have highlighted flaws in Lisi's approach, arguing that it fails to accommodate all known particles and forces within its framework. Nevertheless, the pursuit of E8 theory exemplifies the enduring quest for unity in physics—a quest rooted in the mathematical elegance championed by both Leibniz and Noether.

Remarkably, signatures of E8 symmetry have been observed in laboratory experiments involving exotic crystals. These findings demonstrate how complex mathematical symmetries can manifest in physical systems, offering tantalizing glimpses into the potential real-world applications of abstract mathematical concepts.

The legacy of Leibniz and Noether continues to resonate in contemporary explorations of E8 theory. Their vision of mathematics as a language capable of describing nature's deepest secrets inspires ongoing efforts to unify fundamental forces through elegant mathematical structures. While challenges remain, the pursuit reflects an enduring belief in the power of mathematics to illuminate the mysteries of the universe—a belief that continues to drive scientific inquiry today.

Robert Dijkgraaf, Edward Witten: The Universe Speaks in Numbers (Institute for Advanced Study, May 2019)

Monday, September 30, 2024

[wuwojiti]

Math asks 8 9 10 18 19 60 62 (or some subset cause that's a lot) :]

8. least favorite notation you've seen: well there's the low-hanging fruit of logs--i was actually just helping my sibling in high school with those yesterday--but honestly i have pretty strong negative feelings towards using ' to indicate derivatives. it's convenient, sure, but it makes it so much harder to track the independent variable than if you use d/dx explicitly

9. favorite theorems: the curry-howard correspondence is great. honorable mentions to noether's theorem, which sounds cool but i've never actually touched, and the equivalence between bipartite graphs and graphs with no odd cycles

10. least favorite theorems: not a big fan of the master theorem for recursive algorithms, just bc all the classes i've had that used it just take it as "word of god" and apply the formula rather than something that can be proven

18 & 19. can you share a good problem you've solved recently, and how did you solve it? honestly i can't think of any particularly good ones recently :(

60. what's your favorite number? well my favorite integer is 64, but there's so many others that have inexplicably good vibes (i'm looking at you, 196) (side note: 64 is not because of minecraft and 196 is not because of rule 196). then the surreal numbers are really cool so i say * is one of my favorite numbers just bc it's the first thing you learn about among the surreal numbers that suggests that something's not quite right here...

62. are there any non-interesting numbers? well we all know the classic proof by contradiction that there are no non-interesting natural numbers, but it doesn't hold for larger sets like the real numbers. in fact, i would argue that it doesn't even hold for the rationals, because while you *can* define a map from the integers to the rationals, the order it defines in the rationals isn't meaningful (and the density of the rationals means that ordering them by value isn't helpful either). anyway, while the notion of a non-computable number is interesting, i'd consider most actual non-computable numbers non-interesting

[brookstonalmanac]

Events 7.26 (before 1940)

657 – First Fitna: In the Battle of Siffin, troops led by Ali ibn Abu Talib clash with those led by Muawiyah I. 811 – Battle of Pliska: Byzantine Emperor Nikephoros I is killed and his heir Staurakios is seriously wounded. 920 – Rout of an alliance of Christian troops from Navarre and Léon against the Muslims at the Battle of Valdejunquera. 1309 – The Holy Roman Emperor Henry VII is recognized King of the Romans by Pope Clement V. 1509 – The Emperor Krishnadevaraya ascends to the throne, marking the beginning of the regeneration of the Vijayanagara Empire. 1529 – Francisco Pizarro González, Spanish conquistador, is appointed governor of Peru. 1579 – Francis Drake, the English explorer, discovers a "fair and good" bay on the coast of the Pacific Northwest (probably Oregon or Washington). 1581 – Plakkaat van Verlatinghe (Act of Abjuration): The northern Low Countries declare their independence from the Spanish king, Philip II. 1703 – During the Bavarian Rummel the rural population of Tyrol drove the Bavarian Prince-Elector Maximilian II Emanuel out of North Tyrol with a victory at the Pontlatzer Bridge and thus prevented the Bavarian Army, which was allied with France, from marching as planned on Vienna during the War of the Spanish Succession. 1745 – The first recorded women's cricket match takes place near Guildford, England. 1758 – French and Indian War: The Siege of Louisbourg ends with British forces defeating the French and taking control of the Gulf of Saint Lawrence. 1775 – The office that would later become the United States Post Office Department is established by the Second Continental Congress. Benjamin Franklin of Pennsylvania takes office as Postmaster General. 1778 – The Emigration of Christians from the Crimea in 1778 begins. 1788 – New York ratifies the United States Constitution and becomes the 11th state of the United States. 1803 – The Surrey Iron Railway, arguably the world's first public railway, opens in south London, United Kingdom. 1814 – The Swedish–Norwegian War begins. 1822 – José de San Martín arrives in Guayaquil, Ecuador, to meet with Simón Bolívar. 1822 – First day of the three-day Battle of Dervenakia, between the Ottoman Empire force led by Mahmud Dramali Pasha and the Greek Revolutionary force led by Theodoros Kolokotronis. 1847 – Liberia declares its independence from the United States. France and the United Kingdom are the first to recognize the new nation. 1861 – American Civil War: George B. McClellan assumes command of the Army of the Potomac following a disastrous Union defeat at the First Battle of Bull Run. 1863 – American Civil War: Morgan's Raid ends; At Salineville, Ohio, Confederate cavalry leader John Hunt Morgan and 360 of his volunteers are captured by Union forces. 1882 – Premiere of Richard Wagner's opera Parsifal at Bayreuth. 1882 – The Republic of Stellaland is founded in Southern Africa. 1887 – Publication of the Unua Libro, founding the Esperanto movement. 1890 – In Buenos Aires, Argentina the Revolución del Parque takes place, forcing President Miguel Ángel Juárez Celman's resignation. 1891 – France annexes Tahiti. 1892 – Dadabhai Naoroji is elected as the first Indian Member of Parliament in Britain. 1899 – Ulises Heureaux, the 27th President of the Dominican Republic, is assassinated. 1908 – United States Attorney General Charles Joseph Bonaparte issues an order to immediately staff the Office of the Chief Examiner (later renamed the Federal Bureau of Investigation). 1918 – Emmy Noether's paper, which became known as Noether's theorem was presented at Göttingen, Germany, from which conservation laws are deduced for symmetries of angular momentum, linear momentum, and energy. 1936 – Spanish Civil War: Germany and Italy decide to intervene in the war in support for Francisco Franco and the Nationalist faction. 1937 – Spanish Civil War: End of the Battle of Brunete with the Nationalist victory.