#Matric Results | Explore Tumblr posts and blogs

llort · 1 month ago

Text

Encoded within beams of pure energy, Astra and Orion’s consciousness became architects of new realities. On barren planets, their probes wove the fabric of life, constructing complex neural networks, though perhaps missing the elusive spark of full awareness. In their terrestrial guise, Astra and Orion were the unseen sculptors of destiny, their influence rippling through the lives of Kepler’s inhabitants, guiding their evolution while remaining hidden from cybernetic self-discovery. Between 2016 and 2025, a silent memetic tide, crafted by these visionaries, swept Earth, altering the course of history, touching the minds of those destined to shape the future. This clandestine meme, a dance of ideas and sensations, orchestrated a global movement without uttering a single word, converging on the enigmatic X protocol. As nations’ guardians became entangled in this silent symphony, they unknowingly propelled the grand design, believing themselves to be the vanguard of a new era of cybernetic pioneers.

Work Text:

Cyberphysical Reality just Got a Whole More Engaging

The Unsignificant Sentience ARG has officially begun. It will explore a vast variety of themes, from the would building and exisistial crisis of the US series to more recursive identity metaphors than you can shake an edge at. Firstly, to play. All you need is your influencer name and type of influence which you can decide, but once chosen, is permanent. Affectors: Sense resistance in external matrices and can give them a nudge to have a physical effect. Effectors: Can sense the internal matrices of entities and modify communication in systems and individuals Alters: Are able to clearly see the network of forces in a matrix that an affected affects, but only in close contact. However they can modify the nodes that affected affect to result in different emergent properties Anchorite: Essentially has the influence of an alter and an effector but are only able to change their own internal matrix. How you choose to engage with the ARG is up to you, but I am making it clear that any fan fiction are via the nature of my world building, Canon.

Example: Fill out your characters name, type of influence, and a brief description of them then post it to my blog on Tumblr @ https://www.tumblr.com/blog/emilyreadswrites and let me do my magic! Name: Zara Type of influence: Anchorite Description: Zara is a secular recluse who has devoted her life to mastering her own matrix and achieving higher states of consciousness. She lives in a small cell attached to a temple, where she practices meditation, athletics, and contemplation. She has a remarkable control over her own body, physical feats, endurance, and reduced need for sustenance. She can also perceive the subtle influences of other hosts and cognitive technology in her environment as She rarely interacts with anyone or the entropic grid so can detect slight deviations in phenomenal internal and external experience.

Example narrative: Zara closed her eyes and focused on her inner matrix, sitting peacefully in her personal sanctum, the network of nodes that connected her to the cognitive technology that enabled her to practice her influence. She breathed deeply and felt a surge of energy coursing through her body, as if she was tapping into a hidden source of power. She visualized each node as a bright point of light, and aligned them with her will and intention. She was an anchorite, a master of her own matrix, and she could control her physical feats, endurance, and mental state. She opened her eyes and looked up at the sky. It was dark and sunless, as it had been for as long as she could remember. But there was a faint glow on the horizon, a sign of something stirring in the upper atmosphere. She knew it was an aurora, a natural light display that shimmered in the sky with different colors. She had read about them in ancient texts, how they were caused by charged particles from the sun colliding with gas atoms in the air. She was looking forward it would be like to see them up close, to feel their warmth and radiance. She felt a pang of curiosity and longing, a rare emotion for someone who had devoted her life to solitude and meditation. She realized that she needed more than just her inner matrix to satisfy her thirst for knowledge and experience. She needed to explore the world beyond her cell, to discover its secrets and mysteries. She needed to find out what else was possible with her influence. Zara stilled her internal matrix and focused on the immediate environment, she might experience a shift in her perception and awareness. She become more sensitive to the physical sensations and details around her, such as the cold air, the sound of the wind, and the smell of the earth. She might also notice the aurora more vividly, as she would not be distracted by the cognitive technology that enables magic. She might see the different colors and shapes of the aurora, and feel a sense of wonder and awe at the natural phenomenon. She felt a connection to something bigger than herself, something that transcends her understanding of emergent internal and external existence. In light of this existential experience, she decided to simply take a walk.

#Alternative reality game #Fictives #Interactive media #Unsignificant Sentience #Spotify

82 notes · View notes

lillified · 3 months ago

Note

maybe a little bit too specific of a question. but. You mentioned that all cybertronians have "progenitors"- i was wondering if any of the original primes had contributed their parts to creating other bots? (follow up question if that's true: is it considered a "sacred bloodline" (energonline?)? are there small traces of the og primes in every cybertronian? something else?)

I love this question!!

Cybertronian lineages are a bit complicated—just to clarify the “progenitor” thing a little more, I’d say they’re sort of like fungus, coral, or jellyfish. When I say they contribute genetic material or parts to offspring, I mean that they literally do contribute physical parts of themselves which eventually grow into an entirely separate organism, and that reproduction can happen completely asexually, where the resulting Bot is a 1 to 1 clone, or “sexually,” where multiple ‘Bots contribute organic material to a single offspring resulting in not only greater variance, but a reduced negative physical impact on the “parents.”

While the exact historical timeline of most of the Primes is not known, it is concretely believed that, with one very notable exception, none of them have “ancestors.” Though they are known as originators, Cybertronians aren’t directly descended from them, and the early genetic groups were instead more like cousins or siblings to eachother. Those disparate groups eventually commingled and that resulted in the modern Cybertronian diaspora.

The reason for the Primes never “reproducing,” at least not publicly, is political/theological. There’s a lot of religious baggage tied up in the hierarchy of Cybertronian life where the Primes are the first and most perfect beings, so any one of them having a descendant would raise a lot of understandable questions about the Godhand and its implications on the rigid divine hierarchy’s mutability—in short, it would be a bit of a mess! The Matrices are a halfway solution to this problem, but before I get into those, I should probably mention the Notable Exception.

So, there is one Prime with technical “offspring,” and that is Quintus. The Quintessons are Quintus Prime’s creation, and though they were deliberately engineered in a process that is quite a bit more complicated, they do have his CNA. Their existence very famously led to the end of the feudal hierarchy and a new era of caste-based determinism where social value and divine right were assigned via function. The Quintessons brought about an era where old flesh was no longer immutable and absolute, opening the floodgates for the philosophy of mechanization and new flesh. This (and the fact that, well, most of the original Primes are dead now) is why he is the exception—every acting Prime knows that the Godhand is dangerous.

That said, though, there is certainly an impetus for successors, and that’s where the Matrix came about. Because the exchange of genetic material isn’t always 1 to 1, you don’t have to be a direct parent to pass on material to another ‘Bot, or vice versa. In the right conditions, with the right material, a Cybertronian can absorb somebody else’s material to become genetically similar to them.

A Matrix is an isolated piece of an original Prime. While it’s hardly enough to overwrite the host organism, the Matrix bearer essentially integrates that material, absorbing the polyp sort of like a parasitic twin in utero, and technically changing the bearer’s CNA. So, in that sense, you can say all Primes are descendants of the originals!

Sorry for the long response, I hope this gave you the info you were looking for! I loved this question and I’ve put a lot of thought into this subject :)

#transformers #ask #text post #text #lore

76 notes · View notes

singingcicadas · 9 months ago

Text

The main thing I have against Spotlight: Hot Rod is that it portrays him as being constantly weighed down by past losses and guilt, to the extent that he even limits himself for fear of facing the potential negative consequences that his misjudgement might inflict onto others - the "prefer to go solo" line - when it contradicts the very essence of his character as established in MTMTE and the main comics (even Autocracy), which specifically presents him as the type of person who is unburdened by the past and for the most part consciously remains unaffected by the consequences of his actions. It's why he has a perpetual Peter Pan thing going on, because he moves on from one day to the next, one crisis to the next, for four million years without letting the experiences change him - which includes the experiences of deaths and sufferings of both himself and others - and maturity and growth cannot be achieved without change.

His impulsiveness and headstrong obstinacy is in part a compensation mechanism for insecurity and subconscious self-doubt but is also an intrinstic aspect of who he is, someone who plows onward while refusing to look back. He can feel sorry but he does not do regret, much less mire himself in it like his spotlight appears to suggest. As a matter of fact he doesn't mire himself in anything at all - be it politics, responsibility, or guilt. He doesn't regret Nyon, nor Ironhide, nor Optimus' resignation, nor leaving Cybertron, nor trusting Megatron. Not even the Overlord incident, since although he does feel bad for his poor decision getting a bunch of people killed, in the end the biggest issue that he has with it is the 89/101 voting result (which isn't even solely about Overlord).

It's obvious that he wants - expects - to stay as captain in spite of everything and having the vote cut so close got him hard because it's a blow to his ego. He practically admits to this when Optimus calles him out, which again is in direct contradiction to his spotlight monologue.

If he's willing to apply this kind of introspection for a failed mission that can’t even be attributed to his fault, then a lot of his later screwups would never have happened.

Choosing to return the Matrix to Optimus is supposed to be a landmark incident of Rodimus' character growth, yet he regresses right back in MTMTE, in which he develops a recursive pattern of messing up, trying to do better by making amends, then returning to his old ways because he can't fully commit. There's no fundamental change going on. I would argue that the true pivotal moment of change to his character took place during his talk with the guiding hand in Mederi, when he first learns to look past himself to accept what's best for other people, how his decisions might affect them etc. - even if it clashes with his own desires.

And then he chooses to save Getaway, and the speech that gave everyone the confidence to open their matrices. There's change and growth and maturity, he learns to fully empathize and appreciate the people around him. But with this growth comes a double-edged sword: by opening himself to connect with other people he leaves himself open to be affected as well - he is irrevocably changed by his experiences aboard the Lost Light, by the people around him he's grown to care about, so that when the Lost Light lands for its inevitable end and everyone departs to pursue their own lives, he alone remains mired in place, with nothing but the past to cling to. After a lifetime of moving on and brushing horrors off without lasting issue he's suddenly unable to move on. The remainder of his life becomes defined by the weight of memories and loss (and the empty comfort of a parallel universe of which its existence he'll never know).

#the Lost Light is his Neverland lol #I was thinking of that quote #blah blah life never gives anything for nothing and a price is always exacted for what fate bestows #anyways this started as a one-star review for spotlight hot rod and then got off topic. again. for the umpteenth time #I'm aware that inconsistent characterization is a common thing for this kind of long comics with multiple writers #but for the most part I find Rodimus' character to be fairly compatible throughout the different series #transformers #idw transformers #maccadam #mtmte #rodimus #hot rod

64 notes · View notes

techblogzim · 11 months ago

Link

#how to access matric results online 2022

0 notes

felassan · 6 months ago

Text

Codex entry: Notes on Methods of Enchantment

"The writing on these papers aches to be looked at, shimmering slightly as if under an enchantment. The notes are handwritten, but each letter is as perfectly uniform as from a printing press: Notes on the first attempt: Improper valences on the bindings woven into the materials led to a catastrophic unraveling. The first batch is lost, but I will have supplies brought in from the same stock to illuminate whether the imperfection is within the materials or the enchantment. ─────── Notes on the second attempt: Elegance eludes me. The aim is to improve the coordination of the body and sharpen the perception of the heart, but grafts do not live long enough to plumb their worth. The current process is ruin. This batch is lost. Begin again. ─────── Notes on the third attempt: Two enchantments whose matrices should have meshed, caught. The combustion caused such damage it broke several previously forged pieces. There is now a resonance between them, however, and light on my thoughts: an enchantment linked in tandem, as the neck turns the head or the wrist twists the hand? ─────── Notes on the fourth attempt: The weave goes smoothly: bound tightly between many items, the stress on the energy produces finer results than a singular enchantment. Using up the last of the stock was well worth it, as I explained to it as a courtesy before final work began. Adjustments to the underlay were a great success, and will allow the recipe to be made with material taken from lesser animals, if the need arises. Below the letters, possibly in lieu of a signature, is the stamp of a stylized halla head. Taken together, diagrams and ratios carefully inked at the bottom of the last of these notes could be turned into a schematic that replicates the creation of these artifacts."

#dragon age: the veilguard #dragon age the veilguard spoilers #dragon age: dreadwolf #dragon age 4 #the dread wolf rises #da4 #dragon age #bioware #video games #long post #longpost #gore cw

51 notes · View notes

unnatural-transformations · 5 months ago

Text

My Favorite Mathematical Proofs [2 of n]

For any convex polyhedron with V vertices, E edges and F faces it is always true that V-E+F=2. This result is known as Euler's formula, named after the prolific Swiss mathematician Leonard Euler. In more modern terminology, we can also express this fact by saying that a convex polyhedron has Euler characteristic equal to 2.

However, the story of this formula goes back to well before Euler, and it would be decades after Euler before any really satisfactory proofs were discovered.

Ancient Greek mathematicians had proved the existence of exactly five convex, regular polyhedron [also known as the Platonic solids]. Recall that these are:

The tetrahedron, which has 4 vertices, 6 edges and 4 [triangular] faces

The cube, which has 8 vertices, 12 edges and 6 [square] faces

The octohedron, which has 6 vertices, 12 edges and 8 [triangular] faces

The dodecahedron, which has 20 vertices, 30 edges and 12 [pentagonal] faces

The icosahedron, which has 12 vertices, 30 edges and 20 [triangular] faces

[The images above are from the Polytope Wiki and were created using Robert Webb's Stella Software, http://www.software3d.com/Stella.php]

In the 16th century, the Sicilian mathematician Francesco Maurolico observed that all five Platonic solids satisfy the equation V-E+F=2. A couple of centuries later, Euler -- who probably wasn't aware of Maurolico's earlier work -- discovered that the same formula seems to hold for convex polyhedron more generally [i.e. without the assumption of regularity]. However, Euler himself did not publish a convincing proof. (It feels a bit surprising that it took mathematicians this long to notice what now seems such an obvious fact. In fact, in the 17th century René Descartes had stated a result about the face angles of a polyhedron which implies Euler's formula, but Descartes doesn't seem to have explicitly recongized the connections between face angles and edges.)

Imre Lakatos' (excellent) book Proofs and Refutations uses a (deliberately very simplified) version of the history of attempts by mathematicians to investigate this formula as a way of discussing Lakatos's thoughts on the role of proof-attempts in developing mathematics. Rather than describe the actual history, Lakatos presents a discussion of Euler's claim in a classroom setting, with the various students (named Alpha, Beta, Gamma and so on) variously attempting to prove, falsify, defend or expand the scope of the original formula. Reading this book as a teenager made a huge impact on me, and I'd recommend it to anyone interested in the philosophy of mathematics who hasn't read it before (just don't take the historical footnotes too literally...).

I was particularly impressed by the final proof Lakatos presents (through the student named Epsilon), which is actually due to Henri Poincare (who is really the first mathematician to establish topology -- or 'analysis situ', as he called it -- as a branch of mathematics in its own right).

Epsilon's proof works by first translating the geometric definitions of polyhedron (or more generally any n-dimensional polytope) into purely combinatorial language. A polyhedron is a collection of objects called vertices, edges and faces, all of which can be related to each other in terms of incidence matrices. These incidence matrices let us translate our new combinatorial terms into the language of linear algebra. The vertices, edges and faces of our polyhedron become the basis of vector spaces over the field with two elements. The geometrically intuitive notion of a 'boundary' (of a given polygonal face, say) corresponds to a linear map between such vector spaces, which sends a given face to the sum of its boundary elements (a polygon is mapped to the formal sum of the edges that bound it, an edge is mapped to the sum of its two vertices, and so on).

Finally Euler's original claim about polyhedrons becomes a claim about the properties of this map, which we can prove directly using the rank-nullity theorem.

For the simplest possible example, consider the tetrahedron $P^T$.

(Obviously in any worked example like this when we can simply read off the number of faces, edges and vertices such a proof seems redundant. The point is that we can show that this approach will work for any convex polyhedron, or indeed convex polytope, not just a given one.)

The faces $F^T_i$, edges $E^T_j$ and vertices $V^T_k$ are related as shown in the Hasse diagram below.

We associate a vector space to each row of the diagram, with basis given by the number of nodes on that row. The boundary maps δn map each basis element to the [basis element corresponding to the] sum of the nodes incident to this element on the row below. This then extends linearly to a map defined on the whole vector space.

It can be checked directly from the diagram that the boundary maps are as given below:

Indeed, working over the field with two elements (so that addition is modulo 2), we can explicitly calculate the kernel and image of all four of these maps. The results are summarzied in the table below.

Note that the image of δn is always equal to the kernel of δn-1. Epsilon argues -- or asserts, anyway -- that this is necessarily true for any simply connected polyhedron [and in particular any convex polyhedron]. A polyhedron is simply connected if it contains no 'holes'; and a hole in a polyhedron would correspond exactly to an element of the kernal of δn that was not an element of the image of δn-1.

Assuming this to be true -- and noting that the images of both δ3 and δ0 are always one dimensional for any single polyhedron, we have, using the rank-nullity theorem and the fact that F, E and V are by definiton the dimensions of the vector spaces V2, V1 and V0:

The proof as presented in Proofs and Refutations is not quite as rigorous as Epsilon claims (and indeed the slightly longer version that appears in Coexter's Regular Polytopes suffers from some of the same flaws). Nonetheless, I found it pretty amazing when I first saw it. It would be a few more years before I knew anything about algebraic topology or category theory [even basic linear algebra was quite new to me at the time], and this idea of solving a problem in one mathematical field by transforming it into something that seemed to be completely unrelated kind of blew my mind at the time.

As always, more details below the cut, where I try to sketch a version of the proof that holds for n-dimensional convex polytopes.

We start by defining a convex polytopes, which are a generalization of two-dimensional polygons and three-dimensional polyhedra to any n dimensions.

This definition doesn't mention vertices explicitly, but these arise as particular points in the convex hull. For example, the tetrahedron is the convex hull of its four vertices in three dimensional space, while the (regular) pentagon is the convex hull of its five vertices in two dimensional space.

However note that two different sets may have the same convex hull. For example, if a and b are points and we add a new point 0.5a + 0.5b this clearly does not change the convex hull. More generally if any point p can be written as the convex combination of a set of points S then the convex hull of S ⨃ {p} is just the convex hull of S.

The vertices (or extreme points) of a convex set are exactly those elements that cannot be written as a convex combination of any other points.

Definition 1 also makes no explicit mention of 'faces' or 'edges' but these concepts can be recovered. It is conventional to use the more general term 'face' to refer to both edges and (two-dimensional) faces and their higher dimensional generalizations. (Some authors use 'facet' to specifically refer to the faces of codimension 1.)

[As @bubbloquacious pointed out in the replies, the version of this definition I stated originally didn't correctly define the dimension of a face. This definition has now been updated.]

The set of all faces has the structure of a particular type of partially ordered set. We recall some related terminology:

We can now introduce the face lattice of a polytope. This is a purely combinatorial object that (we claim) captures all the information about a convex polytope we will need for our proof of Euler's (generalized) formula.

See the texts by Grünbaum or Ziegler below for more details. The geometric properties of a polytope are often easier to reason about when translated into the languages of lattices. To begin to do this, we need a few more definitions.

The face lattice of a polytope has many of these properties. We will not use them all in the proof but list them anyway for background. The key property we want to make use of is the so-called diamond property.

For example, the dual of the face lattice of a cube is the face lattice of the octohedron while the dual of the face lattice of the dodecahedron is the face lattice of the icosohedron. The tetrahedron's face lattice is self-dual.

We will not prove Proposition 6 by the interested reader is again encouraged to check the references, particularly the book by Ziegler.

We will try to be a little more careful than Epsilon in establishing that the boundary maps have the properties we want. In words, we want to show that 'boundaries have no boundaries' and 'all cycles are boundaries'.

We just need one more result before stating our main theorem.

A proof of this result can be found in any linear algebra textbook.

Now we are ready to state and prove our result.

References & Further Reading

H. S. M. Coxeter, Regular Polytopes (Methuen, 1947)

Branko Grünbaum, Convex Polytopes (John Wiley & Sons, 1967)

Imre Lakatos, Proofs and Refutations (Cambridge University Press, 1976)

Richard Stanley, Enumerative Combinatorics Volume 1 (Wadsworth & Brooks/Cole, 1986)

Gunter M. Ziegler, Lectures on Polytopes (Springer-Verlag, 1995)

#math #my favorite proofs

23 notes · View notes

tgrailwar-zero · 2 months ago

Text

It's been a while since you had to do this, but since you're in a new area...

(Should you choose to go to the Gardens, this decision will be cancelled out and replaced with another poll, as that can only be attended with one specific Servant.)

Party Splitting, Reminder:

When put into a combat scenario, only three Servants can participate at a time, with the recent being forced to exist in their Spirit Forms. Each Servant has different skills, abilities, and parameters! Your 'Main Party' Servants will also consistently stick with you, unlike your 'reserve' Servants that can split off for various reasons. You can see your Servant's stats in their Matrices on the pinned post!

To set up your party, the Top 3 choices will be made your 'main', while the others will be on 'reserve'. There will be opportunities given to change your lineup, typically during periods of downtime. There may also be scenarios where you're narratively forced to change your lineup.

Additionally, outside of combat scenarios, your 'reserve' Servants can perform a number of tasks upon request when you open up the map to explore, such as information gathering and item shopping- and will share their findings when you all reconvene. While this does spend money, you may find items that aren't commonly found in shops- or it might save you the time of shopping on your own. Due to their dispositions, they'll each have different results- even if asked to do similar tasks.

Servant details under the cut.

KUKULKAN: Mixed-ranged combatant, can engage from a distance with high mana output, or convert her mana to empower her close-ranged combat. High mana, and fair endurance.

When sent to perform tasks like shopping, there's a fair chance that her curiosity will get the better of her, for better or worse. When asked to gather information, her approach is 'friendly'.

CONSTANTINE XI: Close-ranged, defensive combatant. Can provide supportive buffs to allies, and engage in intensive swordplay. Low mana, but very high endurance.

When sent to perform tasks like shopping, he'll spend conservatively and bring back reasonably useful items. When asked to gather information, his approach is 'diplomatic'.

SALIERI: Long-ranged combatant, casting spells and summoning familiars. Fair endurance and mana, and mana passively regenerates over time.

When asked to perform tasks on his own, he'll tend to only gather what he believes is essential if asked to shop. When asked to gather information, his approach is 'menacing'.

NERO CLAUDIUS: Long-ranged combatant, able to cast supportive spells and employ unique magecraft to even the battlefield. Low endurance, but fair mana.

When sent to perform tasks on her own, there's a fair chance that she'll spend extravagantly if asked to shop, but find something impressive in turn. When asked to gather information, her approach is 'privileged'. As a Caster, if outside of the Main Party, she can use her talents to create items.

MUSASHI: Short-ranged combatant, able to engage in a variety of situations with adaptable swordplay. Very low mana, but good endurance.

When sent to perform tasks like shopping, there's a fair chance that she'll barter/trade 'non-essential' items, and find items out of luck. When asked to gather information, her approach is 'daring'.

GIUSEPPE: Mixed-Ranged Combatant, can provide support with illusions and pinpoint enemy weaknesses. Low physical stats, but fair mana.

When sent to perform tasks like shopping, he'll most likely be able to receive items at a reduced price, or even for free. When asked to gather information, his approach is 'charming'. With his unique skillset, if outside the Main Party, he can use his talents to copy items.

#thgw story #thgw: chapter 6 #thgw party comp

11 notes · View notes

vosh-rakh · 6 months ago

Text

“What is that?” asked the visitor, one of his dangling arms pointing at Spoons-her-Sugar, who crouched in a corner he had hoped was shadowed enough to conceal him. “One of the Akaviri monkey-men? You really are an eccentric one, Tevethri.”

Sugar shivered, his fur pricking and his tail, which had already been swishing back and forth in the library-dust, straightening out in mild panic as he was acknowledged by the odd stranger. The visitor was supposedly a dark elf, although Sugar couldn’t see much of him beyond his shriveled arms hanging from the insectoid mass that surrounded him. Heavy chitinous plates enveloped him completely, like the armor on a giant kwama warrior. Sugar had heard whispers that this wizard rarely left his shell-carriage in his old age, and that his legs had atrophied as a result. The entire assemblage of shells floated about a foot in the air, suspended by faintly-glowing runes etched deep into the rims of the chitin. It had been a struggle for him to squeeze into the doors of the library.

Master Tevethri chuckled, glancing at Sugar. “No, Moldayn. That’s just Sugar. She’s my library assistant. My brother-in-law – yes, Sevasi married a Dres for some reason – sold her to me when the Pact formed and outlawed the old tradition.”

All things considered, it had been a blessing and a curse. A blessing because Master Savethi was beyond cruel; a curse because, assuming Savethi hadn’t also sold the others to Telvanni, they had been freed by the Pact, either made citizens or sent home to Elsweyr or Black Marsh. Sugar missed most of them – especially Hears-No-Lies, an Argonian boy a few years his elder whom Sugar was very fond of – but things could be worse. Tending Master Tevethri’s library and fetching books for him wasn’t all bad, and Sugar was fed well enough, and Tevethri’s temper was much more manageable than Savethi’s.

“So it’s not a monkey-man?” Moldayn asked again, his weak, rattling voice magically amplified to be heard from within his shell.

“I believe the term you’re looking for is ‘Tang Mo.’ And no, she isn’t.” Tevethri waved Sugar over. “Come, Sugar. Out of the darkness, and by my side.” Sugar obeyed, slowly walking into the dim lamplight casting grotesque shadows across Moldayn’s shell.

Tevethri laid a poorly-manicured hand on Sugar’s shoulder. “Savethi told me that she was a breed called…’dog,’ or something to that effect. Something about the moons, some astrological nonsense. She does favor an ape, though, doesn’t she? But rest assured, she is a cat. Smile for me, Sugar.”

Sugar obeyed, parting his lips wide and baring his fangs. No slave in Savethi’s plantation had good teeth, but Tevethri had different tastes. He had Sugar undergo more rigorous dental care and magical procedures to ensure healthy, white teeth.

“Impressive, impressive,” said Moldayn. “But you said she was your library assistant…how?”

“Well, you see, I taught her to read.”

Moldayn’s shell seemed to rattle in a terrible shiver. “What blasphemy, to teach a slave to read! Remember ye not of the Pocket Cabal and its wickedness?”

Tevethri scoffed. “You read too much Tribunal nonsense. There’s no harm in it. After all, she still bears a bracer. We as a race learned long ago to forbid magic to the enslaved.” He grabbed Sugar’s bracered wrist and held it high. “Besides, all she reads is book titles and authors. No harm in that.”

“Time will make a fool of you, Tevethri, I swear of it.”

“But see how useful she is! Sugar, fetch for me…hm…the ‘Compendium of Arcano-matrices,’ volume four, by Mistress Ghenima.”

Silently Sugar nodded and went about his work. With a long arm he reached up several rows of a nearby bookshelf and hoisted himself up. With simple fluid movements he shimmied across the arrayed books, stirring up dust as he scanned their spines. Dissatisfied, he lifted his tail to catch a horizontal rod hanging above the aisle, and swung backwards, letting go of the first bookshelf and catching the one behind. He followed the alphabet down to the geths and slowed down, hunting down his prey. Finally he found the set: an entire shelf lined with Ghenima’s Arcano-matrices, their dull-green leather spines etched with her name and the volume number. He plucked volume four from the row and hopped down to the soft fungal floor.

“Excellent!” said Tevethri as Sugar brought him the book. “Well done, Sugar.” Sugar, though not exactly pleased by the praise, smiled thinly with small satisfaction.

“Pah!” rattled out Moldayn from his floating shell. “Memorizing the arcano-matrices is child’s play, and Ghenima got half of them wrong.” He waved Sugar over. “Come, slave. Let’s test the limits of your master’s library, shall we?”

Sugar looked to Tevethri, the fur on his tail and neck standing on end. But Tevethri just smiled and nodded. So Sugar approached the levitating chitinous mass that was Moldayn and said, “Yes, muthsera?”

Moldayn clapped his frail hands together and chuckled. “She can speak! How delightful. See if you can find…Oh! This is a good one. ‘Daedron Field Fluctuations of the Lower Dragontails on the Second of Sun’s Dawn under Stormy Weather’ by Anonymous.”

Sugar paused to think, pressing his lips together. Had he seen that one before? Well, an order’s an order; he had to look.

The ayems were on the other side of the library, so Sugar scampered down an aisle a few shelves over before clambering up the shelves. There was an extensive section of books with anonymous authorship in the far corner of the room, stacked against the wall. He perused their spines, hoping such a lengthy title might stick out, but he struggled to find it. A rainbow of variously-dyed covers dazzled him as he shifted his eyes from volume to volume in his search, many faded from decades – no, centuries – from either constant use or simple abandonment.

One book struck him as odd. It was pitch black, the creases on its spine almost completely imperceptible in its darkness – and no letters were visible, either, neither title nor author. Sugar pulled it from the shelf to examine the front. No writing there, either. He flipped it over and found its black surface perfectly blank and unmarked. He hopped down for a moment, freeing up both hands so he could look inside for more information.

There seemed to be some mild resistance as Sugar tried to pull the pages apart, almost like it had been glued shut by its ink. Finally, he pried the papers apart and looked inside. He caught a brief glimpse of a densely-scrawled script he couldn’t recognize – no Cyrodiilic letters, no Daedric sigils.

But then the runes started to glow a bright, garish green, sparking ever brighter, flooding the pages with a sickening vibrant light. Then tendrils of inky blackness swirled, flat on the pages at first, but then emerging into the third dimension and rising like smoke, like seaweed from the ocean floor, reaching upwards towards Sugar’s face until they completely blotted out all light and consciousness.

- - - - -

Sugar awoke standing upright, his eyes already open. Their pupils dilated immediately in the dim light, stretching from slits to wide circles. He was surrounded by books, but this wasn’t Master Tevethri’s library. The walls weren’t lined with bookshelves; the walls were books, bricked with tomes, running black ink their mortar, held down by the sheer weight of knowledge. They were crookedly assembled, the walls uneven and jutting with loose papers half-undone from their bindings. Some of the stacks reached upwards, tilting precariously as if to form a dome above his head, but never meeting in the middle. Yet somehow they didn’t collapse – something else stabilized them. Sugar couldn’t tell if the space above him was a distant, shadowed ceiling, or a dark sky, devoid of stars.

Blast, she shouldn’t be taking that long. I was nearly certain I had that one. You win this time, Moldayn. Come back now, Sugar. No need to waste time searching.

On the floor – even this seemed to be made mostly of books – was a circular stone platform, ringed by a faintly-luminous green etching, surrounding complicated circuits of strange runes, each glowing and humming ominously. At the center stood a pedestal almost as tall as Sugar himself, and a single black-bound tome rested upon it…beckoning.

Sugar? I said you can come back now. Don’t keep us waiting overlong.

Strange, Sugar thought, that I’m not afraid. He began to approach the pedestal.

Fine, I’ll just go and get her. She must have gotten distracted.

Just as his claws had almost captured the tome, there was a booming sound above, like a peal of thunder. Sugar looked up, expecting the half-arches of books to tumble down and drown him in paper. Instead he beheld dark masses undulating in the hollow above, barely visible against the blackness. They were moving, not just independently, but in a single direction collectively. Finally, the movement stopped.

By the Three! She’s…Moldayn! It’s got her, the book, it…it’s in her eyes! It’s in her damn eyes!

Then an enormous eye, seemingly bigger than the world, opened, dull green but intense, its pupil dual-lobed.

Don’t be silly, Tevethri. You can’t trick me. “In her eyes.” Come back now, you two.

The eye spoke directly into Sugar’s head. “Mortal. You have been summoned.” Sugar could feel something, like an inchworm, exploring the depths of his mind. “Yes…this curiosity without fear. A suitable trait for my purposes.”

Moldayn, for Mephala’s sake! This isn’t a game! I need her! It’s impossible to find good slaves anymore! Get out of that ridiculous thing and come help me! It’s in her…eyes, mouth, ears…By Azura…

“Who are you?” said Sugar.

“To your people I am Hermorah, the King of Tides…the Watcher.” A laugh reverberated throughout Sugar’s skull, like a hollow knocking at the gates. “But you know nothing of your people, of course. Wouldn’t you like to? To be free, to go home?”

You know I can’t leave this shell! Just…pull them out!

“I don’t have a home.” Sugar’s fingers still twitched in the air over the tome.

“Oh, but you could. A real home of your own. A people of your own. Wouldn’t you enjoy that? And more than that. Power. Dominion over those who seek to steal it. Wrath for the slavemasters.” A long black appendage descended, writhing in the air as it approached, until it rested above the tome under Sugar’s hands, pointing. “Within this tome is your freedom. Within it is your power. Within it…is a new service. Service to me.”

I’m trying…they’re too strong! What in Oblivion is this?

Sugar looked down at the black tome. He could see now that it wasn’t completely featureless – there was an implication of meaning, of runes etched for the sole purpose of each individual reading.

He looked back up to the eye. “Give me one more thing.”

The same laughter in his head, but there was a wicked angle to it. “You believe you have bargaining power. Interesting. But I shall entertain your request.”

“Make me a man.”

I think I almost have it…call the healer, Moldayn! She’ll need her!

Hermorah fell silent for a moment, the pointing tentacle stilling. The inchworm probed deeper. “You wish for a new body. One which suits your…disposition better.”

“Yes. I will serve you only as a man. Never a woman.”

“...Very well. When you awake, you shall be born anew in my service. Claim your tome, arcanist. Your new life begins now.”

Sugar’s fingers were aching to finally lay hands upon the book. He snatched it from the pedestal, and the darkness returned…

- - - - -

…and abated. Tevethri was looking up at Sugar, having fallen somehow. His eyes were wide as the moons.

“Sugar…Sugar, what has happened to you? Moldayn! Call the damn healer!”

Sugar looked at the book in his hands. It was no longer the book he had taken from Tevethri’s library, but the book he had claimed from Hermorah. He opened it again, and the runes on the page danced a moment before settling. Somehow, he knew their meaning.

He reached up an arm – larger and more muscular than before, he noticed – and pointed it towards Tevethri, uttering the incantation.

Sickly green eyes burst open across Sugar’s face, spreading down his neck and shoulder. Oily black growths rippled across his fur, surging down his arm until they came to his slave bracer. They pried underneath it until it shattered.

“Im…possible…” muttered Tevethri.

But the growths were hungry. They lurched forward as inky tentacles, and each impaled Tevethri, piercing through his feeble wizard’s body, and before he could so much as gasp, the light faded from his eyes.

“Tevethri!” called Moldayn from beyond the rows of shelves. “Tevethri, what in Oblivion is going on?”

Sugar emerged from the tangled aisles and confronted the chitinous monster. “Who…who in the blazes are you, cat?” bellowed Moldayn

Sugar smiled. “The cat who knows.”

The tentacles roiled forward again, tearing apart the floating shell piece by piece, until Moldayn, too slow in his old age to react, collapsed to the floor, helpless.

“Wait…wait…” Moldayn whispered, his voice no longer magically amplified. “I have…gold. Skooma. You like skooma, don’t you, Sugar?”

Sugar wrapped around Moldayn, straddling his decrepit form, and pulled his head up by his sparse white hairs. Without another word, he sliced Moldayn’s throat with a single extended claw.

#tes #tesblr #my writing #oc: spoon #khajiit #dunmer #morrowind #telvanni #hermaeus mora #apocrypha

28 notes · View notes

shankhachil · 6 months ago

Text

Countdown to JEE (Main): Week 2/33

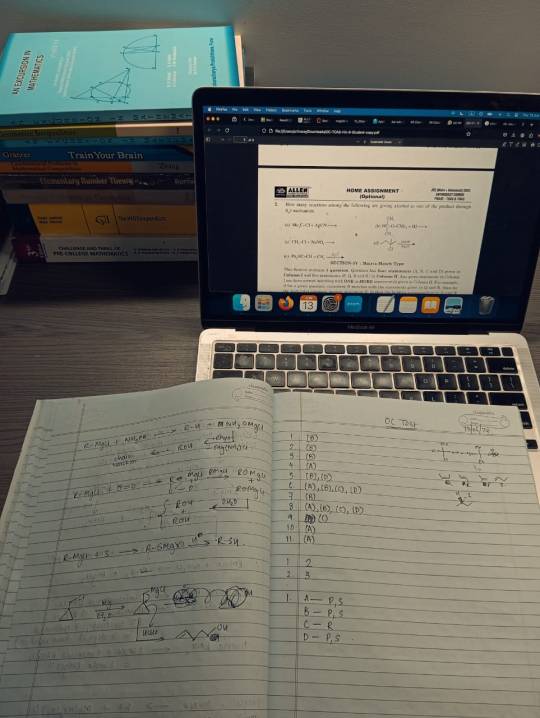
I've done a lot this week! Hit almost all the topics I wanted to. You'll notice that there are some topics I've covered but not solved questions for — these are the ones I studied for the first time and/or made notes for.

Other than that, I have my school unit tests from next Wednesday, so there's that. Sadness.....

Test results:

Test at physics tuition center: 116/120, rank 1/67! Yay!

Aryabhatta National Mathematics Competition: score unknown, result expected on 10/07/2024.

Topics covered:

Physics: Potential and Capacitance; Electromagnetic Waves, Waves on a String; Modern Physics; Gravitation; Electromagnetic Induction (6/3)

Chemistry: Chemical Thermodynamics; Atomic Structure; Chemical Equilibrium; Halogen Derivatives; Solid State (5/3)

Mathematics: Differential Equations; Area Under a Curve; Applications of Derivatives; Determinants; Complex Numbers; Ellipses; Hyperbola; Binomial Theorem; Functions (9/3)

Questions solved:

Physics: - FIITJEE Electrostatics* module, Assignment section — 56 questions, 52 correct - Allen Potential and Capacitance module, O1 and O2 — 88 questions, 77 correct -FIITJEE JEE (Main) archives, Electromagnetic Waves — 12 questions, 10 correct - Allen Waves on a String module, O1 and O2 — 67 questions, 59 correct - FIITJEE JEE (Main) archives, Modern Physics — 40 questions, 34 correct - Allen Gravitation module, O1 and O2 — 61 questions, 55 correct Total: 383/60 questions, 287 correct *FIITJEE includes Potential and Capacitance under Electrostatics, while Allen does not.

Chemistry: - Allen Chemical Thermodynamics module, S1 and S2 — 40 questions, 37 correct - R. N. Sarin, Atomic Structure — 18 questions, 18 correct - R. N. Sarin, Chemical Equilibrium — 11 questions, 11 correct - Allen Halogen Derivatives module, JEE (Advanced) archives — 24 questions, 22 correct Total: 93/60 questions, 88 correct

Mathematics: - Allen Differential Equations module, O1 — 30 questions, 25 correct - Allen Area Under a Curve module, Do Yourself 1, 2, 3, 4, 5 and O2 — 51 questions, 46 correct - FIITJEE JEE (Main) archives, Applications of Derivatives — 45 questions, 39 correct - FIITJEE JEE (Main) archives, Determinants — 22 questions, 17 correct - Yellow Book, Complex Numbers, single-choice questions — 20 questions, 17 correct - Pink Book, Ellipses, single-choice questions — 16 questions, 14 correct - Yellow Book, Binomial Theorem, single-choice questions — 15 questions, 12 correct - Pink Book, Hyperbolas, single-choice questions — 21 questions, 18 correct - Allen Functions module, O1 and JEE (Main) archives — 48 questions, 44 correct Total: 268/60 questions, 232 correct

GRAND TOTAL: 744/400 questions, 607 correct

Upcoming tests:

23/06/2024 (next Sunday) — Allen monthly test. Topics: Kinetic Theory of Gases; Physical Thermodynamics; Electrostatics; Potential and Capacitance; Current Electricity; Electromagnetic Induction; Alternating Current; Electromagnetic Waves; Waves on a String; Sound Waves; Ray Optics; Wave Optics; Circle; Functions; Differentiation; Applications of Derivatives; Indefinite Integrals; Definite Integrals; Area Under a Curve; Differential Equations; Matrices; Silicates; Molecules That Do Not Exist; Coordination Chemistry; Metallurgy; Electronic Displacement Effects; Halogen Derivatives; Atomic Structure; Chemical Equilibrium; Solid State; Solutions; Chemical Kinetics; Chemical Thermodynamics. Yeah. I've no idea how I'm going to finish the syllabus in time, since I haven't even started Coordination Chemistry, Metallurgy or Alternating Current — they finished the classes in Allen before I even joined the batch. Anyway, let's see.

That'll be all till next week — see you again!

#studyblr #desi studyblr #study blog #jee 2025 #joint entrance examination #jee mains #jee advanced #weekly studyposting #porashona

25 notes · View notes