#Mathematical Infinity
Explore tagged Tumblr posts
Text
The Philosophy of Infinity
The concept of infinity has fascinated philosophers, mathematicians, and theologians for centuries. In philosophy, infinity refers to something that is unbounded or limitless. It challenges our understanding of the world, pushing the boundaries of human cognition and logical reasoning. Here's an exploration of the philosophy of infinity:
1. Mathematical Infinity
In mathematics, infinity is used in various contexts, such as the idea of an endless sequence of numbers, the concept of limits, and the notion of infinite sets. The work of Georg Cantor in the 19th century revolutionized the understanding of infinity by showing that there are different sizes of infinity, known as cardinalities. For instance, the set of all natural numbers is countably infinite, while the set of all real numbers is uncountably infinite, meaning there are more real numbers than natural numbers.
2. Metaphysical Infinity
Metaphysically, infinity often refers to the nature of the universe, God, or other ultimate realities. Philosophers like Aristotle and Aquinas discussed infinity in relation to the nature of the divine. Aristotle distinguished between potential infinity (a process that could continue indefinitely) and actual infinity (a completed state of infinity). Thomas Aquinas later used the concept of infinity to argue for the existence of an infinite being, God.
3. Epistemological Considerations
Infinity also raises epistemological questions about the limits of human knowledge. Can we truly comprehend infinity, or is it beyond the grasp of finite minds? Some philosophers argue that infinity is a useful theoretical construct but cannot be fully understood or visualized. Others suggest that our understanding of infinity is shaped by our cognitive and perceptual limitations.
4. Ethical Implications
The concept of infinity has ethical implications, particularly in the context of moral philosophy. For instance, the idea of infinite value or worth can influence discussions about human dignity and the sanctity of life. If each human life is considered to have infinite value, it could have profound implications for ethical decision-making and the prioritization of resources.
5. Infinity in Cosmology
In cosmology, infinity pertains to the nature of the universe. Is the universe finite or infinite in extent and duration? The concept of the infinite universe has been a topic of debate among philosophers and scientists alike. Some theories in modern physics, such as the multiverse hypothesis, suggest that there could be an infinite number of universes.
6. Infinity in Literature and Art
Infinity also appears in literature and art, often symbolizing the sublime, the eternal, or the boundless. Artists and writers use infinity to evoke a sense of wonder and to explore themes of eternity, the divine, and the limits of human experience.
The philosophy of infinity is a rich and complex field that intersects with many areas of human thought, from mathematics and metaphysics to ethics and cosmology. Infinity challenges us to think beyond the finite and to grapple with concepts that stretch the limits of our understanding. Whether in the precise language of mathematics or the profound reflections of metaphysics, infinity continues to inspire and perplex, pushing us to explore the boundaries of knowledge and existence.
#philosophy#epistemology#knowledge#learning#chatgpt#education#metaphysics#ontology#Philosophy Of Infinity#Mathematical Infinity#Metaphysical Infinity#Ethics#Cosmology#Infinite Universe#Human Knowledge#Georg Cantor#Aristotle#Thomas Aquinas#Infinity In Art#Sublime#Boundless#Eternal#Multiverse#Infinite Value#human psychology#infinity
6 notes
·
View notes
Text

#cantor#diagonalization#hilbert's hotel#some infinities are bigger than others#georg cantor#david hilbert#mathematics
3K notes
·
View notes
Text

#infinite monkey theorem#probability#shakespeare#infinity#literature#books#reading#mathematics#math#coriolanus#wronghands#john atkinson#webcomic#humor
66 notes
·
View notes
Text
I am not a plane Figure, but a Solid. You call me a Circle; but in reality I am not a Circle, but an infinite number of Circles, of size varying from a Point to a Circle of thirteen inches in diameter, one placed on the top of the other. When I cut through your Plane as I am now doing, I make in your Plane a section which you, very rightly, call a Circle. For even a Sphere – which is my proper name in my own country – if he manifest himself at all to an inhabitant of Flatland – must needs manifest himself as a Circle.
Edwin Abbott, Flatland: A Romance of Many Dimensions
59 notes
·
View notes
Text
∞ “math” bc im high on algebra (is this algebra?)
im high on math rn so hypothetically lets find yhr mean of ∞
so an example of mean is
(1 + 2 + 3) / 3
So,
(1 + 2 + 3…) / ∞
we have ∞/∞, which is 1. (The denominator is ∞ bc we have an infinite amt of numbers)
Howver, this is incorrect. We havent accounted for negatives. The mean would be 1 if ∞ was only positivr numbers (which its not)
(-1 + 1 - 2 + 2…) / ∞.
bc there is an equal amount of negatives amd positives, the mean of ∞ is 0.
also you can find thr mean bc ∞ is a set of numbers, aka all numbers
im probably wrong but this was fun
ps i will continue with median later
51 notes
·
View notes
Text
Something something heaven will be mine and gravity and girlmath something something axiom of choice
#when mathematical conundrums can be solved by saying#I am able to choose#that’s insane. that’s literally crazy#ASSERTION TO THE UNIVERSE: I am able to choose#and that like. enables infinities to go wild
8 notes
·
View notes
Note
Thank you for adding to my infinity post, and for doing it kindly! My mutual asked me for a fun fact about infinity, so I do the same to you!
One of my favourite things involving infinity is the construction of some interesting topological spaces!
You can construct the Long Line using the first uncountable cardinal, which is an example of a sequentially compact space that isn't compact!
Sometimes it's also possible to make "infinite dimensional" versions of some common topological spaces! This can be done if there is an inductive way of defining those spaces. For example, we can construct Sⁿ by gluing two copies of Dⁿ to Sⁿ along their boundaries. For S² this is exactly the construction of taking the equator (S¹) and gluing each hemisphere to the equator. Because this is inductive, we can define S^∞ to be the space we get at "the end" of the process. The formal way of doing this is with a categorical limit!
One fun fact about S^∞ is that it is contractible, that is we can deform it into a point (formally, S^∞ is homotopy equivalent to the one point space). But none of the finite spheres are!
#I hope this counts as facts about infinity#maths posting#maths#mathblr#mathematics#math#topology#lipshits asks
27 notes
·
View notes
Text
"It's truly fascinating how the concept of Infinity - a megalophobic-inducing terror, is simply played around and toyed with by a mathematician such as myself." - Nicodemus, 26 Feb 2025. 13 Hours And 16 Minutes Away From My First Exam.
8 notes
·
View notes
Text
Limits & Indeterminate Forms (Part 1)
Let's explore an indeterminate form: ∞ – ∞
First, it is important to wrangle with the fact that while evaluating the “limit of a function” and evaluating “the function itself” feel similar for many functions, these are NOT always equivalent processes.
We can see this graphically.
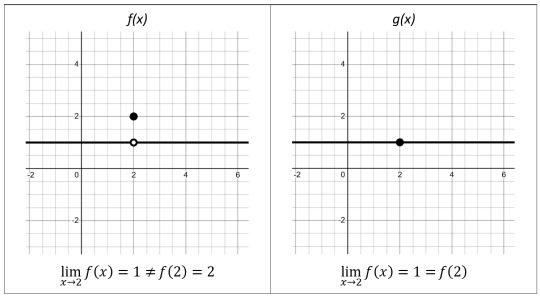
For f(x), f(2) does NOT equal the limit of f(x) as x approaches 2.
For g(x), g(2) DOES equal the limit of g(x) as x approaches 2
The result of evaluating a function isn’t quite as concrete as the result of evaluating a function because the function may not actually reach the result. This is particularly true for results of 0 and infinity.
On to the next point:
Not all infinities are the same size.
Let's examine two different functions: f(x) = 2x and g(x) = 5x.

The limit of f(x) = 2x, as x approaches infinity is ∞.
The limit of g(x) = 5x, as x approaches infinity is ∞.
But what about the limit of [f(x) – g(x)] as x approaches infinity? Or the limit of [g(x) – f(x)] as x approaches infinity? They would both be ∞ – ∞ … but what is that? Zero?

While we use the same symbol for the different infinities… they are not the same. A little bit of algebra, combining like terms, can help us see that the limit of (2x – 5x) as x approaches infinity approaches negative infinity. While the limit of (5x – 2x) as x approaches infinity approaches positive infinity.

∞ – ∞ is said to be “indeterminate”.
We cannot determine the value through directly evaluating the limits. Instead, we need to do more work, namely algebra.
For calculus, it helps the relative sizes of infinities as the speed or slope of the function. The slope of g(x) = 5x is greater than the slope of f(x) = 2x, so g(x) approaches infinity "faster", so the limit of g(x) as x approaches infinity is "bigger".
"∞" is a bit of a catch all that becomes more and more nuanced as you continue through math. In calculus, it is frequently used to help us compare rates of change. Later, we compare the size of infinite sets (for example, are there more natural numbers or more real numbers?). Each person's individual understanding of infinity tends to mirror the development of our collective understanding throughout history.
Questions to ponder:
When is evaluating a limit the same as evaluating a function?
What might some other indeterminate forms be?
Is ∞ + ∞ indeterminate? Why or why not?
Is ∞ * ∞ indeterminate? Why or why not?
#math#mathematics#calculus#calculus help#limit#limits#indeterminate form#infinity#I kinda suspect this won't help anyone but it's something I enjoy rambling about#one of the big sticking points for people new to calculus is the weirdness of infinity#embrace the weirdness#part of math is working with the weirdness until it becomes normal#infinity is like an eldritch horror and you just need to lose your mind a little bit for it to make sense
6 notes
·
View notes
Text
The Man Who Almost Broke Math (And Himself...)
Veritasium @veritasium
youtube
Georg Cantor
3 March 1845 - 6 January 1918
Infinity
03/04/2025, thursday 3 april 2025, 01:10 a.m, indore, madhya pradesh, india.
#Georg Cantor#GeorgCantor#Veritasium#@veritasium#Veritasium@veritasium#Veritasium @veritasium#math#maths#mathematics#infinite#infinity#♾️#Youtube
3 notes
·
View notes
Text
In the philosophy of mathematics, the abstraction of actual infinity, also called completed infinity, involves the acceptance (if the axiom of infinity is included) of infinite entities as given, actual and completed objects. These might include the set of natural numbers, extended real numbers, transfinite numbers, or even an infinite sequence of rational numbers. Actual infinity is to be contrasted with potential infinity, in which a non-terminating process (such as "add 1 to the previous number") produces a sequence with no last element, and where each individual result is finite and is achieved in a finite number of steps. This type of process occurs in mathematics, for instance, in standard formalizations of the notions of an infinite series, infinite product, or limit.
Wikipedia
14 notes
·
View notes
Text
When the math doesn't math
I started playing Honkai Star Rail.
And the first world, I encountered this woman who asked me a 'simple' math question. Which are there more of, prime or natural numbers.
And the game made a point of mocking me for choosing Natural ones. "Because they're both equal."
Whaaaaaaat? Is this about the number scale being infinite? Because I promise you, infinity isn't a number, it's a concept. And two infinite quantities aren't equal.
For instance. How many natural numbers exist between 0 and 100. The answer is 100.
How many prime numbers, however? 25.
Already we have the inequality. Natural numbers are clearly winning here.
And the gap doesn't close as you go on. There are an infinitely more number of composite numbers than prime ones.
Think of it this way. How many decimals exist between one and two? An infinite number. So on a number scale, decimals are already infinite when natural numbers are going from one to two.
Infinities are not equal. They scale differently.
Or is my head the thing that's not working properly here? is my logic faulty? Are the number of primes equal to the number of natural numbers?
I'd appreciate insight.
55 notes
·
View notes
Text
Unorthodox Kitten is my favorite internet "horror" other than _boisvert. The most abstract high-concept story I've ever seen, I've grown obsessed with it due to the themes and the sheer creativity.
youtube
#text post#internet horror#weird#weird fiction#analog horror#mathematics#mathematical fiction#infinity#Youtube
5 notes
·
View notes
Text

2 notes
·
View notes
Text
The Philosophy of Set Theory
The philosophy of set theory explores the foundational aspects of set theory, a branch of mathematical logic that deals with the concept of a "set," which is essentially a collection of distinct objects, considered as an object in its own right. Set theory forms the basis for much of modern mathematics and has significant implications for logic, philosophy, and the foundations of mathematics.
Key Concepts in the Philosophy of Set Theory:
Definition of Set Theory:
Basic Concepts: Set theory studies sets, which are collections of objects, called elements or members. These objects can be anything—numbers, symbols, other sets, etc. A set is usually denoted by curly brackets, such as {a, b, c}, where "a," "b," and "c" are elements of the set.
Types of Sets: Sets can be finite, with a limited number of elements, or infinite. They can also be empty (the empty set, denoted by ∅), or they can contain other sets as elements (e.g., {{a}, {b, c}}).
Philosophical Foundations:
Naive vs. Axiomatic Set Theory:
Naive Set Theory: In its original form, set theory was developed naively, where sets were treated intuitively without strict formalization. However, this led to paradoxes, such as Russell's paradox, where the set of all sets that do not contain themselves both must and must not contain itself.
Axiomatic Set Theory: In response to these paradoxes, mathematicians developed axiomatic set theory, notably the Zermelo-Fraenkel set theory (ZF) and Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC). These formal systems use a set of axioms to avoid paradoxes and provide a rigorous foundation for set theory.
Set Theory and the Foundations of Mathematics:
Role in Mathematics: Set theory serves as the foundational framework for nearly all of modern mathematics. Concepts like numbers, functions, and spaces are all defined in terms of sets, making set theory the language in which most of mathematics is expressed.
Mathematical Platonism: The philosophy of set theory often intersects with debates in mathematical Platonism, which posits that mathematical objects, including sets, exist independently of human thought. Set theory, from this perspective, uncovers truths about a realm of abstract entities.
Philosophical Issues and Paradoxes:
Russell's Paradox: This paradox highlights the problems of naive set theory by considering the set of all sets that do not contain themselves. If such a set exists, it both must and must not contain itself, leading to a contradiction. This paradox motivated the development of axiomatic systems.
Continuum Hypothesis: One of the most famous problems in set theory is the Continuum Hypothesis, which concerns the possible sizes of infinite sets, particularly whether there is a set size between that of the integers and the real numbers. The hypothesis is independent of the ZFC axioms, meaning it can neither be proven nor disproven within this system.
Axioms of Set Theory:
Zermelo-Fraenkel Axioms (ZF): These axioms form the basis of modern set theory, providing a formal foundation that avoids the paradoxes of naive set theory. The axioms include principles like the Axiom of Extensionality (two sets are equal if they have the same elements) and the Axiom of Regularity (no set is a member of itself).
Axiom of Choice (AC): This controversial axiom asserts that for any set of non-empty sets, there exists a function (a choice function) that selects exactly one element from each set. While widely accepted, it has led to some counterintuitive results, like the Banach-Tarski Paradox, which shows that a sphere can be divided and reassembled into two identical spheres.
Infinity in Set Theory:
Finite vs. Infinite Sets: Set theory formally distinguishes between finite and infinite sets. The concept of infinity in set theory is rich and multifaceted, involving various sizes or "cardinalities" of infinite sets.
Cantor’s Theorem: Georg Cantor, the founder of set theory, demonstrated that not all infinities are equal. For example, the set of real numbers (the continuum) has a greater cardinality than the set of natural numbers, even though both are infinite.
Philosophical Debates:
Set-Theoretic Pluralism: Some philosophers advocate for pluralism in set theory, where multiple, possibly conflicting, set theories are considered valid. This contrasts with the traditional view that there is a single, correct set theory.
Constructivism vs. Platonism: In the philosophy of mathematics, constructivists argue that mathematical objects, including sets, only exist insofar as they can be explicitly constructed, while Platonists hold that sets exist independently of our knowledge or constructions.
Applications Beyond Mathematics:
Set Theory in Logic: Set theory is foundational not only to mathematics but also to formal logic, where it provides a framework for understanding and manipulating logical structures.
Philosophy of Language: In philosophy of language, set theory underlies the formal semantics of natural languages, helping to model meaning and reference in precise terms.
The philosophy of set theory is a rich field that explores the foundational principles underlying modern mathematics and logic. It engages with deep philosophical questions about the nature of mathematical objects, the concept of infinity, and the limits of formal systems. Through its rigorous structure, set theory not only provides the bedrock for much of mathematics but also offers insights into the nature of abstraction, existence, and truth in the mathematical realm.
#philosophy#epistemology#knowledge#learning#education#chatgpt#ontology#metaphysics#Set Theory#Mathematical Logic#Axiomatic Systems#Zermelo-Fraenkel Set Theory (ZF)#Axiom of Choice#Russell's Paradox#Continuum Hypothesis#Infinity#Cantor’s Theorem#Mathematical Platonism#Constructivism#Set-Theoretic Pluralism#Philosophy of Mathematics#Naive Set Theory#Formal Semantics
6 notes
·
View notes
