#infinity is like an eldritch horror and you just need to lose your mind a little bit for it to make sense

[existinglimits]

Limits & Indeterminate Forms (Part 1)

Let's explore an indeterminate form: ∞ – ∞

First, it is important to wrangle with the fact that while evaluating the “limit of a function” and evaluating “the function itself” feel similar for many functions, these are NOT always equivalent processes.

We can see this graphically.

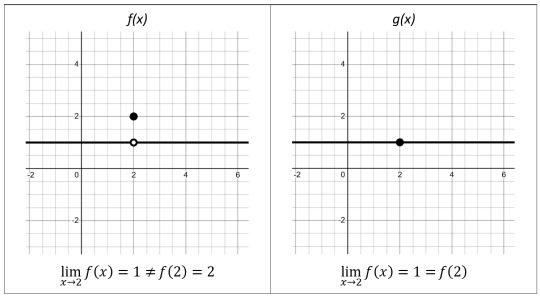
For f(x), f(2) does NOT equal the limit of f(x) as x approaches 2.

For g(x), g(2) DOES equal the limit of g(x) as x approaches 2

The result of evaluating a function isn’t quite as concrete as the result of evaluating a function because the function may not actually reach the result. This is particularly true for results of 0 and infinity.

On to the next point:

Not all infinities are the same size.

Let's examine two different functions: f(x) = 2x and g(x) = 5x.

The limit of f(x) = 2x, as x approaches infinity is ∞.

The limit of g(x) = 5x,  as x approaches infinity is ∞.

But what about the limit of [f(x) – g(x)] as x approaches infinity? Or the limit of [g(x) – f(x)] as x approaches infinity? They would both be ∞ – ∞ … but what is that? Zero?

While we use the same symbol for the different infinities… they are not the same. A little bit of algebra, combining like terms, can help us see that the limit of (2x – 5x) as x approaches infinity approaches negative infinity. While the limit of (5x – 2x) as x approaches infinity approaches positive infinity.

∞ – ∞ is said to be “indeterminate”.

We cannot determine the value through directly evaluating the limits. Instead, we need to do more work, namely algebra.

For calculus, it helps the relative sizes of infinities as the speed or slope of the function. The slope of g(x) = 5x is greater than the slope of f(x) = 2x, so g(x) approaches infinity "faster", so the limit of g(x) as x approaches infinity is "bigger".

"∞" is a bit of a catch all that becomes more and more nuanced as you continue through math. In calculus, it is frequently used to help us compare rates of change. Later, we compare the size of infinite sets (for example, are there more natural numbers or more real numbers?). Each person's individual understanding of infinity tends to mirror the development of our collective understanding throughout history.

Questions to ponder:

When is evaluating a limit the same as evaluating a function?

What might some other indeterminate forms be?

Is ∞ + ∞ indeterminate? Why or why not?

Is ∞ * ∞ indeterminate? Why or why not?