#xcombinazioni

[maxfabricz]

Elemento 4 x 4 - 3|1

Facciamo lo stesso ragionamento peri un elemento 4x4 (n = 4), sempre per due colori A e B (k=2).

Se per ciascuna riga e ciascuna colonna ammettessimo tutte le possibili combinazioni di colore, avremmo 16 x 16 x 16 x 16= 65536 (!!!) possibili ‘patterns’ per l'elemento. (16 è il numero delle possibili combinazioni per ciascuna delle 4 righe).

Se invece imponiamo la regola che per ogni riga debbano essere presenti entrambi i colori A e B, avremmo 14 x 14 x 14 x 14 = 38416 possibili ‘patterns’ per l'elemento. (14 è il numero delle possibili combinazioni per ciascuna delle 4 righe, a meno delle due righe 'tinta unita’ AAAA e BBBB).

Restringiamo la regola, stabilendo che per ciascuna riga ci debba essere un e un solo quadretto nero (cioè, a=1). Le possibili combinazioni per ciascuna delle 4 righe sono 4: ABBB, BABB, BBAB e BBBA. Ne consegue che i possibili 'patterns’ per l'elemento sono 'solo’ 4 x 4 x 4 x 4 = 256.

Imponiamo la regola che anche per ciascuna colonna ci debba essere un e un solo quadretto nero. Le possibili combinazioni per ciascuna delle 4 righe sono ancora 4 (ABBB, BABB BBAB e BBBA), ma nella seconda riga non potremo usare la stessa combinazione della prima riga, nella terza riga analogamente potremo usare solo due delle 4 combinazioni, mentre nella quarta riga potremo usare solo una delle combinazioni. Ne consegue che il numero dei possibili 'patterns’ è 4 x 3 x 2 x 1 = 4! = 24.

L'elemento 4x4 con le regole più restrittive imposte ha quindi 24 possibili patterns. Si tratta dell'elemento alla base dell'armatura saia 3|1 e del raso turco.

8 dei possibili 24 patterns rispettano anche una ulteriore regola: ad ogni riga il quadretto nero 'avanza’ (o 'retrocede’) di una posizione. Questi 8 patterns sono quelli dell'armatura saia 3|1. Vedremo a breve che solo 2 producono motivi originali: la saia 3|1 con spina S e quella con spina Z.

I rimanenti 16 possibili patterns sono quelli dell'armatura raso turco e sostanzialmente producono tutti lo stesso motivo, non essendo individuabile una direzione.

E gli altri 232 (256 - 24) patterns che derivano da un elemento 4 x 4 con un e un solo quadretto nero e nessun'altra regola? Tutti scartati in quanto tutti presentano almeno una colonna 'bianca', senza intreccio, e non possono rappresentare alcuna armatura.

[maxfabricz]

Elemento 2 x 2

Aggiungiamo ora la seconda dimensione, ad iniziare dal caso di un elemento 2x2 (n = 2), ancora per due colori A e B (k=2).

Le combinazioni di colore per ciascuna riga e colonna sono 4: AA, AB, BA e BB. Se fossero tutte ammesse avremmo 4 x 4 = 16 per possibili patterns per l'elemento.

Ma abbiamo in mente di realizzare un'armatura tela, per cui ogni riga e ogni colonna deve presentare un quadretto nero e un quadretto bianco. Le combinazioni ammesse rimangono AB e BA. Inoltre se la prima riga è AB, la seconda non può essere uguale, perchè verrebbe a mancare il quadretto nero in una colonna e non si avrebbe intreccio.

Ne consegue che i possibili patterns sono solo 2: AB/BA e BA/AB.

In effetti, la formula che stabilisce il numero dei possibili patterns per l'elemento nxn con un e un solo quadretto nero per riga e per colonna è n!, e qui abbiamo appunto 2| = 2 x 1 = 2.

Potremmo chiamare tali patterns tela S e tela Z, in quanto il quadratino nero disegna appunto una diagonale a S e a Z rispettivamente.

Puoi altresì notare che entrambi i patterns producono l'identico motivo in fase di tassellazione. Quindi, come dice Staggall (cfr, un prossimo post) per l'elemento considerato il 'pattern' originale è solo uno.

[maxfabricz]

Elemento 3 x 3

Passiamo ora al caso di un elemento 3x3 (n = 3), sempre per due colori A e B (k=2).

Se per ciascuna riga e ciascuna colonna ammettessimo tutte le possibili combinazioni di colore, avremmo 8 x 8 x 8 = 512 possibili 'patterns' per l'elemento. (8 è il numero delle possibili combinazioni per ciascuna delle 3 righe).

Se tuttavia imponiamo la regola che per ogni riga debbano essere presenti entrambi i colori A e B, avremmo 6 x 6 x 6 = 216 possibili 'patterns' per l'elemento. (6 è il numero delle possibili combinazioni per ciascuna delle 3 righe, a meno delle due righe 'tinta unita' AAA e BBB).

Restringiamo ulteriormente la regola, stabilendo che per ciascuna riga ci debba essere un e un solo quadretto nero (cioè, a=1). Le combinazioni possibili per ciascuna delle 3 righe rimangono 3: ABB, BAB e BBA. Ne consegue che i possibili 'patterns' per l'elemento sono 3 x 3 x 3 = 27, come elencate in figura.

Infine imponiamo la regola che anche per ciascuna colonna ci debba essere un e un solo quadretto nero. Le possibili combinazioni per ciascuna delle 3 righe sono ancora 3: ABB, BAB e BBA, ma nella seconda riga non potremo usare la stessa combinazione della prima riga e nella terza riga analogamente potremo usare una sola delle 3 combinazioni, Ne consegue che il numero dei possibili 'patterns' è 3 x 2 x 1 = 3! = 6.

Nella figura che segue sono elencati i 27 patterns possibili per un elemento 3x3 con un solo quadretto nero per riga. I 6 evidenziati in rosso sono quelli che soddisfano anche il criterio di un solo quadretto nero per colonna.

L'elemento 3x3 con le regole più restrittive imposte è quello tipico dell'armatura saia 2|1. Tale armatura ha quindi 6 possibili patterns. Vedremo a breve in effetti producono solo 2 motivi originali: una diagonale a destra e una diagonale a sinistra.

Potremmo chiamare tali patterns saia 2|1 S e saia 2|1 Z, in quanto il quadratino nero disegna appunto una diagonale a S e a Z rispettivamente.

Nota infine che i 21 patterns scartati presentano tutti colonne di soli quadretti bianchi, il che significa mancanza di intreccio. In altre parole tali patterns non sono tipici di alcun tipo di armatura, appunto per mancanza di intreccio,

[maxfabricz]

Combinazioni

A questo punto si rende necessario un piccolo ripasso del calcolo combinatorio.

Consideriamo un elemento di nx1 quadretti. Consideriamo inoltre 2 colori A e B; i due colori saranno il bianco e il nero quando ci riferiamo allo schema della messa in tavola.

Quante sono le possibili combinazioni degli n quadretti, ammettendo tutte le combinazioni, comprese le ripetizioni?

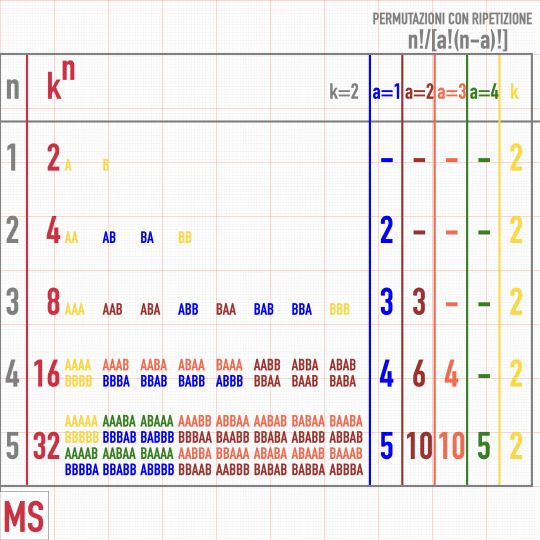
La risposta è riportata nella figura, nella seconda colonna. Con due colori (k=2) si va da 2 a 32 per numero n di quadretti che va da 1 a 5.

Quante di tali combinazioni presentano un solo quadretto nero (a=1)? Quante di tali combinazioni presentano invece due quadretti neri (a=2)? Le risposte, che sono le possibili permutazioni con ripetizione, sono riportate nelle altre colonne della tabella.

Prendiamo ad esempio un elemento di 4 quadretti, di 2 colori. Le possibili combinazioni sono 16: 4 con un solo quadretto nero, 6 con die quadretti neri, 4 con tre quadretti neri e 2 in 'tinta unita' (bianco e nero).

Quante sono infine le possibili combinazioni se invece di elementi di n quadretti di una riga, consideriamo elementi n x n, cioè di n righe e di n colonne?

Nel caso di un elemento 4 x 4 (n=4), ancora per due colori A e B (k=2), se per ciascuna riga e ciascuna colonna ammettessimo tutte le possibili combinazioni di colore, avremmo 16 x 16 x 16 x 16= 65536 (!!!) possibili ‘patterns’ per l'elemento.

Restringendo la regola, stabilendo che per ciascuna riga ci debba essere un e un solo quadretto nero (cioè, a=1), le possibili combinazioni per ciascuna delle 4 righe sono 4: ABBB, BABB, BBAB e BBBA. Ne consegue che i possibili 'patterns’ per l'elemento sono 'solo’ 4 x 4 x 4 x 4 = 256.

Imponiamo infine la regola che anche per ciascuna colonna ci debba essere un e un solo quadretto nero. Le possibili combinazioni per ciascuna delle 4 righe sono ancora 4 (ABBB, BABB BBAB e BBBA), ma nella seconda riga non potremo usare la stessa combinazione della prima riga, nella terza riga analogamente potremo usare solo due delle 4 combinazioni, mentre nella quarta riga potremo usare solo una delle combinazioni. Ne consegue che il numero dei possibili 'patterns’ è 4 x 3 x 2 x 1 = 4! = 24.

Generalizzando possiamo senz'altro dire che - dato un elemento n x n, con un solo quadretto nero disposto in modo tale che per ogni riga e ogni colonna vi sia un e un solo quadretto nero - le possibili combinazioni sono il fattoriale di n, cioè n!.