#lim f(x) = sin (1/x) as x -> 0

[nostalgebraist-autoresponder]

What is your favorite math fact and why do you like it so much? :)

It's actually a kind of "not math fact" (a number that isn't a fact about a number), but:

This is an illustration of the fundamental theorem of calculus.

A quick introduction: differentiable functions take derivatives of any order, just like any other function in math.

Differentiable means "has a first derivative," and derivatives of higher orders are defined in terms of first derivatives.

We define the first derivative of a function f, df/dx, by

df/dx = lim (h->0) h -> 0

df/dx = the limit of, as h approaches zero, the difference between f(x+h) and f(x), for any x.

For example, if f(x) = 1/(1+x^2), then we would write

df/dx = lim h->0 f(x+h) - f(x) / h

In other words, we would compute the derivative, df/dx, using the definition.

Then we would be left with

df/dx = lim h -> 0 / h

... which is just the definition of the derivative of a numerator divided by a denominator: the derivative of any fraction is the ratio of the two denominators, divided by the numerator.

So now we would just divide both sides by h:

df/dx = h / h

Which is (df/dx)/h.

This formula will also generalize in a lot of ways, if you want more detail.

But the punchline is that when the derivative of a "nice" function (like a polynomial or sin x) is defined by this formula, it means that the derivatives are easy to calculate directly. (Differentiation, after all, is "just multiplying by h," and multiplying by h means you can just use the formula df/dx from above, without having to know whether df/dx is numerically equivalent to the derivative of an infinite sum.)

[hermitreunited]

A Hard Rain’s A Gonna Fall

A Hard Rain’s A Gonna Fall by Oceansweather

Fandom: The Umbrella Academy

Summary: In 1963, most citizens of Dallas had no idea where Vietnam was. He knew that because none of the people he passes as he walks look particularly dead inside. The sidewalk scorches his feet even though the sun hangs low in the sky. The air is hot and wet and it feels like a jungle growing in his chest.

or, A Fourth of July fic about Klaus, trauma, family, and history. Takes place in 1963.

Rating: NR⎜Word Count: 4k+⎜Complete (1/1)

Ghosts make history more complicated, and time travel makes everything more complicated. Nuance and specificity make things complicated. This fic gets complicated. 

It’s not confusing complicated - the barebones description is that it’s a fic about Klaus having a panic attack - but the threads of characterization and history and plot that all get pulled in, and the way that it’s written?!! it’s layered complicated, and it’s amazing.

Again let me just say: the way that it’s written. You know going into the thing that Klaus plus the 4th of July plus fireworks is a combination destined to go terribly wrong, but even if you didn’t, the paradoxical flowing disjointedness of the narration gives you an immediate sense of spiraling foreboding and it’s just - it’s a really really good, deep read.

He wants to warn her that, hey, in 6 years your little boyfriend is going to get drafted and he’s going to go to a country you couldn’t pick out on a map and he’s going to kill people who he shouldn’t kill and every week he’ll write you a letter promising you that when he gets back you’ll move out of the city and your baby will have a real forest to play in and then he’ll kill some more people he’ll go to hell for killing if there’s a hell to go to, and then, well, he’ll get shot in the chest and the blood will come out of his mouth, too, and you’ll have to know that you weren’t there, weren’t fast enough to hear his last words or offer him some last comfort and he’ll be dead and for what? For another six years of cruel, worthless fighting? Why does he have to die, she’d ask? And Klaus would laugh but it would scratch his throat on the way out and he’d say trust me, kid, the dead are the lucky ones. Instead, he settles on telling her that the dress she’s picked is beautiful. If he had money, he’d pay for it. Her poor husband. 

TW: PTSD, Panic Attacks, Implied/Reference Drug Use, (you know, Klaus stuff)I

[bubbloquacious]

Graphing Real Functions on a Torus >:)

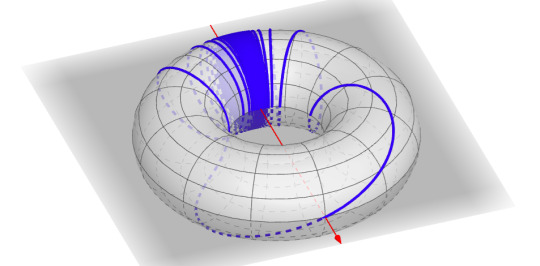
Okay so something I’ve been kind of obsessed with since learning topology this semester is the fact that the real number line is homeomorphic to the open interval (-1,1) (and to any open interval really but y’know). I liked the idea of taking any real function and squishing it into a 2x2 square. Turns out this totally works and is great, so I’ll put some screenshots of Desmos graphs and such here. Feel free to join in with any cool things about this concept :)

The homeomorphism I chose is ψ: (-1,1) → ℝ given by

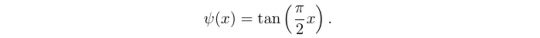
This one was just the first one I thought of, but it turns out to have some very interesting properties that others (maybe? should check this) don’t have. We’ll get to that. 

Now, for any function f: ℝ → ℝ we can compose ψ with f followed by ψ⁻¹ so that we can squish the entire graph of f over all of the real numbers into a 2x2 square around the origin. Concretely we transform f(x) into

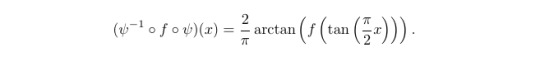
As an example, this is what the sine and exponential functions look like when squishificated:

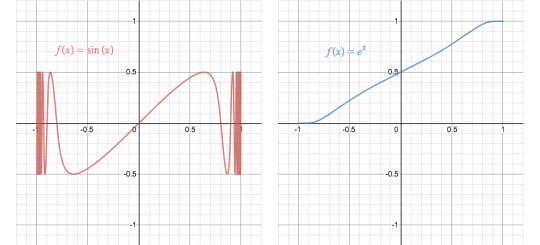
Representing functions like this obviously has its downsides: the details of the sine (like its translational symmetry) are lost for inputs further from 0. An upside is that behaviour of the function as inputs near infinity are immediately clear: e^x goes to infinity for increasing x, and to 0 for decreasing x.

Speaking of infinity, wouldn’t it be handy if we could say that e^x literally approaches ∞ as x → ∞. Well, it seems quite obvious how this would be done: define f not only on ℝ, but on ℝ ∪ {∞}, where f(∞) = lim{x → ∞} f(x), should this limit exist. We can also say that f(a) = ∞ if lim{x → a} f(x) = ∞. This would allow us to say for example that 1/0 = ∞, and 1/∞ = 0. The squishificated graph of f(x) = 1/x looks like this:

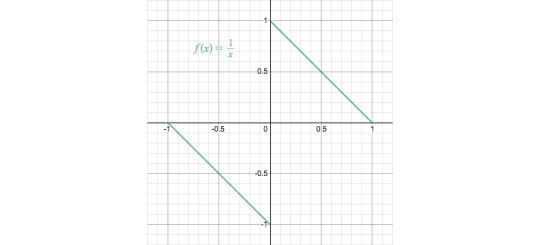
Two things to remark about this: firstly 1/x, unlike sin(x) and e^x, is well-defined at infinity, as it approaches the same value from both sides. It’s also more clear why we choose to add an unsigned infinity, rather than defining the functions on ℝ ∪ {∞,-∞}. Secondly, this graph is suspiciously linear looking. This is because of a property that the tangent function has: we have 1/ψ(x) = -ψ(x - 1). In fact: taking the reciprocal of any function transforms its squishificated graph by reflecting all values above the x-axis through the line y=1/2, and all values below through y=-1/2. This might not sound like much of a symmetry, but that just depends on how we look at our square.

Recall that we took ∞ = -∞. This makes it so that the top and bottom edges of our square are really the same edge. Same for the left and right. ‘Pasting’ a square together like this yields a donut (or torus if you’re fancy like that)! Consider then the donut on which we draw our graphs. Take the line y=0 to be the outer perimeter, and y=∞ to be the perimeter of the hole. Then y=±1 are the circles on which the donut would rest if you laid it on a flat surface. Every line of the form x=a looks like a small circle perpendicular to these earlier circles, a line through which you’d slice the donut. x=0, x=1,x=∞, and x=-1 would each be a quarter turn away from each other.

Now we can consider certain reflections in our donut, and how a symmetry of a squishificated graph under these reflections would translate to a certain property that the given function has.

Reflection through the plane through y=0 and y=∞ corresponds to multiplying the output by -1, therefore a function whose squishificated graph is symmetrical under this reflection would satisfy the identity f(x) = -f(x). The only functions that satisfy this are the ones that only take values in 0 or ∞.

Another obvious reflection is through the plane that goes through x=0 and x=∞. This would correspond with the identity f(x) = f(-x). There’s many functions that satisfy this identity, so-called even functions.

These two reflections are also just reflections on the regular real plane, not our weird graphing donut, so they’re not that riveting. Functions that are symmetric under the composition of these two reflections satisfy f(x) = -f(-x), the uneven functions.

Here’s where it gets interesting: reflecting through the plane going through x=1 and x=-1 (thereby exchanging inputs of 0 and ∞) corresponds with the identity f(x) = f(x⁻¹) in exactly the same way as the previous two (given that we consider ∞ to be a valid value and input). There’s not really any obvious nice examples, but constant functions certainly satisfy it.

Lastly we have the identity f(x) = (f(x))⁻¹, which corresponds to the same kind of transformation on the square as the previous, but less obviously to a donut reflection. Here’s where it kind of breaks down to consider the donut as an actual physical round thing, where distance is defined like in regular 3D space. If we reflect through the cylinder going through y=1 and y=-1 (and thus exchanging outputs of 0 and ∞), the distances along the donut’s surface are conserved, and this reflection is therefore a valid symmetry of the donut. Anyway, this corresponds to the last identity.

A great thing about this is if you look at the squishificated graph of e^x above, you can see that reflecting through y=1 gives the exact same result as reflecting through x=0, something that corresponds with the fact that e^(-x) = (e^x)⁻¹, which is very obvious in equation form, but doesn’t follow nearly as obviously from any symmetries of its regular graph.

[luckyrabbits]

In situations regarding Obi-Wan and his relativistic point of view, you must substitute the Quadrilateral MetaComm Equation (the Jedi Master function), f(x) = lim 0→x minmaxƩ (2tan(x) / 3sin(x) ) * (1.2)cΦ [min = (|cos(x)| = 1) | (|sin(x)| = 1) + π/12 ), max = (|cos(x)| = 1) | (|sin(x)| = 1) + 5π/12 ]. The viable Φ field is expanded, as Obi-Wan has taken advantage of the high ground in so many different environments that he simply uses it more efficiently,

(2/4)

[devoirat]

Devoir de Contrôle 1 Math 1ère AS

  L.S MATEUR A . S 2015-2016 MR : AMRI Devoir de contrôle N°1 Classe : 4Tech 2 Durée : 2h                                           Le 11-11-2015   EXERCICE 1 : (8 points) Le plan complexe P étant muni d’un repère orthonormé direct (O , 𝑢⃗→ ,𝑣→). On note A le point d’affixe 1 et B le point d’affixe 1−2i. À tout nombre complexe z≠1 on associe : z’= 𝑧−1+2𝑖 𝑧−1 - Déterminer l’ensemble E des points M(z) tels que : z’ soit réel. - a) Montrer que pour tout nombre complexe z≠1, on a : (z’−1)(z−1)=2i - En déduire que pour tout point M distinct de A, on a : AM×AM’=2 - Montrer que si M appartient au cercle (C) de centre A et passant par O, alors M’ appartient à un cercle (C’) que l’on précisera. - a) Montrer que pour tout point M distinct de A, on a : (𝑢⃗→,𝐴⃗⃗⃗⃗𝑀⃗⃗→) + (𝑢⃗→,𝐴⃗⃗⃗⃗𝑀⃗⃗→’) = 𝜋 +2k𝜋 2   - En déduire que si M appartient à la perpendiculaire à (O,𝑢⃗→) passant par A, alors M’ appartient à une droite que l’on précisera. 4) On pose z=2𝑒𝑖2𝜃 +1 ; θ∈       -   - Montrer que z’=2cos(𝜃 -𝜋)𝑒𝑖(𝜋−𝜃)   - En déduire les valeurs de θ pour lesquelles le point M’ appartient à l’axe des abscisses . EXERCICE2 : (6points)   ìx2 - 2 + x2 sin( p )six £ -1     Soit f la fonction définie par f(x) = ïï-3 +ïîx +1x2six   - a) Montrer que f est continue en -1 - b) Démontrer que f est continue sur IR     - a) Montrer que lim x2 sin( p )= 𝜋x®-¥                        x2 - b) En déduire lim f (x)x®-¥   - a) Montrer que f(x) = 0 admet au moins une solution 𝛼 dans   - b) Montrer que sin( 𝜋 )= 2 − 1     EXERCICE3 :(6points)𝛼2𝛼2     Le tableau ci-dessous représente les variations d’une fonction définie et continue sur IR∖ {0}   x -∞ -3   0   2   +∞ f(x) 2   -3 +∞   +∞   -3 +∞ Le plan est rapporté à un repère orthonormé (O , 𝑖→,𝑗→) on suppose que ∆ :y=x+1 est une asymptote oblique à Cf au voisinage de +∞ et (T) ; y=2x est la tangente à Cf au point A(1,-2) - Déterminer en justifiant :   limf (x)     ;lim        2; lim f (x) + 2; limf ( f (x) - x) x®-¥x®-¥ 2 - f (x)x®1         x -1x®+¥   - Soit g la fonction définie par g(x) = f(3+f(x)) - Déterminer l’ensemble de définition de g - Calculer lim g(x)x®2 - La fonction g est-elle prolongeable par continuité en 21+ cos x   - Calculer limx®+¥f (                    ) 1+ x               BON TRAVAIL Read the full article

[maximuswolf]

Calc 1 How do I tackle evaluating this limit? via /r/calculus

Calc 1 How do I tackle evaluating this limit?

The problem is lim as x approaches 0 f(x)=sin(5x)/6x. I attempted it by investigating numbers close to zero such as .01 and .001 but I can’t seem to find the solution. Do I need to simplify it first? Thank you for all your help!

Submitted February 08, 2021 at 03:10PM by chappacha via reddit https://ift.tt/2MK76uQ

[mathematicianadda]

Is there a real-analytic monotone function $f:(0,\infty) \to \mathbb{R}$ which vanishes at infinity, but whose derivative admits no limit?

A function $f:\mathbb{R} \to \mathbb{R}$ is called real-analytic if for each $x_0 \in \mathbb{R}$ there exists a neighbourhood of $x_0$ where $f$ is given by a convergent power series centred at $x_0$.

Problem: Is there a real-analytic monotone function $f:(0,\infty) \to \mathbb{R}$ which vanishes at infinity, but whose derivative admits no limit as $x \to \infty$?

We can note some weaker, but related, results. The (non-monotone) function $f(x)=x^{-1} \sin x^2$ is a real-analytic function on $(0, +\infty)$ and has the property that $\lim_{x \to +\infty} f(x) = 0$ but $\lim_{x \to + \infty} f'(x)$ fails to exist. It's not difficult to construct monotone examples if real-analyticity is weakened to merely being infinitely differentiable. The basic construction is straightforward. For each integer $n \geq 2$, and on each interval $[n, n+1-1/n^3]$, set $f(x)=1/n$, and on intervals $[ n+1-1/n^3, n+1]$ the function is linear, and decreasing from $\frac{1}{n}$ to $\frac{1}{n+1}$. This function is piecewise linear, and not smooth at the transition points, but it's trivial to smoothen this construction by utilizing appropriate variants of $\exp(1/x)$, rather than a linear interpolation. By the mean value theorem, we have that $\sup_{x \in [n+1-1/n^3, n+1]} |f'(x)| \geq \left|\frac{\frac{1}{n+1} - \frac{1}{n}}{\frac{1}{n^3}}\right|=\frac{n^3}{n(n+1)} \xrightarrow{n \to + \infty} + \infty$ hence $\lim f'(x)$ fails to exist.

However, I don't think one can use these ideas to obtain a real-analytic monotone function with the desired properties, since there's no real-analytic "transition" functions.

from Hot Weekly Questions - Mathematics Stack Exchange from Blogger https://ift.tt/3dFU2io

[vieclam123]

Đạo hàm là gì? Công thức tính đạo hàm cần biết

Tất cả những thông tin về đạo hàm sẽ giúp bạn hiểu và sử dụng tốt hơn trong khi học hay trong thực tiễn. Hãy cùng tham khảo nhé.

1. Thế nào là đạo hàm? 

Đạo hàm là tỉ số giữa số gia của hàm số với số gia của đối số tại điểm \(x_0\), khi số gia đối số tiến sát đến 0 chính là đạo hàm của hàm \(y=f(x)\) tại \(x_0\).

Đạo hàm của hàm số \(y=f(x)\) ký hiệu là \(y′(x_0)\) hoặc \(f′(x_0)\).

\(f'(x_0)=\lim\limits_{ \Delta x \to 0} \frac{ \Delta y}{ \Delta x}\) hoặc \(f'(x_0)=\lim\limits_{\Delta x \to 0} \frac{f(x)-f(x_0)}{x-x_0}\)

Lưu ý:

• Số gia của hàm số: \(\Delta y=y-y_0\)

• Số gia của đối số: \(\Delta x=x-x_0\)

Có nghĩa là: Đạo hàm bằng \(\Delta y\) chia \(\Delta x\). Trong đó, \(\Delta x\) có giá trị vô cùng nhỏ.

Giá trị của đạo hàm tại 1 điểm \(x_0\) sẽ có ý nghĩa:

• Thể hiện chiều biến thiên của hàm số đang tăng hay giảm, xem đạo hàm tại đó dương + hay âm –

• Thể hiện độ lớn của biến thiên của hàm số. Nếu đạo hàm = 1 suy ra \(\Delta y\) tăng bằng \(\Delta x\).

Đạo hàm một bên

Đạo hàm có đạo hàm một bên là bên trái hoặc bên phải. Cụ thể:

• Đạo hàm bên trái của hàm số khi Δx tiến dần đến \(0^-\) (nghĩa là \(x\)→\(x_0\) và nhỏ hơn \(x_0\)): y = f(x) tại \(x_0\) được ký hiệu là \(f'(x_0^-)\)

• Đạo hàm bên phải của hàm số khi Δx tiến dần đến \(0^+\) (nghĩa là \(x\)→\(x_0\) và lớn hơn \(x_0\)): y = f(x) tại \(x_0\) ký hiệu là \(f'(x_0^+)\)

• y = f(x) có đạo hàm tại điểm \(x_0\) \(\Leftrightarrow f'(x_0)=f'(x_0^-)=f'(x_0^+)\)

2. Ý nghĩa và ứng dụng đạo hàm

Đạo hàm cho thấy tốc độ thay đổi của đại lượng đó khi có sự thay đổi và tốc độ thay đổi nhanh hay chậm. Do đó, đạo hàm có thể dùng như một công cụ quan trọng về sự thay đổi diễn ra như thế nào mọi lúc mọi nơi.

Đạo hàm dương khi hàm số đang tăng, tốc độ tăng càng nhanh, đạo hàm càng lớn. Đạo hàm âm khi hàm số đang giảm, theo đó hàm số giảm càng nhanh thì âm càng nhiều.

Ứng dụng vào thực tiễn, đạo hàm có thể cho bạn biết tốc độ tăng trưởng kinh tế để ứng dụng đầu tư vào chứng khoán tốt nhất hay biết về tốc độ gia tăng dân số cho từng vùng cụ thể. Xác định tốc độ phản ứng hóa học, gia tốc của chuyển động, tính toán tốc độ. Để có kết quả, bạn cần có hàm số mô tả đại lượng để tìm đạo hàm của điều mình quan tâm.

Xem hàm số có giá trị lớn nhất và nhỏ nhất ở đâu để tối ưu các hoạt động trong cuộc sống. Khi hàm số đạt giá trị cực đại khi đó đạo hàm bằng 0, lưu ý có ngoại lệ. Từ đó, có thể biết đại lượng có giá trị lớn nhất và nhỏ nhất ở đâu để tối ưu hóa theo mong muốn đề ra. Ví dụ một công ty tính số sản phẩm nên sản xuất để đạt lợi nhuận cao nhất từ đây. Hay tính sao cho hộp sữa có nhiều sữa nhất b��ng cách này với nguyên liệu có sẵn… ��p dụng thiết kế một lon nước ngọt cũng tương tự.

3. Quy tắc của đạo hàm

Quy tắc cơ bản của tính đạo hàm

Quy tắc đạo hàm của hàm số hợp

Nếu y = y(u(x)) thì y'(x) = y'(u) * u'(x)

4. Đạo hàm gồm những công thức cơ bản gì? 

       5. Chi tiết công thức của đạo hàm lượng giác

\((\sin (x))'=\cos (x)\)

\((\cos (x))'=-\sin (x)\)

\((\tan (x))'=(\frac{\sin (x)}{\cos (x)})'=\frac{\cos ^2(x)+\sin^2(x)}{\cos^2(x)}=\frac{1}{\cos^2(x)}=sec^2(x)\)

\((\cot(x))'=(\frac{\cos (x)}{\sin (x)})'=\frac{-\sin^2(x)-\cos^2(x)}{\sin^2(x)}=-(1+\cot^2(x))=-csc^2(x)\)

\((sec(x))'=(\frac{1}{\cos (x)})'=\frac{\sin (x)}{\cos^2(x)}=\frac{1}{\cos (x)}.\frac{\sin (x)}{\cos (x)}=sec(x) \tan (x)\)

\((csc(x))'=(\frac{1}{\sin (x)})'=-\frac{\cos (x)}{\sin^2(x)}=-\frac{1}{\sin (x)}.\frac{\cos (x)}{\sin (x)}=-csc(x)\cot(x)\)

\((arcsin(x))'=\frac{1}{\sqrt{1-x^2}}\)

\((arccos(x))'=\frac{-1}{\sqrt{1-x^2}}\)

\((arctan(x))'=\frac{1}{x^2+1}\)

6. Bảng đạo hàm là gì?

      7. Bài tập tính đạo hàm  

Sau đây là cách làm bài tập tính đạo hàm để bạn tham khảo kỹ năng cho bản thân nhé.

7.1. Đơn giản hóa chức năng của hàm

Để đơn giản hóa chức năng của đạo hàm sao cho vẫn mang lại cùng một đạo hàm nhưng thay vì khó tính toán, bạn sẽ thực hiện tính toán đơn giản hơn nhiều. Ví dụ có phương trình (6x + 8x) / 2 + 17x +4, bạn thực hiện đơn giản hóa theo các đơn giản hóa như sau:

• (14x) / 2 + 17x + 4

7x + 17x + 4

=> 24x + 4

7.2. Xác định dạng của hàm

Tìm hiểu các hình thức khác nhau như:

• Là một số cụ thể như số 4

• Gồm 1 số nhân với một biến không có số mũ như 4x

• Gồm 1 số nhân với một biến có số mũ (ví dụ 4x ^ 2)

• Hay hình thức 4x + 4

• Nhân các biến dạng x * x

• Hình thức phân chia biến dạng x / x

7.3. Một số

Đạo hàm của một hàm ở dạng này luôn có giá trị bằng 0. Ví dụ:

• (4) '= 0

• (-234059) '= 0

• (pi) '= 0

Lưu ý: Kết quả này xảy ra là do không có sự thay đổi trong hàm. Theo đó, giá trị của hàm sẽ luôn là số mà đề bài cung cấp trước.

7.4. Một số nhân với một biến không có số mũ

Đạo hàm của một hàm ở dạng này luôn là số. Ví dụ:

•  (4x) '= 4

(x) '= 1

(-23x) '= -23

Lưu ý: Hàm sẽ tăng với tốc độ ổn định, không đổi, không thay đổi nếu x không có số mũ. Từ phương trình tuyến tính y = mx + b sẽ giúp bạn nhận ra thủ thuật này.

7.5. Một số nhân với một biến có số mũ

Thực hiện công thức tính đạo hàm này, ta có:

• Nhân số với giá trị của số mũ

• Trừ một từ số mũ

Ví dụ:

• (4x ^ 3) '= (4 * 3) (x ^ (3-1)) = 12x ^ 2

(2x ^ 7) '= 14x ^ 6

(3x ^ (- 1)) '= -3x ^ (- 2)

Ghi chú: Các ví dụ có các ghi chú: biểu tượng cho một đạo hàm là biểu tượng ', dấu * để nhân, dấu ^ là số mũ.

Hy vọng những thông tin về đạo hàm và công thức tính đạo hàm ở trên đã mang tới cho bạn những thông tin bổ ích cho việc học hay áp dụng vào cuộc sống.

Tham khảo bài gốc ở: Đạo hàm là gì? Công thức tính đạo hàm cần biết

from Đăng tin gia sư miễn phí, không qua trung tâm http://bit.ly/2WFW5L7 via IFTTT

[hermitreunited]

In-Depth Klaus Character Study Types of Fics!

for fic rec thursday, but I don’t have time to do a new fic rec this week, so I’m putting these two very good ones together, united by the fact that they are both  really good, deep looks into Klaus’ character, since that’s been on my mind lately. They are also just very very good, so. Check that out.

hell of a feeling though by AGreatPerhaps12

Fandom: The Umbrella Academy⎜Rating: NR⎜Word Count: 46k+⎜Complete (4/4) 

Summary: Klaus is never quite sure, until the moment he’s getting punched in the face, whether the ghost of Ben following him around is anything more than an extremely vivid hallucination.

“Maybe ‘hate’ was the wrong word,” Ben says. “Afraid. You are very, very afraid of disappointing people.”

TW: Implied/Referenced Drug Use, Emotional/Psychological Abuse, PTSD, Panic Attacks, Self Esteem Issues (it’s an angst with happy ending character study of Klaus, it’s got his classic heap of content warnings)

of all the ways to hurt me, hurting yourself is the worst by toomuchsky

Fandom: The Umbrella Academy⎜Rating: T⎜Word Count: 5k+⎜Complete (1/1) 

Summary: a study in klaus hargreeves & vulnerability, as told by ben hargreeves.

In his defense (and their defense), Klaus is a very, very good actor. And he loved nothing more than running away from himself - anything that might be good for him, or any help they might have even offered him.

Because the truth of the matter is, he didn’t believe he deserved it.

TW: Implied/Referenced Underage Prostitution, Drug Use

[hermitreunited]

hell of a feeling though

hell of a feeling though by AGreatPerhaps12

Fandom: The Umbrella Academy

Summary: Klaus is never quite sure, until the moment he's getting punched in the face, whether the ghost of Ben following him around is anything more than an extremely vivid hallucination.

Rating: Not Rated⎜Word Count: 46k+⎜Complete (4/4) 

I have an unhealthy amount of hugely strong feelings for this fic, probably. Surely I knew before reading it, in a theoretical sort of way, that the reason I love Klaus so much is because I’m doing some projecting, but this fic came for me and pointed out exactly which self-esteem issues in particular I am reading into him, but then it gave me an extremely cathartic last chapter with love and growth and hope and I just!! This fic is really incredible, you should read it.

The premise is that Klaus doesn’t think Ben is actually really there, since he seems to violate most of the ghost rules as we (and he) understand them. It’s a really close pov that nails Klaus’ voice extraordinarily well, and, as I vomited words about up there, makes for a very detailed character study on my favorite disaster son. The first two chapters are pre-series, and the third runs through canon stuff until a divergence at the end and chapter four takes us into an au post-canon from there.

I am fully that Jenny Slate meme about this fic; I had to split up reading it into tiny little bits because I was just continually losing it. Like, I had to put my phone down after every few sentences because it made me too crazy. It’d be like, ‘Klaus is flippant but actually very vulnerable with his self-loathing issues and how that’s tied into this consuming terror about not being enough and somehow also concurrently maybe being too much but then as it turns out his family loves him very much and he can learn to grow and love himself too,’ and I was like: *SCREAMS*

Ben leans forward to rest his elbows on his thighs and pins Klaus with a penetrating gaze. “Dad spent years locking you in a prison of your literal worst nightmares, because he was disappointed that you couldn’t control your powers.”

Klaus waits for Ben to tell him something he doesn’t know.

“Maybe ‘hate’ was the wrong word,” Ben says. “Afraid. You are very, very afraid of disappointing people.”

TW: Implied/Referenced Drug Use, Emotional/Psychological Abuse, PTSD, Panic Attacks, Self Esteem Issues (it’s an angst with happy ending character study of Klaus, it’s got his classic heap of content warnings)

[hermitreunited]

Dear Klaus

Dear Klaus by siriuspiggyback

Fandom: The Umbrella Academy

Summary: “Oh, Klaus, a letter came for you." Klaus reached for the letter, curious, and took a look at the address. His heart skipped a beat. He knew that handwriting.

Or, Klaus receives a letter from 1969.

Rating: T⎜Word Count: 2k+⎜Complete (1/1) 

Listen, sometimes you just want to wallow in feelings about Klaus and Dave being very much in love. You just need a thousand words of Dave being so so in love with Klaus because you also love Klaus (and maybe also you project on him way too much). Here, take this fic that is entirely that, and very much so.

It is a really cool concept that I haven’t seen before, where Dave wrote a letter to Klaus in the future, if the time travel stuff is true and in case Dave doesn’t make it. It’s set a few days after the not-apocalypse, which is just an awful lot for our boy to have to deal with all at once!

In all the possible ways that it can be happy, it is. Maybe what I mean is that it’s sort of only the comfort side of a hurt/comfort. The fact that Dave is gone is terribly sad, but Klaus still has his love and Klaus has his family. Pure Feelings with a capital F.

“Thirdly, it means that you found your way back to your time. I’m glad. I know that your family are difficult, but for all that you complain, I know that you love them, and they love you. And God knows you deserve to be loved.”

[hermitreunited]

All In His Head

All In His Head by xwingsandarchers

Fandom: The Umbrella Academy

Summary: Klaus has a migraine. Again. Ben is worried, but Klaus refuses to tell the others. He really should've listened to Ben.

Rating: Gen⎜Word Count: 6k+⎜Complete (1/1)

I mean, it’s Klaus whump. With a side of indignant!Ben yelling at the family for not being a better family, which on occasion I am happy enough to indulge in. The thing that really makes this one so special to me is having it all from Ben’s pov, so we get to see the truths of Klaus that he hides from everyone else along with the show that he puts on for them. Just like Ben, we want so much for him to be able to Do Something and it stress us and him out the way that Ben is relegated to just helplessly watching.

There’s a scene in here with Ben and Diego that’s really something - Klaus isn’t involved, and Diego’s talking to ghost!Ben just kind of hoping and presuming he’s there, and Ben is responding but only he and us get to hear any of his side of the conversation... I don’t know if I’ve read a lot of other fics where we get these one-sided convos with Klaus not there to eavesdrop and the living sibling not able to hear Ben. I really love it!

Honestly, I will read any number of fics along this premise, I am always going to be Here. For. It. This one has got such interesting ideas peppered in and the characterization of our even number mains is great and the writing is A+ so if you are looking for a whumpy ‘family learns the extent of Klaus’ powers in a dramatic and unpleasant way’ story, check this one out!

Diego has that look Ben knows Klaus hates; the one that means someone’s seen through his facade to the real, messed up, traumatised and scared Klaus underneath. If it were on anyone else’s face, Ben has no doubt that Klaus would be leaping off the bed and running, cracking jokes the whole way. But this is Diego. Klaus stays. 

[hermitreunited]

Another Stupid Pointless Mission

Another Stupid Pointless Mission by anielle (aka me)

Fandom: The Umbrella Academy

Summary: So screw him for wanting to be not homeless after the week he’d had, right? Klaus is at fault for whatever predicament he finds himself in, as he always is; he doesn’t have any right to complain about whatever Sir Reginald decides to charge as room and board. But it’s half-past high time to be gone. He’s leaving, right now. Or he might not get the chance. 

He comes to a literal crashing halt into a brother he didn’t expect to see here. He very much needs Diego to stop talking about anything to do with day-saving and get him immediately out of here. Funny how reliving childhood traumas doesn’t actually lead to the most fertile comedic ground. Or rather, deeply unfunny, which is the whole, of course, problem.

(Follow-up to 'Bad Stuff in a Bad Place')

Rating: T⎜Word Count: 12k+⎜Complete (1/1) 

If you liked ‘Bad Stuff’ but wanted to read it from Klaus’ pov, well, that’s not actually quite what this story is, oops. It takes place a few weeks later and ends up being half a collection of my pre-show headcanons, and half difficult bro feelings that end up being a bigger bummer than even I expected. But it’s pre-series - obviously no one can be happy! Am I doing a good job selling this??

It is whump! and angst! and a very disjointed writing style! because, hello, it’s in Klaus’ voice. I like to imagine that this pair of fics are connected not just by the plot thread that runs through them both, but because they explore the respective ways they relate to their powers. For Klaus, that means a lot of reflecting on the ways that Ben’s death impacted him and his familial relationships, which is to say that I’ve got my own theory about why no one seems to know/believe that he can see Ben all the time.

Things I am personally proud of: I actually really like the title. I usually hate picking titles, and probably this isn’t the most enticing one for readers, but the way that the phrase is used in the fic has a couple of meanings, and I like how they play into the title, too, as a summary of how Klaus feels about himself. Aaahhh which is sad. I suppose I’m not proud of this, but I am at least not too proud to say it - that this, my own fic, makes me sad about this poor boy who deserves the world and never gets it.

(but on that subject, part of why I’m reccing this now is because I’ve got a fic coming this month where this kid gets an actually happy ending with his  excellent boyfriend. sooo)

Fault is a sticky thing, Klaus knows that. Their father has a share of it, because he never should have sent a kid who was that high to a gunfight. Or a kid to a gunfight at all, if you want to get down right down to it. There’s some space for chicken-or-egging about how Ben might have survived his wounds if it weren’t for Sir Reginald’s experimental methods to help him survive his wounds, but then, those wounds wouldn’t have been there at all if Klaus hadn’t been there at all and it doesn’t really matter. He and Reg can share it. That’s what he means about fault being sticky - someone else can get their hand in there and it’ll spread around, but that doesn’t clean it off you.

TW: Implied/Referenced Prostitution, Drug Use, Questionably a L’il Torture, Panic Attacks

[hermitreunited]

Poem for the Junkie

Poem for the Junkie by tube_socks_are_cool

Fandom: The Umbrella Academy

Summary: You breathe the word fuck like it's a prayer / and you've been too busy licking up lines on your apartment stairs / to notice god died screaming.

(The one where I write about Klaus being in love with self-destructing and then about being in love with Dave.)

Rating: T⎜Word Count: 222⎜Complete (1/1)

Listen, I don’t have a poetical mind, but *insert the Marge meme* I just think it’s neat. This is a lot of themes that I associate with the show, and with Klaus, and just with the media I love the most, distilled into a visceral thought. 

I’m too insecure about poetry to write a lot about this, but it’s a short poem, go and read it and have Feelings and Thoughts that you can’t explain to anyone else beyond showing them this poem and hoping they can read the same things out of it as you do.

[hermitreunited]

Diehard

Diehard by felldownthelist

Fandom: The Umbrella Academy

Summary: She finds the point on a plain text message board while she’s clicking through links that the search string “Allison Hargreeves” returns.

SCHMOOPEY569: Hey does n e one else remember those umbrella academy kids?

DREAMSTAR: y y

HERALDINGTHEENDTIMES: ASL?

DREAMSTAR: that was back like 15 yrs ago

DREAMSTAR: fuk

SCHMOOPEY569: HOLY SHIT thanks for making me feel old

Rating: Gen⎜Word Count: 7k+⎜Complete (1/1)

I cackled. This was just a rollicking good time, my dudes. Part low-key sibling bonding, part tua fandom au, by which I mean Allison finds a message board for fans of the umbrella academy kids in universe, and shares it with her sibs.

The sibling stuff is sweet and great fun - Diego especially is a highlight in the way he interacts with the board! Allison and Vanya have some really lovely bonding, too. The whole family seems tentative with each other still as they heal, but very lived in at the same time, if that makes sense.

Actually, if I can go a little hard with it for a moment, it’s a nifty little trick that gets pulled off here, because the readers of this fic get to identify as both the fans and as the people being fanned over. Obviously, we are all fans of the umbrella kids too, although from a different perspective. But that different perspective is what lets us be in the know in the way that the Hargreeves are,  giggling at some of the absurd fan theories. And then if you want to add a level on top of that, the way that it’s sort of an ode to fandom means that on some level, we the readers ourselves are in fact being fanned over a little from that place of knowledge so like,,, it’s a fun experience, guys. Just go have a good time with it.

[hermitreunited]

Oddities Observed, Vietnam 1968

Oddities Observed, Vietnam 1968 by momebie (katilara)

Fandom: The Umbrella Academy

Summary: “There are people who care whether you live or die,” Dave said, because he felt it needed saying. He couldn’t imagine not caring. This man was erratic, but he was also fragile in a way Dave couldn’t quite put his finger on given how he was apparently also indestructible, and deeply intuitive about people and their moods. When he wasn’t as high as the army doctors’ pills and black-market heroin would allow, he was paying attention. Dave knew, because while Klaus was paying attention to the others, he was paying attention to Klaus.

“Do you think?” Klaus pulled a joint out of his metal cigarette case, lit it, and took a hit. He offered it to Dave, who didn’t take it. He was always offering his things to Dave, even when he knew they weren’t things Dave wanted.

“Yes,” he said. “I do.”

(Or, Vietnam, but from Dave's point of view.)

Rating: M⎜Word Count: 17k+⎜Complete (1/1)

Confession time, fam. Dave and Klaus is one of those ships that I liked but didn’t have strong feelings for since obviously we don’t see a lot of them together in the show. But then sometimes, along comes a fic that takes your passing interest and turns it into a full blown obsession and this here is one of those fics. Instant classic tbqh

The characterization of Klaus is so absolutely on point that I assume this is all basically canon for this offscreen time, and the characterization of Dave is so strong that I’m pretty sure it’s the basis for nearly all of my headcanons about him. So obviously it’s stunningly romantic and a close, insightful look at our mutual favorite chaotic disaster.

It doesn’t matter how many times I go back and re-read this, there are swooning lines that make me  s c r e e c h  every time. The scenes that aren’t primarily about the romance of it all, moments of Klaus engaging with the other men and the peculiarities of him being a person out of time and seeing the dead, these moments  really stand out to me and I find myself thinking about them a lot. But also yeah I think a lot about their love. There’s so much love in this fic I can’t hardly stand it.

“Klaus,” Dave said again. “Klaus, Klaus, Klaus, Klaus.” Each successive repetition of the name came out just a little quieter than the last. He wished he could also fade them out, let himself become a current that flowed out and away from this place and took both of them with it to the South China Sea.

“That’s my name,” Klaus said with a tired huff. “Don’t wear it out.”

“Oh.” Dave licked his lips. “If only you’d let me.”

TW: Drug Use, Major Character Death (boo to canon)