#joseph fourier

[isomorphismes]

Test functions and [tempered] distributions require the notion of topological vector space … distributions can be traced back to Green's functions in the 1830’s to solve ordinary differential equations … the 1936 work of Sergei Sobolev on hyperbolic PDE’s.

Laurent Schwartz introduced the term "distribution" by analogy with a distribution of electrical charge, possibly including not only point charges but also dipoles and so on.

tempered distribution

topological vector space

(^ if there is a dipole, there must be a notion of subtraction, hence the need for a vector, and to speak of this very conceptually, use a TVS)

[inkliinng]

46 pages in, and there is literally so much. In every chapter. About every character. I cannot fathom 900+ pages of this without my brain turning to mush partway through.

[lindahall]

Georg Ohm – Scientist of the Day

Georg Simon Ohm, a German physicist and mathematician, was born Mar. 16, 1789. Ohm was attracted to the mathematical physics of Joseph Fourier...

learn more

[scotianostra]

26th June 1824 saw the birth of William Thomson, Lord Kelvin, eminent physicist.

Although born in Belfast, Thomson was brought up in Scotland, his father was Professor of Mathematics at Glasgow University and his son took lesson there from the age of ten.

Kelvin attended university classes from the age of 10. He wrote his first scientific paper, under the pseudonym 'PQR', aged only 16.

In his teens he learned French well enough to read the work of eminent French mathematician Jean Baptiste Joseph Fourier. Philip Kelland, Professor of Mathematics at Edinburgh University, had criticised Fourier's work on the theory of heat. Kelvin boldly stated that Kelland was wrong – and later scientists agreed with him.

From 1841 to 1845 Kelvin attended Cambridge University. He was an excellent student – although he shocked his father by spending his allowance on a boat.

After graduating, Kelvin worked in a Paris laboratory with physics professor Victor Regnault.

Kelvin was influenced by the mathematical ideas of George Green, a self-taught miller's son from Nottingham.

He later brought an essay of Green's to the attention of fellow mathematicians and physicists by republishing it in a respected scientific journal. Until then the essay on mathematical analysis, electricity and magnetism had gone largely unnoticed.

In 1846, aged only 22, Kelvin returned to Glasgow to become Professor of Natural Philosophy. He remained in this post for 53 years. Keen to see students involved in practical experiment, he established what became the first university physics laboratory.

Kelvin continued to study the nature of heat. He realised that it would be useful to be able to define extremely low temperatures precisely. In 1848, he proposed an absolute temperature scale, now called The Kelvin Scale.

After further research, Kelvin formulated the second law of thermodynamics. This states that heat will not flow from a colder to a hotter body.

His interest in the transmission of electricity prompted Kelvin's appointment as Director of the Atlantic Telegraph Company in 1856.

The company was to install a cable under the Atlantic Ocean. Atlantic Cable Expeditions in 1857, 1858 and 1865 failed, but communication by cable finally succeeded in 1866.

Kelvin received a knighthood for his efforts in this project.

From 1870 onwards, Kelvin spent many summers on his yacht 'Lalla Rookh', and invented several marine instruments to improve navigation and safety.

He introduced a mariner's compass more accurate than any other in existence, and a machine to predict tide levels worldwide.

In 1884 Kelvin travelled to the United States to give a series of lectures. These were enthusiastically received, and were published in 1904 as the 'Baltimore Lectures'.

Kelvin became a Lord in 1892 and took the name Kelvin because of his Glasgow connections. By the time of his death in 1907, he was an international celebrity, widely respected and honoured.

His success as a synthesizer of theories about energy places him in the same position in 19th-century physics as Sir Isaac Newton has in 17th-century physics or Albert Einstein in 20th-century physics.

Lord Kelvin may have been a smart cookie, but, as seen in te last pic, he got the future of fllight way wrong, I wonder what he thought when the Wright Brothers flwq the first airplane four years before he passed away......

[dailyanarchistposts]

Climate Change and Capitalism

The concept of human-caused climate change is not new. Joseph Fourier first discussed the greenhouse effect in 1824 and suggested human activities could influence global temperatures. Other famous names of chemistry and physics such as Tyndall, Arrhenius and Bell developed this theory and understood its implications. By the early twentieth century there was an understanding in the scientific community that burning fossil fuels could alter the earth’s climate.

By the 1970s, public awareness of the issue had grown and the scientific community began to develop models of how CO2 emissions would affect the future climate. During this period, the oil company Exxon conducted a great deal of research into climate change and global climate modelling. Their findings threatened the company’s profits, so they suppressed the research and instead spent money on a misinformation and lobbying campaign to limit public acceptance and government regulation (see Environmental Research Letters: Bibliography). This was largely successful, with successive governments in the USA and elsewhere questioning the science of climate change and limiting regulation of CO2, despite overwhelming scientific consensus. Misinformation of the public has been supported by many media outlets controlled by the ruling class, allowing governments to stall environmental regulation and treat climate change as a fringe issue.

In more recent times, we’ve seen even the right wing move from the climate denial of George W. Bush to the acceptance of environmental policy by the mainstream. For example, consider David Cameron’s ‘hug a husky’ greenwash. Whilst greenwashing has conceded some small victories, many of the major global players are still delaying any meaningful action as far as possible, whilst promoting false ‘green capitalism’ solutions. Others have accepted climate change, but denied the human cause or that we can do anything about it. Donald Trump claimed in 2016 that climate change was a hoax promoted by China to weaken the economy of the USA, neatly bringing together both economic nationalism and climate denial. By painting the issue as one of national defence and economic necessity, Trump has managed to cast further doubt on the need to lower carbon emissions.

Environmental pollution is one of the great failures of the free market. Fossil fuels are cheap because CO2 is a ‘negative externality’; that is, the cost of emitting it, namely the threat of global environmental change, is not borne by the companies responsible but by society at large. Private companies, therefore, have little incentive to reduce CO2 emissions, and the costs of their products are kept artificially low by this societal subsidy. These emissions have no market value — they add nothing to the cost of a product and yet have huge ramifications for the global climate. The market, therefore, cannot be relied on to fix this problem. The options available to us are to either control the market so that environmental costs are considered, e.g. state capitalism, or to remove the market’s control over our lives altogether.

The longer we delay action on climate change, the more difficult to fix the problem becomes. This pamphlet proposes that the only way to achieve meaningful change is to abandon the capitalist model; to reclaim the energy and production systems from their corporate owners, and bring them into the hands of the people. This is no small task, but offers an escape from the multiple environmental disasters we currently face. We also point out that state power expands in times of crisis and, as such, we must be careful of solutions which increase the power of the state to control our lives. To achieve this, we must consider the maxim of ‘think globally, act locally’ and work towards decentralised solutions which give control of energy and production systems to the people who use them, for the benefit of the whole global ecosystem.

[canmom]

tempted to start pretending Charles Fourier and Joseph Fourier were the same person and telling people the Fourier transform was invented by a utopian socialist who believed we should all live in communes which sometimes fight each other by having massive orgies. because wouldn't it be cool if that was true

[aedislumen]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

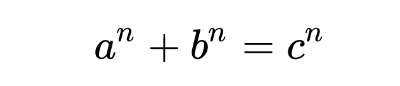
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[inspofromancientworld]

The Science of Discovering the Past: Paleoclimatology

While paleoclimatology or palaeoclimatology is the study of climate predating the narrow span of time we've had instruments to measure it directly and can therefore cover any point in time in the entire history of the world, understanding the past climate of human development allows us to understand human migration, development, and diet. The idea of a changing climate likely began in ancient Egypt, China, and Mesopotamia where prolonged droughts or floods were part of the rise and fall of various dynasties. Historical climatology focuses on the 'effect of climate on civilizations from the emergence of homininis [about 8-4 million years ago] to the present day'. As such, it studies primary sources such chronicles, maps, local histories, paintings, and even rock art, as well as archaeological artifacts. Where there are no records, the techniques of paleoclimatology are used, such as the study of tree rings and ice cores as well as sedimentary rocks.

One of the first writers to write about how humans affect the climate of the land was Theophrastus, an ancient Greek philosopher, who noted in the 4th century BCE that draining marshes made the land more likely to freeze and clearing forests made the land warmer due to receiving more sunlight. In the 1st century BCE, Vitruvius, Roman architect and writer, wrote about selecting the location of cities and the type of architecture based on the local climate.

During the European Renaissance, scholars recorded how deforestation, irrigation, and animal grazing altered the lands of the Mediterranean in records of ancient Greece and Rome, finding it plausible that human interventions caused changes in weather patterns. In 1088, Shen Kuo, Northern Song dynasty sccholar and statesman, wrote in support of climate change based on the discovery of petrified bamboo under the Yanzhou, a dry and arid region, now part of the Yan'an Shaanxi province, which is quite different to the warm, wet climate bamboo typically grows in.

In the 18th and 19th centuries, colonizers who changed forests into cropland noted that doing so shifted the local climate within the course of a human lifetime, with the saying 'rain follows the plow', though others noted that deforestation caused increased run-off and flooding, potentially reducing rainfall as local evaporation patters were shifted. There was also European chauvinism at the time where European academics claimed that the lands inhabited by the 'Caucasian race' were 'naturally superior for the spread of civilization…that the Orientals of the Ancient Near East had heedlessly converted their once lush lands into impoverished deserts'.

By the late 18th century, it was increasingly accepted that there were prehistoric epochs of climate, some of which included glacial advancements across the land, resulting in 'erratics', or boulders that were deposited by glaciers and are far from areas where they were native as was proposed in 1815 by Jean-Pierre Perraudin of those erratics he found in the Val de Bagnes. George-Louis Leclerc, Comte de Buffon, French naturalist, mathematician, and cosmologists, proposed that Earth 'had begun as an incandescent globe and was very gradually cooling' within his Historie Naturelle.

In 1824, Joseph Fourier reasoned that the Earth's atmosphere kept it warmer than it would have been without one and that the atmosphere is inefficient in transmitting infrared light that is emitted by the sun and by the land, acting as an insulator He focused on the changes in land use and how that affected the radiation balance. In 1837, Lois Agassiz developed the theory and term 'Ice Age', a time when glaciers covered much of Europe and North America. John Tyndall continued Fourier's work in 1859, proving that water vapor, hydrocarbons, and carbon dioxide block infrared radiation, increasing the insulation effect of the atmosphere. In the 1890s, scientists worked on finding the infrared radiation of the Moon and found that their measurements were weaker when the Moon was close to the horizon due to the increase in the amount of atmospheric carbon dioxide (CO2), blocking the infrared radiation from the Moon. By 1896, Savante Arrhenius calculated that doubling of atmospheric CO2 could lead to a total warming of 5-6 degrees Celsius. In 1901, Nils Gustaf Ekholm coined the term 'greenhouse effect' for the warming caused by increases of greenhouse gases.

Milutin Milanković (Милутин Миланковић), also spelled Milankovitch, began studying how orbital mechanics effected the paleoclimate with Julius von Hann. They studied the works of John Herschel, astronomer, and Louis Agassiz, geologist, as well as Joseph Adhemar, who pioneered the idea that astronomical changes could cause ice ages. He began with describing how the angle through which the Sun's rays passed through the atmosphere affected the climate in 1912 and 1913. Wilhelm Wien used Milanković's theories to calculate the degree of insolation, the power per unit area received from the sun, to develop a mathematical theory of climate zones. In 1916, he calculated that Mars had an average surface temperature of -17°C and a harsh climate, dampening the belief that there was liquid water on the surface of Mars. Milanković also calculated the change in insolation over the course of 130,000 years based on the procession of the Equinoxes, which effects where in the Earth's orbit the seasons fall. At present, the Northern Hemisphere summer is at the aphelion, when the Earth is farther from the sun, though this was not always the case. In addition to this, he also calculated axial tilt over time and the eccentricity, or how far from circular, of the orbit of the Earth. Between 1925-1928, he wrote Through Distant Worlds and Times, a popular science book that discussed the 'history of astronomy, climatology, and science via a series of imaginary visits to various points in space and time'. He spent much of his career refining his calculations, including pushing his calculations further back in Earth's history as well as working in research on continental drift.

[tastethebloodofmeatthawsmoth]

"If one says to them (i.e., to the civilized) that our swirl of approximately two hundred comets and planets presents but the image of a bee occupying a single cell in the hive; that the other fixed stars, each one surrounded by such a swirl, represent other planets, and that the whole of this vast universe, in its turn, counts only as a single bee in a hive formed of approximately a hundred and thousand sidereal universes, the ensemble of which comprises a biniverse, that then comes the triniverse formed from several thousand biniverses, and so on; finally, that each one of these universes, biniverses, triniverses is a creature, having, like us, its own soul, its own phases of youth and old age, death and birth…….; they will not follow this theme to its end, they will cry out against the insanity, the outrageous daydream; and yet they pose in principle the universal analogy!" - Charles Fourier, quoted by Joseph Dejacque in The Humanisphere

[yourdailyanticistamines]

Yves Saint Laurent: Transparencies - Part 2

Near the end of the exhibition, we got to see the working space of Yves Saint Laurent, which had mostly been preserved since his retirement and death. It was one thing to see his works, which were polished and complete, but another to see his office that was cluttered with books, sketches, and fabrics. It was like being inside his brain. As I stood inside the place where Saint Laurent made history, I felt admiration and awe.

I realized soon after that the emotions I felt there were the exact same as what I felt when I visited the graves of famous mathematicians earlier in the morning at the Cimetière du Père-Lachaise. Math is a lot like fashion, in that the specifics are highly technical, but the value of the finished work is almost entirely dependent on subjective notions of beauty, creativity, and novelty, which are heavily determined by current trends. At least, that is how it is in a short timeframe, but only the works that are truly beautiful stand the test of time. Joseph Fourier died in 1830; his name frequently appears in three different math and physics classes I’m taking this semester, and I will most likely be doing things that are heavily based on his work for the rest of my life. It’s the same with fashion - people will probably still remember Christian Dior’s New Look or Coco Chanel’s little black dress hundreds of years from now.

Looking for graves of significant people, especially mathematicians, physicists, artists, and composers, is a regular hobby of mine. I wasn’t exactly sure myself why I like grave hunting until I visited Saint Laurent’s office and Fourier’s grave - I think I have a desire to leave something beautiful and timeless in the world too.

[okamiz36]

PIXELS ARE NOT SQUARES.

'You may well ask, If a pixel is not a little square, then what is it? And those tiny colored squares on the screens we stare at all day—if they are not pixels, what are they?

To answer these questions, Smith takes us on a grand tour, starting in Napoleonic France, where Jean Baptiste Joseph Fourier proclaimed that the world is made of waves. This idea is easy to grasp when it’s applied to a one- dimensional signal such as music, where the sound produced by an entire symphony orchestra can be decomposed into a set of pure sinusoidal waves of various frequencies. Fourier showed that the same process also works in two or three dimensions. For example, patterns of light and dark in a photograph can be represented by waves extending across the width and height of the image.

But waves are not pixels. Sine waves are smooth and continuous; pixels, whether or not they are little squares, are discrete objects. To get from waves to pixels, Smith leaps ahead a century, from the aftermath of the French Revolution to that of the Russian one, when Vladimir Kotelnikov invented the sampling theorem. Kotelnikov showed that you can capture all the information in a waveform without tracing out the details of its undulations. It’s enough to take samples at discrete points, as long as those points are spaced closely enough that the highest frequency component of the wave is sampled twice in every cycle. Those sample sites, Smith informs us, are the true pixels. They are not little squares but dimensionless points where the wave amplitude is measured. From a set of such point-like samples, the complete image (or sound wave, or any other signal) can be fully reconstructed. And the reconstruction is not just a good approximation; it’s exact. No information is lost in the sampling process.

If pixels, properly understood, are sample points, we are left with the question of what to call all those little squares of color that light up the screen of your phone or computer or television. Smith doesn’t have an inspired answer. He suggests the term display element, but for the most part he grudgingly calls them “spread pixels.”'

Thank you copy and paste, also link here, https://www.americanscientist.org/article/a-pixel-is-not-a-little-square

[xxlet]

Them: ok but you Better not get weird about 17th century mathematicians again

Me: dwdw

Me a drink later: i need to open the grave of joseph fourier and fuck his corpse nasty

[strings0fcontrol]

Hannigram – Post-Fall (1)

He traversed the deathly passages of his mind palace in a slow-motion pace, where sounds dulled to a muted whisper. Yet, amid the eerie silence, an ever-escalating rush of water steadily approached. The once-luxurious carpets beneath his feet were already soaked, yet nothing deterred his advance. As challenging as it was, he pressed on through the eerily vacant corridors, where lights that had once shone brilliantly now flickered uncertainly.

Intermittently, his mind stuttered, and the distant sound of water enveloped him entirely.

It was drawing nearer.

Yet, he continued his frantic search, dashing through rooms in an environment now rendered unrecognizable. His gaze scoured every corner, never relenting. But despite his efforts, the answer remained elusive, forever out of reach.

Then, the water arrived, a force that seized him in its merciless undercurrent. His ears were overwhelmed by the gurgling roar of the ocean, which seemed to rush in and out of him, and the images blurred, never coalescing into distinct shapes. His mind fractured, desperately clinging to the fragile precipice of consciousness.

The encroaching darkness stretched its icy tendrils, almost enveloping him completely.

Yet, he was no ordinary mortal.

He was the MORNINGSTAR, blazing with celestial brilliance.

Lecter stoked the fires within, his dark eyes flaring to life, their radiance surpassing the dark's futile attempts to extinguish him. The distant light beckoned, a mere glimmer on the horizon, akin to a remote, unforgiving moon. He might have welcomed the embrace of death if not for a faint scream in the recesses of his mind—a realization that he had struck the water before anything else, and if he had endured, then it was highly probable that Will was still clinging to life as well. And Hannibal knew, with certainty, that he would not succumb to death until Graham did.

Will had slipped from his grasp, severed in that fleeting moment of darkness. However, if he could just hold on, if Hannibal could remain afloat a while longer in this unending abyss, he might yet discover Graham.

His oxygen supply dwindled, and his body began to entertain the perilous notion of inhaling the liquid, a desperate gambit to defy the odds.

With the utmost restraint, he allowed his head to turn gradually, as if he could peer through the encompassing void. Lecter made the barest of movements, conserving every ounce of energy to prolong his endurance for as long as humanly possible. They found themselves submerged approximately six or seven meters below the water's surface. The impact had been absorbed largely by Hannibal's back, the icy sting of the water's lash still fresh in his senses. Will had been positioned atop him, causing Hannibal to tilt his gaze slightly upward. However, Graham's weight leaned more toward Hannibal's right side, suggesting that Lecter's impact had tilted Will's body, presenting a smaller target area. This implied that Will might have possessed a higher velocity upon impact. As Hannibal's chin dipped in contemplation, he calculated, taking into account the water's density and the relatively subdued movements at this depth, that Will would most likely be situated beneath him.

Within the gradually submerging chamber of mathematics, he pursued the lingering echoes of luminaries like Johannes Kepler, Isaac Newton, Joseph Fourier, and Carl Friedrich Gauss. A portion of his focus remained firmly fixed on what he believed to be the moon, its bright radiance a guiding beacon from the heavens above. This celestial sentinel served as a steadfast reference point to chart his own gradual descent since the moment of impact.

Lecter minimized his movements, intervening with the natural drift as sparingly as possible. This meticulous approach allowed him to discern and retrace the patterns, erupting in a calculation aimed at pinpointing the precise coordinates.

Then, with a resolute surge forward, he sensed it—a faint, trembling presence existing alongside him in the frigid depths. Like a whisper of life, it called, a shadow even darker than the abyss itself. And there, he felt it, the distinct warmth of another body under his touch. It was unmistakable: Will.

Graham hadn't made a single attempt to break the surface, already entangled in a fierce battle with death, his body wracked by convulsions. Lecter pondered whether Will, like himself, had been conscious until just a brief moment ago and deliberately hid himself. However, Will was no swimmer, unlike Hannibal. The doctor had honed his lung capacity for such dire circumstances. It was rather adorable that he attempted to end Lecter with the very thing that had become almost second nature to him. What a deviously clever boy Will could be. Cunning. To annihilate himself meant to obliterate Hannibal in the process. If Will perished, Hannibal would have no purpose to persist, even if he somehow managed to survive. In that move, Graham had effectively checkmated Hannibal, regardless of whether Lecter lived or succumbed.

Regrettably, it had all been rather predictable.

'I don't know if I can save myself. Maybe that's just fine.'

If Will believed that duping him a second time would be a straightforward affair, he was gravely mistaken.

Hannibal could sense it, a feeling akin to butter sizzling in a pan, creeping gradually through his being.

If the fickle hand of time wasn't conspiring against him, he would have gladly remained within this suspended moment indefinitely, contemplating the possibility of cradling Will close and waiting until the enveloping darkness claimed them both.

Yet, a simmering fury churned deep within, a bitterness that bordered on tasting like betrayal. Will had cast them both over the precipice before his wings could fully unfurl and bear him to the heavens. Hannibal had been ensnared by beauty and would have almost welcomed such an end, but an insatiable curiosity lingered, a desire to witness the expression on Will's face—the very revelation denied by the encroaching darkness.

He yearned to glimpse what lay behind those eyes, curious whether it would reveal relief or sheer horror if he were to behold him once more. Hannibal stood at the precipice, with the choice to perish in the embrace of his dream's illusion or awaken to the stark truth.

And that spark of curiosity, that ember of spite, burgeoned into an enraged blaze, becoming the fuel that propelled his ultimate choice.

Approaching the light, a cruel irony indeed, yet Lecter pressed forward with every last ounce of his remaining strength. His body, guided by the residual authority it still possessed, propelled them onward, but the darkness eventually closed in.

Existence melded into an indistinct blur, time unfurled and wavered, and once more, there reigned a profound stillness.

Everything surrounding him appeared dim and remote, save for a single word that echoed relentlessly in his consciousness: 'Hannibal.' Nothing seemed coherent, nothing felt recognizable. The only constants were the persistent sound of the ocean's roar in his ears and the pearls of saltwater cascading down his ebony locks.

Shivering, he sat huddled beneath a colorless blanket, his eyes vacant, mirroring the emptiness that now enveloped his mind.

In a curious way, Will had achieved his goal. No longer was he truly alive; only his body remained, a hollow vessel. As for Will, he was adrift at sea, lost to its fathomless depths.

Beneath it all, the steady hum of a motor provided the backdrop, while the gentle breeze whispered its soft song.

That soothing purr, an oddly familiar sound, as if Will had once known it in a previous life…

Then his eyes gently closed, and along with it, the hum faded into nothingness. Everything ceased to exist.

In this stillness, a fragile tranquility prevailed, yet it lacked the essence of reality.

He knew that, at some point, his eyes would have to reopen, forcing him to confront the unvarnished truth before him.

It felt as though an eternity drifted past before he summoned the courage to unveil what lay hidden on the other side of his closed lids.

And as he cautiously parted his eyelids, what he beheld was…

[scotianostra]

26th June 1824 saw the birth of William Thomson, Lord Kelvin, eminent physicist.

Most people remember William Thomson, or Lord Kelvin as he is universally known nowadays as the man who gave us the Kelvin scale of temperatures but as with most clever people there is a lot more to know about him besides.

Although born in Northern Ireland, William Thomson spent most of his life in Scotland after his father became Professor of Mathematics at Glasgow University. Kelvin attended university classes from the age of 10. He wrote his first scientific paper, under the pseudonym ‘PQR’, aged only 16.

In his teens he learned French well enough to read the work of eminent French mathematician Jean Baptiste Joseph Fourier. Philip Kelland, Professor of Mathematics at Edinburgh University, had criticised Fourier’s work on the theory of heat. Kelvin boldly stated that Kelland was wrong – and later scientists agreed with him.

From 1841 to 1845 Kelvin attended Cambridge University. He was an excellent student – although he shocked his father by spending his allowance on a boat. After graduating, Kelvin worked in a Paris laboratory with physics professor Victor Regnault.

Kelvin was influenced by the mathematical ideas of George Green, a self-taught miller’s son from Nottingham. He later brought an essay of Green’s to the attention of fellow mathematicians and physicists by republishing it in a respected scientific journal. Until then the essay on mathematical analysis, electricity and magnetism had gone largely unnoticed.

In 1846, aged only 22, Kelvin returned to Glasgow to become Professor of Natural Philosophy. He remained in this post for an astonishing 53 years. Keen to see students involved in practical experiment, he established what became the first university physics laboratory. Kelvin continued to study the nature of heat. He realised that it would be useful to be able to define extremely low temperatures precisely. In 1848, he proposed an absolute temperature scale, now called ‘the Kelvin scale’.

After further research, Kelvin formulated the second law of thermodynamics. This states that heat will not flow from a colder to a hotter body.

His interest in the transmission of electricity prompted Kelvin’s appointment as Director of the Atlantic Telegraph Company in 1856. The company was to install a telegraph cable under the Atlantic Ocean. Atlantic Cable Expeditions in 1857, 1858 and 1865 failed, but communication by cable finally succeeded in 1866.

From 1870 onwards, Kelvin spent many summers on his yacht 'Lalla Rookh’, and invented several marine instruments to improve navigation and safety.

He introduced a mariner’s compass more accurate than any other in existence, and a machine to predict tide levels worldwide.

In 1884 Kelvin travelled to the United States to give a series of lectures. These were enthusiastically received, and were published in 1904 as the 'Baltimore Lectures’.

Kelvin became a Lord in 1892 and took the name Kelvin because of his Glasgow connections. By the time of his death in 1907, he was an international celebrity, widely respected and honoured.

The statue in the pics is in Kelvingrove Park, Glasgow.

[imrananwar]

As Easy As (Circles of) Pi: A Love Story in Frequencies - IMRAN®

My fascination with Fourier—and Laplace—transforms began back in the early '80s during my Electrical Engineering days at UET Lahore. These mathematical tools break down any complex signal into a sum of sine and cosine waves, each with its own frequency. It’s a beautiful trick that makes even the most daunting waveforms easier to work with.

The idea goes all the way back to the early 1800s, when Joseph Fourier suggested that even the most intricate patterns—like shifting tides or rustling winds—could be formed from simple, repeating waves. It was revolutionary.

Think of those Spirograph toys we used as kids: plastic gears spinning around to create intricate patterns. Now imagine those circles representing different frequencies, combining and rotating in sync to draw something as elegant as the Pi symbol. Complexity, unspooled into rhythm and rotation—with a touch of childhood wonder.

This image is a collage of four screenshots to illustrate the idea. The short reels/videos I linked in comments below bring it to life in a magical way that feels both modern and nostalgic.

© 2025 IMRAN®

#IMRAN #Fourier #engineering #education #learning #mathematics #Pi

[buttstothemoon]

Joseph Fourier has a paper, not exactly about climate change, but which infers the existence of some kind of "greenhouse" effect occuring in the Earth's atmosphere, published in 1824.