#and if gravity were not quantized (or were quantized but in a way that exhibited certain different properties) we can break countability

[mjec]

You ever think about the fact that our best model of the universe at a micro scale, quantum electrodynamics, tells us really nothing about the nature of the universe at that scale? It is, after all, just a model.

Or is it? If quantum electrodynamics is a vector space that covers at least the minimal representation of all observable distinguishing information in a system, is that the same thing as the system itself? No, it's merely isomorphic to the system. But what does "is" mean if not isomorphic to all observable distinguishing outputs?

At the smallest scale, the thing itself is just the information. It is in the interactions between information that the universe arises.

Unless that's not true. Because after all, isomorphism is itself a concept constrained by the conceptual framework in which it exists. Though on the other hand, that framework is powerful enough to describe the ideas of observation and distinction. Though I guess we're maybe relying on the axiom of choice here; if observation and distinction are neither countable nor chooseable it breaks down. But that they are countable is the fundamental assumption of quantum physics. That's the quantum in question.

[tomasorban]

Fractals, space-time fluctuations, self-organized criticality, quasicrystalline structure.

1. Introduction- Long-range space-time correlations, manifested as the selfsimilar fractal geometry to the spatial pattern, concomitant with inverse power law form for power spectra of space-time fluctuations are generic to spatially extended dynamical systems in nature and are identified as signatures of self-organized criticality. A representative example is the selfsimilar fractal geometry of His-Purkinje system whose electrical impulses govern the interbeat interval of the heart. The spectrum of interbeat intervals exhibits a broadband inverse power law form 'fa' where 'f' is the frequency and 'a' the exponent. Self-organized criticality implies non-local connections in space and time, i.e., long-term memory of short-term spatial fluctuations in the extended dynamical system that acts as a unified whole communicating network.

2.3 Quasicrystalline structure: The flow structure consists of an overall logarithmic spiral trajectory with Fibonacci winding number and quasiperiodic Penrose tiling pattern for internal structure (Fig.1). Primary perturbation ORO (Fig.1) of time period T generates return circulation OR1RO which, in turn, generates successively larger circulations OR1R2, OR2R3, OR3R4, OR4R5, etc., such that the successive radii form the Fibonacci mathematical number series, i.e., OR1/ORO= OR2/OR1 = .= t where t is the golden mean equal to (1+ 5)/2 1.618. The flow structure therefore consists of a nested continuum of vortices, i.e., vortices within vortices. Figure 1: The quasiperiodic Penrose tiling pattern which forms the internal structure at large eddy circulations..

The quasiperiodic Penrose tiling pattern with five-fold symmetry has been identified as quasicrystalline structure in condensed matter physics (Janssen, 1988). The self-organized large eddy growth dynamics, therefore, spontaneously generates an internal structure with the five-fold symmetry of the dodecahedron, which is referred to as the icosahedral symmetry, e.g., the geodesic dome devised by Buckminster Fuller. Incidentally, the pentagonal dodecahedron is, after the helix, nature's second favourite structure (Stevens, 1974). Recently the carbon macromolecule C60, formed by condensation from a carbon vapour jet, was found to exhibit the icosahedral symmetry of the closed soccer ball and has been named Buckminsterfullerene or footballene (Curl and Smalley, 1991). Selforganized quasicrystalline pattern formation therefore exists at the molecular level also and may result in condensation of specific biochemical structures in biological media. Logarithmic spiral formation with Fibonacci winding number and five-fold symmetry possess maximum packing efficiency for component parts and are manifested strikingly in Phyllotaxis (Jean, 1992a,b; 1994) and is common to nature (Stevens, 1974; Tarasov, 1986).

Conclusion: The important conclusions of this study are as follows: (1) the frequency distribution of bases A, C, G,T per 10bp in chromosome Y DNA exhibit selfsimilar fractal fluctuations which follow the universal inverse power law form of the statistical normal distribution, a signature of quantumlike chaos. (2) Quantumlike chaos indicates long-range spatial correlations or ‘memory’ inherent to the self- organized fuzzy logic network of the quasiperiodic Penrose tiling pattern (Fig.1). (3) Such non-local connections indicate that coding exons together with non-coding introns contribute to the effective functioning of the DNA molecule as a unified whole. Recent studies indicate that mutations in introns introduce adverse genetic defects (Cohen, 2002). (4) The space filling quasiperiodic Penrose tiling pattern provides maximum packing efficiency for the DNA molecule inside the chromosome.

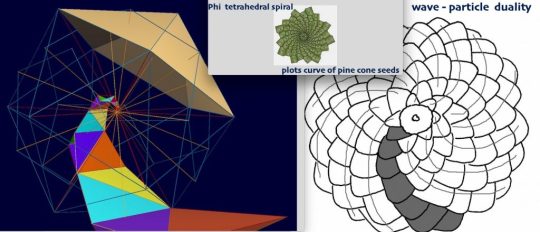
Golden Rhombi quantize to golden ratio tetrahedral building blocks Researchers at the University of Cambridge propose a new simplified method that effectively calculates higher-dimensions. What they find comes to no surprise to researchers of unified physics, as for their calculations to be simplified they have to think in volumes.

Golden ratio scaled phi tetrahedral building blocks model recursive reverse-time reconstructions, and subPlanck phase space (highest fidelity teleportation), demonstrating densest negentropic packing, this plenum reveals power spectra dynamics across scale from SubPlanck, and along with the rotations & overlays of five-fold symmetry axes define quantum mechanics. Fibonacci scaled Phason vectors stretch throughout the quasicrystalline patterns, providing maximum degrees of freedom with hinge variabilities, creating multi-causal non-local quantum gravity effects [300 x light speed], which Dan Winter calls a phase conjugate mirror.

Micro-PSI investorgator Geoff Hodson, shares his observations of the ether/plasma torus the Anu or UPA and 'free' particles (definable voxel voids) that we model as golden tetrahedra which bond together to make golden rhombic structures (voxel void fluctuations) and a volumetric golden ratio spiral that nests perfectly into the stellating dodeca-icosa-dodeca scaffolding waveguide of fractal implosion.

Ten phi tetra's, shaped like an EGG or PINE CONE, spin-collapse from opposite directions [grab a coke can with both hands and twist], becoming the volume of phi spiral conic vectors. The torque spin of both poles is clockwise centripetal [unlike the toroid's inside-outing]. The 180deg out of phase implosion vectors conjugate at the centre, generating a longitudinal wave.

Ten phi tetra's, shaped like an EGG or PINE CONE, spin-collapse from opposite directions [grab a coke can with both hands and twist], becoming the volume of phi spiral conic vectors. The torque spin of both poles is clockwise centripetal [unlike the toroid's inside-outing]. The 180deg out of phase implosion vectors conjugate at the centre, generating a longitudinal wave.

Dan Winter adds: "the unified field appears to be made of a compressible unified substance which behaves like a fluid in the wind. It matters little whether you call it aether, ether, or ‘the space time continuum of curved space’ or, as we choose to call it, the compression and rarefaction of the vacuum as really particle/waves of CHARGE itself. The huge inertia which is clearly present in the vacuum, IS literally like a WIND. So, tilting at windmills with the right approach angle to transform the wind power to a life-giving-energizing advantage and not be blown away by it IS the appropriate way to gain the power of nature. Consider the pine cone or the chicken egg (or DNA proteins ) for example. Along the lines of the windmill analogy, clearly they arrange themselves into the perfect windmill- like configuration to catch the charge in the wind of gravity (the vacuum). That perfect windmill to catch the voltage, the energy - is clearly pine cone (fractal) shaped."

Winter often quotes the research of Charle Leadbeater and Annie Besant, two Theosophists who were able to view the prime aether unit they called an ANU (5th Tattva), this was the smallest unit they could 'see'. Winter is unaware that micro-PSI investorgator Geoff Hodson, was capable of 'seeing' the energy fields far smaller than the ANU (ANU=5th Tattva-EGG-PINE CONE-torus), Hodson shares his observations of the ANU (ether/plasma torus, UPA) and 'free' particles (definable voxel voids) that we model as golden tetrahedra (7th Tattva) which bond together to make golden rhombic structures (6th + 7th Tattvas the energy fields within the vacuum, voxel void fluctuations) and a volumetric golden ratio spiral that nests perfectly into the stellating dodeca-icosa-dodeca scaffolding waveguide of fractal implosion.

"The sight I have of these objects is, I think, improved from the earlier observations (Geoff is referring to Leadbeater & Besant). They're surrounded by a field of spinning particles going round them. The one I've got hold of is like a spinning top — the old-fashioned spinning top, but imagine that with (spinning rapidly) a mist or field round it of at least half its own dimension, of particles spinning (Winter-inertia which is clearly present in the vacuum, IS literally like a WIND) in the same direction much smaller than itself (Winter-the unified field appears to be made of a compressible unified substance which behaves like a fluid in the wind). The Anu is not only the heart-shaped corrugated form that I have described, it is the centre of a great deal of energy and activity and within it. Outside it, as I have said, there's this rushing flood of particles, the corrugations themselves are alive with energy and some of it is escaping — not all of it, but some of it, and this gives it a tremendously dynamic look. Inside, it's almost like a furnace, it is like a furnace (I don't mean in heat) of boiling activity — organised by the bye, yes, in some form of spiral fashion admittedly, but there's a great deal of activity of free, minuter particles (Winter-The huge inertia which is clearly present in the vacuum, IS literally like a WIND). Now, I want to record again the experience of the whole phenomenon being pervaded by countless myriads of minutest conceivable, physically inconceivably minute points of light which I take to be free anu and which for some reason are not caught up in the system of atoms at all but remain unmoved by it and pervade it. These are everywhere. They pervade everything, like ... Strangely unaffected by the tremendous forces at work in the atom and rushes of energy, and so forth, they don't seem to get caught up in those or be affected much by them. If at all. They remain as a virgin atmosphere in which the phenomenon is taking place."

[wumblr]

I spent hours working on this. I'm looking at it as more of a journal entry describing where I'm at with these concepts. It could be riddled with misconceptions, I guess. I would caution you against assuming it's profound, and encourage you to figure it out for yourself.

There is an urge among a certain subset of physicists to derive a fundamental theory from dimensionless constants. This means you would theoretically be able to calculate any salient value by deriving it from other fundamental constants, without requiring any frame of reference, or standard ruler... An even more specific subset of physicists believe that these fundamental dimensionless constants should be "natural" and not "fine tuned," meaning when you derive them from each other, you could multiply or divide something by quantities like 2 or 5 or 10 without too much trouble, but as soon as you find yourself working with values such as 1/137th, you lose "naturalness." Unfortunately, experimental observations of electromagnetic interactions are the origin of the value 1/137.

This does not necessarily mean dimensionless constants are a fool's journey, but I think naturalness might be. I don't see a reasonable expectation at its base -- why should absolutely nothing be fine tuned in a 14 billion year old cosmos? Do you think the laws of physics are timeless and unchanging, or did they evolve over the history of the universe out of the available materials? I could believe that timeless laws require naturalness, but I can't believe in unchanging laws. Experiment shows fine tuning -- perhaps there is a deeper mechanism at play that will explain this in naturalistic terms, but until that mechanism is found, we have to accept the results of experiment at face values.

For contrast, I do see a reasonable expectation for dimensionless constants. It should be possible to define the universe using only pieces of it, without invoking anything exterior to it, including clocks and rulers, i.e. absolute measurements. (This is a multiverse-agnostic stance -- it doesn't matter whether anything outside our universe exists, assuming "outside our universe" means it cannot bear any causal relation to us. If there is a multiverse where gravity pervades the bulk, and exerts influence on our universe due to mass not located in our universe, that would be a different story, because there would be a theoretically detectable causal relation.)

This pursuit is relationalist, and background-independent -- all things ought to be able to be defined in relation to each other and nothing else, without having to invoke a background of aether, or absolute space, or a timeless block universe, or a notion of time that keeps ticking when nothing is happening. Somewhere near the logical conclusions of relationalism, there is a white rabbit. Let's find him.

The thing about dimensionless constants is that you can't have them without scale invariance. If everything is interior to the theory, and you invoke no external absolute ruler unaffected by the circumstances of the experiment -- which seems to me a sensible approach until we can physically experimentally place a ruler outside the universe -- then the fundamental constants are invariant under conformal scale transformations. Things could change size, as a whole or in relation to distant objects, without changing the relationship between them. Drink me.

We can't know whether we're, at present, as the planet travels through space, traversing a rabbithole that will leave us, in comparison to ourselves in the past, a vastly different size. If there was a direction of travel which would change your size as you travel along it, then we would need to come up with a clever way to detect it. If every direction of space is identically warped in this manner, we may not be able to detect it.

Of course, the universe doesn't have to be scale invariant just because the theory allows it, and if I were to pursue this idea on that basis alone, I would be vulnerable to the same error in thinking as outlined for naturalism above. (The universe does not need to be natural just because you can imagine a naturalistic set of constants. The universe does not need to be scale invariant simply because you can imagine how cool it would be.)

True, we seem to have no anomalous experimental results to indicate that scale is varying... Unless we've already seen this indication and interpreted it as something else.

The generally accepted interpretation of general relativity is that, across distances, you must discard the possibility that events can be simultaneous, and objects (and distances) must remain consistent in size. If you discard the possibility that size is immutable, you can reintroduce simultaneity. The theories are dual, meaning they match experiment equally well. We can have a linear conception of time with a notion of simultaneity, or we can have a linear conception of space with a notion of consistent scale. They are interchangeable, but mutually exclusive. Relativity was a choice to preserve the consistency of objects, and so we lost the consistency of time. But time or size could be relative. The two theories imply indistinguishable results.

The generally accepted interpretation of the redshift of distant galaxies is that the universe is expanding, and they are accelerating away from us. But consider the possibility that distant galaxies are increasing in mass -- would this theory produce a similar observable to the expanding interpretation?

Perhaps, and perhaps not. Shouldn't changes in mass under true scale invariance be impossible to detect, if they're changing in a relationally consistent way? Expansion is not a scale transformation -- the distance between objects is expanding, but the objects themselves are not. The relationships among the objects, and the distance between them, are changing. This is not the same as the fundamental values changing in concert. Any true scale transformation preserves the relation.

This would, I suppose, require a caveat that scale invariance applies at fundamental scales, but at scales such as galaxies, invariant processes might provide emergent, scale-variant properties. Particles that gain mass in concert cannot be detected in relation to each other, but collections of particles as large as stars or galaxies might experience additional effects from this increase in mass. Chemical reactions within stellar furnaces may subtly deviate from the predictions governed by the standard model because of this. Perhaps Rubin's observations of anomalous galactic rotation, which led to the theorization of dark matter, are in fact ordinary matter performing ordinary processes in a way that is categorically different from our standard model.

Since I am a pragmatist and a believer in Bohmian mechanics, this caveat works for me. In the historical development of pilot wave theory, de Broglie started from the assumption that wave/particle duality is a little bit of both. I see a similarity in the duality which scale-invariance/relativity can exhibit, so I suspect it's likelier to be a little bit of both scale invariance and relative interactions, depending on which effective theory is relevant to matters at hand.

The generally accepted interpretation of the very early universe is that there was a brief period of uncharacteristically fast expansion we call inflation. This could also be re-envisioned in scale-invariant terms. This is the most dubious assertion I have today, but perhaps the Higgs mechanism was not part of the early universe, and when circumstances arose allowing it to suddenly come into being, all mass in the universe simultaneously changed -- seeming, from our distant perspective, to be indistinguishable from exponentially quick inflation. (The change from "all particles having no mass" to "particles having various masses" is not scale invariant, because the relationships between particle masses change. The change is noticeable because everything didn't change exactly the same amount in relation to each other. Particle mass progressed from "all the same" to "diverse," which is not an invariant transformation.)

People that have written about this include Juan Maldacena, Roger Penrose, Lisa Randall, and Lee Smolin. Each of them took a different direction.

Maldacena developed Anti de Sitter/Conformal Field Theory Correspondence in the 1990s, proving that boundaries of higher dimensional shapes can be theoretically dual to the shapes themselves (AdS/CFT is where "the universe is a projection" comes from, although it's a misconception, because we are not in an Anti de Sitter space). Some of Maldacena's students developed Shape Dynamics in response, where size doesn't matter at all, and difference of shape is the only defining feature for objects (particles don't interact directly with galaxies because they are different shapes, not because one is vastly bigger than the other).

Penrose developed Conformal Cyclic Cosmology, where at the end of time, the universe is indistinguishable from the beginning and thus it "rescales" and restarts the big bang cycle.

Randall noticed a variability inherent to Einstein's equations while looking for testable predictions for the LHC, and developed Warped Geometry in response, positing compactified extra dimensions that only fundamental particles can access.

Smolin is the only one who tries to use the idea to develop a central theory and philosophy of physics, but in order to resolve nonlocality he presumes 1) space is quantizable, 2) networked in a spin-foam, and 3) nonlocal interactions are nonadjacent networking of the quanta of space. I don't like assuming that motion is non-continuous, although that's little more than a hunch, and there are a few other reasons Smolin's work leaves me doubtful, but I might have to finish the book before I can put my finger on them.

Out of these four, I tend to trust Maldacena's conclusions most of all, because he doesn't seem to take them as anything other than mathematical constructs. The other three try to explain the universe.

If I'm going to dip my toe into the philosophy of science, it will be to say this and nothing else: Science does not need to explain the universe, it should merely predict the results of experiments. If we find an explanation for the universe along the way, that's great, and not even entirely implausible -- but this explanation must grant us deeper predictive power, or else it isn't physical science.

In the 2015 physics conferences at LMU in Munich, discussions abounded on how to proceed with regards to naturalness. David Gross put forth an operational definition of scienctific progress in the absence of empirical verification: "Will I continue to work on this?" I think this is a fantastic distinction with great clarifying power, and it's helpful to develop a rubric to admit when you're following unempirical ideas. My concern about this distinction is that it's not distinct enough -- a mathematician might take this idea to vastly different conclusions than a physicist might. Mathematics contain (and should contain) a freedom that physics don't (or at least, shouldn't): the freedom to work without tying that work to reality. Internally consistent mathematics bearing no relation to reality possess a utility not present in internally consistent but unreal physics. Thus the same operational litmus test produces different results in each field.

If time and distance under lightspeed are interchangeable (because distance is defined by the time it takes light to cross it), why assume time is the relative quantity? Does relativity of scale resolve issues that are intractable for relativity of time, or does it create new intractable issues unique to itself? Are the two distinguishable at all, or do they produce exactly the same intractable problems?

In order to unify spacetime, either space or time must become relative, and I'm thinking we might have gone in the wrong direction here. In order to determine this, we might need to go as far in developing relativity of scale as we have for relativity of time. If they produce the same paradoxes, they are dual and indistinguishable. If one produces more, it is wrong.

[scepticaladventure]

9  Light - Some Important Background  18Aug17

Introduction

We observe the Universe, and physics within the Universe, and we try to make sense of it. There is often tension between our natural impression of the physical world and what our models and mathematical logic tell us.

Consider the most important of our senses – sight. Our eyes detect photons of light and our brain composes this information into a visualization of the world around us. That becomes our subjective perceived reality.

Nearly all the information we receive about the Universe arrives in the form of electromagnetic radiation (which I will loosely refer to as ‘light’).

However, light takes time to travel between its source and our eyes (or other detectors such as cameras). Hence all the information we are receiving is already old. We see things not as they are, but as they were when the light was emitted. Which can be a considerable time ago. Which means that we are seeing the objects when they were much younger than they are “now”. In other words, we are seeing back in time to what they looked like then.

Light from the sun takes nearly ten minutes to reach us. Light from the nearest star about 4 years. Light from the nearest spiral galaxy (Andromeda) is about 2 million years old (but Andromeda is becoming closer at about 110 km/sec). Light from distant galaxies and quasars can be billions of years old. In fact our telescopes can see light (microwaves actually) that is so old it originated at the time the early universe became transparent enough for light to travel at all.

Imagine we are at the centre of concentric shells, rather like an infinite onion. At any one moment, we are receiving light from all these shells, but the bigger the shell from which the light originated, the older the information. So what we are seeing is a complete sample of history stretching back over billions of years.

It would be mind boggling exercise to try to reimagine our mental model of what the universe is really like “now” everywhere. The only way I can think to tackle this would be some sort of computerized animation.

Even then there are a range of other distortions to contend with. All the colors we see are affected by the relative speeds between us and the sources of the light. And light is bent by gravity, so some of what we see is not where we think it is. There are other distortions as well, including relativistic distortions. So, in short, what we see is only approximately true. Believing what we see works well for most purposes on everyday earth but it works less well on cosmological time and distance scales.

Light is vital to our Perception of Nature

Electromagnetic radiation is by far the main medium through which we receive information about the rest of the universe. We also receive some information from comets, meteorites, sub-atomic particles, neutrinos and possibly even some gravitational waves, but these sources pale into insignificance compared to the information received from light in all its forms (gamma rays, x-rays, visible light, microwaves, radio waves).

Since we rely so heavily on this form of information it is a concern that the nature of light has perplexed mankind for centuries, and is still causing trouble today.

Hundreds of humanity’s greatest minds have grappled with the nature of light. (Newton, Huygens, Fresnel, Fizeau, Young, Michelson, Einstein, Dirac … the list goes on).

At the same time the topic is still taught and described quite badly, perpetuating endless confusion. Conceptual errors are perpetuated with abandon. For example, radio ways are shown as a set of rings radiating out from the antenna like water ripples in a pond. If this were true then they would lose energy and hence change frequency with increasing distance from source.

Another example:  It is widely taught that Einstein’s work on the photoelectric effect shows that light must exist as quantized packets of energy and that only certain energy levels are possible. I think the equation e = h x frequency (where h is Planck’s constant) does not say this at all. The frequency can be any integral number or any fraction in between. The confusion arises because photons are commonly created by electrons moving between quantized energy levels in atoms, and photons are commonly detected by physical systems which are also quantized. But if a photon arrives which does not have exactly one of these quantised levels of energy and is absorbed, the difference simply ends up in the kinetic energy of the detector. Or so it seems to me.

The Early Experimenters

Most of the progress in gathering evidence about light has been achieved since the middle of the 17th century. Galileo Galilei thought that light must have a finite speed of travel and tried to measure this speed. But he had no idea how enormously fast light travelled and did not have the means to cope with this.

Sir Isaac Newton was born in the year that Galileo died (1642 – which was also the year the English Civil War started and Abel Tasman discovered Tasmania). As well as co-inventing calculus, explaining gravity and the laws of motion, Newton conducted numerous experiments on light, taking advantages of progress in glass, lens and prism manufacturing techniques.  I think Newton is still the greatest physicist ever.

In experiment #42 Newton separated white sunlight into a spectrum of colors. With the aid of a second prism he turned the spectrum back into white light. The precise paths of the beams in his experiments convinced him that light was “corpuscular” in nature. He argued that if light was a wave then it would tend to spread out more.

Other famous scientists of the day (e.g. Huygens) formed an opinion that light was more akin to a water wave. They based this opinion on many experiments with light that demonstrated various diffraction and refraction effects.

Newton’s view dominated due to his immense reputation, but as more and more refraction and diffraction experiments were conducted (e.g. by Fresnel, Brewster, Snell, Stokes, Hertz, Young, Rayleigh etc) light became to be thought of as an electromagnetic wave.

The Wave Model

The model that emerged was that light is a transverse sinusoidal electro-magnetic wave, with magnetic components orthogonal to the electric components. This accorded well with the electromagnetic field equations developed by James Clerk Maxwell.

Light demonstrates a full variety of polarization properties. A good way to model these properties is to imagine that light consists of two electromagnetic sine waves travelling together with a variable phase angle between them. If the phase angle is zero the light is plane polarized. If the phase angle is 90 degrees then the light exhibits circular polarization. And so on. The resultant wave is the vector sum of the two constituent waves.

Most people are familiar with the effect that if you place one linear polarizing filter at right angles to another, then no light passes through both sheets. But if you place a third sheet between the other two, angled at 45 degrees to both the other two filters, then quite a lot of light does get through. How can adding a third filter result in more light getting through?

The answer is that the light leaving the first filter has two components, each at 45 degrees to the first sheet’s plane of polarization. Hence a fair bit of light lines up reasonably well with the interspersed middle sheet. And the light leaving the middle sheet also has two components, each at 45 degrees to its plane of polarization. Hence a fair bit of the light leaving the interspersed sheet lines up reasonably well with the plane of polarization of the last sheet.

Interesting effects were discovered when light passes through crystals with different refractive indices in different planes (see birefringence). Also when light was reflected or refracted using materials with strong electric or magnetic fields across them (see Faraday effect and Kerr effect).

Young’s Double Slit Experiment

Experiments performed by Thomas Young around 1801 are of special interest. Light passing through one slit produces a diffraction pattern analogously to the pattern a water wave might produce. When passed through two parallel slits and then captured on a screen a classic interference pattern can be observed. This effect persists even if the light intensity is so low that it could be thought of as involving just one photon at a time. More on this later.

The Corpuscular Model Returns

At the start of the 20th century, Albert Einstein and others studied experiments that demonstrated that light could produce free electrons when it struck certain types of metal – the photoelectric effect. But only when the incident light was above a characteristic frequency. This experiment was consistent with light being a sort of particle. It helped to revive the corpuscular concept of light.

Arthur Compton showed that the scattering of light through a cloud of electrons was also consistent with light being corpuscular in nature. There were a lot of scattering experiments going on at the time because the atomic structure of atoms was being discovered largely through scattering experiments (refer e.g. Lord Rutherford).

The “light particle” was soon given a new name - the photon.

Wave Particle Duality

Quantum mechanics was being developed at the same time as the corpuscular theory of light re-emerged, and quantum theories and ideas were extended to light. The wave versus particle argument eventually turned into the view that light was both a wave and a particle, (see Complementarity Principle). What you observed depended on how you observed it.

Furthermore, you could never be exactly sure where a photon would turn up (see Heisenberg Uncertainty Principle, Schrodinger Wave equation and Superposition of States).

The wave equation description works well but certain aspects of the model perplexed scientists of the day and have perplexed students of physics ever since. In particular there were many version of Young’s double slit experiments with fast acting shutters covering one or both slits. It turns out that if an experimenter can tell which slit the photons have passed through, the interference pattern vanishes. If it is impossible to determine which slit the photons have passed through, the interference pattern reappears.

It does not matter if the decision to open one slit or the other is made after the photons have left their source – the results are still the same. And if pairs of photons are involved and one of them is forced into adopting a certain state at the point of detection, then the other photons have the equal and opposite states, even though they might be a very long distance away from where their pairs are being detected.

This all led to a variety of convoluted explanations, including the view that the observations were in fact causal factors determining reality. An even more bizarre view is that the different outcomes occur in different universes.

At the same time as all this was going on, a different set of experiments was leading to a radical new approach to understanding the world of physics – Special Relativity. (See an earlier essay in this series.)

The Speed of Light

Waves (water waves, sound waves, waves on a string etc.) typically travel at well-defined speeds in the medium in which they occur. By analogy, it was postulated that light waves must be travelling in an invisible “lumiferous aether” and that this aether filled the whole galaxy (only one galaxy was known at the time) and that light travelled at a well defined speed relative to this aether.

Bradley, Eotvos, Roemer and others showed that telescopes had to lean a little bit one way and then a little bit the other way six months later in order to maintain a fixed image fixed of a distant star. This stellar aberration was interpreted as being caused by the earth moving through the lumiferous aether.

So this should produce a kind of “aether wind”. The speed of light should be faster when it travelling with the wind than if it travelling against the wind. The earth moves quite rapidly in its orbit around the sun. There is a 60 km/sec difference in the velocity of the earth with respect to the “fixed stars” over a six month period due to this movement alone. In addition the surface of the earth is moving quite quickly (about 10 km/sec) due to its own rotation.

In 1886 a famous experiment was carried out in Ohio by Michelson and Morley. They split a beam of light into two paths of equal length but at right angles to each other. The two beams were then recombined and the apparatus was set up to look for interference effects. Light travelling back and forth in a moving medium should take longer to travel if its path lines up with an aether wind than if its path goes across and back the aether wind. (See the swimmer-in-the-stream analogy in an earlier blog).

However, no matter which way the experiment was oriented, no interference effects could be detected. No aether wind or aether wind effects could be found. It became the most famous null experiment in history.

Fizeau measured the speed of light travelling in moving water around a more or less circular path. He sent beams in either direction and looked for small interference effects. He found a small difference in the time of travel (see Sagnac effect), but not nearly as much as if the speed of light was relative to an aether medium through which the earth was moving.

Other ingenious experiments were performed to measure the speed of light. Many of these involved bouncing light off rotating mirrors and suchlike and looking for interference effects. In essence the experimenters were investigating the speed of light over a two-way, back-and-forth path. Some other methods used astronomical approaches. But they all came up with the same answer – about 300 million meters/second (when in a vacuum.)

It did not matter if the source of light is stationary relative to the detection equipment, or whether the source of light is moving towards the detection equipment, or vice versa. The measured or inferred speed of light was always the same. This created an immediate problem – where were the predicted effects of the aether wind?

Some scientists speculated that the earth must drag the aether surrounding it along with it in its heavenly motions. But the evidence from the earlier stellar aberration experiments showed that this could not be the case either.

So the speed of light presented quite a problem.

It was not consistent with the usual behaviour of a wave. Waves ignore the speed of their source and travel at well defined speeds within their particular mediums. If the source is travelling towards the detector, all that happens is that the waves are compressed together. If the source is travelling away from the detector, all that happens is that the waves are stretched out (Doppler shifts).

But if the source is stationary in the medium and the detector is moving then the detected speed of the wave is simply the underlying speed in the medium plus the closing speed of the detector (or minus that speed if the detector is moving away).

The experimenters did not discover these effects for light. They always got the same answer.

Nor is the speed of light consistent with what happens when a particle is emitted. Consider a shell fired from a cannon on a warship. If the warship is approaching the detector, the warship’s speed adds to the speed of the shell. If the detector is approaching the warship then the detector’s speed adds to the measured impact speed of the shell.  This sort of thing did not happen for light.

Lorentz, Poincaré  and Fitzgerald were some of the famous scientists who struggled to explain the experimental results. Between 1892-1895 Hendrik Lorentz speculated that what was going on was that lengths contracted when the experimental equipment was pushed into an aether headwind. But this did not entirely account for the results. So he speculated that time must also slow down in such circumstances. He developed the notion of “local time”.

Quite clearly, the measurement of speed is intimately involved with the measurement of both distance and time duration. Lorentz imagined that when a measuring experiment was moving through the aether, lengths and times distorted in ways that conspired to always give the same result for the speed of light no matter what the orientation to the supposed aether wind.

Lorentz developed a set of equations (Lorentz transformations for 3 dimensional coordinates plus time, as corrected by Poincaré) so that a description of a physical system in one inertial reference frame could be translated to become a description of the same physical system in another inertial reference frame. The laws of physics and the outcome of experiments held true in both descriptions.

Einstein built on this work to develop his famous theory of Special Relativity. But he did not bother to question or explain why the speed of light seemed to be always the same – he just took it as a starting point assumption for his theory.

Many scientists clung to the aether theory. However, as it seemed that the aether was undetectable and Special Relativity became more and more successful and accepted, the aether theory was slowly and quietly abandoned.

Young’s Double Slit Experiment (again)

Reference Wikipedia:  

“The modern double-slit experiment is a demonstration that light and matter can display characteristics of both classically defined waves and particles; moreover, it displays the fundamentally probabilistic nature of quantum mechanical phenomena.

A simpler form of the double-slit experiment was performed originally by Thomas Young in 1801 (well before quantum mechanics). He believed it demonstrated that the wave theory of light was correct. The experiment belongs to a general class of "double path" experiments, in which a wave is split into two separate waves that later combine into a single wave. Changes in the path lengths of both waves result in a phase shift, creating an interference pattern. Another version is the Mach–Zehnder interferometer, which splits the beam with a mirror.

In the basic version of this experiment, a coherent light source, such as a laser beam, shines on a plate pierced by two parallel slits, and the light passing through the slits is observed on a screen behind the plate. The wave nature of light causes the light waves passing through the two slits to interfere, producing bright and dark bands on the screen, as a result that would not be expected if light consisted of classical particles.

However, the light is always found to be absorbed at the screen at discrete points, as individual particles (not waves), the interference pattern appearing via the varying density of these particle hits on the screen.

Furthermore, versions of the experiment that include detectors at the slits find that each detected photon passes through one slit (as would a classical particle), and not through both slits (as a wave would). Such experiments demonstrate that particles do not form the interference pattern if one detects which slit they pass through. These results demonstrate the principle of wave–particle duality. “

In this author’s view, there is so much amiss with this conventional interpretation of Young’s Double Slit Experiment experiment that it hard to know where to begin. I think the paradox is presented in an unhelpful way and then explained in an unsatisfactory way. It is presented as a clash between a wave theory of light and a particle theory of light, and it concludes by saying that light therefore has wave-particle duality.

Deciding that a photon has “wave-particle duality” seems to satisfy most people, but actually it is just enshrining the problem. Just giving the problem a name and saying “that is just the way it is” doesn’t really resolve the issue, it just sweeps it under the carpet.

In this author’s view, what the experimental evidence is telling us is that light is not a wave and that it is not a particle. Neither is it both at the same time (being careful about what that actually means), or one or the other on a whimsy. It is what it is.

Here is just one of the just one of this author’s complaints about the conventional explanation of the double slit experiment. In my opinion, if you place a detector at one slit or the other and you detect a photon then you have destroyed that photon. Photons can only be detected once. To detect a photon is to destroy it.

A detector screen tells you nothing about the path taken by a photon that manages to arrive at the final screen, other than it has arrived. You have to deduce the path by other means.

Wikipedia again:  “The double-slit experiment (and its variations) has become a classic thought experiment for its clarity in expressing the central puzzles of quantum mechanics. Because it demonstrates the fundamental limitation of the ability of an observer to predict experimental results, (the famous physicist and educator) Richard Feynman called it "a phenomenon which is impossible […] to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the mystery [of quantum mechanics].”   Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment.”

There is a class of experiments, known as delayed choice experiments, in which the mode of detection is changed only after the photons have begun their journey. (See Wheeler Delayed Choice Experiments, circa 1980’s  – some of these are thought experiments). The results change depending on the method of detection and seem to produce a paradox.

Reference the Wikipedia article on Young’s slit experiment, quoting John Archibald Wheeler from the 1980’s:  “Actually, quantum phenomena are neither waves nor particles but are intrinsically undefined until the moment they are measured. In a sense, the British philosopher Bishop Berkeley was right when he asserted two centuries ago "to be is to be perceived."

Wheeler went on to suggest that there is no reality until it is perceived, and that the method of perception must determine the phenomena that gave rise to that perception.

They say that fools rush in where angels fear to tread. So, being eminently qualified, the author proposes to have a go at explaining Young’s Double Slit Experiment. But first he would like to suggest a model for photons based on the evidence of the experiments, Einstein’s Special Relativity and some fresh thinking.

[fluxsci]

Elemental Flow - The Orbital Primer pt. 2 (5)

This is it! We have finally reached the conclusion of the orbital arc...or at least the second to last lesson. I’m sure it felt like the Frieza Saga, but I believe that I managed to explain the entirety of orbitals in a concise, but accurate way. Of course, I’ll leave it to you to tell me how I can improve to make this a better story for you. Because, like electrons, we all have to work together here.

In any event, let’s march on and be done with these orbitals. Ah…I can already hear the cheers from the Chemistry 101 students reading this.

Be sure to check out Part 4 for this one. You can’t understand where this one begins without seeing where the other one ends (hence ‘pt. 2’).

Now, it is time to explain the last quantum number.

Spin Quantum Number (s)

Electrons are trying to get rid of their energy in any way possible. Orienting themselves in a way that lowers energy is a good starting point, but they still have plenty of internal energy. In fact, electrons have their own, internal angular momentum, separate from the orbital angular momentum (l).

This was determined after a 1922 experiment by German physicists Otto Stern and Walther Gerlach. The aptly named Stern-Gerlach Experiment involved firing a beam of silver atoms* through a inhomogenous, or uneven, magnetic dipole and observing the results on a detecting wall at the end. The result, surprisingly, was that the beam was deflected in only two directions, landing flush against the wall in two bands.

But how could that be? There’s no way that there should be two, specific places in which the atoms ended up.  

If you think about it, if you threw twenty bar magnets past two huge magnets and looked at where they ended up, they would all be stuck on the wall in random places. After all, you have no idea what direction those magnets were when you threw them or how much attraction or repulsion one magnet had than another one, so you should have no idea exactly how they will come out. Shouldn’t it have been the same for these atoms?

In order to explain the significance of this inconsistency, I’ll need to diverge for a second into the physical quantity of momentum.

Gaining Momentum

Given that we know, from classical linear momentum calculation that there must a velocity, some speed over some time from some position which is usually produced by some force (say that ten times fast), and a mass, or the amount of matter an object has. This tells you how much, in numerical form, an object moves. In fact, you likely already knew the definition of “momentum” without knowing how to put it in words. Classical angular momentum is almost completely the same. The only difference is that an axis is involved, around which your mass rotates.

Thus, the two relative quantities are the moment of inertia and angular velocity. The latter is simply the rate at which rotation occurs. On the other hand, the moment of inertia, also known as the angular mass, is used to depict how much torque, or rotational force, you need to move an object a certain distance around an axis with respect to a certain position. The classic example of this is the tightrope walker.

If it was super easy to cause the one walking on a tightrope to flip around the rope (if gravity didn’t exist), then you would say that their moment of inertia is low. But when one walks across a rope you usually see them stick their arms out or hold a long rod. That single act increases the moment of inertia because you have changed the center of the mass, where the force acts. That is, more rotational force would be needed to rotate the walker. Now, Matthew, why did you go through the effort of explaining momentum here? Patience, viewer! The science will wrap together in a nice ribbon. Just in time for Christmas.

Magnets Start Small

I mentioned, from the now legendary Part 2, that electrons, as charged particles, can generate a magnetic field just by moving. It so happens that we know that electrons are “orbiting” the nucleus, and therefore, they must be exhibiting some sort of magnetic field as it is repeatedly revolving in this closed loop. But we never talked about what that field is doing. It wouldn’t make sense for the magnetic field to just disregard the electron and there is definitely no reason for the electron to not feel the force of the magnetic field.

Image via SchoolPhysics

By the way, if you orient your right-hand’s four fingers so that they are going along the path of the electron and then point out your thumb, that gives you the direction of the magnetic field. Every time. It’s called the Right-Hand Rule.

What would happen if you were to hold your hand on a ball lying on a table and then push your hand forward? The ball would roll in the direction your hand moves. It’s the same with electrons – they experience a rotational force, torque, from the magnetic field. The rotating electron creates another effect, according to electrodynamics. It now becomes a natural magnetic dipole, which is an object that generate magnetic fields that experience torque in such magnetic fields due to the presence of two opposite poles. In many ways, their magnetic effects are just tiny bar magnets. Electrons, too, have a “north” and “south” pole, or, more specifically, two poles at which their magnetic fields are strongest.

Image via Live Science

This is a dipole. You’ve seen bar magnets before.

 So, let’s do a roundup of what we just learned.

 Electrons generate magnetic fields which creates torque on them causing them to rotate and become similar to bar magnets. You should already recognize, then, where the concept of an electron’s angular momentum comes from. Indeed, electrons exhibit their own magnetic moment, from the rotational force, and, coupled with their motion, must create angular momentum!

 This is the origin of the theoretical “spin” that electrons have. Although we, realistically, don’t know if the electrons are spinning or not, this is just a name we give conventionally. You will learn why our convention fails us, especially when it comes to quantum mechanics, later.

 But, I digress. With all of that said…how did the electrons only end up in two places in the Stern-Gerlach Experiment?

 A Discrete Solution

 Stern and Gerlach were smart men. They knew, from Bohr’s prior experimentation of the electron, that it must be quantized. So when they crafted this experiment, they expected a quantized result. That is exactly what they saw. But just because they were correct in their hypothesis doesn’t mean their foundation was solid – a lesson for all of you upcoming scientists.

Image by Bill Watterson

Although that’s a result that you could hypothesize based on an expectation gained after seeing the ice in a glass of water melt, the foundation is all wrong.

The quantum mechanical theory of the time wasn’t correct. Their conclusion that the result was due to the quantization of the electron was not the reason for the quantized result.

 It was because of the electron’s angular momentum was directed in two specific direction. We call these half-spins, since one beam was split evenly into two. Basically, the momentum on the electrons directed the beam either upward or downward according to the direction of their rotational moment.

 A side-note: all elementary particles that hold these spins equal to ½ are called fermions, whereas if their spin value was 1 (what the value would be if the one beam went straight through without any division), it would be called a boson, a word you’ve likely heard before if you’re into physics. These are the two categories in which all particles in the universe reside.

 A Return To Form

 So...how about another summary?

 The Principle Quantum Number (n) determines the energy level, and thus, the electron’s shell. It is conventionally shown with a number from 1 to 5. The Orbital Quantum Number (l) determines where the electrons are with respect to the nucleus. It shows the sub-shell and is typically denoted with a letter (s, p, d or f) according to its number (0, 1, 2 and 3). The Magnetic Quantum Number (m) tells how many subshells there are. It is determined by looking at the subshell and taking the range from -l to l. Lastly, the complex Spin Quantum Number (s) determines whether the electron’s “spin” is +1/2 or -1/2.

 Lastly, there’s the Pauli Exclusion Principle, watching over these Quantum Numbers to make sure they behave themselves. No two electrons can have the same quantum mechanical state within the same atom. It was the aforementioned spin quantum number that proved this; remember that the electrons in the Stern-Gerlach did not simply mix – there was a distinction between +1/2 and -1/2. Furthermore, given that the Principle only works with differing quantum mechanical states, only fermions follow this Principle.

Image via futurespaceprogram

 This opens up a very important piece of orbital theory.

 That spin quantum number shows a great deal, indeed, folks. Because that Pauli Exclusion Principle makes it so that each subshell can only have two electrons – one with the positive spin and one with the negative spin.

 And that, my friends, will guide you into the Aufbau Principle…which we will discuss next time.

 The next lesson will end the Orbital Arc...I hope you’re ready. Because afterward, things will really pick up.

 Please ask questions if you are lost somewhere in these five parts. And share amongst all of your friends – not just the ones interested in science. We can all learn. We just need to light the fire.

*If you understood everything up to this point, you might be able to reason why silver atoms were used. I want to ask you why and give you these three hints to help you: 1) Use the periodic table 2) Orbital Quantum Number 3) Electrons and Protons